A new Coulomb ring-shaped potential via generalized parametric Nikiforov-Uvarov method

Abstract

In this paper, the Schrödinger equation is analytically solved for the Coulomb potential with a novel angle-dependent part. The generalized parametric Nikiforov-Uvarov method is used to obtain energy eigenvalues and corresponding eigenfunctions. We presented the effect of the angle-dependent part on radial solutions and some special cases are also discussed.

Introduction

Noncentral potentials have been studied in various fields of nuclear physics and quantum chemistry, which may be used to the interactions between the deformed pair of nuclei and ring-shaped molecules such as benzene [1–12]. There has been continuous interest in the solutions of the Schrödinger, Klein-Gordon, and Dirac equations for some central and noncentral potentials [13–41]. Yasuk et al. presented an alternative and simple method for the exact solution of the Klein-Gordon equation in the presence of noncentral equal scalar and vector potentials using the Nikiforov-Uvarov method [42]. A spherically harmonic oscillatory ring-shaped potential is proposed, and its exactly complete solutions are presented via the Nikiforov-Uvarov method by Zhang et al. [43]. Bayrak et al. [44] and Chen et al. [45] presented exact solutions of the Schrödinger equation with the Makarov potential using asymptotic iteration method and partial wave method. Souza Dutra and Hott solved the Dirac equation by constructing the exact bound state solutions for a mixing of vector and scalar generalized Hartmann potentials [46]. Kandirmaz et al., using path integral method, investigated the coherent states for a particle in the noncentral Hartmann potential [47]. Chen studied the Dirac equation with the Hartmann potential [48]. A kind of novel angle-dependent (NAD) potential is introduced by Berkdemir [49, 50]:

$$V_{1\theta }\left(\theta \right)=\frac{\gamma +\beta {\sin }^2\theta +\eta {\sin }^4\theta }{{\sin }^2\theta {\cos }^2\theta }.$$

(1)

Hamzavi and Rajabi also solved the Dirac equation for Coulomb plus above the NAD potential when the scalar potential is equal to the vector potential [51]. Very recently, another kind of NAD potential is introduced by Zhang and Huang-Fu [52]:

$$V_{2\theta }\left(\theta \right)=\frac{\gamma +\beta {\cos }^2\theta +\eta {\cos }^4\theta }{{\cos }^2\theta {\sin }^2\theta }.$$

(2)

They solved the Dirac equation for oscillatory potential under a pseudospin symmetry limit. Therefore, the motivation of the present work is to solve the Schrödinger equation with the NAD Coulomb potential:

$$\begin{array}{ll}V\left(r,\theta \right)& =-\frac{A}{r}-\frac{{\mathit{ħ}}^2}{2\mu }\frac{V_{2\theta }\left(\theta \right)}{r^2}\\ =-\frac{A}{r}-\frac{{\mathit{ħ}}^2}{2\mu }\frac{\gamma +\beta {\cos }^2\theta +\eta {\cos }^4\theta }{r^2{\cos }^2\theta {\sin }^2\theta },\end{array}$$

(3)

where A = Zα, $\alpha =\frac{e^2}{\mathit{ħ}c}$ is the fine structure constant, and μ is the reduced mass. In this article, we solve Schrödinger equation with the NAD Coulomb potential (Equation 3) using the generalized parametric Nikiforov-Uvarov method, and we present the effect of the angle-dependent part on radial solutions.

Nikiforov-Uvarov method

To solve second-order differential equations, the Nikiforov-Uvarov method can be used with an appropriate coordinate transformation s = s(r) [53, 54]:

$${\psi }_n^{″}\left(s\right)+\frac{\tilde{\tau }\left(s\right)}{\sigma \left(s\right)}{\psi }_n^{\text{'}}\left(s\right)+\frac{\tilde{\sigma }\left(s\right)}{{\sigma }^2\left(s\right)}{\psi }_n\left(s\right)=0,$$

(4)

where σ(s) and $\tilde{\sigma }\left(s\right)$ are polynomials, at most, of second-degree, and $\tilde{\tau }\left(s\right)$ is a first-degree polynomial. The following equation is a general form of the Schrödinger-like equation written for any potential [55, 56]:

$$\left[\frac{d^2}{d{s}^2}+\frac{{\alpha }_1-{\alpha }_{2}s}{s\left(1-{\alpha }_{3}s\right)}\frac{d}{\mathit{ds}}+\frac{-{\xi }_1{s}^2+{\xi }_{2}s-{\xi }_3}{{\left[s\left(1-{\alpha }_{3}s\right)\right]}^2}\right]{\psi }_n\left(s\right)=0.$$

(5)

According to the Nikiforov-Uvarov method, the eigenfunctions and eigenenergy function become the following equations, respectively:

$$\psi \left(s\right)=s^{{\alpha }_{12}}{\left(1-{\alpha }_{3}s\right)}^{-{\alpha }_{12}-\frac{{\alpha }_{13}}{{\alpha }_3}}{P}_n^{\left({\alpha }_{10}-1,\frac{{\alpha }_{11}}{{\alpha }_3}-{\alpha }_{10}-1\right)}\left(1-2{\alpha }_{3}s\right),$$

(6)

$$\begin{array}{ll}{\alpha }_{2}n& -\left(2n+1\right){\alpha }_5+\left(2n+1\right)\left(\sqrt{{\alpha }_9}+{\alpha }_3\sqrt{{\alpha }_8}\right)\\ +n\left(n-1\right){\alpha }_3+{\alpha }_7+2{\alpha }_3{\alpha }_8+2\sqrt{{\alpha }_8{\alpha }_9}=0,\end{array}$$

(7)

where

$$\begin{array}{ll}{\alpha }_4=\frac{1}{2}\left(1-{\alpha }_1\right),& {\alpha }_5=\frac{1}{2}\left({\alpha }_2-2{\alpha }_3\right),\\ {\alpha }_6={\alpha }_5^2+{\xi }_1,& {\alpha }_7=2{\alpha }_4{\alpha }_5-{\xi }_2,\\ {\alpha }_8={\alpha }_4^2+{\xi }_3& {\alpha }_9={\alpha }_3{\alpha }_7+{\alpha }_3^2{\alpha }_8+{\alpha }_6,\end{array}$$

(8)

and

$$\begin{array}{ll}{\alpha }_{10}={\alpha }_1+2{\alpha }_4+2\sqrt{{\alpha }_8},& {\alpha }_{11}={\alpha }_2-2{\alpha }_5+2\left(\sqrt{{\alpha }_9}+{\alpha }_3\sqrt{{\alpha }_8}\right),\\ {\alpha }_{12}={\alpha }_4+\sqrt{{\alpha }_8},& {\alpha }_{13}={\alpha }_5-\left(\sqrt{{\alpha }_9}+{\alpha }_3\sqrt{{\alpha }_8}\right).\end{array}$$

(9)

In some problems α₃ = 0. For this type of problems when

$$\underset{{\alpha }_3\to 0}{lim}{\mathit{P}}_n^{\left({\alpha }_{10}-1,\frac{{\alpha }_{11}}{{\alpha }_3}-{\alpha }_{10}-1\right)}\left(1-{\alpha }_3\right)s=L_n^{{\alpha }_{10}-1}\left({\alpha }_{11}s\right),$$

(10)

and

$$\underset{{\alpha }_3\to 0}{lim}{\left(1-{\alpha }_{3}s\right)}^{-{\alpha }_{12}-\frac{{\alpha }_{13}}{{\alpha }_3}}=e^{{\alpha }_{13}s},$$

(11)

the solution given in Equation 6 becomes as follows [55, 56]:

$$\psi \left(s\right)=s^{{\alpha }_{12}}{e}^{{\alpha }_{13}s}{L}_n^{{\alpha }_{10}-1}\left({\alpha }_{11}s\right).$$

(12)

Separating variables of the Schrödinger equation with the noncentral potential

In the spherical coordinates, the Schrödinger equation with noncentral potential can be written as follows [57]:

$$\begin{array}{l}-\frac{{\mathit{ħ}}^2}{2\mu }\left[\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial }{\partial r}\right)+\frac{1}{r^2\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial }{\partial \theta }\right)+\frac{1}{r^2{\sin }^2\theta }\frac{{\partial }^2}{\partial {\phi }^2}\right]\psi \left(r,\theta ,\varphi \right)\\ +V\left(r,\theta ,\varphi \right)\psi \left(r,\theta ,\varphi \right)=\mathit{E\psi }\left(r,\theta ,\varphi \right).\end{array}$$

(13)

Let us decompose the spherical wave function as follows:

$$\psi \left(r,\theta ,\varphi \right)=\frac{u\left(r\right)}{r}H\left(\theta \right)\phi \left(\varphi \right),$$

(14)

and also, substituting Equation 3 into Equation 13, we obtain the following equations:

$$\frac{d^{2}u\left(r\right)}{d{r}^2}+\left[\frac{2\mu }{{\mathit{ħ}}^2}\left(E+\frac{A}{r}\right)-\frac{\lambda }{r^2}\right]u\left(r\right)=0,$$

(15a)

$$\frac{1}{\sin \theta }\frac{d}{\mathit{d\theta }}\left(\sin \theta \frac{d}{\mathit{d\theta }}\right)H\left(\theta \right)+\left[\lambda -\frac{m^2}{{\sin }^2\theta }-\frac{\gamma +\beta {\cos }^2\theta +\eta {\cos }^4\theta }{{\cos }^2\theta {\sin }^2\theta }\right]H\left(\theta \right)=0,$$

(15b)

$$\frac{d^2\phi \left(\varphi \right)}{d{\varphi }^2}+m^2\phi \left(\varphi \right)=0,$$

(15c)

where λ and m² are separation constants. It is well known that the solution of Equation 15c is as follows:

$${\mathit{\Phi }}_m\left(\phi \right)=\frac{1}{\sqrt{2\pi }}{e}^{\mathit{im\phi }}m=0,\pm 1,\pm 2,\dots .$$

(16)

Solution of polar angle part

We are now going to derive eigenvalues and eigenfunctions of the polar part of the Schrödinger equation, i.e., Equation 15b, with generalized parametric Nikiforov-Uvarov method. Using transformation s = cos²θ, Equation 15b becomes the following:

$$\begin{array}{ll}\frac{d^{2}H\left(s\right)}{d{s}^2}& +\frac{1-3s}{2s\left(1-s\right)}\frac{\mathit{dH}\left(s\right)}{\mathit{ds}}\\ +\frac{1}{4s^2{\left(1-s\right)}^2}\left(\mathrm{\lambda s}\left(1-s\right)-m^{2}s-\gamma -\mathit{\delta s}-\eta s^2\right)H\left(s\right)=0.\end{array}$$

(17)

Comparing Equations 17 and 5, one obtains the following:

$$\begin{array}{ll}{\alpha }_1=1/2,& {\xi }_1=1/4\left(\lambda +\eta \right),\\ {\alpha }_2=3/2,& {\xi }_2=1/4\left(\lambda -m^2-\delta \right),\\ {\alpha }_3=1,& {\xi }_3=\gamma /4,\end{array}$$

(18)

and

$$\begin{array}{ll}{\alpha }_4=1/4,& \hfill {\alpha }_5=-1/4,\hfill \\ {\alpha }_6=1/16+1/4\left(\mathit{\lambda }+\eta \right),& \hfill {\alpha }_7=-1/8-1/4\left(\mathit{\lambda }-m^2-\delta \right),\hfill \\ {\alpha }_8=1/16+\frac{q}{4},& \hfill {\alpha }_9=1/4\left(m^2+\gamma +\beta +\eta \right),\hfill \\ {\alpha }_{10}=1+\sqrt{\gamma +1/4},& \hfill {\alpha }_{11}=2+\left(\sqrt{m^2+\gamma +\beta +\eta }+\sqrt{\gamma +1/4}\right),\hfill \\ {\alpha }_{12}=1/4+1/2\sqrt{\gamma +1/4},& \hfill {\alpha }_{13}=-1/4-1/2\left(\sqrt{m^2+\gamma +\beta +\eta }+\sqrt{\gamma +1/4}\right).\hfill \end{array}$$

(19)

From Equations 18 and 19 and Equation 7, we obtain the following:

$$\begin{array}{ll}\mathit{\lambda }& =4{\left(\tilde{n}+1/2\right)}^2+2\left(2\tilde{n}+1\right)\left[\sqrt{m^2+\gamma +\beta +\eta }+\sqrt{\gamma +1/4}\right]\\ +2\sqrt{\left(m^2+\gamma +\beta +\eta \right)\left(\gamma +1/4\right)}+m^2+2\gamma +\beta ,\end{array}$$

(20)

where $\tilde{n}$ is a nonnegative integer. For the corresponding wave functions of the polar part, from non-negative Equations 6 and 19, we obtain the following:

$$\begin{array}{l}H\left(s\right)=s^{{\alpha }_{12}}{\left(1-{\alpha }_3\mathit{s}\right)}^{-{\alpha }_{12}-\frac{{\alpha }_{13}}{{\alpha }_3}}{P}_{\tilde{\mathit{n}}}^{\left({\alpha }_{10}-1,\frac{{\alpha }_{11}}{{\alpha }_3}-{\alpha }_{10}-1\right)}\left(1-2{\alpha }_3\mathit{s}\right)\\ =s^{1/4+1/2\sqrt{\gamma +1/4}}{\left(1-s\right)}^{1/2\sqrt{m^2+\gamma +\beta +\eta }}{P}_{\tilde{n}}^{\left(\sqrt{\gamma +1/4},\sqrt{m^2+\gamma +\beta +\eta }\right)}\left(1-2\mathit{s}\right),\end{array}$$

(21)

or equivalently

$$\begin{array}{ll}H\left(\theta \right)=& C_{\tilde{n}m}{\left(\cos \theta \right)}^{1/2+\sqrt{\gamma +1/4}}{\left(\sin \theta \right)}^{\sqrt{m^2+\gamma +\beta +\eta }}\\ P_{\tilde{\mathit{n}}}^{\left(\sqrt{\gamma +1/4},\sqrt{m^2+\gamma +\beta +\eta }\right)}\left(-\cos 2\theta \right),\end{array}$$

(22)

where $C_{\tilde{n}m}$ is the normalization constant.

Solution of the radial equation

For eigenvalues and corresponding eigenfunctions of the radial part, i.e., solution of Equation 15a, we rewrite it as follows:

$$\frac{d^{2}u\left(r\right)}{d{r}^2}+\frac{1}{r^2}\left(-\epsilon r^2+A^{\text{'}}r-\lambda \right)u\left(r\right)=0$$

(23)

where $\epsilon =-\frac{2\mu }{{\mathit{ħ}}^2}E$ and $A^{\text{'}}=\frac{2\mu }{{\mathit{ħ}}^2}A$.

Again, comparing Equations 23 and 5 leads to the following:

$$\begin{array}{l}{\alpha }_1=0,{\xi }_1=\epsilon ,\\ {\alpha }_2=0,{\xi }_2=A^{\prime },\\ {\alpha }_3=0,{\xi }_3=\mathit{\lambda },\end{array}$$

(24)

and

$$\begin{array}{ll}{\alpha }_4=1/2,& \hfill {\alpha }_5=0,\hfill \\ {\alpha }_6=\mathit{\epsilon },& \hfill {\alpha }_7=-A^{\prime },\hfill \\ {\alpha }_8=\mathit{\lambda }+1/4,& \hfill {\alpha }_9=\mathit{\epsilon },\hfill \\ {\alpha }_{10}=1+\sqrt{\mathit{\lambda }+1/4},& \hfill {\alpha }_{11}=2\sqrt{\mathit{\epsilon }},\hfill \\ {\alpha }_{12}=1/2+\sqrt{\mathit{\lambda }+1/4},& \hfill {\alpha }_{13}=-\sqrt{\mathit{\epsilon }}.\hfill \end{array}$$

(25)

The energy eigenvalues of the radial part can be obtained from Equations 24 and 25 and Equation 7 as follows:

$$E=-\frac{2\mu A^2}{{\mathit{ħ}}^2{\left(2n+1+2\sqrt{\mathit{\lambda }+1/4}\right)}^2}$$

(26)

where n is the nonnegative integer. Although one can immediately obtain energy eigenvalues of Equations 15a or 23 from hydrogen problem, here, we have tried the Nikiforov-Uvarov method to show the simplicity of usage of the mentioned method. To find the corresponding radial eigenfunctions, we refer to Equations 11 and 25, and then we obtain the following:

$$\begin{array}{ll}u\left(r\right)& =s^{{\alpha }_{12}}{e}^{{\alpha }_{13}s}{L}_n^{{\alpha }_{10}-1}\left({\alpha }_{11}s\right)\\ =r^{1/2+\sqrt{\mathit{\lambda }+1/4}}{e}^{-\sqrt{\mathit{\epsilon }}r}{L}_n^{\sqrt{\mathit{\lambda }+1/4}}\left(2\sqrt{\mathit{\epsilon }}r\right).\end{array}$$

(27)

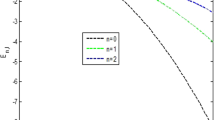
For effect of the angle-dependent part on radial solutions, we substitute Equation 20 into Equation 27, and we obtain the following:

$$E_{n,\tilde{n},m}=-\frac{2\mu {\left(\mathit{Z\alpha }\right)}^2}{{\mathit{ħ}}^2{\left(2n+1+2\sqrt{\begin{array}{c}\hfill \{4{\left(\tilde{n}+1/2\right)}^2+2\left(2\tilde{n}+1\right)\left[\sqrt{m^2+\gamma +\beta +\eta }+\sqrt{\gamma +1/4}\right]\hfill \\ \hfill +2\sqrt{\left(m^2+\gamma +\beta +\eta \right)\left(\gamma +1/4\right)}+m^2+2\gamma +\beta +1/4\}\hfill \end{array}}\right)}^2}.$$

(28)

When γ = η = 0, the potential (Equation 3) reduces to the Hartmann potential, and the energy eigenvalues can be obtained as follows [58]:

$$E_{n,\tilde{n},m}==-\frac{\mu {\left(\mathit{Z\alpha }\right)}^2}{2{\mathit{ħ}}^2{\left(n+\sqrt{m^2+\beta }+\tilde{n}+1\right)}^2}.$$

(29)

Also, when γ = β = η = 0, the potential (Equation 3) reduces to the Coulomb potential, and the energy eigenvalues in Equation 28 reduces to the following [57]:

$$E_{\left(\mathrm{Coulomb}\right)}==-\frac{\mu {\left(\mathit{Z\alpha }\right)}^2}{2{\mathit{ħ}}^2{n}^{\text{'}}{2}^{}}=-\frac{1}{2}\frac{\mu }{c^2}\frac{Z^2{e}^4}{n^{\text{'}}{2}^{}},$$

(30)

where n ′ = n + l + 1 and l = 2ñ + m + 1.

Finally, we can write ψ(r, θ, ϕ) as follows:

$$\begin{array}{ll}\psi \left(r,\theta ,\varphi \right)& =\frac{u\left(r\right)}{r}H\left(\theta \right)\mathit{\Phi }\left(\phi \right)\\ =\frac{C_{n\tilde{n}m}}{\sqrt{2\pi }}{r}^{-\frac{1}{2}+\sqrt{\lambda +\frac{1}{4}}}{e}^{-\sqrt{{\mathit{\epsilon }}^2}r}{L}_n^{2\sqrt{\mathit{\lambda }+\frac{1}{4}}}\left(2\sqrt{{\mathit{\epsilon }}^2}r\right)\\ \times {\left(cos\theta \right)}^{1/2+\sqrt{\gamma +1/4}}{\left(sin\theta \right)}^{\sqrt{m^2+\gamma +\beta +\eta }}\\ P_{\tilde{\mathit{n}}}^{\left(\sqrt{\gamma +1/4},\sqrt{m^2+\gamma +\beta +\eta }\right)}\left(-cos2\theta \right)e^{\mathit{im\phi }}.\end{array}$$

(31)

where $C_{\tilde{n}m}$ is the normalization constant.

Conclusions

We have studied the exact solutions of the Schrödinger equation with the Coulomb plus, a novel angle-dependent potential, using the generalized parametric Nikiforov-Uvarov method. It can be found that this method is a powerful mathematical tool for solving second-order differential equations. The bound-state energy eigenvalues and the corresponding wave functions are obtained. We point that these results may have interesting applications in the study of different quantum mechanical systems and atomic physics [1, 2, 59, 60] and, two special cases, i.e., Hartmann potential and pure Coulomb potential, were also discussed.