Transverse perturbation on three-dimensional ion acoustic waves in electron–positron–ion plasma with high-energy tail electron and positron distribution

Abstract

The basic features of nonlinear ion acoustic (IA) waves are theoretically studied in a superthermal electron–positron–ion (e–p–i) plasma with weakly transverse perturbation. A three-dimensional Kadomtsev–Petviashvili (KP) equation governing evolution of weakly nonlinear IA waves is derived by means of a reductive perturbation method. The energy integral equation is used to study the existence domain of the localized structures. It is found that deviation from thermodynamics equilibrium increases the existence domain of solitary solution and also makes the IA solitary structure more spiky. The ion concentration has an important effect on the existence domain of solitary solution, as for low ion density the primitive domain reduces significantly.

Introduction

Electron–positron–ion (e–p–i) plasma as a particular case of ambiplasma is a quasineutral space plasma containing electrons, positrons, protons, and antiprotons [1]. In the presence of additional positron component in an ordinary electron–ion plasma, the population of ions as well as the restoring force on electron fluid reduces, henceforth it can be predict that the basic features of electrostatic structures affect considerably in an e–p–i plasma. Study of propagation of localized structures in e–p–i plasma has important aspects for researches due to existence of such kind of plasma in the inner regions of the accretion disks surrounding black holes [2], in the early universe [3, 4], in pulsar magnetospheres [5], in the active galactic nuclei [6, 7], in the polar regions of neutron stars [8], at the center of our galaxy [9], and in the plasmas in intense laser fields [10, 11]. Such three-component e–p–i plasmas can also be found in the laboratory plasma; for instance, during the propagation of a short relativistic strong laser pulse in matter, photo production of pairs due to the photon scattering by nuclei can lead to the formation of e–p–i plasmas [10, 11]. Collisions of runaway electrons with plasma ions or thermal electrons in tokamaks (which have also been observed in the Joint European Torus [12] and JT-60U [13]) can lead to production of protons. Therefore, according to the mentioned reasons during the last few decades the propagation properties of electrostatic structures in e–p–i plasma have been attracted a great deal of attention [14–24].

Nonlinear dynamics of IA solitary waves in unmagnetized e–p–i plasmas have been investigated by Popel et al. [14]. They showed that the presence of positrons in electron–ion plasmas significantly reduces the amplitude of IA solitary waves [14]. Small [15] and large [16] amplitude IA double layers have been investigated in an e–p–i plasma. Tiwari et al. [17] studied the influence of positron density and temperature on IA dressed soliton in e–p–i plasma. Subsequently, the IA structures have been studied in the cases of magnetized [18–21], nonplanar [22], quantum [20, 23, 24] e–p–i plasma. These results are useful for understanding of the localized structures in e–p–i plasma with Maxwellian electrons and positrons. However, a number of space, astrophysical and laboratory plasma environments including non-Maxwellian components and the study of such non-Maxwellian plasmas are crucial to the understanding of space, astrophysical and laboratory plasma dynamics, which they can appropriately be described by the generalized Lorantzian (or kappa type) distribution function [25–27]. This distribution function was first employed by Vasyliunas [25] to model space plasma. Observations [25, 28] indicate deviation of particle distribution functions from the Maxwellian. In this case, external forces acting on the neutral space plasma or interaction of wave-particle may lead to formation of suprathermal particles. This kind of particle is often present in space and astrophysical plasma environments, viz., the ionosphere, mesosphere, magnetosphere, lower atmosphere, magneto-sheet, terrestrial plasma-sheet, radiation belts and auroral zones [29–33]. The suprathermal behavior of plasma was also observed in laboratory plasma, for instance in laser–matter interaction and in plasma turbulence [34]. Suprathermal plasmas which are characterized by a long tail in the high-energy region may generally be modeled by a kappa-like distribution. Such distribution is often more appropriate than the Maxwellian (thermal) distribution in a broad range of plasma mediums. In the limit of large values of parameter κ, the κ-distribution reduces to the Maxwellian distribution. Also for low values of κ, they present a hard spectrum including a strong tail with power law form at high speed [35–37], indeed low values of kappa indicate distributions with a high number density of suprathermal particles. Effect of electron suprathermality on the electrostatic excitations has been discussed by a number of authors [38–47]. Ion acoustic solitary waves and double layers in a dense e–p–i magnetoplasma have been studied by Chatterjee et al. [20]. Tribeche and Boubakour [38] studied the effects of superthermal electrons and thermal positrons on IA double layers in e–p–i plasma. They showed that due to the electron superthermality and the relative fraction of positrons, compressive as well as rarefactive double layers exist in such a plasma. Recently, Manouchehrizadeh and Dorranian [48] investigated the basic properties of wake-fields in a magnetized plasma.

The solitary wave is a localized structure that travels with a definite shape due to the mutual balance between the nonlinearity and dispersion terms. A soliton structure which preserves its shape after collision can trap the plasma particles and transfer them over the large distances. This turns out that the solitons can play a vital role in transportation of energy in plasma. The dynamical behavior of solitons in a one-dimensional homogeneous plasma is governed by the well-known Korteweg–deVries (KdV) equation [49]. Different effects such as external magnetic [21, 50] field and inhomogeneous medium [51–54] can modify the propagation properties of soliton. In the presence of the density gradient or boundary in plasma, they may appear in role of a reflector and reflect the soliton waves [55, 56]. In the presence of transverse perturbations a KP equation [57–62] describes the multidimensional solitary structures. Malik et al. [59] studied KP solitons in an inhomogeneous plasmas with finite temperature drifting ions. Boiti et al. [60] investigated properties of solutions of the Kadomtsev–Petviashvili equation in different possible cases. The KP equation in relativistic plasma is also investigated [61].

El-Awady et al. [39] investigated IA soliton propagation in e–p–i plasma with kappa distribution. Oblique propagation of IA waves in a magnetized e–p–i plasma with superthermal electrons has been studied by Alinejad and Mamun [21]. The stability of electrostatic structures has been investigated in a magnetized e–p–i plasma with non-Maxwellian electrons and positrons [49]. They showed that evolution of IA solitary waves in their model was governed by a Zakharov–Kuznetsov type equation. Ghosh et al. [63]. examined effect of superthermal electrons on the IA shock structures in a nonplanar e–p–i plasmas. They derived a KP-Burgers equation to describe the shock structure in their nonplanar e–p–i plasma. Alinejad et al. [64] investigated the effect of electron suprathermality on the IA modulation in dusty plasma.

To complement and give new insights into the previously published work, we propose here to address the propagation properties of weakly nonlinear IA solitary waves in a superthermal e–p–i plasma with transverse perturbation. The reductive perturbation is used to derive the KP equation and then the existence domain of solitons is carefully investigated.

Theoretical model

We consider an electron–positron–ion plasma consisting of inertia less superthermal electron and positron, and inertial ion fluids of densities n _e , n _p and n _i , respectively. The direction of wave propagation lies on the z-axis, and we assume a weak transverse perturbation perpendicular to the z-axis. At equilibrium, the charge neutrality reads as n_e0 = n_i0 + n_p0, where n_e0, n_p0 and n_i0 are the equilibrium density of electrons, positrons, and ions, respectively, and the fractional concentration of electrons with respect to ions can be read as f = n_i0/n_e0 = 1 − n_p0/n_e0. The nonlinear dynamics of the low frequency purely electrostatic perturbation mode (whose phase speed is much less than the electron thermal speed) in a one-fluid model are given by

$$\frac{\mathit{\partial }{n}_i}{\mathit{\partial }t}+\mathrm{\nabla }·(n_i{\mathbf{u}}_i)=0,$$

(1)

$$\frac{\mathit{\partial }{\mathbf{u}}_i}{\mathit{\partial }t}+({\mathbf{u}}_i·\mathrm{\nabla }){\mathbf{u}}_i=-\mathrm{\nabla }\mathit{\varphi }-\frac{{\mathit{\sigma }}_i}{n_i}\mathrm{\nabla }{p}_i,$$

(2)

$$\frac{\mathit{\partial }{p}_i}{\mathit{\partial }t}+({\mathbf{u}}_i·\mathrm{\nabla })p_i+{\mathit{\gamma }}_i{p}_i(\mathrm{\nabla }·{\mathbf{u}}_i)=0,$$

(3)

$${\mathrm{\nabla }}^2\mathit{\varphi }=n_e-f{n}_i-(1-f)n_p,$$

(4)

where n _j (j = e, p, i) is the number density of plasma species normalized by n_j0, u _i  = (u, v, w) is the ion fluid velocity normalized by $c_s=\sqrt{T_e/m_i}$, ϕ is the electrostatic wave potential normalized by T _e /e, the time variable (t) is normalized by ${\mathit{\omega }}_{pi}=\sqrt{4\mathit{\pi }{n}_{e0}{e}^2/m_i}$, the space variable (r) is normalized by λ _D  = c _s /ω _pi , γ _i  = (2 + N)/N (where N is the degrees of freedom), σ _i  = T _i /T _e and the other variables have their usual meaning.

To model the fast superthermal electrons and positrons, we adopt three-dimensional generalized Lorentzian or kappa distribution function [25–27]

$$f_{\mathit{\kappa }}(v)=\frac{n_{e,p0}}{{(\mathit{\pi }\mathit{\kappa }{\mathit{\theta }}^2)}^{3/2}}\frac{\mathrm{\Gamma }(\mathit{\kappa }+1)}{\mathrm{\Gamma }(\mathit{\kappa }-1/2)}{\left(1+\frac{v^2+2q_{i,e}\mathit{\varphi }}{m_{e,p}\mathit{\kappa }{\mathit{\theta }}^2}\right)}^{-1-\mathit{\kappa }},$$

(5)

where θ² = 2T_e,p(κ − 3/2)/κm_e,p is the effective thermal speed, Γ is the gamma function, and κ is a spectral index. In order to find an electron/positron number density with superthermal particles, we integrate the kappa distribution function (5) over the velocity space. Then, the normalized electron and positron number densities are accordingly expressed as

$$n_e={\left(1-\frac{\mathit{\varphi }}{{\mathit{\kappa }}_e-3/2}\right)}^{-{\mathit{\kappa }}_e+1/2},$$

(6)

$$n_p={\left(1+\frac{{\mathit{\sigma }}_p\mathit{\varphi }}{{\mathit{\kappa }}_p-3/2}\right)}^{-{\mathit{\kappa }}_p+1/2},$$

(7)

in which κ_e,p is a spectral index and measures deviation from Maxwellian distribution, as the smaller values of κ_e,p denote the more suprathermal particles in the distribution function tail (and the harder energy spectrum). In the limit of κ_e,p → ∞, the kappa distribution recovers the Maxwellian distribution. It must be noted that the density expressions given by Eqs. (6) and (7) are only valid for κ_e,p > 3/2. Furthermore, Baluku et al. [36] showed that in the weakly nonlinear regime, when we employed the reductive perturbation method, the spectral indexes κ _e and κ _p cannot take the values in the region of 3/2 < κ_e,p < 3. Therefore, in this case we should restrict our attention to the region of κ_e,p > 3. Also σ _p is T _p /T _e with T _e (T _p ) being the electron (positron) temperature.

Derivation of Kadomtsev–Petviashvili equation

We adopt the standard reductive perturbation method to investigate the nonlinear dynamical equation of IA waves in an unmagnetized e–p–i plasmas with transverse perturbation to obtain the KP equation. The stretched coordinates are defined as

$$X=\mathit{\epsilon }x,Y=\mathit{\epsilon }y,\mathit{\xi }={\mathit{\epsilon }}^{1/2}\left(z-Vt\right),\mathit{\tau }={\mathit{\epsilon }}^{3/2}t.$$

(8)

Here, the parameter ɛ refers to a real and small parameter which measures the weakness of the amplitude or dispersion, and V is the phase speed normalized by c _s . The dependent variables are expanded as

$$n_i=1+\mathit{\epsilon }{n}_1+{\mathit{\epsilon }}^2{n}_2+\cdots ,$$

(9a)

$$u={\mathit{\epsilon }}^{3/2}{u}_1+{\mathit{\epsilon }}^{5/2}{u}_2+\cdots ,$$

(9b)

$$v={\mathit{\epsilon }}^{3/2}{v}_1+{\mathit{\epsilon }}^{5/2}{v}_2+\cdots ,$$

(9c)

$$w=\mathit{\epsilon }{w}_1+{\mathit{\epsilon }}^2{w}_2+\cdots ,$$

(9d)

$$\mathit{\varphi }=\mathit{\epsilon }{\mathit{\varphi }}_1+{\mathit{\epsilon }}^2{\mathit{\varphi }}_2+\cdots .$$

(9e)

The appearance of transverse velocity components at a higher order of ɛ (relative to the parallel component w) comes from an anisotropy induced by the influence of transverse perturbation. Then, we use Eqs. (8) and (9a) in Eqs. (1–4), and collect the terms in different powers of ɛ. The lowest order of ɛ leads to

$$w_1=V{n}_{i1},V{w}_1={\mathit{\varphi }}_1+{\mathit{\sigma }}_i{p}_{i1},V{p}_{i1}={\mathit{\gamma }}_i{w}_1,n_{e1}-\left(1-f\right)n_{p1}-f{n}_{i1}=0.$$

(10)

The above equation yields the following linear dispersion relation

$$V=\sqrt{{\mathit{\sigma }}_i{\mathit{\gamma }}_i+\frac{f}{\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+(1-f){\mathit{\sigma }}_p\frac{{\mathit{\kappa }}_p-1/2}{{\mathit{\kappa }}_p-3/2}}}.$$

(11)

We can write the lowest order x and y components of the momentum equation as

$$\frac{\mathit{\partial }{u}_1}{\mathit{\partial }\mathit{\xi }}=\frac{1}{V}\frac{\mathit{\partial }{\mathit{\varphi }}_1}{\mathit{\partial }X}+\frac{{\mathit{\sigma }}_i}{V}\frac{\mathit{\partial }{p}_{i1}}{\mathit{\partial }X},$$

(12a)

$$\frac{\mathit{\partial }{v}_1}{\mathit{\partial }\mathit{\xi }}=\frac{1}{V}\frac{\mathit{\partial }{\mathit{\varphi }}_1}{\mathit{\partial }Y}+\frac{{\mathit{\sigma }}_i}{V}\frac{\mathit{\partial }{p}_{i1}}{\mathit{\partial }Y}.$$

(12b)

The next order in ɛ gives a set of equations in the second-order perturbed quantities, as follows

$$-V\frac{\mathit{\partial }{n}_{i2}}{\mathit{\partial }\mathit{\xi }}+\frac{\mathit{\partial }{n}_{i1}}{\mathit{\partial }\mathit{\tau }}+\frac{\mathit{\partial }{u}_1}{\mathit{\partial }X}+\frac{\mathit{\partial }{v}_1}{\mathit{\partial }Y}+\frac{\mathit{\partial }{w}_2}{\mathit{\partial }\mathit{\xi }}+\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\xi }}(n_{i1}{w}_1)=0,$$

(13a)

$$-V\frac{\mathit{\partial }{w}_2}{\mathit{\partial }\mathit{\xi }}+\frac{\mathit{\partial }{w}_1}{\mathit{\partial }\mathit{\tau }}+w_1\frac{\mathit{\partial }{w}_1}{\mathit{\partial }\mathit{\xi }}-V{n}_{i1}\frac{\mathit{\partial }{w}_1}{\mathit{\partial }\mathit{\xi }}=-\frac{\mathit{\partial }{\mathit{\varphi }}_2}{\mathit{\partial }\mathit{\xi }}-{\mathit{\sigma }}_i\frac{\mathit{\partial }{p}_{i2}}{\mathit{\partial }\mathit{\xi }}-n_{i1}\frac{\mathit{\partial }{\mathit{\varphi }}_1}{\mathit{\partial }\mathit{\xi }},$$

(13b)

$$-V\frac{\mathit{\partial }{p}_{i2}}{\mathit{\partial }\mathit{\xi }}+\frac{\mathit{\partial }{p}_{i1}}{\mathit{\partial }\mathit{\tau }}+{\mathit{\gamma }}_i{p}_{i1}\frac{\mathit{\partial }{w}_1}{\mathit{\partial }\mathit{\xi }}+{\mathit{\gamma }}_i\frac{\mathit{\partial }{w}_2}{\mathit{\partial }\mathit{\xi }}+{\mathit{\gamma }}_i\frac{\mathit{\partial }{u}_1}{\mathit{\partial }X}+{\mathit{\gamma }}_i\frac{\mathit{\partial }{v}_1}{\mathit{\partial }Y}=0,$$

(13c)

$$\frac{{\mathit{\partial }}^2{\mathit{\varphi }}_1}{\mathit{\partial }{\mathit{\xi }}^2}=n_{e2}-(1-f)n_{p2}-f{n}_{i2}.$$

(13d)

Taking the second derivative of (13d) with respect to ξ, and using Eqs. (10–13c), we eliminate the second-order perturbed quantities to obtain the following KP equation,

$$\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\xi }}\left[\frac{\mathit{\partial }{\mathit{\varphi }}_1}{\mathit{\partial }\mathit{\tau }}+A{\mathit{\varphi }}_1\frac{\mathit{\partial }{\mathit{\varphi }}_1}{\mathit{\partial }\mathit{\xi }}+B\frac{{\mathit{\partial }}^3{\mathit{\varphi }}_1}{\mathit{\partial }{\mathit{\xi }}^3}\right]+C\left[\frac{{\mathit{\partial }}^2}{\mathit{\partial }{X}^2}+\frac{{\mathit{\partial }}^2}{\mathit{\partial }{Y}^2}\right]{\mathit{\varphi }}_1=0,$$

(14)

where

$$\begin{array}{c}A=-\frac{\frac{({\mathit{\kappa }}_e-1/2)({\mathit{\kappa }}_e+1/2)}{{({\mathit{\kappa }}_e-3/2)}^2}-(1-f){\mathit{\sigma }}_p^2\frac{({\mathit{\kappa }}_p-1/2)({\mathit{\kappa }}_p+1/2)}{{({\mathit{\kappa }}_p-3/2)}^2}}{2{\left[\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+(1-f){\mathit{\sigma }}_p\frac{{\mathit{\kappa }}_p-1/2}{{\mathit{\kappa }}_p-3/2}\right]}^2\sqrt{\frac{5}{3}{\mathit{\sigma }}_i+\frac{f}{\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+(1-f){\mathit{\sigma }}_p\frac{{\mathit{\kappa }}_p-1/2}{{\mathit{\kappa }}_p-3/2}}}}+\frac{25{\mathit{\sigma }}_i}{18}\frac{\left[\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+(1-f){\mathit{\sigma }}_{p,}\frac{{\mathit{\kappa }}_p-1/2}{{\mathit{\kappa }}_p-3/2}\right]}{\sqrt{\frac{5}{3}{\mathit{\sigma }}_i+\frac{f}{\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+(1-f){\mathit{\sigma }}_p\frac{{\mathit{\kappa }}_p-1/2}{{\mathit{\kappa }}_p-3/2}}}}+\frac{(1+2f)}{2\sqrt{\frac{5}{3}{\mathit{\sigma }}_i+\frac{f}{\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+(1-f){\mathit{\sigma }}_p\frac{{\mathit{\kappa }}_p-1/2}{{\mathit{\kappa }}_p-3/2}}}},\\ B=\frac{1}{2{\left[\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+(1-f){\mathit{\sigma }}_p\frac{{\mathit{\kappa }}_p-1/2}{{\mathit{\kappa }}_p-3/2}\right]}^2\sqrt{\frac{5}{3}{\mathit{\sigma }}_i+\frac{f}{\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+(1-f){\mathit{\sigma }}_p\frac{{\mathit{\kappa }}_p-1/2}{{\mathit{\kappa }}_p-3/2}}}},\\ C=\frac{1+\frac{5{\mathit{\sigma }}_i}{3}\left[\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+(1-f){\mathit{\sigma }}_p\frac{{\mathit{\kappa }}_p-1/2}{{\mathit{\kappa }}_p-3/2}\right]}{2\left[\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+(1-f){\mathit{\sigma }}_p\frac{{\mathit{\kappa }}_p-1/2}{{\mathit{\kappa }}_p-3/2}\right]\sqrt{\frac{5}{3}{\mathit{\sigma }}_i+\frac{f}{\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+(1-f){\mathit{\sigma }}_p\frac{{\mathit{\kappa }}_p-1/2}{{\mathit{\kappa }}_p-3/2}}}}\\ \end{array}$$

(15)

The forthcoming equation is the well-known KP equation, and governs the evolution of the first-order approximation of electrostatic potential corresponding to the IA waves in a superthermal e–p–i plasma. The effect of transverse perturbation leads to appearance of the last term in Eq. (14), as in the absence of this effect the KP Eq. (14) reduces to the usual KdV equation. Thus, the transverse perturbation, through the last term in Eq. (14), affects the properties and existence domain of solitary structures. In the following, we investigate the effect of transverse perturbation on the basic properties as well as the existence domain of solitary structures.

There are several methods to solve the KP equation [60, 62, 65–67]. An exact solution in the form of a solitary wave can be obtained via the generalized expansion method of Eq. (14). For this we transform the independent variables X, Y and ξ into a new coordinate

$$\mathit{\zeta }=l_{X}X+l_{Y}Y+l_{\mathit{\xi }}\mathit{\xi }-U\mathit{\tau }=\mathit{\epsilon }\left(l_{X}x+l_{Y}y\right)+{\mathit{\epsilon }}^{1/2}{l}_{\mathit{\xi }}\left(z-Vt\right)-{\mathit{\epsilon }}^{3/2}Ut,$$

(16)

where U is an arbitrary constant speed, and l _X , l _Y and l _ξ are, respectively, the directional cosines of the wave vector $\stackrel{\rightharpoonup }{k}$ along the x, y and z axes, so that l ² _X  + l ² _Y  + l ² _Z  = 1.

$${\mathit{\varphi }}_1={\mathit{\varphi }}_{\text{max}}sec{h}^2\left(\frac{l_{X}X+l_{Y}Y+l_{\mathit{\xi }}\mathit{\xi }-U\mathit{\tau }}{\mathrm{\Delta }}\right)={\mathit{\varphi }}_{\text{max}}sec{h}^2(\frac{\mathit{\zeta }}{\mathrm{\Delta }}),$$

(17)

where

$${\mathit{\varphi }}_{\text{max}}=3\frac{U{l}_{\mathit{\xi }}-C(l_X^2+l_Y^2)}{A{l}_{\mathit{\xi }}^2},$$

(18a)

and

$$\mathrm{\Delta }=\sqrt{\frac{8B{l}_{\mathit{\xi }}^4}{U{l}_{\mathit{\xi }}-C(l_X^2+l_Y^2)}},$$

(18b)

give the normalized amplitude and width of solitary wave. A further set of solutions of KP equation was presented in Refs. [60, 62, 67]. Using the appropriate scaling, namely ϕ₁ → b₁u, ξ → b₂z′, X → b₃x′, Y → b₃y′, and τ → t′, the KP Eq. (14) reduces to

$${(u_{t^{\prime }}+6u{u}_{z^{\prime }}+u_{z^{\prime }{z}^{\prime }{z}^{\prime }})}_{z^{\prime }}-3u_{x^{\prime }{x}^{\prime }}-3u_{y^{\prime }{y}^{\prime }}=0,$$

(19)

which is equivalent to the standard form of KP equation. The employed coefficients in scaling are given by b₁ = 6B^1/3e^4iπ/3/A, b₂ = B^1/3e^4iπ/3, $b_3=B^{1/6}{C}^{1/2}{e}^{i\mathit{\pi }/6}/\sqrt{3}$. A traveling wave solution u(x′, y′, z′, t′) = u(χ) can be obtained by the repeated homogeneous balance method for Eq. (19), where $\mathit{\chi }=l_{x^{\prime }}{x}^{\prime }+l_{y^{\prime }}{y}^{\prime }+l_{z^{\prime }}{z}^{\prime }-v_{\circ }{t}^{\prime }$, $(l_{x^{\prime }},l_{y^{\prime }},l_{z^{\prime }})$ are positive real numbers such that $l_{x^{\prime }}^2+l_{y^{\prime }}^2+l_{z^{\prime }}^2=1$, and v_o is the incremental soliton speed. For this we use the expansion u = ∑  ⁿ_i=0 h _i Fⁱ and suppose that F′ = αF² + β, where α, β are constant. Then, the general solutions of the standard KP equation can be summarized as follows:

(1) For αβ = −1

$$u(x^{\prime },y^{\prime },z^{\prime },t^{\prime })=\frac{3(l_{y^{\prime }}^2+l_{x^{\prime }}^2)+l_{z^{\prime }}(v_{\circ }+8l_{z^{\prime }}^3)}{6l_{z^{\prime }}^2}-2l_{z^{\prime }}^2{tanh}^2\mathit{\chi },$$

(20)

(2) For α = 1

$$F=\left\{\begin{array}{c}-\sqrt{-\mathit{\beta }}tanh(\sqrt{-\mathit{\beta }}\mathit{\chi }),\text{for}\mathit{\beta }<0\hfill \\ -1/\mathit{\chi },\text{for}\mathit{\beta }=0\hfill \\ \sqrt{\mathit{\beta }}tanh(\sqrt{\mathit{\beta }}\mathit{\chi }),\text{for}\mathit{\beta }>0\hfill \end{array}\right.,$$

(21)

Which lead to the following form for the function u,

$$u(x^{\prime },y^{\prime },z^{\prime },t^{\prime })=\frac{3(l_{y^{\prime }}^2+l_{x^{\prime }}^2)+l_{z^{\prime }}(-v_{\circ }+8\mathit{\beta }{l}_{z^{\prime }}^3)}{6l_{z^{\prime }}^2}+2\mathit{\beta }{l}_{z^{\prime }}^2{tanh}^2(\sqrt{-\mathit{\beta }}\mathit{\chi }),$$

(22a)

$$u(x^{\prime },y^{\prime },z^{\prime },t^{\prime })=\frac{3(l_{y^{\prime }}^2+l_{x^{\prime }}^2)-v_{\circ }{l}_{z^{\prime }}}{6l_{z^{\prime }}^2}-\frac{2l_{z^{\prime }}^2}{{\mathit{\chi }}^2},$$

(22b)

$$u(x^{\prime },y^{\prime },z^{\prime },t^{\prime })=\frac{3(l_{y^{\prime }}^2+l_{x^{\prime }}^2)-l_{z^{\prime }}(v_{\circ }+8\mathit{\beta }{l}_{z^{\prime }}^3)}{6l_{z^{\prime }}^2}-2\mathit{\beta }{l}_{z^{\prime }}^2{tanh}^2(\sqrt{\mathit{\beta }}\mathit{\chi }),$$

(22c)

respectively for β < 0, β = 0, and β > 0.

Energy integral and parametric investigation of solitary wave existence

Kadomtsev and Petviashvili [57] have studied the soliton stability perpendicular to its direction of propagation. They derived a KP equation which governs the evolution of solitons in the presence of transverse perturbation. The solitons remain stable against such perturbations [57, 58]. The profile of soliton solution of KP equation (in contrast to KdV equation) is a function of the sign of dispersion coefficient. Kadomtsev and Petviashvili [57] have shown that in a one-dimensional system with negative dispersion the perturbations can be transformed from soliton to the medium and thus in this case the solitons are stable with respect to the weak transverse perturbations. Kako and Rowlands [58] have considered different types of perturbations on two-dimensional solitons and investigated the stability of IA solitons. Recently, Liu and Zeng [68] presented a new exact solution for the (3 + 1)-dimensional KP equation. To discuss the stability properties of IA solitons, we employ a method based on energy consideration, which it needs to obtain and study of potential energy, namely Sagdeev potential. Using the transformation (16) into Eq. (14) we obtain the following differential equation

$$l_{\mathit{\xi }}\frac{{\mathit{\partial }}^2}{\mathit{\partial }{\mathit{\zeta }}^2}\left[-U{\mathit{\varphi }}_1+\frac{A}{2}{l}_{\mathit{\xi }}{\mathit{\varphi }}_1^2+B{l}_{\mathit{\xi }}^3\frac{{\mathit{\partial }}^2{\mathit{\varphi }}_1}{\mathit{\partial }{\mathit{\zeta }}^2}\right]+C\left[l_X^2+l_Y^2\right]\frac{{\mathit{\partial }}^2{\mathit{\varphi }}_1}{\mathit{\partial }{\mathit{\zeta }}^2}=0,$$

(23)

and after integrating twice, Eq. (23) takes the following form

$$\frac{{\mathit{\partial }}^2{\mathit{\varphi }}_1}{\mathit{\partial }{\mathit{\zeta }}^2}=\frac{U}{B{l}_{\mathit{\xi }}^3}{\mathit{\varphi }}_1-\frac{A}{2B{l}_{\mathit{\xi }}^3}{\mathit{\varphi }}_1^2-\frac{C}{B{l}_{\mathit{\xi }}^4}\left[l_X^2+l_Y^2\right]\frac{{\mathit{\partial }}^2{\mathit{\varphi }}_1}{\mathit{\partial }{\mathit{\zeta }}^2}+c_1{\mathit{\varphi }}_1+c_2$$

(24)

in which c₁and c₂ are the integrating constants. Then, multiplying both sides of Eq. (24) with dϕ₁/dζ and integrating once we can obtain the following energy-like equation

$$\frac{1}{2}{\left(\frac{d{\mathit{\varphi }}_1}{d\mathit{\zeta }}\right)}^2+\mathit{\psi }({\mathit{\varphi }}_1)=0$$

(25)

where ψ(ϕ₁) is the pseudopotential or Sagdeev potential and is given by

$$\mathit{\psi }({\mathit{\varphi }}_1)=\frac{-U{l}_{\mathit{\xi }}+C(l_X^2+l_Y^2)}{2B{l}_{\mathit{\xi }}^4}{\mathit{\varphi }}_1^2+\frac{A}{6B{l}_{\mathit{\xi }}^2}{\mathit{\varphi }}_1^3$$

(26)

To obtain Eq. (26), the appropriate boundary conditions have been employed, namely {ϕ₁; dϕ₁/dζ; d²ϕ₁/dζ²}|_ζ→±∞ → 0, which lead to c₁ = c₂ = 0. Equation (25) is the well-known equation in the form of the “energy integral” of an oscillating particle of unit mass, with velocity ∂ϕ/∂ζ and position ϕ in a potential well ψ(ϕ₁). The first term in Eq. (25) can be considered as the kinetic energy of the unit mass, and ψ(ϕ₁) is the potential energy. Since the kinetic energy is a positive quantity, it requires that ψ(ϕ₁) ≤ 0 for the entire of motion, i.e., in the interval 0 < ϕ < ϕ_max(ϕ_min < ϕ < 0) for the compressive (rarefactive) solitary waves. Where ϕ_max(ϕ_min) is the maximum (minimum) value of ϕ for which ψ(ϕ) = 0.

Furthermore, Eq. (26) describes the Sagdeev potential for IA solitons in a superthermal e–p–i plasma. The limiting case of two-component electron–ion (e–i) plasma can be obtained by substituting f = 1 in Eq. (26), which then reduces to the case for the IA solitary wave in a homogeneous e–i plasma. The existence condition of solitary wave solution (17) requires that $d^2\mathit{\psi }/d{\mathit{\varphi }}_1^2\left|{}_{{\mathit{\varphi }}_1=0}\right.<0$, which implies that

$$\frac{d^2\mathit{\psi }}{d{\mathit{\varphi }}_1^2}\left|{}_{{\mathit{\varphi }}_1=0}\right.=-\frac{U{l}_{\mathit{\zeta }}-C(l_X^2+l_Y^2)}{2B{l}_{\mathit{\zeta }}^4}=\frac{-S}{l_{\mathit{\zeta }}^4}<0$$

(27)

The above expression shows that the solitary wave solution (17) exists whenever the condition

$$S=\left[U{l}_{\mathit{\zeta }}-C\left({l_X}^2+{l_Y}^2\right)\right]/2B>0$$

(28)

is satisfied. The existence domain of solitary wave solution can explore by plotting the curve S = 0 that separates the parameter space into two regions; one in which S > 0 and solitary waves exist and another one where S < 0 and solitary waves do not exist. We note that the sign of S mainly is determined by l _ξ rather than other parameters and in turn, the values of l _ξ that satisfy the existence condition are strongly controlled by arbitrary parameter U. This statement is justified in the following manner. Here we can also obtain an expression which determines the polarity of IA solitons in the present plasma model. Thus, using Eqs. (18a, 28), we can obtain

$$P=\frac{B}{A}S$$

(29)

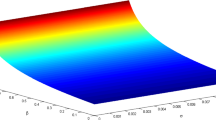
This equation gives a criterion for soliton polarity, in which P > 0 refers to the compressive solitons, while for P < 0 a rarefactive soliton may be predict in the present plasma system. To examine the effect of relevant physical parameters, such as ion/positron concentration, electron/positron superthermality, and ion temperature on the stability properties of IA waves, we have numerically investigated the condition (28). The results are depicted in Figs. 1 and 2. The contour of parameter S in space (f, l _ξ ) is plotted in Fig. 1. The curve S = 0 divides the space (f, l _ξ ) into two parts, one in which S < 0 (area below the curve) and another one where S > 0 (area above the curve). It shows that the solitary wave solution (28) exists at the upper region of the curves, while it cannot exist at the lower region. This figure shows that the existence range of solitons increases as the wave propagation goes more oblique, it is also shown that in the presence of higher concentration of ions the existence domain decreases the threshold values of l _ξ to the higher values of obliqueness. Figure 1a is depicted for non-Maxwellian limit with κ _e  = κ _p  = 3, and Fig. 1b for Maxwellian components, i.e., κ _e  = κ _p  = 100. This figure shows that the threshold values of l _ξ depend on the electron/positron suprathermality, as for the higher (lower) values of κ _e and κ _p the threshold acquire higher (lower) values. We investigated the nature of solitary structures in Fig. 1c, d in the parameter spaces of (f, l _ξ ). A comparison between Fig. 1a with c (or between Fig. 1b with d) shows that only compressive IA solitons support in the present plasma model. To perform a parametric investigation on the existence region of solitary wave solution we repeated Fig. 1 in spaces of (κ _p , l _ξ ), (κ _e , l _ξ ), (σ _i , l _ξ ), and (U, l _ξ ), in Fig. 2a–d, respectively. Figure 2a–b represents that deviation of electrons and positrons from thermodynamics equilibrium increases the primitive range of l _ξ . The electron species and positrons have similar physical properties, such as mass and magnitude of electric charge. But, in the present model the neutrality condition n_e0 = n_i0 + n_p0 causes that the positron population becomes smaller than that of electrons. Accordingly, the positron suprathermality has a weaker effect on the existence domain of solitary structures. Temperature of ions has a destructive effect on the existence domain of soliton solution, as an increase in σ _i leads to decrease of primitive interval (Fig. 2c). The arbitrary parameter U has also an important effect on the sign of parameter S, and thus on the existence domain of soliton solution. Figure 2d shows that the threshold values of l _ξ tend to the lower values for higher values of parameter U. On the other hand, we know that the amplitude of the soliton is controlled by U and its value should be chosen in such a way that the amplitude remains small to establish the assumption of weak nonlinearity. This fact imposes a restriction on the upper value of U. Based on the above findings, henceforth, we fix the value of U at 1 and we shall see in the following that the assumption of weak nonlinearity will be satisfied by this choice. The nature of these IA solitary structures investigated in panels (Fig. 2e–h). It is clear that only in the case of compressive nature, the solitary structures can exist. Thus, the solitary structures in the present plasma model would be excited with positive amplitude. This is a respectable result, because here we have employed the reductive perturbation method, and for this we have to restrict the spectrum indexes κ _p and κ _e to the region 3 < κ _p , κ _e [36]. We found that in this range, the amplitude soliton takes only the positive values.

Fig. 1

The existence domain of solitary solution in space of (f, l _ξ ) in two limits of a non-Maxwellian (with κ _e , κ _p  = 3) and b Maxwellian plasma (κ _e , κ _p  = 100). The other parameters are σ _i  = 0.1, σ _p  = 1, and l _X  = l _Y  = 0.95. The panels a and b are revisited for polarity of solitons, according to Eq. (23), in panels c and d, respectively

Fig. 2

The existence domain of solitary solution: a in space of (κ _p , l _ξ ) with σ _i  = 0.1, σ _p  = 1, f = 0.8, U = 1, κ _e  = 3, l _X  = l _Y  = 0.95, b in space of (κ _e , l _ξ ) with σ _i  = 0.1, σ _p  = 1, f = 0.8, U = 1,κ _p  = 3, l _X  = l _Y  = 0.95, c in space of (σ _i , l _ξ ) with σ _p  = 1, f = 0.8, U = 1, κ _e  = 3, κ _p  = 3, l _X  = l _Y  = 0.95, (d) in space of (U, l _ξ ) with σ _i  = 0.1,σ _p  = 1, f = 0.8, κ _e  = 3, κ _p  = 3, and l _X  = l _Y  = 0.95. The panels a–d are revisited for polarity of solitons, according to Eq. (23), in panels e–h, respectively

A three-dimensional plot of amplitude and width of solitons in spaces (l _ξ , f) and (σ _i , κ _e ) are depicted, respectively in Fig. 3a–d. It can be seen that when ion number density (obliqueness) increases (decreases) and approaches to critical values (at S = 0), the amplitude of solitary potential increases (Fig. 3a) while its width decreases (increases) (Fig. 3b). Then, for values of f and l _ξ greater than critical values, the solitary structure disappears (see also Fig. 1). Similarly, the influence of ion temperature and electron suprathermality on the soliton amplitude and width has been examined in Fig. 3c, d. Deviation of electron components from thermodynamic equilibrium (ion temperature) increases (decreases) the amplitude of IA solitons while its width experiences an inverse effect. This is similar to that observed for IA solitons in a bi-superthermal electron plasma [46]. Consequently, decrease of obliqueness, increase of ion number density, decrease of ion temperature and also deviation from Maxwellian behavior make the IA solitary structure more spiky.

Fig. 3

Three-dimensional plot of a the amplitude and b width of soliton in space of (f, l _ξ ) with σ _i  = 0.1, σ _p  = 1, U = 1, κ _e  = κ _p  = 3, l _X  = l _Y  = 0.95. c The amplitude and d width of soliton in space of (κ _e , σ _i ) with f = 0.8, σ _p  = 1, l _ξ  = 0.9, κ _e  = κ _p  = 3, and l _X  = l _Y  = 0.95

On the other hand, to discuss the formation of IA solitary waves in the present model, we have numerically examined the variation of Sagdeev potential and corresponding electrostatic potential. It should be noted that the amplitude and thickness of the produced IA solitary waves are in relevance with two main characteristic values; ϕ_max and ψ_min, where ϕ_max is the maximum value of ϕ for which ψ(ϕ) = 0, and ψ_min is the minimum value of the Sagdeev potential. Thus, we can predict the amplitude and thickness of DA soliton as $\mathrm{\Delta }={\mathit{\varphi }}_{\text{max}}/\sqrt{\left|{\mathit{\psi }}_{\text{min}}\right|}$ [69]. The corresponding variations of ϕ_max or ∆ against plasma parameters are similar to the variation of the solitary waves amplitude and width, respectively. These properties will be investigated in the Fig. 4. To see what happens when the electron suprathermal index κ _e increases we have studied the variation of Sagdeev potential with respect to the corresponding electrostatic potential in Fig. 4a for different values of κ _e . We observe that the height of IA soliton increases as electrons deviate from thermodynamic equilibrium. This means that the electron superthermality makes the IA solitons more spiky. This is in good agreement with that reported in Ref. [46] for IA solitons in superthermal plasma with two-temperature electrons. Figure 4b shows that the effect of ion number density on the behavior of Sagdeev potential. We can see that when the ion number density increases, both two main characteristic values ϕ_max and ψ_min will increase.

Fig. 4

The behavior of Sagdeev potential ψ(ϕ) with respect to the electrostatic potential ϕ, a for different values of electron suprathermality index κ _e with f = 0.8, b for different values of ion concentration f with κ _e  = 3. The other parameters are σ _p  = 1, l _ξ  = 0.9, κ _p  = 3, and l _X  = l _Y  = 0.9

The behavior of IA solitary profile has been investigated in spaces of (ξ, X) and (ξ, f) in Fig. 5a, b, respectively. Figure 5a represents that how the position of pulse changes in plane of (ξ, X). It is clear that the pulse moves toward the negative direction of ξ as X increases. The one-dimensional model cannot show such behavior. Figure 5b shows evolution of IA solitary profile as a function of the ξ coordinate and ion number density f. The IA solitary structure experiences a decrease (increase) in amplitude (width) with a decreasing f, as for low values of f the IA solitary structure may be disappears. Such behavior could be predicted via Fig. 1, which shows that the existence domain of solitons decreases with a decreasing f.

Fig. 5

Three-dimensional plot of the electrostatic potential: a in space of (ξ, X) with f = 0.8, and b in space of (ξ, f) with X = 1. The other parameters are σ _i  = 0.1σ _p  = 1, l _ξ  = 0.9, κ _e  = κ _p  = 3, l _X  = l _Y  = 0.9, τ = 0.1 and Y = 1

Discussion on the special cases

Here, the nonlinear coefficient A, the dispersion coefficients B and C are dependent on the superthermal index parameter κ, ion concentration f, and ion temperature σ _i . In the following, we consider two special cases of electron–positron (i.e., f → 0) and electron–ion (i.e., f → 1) limits. However, a third case could also be considered for negative ions, which refers to the e–p plasma under the effect of dust grains similar to that discussed by Malik and Malik [70].

1st case: Two-component e–p limit(i.e., f → 0) Let us consider a special case for the limit of f → 0, which infers to a two-component electron–positron (e–p) plasmas. We know that for f ≈ 0 (i.e., a pure e–p plasma) no ions are present and therefore, no IA solitary structures can exist. Thus, in this limit only high frequency waves (such as electron acoustic waves) can propagate, this means that in this limit the present plasma model does not support the excitation of ion acoustic waves. Study of this two-component limit is very interesting due to the fact that e–p plasma is an important constituent of the early Universe [4]. The nonlinear and dispersion coefficients of KP equation in the e–p limit take the following limiting form

$$\begin{array}{c}{A}^{(e-p)}=-\frac{\frac{({\mathit{\kappa }}_e-1/2)({\mathit{\kappa }}_e+1/2)}{{({\mathit{\kappa }}_e-3/2)}^2}-{\mathit{\sigma }}_p^2\frac{({\mathit{\kappa }}_p-1/2)({\mathit{\kappa }}_p+1/2)}{{({\mathit{\kappa }}_p-3/2)}^2}}{2\sqrt{f}{\left[\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+{\mathit{\sigma }}_p\frac{{\mathit{\kappa }}_p-1/2}{{\mathit{\kappa }}_p-3/2}\right]}^{3/2}}+\frac{1}{2\sqrt{f}}{\left[\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+{\mathit{\sigma }}_p\frac{{\mathit{\kappa }}_p-1/2}{{\mathit{\kappa }}_p-3/2}\right]}^{1/2},\\ B^{(e-p)}=\frac{1}{2\sqrt{f}{\left[\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+{\mathit{\sigma }}_p\frac{{\mathit{\kappa }}_p-1/2}{{\mathit{\kappa }}_p-3/2}\right]}^{3/2}},\\ C^{(e-p)}=\frac{1}{2\sqrt{f}{\left[\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+{\mathit{\sigma }}_p\frac{{\mathit{\kappa }}_p-1/2}{{\mathit{\kappa }}_p-3/2}\right]}^{1/2}}.\\ \end{array}$$

(30)

In the Maxwellian limit (with κ _e , κ _p  → ∞) the above expressions get the following form

$$A_M^{(e-p)}=\frac{{\mathit{\sigma }}_p+f(1+{\mathit{\sigma }}_p)}{\sqrt{f(1+{\mathit{\sigma }}_p)}},B_M^{(e-p)}=\frac{1}{2\sqrt{f}{(1+{\mathit{\sigma }}_p)}^{3/2}},C_M^{(e-p)}=\frac{1}{2\sqrt{f(1+{\mathit{\sigma }}_p)}}.$$

(31)

The above Eqs. (30) and (31) show that how the coefficients of KP equation are dependent on the concentration of ions/positrons for low ion density and two Maxwellian and superthermal limits. In this limit the dispersion coefficient B ^(e–p) _M is smaller than the coefficient C ^(e–p) _M with factor of (1 + σ _p ). Parameter S in the limit of low ion density (i.e., f → 0) and in the limit of Maxwellian low ion density (i.e., κ _e , κ _p  → ∞ and f → 0) reduces respectively to the following forms

$$S=U\sqrt{f}{\left(\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+{\mathit{\sigma }}_p\frac{{\mathit{\kappa }}_p-1/2}{{\mathit{\kappa }}_p-3/2}\right)}^{3/2}{l}_{\mathit{\xi }}-\frac{1}{2}\left(\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+{\mathit{\sigma }}_p\frac{{\mathit{\kappa }}_p-1/2}{{\mathit{\kappa }}_p-3/2}\right)\left(l_X^2+l_Y^2\right)$$

(32a)

$$S=U\sqrt{f}{(1+{\mathit{\sigma }}_p)}^{3/2}{l}_{\mathit{\xi }}-\frac{1}{2}(1+{\mathit{\sigma }}_p)(l_X^2+l_Y^2)$$

(32b)

Figure 1 shows that the existence domain of solitary structures is strongly dependent to the ion concentration and suprathermality, as in the Maxwellian limit no soliton solution exists for f ≈ 0 (see Fig. 1b). However, in the non-Maxwellian the existence domain of solitary solution increases but again no soliton solution predicted for limit of f ≈ 0 (see Fig. 1a). Such results can be predicted by Eqs. (32a) and (32b), as these equations show that for f ≈ 0 the parameter S is always negative and therefore, the essential condition for existence of solitary solution cannot be satisfied at f ≈ 0. The behavior of soliton amplitude and width with respect to the ion concentration has been shown respectively in Fig. 3a, b. It can be seen that in the limit of f → 0 the IA soliton becomes more spiky. Of course we see that at f ≈ 0 the solitary structure disappears and system do not supports solitons in the pure e–p limit. It can also be seen from Figs. 4b and 5b that the amplitude (width) of IA soliton decreases (increases) with an decreasing f, and according to Fig. 5b the IA soliton collapses at f ≈ 0.

2stcase; Two-component e–i limit(i.e., f → 1) In the contrast limit, we can consider the electron–ion limit (f → 1), these limits of plasma support ordinary IA waves. The nonlinear and dispersion coefficients of KP equation in the e–i limit reduce to the following form

$$\begin{array}{c}{A}^{(e-i)}=-\frac{1}{2\sqrt{\frac{5}{3}{\mathit{\sigma }}_i+f\frac{{\mathit{\kappa }}_e-3/2}{{\mathit{\kappa }}_e-1/2}}}\frac{({\mathit{\kappa }}_e-1/2)({\mathit{\kappa }}_e+1/2)}{{({\mathit{\kappa }}_e-1/2)}^2}+\left[\frac{25{\mathit{\sigma }}_i}{18}\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}+\frac{1+2f}{2}\right]\frac{1}{\sqrt{\frac{5}{3}{\mathit{\sigma }}_i+f\frac{{\mathit{\kappa }}_e-3/2}{{\mathit{\kappa }}_e-1/2}}},\\ B^{(e-i)}=\frac{1}{2{\left[\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}\right]}^2\sqrt{\frac{5}{3}{\mathit{\sigma }}_i+f\frac{{\mathit{\kappa }}_e-3/2}{{\mathit{\kappa }}_e-1/2}}},\\ C^{(e-i)}=\frac{1+\frac{5{\mathit{\sigma }}_i}{3}\left[\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}\right]}{2\left[\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}\right]\sqrt{\frac{5}{3}{\mathit{\sigma }}_i+f\frac{{\mathit{\kappa }}_e-3/2}{{\mathit{\kappa }}_e-1/2}}}\\ \end{array}$$

(33)

The above expressions can be obtained in the Maxwellian limit (with κ _e , κ _p  → ∞) as follows

$$A_M^{(e-i)}=\frac{\frac{25{\mathit{\sigma }}_i}{18}+f}{\sqrt{\frac{5}{3}{\mathit{\sigma }}_i+f}},B_M^{(e-i)}=\frac{1}{2\sqrt{\frac{5}{3}{\mathit{\sigma }}_i+f}},C_M^{(e-i)}=\frac{1+\frac{5{\mathit{\sigma }}_i}{3}}{2\sqrt{\frac{5}{3}{\mathit{\sigma }}_i+f}}$$

(34)

Equations (33) and (34) describe the limiting behavior of the coefficients of KP equation. It is clear that all of the coefficients A, B, and C in the limits of two-component e–i and Maxwellian plasma, take a simple form as follows $A_M^{(e-i)}=2\left(\frac{25{\mathit{\sigma }}_i}{18}+f\right)B_M^{(e-i)}$, $C_M^{(e-i)}=\left(1+\frac{5{\mathit{\sigma }}_i}{3}\right)B_M^{(e-i)}$. Similar to the Maxellian e–p limit, in the Maxwellian e–i limit also the dispersion coefficient C ^(e–i) _M is greater than the dispersion coefficient B ^(e–i) _M . Parameter S in the limit of low ion density (i.e., f → 0) and in the limit of Maxwellian low ion density (i.e., κ _e , κ _p  → ∞ and f → 0) reduces respectively to the following forms

$$S=U{l}_{\mathit{\xi }}{\left[\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}\right]}^2\sqrt{\frac{5{\mathit{\sigma }}_i}{3}+f\frac{{\mathit{\kappa }}_e-3/2}{{\mathit{\kappa }}_e-1/2}}-\frac{1}{2}\left(1+\frac{5{\mathit{\sigma }}_i}{3}\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}\right)\frac{{\mathit{\kappa }}_e-1/2}{{\mathit{\kappa }}_e-3/2}\left(l_X^2+l_Y^2\right)$$

(35a)

$$S=U{l}_{\mathit{\xi }}\sqrt{\frac{5{\mathit{\sigma }}_i}{3}+f}-\frac{1}{2}\left(1+\frac{5{\mathit{\sigma }}_i}{3}\right)\left(l_X^2+l_Y^2\right)$$

(35b)

Figure 1a shows that in the limit of f → 1 (with κ _e , κ _p  = 3) the existence domain of solitary solution lies in the region of 0.79 < l _ξ  < 1. In the Maxwellian limit (with κ _e , κ _p  = 100) the primitive region of l _ξ for f → 1 reduces to 0.88 < l _ξ  < 1 (see Fig. 1b). Figure 2a, b show that in the limit of f → 1, the effect of positron suprathermality on the primitive region is weaker than the electron suprathermality. Figure 3a shows that the amplitude of IA soliton increases with an increasing f, while the soliton width shows an inverse behavior (see Fig. 3b). This means that the e–i limit supports smaller and wider solitons. Figures 4b and 5b verify that the amplitude (width) of IA soliton increases (decreases) with an increasing f.

Conclusions

A three-dimensional e–p–i plasmas consisting of superthermal electrons and positrons have been considered to examine the effects of transverse perturbation, electron/positron superthermality and ion concentration on the existence, formation and profile of IA solitary waves. Using the reductive perturbation technique we derived a KP equation describing the IA solitary structures. We employed the energy integral equation to study the existence domains of the solitary structures. It is found that the nature of solitary structures in the present model is compressive. The main points of this investigation are summarized as follows:

• 1. We have investigated the existence domain of solitary solution through a parametric analysis and found that this domain is dependent on the suprathermality, ion concentration and ion temperature. While deviation of electrons and positrons from thermodynamics equilibrium increases the primitive range of l _ξ , an increase in ion temperature (through σ _i ) leads to decrease of the primitive interval. Also the existence domain of soliton increases with arbitrary parameter U. We found that in the e–p limit no soliton solution supports by the present model, while the primitive domain of solitons increases with approaching to the e–i limit. In the non-Maxwellian e–i limit, the existence domain of solitary solution lies in the region of 0.79 < l _ξ  < 1, and in the Maxwellian e–i limit the primitive region of l _ξ reduces to 0.88 < l _ξ  < 1.

• 2. It is found that the nonlinear evolution of IA solitary waves in the present e–p–i plasma model is governed by the KP equation, the coefficients of which are found to be significantly modified by the effects of transverse perturbation, suprathermality, ion temperature, and ion concentration.

• 3. The soliton amplitude and width are strongly dependent on the suprathermality, ion concentration and ion temperature. Effect of suprathermality causes to increase (decrease) the amplitude (width) of the solitary structures. This means that deviation of electrons/positrons from thermodynamics equilibrium makes the solitary structure more spiky. The soliton amplitude increases with an increasing f, while the width of soliton shows an inverse behavior. We found that the solitary structure becomes narrower and larger in the e–i limit, while the solitary structure collapses in the e–p limit.

We expect that the present investigation should be useful for understanding the localized electrostatic disturbances in space, astrophysical and laboratory e–p–i plasma.