Evolution of shapes in even–even nuclei using the standard interacting boson model

Abstract

The sd-version of the interacting boson model (IBM) is used to establish the shape phase transitional structure. A simplified Hamiltonian is used which is intermediate between the three dynamical symmetries of U(6), namely the spherical U(5), the prolate and oblate deformed SU(3) and the $\gamma$-unstable O(6) limits. The potential energy surfaces (PESs) to the IBM Hamiltonian have been obtained using the intrinsic state formalism which introduces the shape variables $\beta$ and $\gamma$. The Gadolinium (Gd) and Ruthenium (Ru) isotopic chains have been taken as examples in illustrating the U(5)–SU(3) and U(5)–O(6) shape phase transitions, respectively. We used the standard $\chi ^2$ test to get the IBM Hamiltonian parameters. The fit is performed by minimizing the $\chi ^2$ function for some selected experimental low-lying energy levels, the two neutron separation energies and B(E2) transition rates.

Introduction

The interacting boson model (IBM) [1] was designed to describe the collective quadrupole degrees of freedom in nuclei. The IBM Hamiltonian was written from the beginning in second quantization form in terms of the generators of the unitary Lie algebra U(6) subtended by s and d bosons which carry angular momentum 0 and 2, respectively. The model present three special limits that can be solved easily. These three limits are U(5), SU(3) and O(6) dynamical symmetries appropriate for an harmonic vibrator, axial deformed rotor and $\gamma$-unstable deformed rotor, respectively. Each of these limits is assigned to spherical, axially deformed and deformed with $\gamma$-instability shapes, respectively. Among the transitional Hamiltonian a specially interesting case occurs when it describes a critical point in the transition from a given shape to another. A shape phase transition may be of first or second order, depending on the discontinuity of the first- or second-order derivatives of the order parameter as a function of the control parameters [2–10].

The classical limit of the IBM is defined as its expectation value in a coherent state [10–12] and yields a function of shape variables $\beta$ and $\gamma$ which can be interpreted as a potential energy surface (PES) depending on these parameters. The symmetry E(5) [13] is designed for the critical point of the transition from spherical to deformed $\gamma$-unstable shapes. Later [14, 15] X(5) and Y(5) describe the critical points between spherical and axially deformed shapes and between axial and triaxial deformed shapes, respectively.

In the present work, we use the two parameters sd-IBM-1 Hamiltonian with the intrinsic coherent state method to produce the potential energy surfaces (PESs) for chains of isotopes $^{150-162}$Gd and $^{96-114}$Ru involving nuclei suggested [16–18] to be good candidates for X(5) and E(5) critical point symmetries.

A simplified Hamiltonian of the sd-IBM in the intrinsic condensate state

In this work, we adopt a simplified two-parameter IBM-1 Hamiltonian in the form

$$\begin{aligned} H=\epsilon \hat{n}_d+ a_2 \hat{Q}(\chi ) \cdot \hat{Q}(\chi ) \end{aligned}$$

(1)

where the d-boson number operator $\hat{n}_d$ and the quadrupole operator $Q(\chi )$ are defined as

$$\begin{aligned} \hat{n}_d = d^\dag \cdot \tilde{d} \end{aligned}$$

(2)

$$\begin{aligned} \hat{Q}(\chi ) = s^\dag \tilde{d} + d^\dag \tilde{s} + \chi [d^\dag \times \tilde{d}]^{(2)} \end{aligned}$$

(3)

with $\chi$ the structure parameter of the quadrupole operator of the IBM, and $[d^\dag \times \tilde{d}]^{(2)}$ stands for the $l=2$ tensor coupling of the d-boson creation and annihilation operators $(\tilde{d}_\mu =(-1)^\mu d_{-\mu })$, where $\mu =-2,-1,0,+1,+2$ is the angular momentum projection, and $(\cdot )$ denoting the scalar product.

The geometric interpretation of the Hamiltonian (1) can be derived using the intrinsic condensate state $|N \beta \gamma \rangle$ defined by [10, 11]

$$\begin{aligned} | N \beta \gamma \rangle =\frac{1}{\sqrt{N!}} ({\it \Gamma} _c^\dag )^N |0\rangle \end{aligned}$$

(4)

with

$$\begin{aligned} {\it \Gamma} _c^\dag =\frac{1}{\sqrt{1+\beta ^2}}[s^\dag +\beta \cos \gamma d^\dag _0+\frac{1}{\sqrt{2}} \sin \gamma (d_2^\dag +d_{-2}^\dag )] \end{aligned}$$

(5)

where $\beta$ and $\gamma$ are the geometric parameters. We get the ground state potential energy surface (PES) by calculating the expectation value of the Hamiltonian on the intrinsic boson condensate state:

$$\begin{aligned} \begin{array}{ll} E(N,\beta ,\gamma ,\chi ) &= \langle N \beta \gamma |H|N \beta \gamma \rangle \\ &= \epsilon \frac{N \beta ^2}{1+\beta ^2}+a_2 \Big\{\frac{N}{1+\beta ^2}[5+(1+\chi ^2)\beta ^2] \\ &\quad+\frac{N(N-1)}{(1+\beta ^2)^2} \Big[4 \beta ^2-4\sqrt{\frac{2}{7}} \chi \beta ^3 \cos 3\gamma +\frac{2}{7} \chi ^2 \beta ^4\Big]\Big\} \end{array} \end{aligned}$$

(6)

If we eliminate the contributions of the one-body terms of the quadrupole–quadrupole interaction, then

$$\begin{aligned} E(N,\beta ,\gamma ,\chi )= \frac{A_2 \beta ^2+A_3 \beta ^3 \cos 3\gamma +A_4 \beta ^4}{(1+\beta ^2)^2} \end{aligned}$$

(7)

with

$$\begin{aligned} \begin{array}{ll} A_2 &{}= [\epsilon +4a_2 (N-1)]N \\ A_3 &{}= -4 \sqrt{\frac{2}{7}} \chi a_2 (N-1)N \\ A_4 &{}= \left[\epsilon +\frac{2}{7} \chi ^2 (N-1)a_2\right]N \end{array} \end{aligned}$$

(8)

Minimization of the PES with respect to $\beta$ for a given value of $\chi$, gives the equilibrium value $\beta _m$ defining phase of the system; $\beta _m=0$ corresponding to the symmetric phase while $\beta _m\ne 0$ to the broken symmetry phase. Since $\gamma$ enters the potential (7) only through the $\cos 3\gamma$ dependence in the cubic term, the minimization in this variable can be performed separately. The global minimum is either at $\gamma _m=0 \,(2\pi /3,4\pi /3)$ for $A_3<0$ or at $\gamma _m=\pi /3$ ($\pi ,5\pi /3$) for $A_3>0$. The second possibility can be expected via changing the sign of the corresponding $\beta _m$ and simultaneously setting $\gamma _m=0$.

The IBM phase can be described as follows:

• 1. For $A_3^2< 4A_2 |A_4|$, phase with $\beta _m=0$ interpreted as spherical U(5) dynamical symmetry.

• 2. For $A_3^2> 4A_2 |A_4|$; $A_3<0$, phase with $\beta _m>0$, $\gamma _m=0$ interpreted as prolate deformed SU(3) dynamical symmetry.

• 3. For $A_3^2> 4A_2 |A_4|$; $A_3>0$, phase with $\beta _m>0$, $\gamma _m=\pi /3$ interpreted as oblate deformed $\bar{SU(3)}$ dynamical symmetry.

• 4. The dynamical symmetries O(6) and $\bar{O}(6)$ do not represent separate phases.

For $\beta$ non-zero, the first derivative of Eq. (7) must be zero and the second derivative positive. This gives

$$\begin{aligned} \beta ^3 (4A_4 \beta ^2 + 3A_3 \beta \cos 3\gamma +2A_2)&= 0 \nonumber \\ 12A_4 \beta ^2+6A_3 \beta \cos 3\gamma +2A_2&> 0 \end{aligned}$$

(9)

The solution for $\beta \ne 0$ are obtained if we set $A_3=0$ in equation (9). Then equation (9) gives

$$\begin{aligned} 4A_4 \beta ^2 +2A_2 =0 \end{aligned}$$

(10)

or

$$\begin{aligned} \beta =\pm \sqrt{\frac{-A_2}{2A_4}} \end{aligned}$$

(11)

This requires $A_4$ and $A_2$ to have opposite signs. Since $A_4$ must be positive for bound solutions, $A_2$ must be negative in deformed phase.

The finite $\beta$ solutions corresponds to prolate ($\beta >0$) and oblate ($\beta <0$) equilibrium shapes, separated by a curve corresponding to $A_3=0$. Thus, there are in total, three phases. The spherical-deformed phase transition is generated by a change in sign of $A_2$, while the prolate–oblate correspond to changing the sign of $A_3$.

For $\gamma =0$ (to study the $\beta$ dependence) and in the large N-limit (i.e., N − 1 = N), yield the following coefficients in the PESs

$$\begin{aligned} A_2&= [\epsilon +4a_2 N]N \nonumber \\ A_3&= -4 \sqrt{\frac{2}{7}} \chi a_2 N^2 \\ A_4&= \left[\epsilon +\frac{2}{7} \chi ^2 a_2 N\right]N \nonumber \end{aligned}$$

(12)

providing that $A_2>0$ and $A_3>0$, then the critical point is located at $A_3^2=4A_2 A_4$, which leads to

$$\begin{aligned} 1=-\frac{a_2 N}{\epsilon }\left(4+\frac{2}{7}\chi ^2\right) \end{aligned}$$

(13)

If we introduce the control parameter $\eta$ such that

$$\begin{aligned} \frac{1-\eta }{\eta }=-\frac{a_2 N}{\epsilon } \end{aligned}$$

(14)

Then the critical point is located at

$$\begin{aligned} \eta _c=\frac{4+\frac{2}{7}\chi ^2}{5+\frac{2}{7}\chi ^2} \end{aligned}$$

(15)

At $\eta _c$ the depth of the $\beta =0$ and $\beta \ne 0$ minima is equal.

The antispinodal point for the transition U(5)–SU(3) appears when $A_2=0$, $i.e.,$

$$\begin{aligned} \frac{-a_2 N}{\epsilon }=\frac{1}{4} \end{aligned}$$

(16)

or

$$\begin{aligned} \eta =4/5 \end{aligned}$$

(17)

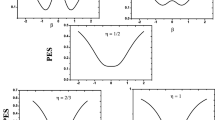
For $\chi =-\sqrt{7}/2$, the critical point is located at $\eta _c=9/11$ and the equilibrium value of the deformation parameter at the critical point is $\beta _0=1/2\sqrt{2}$. At $\eta =1$ the system is in the symmetric phase since the PES has a unique minimum at $\beta =0$. When $\eta$ decreases, one reaches the spinodal point at $\eta <\eta _c$ ($\eta =0.820$) where a second local minimum arises.

The two minima have the same depth at the critical point $\eta _c=9/11$ (0.818). Beyond this value for $\eta >\eta _c$ the symmetric minimum at $\beta =0$ becomes a local minimum till $\eta =4/5$ (0.800) where it becomes antispinodal point. A sketch of this evolution is illustrated in Fig. 1.

Fig. 1

Potential energy surface (PES) as a function of deformation parameters $\beta$ corresponding to U(5)–SU(3) transition for large $N$ limit for different values of control parameter $\eta$

For $\chi =0$ ($A_3=0$), and for large N limit the PES reduces to

$$\begin{aligned} E(N,\beta )=\frac{A_2 \beta ^2+A_4 \beta ^4}{(1+\beta ^2)^2} \end{aligned}$$

(18)

with

$$\begin{aligned} A_2&= (\epsilon +4a_2 N)N \end{aligned}$$

(19)

$$\begin{aligned} A_4&= \epsilon N \end{aligned}$$

(20)

At the critical point $A_2=0$, which leads to

$$\begin{aligned} -\frac{a_2 N}{\epsilon }=\frac{1}{4} \end{aligned}$$

(21)

or

$$\begin{aligned} \frac{1-\eta }{\eta }=\frac{1}{4} \end{aligned}$$

(22)

Then the critical point is located at $\eta _c=4/5$. All the three points, spinodal, critical and antispinodal are located at $\eta =4/5$ and the quantum phase transition between spherical and deformed phase is of the second order. A sketch of this case is illustrated in Fig. 2.

Fig. 2

Potential energy surface (PES) as a function of deformation parameters $\beta$ corresponding to U(5)–O(6) transition for large $N$ limit for three values of control parameter $\lambda$

Table 1 The optimized fitted parameters for the Gd isotopic chain

Table 2 The optimized fitted parameters for the Ru isotopic chain

Fig. 3

Potential energy curves as a function of deformation parameter $\beta$ in the U(5)–SU(3) transition for the even–even Gd isotopic chain obtained from IBM with intrinsic state formalism. The total number of bosons N = 9–15 and $\chi =-\sqrt{7}/2$

Fig. 4

The same as in Fig. 3 but for U(5)–O(6) transition for the even-even Ru isotopics chain. The total number of bosons N = 4–13 and $\chi =0$

Application of the model to the Gd and Ru isotopic chains

We used the $\chi ^2$ test to get the coefficients $A_1,A_2$ and $A_3$ of the PESs. The $\chi ^2$ function is defined in the standard way,

$$\begin{aligned} \chi ^2=\left[ \frac{1}{N_{\rm {data}}-N_{\rm {par}}}\sum ^{N_{\rm {data}}}_{i=1} \left(\frac{\chi ^{\rm {exp}}_{i }(I)-\chi ^{\rm {IBM}}_{i }}{\sigma _i}\right) \right] ^{2} \end{aligned}$$

(23)

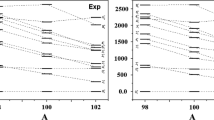
where $N_{\rm {data}}$ is the number of data to be fitted, $N_{\rm {par}}$ is the number of parameters used in the IBM fit, $\chi _i^{\rm {exp}}$ is an experimental energy level [19] or the two-neutron separation energies or the $B(E2)$ values and $\chi _i^{\rm {IBM}}$ is the corresponding calculated IBM value and $\sigma _i$ is the experimental error assigned to each $\chi _i^{exp}$. To perform the fit, we minimized $\chi ^2$ function for the selected energy levels ($2^+_1,4^+_1,6^+_1,8^+_1,0^+_2,2^+_3,4^+_3,2^+_2,3^+_1$ and $4^+_2$) using $A_1,A_2$ and $A_3$ as free parameters.

We apply now the formalism outlined in the previous section to Gd and Ru isotopic chains. In case of Gadolinium chain $^{150-162}_{\qquad \, 64}$Gd we assumed the structure parameters $\chi$ of the quadrupole operator to be equal to $-\sqrt{7}/2$, because some Gd isotopes clearly exhibit the character of the SU(3) dynamical symmetry. Using the optimized fitted parameters shown in Table 1, we calculated the PESs which are illustrated in Fig. 3. The phase diagram exhibits first-order shape phase transition from spherical U(5) to deformed axial symmetric prolate SU(3) when moving from light isotopes to heavy ones. The $^{150}$Gd nucleus still shows a vibrational structure while $^{156-162}$Gd are considered as rather good SU(3) examples.

As an example of isotopic chain in which the structure changes from spherical U(5) to $\gamma$-unstable O(6) symmetry, we have studied the Ruthenium chain $^{96-114}_{\qquad 44}$Ru. The corresponding PESs are plotted in Fig. 4 using the coefficients in Table 2. We considered $\chi =0$ and performed the same process of fitting as applied in Gd chain. The lighter isotopes exhibit a vibrational structure, while the heavier ones present a $\gamma$-unstable behavior with the critical point located of $^{104}$Ru isotope.

Conclusion

In the present work, we have analyzed the shape phase transitions in the framework of a two-parameter simplified truncated sd-IBM1 as a very tractable model for theoretical studies. We used the boson intrinsic coherent state formalism which provides a connection between the IBM and the geometric collective model (GCM) to calculate the PESs. We have analyzed the critical points of the shape phase transitional regions U(5)–SU(3) and U(5)–O(6) in the space of the model parameters. We have investigated the first-order quantum phase transition from spherical U(5) to deformed axial symmetric prolate SU(3) along the chain of $^{150-162}$Gd isotopes and the second-order quantum phase transition from spherical U(5) to $\gamma$-unstable rotor O(6) along the chain of $^{96-114}$Ru isotopes. We find that the critical nuclei characterizing the phase transitions are $^{154}$Gd and $^{104}$Ru. To get the optimized parameter of the PES for each nucleus, a computer-simulated search program is performed to obtain a minimum root mean squared (rms) deviation between calculated and some experimentally selected low-lying energy levels, B(E2) transition rates and two-neutron separation energies.