1 Introduction

The interacting boson model (IBM) provides an algebraic, elegant and powerful model for the description of medium-heavy collective nuclei [1]. In this model, collective excitations in nuclei are described in terms of a system of N interacting (s) and (d) bosons with \(L^\pi =0^+\) and \(2^+\) respectively. The number of bosons N is determined by half the number of valence nucleons. The simplest version of the model (IBM1) do not distinguish between neutron and proton bosons. The sd IBM has dynamical group U(6) with three dynamical symmetry limits U(5), SU(3) and O(6)corresponding to spherical harmonic vibrator, axially deformed rotor and \(\gamma\)-unstable deformed rotor as geometrical analogs. The shape-phase transition from the spherical U(5) dynamical symmetry to the deformed \(\gamma\)-unstable O(6) dynamical symmetry in nuclear isotopic chins in the framework of IBM were studied [2,3,4,5,6,7,8,9,10,11]. The intrinsic coherent state formalism [12,13,14] was introduced to investigate the connection between the IBM, the potential energy surface (PES), the geometric shapes [15] and the phase transitions. The behavior of critical points in the shape phase transition regions can be analyzed on nuclei in the framework of both geometric collective model [16,17,18] and the IBM. The critical point symmetry such as E(5) [19] in IBM is designed to describe the critical point at the transition from spherical U(5) dynamical symmetry to the deformed \(\gamma\)-unstable O(6) dynamical symmetry shapes. The transition between various dynamical symmetries were also studied in framework of catastrophe theory [20, 21], in which the shape-phase diagram depends on two independent combinations of the parameters of the IBM Hamiltonian, called \(r_1\) and \(r_2\), which can be used to classify the equilibrium configurations. Shape phase transitions and critical points in a chain of nuclei can be tested experimentally by measuring observables such as energy ratios \(R_{4/2}=E(4_1^+)/E(2_1^+)\), electromagnetic transitions such as B(E2) values, two-neutron separation energies, isomer shifts and isotopes shifts. In the present paper a detailed study of the shape transition between the spherical vibrator and the deformed \(\gamma\)-unstable rotator in the framework of the IBM (U(5)-O(6)) has been performed by using the intrinsic coherent state formalism and the concept of catastrophe theory, we will apply our results to the Ru, Pd, and Xe even-even chains of isotopes.

2 Outline of the Model

The general interacting boson model (IBM) Hamiltonian with up to two-body interactions can be written in Casimir operators form as:

$$\begin{aligned} H_{sd} = &\; \epsilon C_1\left[ U(5)\right] + k_1 C_2\left[ U(5)\right] + k_2 C_2\left[ O(5)\right] \\ &{}+ k_3 C_2\left[ O(3)\right] + k_4 C_2\left[ SU(3)\right] + k_5 C_2\left[ O(6)\right] \end{aligned}$$
(1)

where \(C_n[G]\) denote the nth -order Casimir operator of the group G, and \(\left\{ k_i\right\} =\left\{ \epsilon , k_1, k_2, k_3, k_4, k_5\right\}\) is the set of the Hamiltonian parameters. The Casimir operators are defined by [22]

$$\begin{aligned} C_1\left[ U(5)\right] =\hat{n}_d \end{aligned}$$
(2)
$$\begin{aligned} C_2\left[ U(5)\right] = \hat{n}_d\left( \hat{n}_d + 4\right) \end{aligned}$$
(3)
$$\begin{aligned} C_2\left[ O(5)\right] = \frac{1}{5} \hat{L}\cdot \hat{L} + 2\hat{T}_3\cdot \hat{T}_3 \end{aligned}$$
(4)
$$\begin{aligned} C_2\left[ O(3)\right] = \hat{L}\cdot \hat{L} \end{aligned}$$
(5)
$$\begin{aligned} C_2\left[ SU(3)\right] = 2\hat{Q}\cdot \hat{Q} + \frac{3}{4}\hat{L}\cdot \hat{L} \end{aligned}$$
(6)
$$\begin{aligned} C_2\left[ O(6)\right] = \hat{N}\left( \hat{N} + 4 \right) - 4\hat{P}\cdot \hat{P} \end{aligned}$$
(7)

where \(\hat{n}_d, \hat{P}, \hat{L}, \hat{Q}, \hat{T}_3\) and \(\hat{T}_4\) are the d-boson number, the pairing, the angular momentum, the quadrupole, the octupole and hexadecapole operators respectively given by:

$$\begin{aligned} \hat{n}_d = \sum _m d_m^\dag d_m \end{aligned}$$
(8)
$$\begin{aligned} \hat{P} = \frac{1}{2}\left( \left( d^\dag \cdot d^\dag \right) - \left( s^\dag \cdot s^\dag \right) \right) \end{aligned}$$
(9)
$$\begin{aligned} \hat{L} = \sqrt{10}\left[ d^\dag \cdot d^\dag \right] ^{(1)} \end{aligned}$$
(10)
$$\begin{aligned} \hat{Q} = \left[ s^\dag \times \tilde{d} + d^\dag \times \tilde{s}\right] ^{(2)} - \chi \left[ d^\dag \times \tilde{d}\right] ^{(2)} \end{aligned}$$
(11)
$$\begin{aligned} \hat{T}_3 = \left[ d^\dag \times \tilde{d}\right] ^{(3)} \end{aligned}$$
(12)
$$\begin{aligned} \hat{T}_4 = \left[ d^\dag \times \tilde{d}\right] ^{(4)} \end{aligned}$$
(13)

with \(\tilde{d}_\mu = (-1)^\mu d_\mu\) and \(\left( t^{(\lambda )}\cdot u^{(\lambda )}\right) = (-1)^\lambda \sqrt{2\lambda +1}\left[ t^{(\lambda )}\times u^{(\lambda )}\right] ^{(0)}\) and \(\left[ t^{(\lambda _1)}\times u^{(\lambda _2)}\right] _\mu ^{(\lambda )} = \sum _{\mu _1\mu _2} \langle \lambda _1\mu _1\lambda _2\mu _2 | \lambda \mu \rangle t^{\lambda _1}_{\mu _1} L^{\lambda _2}_{\mu _2}\) where \(\langle \lambda _1\mu _1\lambda _2\mu _2 | \lambda \mu \rangle\) is a Clebsch-Gordan coefficient. To analyze the geometrical shapes and phase transitions of atomic nuclei, the intrinsic coherent state method is used. In such formalism the eigenfunction of the ground state of the system is [13]

$$\begin{aligned} | N, \beta , \gamma \rangle = \frac{1}{\sqrt{N!(1+\beta ^2)^N}}\left[ s^\dag + \beta \cos \gamma d_0^\dag + \frac{1}{\sqrt{2}}\sin \gamma (d_2^\dag + d_{-2}^\dag )\right] | 0 \rangle \end{aligned}$$
(14)

where \(\beta\) and \(\gamma\) are the deformation parameter and the departure from axial symmetry respectively and \(| 0 \rangle\) is the boson vacuum (inert core). The potential energy surface (PES) is given by the expectation value of the Hamiltonian (1) in the intrinsic coherent state (14). It has the following general form:

$$\begin{aligned} E(\beta , \gamma ) = \frac{A_2 \beta ^2 + A_3 \beta ^3 \cos 3\gamma + A_4 \beta ^4}{(1 + \beta ^2)^2} + C \end{aligned}$$
(15)

where the coefficients \(A_2, A_3, A_4\) and C are given by

$$\begin{aligned} A_2 = \left[ \grave{\lambda } + \left( 8N - \frac{23}{2} + 2\chi ^2 \right) k_4 + 4\left( N-1\right) k_5\right] N \end{aligned}$$
(16)
$$\begin{aligned} A_3 = -8\sqrt{\frac{2}{7}}\chi k_4N(N-1) \end{aligned}$$
(17)
$$\begin{aligned} A_4 = \left[ \grave{\lambda } + k_1(N-1) + \left( \frac{4}{7}\chi ^2 N + \frac{10}{7}\chi ^2 - \frac{7}{2}\right) k_4\right] N \end{aligned}$$
(18)
$$\begin{aligned} C = 10 N k_4 - N(N-1)k_5 \end{aligned}$$
(19)
$$\begin{aligned} \grave{\lambda } = \epsilon + 5 k_1 + 4 k_2 + 6 k_3 \end{aligned}$$
(20)

To reject the U(5) quadratic Casimir operator we put \(k_1 = 0\) and to study the U(5)-O(6) shape transition \((\chi = 0)\) we neglect the SU(3) quadratic Casimir operator \(k_4 = 0\) and in order to remove the dependence on the total boson number N, we divide the parameters \(\epsilon , k_2, k_3\) by N and the parameter \(k_5\) by \(N^2\) in the original Hamiltonian. The PES reads:

$$\begin{aligned} E(\beta ) &= \lambda \frac{\displaystyle \beta ^2}{\displaystyle (1+ \beta ^2)} - \frac{\displaystyle k_5}{(\displaystyle 1 + \beta ^2)^2}\left( 1 - \beta ^2\right) ^2 \\ &{}= \frac{(\displaystyle \lambda + 4k_5)\beta ^2 + \lambda \beta ^4}{\displaystyle (1 + \beta ^2)^2} - k_5 \end{aligned}$$
(21)

with

$$\begin{aligned} \lambda = \epsilon + 4 k_2 + 6 k_3 \end{aligned}$$
(22)

The PES Eq. (21) contains two control parameters \(\lambda\) and \(k_5\) and involves spherical term \(\beta ^2/(1+\beta ^2)\) and a deformed one \(\left[ (1-\beta ^2)/(1+\beta ^2)\right] ^2\) and characterized by N independence, and since it does not depend on \(\gamma\) it corresponds to a \(\gamma\)-unstable geometry. The equilibrium value of \(\beta\) is determined by calculating the first order derivative of the PES Eq. (21) with respect to \(\beta\) which leads to

$$\begin{aligned} \beta \left[ (-4 k_5 + \lambda )\beta ^2 - ( 4k_5 -\lambda )\right] = 0 \end{aligned}$$
(23)

Therefore

$$\begin{aligned} \beta = 0 \ \ \ \ \ \ \ \ \ , \ \ \ \ \ \ \ \ \beta = \pm \sqrt{\frac{\displaystyle -4k_5 - \lambda }{\displaystyle -4k_5 + \lambda }} \end{aligned}$$
(24)

We find that the PES has always a global minimum at \(\beta = 0\) and the equilibrium shape being spherical when \(4k_5 \ge 0\), \(\lambda \ne 0\). For \(\lambda = 0\), \(4k_5 < 0\) the shape becomes deformed (deformed \(\gamma\)-unstable shape). For \(\lambda \ne 0\), \(4k_5\ne 0\), \(5k_5 < \lambda\) shape transition between spherical and deformed occur.

3 Analysis of Critical Points in Terms of Catastrophe Theory

For the general form of the PES

$$\begin{aligned} E(\beta , \gamma ) = g_1\frac{\displaystyle \beta ^2}{\displaystyle 1 + \beta ^2} + \frac{\displaystyle g_2 \beta ^2 + g_3 \beta ^3 \cos 3\gamma + g_4 \beta ^4 + g_0}{\displaystyle (1 + \beta ^2)^2} + C \end{aligned}$$
(25)

the essential parameters \(r_1\) and \(r_2\) of the catastrophe theory [17, 18] are defined as [23]:

$$\begin{aligned} r_1 = \frac{\displaystyle g_1 + g_2 - 2g_0}{\displaystyle g_1 - g_2 + 2g_4} \ \ \ \ , \ \ \ \ r_2 = \frac{\displaystyle -2g_3}{\displaystyle g_1 - g_2 + 2g_4} \end{aligned}$$
(26)

The values of the essential parameters \(r_1\) and \(r_2\) for the dynamical symmetries U(5) and O(6) are \(r_1 = 1, r_2 = 0\) for U(5) and \(r_1 = -1, r_2 = 0\) for O(6). By using the essential parameters \(r_1\) and \(r_2\) the PES can be written as

$$\begin{aligned} E( \beta , \gamma ) = \frac{\displaystyle 1}{\displaystyle 1 + \beta ^2}\left[ \beta ^4 + r_1 \beta ^2 (\beta ^2 + 2 )\right] - r_2 \beta ^3\cos 3\gamma \end{aligned}$$
(27)

In addition, at the antispinodal, critical and spinodal points, yield

$$\begin{aligned} r_{1a} = 0 \end{aligned}$$
(28)
$$\begin{aligned} r_{1c} = \frac{-1}{2} + \frac{1}{2}\sqrt{1 + \frac{\displaystyle 1}{\displaystyle 2} r_2^2} \end{aligned}$$
(29)
$$\begin{aligned} r_{1s} = -1 + \frac{\displaystyle (9 r_2^2 + 16 )^{\frac{3}{2}} -64}{\displaystyle 54 r_2^2} \end{aligned}$$
(30)

The corresponding essential parameters \(r_1\) and \(r_2\) for the PES Eq. (21) are given by

$$\begin{aligned} r_1 = \frac{\displaystyle \lambda + 4k_5}{\displaystyle \lambda -4k_5} \ \ \ \ , \ \ \ \ \ r_2 = 0 \end{aligned}$$
(31)

Introducing the control parameter \(\eta\) such that

$$\begin{aligned} \frac{\displaystyle k_5}{\displaystyle \lambda } = -\frac{\displaystyle 1}{\displaystyle 4}\left( \frac{\displaystyle 1-\eta }{\displaystyle \eta }\right) \end{aligned}$$
(32)

yield

$$\begin{aligned} \frac{\displaystyle \eta }{\lambda } \ E(\beta ) = \frac{\displaystyle (2 \eta - 1)\beta ^2 + \eta \beta ^4}{\displaystyle (1 + \beta ^2)^2} + \frac{1}{4}(1 - \eta ) \end{aligned}$$
(33)
$$\begin{aligned} r_1 = 2\eta -1 \ \ \ \ \ \ \ , \ \ \ \ \ \ \ r_2 = 0 \end{aligned}$$
(34)

From which, it is seen that the transitional region between the U(5) and O(6) limits ic characterized by a straight line. The antispinodal, critical and spinodal points are given by using Eqs. (28), (29), (30)

$$\begin{aligned} \begin{array}{ll} &{}r_{1a} = 0 \ \ \ \ \ , \ \ \ \ \ r_{2a} = 0 \ \ \ \ \ , \ \ \ \ \ \eta _a = 1/2 \\ &{}r_{1c} = 0 \ \ \ \ \ , \ \ \ \ \ r_{2c} = 0 \ \ \ \ \ , \ \ \ \ \ \eta _c = 1/2 \\ &{}r_{1s} = 0 \ \ \ \ \ , \ \ \ \ \ r_{2s} = 0 \ \ \ \ \ , \ \ \ \ \ \eta _s = 1/2 \end{array} \end{aligned}$$
(35)

This shows that the antipinodal, critical and spinodal points coincide, which characterize the second order phase transition U(5)-O(6). The equilibrium value of the deformation parameter \(\beta\) depends on \(\eta\) so that \(\beta _e = 0\) for \(\eta \le 1/2\) and \(\beta _e^2 = 2\eta -1\) for \(\eta \ge 1/2\). That is a spherical minimum for \(\eta < 1/2\) and a deformed one for \(\eta > 1/2\). The phase transition takes place at the critical point \(\eta = 1/2\). The corresponding minimum PES’s are

$$\begin{aligned} \begin{array}{ll} &{}\varepsilon _{min}(\eta ) = 0 \ \ \ \ \ \text{for} \ \ \ \ \ \eta \le 1/2 \ \ \ \\ &{}\varepsilon _{min}(\eta ) = -\frac{\displaystyle (1-2\eta )^2}{\displaystyle 4\eta (1-\eta )} \ \ \ \ \text{for} \ \ \ \ \eta \ge 1/2 \end{array} \end{aligned}$$
(36)

To illustrate the region around the shape phase transition, the PES’s is given in Fig. 1 for five different values of \(\eta\) \((\frac{\displaystyle 1}{\displaystyle 5}, \frac{\displaystyle 1}{\displaystyle 3}, \frac{\displaystyle 1}{\displaystyle 2}, \frac{\displaystyle 2}{\displaystyle 3}, 1)\). For \(\eta < 1/2\) \((\frac{\displaystyle 1}{\displaystyle 5}, \frac{\displaystyle 1}{\displaystyle 3})\), the equilibrium shape is spherical and for \(\eta > 1/2\) \((\frac{\displaystyle 2}{\displaystyle 3}, 1)\) it is deformed. There is no region of coexistence of spherical and deformed. The structure of nuclei at the critical points of the spherical U(5) to deformed unstable O(6) was described by the E(5) symmetry [16].

Fig. 1
figure 1

The evolution of PES’s as a function of deformation parameter \(\beta\) with \(\lambda =4\) and different values of the control parameter \(\eta (1/5, 1/3, 1/2, 2/3, 1)\). A second order phase transition from spherical to deformed shapes occur at \(\eta _c=1/2\)

Full size image

4 Energy Ratios and Electric Transition Rates

The best quantities that exhibit the shape phase transition along isotopic chain are the energy ratios:

$$\begin{aligned} R_{I/2} = E(I_1^+)/E(2_1^+) \end{aligned}$$
(37)

and the electric quadrupole transition rates

$$\begin{aligned} B_{ I+2 / 2} = \frac{\displaystyle B(E2; I+2\rightarrow I)}{\displaystyle B(E2; 2_1^+ \rightarrow 0_1^+)} \end{aligned}$$
(38)

The reduced electric quadrupole transition probability between initial states \(| \alpha _i I_i \rangle\) to final state \(| \alpha _f I_f \rangle\) are given by

$$\begin{aligned} B(E2, \alpha _i, I_i \rightarrow I_f) = \frac{\displaystyle | \langle \alpha _f I_f || \hat{T}(E2)|| \alpha _iI_i \rangle |^2}{\displaystyle 2I_i + 1} \end{aligned}$$
(39)

where the most general form of the electric transition operator in the IBM1 is written as

$$\begin{aligned} \hat{T}_\mu (E2) = e_1\left[ d^\dag \times \tilde{s} + s^\dag \times \tilde{d}\right] _\mu ^{(2)} + e_2\left[ d^\dag \times \tilde{d}\right] _\mu ^{(2)} \end{aligned}$$
(40)

where the coefficient \(e_1\) and \(e_2\) are parameters to fit the data. The energy ratios \(R_{I/2}\) and the electric quadrupole transition rates for the U(5) and O(6) dynamical symmetry limits are given by [1]

$$\begin{aligned} R_{I/2} =\left\{ \begin{array}{ll} \frac{\displaystyle I}{\displaystyle 2}, &{} \hbox {for U(5);} \\ \\ \frac{\displaystyle I}{\displaystyle 8}\left( \frac{\displaystyle I}{\displaystyle 2} + 3\right) , &{} \hbox {for O(6).} \end{array} \right. \end{aligned}$$
(41)
$$\begin{aligned} B_{I+2/2} = \left\{ \begin{array}{ll} \frac{\displaystyle 1}{\displaystyle 2}\left( I+2\right) \left( 1-\frac{\displaystyle I}{\displaystyle 2N}\right) ,&{} {\text{for}\; \text{U}(5);}\\ \\ \frac{\displaystyle 5}{\displaystyle 2}\frac{\displaystyle \left( I+2\right) }{\displaystyle \left( I+5\right) }\left( 1-\frac{\displaystyle I}{\displaystyle 2N}\right) \left( 1 + \frac{\displaystyle I}{\displaystyle 2\left( N+4\right) }\right) &{}\text{for O}(6). \end{array} \right. \end{aligned}$$
(42)

5 Numerical Calculations For Ru, Pd and Xe Isotopic Chains

The studied isotopic chains are \(^{94-110}\)Ru, \(^{100-112}\)Pd and \(^{122-132}\)Xe. For each nucleus the control parameter \(\eta = \lambda /(\lambda -4k_5)\) has been adjusted by fitting the experimental energy levels \(\left( 2_1^+, 4_1^+, 6_1^+, 8_1^+, 10_1^+, 0_2^+, 2_2^+, 3_1^+, 4_2^+\right)\) and the reduced electric quadrupole transition probabilities \(\left( 2_1^+\rightarrow 0_1^+, 4_1^+\rightarrow 2_1^+, 2_2^+\rightarrow 0_1^+, 2_2^+\rightarrow 2_1^+\right)\) to the calculated IBM, by using a simulated search program to minimize the \(\chi ^2\)-function defined in the standard way as

$$\begin{aligned} \chi _E^2 = \frac{ 1}{ N_E}\sum _{i=1}^{N_E} [ E^{exp.}(i) - E^{IBM}(E2) ]^2 \end{aligned}$$
(43)
$$\begin{aligned} \chi _{B(E2)}^2 = \frac{\displaystyle 1}{\displaystyle N_{B(E2)}} \sum _{i=1}^{N_{B(E2)}} \left[ B(E2)^{exp.} - B(E2)^{IBM} \right] ^2 \end{aligned}$$
(44)

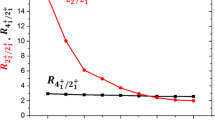
where N is the number of experimental points entering into the fitting procedure and only the low-spin states before the band crossing are included. The experimental data are taken from national nuclear data center (ENSDF database) [24]. The values of the adopted optimized control parameter \(\eta\) for the studied isotopic chains are listed in Table 1. The agreement between the experimental and calculated ones is very good. Since the ground state energy ratio \(R_{4/2} = E(4_1^+)/E(2_1^+)\) is best signature quantity to reflects the shape phase transitions, the \(R_{4/2}\) have been calculated for the studied isotopic chains and illustrated in Fig. 2, compared to the predictions of U(5) \((R_{4/2 = 2})\), O(6) \((R_{4/2 = 2.5})\) and the critical point symmetry E(5)\((R{4/2} = 2.2)\). It is seen from Fig. 2 that the lighter isotopes of Ru and Pd comes to vibrator U(5) limit, while the heavier isotopes tends to the \(\gamma\)-unstable limit O(6), this condition is reversed for the Xe isotopes. From Fig. 2 we observe also that the ratio \(R_{4/2}\) for the nuclei \(^{100}\)Ru, \(^{102}\)Pd and \(^{130}\)Xe lie near the E(5) critical point symmetry.

Fig. 2
figure 2

Evolution of the energy ratios \(R_{4/2}=E(4_1^+)/E(2_1^+)\) changing as a function of mass number for \(^{94-110}\)Ru, \(^{100-112}\)Pd and \(^{122-132}\)Xe isotopic chains compared to the dynamical symmetry limits U(5) and O(6) and the critical point symmetry E(5)

Full size image
Table 1 Values of the control parameter \(\eta\) for each Ru, Pd and Xe isotopic chains (A, N, \(N_B\)) denotes the mass number, the number of neutrons and the total boson number respectively
Full size table

The energy ratio for higher levels \(R_{I/2} = E(I_1^+)/E(2_1^+)\) for the ground state levels \(I_i^+ = 4_1^+\) to \(10_1^+\) are shown in Fig. 3 for the critical \(^{100}\)Ru, \(^{102}\)Pd and \(^{130}\)Xe nuclei, compared to the U(5) and O(6) dynamical symmetry limits. After the introduction of E(5) critical point symmetry [16], we can conclude that the three nuclei \(^{100}\)Ru, \(^{102}\)Pd and \(^{130}\)Xe are good candidate for E(5) symmetry in agreement with Refs [25, 26] on measurements of E1 and \(M_1\) strengths. The characteristic signature of B(E2, \(4_1^+ \rightarrow 2_1^+\)) values normalized to \(B(E2, 2_1^+\rightarrow 0_1^+)\) are listed in Table 2 for \(^{100}\)Ru, \(^{102}\)Pd and \(^{130}\)Xe nuclei and the prediction of U(5) and O(6) dynamical symmetry limits for boson number \(N = 5, 6\). The PES are calculated for the three isotopic chains \(^{94-110}\)Ru, \(^{100-112}\)Pd and \(^{122-132}\)Xe and illustrated in Figs. 4, 5, and 6. We see that the lighter isotopes of Ru and Pd exhibit a vibrational structure, while the heavier one present a \(\gamma\)-unstable behavior with critical points located at \(^{100}\)Ru and \(^{102}\)Pd. For the Xe isotopic chain the structure varies from \(\gamma\)-soft rotor O(6) for \(^{122}\)Xe to harmonic vibrator U(5) for \(^{132}\)Xe. An analysis with catastrophe theory shows that the values of the essential parameters \((r_1, r_2)\) for Ru and Pd isotopic chains evolves from spherical U(5) to deformed \(\gamma\)-unstable O(6) shapes while for Xe isotopic chain the reverse occur. The \((r_1, r_2)\) diagram characterized by a straight line. The pure two dynamical symmetries U(5) and O(6) are (1,0) and (-1,0) respectively. The shape diagram is illustrated in Fig. 7.

Fig. 3
figure 3

The Evolution of the yrast energy ratios \(R_{I/2} = E(I_1^+)/E(2_1^+)\) as a function of nuclear spin I for the critical nuclei \(^{100}\)Ru, \(^{102}\)Pd and \(^{130}\)Xe and comparison with the prediction of U(5) and O(6) dynamical symmetry limits

Full size image
Fig. 4
figure 4

PES’s calculated from IBM as a function of deformation parameter \(\beta\) for the shape phase transition from spherical U(5) to \(\gamma\)-unstable O(6) for \(^{94-110}\)Ru isotopic chain

Full size image
Fig. 5
figure 5

The same as in Fig. 4 but for \(^{100-112}\)Pd isotopic chain

Full size image
Fig. 6
figure 6

The same as in Fig. 4 but for \(^{122-132}\)Xe isotopic chain

Full size image
Fig. 7
figure 7

Shape phase transition for Ru, Pd, Xe isotopic chains in terms of the essential parameters \(r_1, r_2\). For U(5): \(r_1=1, r_2=0\) and for O(6): \(r_1=-1, r_2=0\)

Full size image
Table 2 Comparison of the calculated B(E2) ratios\(R_{4/2}= \frac{B(E2, 4_1^+ \rightarrow 2_1^+)}{B(E2, 2_1^+ \rightarrow 0_1^+)}\), of the ground state bands for the critical nuclei\(^{100}\)Ru (N=6),\(^{102}\)Pu (N=5) and\(^{130}\)Xe (N=5) and the prediction of U(5) and O(6) dynamical symmetry limits
Full size table

6 Real Discussion of The Results

In spite of the consistent Q formalism (CQF) provides a simple and convenient few parameters space for IBM that span the entire Casten triangle, yet we used in the present article the U(5)-O(6) translation Hamiltonian composed of the linear Casimir operator of the limit U(5) and quadratic Casimir operators of the subgroups O(5), O(3) and the limit O(6) with set of four Hamiltonian parameters \(\epsilon , k_2, k_3, k_5\), we reduced this four parameters to only two control parameters \(\lambda\) and \(k_5\).

The PES’s for our isotopic chains are studied with the U(5)-O(6) shape transition of IBM Eq. (1) and the intrinsic state Eq. (14), and formulated in terms of \(\lambda\) and \(k_5\) Eq. (21). To analyze the PES’s and obtain all equilibrium configurations, i.e. to find all critical points, it is preferable to use the successful catastrophe germ of he IBM because this theory translate every set of Hamiltonian parameters to the plane formed by the essential parameters \(r_1, r_2\) which are independent on the combinations of the parameters of the IBM Hamiltonian. In our U(5)-O(6) transition for Ru, Pd and Xe isotopic chains, the essential parameter \(r_2\) vanish, that is the locus of the antispinodal, critical and spinodal points coincide at \(\eta =1/2\). The control parameter \(\eta _a\) of the antispinodal critical point is evaluated by putting the coefficient of \(\beta ^2\) equal zero: \(\lambda +4k_5=0\) and since \((1-\eta )/\eta =-4k_5/\lambda\) which yield \(\eta _a=1/2\).

We presented an investigation of how the N independent control parameter \(\eta\) can affect the position of the critical point in Ru, Pd and Xe isotopes. The results exhibited that the low-lying states are assigned to one of three phases: a U(5) phase, an O(6) phase or a transition phase and the analysis suggested that no triaxial shapes or low-lying shape coexistence configurations appear. These can only be stabilized with the inclusion specific three-body interaction or introduce the \(\gamma\)-parameter. The coexistence of two different nuclear shapes at comparable energies can occur in neutron rich nuclei around \(A\sim 100\) mass region. For instance, we don’t take into account the triaxial and coexistence degrees of freedom when discussing the U(5)-O(6) transition. The experimental data for the ground bands has been fitted by the IBM Hamiltonian for each nucleus by using a simulate search iteration program. We showed in Fig. 2 the calculated results for the energy ratio \(R_{4/2}\). Table 3 include the calculated and experimental energy ratios \(R_{I_1/2_1}\) for only the three critical nuclei \(^{100}\)Ru, \(^{102}\)Pd and \(^{130}\)Xe as an example because we have 22 nuclei. Table 4 contains the original IBM parameters \(\lambda\) and \(k_5\). The parameter \(\eta =\frac{1}{1-4k_5/\lambda }\) are listed in Table 1.

Table 3 Calculated and experimental energy ratios \(R_{I_1/2_1}= E(I^+_1)/E(2_1^+)\) characterize the low-lying spectrum in the critical nuclei \(^{100}\)Ru, \(^{102}\)Pd and \(^{130}\)Xe
Full size table
Table 4 Values of the original optimized best parameters of the Hamiltonian derived from fitting produce for the Ru, Pd and Xe isotopic chains
Full size table

Our calculations include only the positive parity level because the negative parity states in even-even nuclei are formed by including one f-boson or allowing one boson to break into two fermions which occupy a high spin single particle orbit with opposite parity. That is to make negative parity states in even-even nuclei, it is necessary to include f bosons to the sdIBM.

It was suggested that critical points of phase transition U(5)-O(6) can be associated with critical point symmetry E(5) which reproduce the spectra at the critical points. The nuclei \(^{100}\)Ru, \(^{102}\)Pd and \(^{130}\)Xe are near the critical point of the U(5)-O(6) phase transition and can be used as a basis for the prediction of E(5) to compare with experiment.

From the excitation energy systematics for Ru, Pd, and Xe isotopes one observe that, beside the systematic decrease in excitation energy with increase neutron number, the ratio \(E_{4_1^+}/E_{2_1^+}\) reflects a transition from vibrator like nuclei (\(R_{4/2}=2\)) such as in \(^{96}\)Ru (\(R_{4/2}=1.8\)), \(^{102}\)Pd (\(R_{4/2}=2.1\)) to more deformed ones, such as \(^{110}\)Ru (\(R_{4/2}=2.7\)), \(^{112}\)Pd (\(R_{4/2}=2.55\)). Nevertheless this ratio stays clearly below rotational value 3.3 also for the heaviest known isotopes. The \(R_{4/2}\) values for critical nuclei \(^{100}\)Ru, \(^{102}\)Pd are around 2.25 which is near the \(R_{4/2}\) value for the critical point symmetry E(5) (\(R_{4/2}=2.2\)). For the Xe isotopic chain the shape transition is from O(6) to U(5) with increasing the neutron number and \(^{130}\)Xe is the critical nucleus. That is the E(5) predictions cannot be exactly reproduced by all nuclei in each isotopic chain and that the best agreement is close to the calculations for \(^{100}\)Ru, \(^{102}\)Pd and \(^{130}\)Xe nuclei with boson numbers \(N=6, 5, 5\) respectively. These place the yrast \(R_{4/2}\) ratio intermediate between the U(5) value of 2 and the O(6) value of 2.5. Also the yrast B(E2) strength ratio \(B(E2, 4^+_1 \rightarrow 2_1^+ )/B(E2, 2^+_1 \rightarrow 0_1^+ )\) vary continuously along the U(5)-O(6) transition and suggested that \(^{100}\)Ru, \(^{102}\)Pd and \(^{130}\)Xe are well described by E(5) predictions near the value 1.68.

The two essential parameters \(r_1, r_2\) defined according to catastrophe theory combined with the coherent state are used to generater the IBM PES’s to identify the critical phase transition points. The critical nucleus corresponding to the locus (two degenerate minima) in the essential parameter space \(r_1, r_2\). The \(r_1=0\) line corresponds to \((\frac{d^2E}{d\beta ^2})_{\beta =0}=0\), that is to the appearance of the spherical minimum (antispinodal point). Following this approach the nuclei \(^{100}\)Ru, \(^{102}\)Pd and \(^{130}\)Xe have been found to be close to critical. At critical points yield \(r_{1c}=\frac{1}{2}(-1+\sqrt{1+\frac{1}{2}r_2^2})\) so that for U(5) limit \(r_1=1, R_2=0, \beta _2=0\) and for O(6) limit \(r_1=-1, r_2=0, \beta _e=\pm 1\). There is no region of coexistence of spherical and deformed minima.

7 Conclusion

The transition between the spherical vibrational and the deformed \(\gamma\)-unstable is studied using the coherent state formalism of the IBM Hamiltonian in Casimir form after transforming to Q-consistent form. The model is applied to Ru, Pd, and Xe isotopic chains. For each nucleus the IBM control parameter has been fitted to reproduce some selected ground state energies and B(E2) values by using a simulated search programm. The calculated results are in good agreement with the experimental data. The PES’s are calculated using the coherent state formalism and the critical points are extracted and analyzed in framework of catastrophe theory. The \(^{100}\)Ru, \(^{102}\)Pd and \(^{130}\)Xe nuclei have been seen to be a good candidates to the E(5) critical point symmetry.