The effect of multi-directional nanocomposite materials on the vibrational response of thick shell panels with finite length and rested on two-parameter elastic foundations

Abstract

The main purpose of this paper is to investigate the effect of bidirectional continuously graded nanocomposite materials on free vibration of thick shell panels rested on elastic foundations. The elastic foundation is considered as a Pasternak model after adding a shear layer to the Winkler model. The panels reinforced by randomly oriented straight single-walled carbon nanotubes are considered. The volume fractions of SWCNTs are assumed to be graded not only in the radial direction, but also in axial direction of the curved panel. This study presents a 2-D six-parameter power-law distribution for CNTs volume fraction of 2-D continuously graded nanocomposite that gives designers a powerful tool for flexible designing of structures under multi-functional requirements. The benefit of using generalized power-law distribution is to illustrate and present useful results arising from symmetric, asymmetric and classic profiles. The material properties are determined in terms of local volume fractions and material properties by Mori–Tanaka scheme. The 2-D differential quadrature method as an efficient numerical tool is used to discretize governing equations and to implement boundary conditions. The fast rate of convergence of the method is shown and results are compared against existing results in literature. Some new results for natural frequencies of the shell are prepared, which include the effects of elastic coefficients of foundation, boundary conditions, material and geometrical parameters. The interesting results indicate that a graded nanocomposite volume fraction in two directions has a higher capability to reduce the natural frequency than conventional 1-D functionally graded nanocomposite materials.

Introduction

Layered composite materials, due to their thermal and mechanical merits compared to single-composed materials, have been widely used for a variety of engineering applications. However, owing to the sharp discontinuity in the material properties at interfaces between two different layers, there may exist stress concentrations causing severe material failure (Weissenbek et al. 1997). Functionally graded materials are heterogeneous composite materials, in which the material properties vary continuously from one interface to the other. The advantage of using these materials is that they can survive in high thermal gradient environment, while maintaining their structural integrity. Typically, an FGM is made of a ceramic and a metal for the purpose of thermal protection against large temperature gradients. The ceramic material provides a high-temperature resistance due to its low thermal conductivity, while the ductile metal constituent prevents fracture due to its greater toughness. FGMs are now developed for general use as structural elements in extremely high temperature environments. A listing of different applications can be found in Forum (1991). Most of the studies on FGMs have been restricted to thermal stress analysis, thermal buckling, fracture mechanics and optimization (Cho and Tinsley oden 2000; Chunyu et al. 2001; Lanhe 2004). Some researches (Loy et al. 1999; Pradhan et al. 2000; Han et al. 2001; Ng et al. 2001) are based on the classical shell theory, i.e., neglecting the effect of transverse shear deformation. The application of this theory to moderately thick or thick shell structures can lead to serious errors. Using the first and higher order shear deformation theories, some modifications are done to include the effects of transverse shear deformation. In this study, the problem formulations were based on the higher order shear deformation shell theories. Yang and Shen (2003) proposed a semi-analytical approach based on Reddy’s higher order shear deformation shell theory, for free vibration and dynamic instability of FGM cylindrical panels under combined static and periodic axial forces and thermal loads. Free vibration and stability of functionally graded shallow shells according to a 2-D higher order deformation theory were investigated by Matsunaga (2008). Free vibration analysis of functionally graded curved panels was carried out using a higher order formulation by Pradyumna and Bandyopadhyay (2008). They used a C0 finite element formulation to carry out the analysis. Using a 2-D higher order shear deformation theory, vibration and buckling analyses of simply supported circular cylindrical shells made of functionally graded materials (FGMs) were studied by Matsunaga (2009). He used the method of power series expansion of continuous displacement components to solve the problem. In all of the above studies the variation of the radius through the thickness was not considered and the problem formulations were based on the constant mean radius of curvature.

Two-dimensional theories reduce the dimensions of problems from three to two by introducing some assumptions in mathematical modeling leading to simpler expressions and derivation of solutions. However, these simplifications inherently bring errors and therefore may lead to unreliable results for relatively thick panels. As a result, three-dimensional analysis of panels not only provides realistic results, but also allows further physical insights, which cannot otherwise be predicted by the two-dimensional analysis. There are some studies on free vibration analysis of isotropic and composite panels and shells based on the three-dimensional elasticity formulation (Chern and Chao 2000).

Structures resting on elastic foundations with different shapes, sizes, and thickness variations and boundary conditions have been the subject of investigations, and those play an important role in aerospace, marine, civil, mechanical, electronic and nuclear engineering problems. For example, plates and shells are used in various kinds of industrial applications such as the analysis of reinforced concrete pavement of roads, airport runways and foundations of buildings. The Pasternak model (also referred to as the two-parameter model) was widely used to describe the mechanical behavior of the foundation, in which the well-known Winkler model is a special case.

The most serious deficiency of the Winkler foundation model is to have no interaction between the springs. In other words, the springs in this model are assumed to be independent and unconnected. The Winkler foundation model is fairly improved by adopting the Pasternak foundation model, a two-parameter model, in which the shear stiffness of the foundation is considered. The evident importance in practical applications, investigations on the dynamic characteristics of FGM plates and panels on elastic foundations are still limited in number. Yas and Tahouneh (2012) investigated the free vibration analysis of thick FG annular plates on elastic foundations via differential quadrature method based on the three-dimensional elasticity theory and Tahouneh and Yas (2012) investigated the free vibration analysis of thick FG annular sector plates on Pasternak elastic foundations using DQM. Tahouneh et al. (2013) studied free vibration characteristics of annular continuous grading fiber reinforced (CGFR) plates resting on elastic foundations using DQM. More recently, (Tahouneh and Naei 2014) achieved the natural frequencies of thick multi-directional functionally graded rectangular plates resting on a two-parameter elastic foundation via 2-D differential quadrature method, The proposed rectangular plates had two opposite edges simply supported, while all possible combinations of free, simply supported and clamped boundary conditions were applied to the other two edges. Farid et al. (2010) presented free vibration analysis of initially stressed thick simply supported functionally graded curved panel resting on two-parameter elastic foundation (Pasternak model), subjected in thermal environment was studied using the three-dimensional elasticity formulation. Tahouneh (2014) investigated free vibration analysis of continuous grading fiber reinforced (CGFR) FG annular sector plates on two-parameter elastic foundations under various boundary conditions, based on the three-dimensional theory of elasticity. The plates with simply supported radial edges and arbitrary boundary conditions on their circular edges were considered.

Recently, nanocomposites have significant importance for engineering applications that require high levels of structural performance and multi-functionality. Carbon nanotubes (CNTs) have demonstrated exceptional mechanical, thermal and electrical properties. These materials are considered as one of the most promising reinforcement materials for high performance structural and multi-functional composites with vast application potentials (Esawi and Farag 2007; Thostenson et al. 2001). Most studies on carbon nanotube-reinforced composites (CNTRCs) have focused on their material properties (Esawi and Farag 2007; Thostenson et al. 2001; Dai 2002; Kang et al. 2006; Lau et al. 2006). Gojny et al. (2005) focused on the evaluation of the different types of the CNTs applied, their influence on the mechanical properties of epoxy-based nanocomposites and the relevance of surface fictionalization. Fidelus et al. (2005) investigated thermo-mechanical properties of epoxy-based nanocomposites based on low weight fraction of randomly oriented single-and multi-walled CNTs. Han and Elliott (2007) determined the elastic modulus of composite structures under CNTs reinforcement by molecular dynamic simulation and investigated the effect of volume fraction of SWNTs on mechanical properties of nanocomposites. Manchado et al. (2005) blended small amounts of arc-SWNT into isotactic polypropylene and observed the modulus increase from 0.85 to 1.19 GPa at 0.75 wt%. In addition, the strength increased from 31 to 36 MPa by 0.5 wt%. Both properties were observed to fall off at higher loading levels. These investigations and (Mokashi et al. 2007; Zhu et al. 2007) have shown that the addition of small amount of carbon nanotube in the matrix can considerably improve the mechanical, electrical and thermal properties of polymeric composites. This behavior, combined with their low density makes them suitable for transport industries, especially for aeronautic and aerospace applications where the reduction of weight is crucial in order to reduce the fuel consumption.

The properties of the CNT-reinforced composites (CNTRCs) depend on a variety of parameters including CNT geometry and the inter-phase between the matrix and CNT. Interfacial bonding in the inter-phase region between embedded CNT and its surrounding polymer is a crucial issue for the load transferring and reinforcement phenomena Shokrieh and Rafiee (2010). The traditional approach to fabricating nanocomposites implies that the nanotube is distributed either uniformly or randomly such that the resulting mechanical, thermal, or physical properties do not vary spatially at the macroscopic level. Experimental and numerical studies concerning CNTRCs have shown that distributing CNTs uniformly as the reinforcements in the matrix can achieve moderate improvement of the mechanical properties only (Seidel and Lagoudas 2006). This is mainly due to the weak interface between the CNTs and the matrix where a significant material property mismatch exists. The concept of FGM can be utilized for the management of a material’s microstructure, so that the vibrational behavior of a plate/shell structure reinforced by CNTs can be improved. According to a comprehensive survey of literature, the authors found that there are few research studies on the mechanical behavior of functionally graded CNTRC structures. For the first time, Shen (2009) suggested that the nonlinear bending behavior can be considerably improved through the use of a functionally graded distribution of CNTs in the matrix. He introduced the CNT efficiency parameter to account load transfer between the nanotube and polymeric phases.

Due to intrinsic complexity of the formulations based on the three-dimensional elasticity, powerful numerical methods are needed to solve the governing equations. The differential quadrature method (DQM) is a relatively new numerical technique in structural analysis. A review of the early developments in the differential quadrature method can be found in papers by (Bert and Malik 1997).

This paper is motivated by the lack of studies in the technical literature concerning to the three-dimensional vibration analysis of thick bidirectional nanocomposite curved panels resting on a two-parameter elastic foundation reinforced by randomly oriented straight single-walled carbon nanotubes CNTs. To the authors’ best knowledge, research on the vibration of thick curved panels reinforced by randomly oriented straight single-walled carbon nanotubes which are graded in both direction including axial and radial directions has not been seen until now. The volume fractions of randomly straight single-walled carbon nanotubes SWCNTs are assumed to be graded in the thickness and also axial directions of the curved panels. The direct application of CNT properties in micromechanics models for predicting material properties of the nanotube/polymer composite is inappropriate without taking into account the effects associated with the significant size difference between a nanotube and a typical carbon fiber (Odegard et al. 2003). In other words, continuum micromechanics equations cannot capture the scale difference between the nano and micro-levels. In order to overcome this limitation, a virtual equivalent fiber consisting of nanotube and its inter-phase which is perfectly bonded to surrounding resin is applied.

This study presents a novel 2-D six-parameter power-law distribution for CNTs volume fraction of 2-D functionally graded nanocomposite materials that gives designers a powerful tool for flexible designing of structures under multi-functional requirements. Various material profiles along the radial and axial directions are illustrated by using the 2-D power-law distribution. The effective material properties at a point are determined in terms of the local volume fractions and the material properties by the Mori–Tanaka scheme. A sensitivity analysis is performed, and the natural frequencies are calculated for different sets of boundary conditions and different combinations of the geometric, material, and foundation parameters. Therefore, very complex combinations of the material properties, boundary conditions, and foundation stiffness are considered in the present semi-analytical solution approach.

Problem description

In this section, a virtual equivalent fiber consisting of a nanotube and its inter-phase which is perfectly bonded to surrounding resin is introduced to obtain the mechanical properties of the carbon nanotube/polymer composite by using the results of multi-scale FEM Shokrieh and Rafiee (2010). The equivalent fiber for SWCNT with chiral index of (10, 10) is a solid cylinder with diameter of 1.424 nm. The inverse of the rule of mixture is used to calculate material properties of equivalent fiber (Tsai et al. 2003):

$$\begin{aligned} &E_{\text{LEF}} = \frac{{E_{\text{LC}} }}{{V_{\text{EF}} }} - \frac{{E_{\text{M}} V_{\text{M}} }}{{V_{\text{EF}} }}, \hfill \\ &\frac{1}{{E_{\text{TEF}} }} = \frac{1}{{E_{\text{TC}} V_{\text{EF}} }} - \frac{{V_{M} }}{{E_{M} V_{\text{EF}} }}, \hfill \\ &\frac{1}{{G_{\text{EF}} }} = \frac{1}{{G_{C} V_{\text{EF}} }} - \frac{{V_{M} }}{{G_{M} V_{\text{EF}} }}, \hfill \\ &\upsilon_{\text{EF}} = \frac{{\upsilon_{C} }}{{V_{\text{EF}} }} - \frac{{\upsilon_{M} V_{M} }}{{V_{\text{EF}} }}, \hfill \\ \end{aligned}$$

(1)

where $E_{\text{LEF}}$, $E_{\text{TEF}}$, $G_{\text{EF}}$, $\upsilon_{\text{EF}}$, $E_{\text{LC}}$, $E_{\text{TC}}$, $G_{C}$, $\upsilon_{C}$, $E_{M}$, $G_{M}$, $\upsilon_{M}$, $V_{\text{EF}}$ and $V_{M}$ are longitudinal modulus of equivalent fiber, transverse modulus of equivalent fiber, shear modulus of equivalent fiber, Poisson’s ratio of equivalent fiber, longitudinal modulus of composites, transverse modulus of composites, shear modulus of composites, Poisson’s ratio of composites, modulus of matrix, shear modulus of matrix, Poisson’s ratio of matrix, volume fraction of the equivalent fiber and volume fraction of the matrix, respectively. $E_{\text{LC}}$, $G_{C}$, and $E_{\text{TC}}$ are obtained from multi-scale FEM or molecular dynamics (MD) simulations. It should be mentioned that the volume fraction of the equivalent fiber is assumed to be 7.5 % (Shokrieh and Rafiee 2010) and Poly {(mphenylenevinylene)-co-[(2,5-dioctoxy-p-phenyle) vinylene]}, referred to as (PmPV), is selected as a matrix material:

$$E^{m} = 2.1\,{\text{Gpa}},\;\rho^{m} = 1150\,{\text{kg/m}}^{ 3} ,\;\upsilon^{m} = 0.34 .$$

The material properties adopted for equivalent fiber are (Shokrieh and Rafiee 2010):

$$\begin{aligned} &E_{1}^{cn} = 649.12\,{\text{Gpa}},\; \hfill \\ &E_{1}^{cn} = 11.27\,{\text{Gpa}},\; \hfill \\ &\upsilon = 0.284,\; \hfill \\ &G^{cn} = 5.13\,{\text{Gpa}},\; \hfill \\ &\rho^{cn} = 1400\,{\text{kg/m}}^{ 3} \hfill \\ \end{aligned}$$

Composites reinforced with aligned, straight CNTs

Following the standard MT derivation, one can develop the expression for effective composite stiffness C. This is obtained by using an equivalent fiber having the effective CNT properties in the MT approach which is given as (Shi et al. 2004):

$$C = C_{m} + f_{r} \left\langle {\left({C_{r} - C_{m} } \right)A_{r} } \right\rangle \left({f_{m} I + f_{r} \left\langle {A_{r} } \right\rangle } \right)^{ - 1} ,$$

(2)

where $f_{r}$ and $f_{m}$ are the fiber and matrix volume fractions, respectively. $C_{m}$ is the stiffness tensor of the matrix material; $C_{r}$ is the stiffness tensor of the equivalent fiber; I is the forth order identity tensor and $A_{r}$ is the dilute strain-concentration tensor of the rth phase for the fiber which is given as:

$$A_{r} = \left[ {I + S\left({C_{m} } \right)^{ - 1} \left({C_{r} - C_{m} } \right)} \right]^{ - 1} ,$$

(3)

where S is Eshelby’s tensor, as given by (Eshelby 1957) and (Mura 1982). The terms enclosed by angle brackets in Eq. (2) represent the average value of the term over all orientations defined by transformation from the local fiber coordinates (O-x′ ₁ x′ ₂ x′ ₃) to the global coordinates (O-x ₁ x ₂ x ₃) (Fig. 1). Assume axis x ₂ as the direction along the aligned nanotube. The elastic properties of the nanocomposite are determined from the average strain obtained in the representative volume element. The matrix is assumed to be elastic and isotropic, with Young’s modulus $E_{m}$ and Poisson’s ratio $\upsilon_{m}$. Each straight CNT is modeled as a long fiber with transversely isotropic elastic properties and has a stiffness matrix given by Eq. (1). Therefore, the composite is also transversely isotropic, with five independent elastic constants. The substitution of nonvanishing components of the Eshelby tensor S for a straight, long fiber along the x ₂-direction (Shi et al. 2004) in Eq. (3) gives the dilute mechanical strain concentration tensor. Then, the substitution of Eq. (3) into Eq. (2) gives the tensor of effective elastic moduli of the composite reinforced by aligned, straight CNTs. The axial and transverse Young’s modulus of the composite can be calculated from the Hill’s elastic modulus as (Shi et al. 2004):

$$\begin{aligned} E_{1} = n - \frac{{l^{2} }}{k}, \hfill \quad E_{2} = \frac{{4m\left({kn - l^{2} } \right)}}{{kn - l^{2} + mn}} \hfill \\ \end{aligned} ,$$

(4)

where k, l, m and n are its plane-strain bulk modulus normal to the fiber direction, cross-modulus, transverse shear modulus, axial modulus and axial shear modulus, respectively, and can be found in the Appendix. As mentioned before, the CNTs are transversely isotropic and have a stiffness matrix given below:

$$C_{r} = \left[ {\begin{array}{*{20}c} {\frac{1}{{E_{L} }}} & {\frac{{ - \upsilon_{TL} }}{{E_{T} }}} & {\frac{{ - \upsilon_{ZL} }}{{E_{Z} }}} & 0 & 0 & 0 \\ {\frac{{ - \upsilon_{LT} }}{{E_{L} }}} & {\frac{1}{{E_{T} }}} & {\frac{{ - \upsilon_{ZT} }}{{E_{Z} }}} & 0 & 0 & 0 \\ {\frac{{ - \upsilon_{LZ} }}{{E_{L} }}} & {\frac{{ - \upsilon_{TZ} }}{{E_{T} }}} & {\frac{1}{{E_{Z} }}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {\frac{1}{{G_{TZ} }}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{1}{{G_{ZL} }}} & 0 \\ 0 & 0 & 0 & 0 & 0 & {\frac{1}{{G_{LT} }}} \\ \end{array} } \right]$$

(5)

where $E_{L} ,\;E_{T} ,\;E_{Z} ,\;G_{TZ} ,\;G_{ZL} ,\;G_{LT} ,\;\upsilon_{LT} ,\;\upsilon_{LZ} ,\;\upsilon_{TZ}$ are material properties of the equivalent fiber which can be determined from the inverse of the rule of mixture.

Fig. 1

Representative volume element (RVE) with randomly oriented, straight CNT

Composites reinforced with randomly oriented, straight CNTs

The effective properties of composites with randomly oriented non-clustered CNTs, such as in Fig. 1, are studied in this section. The resulting effective properties for the randomly oriented CNT composite are isotropic, despite the CNTs having transversely isotropic effective properties. The orientation of a straight CNT is characterized by two Euler angles α and β, as shown in Fig. 1. When CNTs are completely randomly oriented in the matrix, the composite is then isotropic, and its bulk modulus k and shear modulus G are derived as:

$$k = k_{m} + \frac{{f_{r} \left({\delta_{r} - 3K_{m} \alpha_{r} } \right)}}{{3\left({f_{m} + f_{r} \alpha_{r} } \right)}},G = G_{m} + \frac{{f_{r} \left({\eta_{r} - 2G_{m} \beta_{r} } \right)}}{{2\left({f_{m} + f_{r} \beta_{r} } \right)}} ,$$

(6)

where $\alpha_{r} ,\beta_{r} ,\delta_{r}$ and $\eta_{r}$ can be found in the Appendix. The effective Young’s modulus $E$ and Poisson’s ratio $\upsilon$ of the composite is given by:

$$E = \frac{9KG}{3K\, + G},\quad \upsilon = \frac{3K - 2G}{6K + 2G}$$

(7)

Functionally graded carbon nanotube-reinforced

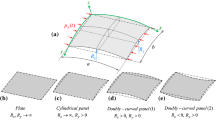
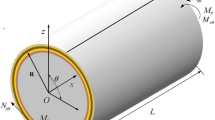
Consider a bidirectional nanocomposite curved panel rested on two-parameter elastic foundations as shown in Fig. 2. A cylindrical coordinate system (r, θ, z) is used to label the material point of the panel. The inner surface is continuously in contact with an elastic medium that acts as an elastic foundation represented by the Winkler/Pasternak model with K _w and K _g that are Winkler and shear coefficients of Pasternak foundation, respectively.

Fig. 2

The sketch of an elastically supported thick bidirectional nanocomposite cylindrical panel resting on a two-parameter elastic foundation and setup of the coordinate system

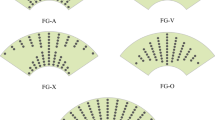
One of the well-known power-law distributions which is widely considered by the researchers is three- or four-parameter power-law distribution. The benefit of using such power-law distributions is to illustrate and present useful results arising from symmetric and asymmetric profiles. Consider V _c (volume fraction of the CNTs) in form of f(z) × g(r), f(z) and g(r) are both the three-parameter power-law distribution. They can be used to illustrate symmetric, asymmetric and classical profiles along the axial and radial directions of the curved panels, respectively. So by considering V _c as f(z) × g(r), one can present a 2-D six-parameter power-law distribution which is useful to illustrate different types of volume fraction profiles, including classical–classical, symmetric–symmetric and classical–symmetric in both directions.

In order to investigate 3-D dynamic response of thick bidirectional nanocomposite curved panels resting on a two-parameter elastic foundation, it is assumed that the volume fraction of the CNTs follows a 2-D six-parameter power-law distribution:

$$V_{c} = \left({(V_{b} - V_{a} )\left({\left({\frac{1}{2} - \frac{r - R}{h}} \right) + \alpha_{r} \left({\frac{1}{2} + \frac{r - R}{h}} \right)^{{\beta_{r} }} } \right)^{{\gamma_{r} }} + V_{a} } \right)\;\left({1 - \left({\frac{z}{{L_{z} }}} \right) + \alpha_{z} \left({\frac{z}{{L_{z} }}} \right)^{{\beta_{z} }} } \right)^{{\gamma_{{_{z} }} }} ,$$

(8)

where the radial volume fraction index $\gamma_{r}$, and the parameters $\alpha_{r}$, $\beta_{r}$ and the axial volume fraction index $\gamma_{z}$, and the parameters $\alpha_{z}$, $\beta_{z}$ govern the material variation profile through the radial and axial directions, respectively. The volume fractions V _a and V _b , which have values that range from 0 to 1, denote the maximum and minimum volume fraction of CNTs. With assumption V _b  = 1 and V _a  = 0.3, some material profiles in the radial [η _r  = (r − R)/h] and axial (η _z  = z/L _z ) directions are illustrated in Figs. 3, 4 and 5. As can be seen from Fig. 3, the classical volume fraction profiles in the radial and axial directions are presented as special case of the 2-D power-law distribution by setting $\gamma_{r} = \gamma_{z} = 4,$ and $\alpha_{r} = \alpha_{z} = 0$. In Fig. 3, The CNTs volume fraction decreases in the axial direction from 1 at η _z  = −0.5 to 0 at η _z  = 0.5. With another choice of the parameters $\alpha_{z}$, $\beta_{z}$, $\alpha_{r}$ and $\beta_{r}$, it is possible to obtain volume fraction profiles along the radial and axial directions of the panel as shown in Fig. 4. This figure shows a classical profile versus η _r and a symmetric profile versus η _z . As observed, volume fraction on the lower edge (η _z  = −0.5) is the same as that on the upper edge (η _z  = 0.5). Figure 5 illustrates symmetric profiles through the radial and axial directions obtained by setting $\beta_{r} = \beta_{z} = 2,$ and $\alpha_{r} = \alpha_{z} = 1$. In the following, we have compared several different volume fraction profiles of conventional 1-D and 2-D continuously graded nanocomposite with appropriate choice of the radial and axial parameters of the 2-D six-parameter power-law distribution, as shown in Table 1. It should be noted that the notation classical–symmetric indicates that the 2-D nanocomposite curved panel has classical and symmetric volume fraction profiles in the radial and axial directions, respectively.

Fig. 3

Variations of the classical volume fraction profile in the radial and axial directions $(\gamma_{r} = \gamma_{z} = 4,\alpha_{r} = \alpha_{z} = 0)$

Fig. 4

Variations of the volume fraction profile along the radial and axial directions of the curved panels $(\gamma_{r} = \gamma_{z} = 3,\alpha_{r} = 0,\alpha_{z} = 1,\beta_{z} = 2)$

Fig. 5

Variations of the symmetric volume fraction profile along the radial and axial directions of the curved panels $(\gamma_{r} = \gamma_{z} = 3,\alpha_{r} = \alpha_{z} = 1,\beta_{z} = \beta_{r} = 2)$

Table 1 Various volume fraction profiles, different parameters, and volume fraction indices of 2-D power-law distributions

The basic formulations

The mechanical constitutive relation that relates the stresses to the strains is as follows:

$$\left[ {\begin{array}{*{20}c} {\sigma_{r} } \\ {\sigma_{\theta } } \\ {\sigma_{z} } \\ {\tau_{z\theta } } \\ {\tau_{rz} } \\ {\tau_{r\theta } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{13} } & 0 & 0 & 0 \\ {C_{12} } & {C_{22} } & {C_{23} } & 0 & 0 & 0 \\ {C_{13} } & {C_{23} } & {C_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{66} } \\ \end{array} } \right]\;\left[ {\begin{array}{*{20}c} {\varepsilon_{r} } \\ {\varepsilon_{\theta } } \\ {\varepsilon_{z} } \\ {\gamma_{z\theta } } \\ {\gamma_{rz} } \\ {\gamma_{r\theta } } \\ \end{array} } \right].$$

(9)

In the absence of body forces, the governing equations are as follows:

$$\begin{aligned} & \frac{{\partial \sigma_{r} }}{\partial r} + \frac{1}{r}\,\,\frac{{\partial \tau_{r\theta } }}{\partial \theta } + \frac{{\partial \tau_{rz} }}{\partial z} + \frac{{\sigma_{r} - \sigma_{\theta } }}{r} = \rho \frac{{\partial^{2} u_{r} }}{{\partial t^{2} }}, \\ & \frac{{\partial \tau_{r\theta } }}{\partial r} + \frac{1}{r}\,\,\frac{{\partial \sigma_{\theta } }}{\partial \theta } + \frac{{\partial \tau_{\theta z} }}{\partial z} + \frac{{2\tau_{r\theta } }}{r} = \rho \frac{{\partial^{2} u_{\theta } }}{{\partial t^{2} }}, \\ & \frac{{\partial \tau_{rz} }}{\partial r} + \frac{1}{r}\,\,\frac{{\partial \tau_{\theta z} }}{\partial \theta } + \frac{{\partial \sigma_{z} }}{\partial z} + \frac{{\tau_{rz} }}{r} = \rho \frac{{\partial^{2} u_{z} }}{{\partial t^{2} }} \\ \end{aligned}$$

(10)

Strain–displacement relations are expressed as:

$$\begin{aligned} & \varepsilon_{r} = \frac{{\partial u_{r} }}{\partial r},\varepsilon_{\theta } = \frac{{u_{r} }}{r} + \frac{1}{r}\frac{{\partial u_{\theta } }}{\partial \theta },\varepsilon_{z} = \frac{{\partial u_{z} }}{\partial z}, \\ & \gamma_{\theta z} = \frac{{\partial u_{\theta } }}{\partial z} + \frac{1}{r}\frac{{\partial u_{z} }}{\partial \theta },\gamma_{rz} = \frac{{\partial u_{r} }}{\partial z} + \frac{{\partial u_{z} }}{\partial r}, \\ & \gamma_{r\theta } = \frac{1}{r}\frac{{\partial u_{r} }}{\partial \theta } + \frac{{\partial u_{\theta } }}{\partial r} - \frac{{u_{\theta } }}{r} \\ \end{aligned}$$

(11)

where u _r , u _θ and u _z are radial, circumferential and axial displacement components, respectively. Upon substitution Eq. (11) into (9) and then into (10), the equations of motion in terms of displacement components with infinitesimal deformations can be written as:

$$\begin{aligned} c_{11} \frac{{\partial^{2} u_{r} }}{{\partial r^{2} }} + c_{12} \left({ - \frac{1}{{r^{2} }}\,\,\frac{{\partial u_{\theta } }}{\partial \theta } + \frac{1}{r}\,\,\,\frac{{\partial^{2} u_{\theta } }}{\partial r\partial \theta } + \frac{1}{r}\,\,\frac{{\partial u_{r} }}{\partial r} - \frac{1}{{r^{2} }}\,\,u_{r} } \right) \hfill \\ \quad \quad + c_{13} \frac{{\partial^{2} u_{z} }}{\partial r\partial z} + \frac{{\partial c_{11} }}{\partial r}\frac{{\partial u_{r} }}{\partial r} + \frac{{\partial c_{12} }}{\partial r}\left({\frac{{u_{r} }}{r} + \frac{1}{r}\frac{{\partial u_{\theta } }}{\partial \theta }} \right) \hfill \\ \quad \quad + \frac{{\partial c_{13} }}{\partial r}\frac{{\partial u_{z} }}{\partial z} + \frac{{c_{66} }}{r}\left({\frac{{\partial^{2} u_{\theta } }}{\partial \theta \partial r} + \frac{1}{r}\,\,\frac{{\partial^{2} u_{r} }}{{\partial \theta^{2} }} - \frac{1}{r}\,\,\frac{{\partial u_{\theta } }}{\partial \theta }} \right) \hfill \\ \quad \quad + c_{55} \left({\frac{{\partial^{2} u_{r} }}{{\partial z^{2} }} + \frac{{\partial^{2} u_{z} }}{\partial z\partial r}} \right) + \frac{1}{r}\left({c_{11} \frac{{\partial u_{r} }}{\partial r} + c_{12} (\frac{{u_{r} }}{r} + \frac{1}{r}\frac{{\partial u_{\theta } }}{\partial \theta }} \right) \hfill \\ \quad \quad + c_{13} \frac{{\partial u_{z} }}{\partial z} - c_{12} \frac{{\partial u_{r} }}{\partial r} - c_{22} \left({\frac{{u_{r} }}{r} + \frac{1}{r}\frac{{\partial u_{\theta } }}{\partial \theta }) - c_{23} \frac{{\partial u_{z} }}{\partial z}} \right) \hfill \\ \quad = \rho \frac{{\partial^{2} u_{r} }}{{\partial t^{2} }} \hfill \\ \end{aligned}$$

(12)

$$\begin{aligned} c_{66} \left({\frac{ - 1}{{r^{2} }}\frac{{\partial u_{r} }}{\partial \theta } + \frac{1}{r}\frac{{\partial^{2} u_{r} }}{\partial r\partial \theta } + \frac{{\partial^{2} u_{\theta } }}{{\partial r^{2} }} + \frac{{u_{\theta } }}{{r^{2} }} - \frac{1}{r}\frac{{\partial u_{\theta } }}{\partial r}} \right) + \frac{{\partial c_{66} }}{\partial r}\left({\frac{1}{r}\frac{{\partial u_{r} }}{\partial \theta } + \frac{{\partial u_{\theta } }}{\partial r} - \frac{{u_{\theta } }}{r}} \right) \hfill \\ \quad + \frac{1}{r}\left({c_{12} \frac{{\partial^{2} u_{r} }}{\partial \theta \partial r} + c_{22} \left({\frac{1}{r}\frac{{\partial u_{r} }}{\partial \theta } + \frac{1}{r}\frac{{\partial^{2} u_{\theta } }}{{\partial \theta^{2} }}} \right) + c_{23} \frac{{\partial^{2} u_{z} }}{\partial \theta \partial z}} \right) + c_{44} \left({\frac{{\partial^{2} u_{\theta } }}{{\partial z^{2} }} + \frac{1}{r}\frac{{\partial^{2} u_{z} }}{\partial z\partial \theta }} \right) \hfill \\ \quad + \frac{{2c_{66} }}{r}\left({\frac{1}{r}\frac{{\partial u_{r} }}{\partial \theta } + \frac{{\partial u_{\theta } }}{\partial r} - \frac{{u_{\theta } }}{r}} \right) = \rho \frac{{\partial^{2} u_{\theta } }}{{\partial t^{2} }} \hfill \\ \end{aligned}$$

(13)

$$\begin{aligned} c_{55} \left({\frac{{\partial^{2} u_{r} }}{\partial r\partial z} + \frac{{\partial^{2} u_{z} }}{{\partial r^{2} }}} \right) + \frac{{\partial c_{55} }}{\partial r}\left({\frac{{\partial u_{r} }}{\partial z} + \frac{{\partial u_{z} }}{\partial r}} \right) + \frac{{c_{44} }}{r}\left({\frac{{\partial^{2} u_{\theta } }}{\partial \theta \partial z} + \frac{1}{r}\frac{{\partial^{2} u_{z} }}{{\partial \theta^{2} }}} \right) \hfill \\ \quad \quad + c_{13} \frac{{\partial^{2} u_{r} }}{\partial z\partial r} + c_{23} \left({\frac{1}{r}\frac{{\partial u_{r} }}{\partial z} + \frac{1}{r}\frac{{\partial^{2} u_{\theta } }}{\partial \theta \partial z}} \right) + c_{33} \frac{{\partial^{2} u_{z} }}{{\partial z^{2} }} + \frac{{c_{55} }}{r}\left({\frac{{\partial u_{r} }}{\partial z} + \frac{{\partial u_{z} }}{\partial r}} \right) \hfill \\ \quad = \rho \frac{{\partial^{2} u_{z} }}{{\partial t^{2} }} \hfill \\ \end{aligned}.$$

(14)

The boundary conditions at the concave and convex surfaces, r = r _i and r _o , respectively, can be described as follows:

• At r = r _o , r _i

  $$\tau_{rz} = \tau_{r\theta } = 0,\;\sigma_{r} = \left\{ {\begin{array}{*{20}c} { - k_{w} u_{r} + k_{g} \left\{ {\frac{{\partial^{2} u_{r} }}{{\partial z^{2} }} + \frac{1}{{r^{2} }}\frac{{\partial^{2} u_{r} }}{{\partial \theta^{2} }}} \right\}} & {{\text{at}}\,r = r_{i} } \\ 0 & {{\text{at}}\,r = r_{o} } \\ \end{array} } \right.$$

  (15)

In this investigation, three different types of classical boundary conditions at edges z = 0 and L _z of the panel can be stated as follows:

• Simply supported (S):

  $$U_{r} = U_{\theta } = \sigma_{z} = 0$$

  (16)

• Clamped (C):

  $$U_{r} = U_{\theta } = U_{z} = 0$$

  (17)

• Free (F):

  $$\sigma_{z} = \sigma_{z\theta } = \sigma_{zr} = 0$$

  (18)

For the curved panels with simply supported at one pair of opposite edges, the displacement components can be expanded in terms of trigonometric functions in the direction normal to these edges. In this work, it is assumed that the edges θ = 0 and θ = Φ are simply supported. Hence,

$$\begin{aligned} & u_{r} (r,\theta ,z,t) = \sum\limits_{m = 1}^{\infty } {U_{r} } (r,z)\sin \left({\frac{m\pi }{\varPhi }\theta } \right)e^{i\omega t} , \\ & u_{\theta } (r,\theta ,z,t) = \sum\limits_{m = 1}^{\infty } {U_{\theta } } (r,z)\cos \left({\frac{m\pi }{\varPhi }\theta } \right)e^{i\omega t} , \\ & u_{z} (r,\theta ,z,t) = \sum\limits_{m = 1}^{\infty } {U_{z} } (r,z)\sin \left({\frac{m\pi }{\varPhi }\theta } \right)e^{i\omega t} \\ \end{aligned}$$

(19)

where m is the circumferential wave number, $\omega$ is the natural frequency and i (=$\sqrt { - 1}$) is the imaginary number. Substituting for displacement components from Eq. (19) into Eqs. (12, 13, 14), one gets

Equation (12):

$$\begin{aligned} c_{11} \frac{{\partial^{2} U_{r} }}{{\partial r^{2} }} + c_{12} \left({\frac{m\pi }{{\varPhi r^{2} }}U_{\theta } - \frac{m\pi }{\varPhi r}\frac{{\partial U_{\theta } }}{\partial r} + \frac{1}{r}\frac{{\partial U_{r} }}{\partial r} - \frac{1}{{r^{2} }}U_{r} } \right) + c_{13} \frac{{\partial^{2} U_{z} }}{\partial r\partial z} + \frac{{\partial c_{11} }}{\partial r}\frac{{\partial U_{r} }}{\partial r} \hfill \\ \quad \quad + \frac{{\partial c_{12} }}{\partial r}\left({\frac{1}{r}U_{r} - \frac{m\pi }{\varPhi r}U_{\theta } } \right) + \frac{{\partial c_{13} }}{\partial r}\frac{{\partial U_{z} }}{\partial z} \hfill \\ \quad \quad + \frac{{c_{66} }}{r}\left({ - \frac{m\pi }{\varPhi }\frac{{\partial U_{\theta } }}{\partial r} - \frac{1}{r}\left({\frac{m\pi }{\varPhi }} \right)^{2} U_{r} + \frac{m\pi }{\varPhi r}U_{\theta } } \right) + c_{55} \left({\frac{{\partial^{2} U_{r} }}{{\partial z^{2} }} + \frac{{\partial^{2} U_{z} }}{\partial z\partial r}} \right) \hfill \\ \quad \quad + \frac{1}{r}\left({(c_{11} \frac{{\partial U_{r} }}{\partial r} + c_{12} \left({\frac{1}{r}U_{r} - \frac{m\pi }{\varPhi r}U_{\theta } } \right) + \; c_{13} \frac{{\partial U_{z} }}{\partial z} - c_{12} \frac{{\partial U_{r} }}{\partial r} - c_{22} \left({\frac{1}{r}U_{r} - \frac{m\pi }{\varPhi r}U_{\theta } } \right) - c_{23} \frac{{\partial U_{z} }}{\partial z}} \right) \hfill \\ \quad = - \rho \omega^{2} U_{r} \hfill \\ \end{aligned}$$

(20)

Equation (13):

$$\begin{aligned} c_{66} \left({ - \frac{m\pi }{{\varPhi r^{2} }}U_{r} + \frac{m\pi }{\varPhi r}\frac{{\partial U_{r} }}{\partial r} + \frac{{\partial^{2} U_{\theta } }}{{\partial r^{2} }} + \frac{{U_{\theta } }}{{r^{2} }} - \frac{1}{r}\frac{{\partial U_{\theta } }}{\partial r}} \right) \hfill \\ \quad \quad + \frac{{\partial c_{66} }}{\partial r}\left({\frac{m\pi }{\varPhi r}U_{r} + \frac{{\partial U_{\theta } }}{\partial r} - \frac{{U_{\theta } }}{r}} \right) \hfill \\ \quad \quad + \frac{1}{r}\left({c_{12} \frac{m\pi }{\varPhi }\frac{{\partial U_{r} }}{\partial r} + c_{22} \left({\frac{m\pi }{\varPhi r}U_{r} - \frac{1}{r}\left({\frac{m\pi }{\varPhi }} \right)^{2} U_{\theta } } \right) + c_{23} \frac{m\pi }{\varPhi }\frac{{\partial U_{z} }}{\partial z}} \right) \hfill \\ \quad \quad + c_{44} \left({\frac{{\partial^{2} U_{\theta } }}{{\partial z^{2} }} + \frac{m\pi }{\varPhi r}\frac{{\partial U_{z} }}{\partial z}} \right) + \frac{{2c_{66} }}{r}\left({\frac{m\pi }{\varPhi r}U_{r} + \frac{{\partial U_{\theta } }}{\partial r} - \frac{{U_{\theta } }}{r}} \right) \hfill \\ \quad = - \rho \omega^{2} U_{\theta } \hfill \\ \end{aligned}$$

(21)

Equation (14):

$$\begin{aligned} &c_{55} \left({\frac{{\partial^{2} U_{r} }}{\partial r\partial z} + \frac{{\partial^{2} U_{z} }}{{\partial r^{2} }}} \right) + \frac{{\partial c_{55} }}{\partial r}\left({\frac{{\partial U_{r} }}{\partial z} + \frac{{\partial U_{z} }}{\partial r}} \right) \\&\quad \quad + \frac{{c_{44} }}{r}\left({ - \frac{m\pi }{\varPhi }\frac{{\partial U_{\theta } }}{\partial z} - \frac{1}{r}\left({\frac{m\pi }{\varPhi }} \right)^{2} U_{z} } \right) + c_{13} \frac{{\partial^{2} U_{r} }}{\partial z\partial r}\\&\quad \quad + c_{23} \left({\frac{1}{r}\frac{{\partial U_{r} }}{\partial z} - \frac{m\pi }{\varPhi r}\frac{{\partial U_{\theta } }}{\partial z}} \right) + c_{33} \frac{{\partial^{2} U_{z} }}{{\partial z^{2} }} + \frac{{c_{55} }}{r}\left({\frac{{\partial U_{r} }}{\partial z} + \frac{{\partial U_{z} }}{\partial r}} \right)\\ &\quad = - \rho \omega^{2} U_{z} \hfill \\ \end{aligned}$$

(22)

The geometrical and natural boundary conditions stated in Eq. (15) can also be simplified as follows

Equation (15):

$$\begin{aligned} \frac{{\partial U_{r} }}{\partial z} + \frac{{\partial U_{z} }}{\partial r} = \frac{m\pi }{\varPhi r}U_{r} + \frac{{\partial U_{\theta } }}{\partial r} - \frac{{U_{\theta } }}{r} = 0, \hfill \\ \left\{ \begin{aligned} \begin{array}{*{20}c} \begin{aligned} c_{11} \frac{{\partial U_{r} }}{\partial r} + c_{12} \left({\frac{{U_{r} }}{r} - \frac{m\pi }{\varPhi r}U_{\theta } } \right) + c_{13} \frac{{\partial U_{z} }}{\partial z} \hfill \\ \quad + k_{w} U_{r} - k_{g} \left\{ {\frac{{\partial^{2} U_{r} }}{{\partial z^{2} }} - \left({\frac{m\pi }{\varPhi r}} \right)^{2} U_{r} } \right\} = 0 \hfill \\ \end{aligned} & {at\;r = r_{i} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {c_{11} \frac{{\partial U_{r} }}{\partial r} + c_{12} \left({\frac{{U_{r} }}{r} - \frac{m\pi }{\varPhi r}U_{\theta } } \right) + c_{13} \frac{{\partial U_{z} }}{\partial z} = 0} & {at\;r = r_{o} } \\ \end{array} \hfill \\ \end{aligned} \right. \hfill \\ \end{aligned}$$

(23)

The boundary conditions stated in Eqs. (16, 17, 18) can also be simplified; however, for the sale of brevity, they are not shown here.

2-D DQM solution of governing equations

It is difficult to solve analytically the equations of motion, if it is not impossible. Hence, one should use an approximate method to find a solution. Here, the differential quadrature method (DQM) is employed. One can compare DQM solution procedure with the other two widely used traditional methods for plate analysis, i.e., Rayleigh–Ritz method and FEM. The main difference between the DQM and the other methods is how the governing equations are discretized. In DQM, the governing equations and boundary conditions are directly discretized, and thus elements of stiffness and mass matrices are evaluated directly. But in Rayleigh–Ritz and FEMs, the weak form of the governing equations should be developed and the boundary conditions are satisfied in the weak form. Generally by doing so larger number of integrals with increasing amount of differentiation should be done to arrive at the element matrices. In addition, the number of degrees of freedom will be increased for an acceptable accuracy.

The basic idea of the DQM is the derivative of a function, with respect to a space variable at a given sampling point, is approximated as a weighted linear sum of the sampling points in the domain of that variable. In order to illustrate the DQ approximation, consider a function $f(\xi ,\eta )$ defined on a rectangular domain $0 \le \xi \le a$ and $0 \le \eta \le b$. Let in the given domain, the function values be known or desired on a grid of sampling points. According to DQM method, the rth derivative of the function $f(\xi ,\eta )$ can be approximated as:

$$\begin{aligned} \frac{{\partial^{r} f(\xi ,\eta )}}{{\partial \xi^{r} }}|(\xi ,\eta ) = (\xi_{i} ,\eta_{j} ) \hfill \\ \quad = \sum\limits_{m = 1}^{{N_{\xi } }} {A_{im}^{\xi (r)} f_{mj} } \quad for\;i = 1,2, \ldots ,N_{\xi } \;and\;r = 1,2, \ldots ,N_{\xi } - 1 \hfill \\ \end{aligned}$$

(24)

where $N_{\xi }$ represents the total number of nodes along the $\xi$-direction. From this equation one can deduce that the important components of DQM approximations are the weighting coefficients $(A_{ij}^{\xi (r)} )$ and the choice of sampling points. In order to determine the weighting coefficients, a set of test functions should be used in Eq. (24). The weighting coefficients for the first-order derivatives in $\xi_{{}}$-direction are thus determined as (Bellman and Casti 1971):

$$A_{ij}^{\xi } = \left\{ {\begin{array}{*{20}c} {\frac{1}{a}\frac{{M(\xi_{i} )}}{{(\xi_{i} - \xi_{j} )M(\xi_{j} )}}} & {for\;i \ne j} \\ { - \sum\limits_{\begin{subarray}{l} j = 1 \\ i \ne j \end{subarray} }^{{N_{\xi } }} {A_{ij}^{\xi } } } & {for\;i = j} \\ \end{array} } \right.\;;\,\;\;i,j = 1,2, \ldots ,N_{\xi } ,$$

(25)

where

$$M(\xi_{i} ) = \prod\limits_{j = 1,i \ne j}^{{N_{\xi } }} {(\xi_{i} } - \xi_{j} )$$

(26)

The weighting coefficients of the second-order derivative can be obtained in the matrix form (Bellman and Casti 1971):

$$\left[ {B_{ij}^{\xi } } \right] = \left[ {A_{ij}^{\xi } } \right]\left[ {A_{ij}^{\xi } } \right] = \left[ {A_{ij}^{\xi } } \right]^{2}$$

(27)

In a similar manner, the weighting coefficients for the $\eta$-direction can be obtained.

The natural and simplest choice of the grid points is equally spaced points in the direction of the coordinate axes of computational domain. It was demonstrated that non-uniform grid points gives a better result with the same number of equally spaced grid points (Bellman and Casti 1971). It is shown (Shu and Wang 1999) that one of the best options for obtaining grid points is Chebyshev–Gauss–Lobatto quadrature points:

$$\begin{gathered} \frac{{\xi _{i} }}{a} = \frac{1}{2}\left\{ {1 - \cos \left[ {\frac{{(i - 1)\pi }}{{(N_{\xi } - 1)}}} \right]} \right\}, \hfill \\ \frac{{\eta _{j} }}{b} = \frac{1}{2}\left\{ {1 - \cos \left[ {\frac{{(j - 1)\pi }}{{(N_{\eta } - 1)}}} \right]} \right\}\quad {\text{for}}\;\;i = 1,2, \ldots ,N_{\xi }; \hfill \\ \end{gathered}$$

(28.1, 2)

${\text{j}} = 1, 2, \ldots ,N_{\eta } ,$where $N_{\xi }$ and $N_{\eta }$ are the total number of nodes along the $\xi$- and $\eta$-directions, respectively. At this stage, the DQ method can be applied to discretize the equations of motion (20, 21, 22). As a result, at each domain grid point (r _i ,z _j ) with i = 2,…, N _r  − 1 and j = 2,…, N _z  − 1, the discretized equations take the following forms.

Equation (20):

$$\begin{aligned} \left({c_{11} } \right)_{ij} \sum\limits_{n = 1}^{{N_{r} }} {B_{in}^{r} U_{rnj} } + \left({c_{12} } \right)_{ij} \left({\frac{m\pi }{{\varPhi r_{i}^{2} }}U_{\theta ij} - \frac{m\pi }{{\varPhi r_{i} }}\sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{\theta nj} } + \frac{1}{{r_{i} }}\sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{rnj} } - \frac{{U_{rij} }}{{r_{i}^{2} }}} \right) \hfill \\ \quad \quad + \left({c_{13} } \right)_{ij} \sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{v = 1}^{{N_{z} }} {A_{jv}^{z} A_{in}^{r} U_{znv} } } + \left({\frac{{\partial c_{11} }}{\partial r}} \right)_{ij} \sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{rnj} } + \left({\frac{{\partial c_{12} }}{\partial r}} \right)_{ij} \left({\frac{1}{{r_{i} }}U_{rij} - \frac{m\pi }{{\varPhi r_{i} }}U_{\theta ij} } \right) \hfill \\ \quad \quad + \left({\frac{{\partial c_{13} }}{\partial r}} \right)_{ij} \sum\limits_{n = 1}^{{N_{z} }} {A_{jn}^{z} U_{zin} } + \frac{{\left({c_{66} } \right)_{ij} }}{{r_{i} }}\left({ - \frac{m\pi }{\varPhi }\sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{\theta nj} - \frac{1}{{r_{i} }}\left({\frac{m\pi }{\varPhi }} \right)^{2} U_{rij} } + \frac{m\pi }{{\varPhi r_{i} }}U_{\theta ij} } \right) \hfill \\ \quad \quad + \left({c_{55} } \right)_{ij} \left({\sum\limits_{n = 1}^{{N_{z} }} {B_{jn}^{z} U_{rin} } + \sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{v = 1}^{{N_{z} }} {A_{jv}^{z} A_{in}^{r} U_{znv} } } } \right) \hfill \\ \quad \quad + \frac{1}{{r_{i} }}\left({(c_{11} )_{ij} \sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{rnj} } + \left({c_{12} } \right)_{ij} \left({\frac{{U_{rij} }}{{r_{i} }} - \frac{m\pi }{{\varPhi r_{i} }}U_{\theta ij} } \right) + \left({c_{13} } \right)_{ij} \sum\limits_{n = 1}^{{N_{z} }} {A_{jn}^{z} U_{zin} } - \left({c_{12} } \right)_{ij} \sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{rnj} } - \left({c_{22} } \right)_{ij} \left({\frac{{U_{rij} }}{{r_{i} }} - \frac{m\pi }{{\varPhi r_{i} }}U_{\theta ij} } \right) - \left({c_{23} } \right)_{ij} \sum\limits_{n = 1}^{{N_{z} }} {A_{jn}^{z} U_{zin} } } \right) \hfill \\ \quad = - \rho_{ij} \omega^{2} U_{rij} \hfill \\ \end{aligned}$$

(29)

Equation (21):

$$\begin{aligned} \left({c_{66} } \right)_{ij} \left({ - \frac{1}{{r_{i}^{2} }}\frac{m\pi }{\varPhi }U_{rij} + \frac{m\pi }{{\varPhi r_{i} }}\sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{rnj} } + \sum\limits_{n = 1}^{{N_{r} }} {B_{in}^{r} U_{\theta nj} } + \frac{{U_{\theta ij} }}{{r_{i}^{2} }} - \frac{1}{{r_{i} }}\sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{\theta nj} } } \right) \hfill \\ \quad \quad + \left({\frac{{\partial c_{66} }}{\partial r}} \right)_{ij} \left({\frac{m\pi }{{\varPhi r_{i} }}U_{rij} + \sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{\theta nj} } - \frac{{U_{\theta ij} }}{{r_{i} }}} \right) \hfill \\ \quad \quad + \frac{1}{{r_{i} }}\left({\left({c_{12} } \right)_{ij} \frac{m\pi }{\varPhi }\sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{rnj} } + \left({c_{22} } \right)_{ij} \left({\frac{m\pi }{{\varPhi r_{i} }}U_{rij} - \frac{1}{{r_{i} }}\left({\frac{m\pi }{\varPhi }} \right)^{2} U_{\theta ij} } \right) + \left({c_{23} } \right)_{ij} \frac{m\pi }{\varPhi }\sum\limits_{n = 1}^{{N_{z} }} {A_{jn}^{z} U_{zin} } } \right) \hfill \\ \quad \quad + \left({c_{44} } \right)_{ij} \left({\sum\limits_{n = 1}^{{N_{z} }} {B_{jn}^{z} U_{\theta in} } + \frac{m\pi }{{\varPhi r_{i} }}\sum\limits_{n = 1}^{{N_{z} }} {A_{jn}^{z} U_{zin} } } \right) \hfill \\ \quad \quad + \frac{{2\left({c_{66} } \right)_{ij} }}{{r_{i} }}\left({\frac{m\pi }{{\varPhi r_{i} }}U_{rij} + \sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{\theta nj} } - \frac{{U_{\theta ij} }}{{r_{i} }}} \right) \hfill \\ \quad = - \rho_{ij} \omega^{2} U_{\theta ij} \hfill \\ \end{aligned}$$

(30)

Equation (22):

$$\begin{aligned} &\left({c_{55} } \right)_{ij} \left({\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{v = 1}^{{N_{z} }} {A_{jv}^{z} A_{in}^{r} U_{rnv} } } + \sum\limits_{n = 1}^{{N_{r} }} {B_{in}^{r} U_{znj} } } \right) + \left({\frac{{\partial c_{55} }}{\partial r}} \right)_{ij}\times \left({\sum\limits_{n = 1}^{{N_{z} }} {A_{jn}^{z} U_{rin} } + \sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{znj} } } \right) \hfill \\ &\quad \quad+ \frac{{\left({c_{44} } \right)_{ij} }}{{r_{i} }}\left({ - \frac{m\pi }{\varPhi }\sum\limits_{n = 1}^{{N_{z} }} {A_{jn}^{z} U_{\theta in} } - \frac{1}{{r_{i} }}\left({\frac{m\pi }{\varPhi }} \right)^{2} U_{zij} } \right) + \left({c_{13} } \right)_{ij} \sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{v = 1}^{{N_{z} }} {A_{jv}^{z} A_{in}^{r} U_{rnv} } } \hfill \\ &\quad \quad + \left({c_{23} } \right)_{ij} \left({\frac{1}{{r_{i} }}\sum\limits_{n = 1}^{{N_{z} }} {A_{jn}^{z} U_{rin} } - \frac{m\pi }{{\varPhi r_{i} }}\sum\limits_{n = 1}^{{N_{z} }} {A_{jn}^{z} U_{\theta in} } } \right) + \left({c_{33} } \right)_{ij} \sum\limits_{n = 1}^{{N_{z} }} {B_{jn}^{z} U_{zin} } \hfill \\ &\quad \quad + \frac{{\left({c_{55} } \right)_{ij} }}{{r_{i} }}\left({\sum\limits_{n = 1}^{{N_{z} }} {A_{jn}^{z} U_{rin} } + \sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{znj} } } \right) \hfill \\ & = - \rho_{ij} \omega^{2} U_{zij} \hfill \\ \end{aligned}$$

(31)

where $A_{ij}^{r}$, $A_{ij}^{z}$ and $B_{ij}^{r}$, $B_{ij}^{z}$ are the first- and second-order DQ weighting coefficients in the r- and z-directions, respectively. The DQ method can also be applied to discretize the boundary conditions at r = r _i and r _o as follows. Equation (23):

$$\begin{aligned} \sum\limits_{n = 1}^{{N_{z} }} {A_{jn}^{z} U_{rin} } + \sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{znj} } = 0, \hfill \\ \frac{m\pi }{{\varPhi r_{i} }}U_{rij} + \sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{\theta nj} } - \frac{{U_{\theta ij} }}{{r_{i} }} = 0, \hfill \\ \left({c_{11} } \right)_{ij} \sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{rnj} } + \left({c_{12} } \right)_{ij} \left({\frac{{U_{rij} }}{{r_{i} }} - \frac{m\pi }{{\varPhi r_{i} }}U_{\theta ij} } \right) + \left({c_{13} } \right)_{ij} \sum\limits_{n = 1}^{{N_{z} }} {A_{jn}^{z} U_{zin} } \hfill \\ \left\{ {k_{w} U_{rij} - k_{g} \left({\sum\limits_{n = 1}^{{N_{z} }} {B_{jn}^{z} U_{rin} - \left({\frac{m\pi }{{\varPhi r_{i} }}} \right)^{2} U_{rij} } } \right)} \right\}\delta_{1i} = 0 \hfill \\ \end{aligned}$$

(32)

where i = 1 at r = r _i and i = N _r at r = r _o , and j = 1,2,…,N _z ; also δ _ij is the Kronecker delta. The boundary conditions at z = 0 and L _z stated in Eqs. (16, 17, 18), become Eq. (16):

• Simply supported (S):

  $$\begin{aligned} U_{rij} = U_{\theta ij} = 0, \hfill \\ \left({c_{13} } \right)_{ij} \sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{rnj} } + \left({c_{23} } \right)_{ij} \left({\frac{{U_{rij} }}{{r_{i} }} - \frac{m\pi }{{\varPhi r_{i} }}U_{\theta ij} } \right) + \left({c_{33} } \right)_{ij} \sum\limits_{n = 1}^{{N_{z} }} {A_{jn}^{z} U_{zin} } = 0 \hfill \\ \end{aligned}$$

  (33)

Equation (17):

• Clamped (C):

  $$U_{rij} = U_{\theta ij} = U_{zij} 0$$

  (34)

Equation (18):

• Free (F):

  $$\begin{aligned} \left({c_{13} } \right)_{ij} \sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{rnj} } + (c_{23} )_{ij} \left({\frac{{U_{rij} }}{{r_{i} }} - \frac{m\pi }{{\varPhi r_{i} }}U_{\theta ij} } \right) + \left({c_{33} } \right)_{ij} \sum\limits_{n = 1}^{{N_{z} }} {A_{jn}^{z} U_{zin} } = 0, \hfill \\ \sum\limits_{n = 1}^{{N_{z} }} {A_{jn}^{z} U_{\theta in} } + \frac{m\pi }{{\varPhi r_{i} }}U_{zij} = 0, \hfill \\ \sum\limits_{n = 1}^{{N_{z} }} {A_{jn}^{z} U_{rin} } + \sum\limits_{n = 1}^{{N_{r} }} {A_{in}^{r} U_{znj} } = 0 \hfill \\ \end{aligned}$$

  (35)

In the above equations i = 2,…,N _r  − 1; also j = 1 at z = 0 and j = N _z at z = L _z .

In order to carry out the eigenvalue analysis, the domain and boundary nodal displacements should be separated. In vector forms, they are denoted as {d} and {b}, respectively. Based on this definition, the discretized form of the equations of motion and the related boundary conditions can be represented in the matrix form as:Equations of motion, Eqs. (29, 30, 31):

$$\left[ {\left[ {K_{db} } \right]\left[ {K_{dd} } \right]} \right]\left\{ \begin{aligned} \left\{ b \right\} \hfill \\ \left\{ d \right\} \hfill \\ \end{aligned} \right\} - \omega^{2} \left[ M \right]\left\{ d \right\} = \left\{ 0 \right\}\,$$

(36)

Boundary conditions, Eq. (32) and Eqs. (33, 34, 35):

$$\left[ {K_{bd} } \right]\left\{ d \right\} + \left[ {K_{bb} } \right]\left\{ b \right\} = \left\{ 0 \right\}\,$$

(37)

Eliminating the boundary degrees of freedom in Eq. (36) using Eq. (37), this equation becomes

$$\left[ K \right] - \omega_{{}}^{2} \left[ M \right]\left\{ d \right\} = \left\{ 0 \right\} ,$$

(38)

where $\left[ K \right] = \left[ {K_{dd} } \right] - \left[ {K_{db} } \right]\left[ {K_{bb} } \right]^{{\text{ - }1}} \left[ {K_{bd} } \right]$. The above eigenvalue system of equations can be solved to find the natural frequencies and mode shapes of the curved panel.

Numerical results and discussion

Convergence and comparison studies

Due to lack of appropriate results for free vibration of CGCNTR cylindrical panels reinforced by oriented CNTs for direct comparison, validation of the presented formulation is conducted in two ways. Firstly, the results are compared with those of FGM composite cylindrical panels and then, the results of the presented formulations are given in the form of convergence studies with respect to N _r and N _z , the number of discrete points distributed along the radial and axial directions, respectively. To validate the proposed approach its convergence and accuracy are demonstrated via different examples. The obtained natural frequencies based on the three-dimensional elasticity formulation are compared with those of the power series expansion method for both FGM curved panels with and without elastic foundations (Matsunaga 2008; Pradyumna and Bandyopadhyay 2008; Farid et al. 2010). In these studies the material properties of functionally graded materials are assumed as follows:

• Metal (Aluminum, Al):

  $$E_{m} = 70* 10^{ 9} \;{\text{Pa}},\rho_{m} = 2 70 2\;{\text{K}}_{\text{g}} / {\text{m}}^{3} ,\upsilon_{m} = 0. 3$$

• Ceramic (Alumina, Al₂O₃):

  $$E_{c} = 3 80* 10^{ 9} \;{\text{Pa}},\rho_{c} = 3 800\;{\text{K}}_{\text{g}} / {\text{m}}^{ 3} ,\upsilon_{c} = 0. 3$$

Subscripts M and C refer to the metal and ceramic constituents which denote the material properties of the outer and inner surfaces of the panel, respectively. To validate the analysis, results for FGM cylindrical shells are compared with similar ones in the literature, as shown in Table 2. The comparison shows that the present results agreed well with those in the literatures. Besides the fast rate of convergence of the method being quite evident, it is found that only 13 grid points (N _r  = N _z  = 13) along the radial and axial directions can yield accurate results. Further validation of the present results for isotropic FGM cylindrical panel is shown in Table 3. In this table, comparison is made for different L _z /R and L _z /h ratios, and it is observed there is good agreement between the results.

Table 2 Comparison of the normalized natural frequency of an FGM composite curved panel with four edges simply supported $(\varOmega_{11} = \omega_{11} R\varPhi \sqrt {{{\rho_{m} h} \mathord{\left/ {\vphantom {{\rho_{m} h} D}} \right. \kern-0pt} D}} ,D = {{E_{m} h^{3} } \mathord{\left/ {\vphantom {{E_{m} h^{3} } {12(1 - \upsilon_{m}^{2} }}} \right. \kern-0pt} {12(1 - \upsilon_{m}^{2} }}))$

Table 3 Comparison of the normalized natural frequency of an FGM composite curved panel for various L _Z /R and L _Z /h ratios

As another example, the convergence and accuracy of the method are investigated by evaluating the first three natural frequency parameters of the FG curved panel resting on Pasternak foundations. The non-dimensional forms of the elastic foundation coefficients are defined as K _w  = k _w R/G _c and K _g  = k _g /(G _c R) in which G _c is the shear modulus of elasticity of the ceramic layer. The results are prepared for different thickness-to-mean radius ratios and different values of the DQ grid points along the radial and axial directions, respectively, are shown in Table 4. Also, one can see that excellent agreement exists between the results.

Table 4 Comparison of the first three non-dimensional natural frequency parameters of panel on an elastic foundation $(\varpi_{mn} = \, \omega_{mn} h\sqrt {{{\rho_{C} } \mathord{\left/ {\vphantom {{\rho_{C} } {E_{C} }}} \right. \kern-0pt} {E_{C} }}} ,P = 1,\varPhi = 60^{\circ},N_{r} = N_{z} = 13)$

Parametric studies

After demonstrating the convergence and accuracy of the present method, parametric studies for 3-D vibration analysis of thick curved panels resting on a two-parameter elastic foundation reinforced by randomly oriented straight single-walled carbon nanotubes for various CNTs volume fraction distribution, length-to-mean radius ratio, elastic coefficients of foundation and different combinations of free, simply supported and clamped boundary conditions along the axial direction of the curved panel, are computed. The boundary conditions of the panel are specified by the letter symbols, for example, S–C–S–F denotes a curved panel with edges θ = 0 and Φ simply supported (S), edge z = 0 clamped (C) and edge z = L _z free (F).

The non-dimensional natural frequency, Winkler and shearing layer elastic coefficients are as follows:

$$\begin{aligned} \varOmega_{mn} = \omega_{mn} 10h\sqrt {{{\rho_{m} } \mathord{\left/ {\vphantom {{\rho_{m} } {E_{m} }}} \right. \kern-0pt} {E_{m} }}} , \hfill \\ K_{w} = \frac{{k_{w} R}}{{G_{m} }},\mathop {}\limits^{{}} K_{g} = \frac{{k_{g} }}{{G_{m} R}}, \hfill \\ \end{aligned}$$

(39)

where ρ _m , E _m and G _m represent the mass density, Young’s modulus and shear modulus of the matrix, respectively.

The effect of the Winkler elastic coefficient on the fundamental frequency parameters for different boundary conditions is shown in Figs. 6, 7 and 8. It is observed that the fundamental frequency parameters converge with increasing Winkler elastic coefficient of the foundation. According to these figures, the lowest frequency parameter is obtained by using classical–classical volume fraction profile. On the contrary, the 1-D FG panel with symmetric volume fraction profile has the maximum value of the frequency parameter. Therefore, a graded CNTs volume fraction in two directions has higher capabilities to reduce the frequency parameter than conventional 1-D nanocomposite. It is also observed from Figs. 6, 7 and 8, for the large values of Winkler elastic coefficient, the shearing layer elastic coefficient has less effect and the results become independent of it, in other words the non-dimensional natural frequencies converge with increasing Winkler foundation stiffness.

Fig. 6

Variations of fundamental frequency parameters of a bidirectional S–C–S–C nanocomposite curved panels resting on a two-parameter elastic foundation with Winkler elastic coefficient for different volume fraction profiles (K _g  = 100, R/h = L _z /R = 3.5, γ _r  = 2, Φ = 135°)

Fig. 7

Variations of fundamental frequency parameters of a bidirectional S–C–S–S nanocomposite curved panels resting on a two-parameter elastic foundation with Winkler elastic coefficient for different volume fraction profiles (K _g  = 100, R/h = L _z /R = 3.5, γ _r  = 2, Φ = 135°)

Fig. 8

Variations of fundamental frequency parameters of a bidirectional S–F–S–F nanocomposite curved panels resting on a two-parameter elastic foundation with Winkler elastic coefficient for different volume fraction profiles (K _g  = 100, R/h = L _z /R = 3.5, γ _r  = 2, Φ = 135°)

The influence of shearing layer elastic coefficient on the non-dimensional natural frequency for S–C–S–C, S–C–S–S and S–F–S–F bidirectional nanocomposite curved panel resting on a two-parameter elastic foundation, is shown in Figs. 9, 10 and 11. It is observed that the variation of Winkler elastic coefficient has little effect on the non-dimensional natural frequency at different values of shearing layer elastic coefficient. It is clear that with increasing the shearing layer elastic coefficient of the foundation, the frequency parameters increase to some limit values and for the large values of shearing layer elastic coefficient, the frequency parameters become independent of it.

Fig. 9

Variations of fundamental frequency parameters of a bidirectional S–C–S–C nanocomposite curved panels resting on a two-parameter elastic foundation with the shearing layer elastic coefficient (R/h = L _z /R = 3.5, γ _r  = γ _z  = 2, α _r  = α _z  = 0, Φ = 135°)

Fig. 10

Variations of fundamental frequency parameters of a bidirectional S–C–S–S nanocomposite curved panels resting on a two-parameter elastic foundation with the shearing layer elastic coefficient (R/h = L _z /R = 3.5, γ _r  = γ _z  = 2, α _r  = α _z  = 0, Φ = 135°)

Fig. 11

Variations of fundamental frequency parameters of a bidirectional S–F–S–F nanocomposite curved panels resting on a two-parameter elastic foundation with the shearing layer elastic coefficient (R/h = L _z /R = 3.5, γ _r  = γ _z  = 2, α _r  = α _z  = 0, Φ = 135°)

The variations of fundamental frequency parameters of bidirectional nanocomposite curved panels resting on an elastic foundation with length-to-mean radius ratio (L _z /R) for different types of volume fraction profiles are depicted in Figs. 12, 13 and 14. It can also be inferred from these figures that the frequency is greatly influenced in that fundamental frequency parameter decreases steadily as length-to-mean radius ratio (L _z /R) becomes larger and remains almost unaltered for the large values of length-to-mean radius ratio. As can be seen from this figure, for the all length-to-mean radius ratio (L _z /R), classical–classical volume fraction profile has the lowest frequencies followed by classical–symmetric, classical, symmetric–symmetric and symmetric profiles.

Fig. 12

Variations of fundamental frequency parameters of two-dimensional continuously graded S–C–S–C nanocomposite curved panels resting on an elastic foundation with L _z /R ratio for different volume fraction profiles (K _w  = K _g  = 100, R/h = 3.5, γ _z  = 2, Φ = 135°)

Fig. 13

Variations of fundamental frequency parameters of two-dimensional continuously graded S–C–S–S nanocomposite curved panels resting on an elastic foundation with L _z /R ratio for different volume fraction profiles (K _w  = K_g = 100, R/h = 3.5, γ _z  = 2, Φ = 135°)

Fig. 14

Variations of fundamental frequency parameters of two-dimensional continuously graded S–F–S–F nanocomposite curved panels resting on an elastic foundation with L _z /R ratio for different volume fraction profiles (K _w  = K _g  = 100, R/h = 3.5, γ _z  = 2, Φ = 135°)

The variations of fundamental frequency parameters of bidirectional nanocomposite curved panels with length-to-mean radius ratio (L _z /R), and the volume fraction index through the radial direction of the panels for S–F–S–F boundary conditions are shown in Fig. 15, by considering $(\alpha_{r} = \alpha_{z} = 0,\gamma_{z} = 2,K_{w} = K_{g} = 100)$ for classical–classical 2-D nanocomposite curved panels. Confirming the effect of length-to-mean radius ratio on the natural frequency already shown in the Figs. 12, 13 and 14, it is found that the frequency parameter decreases by increasing the radial volume fraction index $(\gamma_{r} )$. This behavior is also observed for other boundary conditions, not shown here for brevity.

Fig. 15

Variations of fundamental frequency parameters of bidirectional nanocomposite curved panels with length-to-mean radius ratio (L _z /R), and the volume fraction index through the radial direction of the panels for S–F–S–F boundary condition (K _w  = K _g  = 100, R/h = 3.5, γ _z = 2, α _r  = α _z  = 0, Φ = 135°)

Conclusion remarks

In this research work, free vibration of thick bidirectional nanocomposite curved panels resting on a two-parameter elastic is investigated based on three-dimensional theory of elasticity. The elastic foundation is considered as a Pasternak model with adding a shear layer to the Winkler model. Three complicated equations of motion for the curved panel under consideration are semi-analytically solved by using 2-D differential quadrature method. Using the 2-D differential quadrature method along the radial and axial directions, allows one to deal with curved panel with arbitrary thickness distribution of material properties and also to implement the effects of the elastic foundations as a boundary condition on the lower surface of the curved panel efficiently and in an exact manner. The volume fractions of randomly oriented straight single-walled carbon nanotubes (SWCNTs) are assumed to be graded not only in the radial direction, but also in axial direction of the curved panel. The direct application of CNTs properties in micromechanics models for predicting material properties of the nanotube/polymer composite is inappropriate without taking into account the effects associated with the significant size difference between a nanotube and a typical carbon fiber. In other words, continuum micromechanics equations cannot capture the scale difference between the nano and micro-levels. In order to overcome this limitation, a virtual equivalent fiber consisting of nanotube and its inter-phase which is perfectly bonded to surrounding resin is applied. In this research work, an equivalent continuum model based on the Eshelby–Mori–Tanaka approach is employed to estimate the effective constitutive law of the elastic isotropic medium (matrix) with oriented straight CNTs. The effects of elastic foundation stiffness parameters, various geometrical parameters on the vibration characteristics of CGCNTR curved panel, are investigated, and also, different types of volume fraction profiles along the radial and axial directions of the panels and elastic coefficients of foundation of bidirectional curved panels resting on a two-parameter elastic foundation are studied. Moreover, vibration behavior of 2-D continuously graded nanocomposite panels are compared with conventional one-dimensional nanocomposite panels. From this study, some conclusions can be made:

• It is observed, for the large values of Winkler elastic coefficient, the shearing layer elastic coefficient has less effect and the results become independent of it, in other words the non-dimensional natural frequencies converge with increasing Winkler foundation stiffness.

• The results show that the variation of Winkler elastic coefficient has little effect on the non-dimensional natural frequency at different values of shearing layer elastic coefficient. It is clear that with increasing the shearing layer elastic coefficient of the foundation, the frequency parameters increase to some limit values and for the large values of shearing layer elastic coefficient; the frequency parameters become independent of it.

• The frequency parameter decreases rapidly with the increase of the length-to-mean radius ratio and then remains almost unaltered for the long cylindrical panel (L _z /R > 5).

• The interesting results show that the lowest magnitude frequency parameter is obtained by using a classical–classical volume fraction profile. It can be concluded that a graded CNTs volume fraction in two directions has higher capabilities to reduce the natural frequency than a conventional 1-D nanocomposite.

• It is found that the frequency parameter decreases by increasing the radial volume fraction index $(\gamma_{r} )$.

• For the all length-to-mean radius ratio (L _z /R), classical–classical volume fraction profile has the lowest frequencies followed by classical–symmetric, classical, symmetric–symmetric and symmetric profiles.

Based on the achieved results, using 2-D six-parameter power-law distribution leads to a more flexible design so that maximum or minimum value of natural frequency can be obtained in a required manner.

Appendix

The Hill’s elastic moduli are found as (Shi et al. 2004):

$$\begin{aligned} \varepsilon_{r} = k = \frac{{E_{m} \{ E_{m} f_{m} + 2k_{r} (1 + \upsilon_{m} )[1 + f_{r} (1 - 2\upsilon_{m} )]\} }}{{2(1 + \upsilon_{m} )[E_{m} (1 + f_{r} - 2\upsilon_{m} ) + 2f_{m} k_{r} (1 - \upsilon_{m} - 2\upsilon_{m}^{2} )]}}, \hfill \\ l = \frac{{E_{m} \{ \upsilon_{m} f_{m} [E_{m} + 2k_{r} (1 + \upsilon_{m} )] + 2f_{r} k_{r} (1 - \upsilon_{m}^{2} )\} }}{{(1 + \upsilon_{m} )[E_{m} (1 + f_{r} - 2\upsilon_{m} ) + 2f_{m} k_{r} (1 - \upsilon_{m} - 2\upsilon_{m}^{2} )]}}, \hfill \\ n = \frac{{E_{m}^{2} f_{m} (1 + f_{r} - f_{m} \upsilon_{m} ) + 2f_{m} f_{r} (k_{r} n_{r} - l_{r}^{2} )(1 + \upsilon_{m} )^{2} (1 - 2\upsilon_{m} )}}{{(1 + \upsilon_{m} )[E_{m} (1 + f_{r} - 2\upsilon_{m} ) + 2f_{m} k_{r} (1 - \upsilon_{m} - 2\upsilon_{m}^{2} )]}} \hfill \\ \quad + \frac{{E_{m} [2f_{m}^{2} k_{r} (1 - \upsilon_{m} ) + f_{r} n_{r} (1 + f_{r} - 2\upsilon_{m} ) - 4f_{m} l_{r} \upsilon_{m} ]}}{{E_{m} (1 + f_{r} - 2\upsilon_{m} ) + 2f_{m} k_{r} (1 - \upsilon_{m} - 2\upsilon_{m}^{2} )}}, \hfill \\ p = \frac{{E_{m} [E_{m} f_{m} + 2p_{r} (1 + \upsilon_{m} )(1 + f_{r} )]}}{{2(1 + \upsilon_{m} )[E_{m} (1 + f_{r} ) + 2f_{m} p_{r} (1 + \upsilon_{m} )]}}, \hfill \\ k = \frac{{E_{m} [E_{m} f_{m} + 2m_{r} (1 + \upsilon_{m} )(3 + f_{r} - 4\upsilon_{m} )]}}{{2(1 + \upsilon_{m} )\{ E_{m} [f_{m} + 4f_{r} (1 - \upsilon_{m} )] + 2f_{m} m_{r} (3 - \upsilon_{m} - 4\upsilon_{m}^{2} )\} }}, \hfill \\ \end{aligned}$$

$$\begin{aligned} \alpha_{r} = \frac{{3\left({K_{m} + G_{m} } \right) + k_{r} + l_{r} }}{{3\left({k_{r} + G_{m} } \right)}} \hfill \\ \beta_{r} = \frac{1}{5}\left[ {\frac{{4G_{m} + 2k_{r} + l_{r} }}{{3\left({G_{m} + k_{r} } \right)}} + \frac{{4G_{m} }}{{G_{m} + p_{r} }} + \frac{{2\left[ {G_{m} \frac{{\left({3K_{m} + G_{m} } \right)}}{{}} + G_{m} \left({3K_{m} + 7G_{m} } \right)} \right]}}{{G_{m} \left({3K_{m} + G_{m} } \right) + m_{r} \left({3K_{m} + 7G_{m} } \right)}}} \right] \hfill \\ \delta_{r} = \frac{1}{3}\left[ {n_{r} + 2l_{r} + \frac{{\left({2k_{r} + l} \right)\left({3K_{m} + 2G_{m} - l_{r} } \right)}}{{G_{m} + k_{r} }}} \right] \hfill \\ \eta_{r} = \frac{1}{5}\left[ {\frac{2}{3}\left({n_{r} - l_{r} } \right) + \frac{{8G_{m} p_{r} }}{{G_{m} + p_{r} }} + \frac{{2\left({k_{r} - l_{r} } \right)\left({2G_{m} + l_{r} } \right)}}{{3\left({G_{m} + k_{r} } \right)}}} \right] + \frac{1}{5}\left[ {\frac{{8m_{r} G_{m} \left({3K_{m} + 4G_{m} } \right)}}{{3K_{m} \left({m_{r} + G_{m} } \right) + G_{m} \left({7m_{r} + G_{m} } \right)}}} \right]. \hfill \\ \end{aligned}$$