Introduction

Heat exchangers play a key role in cooling systems and power cycles thanks to their anomalous thermal features, contact surface area and the great heat transfer coefficient. Depending on the application, type of the coolant, the rate of cooling and amount of the heat transfer rate, different models and standards have been defined to fabricate efficient heat exchanging media [1,2,3,4,5,6,7]. When it comes to the surface cooling technology, liquid blocks and heat sinks are pioneer types of heat exchanging media with the capability to remove the significant amount of thermal heat dissipated from the heating surface using a very small space [4, 8,9,10]. For instance, to cool a central processing unit (CPU), normally a heat sink equipped with a forced convective fan is used which is not only a noiseless technology but also an efficient conductive/convective cooling system. However, air and conventional coolants used in such systems have reached their limitations [11,12,13,14]. For example, the thermal conductivity of water is around 0.59 W/m K, which is way lower than other coolants such as liquid metals, silicone-based liquid coolants and oil-based working fluids [12, 15, 16]. Thereby, seeking some alternatives to replace the conventional coolant has been targeted by the researchers.

Since nanofluid was introduced in Aragon National Laboratories (ANL) [17, 18], extensive studies have been conducted to further understand the micro-mechanisms involved in the nanofluids. By a definition, a nanofluid is a colloidal mixture of a conventional coolant and some conductive particles with the nominal size of zero to 100 nano-meters [19,20,21,22]. The presence of these nanoparticles can intensify some thermo-physical properties of the nanofluids including thermal conductivity, heat capacity, and density. Together with these properties, viscosity has also been reported to be changed due to the particle–particle behaviour [23,24,25,26,27]. Thanks to the changes occurred in the physical properties of the coolant, an enhancement in the heat transfer coefficient has been reported in the literature [28,29,30], while there are some studies that vote against the enhancement of heat transfer due to the nanofluids [31,32,33]. Such controversial reports are the main driver for further study on nanofluids. That being said, much effort has been made to implement nanofluid for cooling purposes not only in the heat exchangers but also in cooling systems. For example, in several studies conducted by Sarafraz et al., on various groups of nanofluids [12, 34,35,36,37] and base fluids [34, 38,39,40,41,42,43] and for different thermodynamic systems [11, 37, 44,45,46,47,48], the heat transfer characteristics of carbon nanotube-based nanofluid inside the various heat exchangers were investigated. They also conducted the experiments on some modified surfaces with circular fins, rectangular channels and tubular cross sections with the view to enhance the heat transfer coefficient, bubble formation (in two-phase experiments) while taking advantages of nanofluid to enhance the thermo-physical properties of the water. They found out that the HTC on the smooth heating surface decreased, while for the modified one, the HTC increased by 56% and 77% for wt% = 0.1 and wt% = 0.3, respectively. They also noticed that the bubble formation might be affected due to the presence of nanofluids which created a fouling layer on the surface resulting in the change in HTC.

Apart from two-phase experiments, some researchers focused on the nanofluid’s physical properties. Much effort has made to investigate the influence of nanoparticles on the enhancement of the thermal conductivity and the density of nanofluids with the view to enhance the HTC and the ability of nanofluid for thermal energy storage. It has been shown that such conductive particles have plausible influence on the heat capacity, thermal conductivity and density of the base fluid. However, disadvantage of presence of nanoparticles is reflected in the increase in the value of the pressure drop and also a deterioration in the HTC in boiling and evaporation studies [49,50,51,52,53].

There are other groups of study focusing on the potential of nanofluids on the enhancement of the forced convective heat transfer in the cooling and heating systems. For example, in an empirical study performed by Han et al. [54], several experiments were conducted to identify and measure the effect of aluminium oxide nanofluid on the HTC of the system in a pipe–pipe heat exchanging medium. They showed that the HTC of the nanofluid can be increased with an increase in the concentration, film temperature and flow rate of nanofluid. A maximum enhancement of ~ 24% for the largest concentration of nanoparticles was reported. Similar findings were also demonstrated by Bahraei et al. [55] by doing some experiments on a mini-channel heat exchanging system. They reported 53% enhancement in the HTC of nanofluid. Sarkar et al. [56] experimentally evaluated the heat transfer performance of a PHE (plate heat exchanger) working with a mixture of two different nanofluids. The HTC increased by 39.1% in comparison with the base fluid. Vinod et al. [57], conducted some experiments on various nanofluids including iron oxide, alumina and copper oxide in a shell and tube cooler. He found that the HTC of the system increased significantly which was attributed to the presence of the nanoparticles. In another research conducted by Kumar et al. [58], the HTC of a nanofluid inside a PHE was experimentally measured and it was found that not only the HTC of the system is improved but also the exergic efficiency of the system can be increased which is due to the heat dissipation with nanoparticles. Also, Brownian motion and thermo-phoresis phenomena were responsible for these enhancements. Anoop et al. [59] studied the potential effect of silica nanofluid on the HTC and pressure drop in an industrial heat exchanger with the view to put one step forward towards the commercialization of nanofluids. Their results were later confirmed by Peyghambarzadeh et al. [60,61,62]. Despite the promising enhancement in the HTC, still pumping power, pressure drop and friction factors were the main challenging parameters. The enhancement in the pressure drop was attributed to the frictional forces caused by nanoparticles. Such enhancement in frictional forces further increased the viscosity of nanofluid resulting in the pressure drop enhancement. Hence, no firm conclusion was made on the nanofluids unless more experiments are conducted.

Facing the above literature, further investigation is required on the plausible application of the nanofluids as the working fluid inside the heat exchanging medium. Zirconia nanoparticles have plausible thermo-physical characteristics and have recently been used for various applications including two-phase flow systems. However, the thermal performance of zirconia nanofluid dispersed in water in a microchannel under a single-phase flow regime has not been investigated yet. Also, it is expected that by combining the plausible thermal performance of the zirconia nanofluid with the advantages offered by a microchannel, anomalous heat transfer coefficient and thermal performance can be achieved. Hence, in the present research, for the first time, an experimental study is conducted on the heat transfer characteristics of the zirconia nanofluid in a microchannel heat exchanging system. Influence of the fluid flow rate and the heat flux on the HTC, pressure drop and the friction factor of the system is experimentally investigated. Also, the thermo-physical properties of the nanofluids were experimentally measured and compared with the base fluid to better understand the role of the thermo-physical properties on the enhancement and/or deterioration of the heat transfer inside the microchannel.

Experimental

Test rig

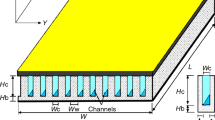
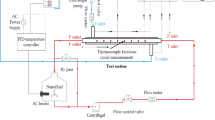
Figure 1a shows the schematic diagram of the experimental setup used in the present research consisting of three main units including but not limited to the circulation part (pipes, pumps, and valves), the microchannel heat exchanger (microchannel block and hosing) and the measurement instruments (pressure sensors, flow meter and thermocouples). The microchannel block is a copper-made cooling block with 25 microchannels with the cross section of 200 µm × 200 µm, which is created with a CNC machining system and also a water jet at 10 MPa to produce the channels with the same roughness. The detailed specifications of the microchannel used in this research have been presented in Fig. 1b. The temperature and the pressure of the nanofluid are constantly monitored with two pressure transmitters (accuracy: 0.1% of reading, purchased from Omega) and two k-type thermocouples (accuracy: 0.1 K, manufactured by RS components) located before and after the test section. A pump is used to circulate the nanofluid within the system. The heat is applied with a flat square heater (manufactured by 3 M, 400 W) by attaching it to the bottom of the microchannel. The flow rate of the nanofluid is constantly monitored with an ultrasonic flow meter (purchased from Cinergy 3, accuracy: 0.1% reading).

Fig. 1
figure 1

a A schematic diagram of the experimental setup used in the present research. b Detailed specifications of the microchannel used in the present research

Full size image

Before running the experiments, the experimental setup was calibrated with deionised water and the system was de-aerated with a vacuum pump to ensure the single-phase heat transfer regime within the system. All the sensors and the instruments were connected to a data logger (manufactured by NI) with frequency of 1 kHz to collect the data and process them with a computer.

The roughness of channels was measured and monitored using a profile-meter (Manufactured by Diverson with the precision of 0.1 µm). Experiments were conducted at various operating conditions represented in Table 1.

Table 1 The experimental conditions used for the present research
Full size table

Nanofluid formulation

The zirconia nanoparticles (20 nm) were purchased from Aztech chemical Co. and were used as purchased. An ultrasonic with 400-W power was also implemented to uniformly disperse the particles within the base fluid. Deionized water was used as the base fluid. To prepare the nanofluids, a desired mass of nanoparticles was dispersed in deionized water (hereafter DI water), followed by adding surfactant (Nonylphenol ethoxilate, NPE) into the base fluid. To crack the agglomeration of the nanoparticles due to the particle–particle attractive forces, an ultrasonic homogeniser was employed at 400 W and 24 kHz). The nanofluids were prepared at wt% = 0.1–0.3. Also, to stabilise the prepared nanofluids, pH of the nanofluids was set to the value in which the zeta potential is out of the range of − 20 to + 20 mV. This is because, in this condition, the longest stability can be achieved. Note that, the time-settlement experiments were used. At first, a sedimentation layer of 1 mm at the bottom of the vessel was targeted and time was measured unless the 1 mm deposition is seen at the bottom of the vessel. The measured time corresponds to the stability of the nanofluid. Notably, the zeta potential was measured using zeta sizer (manufactured by Malvern instrument, accuracy: 1% of reading value). Table 2 shows the results of the stability analysis of the nanofluids. The longest stability belonged to nanofluid at wt% = 0.3 for 8 days. Notably, according to the literature, the zeta potential of a stable nanofluid must not be within the range of − 20 mV < zeta potential < + 20 mV. Hence, we used the sonication, pH setting and stirring to enhance the zeta potential to value smaller than − 20 mV.

Table 2 Summary of the stability tests performed on the nanofluids
Full size table

As can be seen, the prepared nanofluids were stable for more than 2 weeks. The stability of the nanofluids did not change over this period of time. Also, during the test, neither agglomeration nor clustering and deposition were observed in the system.

Data reduction and uncertainty disclosure

For estimating the heat transfer between the microchannel and the working fluid, following equation was implemented:

$$Q = \dot{m} \times C_{\text{p}} \left( {T_{\text{out}} - T_{\text{in}} } \right),$$
(1)

where Q is the heat transfer amount, \(\dot{m}\) is the mass flow rate of working fluid, T is the temperature of working fluid and in and out stand for inlet and outlet. Cp is the specific heat of working fluid. To obtain the heat applied to the microchannel block, the Joule’s effect was utilised according to the following equation:

$$Q = V\; \times \;I,$$
(2)

where V and I are the voltage applied to the heater and the current passing through the heating element’s circuit. The convective heat transfer between fluid and microchannel is estimated using the following equation:

$$Q_{{{\text{conv}} .}} \; = \;\frac{Q}{A} = \frac{{\dot{m} \times C_{\text{p}} \left( {T_{\text{out}} - T_{\text{in}} } \right)}}{{NI\left( {2\eta H + W} \right)}},$$
(3)

where N, H, and l are the number of channels, the height of the microchannels and also the length of each channel, while W is the width of each channel. The Fin’s efficiency is a key parameter which can be obtained with the following equation:

$$\eta = \frac{{\text{Tan} h\left( {mH} \right)}}{mH},$$
(4)

and

$$m = \sqrt {\frac{{2h_{\text{av}} }}{W \times k}} .$$
(5)

In the above equation, k is copper’s thermal conductivity and hav is the average HTC calculating with the following equation:

$$h_{\text{av}} = \frac{1}{l}\int\limits_{0}^{l} {h_{z} {\text{d}}z} .$$
(6)

In this equation, l is the distance from the entrance region of the microchannel to a specific location for which the HTC is calculated:

$$h_{\text{az}} = \frac{{Q_{\text{conv}} }}{{T_{{{\text{w,}}\,{\text{z}}}} - T_{{{\text{b,}}\,{\text{Z}}}} }},$$
(7)

where Tw,z is the surface temperature of the microchannel at each location, Tb,z is the mean temperature of the fluid. Since thermocouples are not exactly located on the surface of the microchannel, the corrected surface temperature can be calculated using the following equation:

$$T_{{{\text{w,}}\,{\text{z}}}} = T_{\text{th}} - Q^{\prime\prime}_{\text{conv}} \times \frac{s}{k},$$
(8)

where s is the small conductive gap between the surface of each channel and the exact location of each thermocouple following the literature [63]. The average temperature of fluid is calculated with the following equation [64]:

$$T_{{{\text{b,}}\,{\text{z}}}} = \frac{z}{l}T_{\text{out}} + \left( {1 - \frac{z}{l}} \right)T_{\text{in}} ,$$
(9)

where z and l are the axial positions of the thermocouples and the length of the microchannel, respectively. To calculate the thermal–hydraulic performance of the microchannel, following equation was used:

$${\text{Thermo - hydraulic}}\;{\text{performance}} = \frac{Nu}{{Nu_{\text{w}} }} \times \left( {\frac{fw}{f}} \right)^{0.3} .$$
(10)

Here, the friction factor can be calculated with the following equation:

$$f = \frac{{\Delta P_{\text{nf}} }}{{\frac{L}{{D_{{{\text{hyd}}.}} }} \times \frac{{2u^{2} }}{{\rho_{\text{nf}} }}}},$$
(11)

where L is the length of microchannel, u is the average bulk velocity (m/s), and Dhyd. is the hydraulic diameter of the each microchannel.

To check the uncertainty of the experiments, Kline–McClintock [65] equation was applied as follows:

$$\Delta R = \sqrt {\left( {\frac{\partial R}{{\partial x_{1} }}\Delta x_{1} } \right)^{2} + \left( {\frac{\partial R}{{\partial x_{2} }}\Delta x_{2} } \right)^{2} + \left( {\frac{\partial R}{{\partial x_{3} }}\Delta x_{3} } \right) + \cdots } ,$$
(12)

where R is a function of the independent variables of x1, x2, x3,…, xn, R = R (x1, x2, x3,…, xn), and \(\Delta x_{1} ,\,\Delta x_{2} ,\,\Delta x_{3} , \ldots ,\Delta x_{n}\) are the uncertainties in these independent variables that can be obtained from the uncertainty of the utilized instruments presented in Table 3. The results of the uncertainty analysis have been represented in the table as well.

Table 3 The uncertainty of the instruments and the parameters used in the present research
Full size table

Results and discussion

Heat flux

Apart from the fluid flow, the heat flux was found to intensify the heat transfer coefficient. Figure 2 presents the dependence of heat transfer coefficient on the applied heat flux for various concentrations of nanofluid. As can be seen, with an increase in the applied heat flux to nanofluid, the heat transfer coefficient increases. For example, for wt% = 0.1 and at heat flux = 20 kW/m2, the heat transfer coefficient is 1490 W/m2 K, while the HTC is 3510 W/(m2K) at the applied heat flux of 70 kW/m2. Again, an increase in the mass concentration of nanofluid enhances the heat transfer coefficient, which can be attributed to the enhancement in the physical properties of the nanofluid.

Fig. 2
figure 2

The dependence of heat transfer coefficient on the applied heat flux and for various mass concentrations of nanofluids

Full size image

Fluid flow

Figure 3 presents the dependence of heat transfer coefficient on the Reynolds number (an index for fluid flow inside the system) for various weight concentration of zirconia/water nanofluids. As can be seen, with an increase in the Reynolds number, the overall heat transfer coefficient of the micro heat exchanger increases. For example, for wt% = 0.3, at Re = 300, the heat transfer coefficient is ~ 2560 W/m2 K, while at Re = 1200, it increases to 5177 W/m2. K. The maximum enhancement measured for the HTC of the nanofluid was 102.1% at wt% = 0.3 and for Reynolds number 1200. The enhancement in the heat transfer coefficient can be attributed to the presence of nanoparticles within the base fluid. Interestingly, with an increase in the heat flux applied to the microheat exchanger, the heat transfer coefficient is also increased. Notably, the nanoparticles enhance the thermal conductivity of the base fluid together with the intensification in the Brownian motion and thermo-phoresis phenomena. In fact, each nanoparticle acts as an energy carrier in a way that it absorbs the energy in high-temperature locations and due to the Brownian motion, it transfers the thermal energy to the cold locations due to the thermo-phoresis effect. Hence, thermo-phoresis is another mechanism which shifts the nanoparticles from a hot region to the cold ones resulting in the better heat transfer.

Fig. 3
figure 3

Dependence of heat transfer coefficient on Reynolds number and for various mass concentrations of nanofluids

Full size image

Mass concentration

Figure 3 (the above figure) also represents the dependence of heat transfer coefficient on Reynolds number for various mass concentrations of nanofluids. As can be seen, with an increase in the mass concentration of nanofluid, the heat transfer coefficient increases. For example, at Re = 500, for wt% = 0.1 and at 40 °C, the heat transfer coefficient is 2890 W/m2 K, while for the same Re number and at wt % = 0.3, it is 3390 W/m2 K, increasing by 17.3%. The enhancement in the heat transfer coefficient can be attributed to the increase in the thermal conductivity and other physical properties of the nanofluid, which has been discussed in Sect. “Thermo-hydraulic performance analysis”. Still, the enhancement in the Brownian motion is the main reason for the enhancement of the heat transfer coefficient at larger Reynolds numbers, which is in accordance with the results published in the literature [66, 67].

Pressure drop

Figure 4 presents the dependence of pressure drop on the Reynolds number for various mass concentrations of nanofluids. As can be seen, with an increase in the Reynolds number, the pressure drop inside the microchannel increases. For example, at Re = 400 and wt% = 0.3, the pressure drop is 14 kPa, while by increasing the Reynolds number to 1200, the pressure drop increases 364% reaching 65 kPa. Likewise, with an increase in the mass concentration of nanofluids, the pressure drop increases inside the microchannel. For example, for a given Reynolds number 1000, at wt% = 0.1, the pressure drop was 41 kPa, while it can reach 48 kPa.

Fig. 4
figure 4

Dependence of pressure drop on Reynolds number and for various mass concentration of nanofluids

Full size image

The increase in the pressure drop is associated with the increase in the viscosity of nanofluid due to the frictional forces between the layers of the fluid. In fact, the presence of nanoparticles increases the frictional forces resulting in the increase in viscosity and the pressure drop of the microchannel.

Friction factor

Figure 5 presents the dependence of friction factor on the Reynolds number for various mass concentration of nanofluids. As can be seen, the friction factor, regardless of its value, follows the Darcy equation for the laminar region (64/Re). Likewise, the presence of nanoparticles increased the friction factor. For example, for a given Reynolds number of 300, at wt% = 0.1, the friction factor is 0.22, while at wt% = 0.3, it reaches 0.2488 increasing by 13.9%. Hence, a trade-off behaviour between the heat transfer coefficient and the pressure drop was identified. In one hand, the presence of nanoparticles increased the heat transfer coefficient, while on the other hand, it also decreased the pressure drop due to the enlargement in the viscosity. Thereby, for the better assessment, thermal performance of the system was evaluated and discussed in Fig. 6.

Fig. 5
figure 5

Dependence of friction factor on Reynolds number and for various mass concentrations of nanofluids

Full size image
Fig. 6
figure 6

Dependence of thermal performance of the system on Reynolds number and for various mass concentrations of nanofluids

Full size image

Thermo-hydraulic performance analysis

Figure 6 presents the dependence of thermal performance of system on Reynolds number for various mass concentrations of nanofluids. As can be seen, the effect of HTC on thermal performance is stronger than that observed for the pressure drop. It means that despite the increase in the value of pressure drop, thermal performance of the system increases. For example, the thermal performance of the system at Re = 600 and wt% = 0.1 is 1.07, while for the same conditions and wt% = 0.3, the thermal performance is 1.19. The maximum enhancement in thermal performance of the system was at the largest Reynolds number and wt% of nanofluids, which was 1.13 for Re = 1200 and wt% = 0.3.

Physical properties of the zirconia nanofluid

Figure 7 presents the dependence of thermo-physical properties on the mass concentrations of nanofluids. Since the experiments were conducted at 40 °C, the measurements of physical properties were conducted at the average temperature of 40 °C and it is assumed that the physical properties of nanofluids remain constant in the range of 40–60 °C, which is a valid assumption [43, 68]. As can be seen, with an increase in the mass concentrations of nanoparticles, the thermal conductivity, density and viscosity of the base fluid increase, while the heat capacity of the nanofluid decreases. The decreases in the heat capacity are largely due to the reduction in the mass fraction of water which has the higher heat capacity, while mass fraction of zirconia increases which has the lower heat capacity. Hence, the total heat capacity of the mixture decreases. For thermal conductivity and density and viscosity, the same explanations are applied. Thermal conductivity, density, and viscosity of zirconia are larger than water resulting in the enhancement of these properties. Therefore, zirconia/water nanofluid offers better thermal properties than water. This is conjunction with the previous studies conducted on nanofluids and particulate fluids [69,70,71,72,73,74,75,76,77,78]. 

Fig. 7
figure 7

Dependence of physical properties of nanofluids on the mass concentrations of nanofluids

Full size image

Figure 8a–c shows the variation of the thermo-physical properties of the nanofluid with temperature within the range of 40–60 °C. As can be seen in Fig. 8a, the thermal conductivity of the nanofluid slightly increases with an increase in the temperature of the system, while it is significantly improved with an increase in the mass concentration of the nanofluid. The highest thermal conductivity of the nanofluid was obtained at wt% = 0.3 (33% enhancement over the pure water, k = 0.61 W/(mK)). The same trend was also observed for the heat capacity and also the viscosity of the nanofluid such that the influence of the temperature of the nanofluid on its thermal properties is very insignificant in comparison with the mass concentration of the nanofluid. Also, a particle size count test was performed to ensure that the size of the nanoparticles is the same. As can be seen in Fig. 8d, the size distribution profile of the nanoparticles showed that the dominant size of the nanoparticles is 20 nm, which is in accordance with the size claimed by the manufacturer.

Fig. 8
figure 8

Variation of thermo-physical properties of the nanofluid with temperature, a thermal conductivity with temperature, b heat capacity with temperature, c viscosity with temperature, d particle size distribution of the nanoparticle sample

Full size image

Validation

Figure 9 presents the results of a rough comparison between the data experimentally measured with the test rig for deionized water and those reported in the literature for other microchannel tests including Azizi et al. [64], Peyghambarzadeh et al. [60] and Sarafraz et al. [25, 47] works. As can be seen, the results showed that there is a very good agreement (~ ±10%) between the data and the literature, which further improves the accuracy and reliability of the test rig for measuring the heat transfer coefficient. For the pressure drop, again a fair agreement with the experimental data reported in the literature was seen within the ~ ±9.1% compared to the results published in the literature [60, 64].

Fig. 9
figure 9

A rough comparison between the experimental results and those reported in the literature

Full size image

Conclusion

Experimental investigation was conducted on the potential of zirconia/water nanofluid to be utilised in a microchannel as a coolant and the following conclusions were made:

  1. 1.

    Results showed that with an increase in the applied heat flux to the microchannel, the heat transfer coefficient increased. The maximum enhancement in the heat transfer coefficient due to the heat flux increment was 181% and for wt% = 0.3. This also further proved that nanofluids have the potential to be utilised in high heat flux conditions as they have plausible heat transfer coefficient at high heat flux conditions.

  2. 2.

    An increase in the flow rate of nanofluid increased the heat transfer coefficient together with the pressure drop showing that there is a trade-off between pressure drop, friction factor and heat transfer coefficient. Hence, determination of thermal performance was found to be a key parameter which shows the real enhancement/reduction in the thermal performance of the system.

  3. 3.

    Thermo-hydraulic performance of the system increased at any mass concentrations, flow rate and heat flux (compared to water) and the effect of heat transfer enhancement on the thermal performance of the system was stronger than pressure drop showing the plausible thermal features of nanofluids for cooling applications.

  4. 4.

    Thermal conductivity, heat capacity and density of water were enhanced by adding the zirconia nanoparticles. These physical properties enhanced the heat transfer within the nanofluid. Brownian motion and thermos-phoresis were the main contributing mechanisms to the heat transfer enhancement.

Overall, the zirconia nanofluid showed a great thermal performance despite a pressure drop augmentation. Hence, this nanofluid is recommended for the thermal applications provided the optimum mass concentration of the nanoparticles is identified to minimise the trade-off between the pressure drop and Nusselt number.