Abstract
An experimental investigation was performed with the view to assess the heat transfer characteristics of a water-based nanofluid in a micro heat exchanger employed to quench a high heat flux heater for industrial and microelectronic cooling applications. The experiments were conducted at heat fluxes 10–70 kW/m2 and for nanofluids at various mass concentrations of 0.1–0.3% and passing flow rates of 0.1–5 l/min. Thermo-physical properties of the nanofluid including thermal conductivity, heat capacity, density and viscosity of nanofluid were experimentally measured at 40 °C close to the temperature of the experiments. Results showed that the heat transfer coefficient and pressure drop were augmented by 40.1% and 67% at wt% = 0.3 compared to the base fluid, respectively. The enhancement in the heat transfer coefficient was associated with the improvement in the thermal conductivity of the base fluid together with the intensification of Brownian motion and thermo-phoresis effect. The increase in the pressure drop was also attributed to the increase in the viscosity of the working fluid which induces layer–layer frictional forces in the bulk of the coolant in micro heat exchanger.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Heat exchangers play a key role in cooling systems and power cycles thanks to their anomalous thermal features, contact surface area and the great heat transfer coefficient. Depending on the application, type of the coolant, the rate of cooling and amount of the heat transfer rate, different models and standards have been defined to fabricate efficient heat exchanging media [1,2,3,4,5,6,7]. When it comes to the surface cooling technology, liquid blocks and heat sinks are pioneer types of heat exchanging media with the capability to remove the significant amount of thermal heat dissipated from the heating surface using a very small space [4, 8,9,10]. For instance, to cool a central processing unit (CPU), normally a heat sink equipped with a forced convective fan is used which is not only a noiseless technology but also an efficient conductive/convective cooling system. However, air and conventional coolants used in such systems have reached their limitations [11,12,13,14]. For example, the thermal conductivity of water is around 0.59 W/m K, which is way lower than other coolants such as liquid metals, silicone-based liquid coolants and oil-based working fluids [12, 15, 16]. Thereby, seeking some alternatives to replace the conventional coolant has been targeted by the researchers.
Since nanofluid was introduced in Aragon National Laboratories (ANL) [17, 18], extensive studies have been conducted to further understand the micro-mechanisms involved in the nanofluids. By a definition, a nanofluid is a colloidal mixture of a conventional coolant and some conductive particles with the nominal size of zero to 100 nano-meters [19,20,21,22]. The presence of these nanoparticles can intensify some thermo-physical properties of the nanofluids including thermal conductivity, heat capacity, and density. Together with these properties, viscosity has also been reported to be changed due to the particle–particle behaviour [23,24,25,26,27]. Thanks to the changes occurred in the physical properties of the coolant, an enhancement in the heat transfer coefficient has been reported in the literature [28,29,30], while there are some studies that vote against the enhancement of heat transfer due to the nanofluids [31,32,33]. Such controversial reports are the main driver for further study on nanofluids. That being said, much effort has been made to implement nanofluid for cooling purposes not only in the heat exchangers but also in cooling systems. For example, in several studies conducted by Sarafraz et al., on various groups of nanofluids [12, 34,35,36,37] and base fluids [34, 38,39,40,41,42,43] and for different thermodynamic systems [11, 37, 44,45,46,47,48], the heat transfer characteristics of carbon nanotube-based nanofluid inside the various heat exchangers were investigated. They also conducted the experiments on some modified surfaces with circular fins, rectangular channels and tubular cross sections with the view to enhance the heat transfer coefficient, bubble formation (in two-phase experiments) while taking advantages of nanofluid to enhance the thermo-physical properties of the water. They found out that the HTC on the smooth heating surface decreased, while for the modified one, the HTC increased by 56% and 77% for wt% = 0.1 and wt% = 0.3, respectively. They also noticed that the bubble formation might be affected due to the presence of nanofluids which created a fouling layer on the surface resulting in the change in HTC.
Apart from two-phase experiments, some researchers focused on the nanofluid’s physical properties. Much effort has made to investigate the influence of nanoparticles on the enhancement of the thermal conductivity and the density of nanofluids with the view to enhance the HTC and the ability of nanofluid for thermal energy storage. It has been shown that such conductive particles have plausible influence on the heat capacity, thermal conductivity and density of the base fluid. However, disadvantage of presence of nanoparticles is reflected in the increase in the value of the pressure drop and also a deterioration in the HTC in boiling and evaporation studies [49,50,51,52,53].
There are other groups of study focusing on the potential of nanofluids on the enhancement of the forced convective heat transfer in the cooling and heating systems. For example, in an empirical study performed by Han et al. [54], several experiments were conducted to identify and measure the effect of aluminium oxide nanofluid on the HTC of the system in a pipe–pipe heat exchanging medium. They showed that the HTC of the nanofluid can be increased with an increase in the concentration, film temperature and flow rate of nanofluid. A maximum enhancement of ~ 24% for the largest concentration of nanoparticles was reported. Similar findings were also demonstrated by Bahraei et al. [55] by doing some experiments on a mini-channel heat exchanging system. They reported 53% enhancement in the HTC of nanofluid. Sarkar et al. [56] experimentally evaluated the heat transfer performance of a PHE (plate heat exchanger) working with a mixture of two different nanofluids. The HTC increased by 39.1% in comparison with the base fluid. Vinod et al. [57], conducted some experiments on various nanofluids including iron oxide, alumina and copper oxide in a shell and tube cooler. He found that the HTC of the system increased significantly which was attributed to the presence of the nanoparticles. In another research conducted by Kumar et al. [58], the HTC of a nanofluid inside a PHE was experimentally measured and it was found that not only the HTC of the system is improved but also the exergic efficiency of the system can be increased which is due to the heat dissipation with nanoparticles. Also, Brownian motion and thermo-phoresis phenomena were responsible for these enhancements. Anoop et al. [59] studied the potential effect of silica nanofluid on the HTC and pressure drop in an industrial heat exchanger with the view to put one step forward towards the commercialization of nanofluids. Their results were later confirmed by Peyghambarzadeh et al. [60,61,62]. Despite the promising enhancement in the HTC, still pumping power, pressure drop and friction factors were the main challenging parameters. The enhancement in the pressure drop was attributed to the frictional forces caused by nanoparticles. Such enhancement in frictional forces further increased the viscosity of nanofluid resulting in the pressure drop enhancement. Hence, no firm conclusion was made on the nanofluids unless more experiments are conducted.
Facing the above literature, further investigation is required on the plausible application of the nanofluids as the working fluid inside the heat exchanging medium. Zirconia nanoparticles have plausible thermo-physical characteristics and have recently been used for various applications including two-phase flow systems. However, the thermal performance of zirconia nanofluid dispersed in water in a microchannel under a single-phase flow regime has not been investigated yet. Also, it is expected that by combining the plausible thermal performance of the zirconia nanofluid with the advantages offered by a microchannel, anomalous heat transfer coefficient and thermal performance can be achieved. Hence, in the present research, for the first time, an experimental study is conducted on the heat transfer characteristics of the zirconia nanofluid in a microchannel heat exchanging system. Influence of the fluid flow rate and the heat flux on the HTC, pressure drop and the friction factor of the system is experimentally investigated. Also, the thermo-physical properties of the nanofluids were experimentally measured and compared with the base fluid to better understand the role of the thermo-physical properties on the enhancement and/or deterioration of the heat transfer inside the microchannel.
Experimental
Test rig
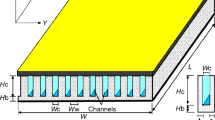
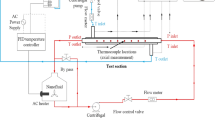
Figure 1a shows the schematic diagram of the experimental setup used in the present research consisting of three main units including but not limited to the circulation part (pipes, pumps, and valves), the microchannel heat exchanger (microchannel block and hosing) and the measurement instruments (pressure sensors, flow meter and thermocouples). The microchannel block is a copper-made cooling block with 25 microchannels with the cross section of 200 µm × 200 µm, which is created with a CNC machining system and also a water jet at 10 MPa to produce the channels with the same roughness. The detailed specifications of the microchannel used in this research have been presented in Fig. 1b. The temperature and the pressure of the nanofluid are constantly monitored with two pressure transmitters (accuracy: 0.1% of reading, purchased from Omega) and two k-type thermocouples (accuracy: 0.1 K, manufactured by RS components) located before and after the test section. A pump is used to circulate the nanofluid within the system. The heat is applied with a flat square heater (manufactured by 3 M, 400 W) by attaching it to the bottom of the microchannel. The flow rate of the nanofluid is constantly monitored with an ultrasonic flow meter (purchased from Cinergy 3, accuracy: 0.1% reading).
Before running the experiments, the experimental setup was calibrated with deionised water and the system was de-aerated with a vacuum pump to ensure the single-phase heat transfer regime within the system. All the sensors and the instruments were connected to a data logger (manufactured by NI) with frequency of 1 kHz to collect the data and process them with a computer.
The roughness of channels was measured and monitored using a profile-meter (Manufactured by Diverson with the precision of 0.1 µm). Experiments were conducted at various operating conditions represented in Table 1.
Nanofluid formulation
The zirconia nanoparticles (20 nm) were purchased from Aztech chemical Co. and were used as purchased. An ultrasonic with 400-W power was also implemented to uniformly disperse the particles within the base fluid. Deionized water was used as the base fluid. To prepare the nanofluids, a desired mass of nanoparticles was dispersed in deionized water (hereafter DI water), followed by adding surfactant (Nonylphenol ethoxilate, NPE) into the base fluid. To crack the agglomeration of the nanoparticles due to the particle–particle attractive forces, an ultrasonic homogeniser was employed at 400 W and 24 kHz). The nanofluids were prepared at wt% = 0.1–0.3. Also, to stabilise the prepared nanofluids, pH of the nanofluids was set to the value in which the zeta potential is out of the range of − 20 to + 20 mV. This is because, in this condition, the longest stability can be achieved. Note that, the time-settlement experiments were used. At first, a sedimentation layer of 1 mm at the bottom of the vessel was targeted and time was measured unless the 1 mm deposition is seen at the bottom of the vessel. The measured time corresponds to the stability of the nanofluid. Notably, the zeta potential was measured using zeta sizer (manufactured by Malvern instrument, accuracy: 1% of reading value). Table 2 shows the results of the stability analysis of the nanofluids. The longest stability belonged to nanofluid at wt% = 0.3 for 8 days. Notably, according to the literature, the zeta potential of a stable nanofluid must not be within the range of − 20 mV < zeta potential < + 20 mV. Hence, we used the sonication, pH setting and stirring to enhance the zeta potential to value smaller than − 20 mV.
As can be seen, the prepared nanofluids were stable for more than 2 weeks. The stability of the nanofluids did not change over this period of time. Also, during the test, neither agglomeration nor clustering and deposition were observed in the system.
Data reduction and uncertainty disclosure
For estimating the heat transfer between the microchannel and the working fluid, following equation was implemented:
where Q is the heat transfer amount, \(\dot{m}\) is the mass flow rate of working fluid, T is the temperature of working fluid and in and out stand for inlet and outlet. Cp is the specific heat of working fluid. To obtain the heat applied to the microchannel block, the Joule’s effect was utilised according to the following equation:
where V and I are the voltage applied to the heater and the current passing through the heating element’s circuit. The convective heat transfer between fluid and microchannel is estimated using the following equation:
where N, H, and l are the number of channels, the height of the microchannels and also the length of each channel, while W is the width of each channel. The Fin’s efficiency is a key parameter which can be obtained with the following equation:
and
In the above equation, k is copper’s thermal conductivity and hav is the average HTC calculating with the following equation:
In this equation, l is the distance from the entrance region of the microchannel to a specific location for which the HTC is calculated:
where Tw,z is the surface temperature of the microchannel at each location, Tb,z is the mean temperature of the fluid. Since thermocouples are not exactly located on the surface of the microchannel, the corrected surface temperature can be calculated using the following equation:
where s is the small conductive gap between the surface of each channel and the exact location of each thermocouple following the literature [63]. The average temperature of fluid is calculated with the following equation [64]:
where z and l are the axial positions of the thermocouples and the length of the microchannel, respectively. To calculate the thermal–hydraulic performance of the microchannel, following equation was used:
Here, the friction factor can be calculated with the following equation:
where L is the length of microchannel, u is the average bulk velocity (m/s), and Dhyd. is the hydraulic diameter of the each microchannel.
To check the uncertainty of the experiments, Kline–McClintock [65] equation was applied as follows:
where R is a function of the independent variables of x1, x2, x3,…, xn, R = R (x1, x2, x3,…, xn), and \(\Delta x_{1} ,\,\Delta x_{2} ,\,\Delta x_{3} , \ldots ,\Delta x_{n}\) are the uncertainties in these independent variables that can be obtained from the uncertainty of the utilized instruments presented in Table 3. The results of the uncertainty analysis have been represented in the table as well.
Results and discussion
Heat flux
Apart from the fluid flow, the heat flux was found to intensify the heat transfer coefficient. Figure 2 presents the dependence of heat transfer coefficient on the applied heat flux for various concentrations of nanofluid. As can be seen, with an increase in the applied heat flux to nanofluid, the heat transfer coefficient increases. For example, for wt% = 0.1 and at heat flux = 20 kW/m2, the heat transfer coefficient is 1490 W/m2 K, while the HTC is 3510 W/(m2K) at the applied heat flux of 70 kW/m2. Again, an increase in the mass concentration of nanofluid enhances the heat transfer coefficient, which can be attributed to the enhancement in the physical properties of the nanofluid.
Fluid flow
Figure 3 presents the dependence of heat transfer coefficient on the Reynolds number (an index for fluid flow inside the system) for various weight concentration of zirconia/water nanofluids. As can be seen, with an increase in the Reynolds number, the overall heat transfer coefficient of the micro heat exchanger increases. For example, for wt% = 0.3, at Re = 300, the heat transfer coefficient is ~ 2560 W/m2 K, while at Re = 1200, it increases to 5177 W/m2. K. The maximum enhancement measured for the HTC of the nanofluid was 102.1% at wt% = 0.3 and for Reynolds number 1200. The enhancement in the heat transfer coefficient can be attributed to the presence of nanoparticles within the base fluid. Interestingly, with an increase in the heat flux applied to the microheat exchanger, the heat transfer coefficient is also increased. Notably, the nanoparticles enhance the thermal conductivity of the base fluid together with the intensification in the Brownian motion and thermo-phoresis phenomena. In fact, each nanoparticle acts as an energy carrier in a way that it absorbs the energy in high-temperature locations and due to the Brownian motion, it transfers the thermal energy to the cold locations due to the thermo-phoresis effect. Hence, thermo-phoresis is another mechanism which shifts the nanoparticles from a hot region to the cold ones resulting in the better heat transfer.
Mass concentration
Figure 3 (the above figure) also represents the dependence of heat transfer coefficient on Reynolds number for various mass concentrations of nanofluids. As can be seen, with an increase in the mass concentration of nanofluid, the heat transfer coefficient increases. For example, at Re = 500, for wt% = 0.1 and at 40 °C, the heat transfer coefficient is 2890 W/m2 K, while for the same Re number and at wt % = 0.3, it is 3390 W/m2 K, increasing by 17.3%. The enhancement in the heat transfer coefficient can be attributed to the increase in the thermal conductivity and other physical properties of the nanofluid, which has been discussed in Sect. “Thermo-hydraulic performance analysis”. Still, the enhancement in the Brownian motion is the main reason for the enhancement of the heat transfer coefficient at larger Reynolds numbers, which is in accordance with the results published in the literature [66, 67].
Pressure drop
Figure 4 presents the dependence of pressure drop on the Reynolds number for various mass concentrations of nanofluids. As can be seen, with an increase in the Reynolds number, the pressure drop inside the microchannel increases. For example, at Re = 400 and wt% = 0.3, the pressure drop is 14 kPa, while by increasing the Reynolds number to 1200, the pressure drop increases 364% reaching 65 kPa. Likewise, with an increase in the mass concentration of nanofluids, the pressure drop increases inside the microchannel. For example, for a given Reynolds number 1000, at wt% = 0.1, the pressure drop was 41 kPa, while it can reach 48 kPa.
The increase in the pressure drop is associated with the increase in the viscosity of nanofluid due to the frictional forces between the layers of the fluid. In fact, the presence of nanoparticles increases the frictional forces resulting in the increase in viscosity and the pressure drop of the microchannel.
Friction factor
Figure 5 presents the dependence of friction factor on the Reynolds number for various mass concentration of nanofluids. As can be seen, the friction factor, regardless of its value, follows the Darcy equation for the laminar region (64/Re). Likewise, the presence of nanoparticles increased the friction factor. For example, for a given Reynolds number of 300, at wt% = 0.1, the friction factor is 0.22, while at wt% = 0.3, it reaches 0.2488 increasing by 13.9%. Hence, a trade-off behaviour between the heat transfer coefficient and the pressure drop was identified. In one hand, the presence of nanoparticles increased the heat transfer coefficient, while on the other hand, it also decreased the pressure drop due to the enlargement in the viscosity. Thereby, for the better assessment, thermal performance of the system was evaluated and discussed in Fig. 6.
Thermo-hydraulic performance analysis
Figure 6 presents the dependence of thermal performance of system on Reynolds number for various mass concentrations of nanofluids. As can be seen, the effect of HTC on thermal performance is stronger than that observed for the pressure drop. It means that despite the increase in the value of pressure drop, thermal performance of the system increases. For example, the thermal performance of the system at Re = 600 and wt% = 0.1 is 1.07, while for the same conditions and wt% = 0.3, the thermal performance is 1.19. The maximum enhancement in thermal performance of the system was at the largest Reynolds number and wt% of nanofluids, which was 1.13 for Re = 1200 and wt% = 0.3.
Physical properties of the zirconia nanofluid
Figure 7 presents the dependence of thermo-physical properties on the mass concentrations of nanofluids. Since the experiments were conducted at 40 °C, the measurements of physical properties were conducted at the average temperature of 40 °C and it is assumed that the physical properties of nanofluids remain constant in the range of 40–60 °C, which is a valid assumption [43, 68]. As can be seen, with an increase in the mass concentrations of nanoparticles, the thermal conductivity, density and viscosity of the base fluid increase, while the heat capacity of the nanofluid decreases. The decreases in the heat capacity are largely due to the reduction in the mass fraction of water which has the higher heat capacity, while mass fraction of zirconia increases which has the lower heat capacity. Hence, the total heat capacity of the mixture decreases. For thermal conductivity and density and viscosity, the same explanations are applied. Thermal conductivity, density, and viscosity of zirconia are larger than water resulting in the enhancement of these properties. Therefore, zirconia/water nanofluid offers better thermal properties than water. This is conjunction with the previous studies conducted on nanofluids and particulate fluids [69,70,71,72,73,74,75,76,77,78].
Figure 8a–c shows the variation of the thermo-physical properties of the nanofluid with temperature within the range of 40–60 °C. As can be seen in Fig. 8a, the thermal conductivity of the nanofluid slightly increases with an increase in the temperature of the system, while it is significantly improved with an increase in the mass concentration of the nanofluid. The highest thermal conductivity of the nanofluid was obtained at wt% = 0.3 (33% enhancement over the pure water, k = 0.61 W/(mK)). The same trend was also observed for the heat capacity and also the viscosity of the nanofluid such that the influence of the temperature of the nanofluid on its thermal properties is very insignificant in comparison with the mass concentration of the nanofluid. Also, a particle size count test was performed to ensure that the size of the nanoparticles is the same. As can be seen in Fig. 8d, the size distribution profile of the nanoparticles showed that the dominant size of the nanoparticles is 20 nm, which is in accordance with the size claimed by the manufacturer.
Validation
Figure 9 presents the results of a rough comparison between the data experimentally measured with the test rig for deionized water and those reported in the literature for other microchannel tests including Azizi et al. [64], Peyghambarzadeh et al. [60] and Sarafraz et al. [25, 47] works. As can be seen, the results showed that there is a very good agreement (~ ±10%) between the data and the literature, which further improves the accuracy and reliability of the test rig for measuring the heat transfer coefficient. For the pressure drop, again a fair agreement with the experimental data reported in the literature was seen within the ~ ±9.1% compared to the results published in the literature [60, 64].
Conclusion
Experimental investigation was conducted on the potential of zirconia/water nanofluid to be utilised in a microchannel as a coolant and the following conclusions were made:
-
1.
Results showed that with an increase in the applied heat flux to the microchannel, the heat transfer coefficient increased. The maximum enhancement in the heat transfer coefficient due to the heat flux increment was 181% and for wt% = 0.3. This also further proved that nanofluids have the potential to be utilised in high heat flux conditions as they have plausible heat transfer coefficient at high heat flux conditions.
-
2.
An increase in the flow rate of nanofluid increased the heat transfer coefficient together with the pressure drop showing that there is a trade-off between pressure drop, friction factor and heat transfer coefficient. Hence, determination of thermal performance was found to be a key parameter which shows the real enhancement/reduction in the thermal performance of the system.
-
3.
Thermo-hydraulic performance of the system increased at any mass concentrations, flow rate and heat flux (compared to water) and the effect of heat transfer enhancement on the thermal performance of the system was stronger than pressure drop showing the plausible thermal features of nanofluids for cooling applications.
-
4.
Thermal conductivity, heat capacity and density of water were enhanced by adding the zirconia nanoparticles. These physical properties enhanced the heat transfer within the nanofluid. Brownian motion and thermos-phoresis were the main contributing mechanisms to the heat transfer enhancement.
Overall, the zirconia nanofluid showed a great thermal performance despite a pressure drop augmentation. Hence, this nanofluid is recommended for the thermal applications provided the optimum mass concentration of the nanoparticles is identified to minimise the trade-off between the pressure drop and Nusselt number.
Abbreviations
- A :
-
The microchannel surface area, m2
- \(C_{\text{p}}\) :
-
The heat capacity of the eutectic, kJ/kg °C
- d :
-
Diameter of the microchannel (hydraulic diameter), m
- f :
-
Friction factor
- H :
-
Height of microchannel, m
- I :
-
Digital current, A
- k :
-
Thermal conductivity, W/m °C
- L or L :
-
Length, m
- m :
-
Fin constant
- \(\dot{m}\,\) :
-
Mass flow rate, kg/m2 s
- N :
-
Number of microchannel
- Q :
-
Heat transfer, W
- Qʹʹ:
-
Applied heat flux, kW/m2
- s :
-
Distance between thermocouple and wall of microchannel, m
- T :
-
Temperature, °C
- u :
-
Fluid mean velocity, m/s
- V :
-
Voltage, V
- W :
-
Width of microchannel, m
- z :
-
Axial distance, m
- \(\eta\) :
-
Efficiency of the fin
- \(\rho\) :
-
Density, kg/m3
- \(\nu\) :
-
Fluid flow rate, m/s
- \(\mu\) :
-
Viscosity, cP
References
Mohammed H, Bhaskaran G, Shuaib N, Saidur R (2011) Heat transfer and fluid flow characteristics in microchannels heat exchanger using nanofluids: a review. Renew Sustain Energy Rev 15:1502–1512
Pettigrew M, Taylor C (1991) Fluidelastic instability of heat exchanger tube bundles: review and design recommendations. J Pressure Vessel Technol 113:242–256
Huminic G, Huminic A (2012) Application of nanofluids in heat exchangers: a review. Renew Sustain Energy Rev 16:5625–5638
Nakhjavani M, Nikounezhad N, Ashtarinezhad A, Shirazi FH (2016) Human lung carcinoma reaction against metabolic serum deficiency stress. Iran J Pharm Res 15:817
Bahiraei M, Salmi HK, Safaei MR (2019) Effect of employing a new biological nanofluid containing functionalized graphene nanoplatelets on thermal and hydraulic characteristics of a spiral heat exchanger. Energy Convers Manage 180:72–82
Goodarzi M, Amiri A, Goodarzi MS, Safaei MR, Karimipour A, Languri EM, Dahari M (2015) Investigation of heat transfer and pressure drop of a counter flow corrugated plate heat exchanger using MWCNT based nanofluids. Int Commun Heat Mass Transfer 66:172–179
Goodarzi M, Kherbeet AS, Afrand M, Sadeghinezhad E, Mehrali M, Zahedi P, Wongwises S, Dahari M (2016) Investigation of heat transfer performance and friction factor of a counter-flow double-pipe heat exchanger using nitrogen-doped, graphene-based nanofluids. Int Commun Heat Mass Transfer 76:16–23
Sarafraz M, Arya A, Hormozi F, Nikkhah V (2017) On the convective thermal performance of a CPU cooler working with liquid gallium and CuO/water nanofluid: a comparative study. Appl Therm Eng 112:1373–1381
Arya A, Shahmiry S, Nikkhah V, Sarafraz MM (2017) Cooling of high heat flux flat surface with nanofluid assisted convective loop: experimental assessment. Arch Mech Eng 64:519–531
Bahmani MH, Sheikhzadeh G, Zarringhalam M, Akbari OA, Alrashed AA, Shabani GAS, Goodarzi M (2018) Investigation of turbulent heat transfer and nanofluid flow in a double pipe heat exchanger. Adv Powder Technol 29:273–282
Sarafraz MM, Hormozi F (2014) Forced convective and nucleate flow boiling heat transfer to alumnia nanofluids. Periodica Polytech Chem Eng 58:37–46
Sarafraz M, Nikkhah V, Nakhjavani M, Arya A (2017) Fouling formation and thermal performance of aqueous carbon nanotube nanofluid in a heat sink with rectangular parallel microchannel. Appl Therm Eng 123:29–39
Abdollahi A, Darvanjooghi MHK, Karimipour A, Safaei MR (2018) Experimental study to obtain the viscosity of CuO-loaded nanofluid: effects of nanoparticles’ mass fraction, temperature and basefluid’s types to develop a correlation. Meccanica 53:3739–3757
Karimipour A, Bagherzadeh SA, Goodarzi M, Alnaqi AA, Bahiraei M, Safaei MR, Shadloo MS (2018) Synthesized CuFe2O4/SiO2 nanocomposites added to water/EG: evaluation of the thermophysical properties beside sensitivity analysis & EANN. Int J Heat Mass Transf 127:1169–1179
Alrashed AA, Karimipour A, Bagherzadeh SA, Safaei MR, Afrand M (2018) Electro-and thermophysical properties of water-based nanofluids containing copper ferrite nanoparticles coated with silica: experimental data, modeling through enhanced ANN and curve fitting. Int J Heat Mass Transf 127:925–935
Alrashed AA, Gharibdousti MS, Goodarzi M, de Oliveira LR, Safaei MR, Bandarra Filho EP (2018) Effects on thermophysical properties of carbon based nanofluids: experimental data, modelling using regression, ANFIS and ANN. Int J Heat Mass Transf 125:920–932
Eastman JA, Choi S, Li S, Yu W, Thompson L (2001) Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl Phys Lett 78:718–720
Keblinski P, Phillpot S, Choi S, Eastman J (2002) Mechanisms of heat flow in suspensions of nano-sized particles (nanofluids). Int J Heat Mass Transf 45:855–863
Eastman J, Choi U, Li S, Thompson L, Lee S (1996) Enhanced thermal conductivity through the development of nanofluids. In: MRS online proceedings library archive, p 457
Abbassi MA, Safaei MR, Djebali R, Guedri K, Zeghmati B, Alrashed AA (2018) LBM simulation of free convection in a nanofluid filled incinerator containing a hot block. Int J Mech Sci 144:172–185
Maleki H, Safaei MR, Togun H, Dahari M (2018) Heat transfer and fluid flow of pseudo-plastic nanofluid over a moving permeable plate with viscous dissipation and heat absorption/generation. J Therm Anal Calorim 2018:1–12
Bahrami M, Akbari M, Bagherzadeh SA, Karimipour A, Afrand M, Goodarzi M (2018) Develop 24 dissimilar ANNs by suitable architectures & training algorithms via sensitivity analysis to better statistical presentation: measure MSEs between targets and ANN for Fe–CuO/Eg–water nanofluid. Phys A Stat Mech Appl 519:159–168
Sarafraz M, Arjomandi M (2018) Demonstration of plausible application of gallium nano-suspension in microchannel solar thermal receiver: experimental assessment of thermo-hydraulic performance of microchannel. Int Commun Heat Mass Transfer 94:39–46
Sarafraz M, Arjomandi M (2018) Thermal performance analysis of a microchannel heat sink cooling with copper oxide-indium (CuO/In) nano-suspensions at high-temperatures. Appl Therm Eng 137:700–709
Sarafraz M, Arya H, Arjomandi M (2018) Thermal and hydraulic analysis of a rectangular microchannel with gallium-copper oxide nano-suspension. J Mol Liq 263:382–389
Sarafraz M, Arya H, Saeedi M, Ahmadi D (2018) Flow boiling heat transfer to MgO-therminol 66 heat transfer fluid: experimental assessment and correlation development. Appl Therm Eng 138:552–562
Maleki H, Safaei MR, Alrashed AA, Kasaeian A (2018) Flow and heat transfer in non-Newtonian nanofluids over porous surfaces. J Therm Anal Calorim 2018:1–12
Murshed SS, De Castro CN, Lourenço M, Lopes M, Santos F (2011) A review of boiling and convective heat transfer with nanofluids. Renew Sustain Energy Rev 15:2342–2354
Hosseini SM, Safaei MR, Goodarzi M, Alrashed AA, Nguyen TK (2017) New temperature, interfacial shell dependent dimensionless model for thermal conductivity of nanofluids. Int J Heat Mass Transf 114:207–210
Arani AAA, Akbari OA, Safaei MR, Marzban A, Alrashed AA, Ahmadi GR, Nguyen TK (2017) Heat transfer improvement of water/single-wall carbon nanotubes (SWCNT) nanofluid in a novel design of a truncated double-layered microchannel heat sink. Int J Heat Mass Transf 113:780–795
Wang X-Q, Mujumdar AS (2007) Heat transfer characteristics of nanofluids: a review. Int J Therm Sci 46:1–19
Das SK, Choi SU, Patel HE (2006) Heat transfer in nanofluids—a review. Heat Transfer Eng 27:3–19
Aghaei A, Sheikhzadeh GA, Goodarzi M, Hasani H, Damirchi H, Afrand M (2018) Effect of horizontal and vertical elliptic baffles inside an enclosure on the mixed convection of a MWCNTs-water nanofluid and its entropy generation. Eur Phys J Plus 133:486
Arya A, Sarafraz M, Shahmiri S, Madani S, Nikkhah V, Nakhjavani S (2018) Thermal performance analysis of a flat heat pipe working with carbon nanotube-water nanofluid for cooling of a high heat flux heater. Heat Mass Transf 54:985–997
Sarafraz M, Hormozi F (2016) Heat transfer, pressure drop and fouling studies of multi-walled carbon nanotube nano-fluids inside a plate heat exchanger. Exp Thermal Fluid Sci 72:1–11
Sarafraz M, Hormozi F, Nikkhah V (2016) Thermal performance of a counter-current double pipe heat exchanger working with COOH–CNT/water nanofluids. Exp Thermal Fluid Sci 78:41–49
Sarafraz M, Hormozi F, Silakhori M, Peyghambarzadeh S (2016) On the fouling formation of functionalized and non-functionalized carbon nanotube nano-fluids under pool boiling condition. Appl Therm Eng 95:433–444
Nakhjavani M, Nikkhah V, Sarafraz M, Shoja S, Sarafraz M (2017) Green synthesis of silver nanoparticles using green tea leaves: experimental study on the morphological, rheological and antibacterial behaviour. Heat Mass Transf 53:3201–3209
Nikkhah V, Sarafraz M, Hormozi F (2015) Application of spherical copper oxide (II) water nano-fluid as a potential coolant in a boiling annular heat exchanger. Chem Biochem Eng Q 29:405–415
Salari E, Peyghambarzadeh M, Sarafraz MM, Hormozi F (2016) Boiling heat transfer of alumina nano-fluids: role of nanoparticle deposition on the boiling heat transfer coefficient. Periodica Polytech Chem Eng 60:252–258
Salari E, Peyghambarzadeh S, Sarafraz M, Hormozi F, Nikkhah V (2017) Thermal behavior of aqueous iron oxide nano-fluid as a coolant on a flat disc heater under the pool boiling condition. Heat Mass Transf 53:265–275
Sarafraz M (2013) Experimental investigation on pool boiling heat transfer to formic acid, propanol and 2-butanol pure liquids under the atmospheric pressure. J Appl Fluid Mech 6:73–79
Sarafraz M, Hormozi F (2014) Application of thermodynamic models to estimating the convective flow boiling heat transfer coefficient of mixtures. Exp Thermal Fluid Sci 53:70–85
Sarafraz M, Hormozi F, Kamalgharibi M (2014) Sedimentation and convective boiling heat transfer of CuO–water/ethylene glycol nanofluids. Heat Mass Transf 50:1237–1249
Sarafraz M, Hormozi F, Peyghambarzadeh S, Vaeli N (2015) Upward flow boiling to DI-water and Cuo nanofluids inside the concentric annuli. J Appl Fluid Mech 8:4
Sarafraz M, Nikkhah V, Madani S, Jafarian M, Hormozi F (2017) Low-frequency vibration for fouling mitigation and intensification of thermal performance of a plate heat exchanger working with CuO/water nanofluid. Appl Therm Eng 121:388–399
Sarafraz M, Nikkhah V, Nakhjavani M, Arya A (2018) Thermal performance of a heat sink microchannel working with biologically produced silver-water nanofluid: experimental assessment. Exp Thermal Fluid Sci 91:509–519
Sarafraz MM, Peyghambarzadeh S, Alavi FS (2012) Experimental studies on nucleate pool boiling heat transfer to ethanol/MEG/DEG ternary mixture as a new coolant. Chem Ind Chem Eng Q 18:577–586
Choi S, Zhang Z, Yu W, Lockwood F, Grulke E (2001) Anomalous thermal conductivity enhancement in nanotube suspensions. Appl Phys Lett 79:2252–2254
Chon CH, Kihm KD, Lee SP, Choi SU (2005) Empirical correlation finding the role of temperature and particle size for nanofluid (Al2O3) thermal conductivity enhancement. Appl Phys Lett 87:153107
Fan L, Khodadadi JM (2011) Thermal conductivity enhancement of phase change materials for thermal energy storage: a review. Renew Sustain Energy Rev 15:24–46
Rahimi Gheynani A, Ali Akbari O, Zarringhalam M, Ahmadi Sheikh Shabani G, Alnaqi AA, Goodarzi M, Toghraie D (2018) Investigating the effect of nanoparticles diameter on turbulent flow and heat transfer properties of non-Newtonian carboxymethyl cellulose/CuO fluid in a microtube. Int J Numer Methods Heat Fluid Flow
Alrashed AA, Akbari OA, Heydari A, Toghraie D, Zarringhalam M, Shabani GAS, Seifi AR, Goodarzi M (2018) The numerical modeling of water/FMWCNT nanofluid flow and heat transfer in a backward-facing contracting channel. Phys B 537:176–183
Han D, He W, Asif F (2017) Experimental study of heat transfer enhancement using nanofluid in double tube heat exchanger. Energy Procedia 142:2547–2553
Bahiraei M, Godini A, Shahsavar A (2018) Thermal and hydraulic characteristics of a minichannel heat exchanger operated with a non-Newtonian hybrid nanofluid. J Taiwan Inst Chem Engineers 84:149–161
Bhattad A, Sarkar J, Ghosh P (2018) Discrete phase numerical model and experimental study of hybrid nanofluid heat transfer and pressure drop in plate heat exchanger. Int Commun Heat Mass Transfer 91:262–273
Naik BAK, Vinod AV (2018) Heat transfer enhancement using non-Newtonian nanofluids in a shell and helical coil heat exchanger. Exp Thermal Fluid Sci 90:132–142
Kumar V, Tiwari AK, Ghosh SK (2017) Characterization and performance of nanofluids in plate heat exchanger. Mater Today Proc 4:4070–4078
Anoop K, Cox J, Sadr R (2013) Thermal evaluation of nanofluids in heat exchangers. Int Commun Heat Mass Transfer 49:5–9
Peyghambarzadeh S, Hashemabadi S, Chabi A, Salimi M (2014) Performance of water based CuO and Al2O3 nanofluids in a Cu–Be alloy heat sink with rectangular microchannels. Energy Convers Manage 86:28–38
Chabi A, Zarrinabadi S, Peyghambarzadeh S, Hashemabadi S, Salimi M (2017) Local convective heat transfer coefficient and friction factor of CuO/water nanofluid in a microchannel heat sink. Heat Mass Transf 53:661–671
Peyghambarzadeh S, Hashemabadi S, Jamnani MS, Hoseini S (2011) Improving the cooling performance of automobile radiator with Al2O3/water nanofluid. Appl Therm Eng 31:1833–1838
Kumar R, Varma H, Agrawal K, Mohanty B (2001) A comprehensive study of modified Wilson plot technique to determine the heat transfer coefficient during condensation of steam and R-134a over single horizontal plain and finned tubes. Heat Transfer Eng 22:3–12
Azizi Z, Alamdari A, Malayeri M (2015) Convective heat transfer of Cu–water nanofluid in a cylindrical microchannel heat sink. Energy Convers Manage 101:515–524
Kline SA, McClintock FA (1953) Describing uncertainties in single-sample experiments. ASME Mech Eng 75:3–8
Prasher R (2005) Brownian-motion-based convective-conductive model for the thermal conductivity of nanofluidsASME 2005 summer heat transfer conference collocated with the ASME 2005 Pacific rim technical conference and exhibition on integration and packaging of MEMS, NEMS, and electronic systems American society of mechanical engineers, pp 343–353
Evans W, Fish J, Keblinski P (2006) Role of Brownian motion hydrodynamics on nanofluid thermal conductivity. Appl Phys Lett 88:093116
Nikkhah V, MM Sarafraz MM, Hormozi F, Peyghambarzadeh SM (2015) Particulate fouling of CuO–water nanofluid at isothermal diffusive condition inside the conventional heat exchanger-experimental and modeling. Exp Thermal Fluid Sci 60:83–95
Sarafraz MM, Peyghambarzadeh SM (2012) Nucleate pool boiling heat transfer to Al2O3-water and TiO2-water nanofluids on horizontal smooth tubes with dissimilar homogeneous materials. Chem Biochem Eng Q 26:199–206
Peyghambarzadeh SM, Sarafraz MM, Vaeli N, Ameri E, Vatani A, Jamialahmadi M (2013) Forced convective and subcooled flow boiling heat transfer to pure water and n-heptane in an annular heat exchanger. Ann Nucl Energy 53:401–410
Salari E, Peyghambarzadeh SM, Sarafraz MM, Hormozi F (2016) Boiling thermal performance of TiO2 aqueous nanofluids as a coolant on a disc copper block. Periodica Polytech Chem Eng 60:106–122
Sarafraz MM, Peyghambarzadeh SM (2012) Influence of thermodynamic models on the prediction of pool boiling heat transfer coefficient of dilute binary mixtures. Int Commun Heat Mass Transfer 39(8):1303–1310
Sarafraz MM, Peyghambarzadeh SM, Alavifazel SA (2012) Enhancement of nucleate pool boiling heat transfer to dilute binary mixtures using endothermic chemical reactions around the smoothed horizontal cylinder. Heat Mass Transfer 48(10):1755–1765
Sarafraz MM, Peyghambarzadeh SM, Alavi Fazel SA, Vaeli N (2013) Nucleate pool boiling heat transfer of binary nano mixtures under atmospheric pressure around a smooth horizontal cylinder. Periodica Polytech Chem Eng 57(1–2):71
Sarafraz MM, Peyghambarzadeh SM, Vaeli N (2012) Subcooled flow boiling heat transfer of ethanol aqueous solutions in vertical annulus space. Chem Indus Chem Eng Quart 18(2):315–327
Sarafraz MM, Hormozi F, Kamalgharibi M (2014) Sedimentation and convective boiling heat transfer of CuO-water/ethylene glycol nanofluids. Heat Mass Transfer 50(9):1237–1249
Sarafraz MM, Hormozi F, Nikkhah V (2016) Thermal performance of a counter-current double pipe heat exchanger working with COOH-CNT/water nanofluids. Exp Thermal Fluid Sci 78:41–49
Sarafraz MM, Hormozi F, Peyghambarzadeh SM (2014) Thermal performance and efficiency of a thermosyphon heat pipe working with a biologically ecofriendly nanofluid. Int Commun Heat Mass Transf 57:297–303
Acknowledgements
The authors of this work tend to appreciate Yazd University for their financial supports.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Nikkhah, V., Nakhjavani, S. Thermal performance of a micro heat exchanger (MHE) working with zirconia-based nanofluids for industrial cooling. Int J Ind Chem 10, 193–204 (2019). https://doi.org/10.1007/s40090-019-0183-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40090-019-0183-6