Numerical analysis and simulation for Rayleigh beam equation with dynamical boundary controls

Abstract

In this paper, the Rayleigh beam system with two dynamical boundary controls is treated. Theoretically, the well-posedness of the weak solution is obtained. Later, we discretize the system by using the Implicit Euler scheme in time and the $P^3$ Hermite finite element in space. In addition, we show the decay of the discrete energy and we establish some a priori error estimates. Finally, some numerical simulations are presented.

1 Introduction

In [1], Wehbe considered the Rayleigh beam equation with two dynamical boundary controls and the energy decay was theoretically established. In [2], the authors consider a clamped Rayleigh beam equation subject to only one dynamical boundary feedback. First, they considered the Rayleigh beam equation subject to only one dynamical boundary control moment, and later, they considered the Rayleigh beam equation subject to only one dynamical boundary control force and established in both cases a theoretical energy decay.

In [3], Rao considered the exact controllability of a hybrid system consisting of an elastic beam, clamped at one end and attached at the other end to a rigid antenna. Such a system is governed by one partial differential equation and two ordinary differential equations. Using the HUM method, they proved that the hybrid system is exactly controllable in an arbitrarily short time in the usual energy space.

In [4], the authors established, using a multiplier method, the polynomial energy decay rate for the smooth solutions of Kirchhoff plates equations. Consequently, they obtained the strong stability in the absence of compactness of the infinitesimal operator.

In [5], Rincon and Copetti studied numerically a locally damped wave equation. Error estimates for the semi-discrete and fully discrete schemes in the energy norm were provided.

In [6], a dynamic contact problem between a viscoelastic beam and a deformable obstacle is considered. The classical Timoshenko beam model is used and the contact is modeled using the well-known normal compliance contact condition. Fully discrete approximations were introduced, A priori error estimates were proved to obtain the linear convergence of the algorithm under an additional regularity condition. A numerical analysis for Bresse system is done in [8] and [7].

The aim of this paper is to study numerically the equation of Rayleigh beam, which is clamped at one end and subjected to two dynamical boundary controls at the other end. At an instant time t, the position y(x, t) of a given point x of the beam is governed by the following system of equations:

$$\begin{aligned} \left\{ \begin{array}{lll} y_{tt}-\gamma y_{xxtt}+y_{xxxx}&{}=&{}0, \\ y(0,t)=y_x(0,t)&{}=&{}0,\\ y_{xx}(1,t)+\eta (t)&{}=&{}0,\\ y_{xxx}(1,t)-\gamma y_{xtt}(1,t)&{}=&{}\xi (t), \end{array}\right. \end{aligned}$$

(1)

where $\gamma >0$ is a physical constant, and $\xi$ and $\eta$ designate, respectively, the dynamical boundary force and moment controls applied at the free end of the beam. The dynamical controls $\xi$ and $\eta$ are given by the following integral system:

$$\begin{aligned} \left\{ \begin{array}{lll} \eta _t(t)-y_{xt}(1,t)+\eta (t)&{}=&{}0, \\ \xi _t(t)-y_t(1,t)+\xi (t)&{}=&{}0, \end{array}\right. \end{aligned}$$

(2)

where $0<x<1, ~t>0$ and the following initial conditions:

$$\begin{aligned} y(x,0)=y_0(x), \ \ y_t(x,0)=y_1(x), \ \ 0<x<1, \ \ \eta (0)=\eta _0, \xi (0)=\xi _0\in \mathbb {R}. \end{aligned}$$

Let y be a smooth solution of the system (1)–(2). The associated energy E(t) is defined by:

$$\begin{aligned} E(t)=\frac{1}{2}\Big (\int _0^1\left( |y_t|^2+\gamma |y_{xt}|^2+|y_{xx}|^2\right) \mathrm{d}x+|\eta (t)|^2+|\xi (t)|^2\Big ). \end{aligned}$$

(3)

A straightforward calculations yields:

$$\begin{aligned} E'(t)=-\left| \eta (t)\right| ^2-\left| \xi (t)\right| ^2\le 0. \end{aligned}$$

(4)

Hence, system (1)–(2) is dissipative in the sense that the energy E(t) is a decreasing function of the time.

The notion of a dynamical control has been studied for the first time by the automaticians in the finite-dimensional case (see Francis [9]). While, in the infinite-dimensional case, the notion of dynamical controls was studied by Russell [10].

Our purpose is to use the finite-element method and to obtain error estimates for the approximation of (1). Moreover, a fully discrete implicit scheme is proposed and analyzed. An outline of the contents of this paper is as follows. In Sect. 2, we show the well-posedness using the Faedo–Galerkin method (see[11]), as well as some regularity results. In Sect. 3, a semi-discrete Galerkin approximation to the solution of (1.1) is analyzed, and in Sect. 4, a fully discrete scheme is considered. We use the $P^3$ Hermite functions in space and the backward Euler method in time. We show that the fully discrete energy decays and derive some stability and error estimates. Finally, the results of numerical experiments illustrating the theoretical results are presented in the last section.

2 Existence and uniqueness

Denote by |.| and (., .) the norm and scalar product in $L^2(0,1)$, respectively, and introduce the energy space:

$$\begin{aligned} V=H^2_E(0,1)=\{\chi \in H^2(0,1)/\chi (0)=\chi _x(0)=0\}. \end{aligned}$$

Denote also by

$$\begin{aligned} H^1_E(0,1)=\{\chi \in H^1(0,1)/\chi (0)=0\}. \end{aligned}$$

Multiply (1)$_1$ by a test function $\upsilon \in H^2_E(0,1)$, and then use Green’s formula with the initial and boundary conditions to obtain the weak form of (1).

Find $y(.,t) \in H^2_E(0,1)$, $\xi (t)\in \mathbb {R}$ and $\eta (t)\in \mathbb {R}$, such that, for all $\upsilon \in H^2_E(0,1)$:

$$\begin{aligned} \left\{ \begin{array}{ll} \left( y_{tt},\upsilon \right) +\gamma \left( y_{xtt},\upsilon _x\right) +\left( y_{xx},\upsilon _{xx}\right) +\xi \upsilon (1)+\eta \upsilon _x(1)=0,&{}\\ \eta _t(t)-y_{xt}(1,t)+\eta (t)=0,&{} \\ \xi _t(t)-y_t(1,t)+\xi (t)=0.&{}\\ \end{array} \right. \end{aligned}$$

(5)

The next theorem provides us with the existence and uniqueness of the solution of (1)–(2) using the Faedo–Galerkin method.

Theorem 2.1

Assume that $y_0,y_1\in H_E^2(0,1)$. Then, for each $T>0$, there exist a unique solution to (1)–(2) under the following regularity:

• (1) $y\in L^\infty (0,T,H^2_E(0,1)\cap H^3(0,1)),$

• (2) $y_t \in L^\infty (0,T,H^2_E(0,1)),$

• (3) $y_{tt} \in L^\infty (0,T,H^1_E(0,1)),$

• (4) $\xi , \xi _t, \eta , \eta _t \in L^\infty (0,T)\cap L^2(0,T),$

• (5) $\left( \gamma y_{tt}-y_{xx}\right) _{xx}=y_{tt}\in L^\infty (0,T,H^1_E(0,1)),$

• (6) $y_{tt}-\gamma y_{xxtt}+y_{xxxx}=0 \, a.e\, in \, (0,1)\times (0,T),$

• (7) $y_{xx}(1,t)+\eta (t)=0,$

• (8) $y_{xxx}(1,t)-\gamma y_{xtt}(1,t)=\xi (t),$

• (9) $y(0)=y_0, \,y_t(0)=y_1,\, \xi (0)=\xi _0, \, and \, \eta (0)=\eta _0.$

Proof

Let $V_m$ be the subspace spanned by $\{\phi _1, \phi _2,...,\phi _m\}$, where $\{\phi _i\}_{i=1}^\infty$ is a smooth basis for V.

There exist two sequences (see [11] p. 513) $(y_0^m)$ and $(y_1^m)$, such that:

$$\begin{aligned} \left\{ \begin{array}{ll} \forall m,\, y_0^m\in V_m,\,\,y_0^m\rightarrow y_0\,\, \text {in}\,V,&{}\\ \forall m,\, y_1^m\in V_m,\,\,y_1^m\rightarrow y_1\,\, \text {in}\,V.&{}\\ \end{array} \right. \end{aligned}$$

(6)

Hence, we have to find $y^m(x,t)=\displaystyle \sum _{i=1}^{m} d_\mathrm{im}(t)\phi _i(x)$, $\xi ^m$ and $\eta ^m \in \mathbb {R},$ satisfying $\forall \upsilon \in V_m$:

$$\begin{aligned} \left\{ \begin{array}{ll} \left( y^m_{tt},\upsilon \right) +\gamma \left( y^m_{xtt},\upsilon _x\right) +\left( y^m_{xx},\upsilon _{xx}\right) +\xi ^m\upsilon (1)+\eta ^m\upsilon _x(1)=0,&{}\\ \eta ^m_t(t)-y^m_{xt}(1,t)+\eta ^m(t)=0,&{} \\ \xi ^m_t(t)-y^m_t(1,t)+\xi ^m(t)=0,&{}\\ \end{array} \right. \end{aligned}$$

(7)

with the initial conditions $y^m(x,0)=y_0^m, y^m_t(x,0)=y_1^m, \xi ^m(0)=\xi _0, \eta ^m(0)=\eta _0$ and $\upsilon \in V_m.$ This initial value problem has a local solution on $[0,T_m]\times [0,T_m]\times [0,T_m]$ by the standard ODE theory. The a priori estimates established below allow us to extend the solution to $[0,T]\times [0,T]\times [0,T]$ for any given T.

Estimate I:

Take $\upsilon =2y_t^m$ in (7)$_1$ to get:

$$\begin{aligned} 2\left( y^m_{tt},y^m_t\right) +2\gamma \left( y^m_{xtt},y^m_{xt}\right) +2\left( y^m_{xx},y^m_{xxt}\right) +2\xi ^my^m_t(1,t)+2\eta ^my^m_{xt}(1,t)=0. \end{aligned}$$

Using (7)$_2$ and (7)$_3$, we obtain:

$$\begin{aligned} \frac{d}{\mathrm{d}t} \left( |y^m_t|^2+\gamma |y^m_{xt}|^2+|y^m_{xx}|^2+|\xi ^m|^2+|\eta ^m|^2\right) +2|\xi ^m|^2+2|\eta ^m|^2=0. \end{aligned}$$

Integrating from 0 to t yields:

$$\begin{aligned} \begin{array}{ll} |y^m_t|^2+\gamma |y^m_{xt}|^2+|y^m_{xx}|^2+|\xi ^m|^2+|\eta ^m|^2+2\displaystyle \int _{0}^{t}\left( |\xi ^m|^2+|\eta ^m|^2\right) ds=\\ \\ |y^m_1|^2+\gamma |y^m_{1x}|^2+|y^m_{0xx}|^2+|\xi ^m_0|^2+|\eta ^m_0|^2\le \\ \\ C\left( |y_1|^2+\gamma |y_{1x}|^2+|y_{0xx}|^2+|\xi _0|^2+|\eta _0|^2\right) . \end{array} \end{aligned}$$

The assumption on the initial data gives the following:

$y^m$ is bounded in $L^\infty (0,T,H^2_E(0,1))$,

$y^m_t$ is bounded in $L^\infty (0,T,H^1_E(0,1))$,

$\xi ^m$ and $\eta ^m$ are bounded in $L^\infty (0,T)\cap L^2(0,T)$,

and the solution can be extended to $[0,T]\times [0,T]\times [0,T]$. Also, there exist three sub-sequences still denoted by $(y^m), (\xi ^m), (\eta ^m),$ such that

$y^m\longrightarrow y$ weak-star in $L^\infty (0,T,H^2_E(0,1)),$

$y^m_t\longrightarrow y_t$ weak-star in $L^\infty (0,T,H^1_E(0,1)),$

$\xi ^m\longrightarrow \xi$ weak-star in $L^\infty (0,T),$

$\xi ^m\longrightarrow \xi$ weak in $L^2(0,T),$

$\eta ^m\longrightarrow \eta$ weak-star in $L^\infty (0,T),$ and

$\eta ^m\longrightarrow \eta$ weak in $L^2(0,T).$

Estimate II:

Differentiating (7) with respect to t and let $\hat{y}^m=y_t^m$, we get:

$$\begin{aligned} \left\{ \begin{array}{ll} \left( \hat{y}^m_{tt},\upsilon \right) +\gamma \left( \hat{y}^m_{xtt},\upsilon _x\right) +\left( \hat{y}^m_{xx},\upsilon _{xx}\right) +\xi ^m_t\upsilon (1)+\eta ^m_t\upsilon _x(1)=0,&{}\\ \eta ^m_{tt}(t)-\hat{y}^m_{xt}(1,t)+\eta ^m_t(t)=0,&{} \\ \xi ^m_{tt}(t)-\hat{y}^m_t(1,t)+\xi ^m_t(t)=0.&{}\\ \end{array} \right. \end{aligned}$$

(8)

Take $\upsilon =2\hat{y}^m_t$ in (8)$_1$:

$$\begin{aligned} 2\left( \hat{y}^m_{tt},\hat{y}^m_t\right) +2\gamma \left( \hat{y}^m_{xtt},\hat{y}^m_{xt}\right) +2\left( \hat{y}^m_{xx},\hat{y}^m_{xxt}\right) +2\xi ^m_t\hat{y}^m_t(1,t)+2\eta ^m_t\hat{y}^m_{xt}(1,t)=0; \end{aligned}$$

use (8)$_2$ and (8)$_3$ to obtain:

$$\begin{aligned} \frac{d}{\mathrm{d}t} \left( |\hat{y}^m_t|^2+\gamma |\hat{y}^m_{xt}|^2+|\hat{y}^m_{xx}|^2+|\xi ^m_t|^2+|\eta ^m_t|^2\right) +2|\xi ^m_t|^2+2|\eta ^m_t|^2=0. \end{aligned}$$

Integrating from 0 to t, we get:

$$\begin{aligned} \begin{array}{ll} |\hat{y}^m_t|^2+\gamma |\hat{y}^m_{xt}|^2+|\hat{y}^m_{xx}|^2+|\xi ^m_t|^2+|\eta ^m_t|^2+2\displaystyle \int _{0}^{t}\left( |\xi ^m_t|^2+|\eta ^m_t|^2\right) ds=\\ \ |y^m_{tt}(0)|^2+\gamma |y^m_{xtt}(0)|^2+|y^m_{xx}(0)|^2+|\xi ^m_t(0)|^2+|\eta ^m_t(0)|^2. \end{array} \end{aligned}$$

(9)

We have to bound $|y^m_{tt}(0)|$, $|y^m_{xtt}(0)|$, $|\xi ^m_t(0)|$, and $|\eta ^m_t(0)|$.

Use after integrating by parts (7)$_1)$ with $\upsilon =y^m_{tt}(0)$ and $t=0$, we get:

$$\begin{aligned} |y^m_{tt}(0)|^2+\gamma |y^m_{xtt}(0)|^2=-(y^m_{xx}(0),y^m_{tt}(0))\le \frac{1}{2}|y^m_{xx}(0)|^2+\frac{1}{2}|y^m_{tt}(0)|^2; \end{aligned}$$

hence:

$$\begin{aligned} |y^m_{tt}(0)|^2\le C\, \text {and} \, |y^m_{xtt}(0)|^2\le C. \end{aligned}$$

Now, use (7)$_2$ for $t=0$ to obtain:

$\eta _t^m(0)=y^m_{xt}(1,0)-\eta ^m(0)=y^m_{1x}(1)-\eta _0.$

Note that

$$\begin{aligned} y^m_{1x}(1)=\int _{0}^{1}y^m_{1xx}(x)\mathrm{d}x\le C|y^m_{1xx}|\le C|y_{1xx}|, \end{aligned}$$

and the regularity on the initial data gives:

$$\begin{aligned} |\eta _t^m(0)|\le C|y_{1xx}|+|\eta _0|\le C. \end{aligned}$$

In the same way, we get:

$$\begin{aligned} |\xi _t^m(0)\le C|y_{1x}|+|\xi _0|\le C. \end{aligned}$$

Combine these results with (9) to get:

$$\begin{aligned} \begin{array}{ll} |\hat{y}^m_t|^2+\gamma |\hat{y}^m_{xt}|^2+|\hat{y}^m_{xx}|^2+|\xi ^m_t|^2+|\eta ^m_t|^2+2\displaystyle \int _{0}^{t}\left( |\xi ^m_t|^2+|\eta ^m_t|^2\right) ds=\\ \ |y^m_{tt}(0)|^2+\gamma |y^m_{xtt}(0)|^2+|y^m_{xx}(0)|^2+|\xi ^m_t(0)|^2+|\eta ^m_t(0)|^2; \end{array} \end{aligned}$$

therefore:

$\hat{y}^m$ is bounded in $L^\infty (0,T,H^2_E(0,1))$,

$\hat{y}^m_t$ is bounded in $L^\infty (0,T,H^1_E(0,1))$, and

$\xi ^m_t$ and $\eta ^m_t$ are bounded in $L^\infty (0,T)\cap L^2(0,T)$.

We conclude that

$y^m_t\longrightarrow y_t$ weak star in $L^\infty (0,T,H^2_E(0,1)),$

$y^m_{tt}\longrightarrow y_{tt}$ weak star in $L^\infty (0,T,H^1_E(0,1)),$

$\xi ^m_t\longrightarrow \xi _t$ weak star in $L^\infty (0,T),$

$\xi ^m_t\longrightarrow \xi _t$ weak in $L^2(0,T),$

$\eta ^m_t\longrightarrow \eta _t$ weak star in $L^\infty (0,T),$ and

$\eta ^m_t\longrightarrow \eta _t$ weak in $L^2(0,T).$

Using the convergence results, we can pass to the limit $m\rightarrow +\infty$ in (7) to obtain:

$$\begin{aligned} \left\{ \begin{array}{ll} \left( y_{tt},\upsilon \right) +\gamma \left( y_{xtt},\upsilon _x\right) +\left( y_{xx},\upsilon _{xx}\right) +\xi \upsilon (1)+\eta \upsilon _x(1)=0,&{}\\ \eta _t(t)-y_{xt}(1,t)+\eta (t)=0,&{} \\ \xi _t(t)-y_t(1,t)+\xi (t)=0.&{}\\ \end{array} \right. \end{aligned}$$

(10)

Using (10)$_1$ for $\upsilon \in D(0,1)$, we get:

$$\begin{aligned} \left( \gamma y_{tt}-y_{xx},\upsilon _{xx}\right) =(y_{tt},\upsilon ), \end{aligned}$$

and since, $y_{tt}\in L^\infty (0,T,H^1_E(0,1)),$ we get:

$\gamma y_{tt}-y_{xx}\in H^3(0,1),$ a.e $t\in [0,T],$ and:

$$\begin{aligned} y_{tt}-\gamma y_{xxtt}+y_{xxxx}=0 \quad a.e \quad in \quad (0,1)\times (0,T). \end{aligned}$$

However, $y_{tt}(.,t) \in H^1(0,1)$, so

$y_{xx}(.,t)\in H^1(0,1)$; that is, $y(.,t)\in H^3(0,1).$

Using Greens formula to Eq. (10)$_1$, we get $\forall \upsilon \in V:$

$$\begin{aligned} \begin{array}{ll} \left( y_{tt},\upsilon \right) -\gamma \left( y_{xxtt},\upsilon \right) +\left( y_{xxxx},\upsilon \right) +\\ \\ \left( \gamma y_{xtt}(1,t)-y_{xxx}(1,t)+\xi (t)\right) \upsilon (1)+\left( y_{xx}(1,t)+\eta \right) \upsilon _x(1)=0;\\ \end{array} \end{aligned}$$

hence:

$$\begin{aligned} \big [\gamma y_{xtt}(1,t)-y_{xxx}(1,t)+\xi (t)\big ]\upsilon (1)+\big [y_{xx}(1,t)+\eta \big ]\upsilon _x(1)=0, \end{aligned}$$

(11)

use (11) with $\upsilon \in V$ such that $\upsilon (1)=0,\, \upsilon _x(1)\ne 0$, we get:

$$\begin{aligned} y_{xx}(1,t)+\eta =0, \end{aligned}$$

use (11) again with $\upsilon \in V$, such that $\upsilon (1)\ne 0,\, \upsilon _x(1)=0$, we get:

$$\begin{aligned} y_{xxx}(1,t)-\gamma y_{xtt}(1,t)=\xi (t), \end{aligned}$$

and so, $(y,\xi ,\eta )$ verify the boundary conditions.

Uniqueness:

let $(y_1,\xi _1,\eta _1)$ and $(y_2,\xi _2,\eta _2)$ be two solutions and take

$w=y_1-y_2,\, \sigma =\xi _1-\xi _2$ and $\lambda =\eta _1-\eta _2$, and then, we have:

$$\begin{aligned} \left\{ \begin{array}{ll} \left( w_{tt},\upsilon \right) +\gamma \left( w_{xtt},\upsilon _x\right) +\left( w_{xx},\upsilon _{xx}\right) +\sigma \upsilon (1)+\lambda \upsilon _x(1)=0,&{}\\ \lambda _t(t)-w_{xt}(1,t)+\lambda (t)=0,&{} \\ \sigma _t(t)-w_t(1,t)+\sigma (t)=0.&{}\\ \end{array} \right. \end{aligned}$$

Take $\upsilon =2w_t$, and then integrate from 0 to t to obtain:

$$\begin{aligned} \begin{aligned}&|w_t|^2+\gamma |w_{xt}|^2+|w_{xx}|^2+|\sigma |^2+|\lambda |^2+2\int _{0}^{t}(|\sigma |^2+|\lambda |^2)ds=\\&|w_t(0)|^2+\gamma |w_{xt}(0)|^2+|w_{xx}(0)|^2+|\sigma (0)|^2+|\lambda (0)|^2=0.\\ \end{aligned} \end{aligned}$$

Therefore, $w_t=w_{xt}=w_{xx}=0$; therefore, $w=\sigma =\lambda =0.$ $\square$

3 Semi-discrete approximation

Let $0=x_0<x_1<\cdots <x_{s+1}=1$ be a uniform partition of the interval $I=(0,1)$ into sub-intervals $I_j=(x_{j-1},x_j),j=1,...,s+1$ of length $h=\frac{1}{s+1}$, and we denote by $V_E^h\subset H^2_E(I)$ the space:

$$\begin{aligned} V_E^h=\{\chi \in H^2_E(I)\cap C^1([0,1])\, \text {such that}\,\chi _{|_{[x_j,x_{j+1}]}} \in \mathbb {P}_3\, \text {for all} \, 0\le j\le s+1\}, \end{aligned}$$

and by $\pi ^h_E$, the elliptic projection $\pi ^h_E: H^2_E(I)\longrightarrow V_E^h$, defined by:

$$\begin{aligned} (\pi ^h_E\psi )(x_i)=\psi (x_i) \, \text {and}\,(\pi ^h_E\psi )_x(x_i)=\psi _x(x_i) \,\, \forall \psi \in H^2_E(I), \end{aligned}$$

and satisfying the following estimate (see [12]):

$$\begin{aligned} |\psi -\pi ^h_E\psi |_{H^1(I)}\le Ch|\psi _{xx}|, \quad \forall \psi \in H^2_E(I). \end{aligned}$$

(12)

Moreover, for all $\psi \in H^2_E(I)\cap H^3(I)$, we have:

$$\begin{aligned} |\psi _{xx}-(\pi ^h_E\psi )_{xx}|\le Ch|\psi _{xxx}|. \end{aligned}$$

(13)

We admit the following lemma:

Lemma 3.1

For all $\psi \in H^2_E(I)$ and $\chi \in V_E^h$, we have:

$$\begin{aligned} ((\pi ^h_E\psi )_{xx},\chi _{xx})=(\psi _{xx},\chi _{xx}). \end{aligned}$$

The semi-discrete finite element to (5) is to find for all $0 \le t\le T,$ $y^h(t)\in V_E^h$ and $\xi ^h(t),\eta ^h(t)\in \mathbb {R}$, such that

$$\begin{aligned} \left\{ \begin{array}{ll} \left( y^h_{tt},W\right) +\gamma \left( y^h_{xtt},W_x\right) +\left( y^h_{xx},W_{xx}\right) +\xi ^hW(1)+\eta ^hW_x(1)=0,&{}\\ \eta ^h_t(t)-y^h_{xt}(1,t)+\eta ^h(t)=0,&{} \\ \xi ^h_t(t)-y^h_t(1,t)+\xi ^h(t)=0.&{}\\ \end{array} \right. \end{aligned}$$

(14)

$\forall W\in V_E^h$, with $y^h(0)=\pi ^h_Ey_0$, $y^h_t(0)=\pi ^h_Ey_1$, $\xi ^h(0)=\xi _0,$ and $\eta ^h(0)=\eta _0$.

Lemma 3.2

$|(\pi ^h_Ey_i)_{xx}|^2=|y_{ixx}|^2$, $|(\pi ^h_Ey_i)_x|^2\le C|y_{ixx}|^2$, and

$|\pi ^h_Ey_i|^2\le C|y_{ixx}|^2$, for $i=0,1.$

Proof

$\forall \chi \in V_E^h$, we have by lemma (3.1):

$$\begin{aligned} ((\pi ^h_Ey_i)_{xx},\chi _{xx})=(y_{ixx},\chi _{xx}), \end{aligned}$$

choose $\chi =\pi ^h_Ey_i \in V_E^h$, and use lemma (3.1) again, we get:

$$\begin{aligned} |(\pi ^h_Ey_i)_{xx}|^2=(y_{ixx},(\pi ^h_Ey_i)_{xx})=(y_{ixx},y_{ixx})=|y_{ixx}|^2. \end{aligned}$$

Now:

$|(\pi ^h_Ey_i)_x|^2=|y_{ix}-(\pi ^h_Ey_i)_x+y_{ix}|^2\le 2|y_{ix}-(\pi ^h_Ey_i)_x|^2+2|y_{ix}|^2$.

Using (12) and the Poincare inequality, we get:

$|(\pi ^h_Ey_i)_x|^2\le C|y_{ixx}|^2$,

Poincare inequality again yields:

$|\pi ^h_Ey_i|^2\le C|(\pi ^h_Ey_i)_x|^2\le C|y_{ixx}|^2$. $\square$

Define the semi-discrete energy by:

$$\begin{aligned} E^h(t)=\frac{1}{2}\left( \int _0^1(|y^h_t|^2+\gamma |y^h_{xt}|^2+|y^h_{xx}|^2)\mathrm{d}x+|\xi ^h|^2+|\eta ^h|^2\right) . \end{aligned}$$

To show that the semi-discrete energy decays, we choose $W=2y^h_t$, as a test function in (14), and

hence:

$$\begin{aligned} 2\left( y^h_{tt},y^h_t\right) +2\gamma \left( y^h_{xtt},y^h_{xt}\right) +2\left( y^h_{xx},y^h_{xxt}\right) +2\xi ^hy^h_t(1,t)+2\eta ^hy^h_{xt}(1,t)=0. \end{aligned}$$

Using (14)$_2$ and (14)$_3$ to obtain:

$$\begin{aligned} \frac{d}{\mathrm{d}t} \left( |y^h_t|^2+\gamma |y^h_{xt}|^2+|y^h_{xx}|^2+|\xi ^h|^2+|\eta ^h|^2\right) +2|\xi ^h|^2+2|\eta ^h|^2=0. \end{aligned}$$

Therefore, we have:

$$\begin{aligned} \frac{d}{\mathrm{d}t}E^h(t)\le 0. \end{aligned}$$

Finally, integrating from 0 to t to get stability:

$$\begin{aligned} \begin{array}{ll} |y^h_t|^2+\gamma |y^h_{xt}|^2+|y^h_{xx}|^2+|\xi ^h|^2+|\eta ^h|^2+2\displaystyle \int _{0}^{t}\left( |\xi ^h|^2+|\eta ^h|^2\right) ds=\\ \\ |y^h_t(0)|^2+\gamma |y^h_{xt}(0)|^2+|y^h_{xx}(0)|^2+|\xi ^h(0)|^2+|\eta ^h(0)|\le \\ \\ C\left( |\pi ^h_Ey_1|^2+\gamma |(\pi ^h_Ey_1)_x|^2+|(\pi ^h_Ey_0)_{xx}|^2+|\xi _0|^2+|\eta _0|\right) \le C. \end{array} \end{aligned}$$

Where we used lemma (3.2) and the regularity on the initial data, and hence:

$$\begin{aligned} E^h(t)\le C. \end{aligned}$$

The next theorem provides us with an error bounds for the piecewise linear approximation (14).

Theorem 3.3

Under the assumption of Theorem (2.1), the estimate

$$\begin{aligned} |y_t-y^h_t|^2+\gamma |y_{xt}-y^h_{xt}|^2+|y_{xx}-y^h_{xx}|^2+|\xi -\xi ^h|^2+|\eta -\eta ^h|^2\le Ch^2, \end{aligned}$$

holds for all $0\le t\le T.$

Proof

Introducing $\hat{y}=y_t$ and $\hat{y}^h=y^h_t$, hence the continuous (5) and the semi-discrete (14) problems can be written as:

$$\begin{aligned} \left\{ \begin{array}{ll} (\hat{y}_t,\upsilon )+\gamma (\hat{y}_{xt},\upsilon _x)+(y_{xx},\upsilon _{xx})+\xi \upsilon (1)+\eta \upsilon _x(1)=0,\\ \\ \eta _t(t)-y_{xt}(1,t)+\eta (t)=0,\\ \\ \xi _t(t)-y_t(1,t)+\xi (t)=0, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{array}{ll} (\hat{y}^h_t,W)+\gamma (\hat{y}^h_{xt},W_x)+(y^h_{xx},W_{xx})+\xi ^hW(1)+\eta ^hW_x(1)=0,\\ \\ \eta ^h_t(t)-y^h_{xt}(1,t)+\eta ^h(t)=0,\\ \\ \xi ^h_t-(t)y^h_t(1,t)+\xi ^h(t)=0, \end{array} \right. \end{aligned}$$

for all $W\in V_E^h$ and $\upsilon \in H^2_E(I)$.

In particular, the first equality is true $\forall W \in V_E^h.$

Take $\upsilon =W\in V_E^h$ and subtract the two equalities to get:

$$\begin{aligned} (\hat{y}_t-\hat{y}^h_t,W)+\gamma (\hat{y}_{xt}-\hat{y}^h_{xt},W_x)+(y_{xx}-y^h_{xx},W_{xx})+(\xi -\xi ^h)W(1)+(\eta -\eta ^h)W_x(1)=0; \end{aligned}$$

that is:

$$\begin{aligned} \left\{ \begin{array}{ll} (\hat{y}_t-\pi ^h_E\hat{y}_t+\pi ^h_E\hat{y}_t-\hat{y}^h_t,W)+\gamma (\hat{y}_{xt}-\pi ^h_E\hat{y}_{xt}+\pi ^h_E\hat{y}_{xt}-\hat{y}^h_{xt},W_x)+\\ \\ (y_{xx}-\pi ^h_Ey_{xx}+\pi ^h_Ey_{xx}-y^h_{xx},W_{xx})+(\xi -\xi ^h)W(1)+(\eta -\eta ^h)W_x(1)=0. \end{array} \right. \end{aligned}$$

Let $\hat{e}^h=\hat{y}^h-\pi ^h_E\hat{y}$ and $e^h=y^h-\pi ^h_Ey$, and we get:

$$\begin{aligned} \left\{ \begin{array}{ll} (\hat{e}^h_t,W)+\gamma (\hat{e}^h_{xt},W_x)+(e^h_{xx},W_{xx})-(\xi -\xi ^h)W(1)-(\eta -\eta ^h)W_x(1)=\\ \\ (\hat{y}_t-\pi ^h_E\hat{y}_t,W)+\gamma (\hat{y}_{xt}-\pi ^h_E\hat{y}_{xt},W_x)+(y_{xx}-\pi ^h_Ey_{xx},W_{xx}). \end{array} \right. \end{aligned}$$

Take $W=\hat{e}^h\in V_E^h$ and use (13), to obtain:

$(\pi ^h_E\hat{y})(1)=(\pi ^h_E\hat{y})(x_s)=y_t(x_s)=y_t(1)=\xi _t+\xi$,

$(\pi ^h_E\hat{y})_x(1)=(\pi ^h_E\hat{y}_x)(x_s)=y_{xt}(x_s)=y_{xt}(1)=\eta _t+\eta$, and

hence $W(1)=\hat{e}^h(1)=\hat{y}^h(1)-(\pi ^h_E\hat{y})(1)=(\xi ^h_t-\xi _t)+(\xi ^h-\xi )$,

also, $W_x(1)=(\eta ^h_t-\eta _t)+(\eta ^h-\eta );$

therefore:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{1}{2}\frac{d}{\mathrm{d}t}\big [|\hat{e}^h|^2+\gamma |\hat{e}^h_x|^2+|e^h_{xx}|^2+|\xi -\xi ^h|^2+|\eta -\eta ^h|^2\big ]+ |\xi -\xi ^h|^2+|\eta -\eta ^h|^2=\\ \\ (\hat{y}_t-\pi ^h_E\hat{y}_t,\hat{e}^h)+\gamma (\hat{y}_{xt}-\pi ^h_E\hat{y}_{xt},\hat{e}^h_x)+(y_{xx}-\pi ^h_Ey_{xx},\hat{e}^h_{xx}).\\ \end{array} \right. \end{aligned}$$

(15)

Using (12), we have:

$(\hat{y}_t-\pi ^h_E\hat{y}_t,\hat{e}^h)\le 2|\hat{y}_t-\pi ^h_E\hat{y}_t|^2+2|\hat{e}^h|^2 \le 2Ch^2|\hat{y}_{tx}|^2+2|\hat{e}^h|^2,$

and $(\hat{y}_{xt}-\pi ^h_E\hat{y}_{xt},\hat{e}^h_x)\le 2Ch^2|\hat{y}_{xxt}|^2+2|\hat{e}^h_x|^2.$

Lemma (3.1) yields:

$(y_{xx}-\pi ^h_Ey_{xx},\hat{e}^h_{xx})=0.$

Combining these results with (15) to obtain:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{1}{2}\frac{d}{\mathrm{d}t}\big [|\hat{e}^h|^2+\gamma |\hat{e}^h_x|^2+|e^h_{xx}|^2+|\xi -\xi ^h|^2+|\eta -\eta ^h|^2\big ]+\\ \\ |\xi -\xi ^h|^2+|\eta -\eta ^h|^2\le 2Ch^2|\hat{y}_{tx}|^2+2C\gamma h^2|\hat{y}_{xxt}|^2+2\gamma |\hat{e}^h_x|^2+2|\hat{e}^h|^2. \end{array} \right. \end{aligned}$$

Integrating from 0 to t, we find:

$$\begin{aligned} \left\{ \begin{array}{ll} |\hat{e}^h|^2+\gamma |\hat{e}^h_x|^2+|e^h_{xx}|^2+|\xi -\xi ^h|^2+|\eta -\eta ^h|^2+ \displaystyle \int _0^t|\xi -\xi ^h|^2+|\eta -\eta ^h|^2)ds\le \\ \\ 2Ch^2\displaystyle \int _0^t\Big (|\hat{y}_{tx}|^2+\gamma |\hat{y}_{xxt}|^2\Big )ds+2\displaystyle \int _0^t\Big (|\hat{e}^h|^2+\gamma |\hat{e}^h_x|^2\Big )ds+\\ \\ |\hat{e}^h(0)|^2+\gamma |\hat{e}^h_x(0)|^2+ |e^h_{xx}(0)|^2+|\xi (0)-\xi ^h(0)|^2+(|\eta (0)-\eta ^h(0)|^2. \end{array} \right. \end{aligned}$$

Use (12) to obtain:

$\left| \hat{e}^h(0)\right| =|\hat{y}^h(0)-\pi ^h_E\hat{y}(0)|=|\pi ^h_Ey_1-\hat{y}(0)|=|\pi ^h_Ey_1-y_1|\le Ch|y_{1xx}|$,

and

$|\hat{e}^h_x(0)|\le Ch|y_{1xx}|$.

By (13), we have:

$|e^h_{xx}(0)|=|y^h_{xx}(0)-\pi ^h_Ey_{xx}(0)|=|y_{0xx}-\pi ^h_Ey_{0xx}|\le Ch|y_{0xxx}|$.

Use the above estimates with the fact that:

$$\begin{aligned} \xi (0)-\xi ^h(0)=\eta (0)-\eta ^h(0)=0, \end{aligned}$$

we get:

$$\begin{aligned} \left\{ \begin{array}{ll} |\hat{e}^h|^2+\gamma |\hat{e}^h_x|^2+|e^h_{xx}|^2+|\xi -\xi ^h|^2+|\eta -\eta ^h|^2+\\ \\ \displaystyle \int _0^t|\xi -\xi ^h|^2+|\eta -\eta ^h|^2)ds\le \\ \\ C\gamma h^2|y_{1xx}|^2+Ch^2|y_{0xxx}|^2+ 2Ch^2\displaystyle \int _0^t\Big (|\hat{y}_{tx}|^2+\gamma |\hat{y}_{xxt}|^2\Big )ds\\ \\ +2\displaystyle \int _0^t\Big (|\hat{e}^h|^2+\gamma |\hat{e}^h_x|^2\Big )ds. \end{array} \right. \end{aligned}$$

The regularity on $y_0, y_1$, and y, gives:

$$\begin{aligned} \begin{array}{ll} |\hat{e}^h|^2+\gamma |\hat{e}^h_x|^2+|e^h_{xx}|^2+|\xi -\xi ^h|^2+|\eta -\eta ^h|^2\le \\ \qquad Ch^2+2\displaystyle \int _0^t\Big (|\hat{e}^h|^2+\gamma |\hat{e}^h_x|^2\Big )ds.\\ \end{array} \end{aligned}$$

Applying Gronwall inequality, to obtain:

$$\begin{aligned} |\hat{e}^h|^2+\gamma |\hat{e}^h_x|^2\le Ch^2+Ch^2\int _0^te^{C(t-s)}ds\le Ch^2. \end{aligned}$$

Therefore:

$|\hat{e}^h|^2+\gamma |\hat{e}^h_x|^2+|e^h_{xx}|^2+|\xi -\xi ^h|^2+|\eta -\eta ^h|^2\le Ch^2.$

Finally:

$$\begin{aligned} \left\{ \begin{array}{ll} |y_t-y_t^h|^2+\gamma |y_{xt}-y^h_{xt}|^2+|y_{xx}-y^h_{xx}|^2+|\xi -\xi ^h|^2+|\eta -\eta ^h|^2=\\ \\ |y_t-\pi ^h_Ey_t+\pi ^h_Ey_t-y_t^h|^2+|y_{xt}-\pi ^h_Ey_{xt}+\pi ^h_Ey_{xt}-y^h_{xt}|^2+\\ \\ |y_{xx}-\pi ^h_Ey_{xx}+\pi ^h_Ey_{xx}-y^h_{xx}|^2 +|\xi -\xi ^h|^2+|\eta -\eta ^h|^2\le \\ \\ C(|\hat{e}^h|^2+\gamma |e^h_{xt}|^2+|\xi -\xi ^h|^2+|\eta -\eta ^h|^2)+\\ \\ C(|y_t-\pi ^h_Ey_t|^2+|y_{xt}-\pi ^h_Ey_{xt}|^2+|y_{xx}-\pi ^h_Ey_{xx}|^2)\le \\ \\ Ch^2(|y_{xxt}|^2+|y_{xxt}|^2+|y_{xxx}|^2)+Ch^2\le Ch^2, \end{array} \right. \end{aligned}$$

where we used the regularity on y. $\square$

4 Fully discrete approximation

In this section, we introduce a fully discrete finite-element method to (11).

Given an integer $N>0$, our numerical scheme can be stated as find $y^n$, $n=2,...,N$ and $\xi ^n, \eta ^n$, $n=1,...,N,$ such that, $\forall W\in V_E^h$, we have:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{1}{(\Delta t)^2}(y^{n+1}-2y^n+y^{n-1},W)+\displaystyle \frac{\gamma }{(\Delta t)^2}(y_x^{n+1}-2y_x^n+y_x^{n-1},W_x)+\\ (y^{n+1}_{xx},W_{xx})+\xi ^{n+1}W(1)+\eta ^{n+1}W_x(1)=0,\\ \frac{1}{\Delta t}(\eta ^{n+1}-\eta ^n)-\frac{1}{\Delta t}(y_x^{n+1}(1)-y_x^n(1))+\eta ^{n+1}=0,\\ \frac{1}{\Delta t}(\xi ^{n+1}-\xi ^n)-\frac{1}{\Delta t}(y^{n+1}(1)-y^n(1))+\xi ^{n+1}=0,\\ \end{array} \right. \end{aligned}$$

(16)

where $\Delta t={T}/{N}$ is the time step, $y^0=\pi ^h_Ey_0$, $y^1=y^0+\Delta t\pi ^h_Ey_1$, $\xi ^0=\xi _0$, and $\eta ^0=\eta _0$.

Writing $y^n(x)=\displaystyle \sum _{i=1}^{2s+2}c_i^n\mu _i(x)$, where $\{\mu _i\}_{i=1}^{2s+2}$ is a $\mathbb {P}^3$ Hermite basis for $V_E^h$, which will be defined in Sect. 5. We find that the method defined requires the linear system of $(2s+4)$ algebraic equations which can be written in the matrix form as:

$$\begin{aligned} \begin{array}{ll} MC^{n+1}=KC^n+LC^{n-1},\quad \text{ for }\quad n=1,2,\ldots N. \end{array} \end{aligned}$$

(17)

Here:

$$\begin{aligned} \begin{array}{lll} &{}M=\Big [A+\gamma B+(\Delta t)^2D+(\Delta t)^2E+F+G\Big ],\\ &{}K = \Big [2A+2\gamma B+F'+G'\Big ],\\ &{}L= \Big [-A-\gamma B\Big ],\\ \end{array} \end{aligned}$$

with

$$\begin{aligned} \left\{ \begin{array}{lllll} &{}A_{ij}=(\mu _i,\mu _j), A_{(2s+4)j}=A_{i(2s+4)}=A_{(2s+3)j}=A_{i(2s+3)}=0, \quad \forall ~ 1\le i,j\le 2s+4, \\ &{}B_{ij}=(\mu _{ix},\mu _{jx}), B_{i(2s+4)}=B_{j(2s+4)}=B_{i(2s+3)}=B_{j(2s+3)}=0, \quad \forall ~ 1\le i,j\le 2s+4, \\ &{}D_{ij}=(\mu _{ixx},\mu _{jxx}), D_{i(2s+4)}=D_{j(2s+4)}=D_{i(2s+3)}=D_{j(2s+3)}=0, \quad \forall ~ 1\le i,j\le 2s+4, \\ &{} E_{ij}=0, \quad \forall ~ 1\le i,j\le 2s+4, ~{\text{ except }}~ E_{s+1,2s+4}=E_{2s+2,2s+3}=1,\\ &{} F_{ij}=0, \quad \forall ~ 1\le i,j\le 2s+4,~ {\text{ except }}~ F_{2s+3,2s+2}=-1 , F_{2s+3,2s+3}=1+\Delta t,\\ &{} F'_{ij}=0, \quad \forall ~ 1\le i,j\le 2s+4,~ {\text{ except }}~ F'_{2s+3,2s+2}=-1 \, F'_{2s+3,2s+3}=1,\\ &{} G_{ij}=0, \quad \forall ~ 1\le i,j\le 2s+4,~ {\text{ except }}~ G_{2s+4,s+1}=-1, \,G_{2s+4,2s+4}=1+\Delta t,\\ &{} G'_{ij}=0, \quad \forall ~ 1\le i,j\le 2s+4,~ {\text{ except }}~ G'_{2s+4,s+1}=-1, \,G'_{2s+4,2s+4}=1.\\ \end{array} \right. \end{aligned}$$

(18)

And $C^n=(c^n_1,c^n_2,...,c^n_{2s+2},\eta ^n,\xi ^n)^T$, is the vector to be determined at each time step. Since the matrix M is non-singular, the system has a unique solution.

In a similar manner to the continuous case, the decay of the energy associated with the fully discrete problem and stability estimates are proved.

Let

$$\begin{aligned} \hat{y}^{n+1}=\displaystyle (y^{n+1}-y^n)/{\Delta t},\hat{\xi }^{n+1}=\displaystyle ({\xi ^{n+1}-\xi ^n})/{\Delta t}\quad \text{ and }\quad \hat{\eta }^{n+1}=\displaystyle ({\eta ^{n+1}-\eta ^n})/{\Delta t} \end{aligned}$$

define the energy of the fully discrete problem by:

$$\begin{aligned} E^{n+1}=\frac{1}{2}\big (|\hat{y}^{n+1}|^2+\gamma |\hat{y}^{n+1}_x|^2+|y^{n+1}_{xx}|^2+|\xi ^{n+1}|^2+|\eta ^{n+1}|^2\big ), n=0,1,\cdots ,(N-1). \end{aligned}$$

(19)

Taking, $W=\hat{y}^{n+1}$ in (16)$_1$, we get:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{1}{\Delta t}(\hat{y}^{n+1}-\hat{y}^n,\hat{y}^{n+1})+\displaystyle \frac{\gamma }{\Delta t}(\hat{y}_x^{n+1}-\hat{y}_x^n,\hat{y}^{n+1}_x)+\\ (y^{n+1}_{xx},\hat{y}^{n+1}_{xx})+\xi ^{n+1}\hat{y}^{n+1}(1)+\eta ^{n+1}\hat{y}_x^{n+1}(1)=0. \end{array} \right. \end{aligned}$$

Using (16)$_2$ and (16)$_3$, we get:

$\hat{y}_x^{n+1}(1)=\hat{\eta }^{n+1}+\eta ^{n+1},$ and

$\hat{y}^{n+1}(1)=\hat{\xi }^{n+1}+\xi ^{n+1}:$

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{1}{\Delta t}(\hat{y}^{n+1}-\hat{y}^n,\hat{y}^{n+1})+\displaystyle \frac{\gamma }{\Delta t}(\hat{y}_x^{n+1}-\hat{y}_x^n,\hat{y}^{n+1}_x)+(y^{n+1}_{xx},\hat{y}^{n+1}_{xx})+\\ |\xi ^{n+1}|^2+\xi ^{n+1}\hat{\xi }^{n+1}+|\eta ^{n+1}|^2+\eta ^{n+1}\hat{\eta }^{n+1}=0. \end{array} \right. \end{aligned}$$

Using the elementary equality:

$$\begin{aligned} (a,b)=\frac{1}{2}(|a|^2+|b|^2-|a-b|^2), \quad \forall a,b\in \mathbb {R}. \end{aligned}$$

(20)

We get:

$$\begin{aligned} \left\{ \begin{array}{llll} \displaystyle \frac{1}{2\Delta t}\left[ |\hat{y}^{n+1}-\hat{y}^n|^2+|\hat{y}^{n+1}|^2-|\hat{y}^n|^2\right] \\ +\displaystyle \frac{\gamma }{2\Delta t}\left[ |\hat{y}_x^{n+1}-\hat{y}_x^n|^2+|\hat{y}_x^{n+1}|^2-|\hat{y}_x^n|^2\right] \\ +\displaystyle \frac{1}{2\Delta t}\left[ |y_{xx}^{n+1}-y_{xx}^n|^2+|y_{xx}^{n+1}|^2-|y_{xx}^n|^2\right] \\ +\displaystyle \frac{1}{2\Delta t}\left[ |\eta ^{n+1}-\eta ^n|^2+|\eta ^{n+1}|^2-|\eta ^n|^2\right] \\ +\displaystyle \frac{1}{2\Delta t}\left[ |\xi ^{n+1}-\xi ^n|^2+|\xi ^{n+1}|^2-|\xi ^n|^2\right] \\ +|\xi ^{n+1}|^2+|\eta ^{n+1}|^2=0.\\ \end{array} \right. \end{aligned}$$

(21)

Therefore:

$$\begin{aligned} \big ({E^{n+1}-E^n}\big )/{\Delta t}\le 0. \end{aligned}$$

For the stability, we multiply (21) by $2\Delta t$ and sum from $i=1$ to n, to get:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \sum _{i=1}^n(|\hat{y}^{i+1}-\hat{y}^i|^2)+|\hat{y}^{n+1}|^2+\gamma \displaystyle \sum _{i=1}^n(|\hat{y}_x^{i+1}-\hat{y}_x^i|^2)+\gamma |\hat{y}_x^{n+1}|^2+\\ \\ \displaystyle \sum _{i=1}^n(|y_{xx}^{i+1}-y_{xx}^i|^2)+|y_{xx}^{n+1}|^2 +\displaystyle \sum _{i=1}^n(|\eta ^{i+1}-\eta ^i|^2)+|\eta ^{n+1}|^2+\\ \\ \displaystyle \sum _{i=1}^n(|\xi ^{i+1}-\xi ^i|^2)+|\xi ^{n+1}|^2 +\displaystyle \sum _{i=1}^n(|\eta ^{i+1}|^2)+\displaystyle \sum _{i=1}^n(|\xi ^{i+1}|^2)=\\ \\ |\hat{y}^1|^2+\gamma |\hat{y}^1_x|^2+|y^1_{xx}|^2+|\eta ^1|^2+|\xi ^1|^2.\\ \end{array} \right. \end{aligned}$$

Use lemma (3.2) and the definitions of $y^1$ and $\hat{y}^1$, to obtain:

$$\begin{aligned} |\hat{y}^1|=|\pi ^h_Ey_1|\le C|y_{1xx}|\le C, \end{aligned}$$

and

$$\begin{aligned} |\hat{y}_x^1|=|(\pi ^h_Ey_1)_x|\le C|y_{1xx}|\le C. \end{aligned}$$

Using lemma (3.2), we get:

$|y^1_{xx}|=|(\pi ^h_Ey_0)_{xx}+\Delta t(\pi ^h_Ey_1)_{xx}|\le |(\pi ^h_Ey_0)_{xx}|+|\Delta t(\pi ^h_Ey_1)_{xx}|=|y_{0xx}+\Delta ty_{1xx}|\le C$.

To bound $\eta ^1$, we use (16)$_2$ for $n=0$ , the second part of (13) with $x_s=1$, the definition of $y^1$, and the fact that $\displaystyle y_1(1)\le |y_{1x}|$.

Therefore, we have:

$$\begin{aligned} \left\{ \begin{array}{ll} |\eta ^1|=\displaystyle \frac{1}{1+\Delta t}|\eta ^0+\Delta t(\pi ^h_Ey_1)(1)| \le \displaystyle \frac{1}{1+\Delta t}(|\eta ^0|+|\Delta ty_1(1)|)\\[8pt] \qquad \le \displaystyle \frac{1}{1+\Delta t}(|\eta ^0|+C|y_{1x}|)\le C. \end{array} \right. \end{aligned}$$

In the same way, we use (16)$_3$ to get $|\xi ^1|\le C$.

Therefore:

$$\begin{aligned} E^{n+1}\le C. \end{aligned}$$

4.1 Error Estimate

Theorem 4.1

Assume that the assumption of theorem 2.1 holds, and then, if $y\in H^3(0,T,L^2(I))\cap H^2(0,T,H^2(I))$ and $\eta , \xi \in H^2(0,T)$ we have:

$$\begin{aligned} |y_t(t_n)-\hat{y}^n|^2+\gamma |\hat{y}_x(t_n)-\hat{y}_x^n|^2+|y_{xx}(t_n)-y^n_{xx}|^2+|\eta (t_n)-\eta ^n|^2+|\xi (t_n)-\xi ^n|^2\le C\Big [(\Delta t)^2+h^2\Big ], \end{aligned}$$

where C is independent of t and h.

Proof  

We use the standard decompositions:

$$\begin{aligned} \left\{ \begin{array}{ll} y^n-y(t_n)=y^n-\pi ^h_Ey(t_n)+\pi ^h_Ey(t_n)-y(t_n)=e^n+\rho ^n,\\ \\ \hat{y}_x^n-\hat{y}_x(t_n)=y_x^n-\pi ^h_E\hat{y}_x(t_n)+\pi ^h_E\hat{y}_x(t_n)-\hat{y}_x(t_n)=\hat{e}_x^n+\hat{\rho }_x^n,\\ \end{array} \right. \end{aligned}$$

where:

$$\begin{aligned} \left\{ \begin{array}{ll} e^n=y^n-\pi ^h_Ey(t_n),\quad \rho ^n=\pi ^h_Ey(t_n)-y(t_n),\\ b^n=\xi ^n-\xi (t_n),\quad d^n=\eta ^n-\eta (t_n), \\ \hat{e}^n=\hat{y}^n-\pi ^h_E\hat{y}(t_n),\\ \hat{\rho }^n=\pi ^h_E\hat{y}(t_n)-\hat{y}(t_n),\\ \hat{b}^n=\hat{\xi }^n-\hat{\xi }(t_n),\quad \hat{d}^n=\hat{\eta }^n-\hat{\eta }(t_n). \end{array} \right. \end{aligned}$$

Let us rewrite (16)$_1$ as:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{1}{\Delta t}(\hat{y}^{n+1}-\hat{y}^n,W)+\frac{\gamma }{\Delta t}(\hat{y}^{n+1}_x-\hat{y}^n_x,W_x)+(y_{xx}^{n+1},W_{xx})\\ \quad +\xi ^{n+1}W(1)+\eta ^{n+1}W_x(1)=0, \forall W\in V_E^h; \end{array} \right. \end{aligned}$$

therefore:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{1}{\Delta t}(\hat{e}^{n+1}-\hat{e}^n,W)+\frac{\gamma }{\Delta t}(\hat{e}^{n+1}_x-\hat{e}_x^n,W_x)+\\ (e^{n+1}_{xx},W_{xx})+\xi ^{n+1}W(1)+\eta ^{n+1}W_x(1)=\\ \quad -\displaystyle \frac{1}{\Delta t}\left( \pi ^h_E\hat{y}(t_{n+1})-\pi ^h_E\hat{y}(t_n),W\right) \\ \quad -\displaystyle \frac{\gamma }{\Delta t}\left( \left( \pi ^h_E\hat{y}(t_{n+1})\right) _x-\left( \pi ^h_E\hat{y}(t_{n})\right) _x,W_x\right) -\left( \left( \pi ^h_Ey(t_{n+1})\right) _{xx},W_{xx}\right) . \end{array} \right. \end{aligned}$$

Using lemma (3.1), we get:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{1}{\Delta t}(\hat{e}^{n+1}-\hat{e}^n,W)+\frac{\gamma }{\Delta t}(\hat{e}^{n+1}_x-\hat{e}_x^n,W_x)+\\ (e^{n+1}_{xx},W_{xx})+\xi ^{n+1}W(1)+\eta ^{n+1}W_x(1)=\\ \quad -\displaystyle \frac{1}{\Delta t}\left( \pi ^h_E\hat{y}(t_{n+1})-\pi ^h_E\hat{y}(t_n),W\right) \\ \quad -\displaystyle \frac{\gamma }{\Delta t}\left( \left( \pi ^h_E\hat{y}(t_{n+1})\right) _x-\left( \pi ^h_E\hat{y}(t_{n})\right) _x,W_x\right) -(y_{xx}(t_{n+1}),W_{xx}). \end{array} \right. \end{aligned}$$

Using (5) with $t=t_{n+1}$ and $\upsilon =W$, we get:

$$\begin{aligned} \begin{array}{ll} (y_{xx}(t_{n+1}),W_{xx})\\ \quad =-\displaystyle \frac{\gamma }{\Delta t}\left( \hat{y}_x(t_{n+1})-\hat{y}(t_{n})_x,W_x\right) -(\hat{y}_t(t_{n+1}),W)-\xi (t_{n+1})W(1)-\eta (t_{n+1})W_x(1); \end{array} \end{aligned}$$

therefore:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{1}{\Delta t}(\hat{e}^{n+1}-\hat{e}^n,W)+\frac{\gamma }{\Delta t}(\hat{e}^{n+1}_x-\hat{e}_x^n,W_x)+(e^{n+1}_{xx},W_{xx}) +\xi ^{n+1}W(1)+\eta ^{n+1}W_x(1)=\\ \quad -\displaystyle \frac{1}{\Delta t}\left( \pi ^h_E\hat{y}(t_{n+1})-\pi ^h_E\hat{y}(t_n),W\right) -\displaystyle \frac{\gamma }{\Delta t}\left( \left( \pi ^h_E\hat{y}(t_{n+1})\right) _x-\left( \pi ^h_E\hat{y}(t_{n})\right) _x,W_x\right) \\ \quad +\displaystyle \frac{\gamma }{\Delta t}\left( \hat{y}_x(t_{n+1})-\hat{y}(t_{n})_x,W_x\right) +(\hat{y}_t(t_{n+1}),W)+\xi (t_{n+1})W(1)+\eta (t_{n+1})W_x(1); \end{array} \right. \end{aligned}$$

hence:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{1}{\Delta t}(\hat{e}^{n+1}-\hat{e}^n,W)+\frac{\gamma }{\Delta t}(\hat{e}^{n+1}_x-\hat{e}_x^n,W_x)+(e^{n+1}_{xx},W_{xx}) +b^{n+1}W(1)+d^{n+1}W_x(1)=\\ \displaystyle \frac{\gamma }{\Delta t}\Big (\hat{\rho }^n_x-\hat{\rho }^{n+1}_x,W_x\Big )+ \Big (\hat{y}_t(t_{n+1})-\displaystyle \frac{\pi ^h_E\hat{y}(t_{n+1})-\pi ^h_E\hat{y}(t_n)}{\Delta t},W\Big ).\\ \end{array} \right. \end{aligned}$$

Take $W=\hat{e}^{n+1}$, and use the fact that:

$$\begin{aligned} \left\{ \begin{array}{ll} &{}\hat{e}^{n+1}(1)=\hat{y}^{n+1}(1)-(\pi ^h_E\hat{y}(t_{n+1}))(1)\\ &{} = \hat{\xi }^{n+1}+\xi ^{n+1}-\hat{y}(1,t_{n+1})\\ &{} = \hat{\xi }^{n+1}+\xi ^{n+1}-\hat{\xi }(t_{n+1})-\xi (t_{n+1})\\ &{} =\left( \hat{\xi }^{n+1}-\hat{\xi }(t_{n+1})\right) + \left( \xi ^{n+1}-\xi (t_{n+1})\right) \\ &{} =b^{n+1}+\hat{b}^{n+1}, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{array}{ll} &{}\hat{e}_x^{n+1}(1)=\hat{y}_x^{n+1}(1)-(\pi ^h_E\hat{y}(t_{n+1}))_x(1)\\ &{} = \hat{\eta }^{n+1}+\eta ^{n+1}-\hat{y}_x(1,t_{n+1})\\ &{} = \hat{\eta }^{n+1}+\eta ^{n+1}-\hat{\eta }(t_{n+1})-\eta (t_{n+1})\\ &{} =\left( \hat{\eta }^{n+1}-\hat{\eta }(t_{n+1})\right) + \left( \eta ^{n+1}-\eta (t_{n+1})\right) \\ &{} =d^{n+1}+\hat{d}^{n+1}, \end{array} \right. \end{aligned}$$

we get:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{1}{\Delta t}(\hat{e}^{n+1}-\hat{e}^n,\hat{e}^{n+1})+\frac{\gamma }{\Delta t}(\hat{e}^{n+1}_x-\hat{e}_x^n,\hat{e}^{n+1}_x)+(e^{n+1}_{xx},\hat{e}^{n+1}_{xx})+\\ |b^{n+1}|^2+|d^{n+1}|^2+b^{n+1}\hat{b}^{n+1}+d^{n+1}\hat{d}^{n+1}=\\ \displaystyle \frac{\gamma }{\Delta t}\Big (\hat{\rho }^n_x-\hat{\rho }^{n+1}_x,\hat{e}^{n+1}_x\Big )+ \Big (\hat{y}_t(t_{n+1})-\displaystyle \frac{\pi ^h_E\hat{y}(t_{n+1})-\pi ^h_E\hat{y}(t_n)}{\Delta t},\hat{e}^{n+1}\Big ).\\ \end{array} \right. \end{aligned}$$

(22)

Note that:

$$\begin{aligned} \displaystyle \xi _t(t_{n+1})=\frac{\xi (t_{n+1})-\xi (t_n)}{\Delta t}+\frac{1}{\Delta t}\displaystyle \int _{t_n}^{t_{n+1}}(s-t_n)\xi _{tt}(s)ds; \end{aligned}$$

therefore:

$$\begin{aligned} \left\{ \begin{array}{ll} \hat{b}^{n+1}=\hat{\xi }^{n+1}-\hat{\xi }(t_{n+1})\\ \quad = \displaystyle \frac{1}{\Delta t}\Big [(\xi ^{n+1}-\xi (t_{n+1}))-(\xi ^n-\xi (t_n))- \displaystyle \int _{t_n}^{t_{n+1}}(s-t_n)\xi _{tt}(s)ds\Big ]\\ \quad =\displaystyle \frac{1}{\Delta t}[b^{n+1}-b^n-\theta ^{n+1}], \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} \theta ^{n+1}=\displaystyle \int _{t_n}^{t_{n+1}}(s-t_n)\xi _{tt}(s)ds. \end{aligned}$$

Therefore, (20) gives:

$$\begin{aligned} \left\{ \begin{array}{ll} b^{n+1}\hat{b}^{n+1}=\frac{1}{\Delta t}b^{n+1}\Big (b^{n+1}-b^n\Big )-\frac{1}{\Delta t}b^{n+1}\theta ^{n+1}=\\ \quad \displaystyle \frac{1}{2\Delta t}\Big [|b^{n+1}-b^n|^2+|b^{n+1}|^2-|b^n|^2\Big ]-\frac{1}{\Delta t}b^{n+1}\theta ^{n+1}\ge \\ \displaystyle \frac{1}{2\Delta t}\Big [|b^{n+1}-b^n|^2+|b^{n+1}|^2-|b^n|^2\Big ]-|b^{n+1}|^2-\frac{1}{4\Delta t}|\theta ^{n+1}|^2,\\ \end{array} \right. \end{aligned}$$

where we used Young’s Inequality $\Big (\pm ab\le \delta a^2+\frac{1}{4\delta }b^2\Big )$, with $\delta =\Delta t$. In the same way, we show that:

$$\begin{aligned} \begin{array}{ll} d^{n+1}\hat{d}^{n+1}\ge \displaystyle \frac{1}{2\Delta t}\Big [|d^{n+1}-d^n|^2+|d^{n+1}|^2-|d^n|^2\Big ]-|d^{n+1}|^2-\frac{1}{4\Delta t}|\phi ^{n+1}|^2,\\ \end{array} \end{aligned}$$

where

$$\begin{aligned} \phi ^{n+1}=\displaystyle \int _{t_n}^{t_{n+1}}(s-t_n)\eta _{tt}(s)ds. \end{aligned}$$

Combine the above with (22) to obtain:

$$\begin{aligned} \left\{ \begin{array}{ll} &{}\displaystyle \frac{1}{2\Delta t}\left[ |\hat{e}^{n+1}-\hat{e}^n|^2+|\hat{e}^{n+1}|^2-|\hat{e}^n|^2\right] \\ &{}\displaystyle \quad + \displaystyle \frac{\gamma }{2\Delta t}\left[ |\hat{e}^{n+1}_x-\hat{e}^n_x|^2+|\hat{e}^{n+1}_x|^2-|\hat{e}^n_x|^2\right] \\ &{}\displaystyle \quad + \displaystyle \frac{1}{2\Delta t}\left[ |e^{n+1}_{xx}-e^n_{xx}|^2+|e^{n+1}_{xx}|^2-|e^n_{xx}|^2\right] \\ &{}\displaystyle \quad \displaystyle \frac{1}{2\Delta t}\left[ |b^{n+1}-b^n|^2+|b^{n+1}|^2-|b^n|^2\right] +\\ &{}\displaystyle \quad \displaystyle \frac{1}{2\Delta t}\left[ |d^{n+1}-d^n|^2+|d^{n+1}|^2-|d^n|^2\right] \le \\ &{}\displaystyle \quad \displaystyle \frac{\gamma }{\Delta t}\Big (\hat{\rho }^n_x-\hat{\rho }^{n+1}_x,\hat{e}^{n+1}_x\Big )+ \Big (\hat{y}_t(t_{n+1})-\displaystyle \frac{\pi ^h_E\hat{y}(t_{n+1})-\pi ^h_E\hat{y}(t_n)}{\Delta t},\hat{e}^{n+1}\Big )+\\ &{}\displaystyle \quad \displaystyle \frac{1}{4\Delta t}|\theta ^{n+1}|^2+\displaystyle \frac{1}{4\Delta t}|\phi ^{n+1}|^2=\\ &{}\displaystyle \quad \displaystyle \frac{\gamma }{\Delta t}H+I+\displaystyle \frac{1}{4\Delta t}J+\displaystyle \frac{1}{4\Delta t}K. \end{array} \right. \end{aligned}$$

(23)

Using the definition of $\hat{\rho }$ and (12), we get:

$$\begin{aligned} |\hat{\rho }^{n+1}_x-\hat{\rho }^n_x|^2=\displaystyle \int _{t_n}^{t_{n+1}}|\hat{\rho }_{xt}(s)|^2ds= \displaystyle \int _{t_n}^{t_{n+1}}\Big |\left( \pi ^h_E\hat{y}(s)\right) _{xt}-\hat{y}_{xt}(s)\Big |^2ds\le Ch^2\displaystyle \int _{t_n}^{t_{n+1}}|\hat{y}_{xxt}(s)|^2ds; \end{aligned}$$

hence:

$$\begin{aligned} H=\Big (\hat{\rho }^n_x-\hat{\rho }^{n+1}_x,\hat{e}^{n+1}_x\Big )\le 2|\hat{\rho }^{n+1}_x-\hat{\rho }^n_x|^2+2|\hat{e}^{n+1}_x|^2\le 2Ch^2\displaystyle \int _{t_n}^{t_{n+1}}|\hat{y}_{xxt}(s)|^2ds+2|\hat{e}^{n+1}_x|^2. \end{aligned}$$

Moreover:

$$\begin{aligned} \begin{array}{ll} &{}\Big |\hat{y}_t(t_{n+1})-\displaystyle \frac{\pi ^h_E\hat{y}(t_{n+1})-\pi ^h_E\hat{y}(t_n)}{\Delta t}\Big |\le \Big |\hat{y}_t(t_{n+1})-\displaystyle \frac{\hat{y}(t_{n+1})-\hat{y}(t_n)}{\Delta t}\Big |\\ &{} + \frac{1}{\Delta t}\Big |(\hat{y}(t_{n+1})-\hat{y}(t_n))-(\pi ^h_E\hat{y}(t_{n+1})-\pi ^h_E\hat{y}(t_n))\Big |=I_1+I_2. \end{array} \end{aligned}$$

We have to bound $I_{1}$ and $I_{2}$:

$$\begin{aligned} \begin{array}{ll} I_1&{}=\Big |\hat{y}_t(t_{n+1})-\displaystyle \frac{\hat{y}(t_{n+1})-\hat{y}(t_n)}{\Delta t}\Big |= \Big |\displaystyle \frac{1}{\Delta t}\displaystyle \int _{t_n}^{t_{n+1}}(s-t_n)\hat{y}_{tt}(s)ds\Big |\\ &{} \le \displaystyle \frac{1}{\Delta t}\Big (\displaystyle \int _{t_n}^{t_{n+1}}(s-t_n)^2ds\Big )^{\frac{1}{2}}\Big (\int _{t_n}^{t_{n+1}}|\hat{y}_{tt}(s)|^2ds\Big )^{\frac{1}{2}}\\ &{} = \displaystyle \frac{(\Delta t)^{\frac{1}{2}}}{3}\Big (\displaystyle \int _{t_n}^{t_{n+1}}|\hat{y}_{tt}(s)|^2ds\Big )^{\frac{1}{2}}, \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{ll} I_2=\frac{1}{\Delta t}\Big |(\hat{y}(t_{n+1})-\hat{y}(t_n))-(\pi ^h_E\hat{y}(t_{n+1})-\pi ^h_E\hat{y}(t_n))\Big |=\\ \frac{1}{\Delta t}\Big |\displaystyle \int _{t_n}^{t_{n+1}}\hat{\rho }_t(s)ds\Big |\le \frac{1}{\Delta t}\Big (\Delta t\displaystyle \int _{t_n}^{t_{n+1}}|\hat{\rho }_t(s)|^2ds\Big )^{1/2}, \end{array} \end{aligned}$$

again

$$\begin{aligned} \Big |\hat{\rho }_t(s)\Big |=\Big |\left( \pi ^h_E\hat{y}(s)\right) _t-\hat{y}_t(s)\Big |\le Ch\Big |\hat{y}_{xxt}(s)\Big |; \end{aligned}$$

hence:

$$\begin{aligned} I_2\le Ch(\Delta t)^{\frac{1}{2}}\Big (\displaystyle \int _{t_n}^{t_{n+1}}|y_{xxtt}(s)|^2ds\Big )^{\frac{1}{2}}. \end{aligned}$$

Young’s Inequality with $\delta =\Delta t$ gives:

$$\begin{aligned} \begin{array}{ll} I=\Big (\hat{y}_t(t_{n+1})-\displaystyle \frac{\pi ^h_E\hat{y}(t_{n+1})-\pi ^h_E\hat{y}(t_n)}{\Delta t},\hat{e}^{n+1}\Big )\le \\ 2\Delta tI_1^2+2\Delta tI_2^2+\displaystyle \frac{2}{\Delta t}|\hat{e}^{n+1}|^2\le \displaystyle \frac{2(\Delta t)^2}{9}\displaystyle \int _{t_n}^{t_{n+1}}|\hat{y}_{tt}(s)|^2ds+\\ Ch^2(\Delta t)^2\displaystyle \int _{t_n}^{t_{n+1}}|y_{xxtt}(s)|^2ds+\displaystyle \frac{2}{\Delta t}|\hat{e}^{n+1}|^2. \end{array} \end{aligned}$$

Using the Cauchy–Schwarz inequality, we get:

$$\begin{aligned} \theta ^{n+1}=\displaystyle \int _{t_n}^{t_{n+1}}(s-t_n)\xi _{tt}(s)ds\le C(\Delta t)^{\frac{3}{2}}\Big (\displaystyle \int _{t_n}^{t_{n+1}}| \xi _{tt}(s)|^2ds\Big )^{\frac{1}{2}}; \end{aligned}$$

hence:

$$\begin{aligned} J=|\theta ^{n+1}|^2\le C(\Delta t)^3\displaystyle \int _{t_n}^{t_{n+1}}|\xi _{tt}(s)|^2ds; \end{aligned}$$

also:

$$\begin{aligned} K=|\phi ^{n+1}|^2\le C(\Delta t)^3\displaystyle \int _{t_n}^{t_{n+1}}|\eta _{tt}(s)|^2ds. \end{aligned}$$

The above estimates together with (23) give:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{1}{2\Delta t}\left[ |\hat{e}^{n+1}-\hat{e}^n|^2+|\hat{e}^{n+1}|^2-|\hat{e}^n|^2\right] +\\ \displaystyle \frac{\gamma }{2\Delta t}\left[ |\hat{e}^{n+1}_x-\hat{e}^n_x|^2+|\hat{e}^{n+1}_x|^2-|\hat{e}^n_x|^2\right] +\\ \displaystyle \frac{1}{2\Delta t}\left[ |e^{n+1}_{xx}-e^n_{xx}|^2+|e^{n+1}_{xx}|^2-|e^n_{xx}|^2\right] +\\ \displaystyle \frac{1}{2\Delta t}\left[ |b^{n+1}-b^n|^2+|b^{n+1}|^2-|b^n|^2\right] +\\ \displaystyle \frac{1}{2\Delta t}\left[ |d^{n+1}-d^n|^2+|d^{n+1}|^2-|d^n|^2\right] \le \\ \displaystyle \frac{2\gamma Ch^2}{\Delta t}\displaystyle \int _{t_n}^{t_{n+1}}|\hat{y}_{xxt}(s)|^2ds+\displaystyle \frac{2\gamma }{\Delta t}|\hat{e}^{n+1}_x|^2+\\ \displaystyle \frac{2(\Delta t)^2}{9}\displaystyle \int _{t_n}^{t_{n+1}}|\hat{y}_{tt}(s)|^2ds+C(\Delta t)^2h^2\displaystyle \int _{t_n}^{t_{n+1}}|y_{ttxx}(s)|^2ds+\displaystyle \frac{2}{\Delta t}|\hat{e}^{n+1}|^2+\\ C(\Delta t)^2\displaystyle \int _{t_n}^{t_{n+1}}|\xi _{tt}(s)|^2ds+C(\Delta t)^2\displaystyle \int _{t_n}^{t_{n+1}}|\eta _{tt}(s)|^2ds.\\ \end{array} \right. \end{aligned}$$

Multiply by $2\Delta t$ and sum from $i=1$ to n:

$$\begin{aligned} \left\{ \begin{array}{llllll} \displaystyle \sum _{i=1}^n|\hat{e}^{i+1}-\hat{e}^i|^2+|\hat{e}^{n+1}|^2+\gamma \displaystyle \sum _{i=1}^n|\hat{e}_x^{i+1}-\hat{e}_x^i|^2+ \gamma |\hat{e}_x^{n+1}|^2+\\ \\ \displaystyle \sum _{i=1}^n|e_{xx}^{i+1}-e_{xx}^i|^2+|e_{xx}^{n+1}|^2+\displaystyle \sum _{i=1}^n|b^{i+1}-b^i|^2+|b^{n+1}|^2+\\ \\ \ \displaystyle \sum _{i=1}^n|b^{i+1}-b^i|^2+|d^{n+1}|^2\\ \\ \le C(\Delta t)^2\Big (\displaystyle \int _{t_1}^{t_{n+1}}|\hat{y}_{tt}(s)|^2ds+h^2\displaystyle \int _{t_1}^{t_{n+1}}|y_{ttxx}(s)|^2ds+ \displaystyle \int _{t_1}^{t_{n+1}}|\xi _{tt}(s)|^2ds+\\ \\ \displaystyle \int _{t_1}^{t_{n+1}}|\eta _{tt}(s)|^2ds\Big )+4\displaystyle \sum _{i=1}^n\Big [|\hat{e}^{i+1}|^2+\gamma |\hat{e}_x^{i+1}|^2\Big ]+|\hat{e}^1|^2+|\hat{e}^1_x|^2+|e^1_{xx}|^2+|b^1|^2+|d^1|^2\le C\\ \\ (\Delta t)^2\Big [\left\| y_{ttt}\right\| ^2_{L^2(0,T,L^2(I))}+h^2\left\| y_{tt}\right\| ^2_{L^2(0,T,H^2_E(I))}+\left\| \xi _{tt}\right\| ^2_{L^2(0,T)}+\left\| \eta _{tt}\right\| ^2_{L^2(0,T)}\Big ]+\\ \\ 4\displaystyle \sum _{i=1}^n\Big [|\hat{e}^{i+1}|^2+\gamma |\hat{e}_x^{i+1}|^2\Big ] +|\hat{e}^1|^2+|\hat{e}^1_x|^2+|e^1_{xx}|^2+|b^1|^2+|d^1|^2\\ \\ \le C(\Delta t)^2+Ch^2(\Delta t)^2+|\hat{e}^1|^2+|\hat{e}^1_x|^2+|e^1_{xx}|^2+|b^1|^2+|d^1|^2 + 4\displaystyle \sum _{i=1}^n\Big [|\hat{e}^{i+1}|^2+\gamma |\hat{e}_x^{i+1}|^2\Big ]. \end{array} \right. \end{aligned}$$

(24)

We have to bound $|e^1_{xx}|$, $|\hat{e}^1_x|$, $|\hat{e}^1|$, $|b^1|$, and $|d^1|$:

$$\begin{aligned} \left\{ \begin{array}{ll} &{}(e^1_{xx},\upsilon _{xx})=(y^1_{xx}-(\pi ^h_Ey(t_1))_{xx},\upsilon _{xx}) = (y^0_{xx}+\Delta t(\pi ^h_Ey_1)_{xx}-(\pi ^h_Ey(t_1))_{xx},\upsilon _{xx})\\ &{} = ((\pi ^h_Ey_0)_{xx}+\Delta t(\pi ^h_Ey_1)_{xx}-(\pi ^h_Ey(t_1))_{xx},\upsilon _{xx})= (y_{0xx}+y_{1xx}-y_{xx}(t_1),\upsilon _{xx})\\ &{} =(y_{xx}(0)+\Delta ty_{xxt}(0)-y_{xx}(t_1),\upsilon _{xx}), \end{array} \right. \end{aligned}$$

where we used the definition of $\pi ^h_E, y^1$ and $y^0$.

However:

$$\begin{aligned} y_{xx}(t_1)=y_{xx}(0)+\Delta ty_{xxt}(0)+\frac{(\Delta t)^2}{2}y_{xxtt}(\tau _1); \end{aligned}$$

so:

$$\begin{aligned} (e^1_{xx},\upsilon _{xx})=\Big (-\frac{(\Delta t)^2}{2}y_{xxtt}(\tau _1),\upsilon _{xx}\Big ). \end{aligned}$$

Choosing $\upsilon =e^1$, we get:

$$\begin{aligned} |e^1_{xx}|^2\le \frac{1}{2}(\Delta t)^2|y_{xxtt}(\tau _1)||e^1_{xx}|, \quad \text{ that } \text{ is, }\quad |e^1_{xx}|\le C(\Delta t)^2. \end{aligned}$$

To bound $|\hat{e}^1|$ and $|\hat{e}^1_x|$, we will bound $|\hat{e}^1_{xx}|$, and then, we use the Poincare inequality.

Knowing that, $\hat{y}^1=({y^1-y^0})/{\Delta t}$ and $y^1=y^0+\Delta t\pi ^h_Ey_1.$

We have:

$$\begin{aligned} \left\{ \begin{array}{llll} &{}(\hat{e}^1_{xx},\upsilon _{xx})=(\hat{y}^1_{xx}-(\pi ^h_E\hat{y}(t_1))_{xx},\upsilon _{xx})\\ &{} =\displaystyle \frac{1}{\Delta t}(y^1_{xx}-y^0_{xx},\upsilon _{xx})-(\pi ^h_E\hat{y}(t_1))_{xx},\upsilon _{xx})\\ &{} =\displaystyle \left( (\pi ^h_Ey_1)_{xx},\upsilon _{xx}\right) -((\pi ^h_E\hat{y}(t_1))_{xx},\upsilon _{xx})\\ &{} =\displaystyle (y_{1xx},\upsilon _x)-(y_{xxt}(t_1),\upsilon _{xx})\\ &{} =\displaystyle (y_{xxt}(0)-y_{xxt}(t_1),\upsilon _{xx}), \end{array} \right. \end{aligned}$$

but, $y_{xxt}(t_1)=y_{xxt}(0)+\Delta ty_{xxtt}(\tau _2)$,    so,   $(\hat{e}^1_x,\upsilon _x)=-\Delta t(y_{ttx}(\tau _2),\upsilon _x).$

Choose $\upsilon =\hat{e}^1$, we get:

$$\begin{aligned} |\hat{e}^1_{xx}|^2\le C\Delta t|(y_{xxtt}(\tau _2)||\hat{e}^1_{xx}|, \text{ and } \text{ hence } |\hat{e}^1_{xx}|\le C\Delta t. \end{aligned}$$

Using Poincare inequality, we get $|\hat{e}^1|\le C|\hat{e}^1_x|\le C|\hat{e}^1_{xx}|\le \Delta t.$

To bound $|b^1|$, we use the fact:

$$\begin{aligned} \eta (t_1)=\eta (t_0)+\Delta t \eta _t(\sigma ), with 0<\sigma <t_1; \end{aligned}$$

therefore, we have:

$$\begin{aligned} |b^1|=|\eta ^1-\eta (t_1)|=|\eta ^1-\eta ^0+\eta (0)-\eta (t_1)|=\Delta t|\hat{\eta }^1-\eta _t(\sigma )|\le C\Delta t. \end{aligned}$$

Also, $|d^1|\le C \Delta t$.

Using (24) and the above estimates, we get:

$$\begin{aligned} \left\{ \begin{array}{ll} &{}|\hat{e}^{n+1}|^2+\gamma |\hat{e}_x^{n+1}|^2+|e_{xx}^{n+1}|^2+|b^{n+1}|^2+|d^{n+1}|^2\\ &{} \le C(\Delta t)^2+Ch^4+4C\displaystyle \sum _{i=1}^n\Big [|\hat{e}^{i+1}|^2+\gamma |\hat{e}^i_x|^2\Big ]. \end{array} \right. \end{aligned}$$

Applying the discrete Gronwall inequality to obtain:

$$\begin{aligned}&|\hat{e}^{n+1}|^2+\gamma |\hat{e}_x^{n+1}|^2+|e_{xx}^{n+1}|^2+|b^{n+1}|^2+|d^{n+1}|^2\le C\Big [(\Delta t)^2+h^4\Big ]. \end{aligned}$$

Now:

$$\begin{aligned} \left\{ \begin{array}{ll} &{}|y_t(t_n)-\hat{y}^n|^2+\gamma |y_{xt}(t_n)-\hat{y}_x^n|^2+|y_{xx}(t_n)-y_{xx}^n|^2+|\xi (t_n)-\xi ^n|^2+|\eta (t_n)-\eta ^n|^2\\ &{} \le C\big [|\hat{e}^{n+1}|^2+\gamma |\hat{e}_x^{n+1}|^2+|e_{xx}^{n+1}|^2+|b^{n+1}|^2+|d^{n+1}|^2+|\hat{\rho }^n|^2+\gamma |\hat{\rho }^n_x|^2 +|\rho ^n_{xx}|^2\big ]\\ &{} \le C\Big [(\Delta t)^2+(\Delta t)^4+h^4\Big ]+C\big [|\hat{\rho }^n|^2+\gamma |\hat{\rho }^n_x|^2+ |\rho ^n_{xx}|^2\big ]. \end{array} \right. \end{aligned}$$

Using (12), we have:

$$\begin{aligned} |\hat{\rho }^n|=|\pi ^h_E\hat{y}(t_n)-\hat{y}(t_n)|\le Ch|\hat{y}_{xx}(t_n)|\le Ch, \end{aligned}$$

also $|\hat{\rho }^n_x|\le Ch$ and $|\rho ^n_{xx}|\le Ch.$ Hence:

$$\begin{aligned} \left\{ \begin{array}{ll} &{}|y_t(t_n)-\hat{y}^n|^2+\gamma |y_{xt}(t_n)-\hat{y}_x^n|^2+|y_{xx}(t_n)-y_{xx}^n|^2+|\xi (t_n)-\xi ^n|^2+|\eta (t_n)-\eta ^n|^2\le \\ \\ &{}C(h^2+h^4+(\Delta t)^2). \end{array}\ \right. \end{aligned}$$

Finally:

$$\begin{aligned} |y_t(t_n)-\hat{y}^n|^2+\gamma |y_{xt}(t_n)-\hat{y}_x^n|^2+|y_{xx}(t_n)-y_{xx}^n|^2+|\xi (t_n)-\xi ^n|^2+|\eta (t_n)-\eta ^n|^2\le C(h^2+(\Delta t)^2). \quad \qquad \qquad \qquad \square \end{aligned}$$

5 Finite-element method

In the finite-element method, the basis functions are usually polynomials of any degree, defined in each finite element. In this paper, we are going to use the Hermite finite element (see [12] Page 168).

To define a basis for $V^h_E$, we introduce the two reference functions:

$$\begin{aligned} \phi (x)=\left\{ \begin{array}{llll} &{}\displaystyle (1+x)^2(1-2x) \quad \text {if}\, x\in [-1,0],\\ &{}\displaystyle (1-x)^2(1+2x) \quad \text {if}\, x\in [0,1],\\ &{} 0 \qquad \mathrm{else where}, \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \psi (x)=\left\{ \begin{array}{ll} &{}\displaystyle x(1+x)^2 \quad \text {if}\, x\in [-1,0],\\ &{}\displaystyle x(1-x)^2 \quad \text {if}\, x\in [0,1],\\ &{} 0 \qquad \mathrm{else where}. \end{array} \right. \end{aligned}$$

Define the following bases functions by:

$$\begin{aligned} \phi _j(x)=\phi \Big (\frac{x-x_j}{h}\Big )\,\, \forall \,1\le j\le s+1 \end{aligned}$$

and

$$\begin{aligned} \psi _j(x)=h\psi \Big (\frac{x-x_j}{h}\Big )\,\, \forall \,1\le j\le s+1. \end{aligned}$$

Note that, for all $1\le i,j\le s+1$, we have:

$$\begin{aligned} \phi _j(x_i)=\delta _{ij},\phi _{jx}(x_i)=0,\psi _j(x_i)=0\, \text {and}\,\psi _{jx}(x_i)=\delta _{ij}. \end{aligned}$$

With the above, $V^h_E$ becomes a subspace of $H^2_E(I)$ of dimension $2s+2$, and for all $y^h\in V^h_E$, $y^h$ can be written in the form:

$$\begin{aligned} y^h(x)=\displaystyle \sum _{j=1}^{s+1}y^h(x_j)\phi _j(x)+\displaystyle \sum _{j=1}^{s+1}y^h_x(x_j)\psi _j(x)\, \forall x\in [0,1]. \end{aligned}$$

let us rename the basis as $\{\mu _i\}_{i=1}^{2s+2}$, where:

$$\begin{aligned} \begin{array}{ll} \mu _i(x)=\phi _i(x)=\phi \Big (\frac{x-x_i}{h}\Big )\,\, \forall \,1\le i\le s+1,\\ \mu _i(x)=\psi _{i-s-1}(x)=h\psi \Big (\frac{x-x_{i-s-1}}{h}\Big )\,\, \forall \,s+2\le j\le 2s+2.\\ \end{array} \end{aligned}$$

5.1 Numerical simulations

The numerical analysis is performed for $\gamma =0.1$, $\Delta t=0.05$, $h=1/15$, $y_0(x)=x^2(1-x)$, $y_1(x)=-x^2(1-x)$, $\eta _0=3/(1+\Delta t)$, $\eta _1=(4(20+\Delta t))/(5(1+\Delta t))$, $\xi _0=1$, and $\xi _1=1/(1 + \Delta t)$.

Fig. 1

Position $y^n(x,t)$

Fig. 2

Moment control $\eta ^n$

Fig. 3

Force control $\xi ^n$

Fig. 4

Full discrete energy $E^n.$

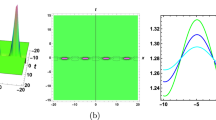
The graphs in Figs.  1, 2, 3, and 4 represent, respectively, the time evolution of the beam’s position $y^n(x,t)$, moment control $\eta ^n$, force control $\xi ^n$, and the discrete energy $E^n$.