1 Introduction

Countries across the world were affected by the 2019 novel coronavirus disease (COVID-19), an infectious disease caused by the recently discovered severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). The Philippines’ Department of Health (DOH) confirmed the first positive case in the country last 30 January, 2020. On 7 March, DOH announced that the fifth case of COVID-19 is the first case of local transmission. Due to the increasing number of community transmission of COVID-19, Metro Manila, and the entire Luzon were placed under enhanced community quarantine (ECQ) last March 16.

Several control measures are being done to minimize the spread of this contagious disease such as social distancing, case isolation, household quarantine, and school and university closure (Ferguson et al. 2020). Following China’s containment efforts, several countries adopted broad community quarantines or lockdowns as a means of controlling the spread of COVID-19 (Anderson et al. 2020; Cohen and Kupferschmidt 2020). However, amidst community quarantines and lockdowns, there are working classes who continue to provide essential services for healthcare, medicine, security, food, retail, and transport. This group of workers became collectively referred to as the frontliners. The nature of their work, being in close proximity and in frequent interaction with the public, put them at a higher risk of getting infected (WHO 2020a, b; Kiersz 2020; Heinzerling et al. 2020; Gamio 2020), and once infected, their continuous contact with the public can make them superspreaders.

On 11 May, DOH announced that 1991 (17.96%) healthcare workers were infected among 11,086 total COVID-19 confirmed cases and this is 1.5% of the Philippines’ health system workforce (DOH 2020; Dayrit 2018). Healthcare workers are at high risk when they are doing physical examinations and placing respiratory devices to an infected person (Heinzerling et al. 2020; Ferioli et al. 2020). Persons needing medical help put healthcare workers at high risk if they fail to disclose any coronavirus symptoms (The Philippine Star 2020). In addition, healthcare workers are at risk because of the insufficient number of available protective equipment and the unavailability of diagnostic tests (Ali et al. 2020; Heinzerling et al. 2020; Ferioli et al. 2020). When frontliners unknowingly become exposed to the virus, they can unintentionally transmit the virus to patients and the general public. This led to the implementation of more stringent precautionary measures for frontliners especially healthcare workers (Ersoy 2020). Due to the huge impact of COVID-19 transmission between the frontliners and the general public, health authorities need to determine possible interventions to protect both groups.

In this study, we formulate a mathematical model on the transmission dynamics of COVID-19 between the frontliners and the general public. We assume different basic reproduction numbers for the frontliners and the general public. We also consider a parameter for the susceptibility of an exposed individual with varying values for the frontliners and the general public. This parameter can be decreased through some level of protection. We examine the model simulations and perform sensitivity analysis to determine which parameters have significant effects to the model output. The key parameters in mathematical models of the spread of COVID-19 are the basic reproduction number which refers to the average number of secondary cases generated from a contagious person, and a dispersion parameter that can provide further information about outbreak dynamics and potential for superspreading events (Riou and Althaus 2020). As of May 2020, the basic reproduction number of COVID-19 is estimated to be around 1.5–4 (Rabajante 2020). Model parameters for the spread of the disease are usually considered constant for the entire population with time variation (Liu et.al. 2020). However, these parameters vary considering the heterogeneity of the population, location of virus transmission, and socio-economic and political factors (Rabajante 2020).

2 Mathematical model

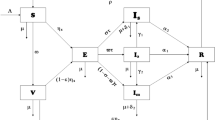
We consider an extended susceptible-exposed-infected-recovered (SEIR) compartment model to study the dynamics of the transmission of COVID-19 (Fig. 1). The model has two mutually exclusive populations: the general public and the frontliners. Frontliners refer to working classes that provide continued services during disease outbreaks such as healthcare workers, customer service and retail personnel, food service crews, and transport or delivery workers.

Fig. 1
figure 1

Extended susceptible–exposed–infected–recovered model Framework of COVID-19 transmission between the frontliners and the general public. Two mutually exclusive populations with separate compartments for susceptible, exposed, infected, and recovered are used to represent the dynamics of the transmission of the COVID-19 disease between these two populations

Full size image

In the model, the general public and the frontliners are compartmentalized to susceptible, exposed, infected, and recovered. The numbers of susceptible individuals from the general public and from the frontliners are \(S_{1}\) and \(S_{2}\), respectively. The numbers of individuals exposed to the disease are \(E_{1}\) for the general public and \(E_{2}\) for the frontliners. For the number of infected, \(I_{1}\) is for the general public and \(I_{2}\) is for the frontliners. From the infected, the number of those that are in isolation are denoted by \({\text{Is}}_{1}\) for the general public and \({\text{Is}}_{2}\) for the frontliners. The numbers of recovered individuals from the general public and from the frontliners are \(R_{1}\) and \(R_{2}\), respectively.

The general public and the frontliners are assigned different parameter values for basic reproduction number and susceptibility depending on the exposure to the disease. We refer to \(\beta_{1}\) and \(\beta_{2}\) as exposure rates for the general public and the frontliners. The exposure rate is the number of new exposed individuals caused by an infectious individual per unit of time. The rates at which an exposed individual from the general public and an exposed frontliner become susceptible are by \(\mu_{1}\) and \(\mu_{2}\), respectively. Exposed individuals become infected with the disease at a rate of \(\alpha_{1}\) for the general public and \(\alpha_{2}\) for the frontliners. The rate at which infected individuals are being isolated in a health facility is \(iso_{1}\) for the general public and \({\text{iso}}_{2}\) for the frontliners. The rate of imported cases of infection is \({\text{Import}}_{1}\) for the general public and \({\text{Import}}_{2}\) for the frontliners. For the non-isolated infected individuals, the recovery rates are \(\gamma_{1}\) for the general public and \(\gamma_{2}\) for the frontliners, and the death rates are \(m_{1}\) for the general public and \(m_{2}\) for the frontliners. On the other hand, for the isolated infected individuals, the recovery rates are \(\gamma_{1}^{*}\) for the general public and \(\gamma_{2}^{*}\) for the frontliners, and the death rates are \(m_{{{\text{Is}}_{{1}} }}\) for the general public and \(m_{{{\text{Is}}_{2} }}\) for the frontliners. Recovered individuals become susceptible again at a rate of \(\rho_{1}\) for the general public and \(\rho_{2}\) for the frontliners.

The dynamics in the extended SEIR sel we used in the study is described by the following equations.

$$\frac{{{\text{d}}S_{1} }}{{{\text{d}}t}}\, = \, - \beta_{1} I_{1} \frac{{S_{1} }}{N}\, + \,\rho_{1} R_{1} \, - \,\beta_{2} I_{2} \frac{{S_{1} }}{N}\, + \,\mu_{1} E_{1} ,$$
$$\frac{{{\text{d}}E_{1} }}{{{\text{d}}t}}\, = \,\beta_{1} I_{1} \frac{{S_{1} }}{N}\, + \,\beta_{2} I_{2} \frac{{S_{1} }}{N}\, - \,\alpha_{1} E_{1} \, - \,\mu_{1} E_{1} ,$$
$$\frac{{{\text{d}}I_{1} }}{{{\text{d}}t}}\, = \,\alpha_{1} E_{1} \, - \,\gamma_{1} I_{1} \, - \,{\text{iso}}_{1} I_{1} \, - \,m_{1} I_{1} \, + \,{\text{Im}} {\text{port}}_{1} ,$$
$$\frac{{{\text{d}}Is_{1} }}{{{\text{d}}t}}\, = \,{\text{iso}}_{1} I_{1} \, - \,\gamma_{1}^{*} Is_{1} \, - \,m_{{Is_{1} }} Is_{1} ,$$
$$\frac{{{\text{d}}R_{1} }}{{{\text{d}}t}}\, = \,\gamma_{1} I_{1} \, - \,\rho_{1} R_{1} \, + \,\gamma_{1}^{*} {\text{Is}}_{1} ,$$
$$\frac{{{\text{d}}S_{2} }}{{{\text{d}}t}}\, = \, - \beta_{1} I_{1} \frac{{S_{2} }}{N}\, + \,\rho_{2} R_{2} \, - \,\beta_{2} I_{2} \frac{{S_{2} }}{N}\, + \,\mu_{2} E_{2} ,$$
$$\frac{{{\text{d}}E_{2} }}{{{\text{d}}t}}\, = \,\beta_{1} I_{1} \frac{{S_{2} }}{N}\, + \,\beta_{2} I_{2} \frac{{S_{2} }}{N}\, - \,\alpha_{2} E_{2} \, - \,\mu_{2} E_{2} ,$$
$$\frac{{{\text{d}}I_{2} }}{{{\text{d}}t}}\, = \,\,\alpha_{2} E_{2} \, - \,\gamma_{2} I_{2} \, - \,{\text{iso}}_{2} I_{2} \, - \,m_{2} I_{2} \, + \,{\text{Import}}_{2} ,$$
$$\frac{{{\text{dIs}}_{2} }}{{{\text{d}}t}}\, = \,{\text{iso}}_{2} I_{2} \, - \,\gamma_{2}^{*} {\text{Is}}_{2} \, - \,m_{{Is_{2} }} {\text{Is}}_{2} ,$$
$$\frac{{{\text{d}}R_{2} }}{{{\text{d}}t}}\, = \,\gamma_{2} I_{2} \, - \,\rho_{2} R_{2} \, + \,\gamma_{2}^{*} {\text{Is}}_{2} ,$$
$$\beta_{1} \, = \,\frac{{R_{01} }}{\tau }\frac{{\left( {S_{1} \left( 0 \right)\, + \,E_{1} \left( 0 \right)\, + \,I_{1} \left( 0 \right)\, + \,S_{2} \left( 0 \right)\, + \,E_{2} \left( 0 \right)\, + \,I_{2} \left( 0 \right)} \right)}}{{S_{1} \left( 0 \right)\, + \,S_{2} \left( 0 \right)}},$$
$$\beta_{2} \, = \,\frac{{R_{02} }}{\tau }\frac{{\left( {S_{1} \left( 0 \right)\, + \,E_{1} \left( 0 \right)\, + \,I_{1} \left( 0 \right)\, + \,S_{2} \left( 0 \right)\, + \,E_{2} \left( 0 \right)\, + \,I_{2} \left( 0 \right)} \right)}}{{S_{1} \left( 0 \right)\, + \,\,S_{2} \left( 0 \right)}}.$$

In the simulations, certain parameter values are based on previous findings. Table 1 shows descriptions of the parameters in the SEIR model, the default parameter values used in the simulations, and the references for these parameter values. The succeeding section discusses the sensitivity analysis of the parameters.

Table 1 Description of parameters and parameter values
Full size table

The reproduction number describes the expected number of individuals that can be infected by a single infected person. We use 2.5 as the average number of secondary cases generated from an infectious public individual. This is based on the reproduction number in the early stages of COVID-19 in China (Anderson et al. 2020). On the other hand, since frontliners have higher exposure than the general public, we set the average number of secondary cases generated from an infectious frontliner to be 10. The exposure rates \(\beta_{1}\) and \(\beta_{2}\) are computed from the reproduction number, the infection period, and the number of susceptible individuals.

We assume that the infection rates, isolation rates, recovery rates, death rates, susceptibility rates, and rate of imported cases are the same for the general public and the frontliners. In the simulations, we use the same parameter values for the general public and the frontliners for these rates. We set the infection rate at 10/14 (Rabajante 2020), where we assume 10 new infections within 14 days from those who are exposed. We assume that the death rate of infected individuals is 0.03/14 (Chen 2020). We attribute the protection levels of the public and the frontliners to the recommendations of WHO: protection measures such as wearing masks, frequent hand hygiene, and wearing PPEs in the case of the frontliners. The parameters \(\mu_{1}\) and \(\mu_{2}\) can be considered as protection levels since these are the percentages of exposed individuals that are again classified as being susceptible. If the protection measures done by the community is effective, these protection parameters are set close to 1.

3 Simulation results

For the simulation, we use parameter values indicated in Table 1. We consider 200 days starting from the onset of the spread of the disease with initial values for population sizes indicated in Table 2. We vary parameter values for the basic reproduction number and susceptibility rate. We observe the number of non-isolated infected individuals for both the frontliners and the general public. The following are our observations.

Table 2 Initial values for the population of frontliners and the general public
Full size table

The parameters \(\mu_{1}\) and \(\mu_{2}\) quantify the protection of the general public and the frontliners when they are exposed to the disease. Higher values for these parameters indicate the effectiveness of the preventive measures (e.g. social distancing, use of protective gears, and self-sanitizing) against infection. We vary the values for \(\mu_{1}\) and \(\mu_{2}\) and observe how these affect the dynamics of the infection through the general public and the frontliners.

First, we increase the protection \(\mu_{1}\) of the general public, for a fixed value of \(\mu_{2}\). We obtain the following insights: (i) as \(\mu_{1}\) increases, there is a flattening in the peak of the number of infected for both populations (Figs. 2a–d), which means increasing the protection of the general public causes a significant decrease in the number of infected individuals; and (ii) as \(\mu_{1}\) increases, the peaks of the number of infected for each population happen at a later time (Fig. 2), which implies a slower increase in the number of infected individuals.

Fig. 2
figure 2

Predicted number of infected public individuals and frontliners when we increase the initial values of the compartments S, E and I with fixed values of \(\mu_{2}\) and varying values of \(\mu_{1}\). Parameter values used: \(R_{01} = 2.5,\;R_{02} = 10,\) \(\tau = 14,\) , \(\gamma_{1} = \gamma_{2} = 0.96/14\),\(\gamma_{1} * = \gamma_{2} * = 0.98/14\), \(m_{1} = m_{2} = 0.03/14\), \(m_{{{\text{Is1}}}} \, = \,m_{{{\text{Is}}2}} \, = \,0.02/14,\;{\text{Import}}_{1} \, = \,{\text{Import}}_{2} \,\, = \,0.1.\) a–d Initial population \(S_{1} = 10,000\), \(E_{1} = 0,I_{1} = 1\), \(Is_{1} = 0\), \(R_{1} = 0\), \(S_{2} = 100\), \(E_{2} = 10,I_{2} = 0\), \(Is_{2} = 0\), \(R_{2} = 0\). e–h Initial population \(S_{1} = 100,000\), \(E_{1} = 0,I_{1} = 1\) 0, \(Is_{1} = 0\), \(R_{1} = 0\), \(S_{2} = 1000\), \(E_{2} = 100,I_{2} = 0\), \(Is_{2} = 0\), \(R_{2} = 0\). a–h \(\mu_{1}\) = 0, 0.1,0.5, 0.9. a, e \(\mu_{2}\) = 0. b, f \(\mu_{2}\) = 0.1. c, g \(\mu_{2}\) = 0.5. d, h \(\mu_{2}\) = 0.9

Full size image

Second, we significantly change the initial values of the compartments S, E, and I but with varying values of both \(\mu_{1}\) and \(\mu_{2}\) (Fig. 3). We observe that the peaks are reached after almost the same number of days regardless of the initial population size.

Fig. 3
figure 3

Predicted number of infected public individuals and frontliners when we increase the initial values of the compartments S, E and I with fixed values of \(\mu_{1}\) and \(\mu_{2}\). Parameter used: \(R_{01} = 2.5,R_{02} = 10,\) \(\tau = 14,\) \(iso_{1} = iso_{2} = 0.01/14,\alpha_{1} = \alpha_{2} = 10/14\), \(\gamma_{1} = \gamma_{2} = 0.96/14\),\(\gamma_{1} * = \gamma_{2} * = 0.98/14\), \(m_{1} = m_{2} = 0.03/14\), \(m_{{{\text{Is}}1}} \, = \,m_{{{\text{Is}}2}} \, = \,0.02/14\). (Parameter 1) Initial population \(S_{1} = 10,000\), \(E_{1} = 0,I_{1} = 1\), \({\text{Is}}_{1} = 0\), \(R_{1} = 0\), \(S_{2} = 100\), \(E_{2} = 10,I_{2} = 0\), \({\text{Is}}_{2} = 0\), \(R_{2} = 0\). (Parameter 2) Initial population \(S_{1} = 100,000\), \(E_{1} = 0,I_{1} = 10\), \(Is_{1} = 0\), \(R_{1} = 0\), \(S_{2} = 1000\), \(E_{2} = 100,I_{2} = 0\), \(Is_{2} = 0\), \(R_{2} = 0\). a \(\mu_{1}\) = 0, \(\mu_{2}\) = 0. b \(\mu_{1}\) = 0.1, \(\mu_{2}\) = 0.9. c \(\mu_{1}\) = 0.5, \(\mu_{2}\) = 0.5. d \(\mu_{1}\) = 0.9, \(\mu_{2}\) = 0.1

Full size image

Third, we increase the protection \(\mu_{2}\) of the frontliners for a fixed value of \(\mu_{1}\) and also vary the population of frontliners (Fig. 4). The number of infected frontliners decreased but there is no significant effect on the number of infected public individuals. Moreover, when the initial population of frontliners increased ten times, the peak on the number of infected public individuals significantly increased by 43.48% of the total number of susceptible public individuals.

Fig. 4
figure 4

Predicted number of infected public individuals and frontliners when we increase the initial values of the compartments S, E and I of the frontliners ten times with fixed values of \(\mu_{1}\) and varying values of \(\mu_{2}\). Parameter used: \(S_{1} = 10,000\), \(E_{1} = 0,I_{1} = 1\), \(Is_{1} = 0\), \(R_{1} = 0\), \(R_{01} = 2.5,\;R_{02} = 10,\) \(\tau = 14,\) \({\text{iso}}_{1} = {\text{iso}}_{2} = 0.01/14,\;\alpha_{1} = \alpha_{2} = 10/14\), \(\gamma_{1} = \gamma_{2} = 0.96/14\),\(\gamma_{1} * = \gamma_{2} * = 0.98/14\), \(m_{1} = m_{2} = 0.03/14\), \(m_{Is1} = m_{Is2} = 0.02/14\). a Initial population \(S_{2} = 100\), \(E_{2} = 10,I_{2} = 0\), \({\text{Is}}_{2} = 0\), \(R_{2} = 0\). b Initial population \(S_{2} = 1000\), \(E_{2} = 100,I_{2} = 0\), \({\text{Is}}_{2} = 0\), \(R_{2} = 0\). a–b \(\mu_{1}\) = 0, \(\mu_{2}\) = 0, 0, 0.1, 0.5, 0.9

Full size image

Lastly, we observe the effect of average secondary infections \(R_{01}\) and \(R_{02 }\) produced by an infectious public individual and an infectious frontliner, respectively. It was observed that a decrease in \(R_{01}\) will considerably reduce the number of infected in the general public and the frontliners (Fig. 5a). The combined effect of average secondary infections (\(R_{01}\) and \(R_{02}\)) and protection (\(\mu_{1}\) and \(\mu_{2}\)) was also explored. Figure 5b shows that the most effective way to minimize the number of infected individuals is a combination of reduced reproduction number \((R_{01} )\) and improved protection for the general public (\(\mu_{1}\)). This agrees with the policies currently being implemented that the general public should observe several preventive measures.

Fig. 5
figure 5

Predicted number of infected public individuals and frontliners. a Number of infected when we vary \(R_{0 }\) with fixed values of \(\mu_{1}\) and \(\mu_{2}\). b Number of infected when we vary \(R_{0}\), \(\mu_{1}\) and \(\mu_{2}\). Parameter used: Initial population \(S_{1} = 100,000\), \(E_{1} = 0,\;I_{1} = 1\) 0, \({\text{Is}}_{1} = 0\), \(R_{1} = 0\), \(S_{2} = 1000\), \(E_{2} = 100,I_{2} = 0\), \({\text{Is}}_{2} \, = \,0\), \(R_{2} = 0\), \(R_{01} = 2.5,\;R_{02} = 10,\) \(\tau = 14,\) \({\text{iso}}_{1} \, = \,{\text{iso}}_{2} \, = \,0.01/14,\;\alpha_{1} = \alpha_{2} = 10/14\), \(\gamma_{1} = \gamma_{2} = 0.96/14\), \(\gamma_{1} * = \gamma_{2} * = 0.98/14\), \(m_{1} = m_{2} = 0.03/14\), \(m_{Is1} = m_{Is2} = 0.02/14\). a \(\mu_{1}\) = 0, \(\mu_{2}\) = 0

Full size image

4 Sensitivity analysis

Sensitivity analysis is a method used to identify the effect of each parameter in the model outcome. Its aim is to identify the parameters that most influence the model output and quantify how uncertainty in the input affects model outputs (Marino et al. 2008). In this study, we are interested in the number of infected individuals of both the general public \(I_{1}\) and the frontliners \(I_{2}\). We employ a method called partial rank correlation coefficient (PRCC) analysis, which is a global sensitivity analysis technique that is proven to be the most reliable and efficient sampling-based method. To implement PRCC analysis, Latin hypercube sampling (LHS) is used in obtaining input parameter values. This is a stratified sampling without replacement technique proposed by Mckay et al. (Marino et al. 2008). Here, the uniform distribution is assigned to every parameter and simulation is done 10,000 times. The maximum and minimum values of the parameters are set as ± 90% of the default values listed in Table 1 with values of \(\mu_{1}\) and \(\mu_{2}\) set to 0.1.

PRCC values, which range from −1 to 1, are computed at different time points, specifically in the days \(t = 40k, \;k = 0,1,2,3,4, 5\) using the MATLAB function partialcorr. In Fig. 6, each bar corresponds to a PRCC value at an instance. The value of 1 takes a perfect positive linear relationship while −1 means a perfect negative linear relationship. Also, a large absolute PRCC value would mean a large correlation of the parameter with the model outcome, that is, a minute change to a sensitive parameter would affect the dynamics of the model output.

Fig. 6
figure 6

PRCC values depicting the sensitivities of the model output (infected population) with respect to model parameters

Full size image

Parameters \(R_{01} , \tau , \alpha_{1} , \gamma_{1}\) and \(R_{02}\) are found to have high PRCC values (> 0.5 or < −0.5). Among these, \(R_{01} , \alpha_{1}\) and \(R_{02}\) have positive PRCC values which mean that an increase in the values of these parameters will result in an increase in the infected population. In contrast, \(\tau\) and \(\gamma_{1}\) have negative PRCC values which indicate that an increase in these values will consequently result in a decrease in the infected population.

5 Discussion

We investigated the transmission dynamics of COVID-19 between frontliners and the general public using an extended susceptible–exposed–infected–recovered (SEIR) Compartment Model. The model has two mutually exclusive populations: the general public and the frontliners. Compartments for frontliners were incorporated in the usual SEIR model to represent those individuals who are frequently in contact with other people to provide essential services during a pandemic. Since frontliners have frequent interaction with the population, we set a higher basic reproduction number for frontliners compared to the general public. The sensitivity of the model parameters was determined to evaluate parameters with significant impact on the model output, in this case, the infected population of both the general public and frontliners. It was observed that the infected population is sensitive to the changes in the basic reproduction numbers of the general public \(R_{01}\) and of the frontliners \(R_{02}\), the infection period \(\tau ,\) the infection rate of an exposed public individual \(\alpha_{1} ,\) and the recovery rate of a non-isolated infected public individual \(\gamma_{1}\).

The model cannot be immediately utilized to make predictions on the spread of COVID-19 but it can provide insights on the transmission of the disease between two populations with different characteristics in terms of factors affecting disease transmissions such as the basic reproduction number and susceptibility rate. This can help in developing sound decisions and effective strategies in mitigating the spread of the disease. Simulations of the model show that both the frontliners and the general public should be protected against a spreading disease. The frontliners can be protected by providing them the necessary protective equipment. Strict implementations of the policies of the ECQ like physical distancing and wearing facemasks can protect the public from getting infected. Moreover, informing the public about the disease and the importance of precautionary measures will be very useful to control the spread of the disease.

One of the goals in controlling the spread of a disease is to flatten the epidemic curve so as not to overwhelm the country’s health system and to allow more time until a vaccine is developed. Our model showed that prioritizing only the protection of the frontliners cannot flatten the epidemic curve. On the other hand, protecting only the general public from the disease will significantly flatten the epidemic curve but the infection risk faced by the frontliners is still high, which can eventually affect their capability to provide services during an epidemic. In addition, if the control measures for the public are less strict, we can expect the number of secondary cases to be higher.

Simulations also revealed that a decrease in the average secondary infections by an infected individual, who is a part of the general public, will effectively reduce the infections in both populations. Mass testing will allow for the detection of asymptomatic cases and their immediate isolation can prevent further infection of other healthy individuals. Personal health and social practices that can prevent an individual from getting infected should be observed. These can be in the form of good personal hygiene, physical distancing, and self-isolation if an individual shows even minor symptoms.

Some asymptomatic individuals are less infectious compared to symptomatic ones (Gao et al. 2020). We incorporated this in the model by splitting the compartment for infected individuals into symptomatic (\(I^{s}\)) and asymptomatic (\(I^{as}\)) subcompartments. However, if an asymptomatic subcompartment is added, the dynamics of the infected population is unchanged if parameters \(\mu_{1}\) and \(\mu_{2}\) are varied (see Figs. 2, 7). This is also the case when other parameters that were varied in the original model are also varied in the revised model (with a subcompartment for asymptomatic individuals) as seen in Figs. 3, 4, 5, 8, 9, and 10.

Fig. 7
figure 7

Predicted number of infected public individuals and frontliners when infected individuals are divided to symptomatic \(\left( {I^{{\text{s}}} } \right)\) and asymptomatic \(\left( {I^{{{\text{as}}}} } \right)\) and if we increase the initial values of the compartments S, E, Is and \(I^{{{\text{as}}}}\) with fixed values of \(\mu_{2}\) and varying values of \(\mu_{1}\). Parameter used: \(R_{01} = 2.5,\) \(R_{02} = 10,\) \(\tau = 14,iso_{1} = iso_{2} = 0.01/14,\) \(\alpha_{1} = \alpha_{2} = 10/14\), \(\gamma_{1} = \gamma_{2} = 0.96/14\), \(\gamma_{1}^{*} = \gamma_{2}^{*} = 0.98/14\), \(m_{1} = m_{2} = 0.03/14\), \(Import_{1} = Import_{2} = 0.1.\) a–d Initial population \(S_{1} = 10,000\), \(E_{1} = 0, I^{s}_{1} = 0, I^{as}_{1} = 0\), \(Is_{1} = 0\), \(R_{1} = 0\), \(S_{2} = 100\), \(E_{2} = 10,\;I^{{\text{s}}}_{2} \, = \,0, \;I^{{{\text{as}}}}_{2} \, = \,0\), \(Is_{2} = 0\), \(R_{2} = 0\). e–h Initial population \(S_{1} = 100,000\), \(E_{1} = 0, I^{s}_{1} = 8, I^{as}_{1} = 2\), \(Is_{1} = 0\), \(R_{1} = 0\), \(S_{2} = 1000\), \(E_{2} = 100,\;I^{{\text{s}}}_{2} \,\, = \,0, \;I^{{{\text{as}}}}_{2} \, = \,0,\) \(Is_{2} = 0\), \(R_{2} = 0\). a–h \(\mu_{1}\) = 0, 0.1,0.5, 0.9. a, e \(\mu_{2}\) = 0. b, f \(\mu_{2}\) = 0.1. c, g \(\mu_{2}\) = 0.5. d, h \(\mu_{2}\) = 0.9

Full size image
Fig. 8
figure 8

Predicted number of infected public individuals and frontliners when infected individuals are divided to symptomatic \(\left( {I^{{\text{s}}} } \right)\) and asymptomatic \(\left( {I^{{{\text{as}}}} } \right)\) and when we increase the initial values of the compartments S, E, Is and \(I^{{{\text{as}}}}\) with fixed values of \(\mu_{1}\) and \(\mu_{2}\). Parameter used: \(R_{01} = 2.5,R_{02} = 10,\) \(\tau = 14,\) \({\text{iso}}_{1} \, = \,{\text{iso}}_{2} \, = \,0.01/14,\;\alpha_{1} = \alpha_{2} = 10/14\), \(\gamma_{1} = \gamma_{2} = 0.96/14\),\(\gamma_{1} * = \gamma_{2} * = 0.98/14\), \(m_{1} = m_{2} = 0.03/14\), \(m_{Is1} = m_{Is2} = 0.02/14\). (Parameter 1) Initial population \(S_{1} = 10,000\), \(E_{1} = 0,^{{}} I^{{\text{s}}}_{1} \, = 0, \;I^{{{\text{as}}}}_{1} = 0,\) \(Is_{1} = 0\), \(R_{1} = 0\), \(S_{2} = 100\), \(E_{2} \, = \,10,\;I^{{\text{s}}}_{2} \, = \,0, \,I^{{{\text{as}}}}_{2} \, = \,0\), \({\text{Is}}_{2} = 0\), \(R_{2} = 0\). (Parameter 2) Initial population \(S_{1} = 100,000\), \(E_{1} = 0,I^{s}_{1} = 8, I^{as}_{1} = 2\), \({\text{Is}}_{1} = 0\), \(R_{1} = 0\), \(S_{2} = 1000\), \(E_{2} \, = \,100,\; I^{{\text{s}}}_{2} \, = \,0,\; I^{{{\text{as}}}}_{2} = 0\), \(Is_{2} = 0\), \(R_{2} = 0\). a \(\mu_{1}\) = 0, \(\mu_{2}\) = 0. b \(\mu_{1}\) = 0.1, \(\mu_{2}\) = 0.9. c \(\mu_{1}\) = 0.5, \(\mu_{2}\) = 0.5. d \(\mu_{1}\) = 0.9, \(\mu_{2}\) = 0.1

Full size image
Fig. 9
figure 9

Predicted number of infected public individuals and frontliners when infected individuals are divided to symptomatic \(\left( {I^{{\text{s}}} } \right)\) and asymptomatic \(\left( {I^{{{\text{as}}}} } \right)\) and when we increase the initial values of the compartments S, E, Is and \(I^{{{\text{as}}}}\) of the frontliners ten times with fixed values of \(\mu_{1}\) and varying values of \(\mu_{2}\). Parameter used: \(S_{1} = 10000\), \(E_{1} = 0,\; I^{s}_{1} = 0,\; I^{as}_{1} = 0\), \(Is_{1} = 0\), \(R_{1} = 0\), \(R_{01} = 2.5,\;R_{02} = 10,\) \(\tau = 14,\) \(iso_{1} = iso_{2} = 0.01/14,\alpha_{1} = \alpha_{2} = 10/14\), \(\gamma_{1} = \gamma_{2} = 0.96/14\), \(\gamma_{1}^{*} = \gamma_{2}^{*} = 0.98/14\), \(m_{1} = m_{2} = 0.03/14\), \(m_{Is1} = m_{Is2} = 0.02/14\). (a) Initial population \(S_{2} = 100\), \(E_{2} = 10,I^{s}_{2} = 0, I^{as}_{2} = 0\), \({\text{Is}}_{2} = 0\), \(R_{2} = 0\). (b) Initial population \(S_{2} = 1000\), \(E_{2} = 100,I^{s}_{2} = 0, I^{as}_{2} = 0\), \({\text{Is}}_{2} = 0\), \(R_{2} = 0\). (a–b) \(\mu_{1}\) = 0, \(\mu_{2}\) = 0, 0, 0.1, 0.5, 0.9

Full size image
Fig. 10
figure 10

Predicted number of infected public individuals and frontliners when infected individuals are divided to symptomatic \(\left( {I^{{\text{s}}} } \right)\) and asymptomatic \(\left( {I^{{{\text{as}}}} } \right)\) and when the level of protection varies. a Number of infected when we vary \(R_{0 }\) with fixed values of \(\mu_{1}\) and \(\mu_{2}\). b Number of infected when we vary \(R_{0}\), \(\mu_{1}\) and \(\mu_{2}\). Parameter used: Initial population \(S_{1} = 100,000\), \(E_{1} \, = \,0,\;I^{{\text{s}}}_{1} \, = \,0,\; I^{{{\text{as}}}}_{1} = 0\), \({\text{Is}}_{1} = 0\), \(R_{1} = 0\), \(S_{2} = 1000\), \(E_{2} = 100,\;I^{{\text{s}}}_{2} = 0, \;I^{{{\text{as}}}}_{2} = 0\), \(Is_{2} = 0\), \(R_{2} = 0\),\(R_{01} = 2.5,R_{02} = 10,\) \(\tau = 14,\) \({\text{iso}}_{1} \, = \,{\text{iso}}_{2} \, = \,0.01/14,\;\alpha_{1} = \alpha_{2} = 10/14\), \(\gamma_{1} = \gamma_{2} = 0.96/14\),\(\gamma_{1} * = \gamma_{2} * = 0.98/14\), \(m_{1} = m_{2} = 0.03/14\), \(m_{{{\text{Is1}}}} \, = \,m_{{{\text{Is}}2}} \, = \,0.02/14\). a \(\mu_{1}\) = 0, \(\mu_{2}\) = 0

Full size image

We also note that the results from our model can be observed in the behavior of the actual COVID-19 infection in the Philippines from 1 July to 10 November 2020. Although the numerical values may vary, a similar trend of both the number of infected frontliners and the total number of case infections in the Philippines (most of which are from the general public) can be seen in the results presented from our model (Figs. 11, 12). The number of infected frontliners might have a smaller peak compared to that of the infected general public due to the small number of the actual frontliner population. Regardless, they are still responsible for handling the general public which puts them at a higher risk of being infected.

Fig.11
figure 11

Source: DOH Data Drop. Retrieved from https://www.doh.gov.ph/covid19tracker.)

Number of active COVID-19 cases frontliners (doctors, nurses, and others) in the Philippines from 1 July to 10 November 2020. (

Full size image
Fig. 12
figure 12

Source: DOH Data Drop. Retrieved from https://www.doh.gov.ph/covid19tracker.)

Reported COVID-19 new cases in the Philippines from 1 July to 10 November 2020. (

Full size image

The model may be further improved by considering factors such as differences in the dynamics between age categories and some behavioral changes that may result in immunity from the disease. An optimal control problem to determine methods to lessen the spread of the infection can also be formulated. This will determine the most effective strategies in controlling the spread of the disease and when these strategies should be implemented.