Abstract
Introduction
The self-thinning relationship established by Reineke in 1933 assumes a relationship between the number of stems and the quadratic mean diameter in fully stocked pure stands. This rule is extensively used for management purposes, but it has been initially calibrated for pure, even-aged stands for relatively few species.
Objectives
Here, we extend this relationship to mixed-species and mixed-size forests through a generalized modeling approach. Reineke’s rule can be seen as a particular case of this generalized approach. Resource sharing is taken as a starting point; thus, both site fertility and diameter heterogeneity are taken into account.
Discussion
Calibration on actual inventories is made on a dataset of 82 French stands. The theoretical relationship is successfully adjusted for species in which enough data were available, namely, common beech (Fagus sylvatica L.), oak (Quercus petraea [Mattuschka] Liebl and Quercus robur L.), and Norway spruce (Picea abies [L.] Karst).
Conclusion
Self-thinning exponents obtained for beech and oak (1.86 and 1.76, respectively) can be used in the mixed-species equation that we developed. These results encourage calibrating the parameters for other species if appropriate data are available.
Similar content being viewed by others
1 Introduction
Natural mortality is a major concern for foresters. Tree death occurs from diverse biotic or abiotic causes, some of them being considered to be random (Puettman et al. 1992). Nevertheless, the fraction of mortality directly or indirectly induced by competition between trees (called self-thinning) depends on the stocking per hectare and their relative growth and position (Reynolds and Ford 2005; Weiskittel et al. 2009). If the availability of light, water, nutrients, or even geometrical space is limited, the growth of a tree is restricted, leading to weakness or even death. The remaining trees will thus grow better, to the fullest potential of each site. That is why resource sharing can be seen as a starting point for modeling self-thinning (Enquist and Niklas 2001). Without anthropogenic action, stand density increases toward an upper limit, and the smallest trees or trees with less vigor die.
Mortality is a component of stand dynamics which is taken into account in growth models (Puettman et al. 1992; Berger and Hildenbrandt 2000; Enquist and Niklas 2001). Nevertheless, even if simple inventories allow the quantification of mortality, it is impossible to make all possible factors explicit. Thus, general approaches such as self-thinning laws are used to estimate a theoretical maximum density (Reineke 1933). By comparing this theoretical value with the actual density, it is possible to calculate an estimate of competition (Shaw 2006).
Considerable work has been conducted in relation to this topic over the last 80 years, often with contradictory results (Weller 1987). Initial works dealt with pure and even-aged forests or plantations (Reineke 1933; Yoda et al. 1963). Some authors pointed several difficulties to extend the relationship to mixed stands (Shaw 2006). Approaches dealing with species cohorts (Long and Daniel 1990) or fixed exponents (Ducey and Knapp 2010) as well as relative basal area for different species (Puettman et al. 1992; Weiskittel et al. 2009) have successfully overcome some of these difficulties. Here, the aim was to build a theoretical relationship as a generalization of the classical self-thinning equation to mixed stands. We also present a procedure for estimating the parameters of this law and compare the results with classical methods.
2 Self-thinning equation
2.1 Reineke’s reference equation
The first self-thinning rule was developed by Reineke (1933). It models the relationship between stem density (N) and quadratic mean diameter at breast height (QMD) in a pure, even-aged stand (Eq. 1) described in log–log coordinates (Zeide 2010).
where N is the number of trees per hectare, k is a species-specific constant, and QMD is the quadratic mean diameter (in centimeters).
In this equation, the slope of the self-thinning line is a constant found equal to −1.605 for all species, k being the only species-dependent parameter. Contrary to his expectations, Reineke did not find any influence of age or site quality on the values of the parameters, which were considered as universal.
Reineke’s results have been used extensively for management purposes (Castedo-Dorado et al. 2009) and in growth models (Enquist and Niklas 2001; Mäkelä et al. 2000). Indeed, one classical approach to density consists of comparing the actual number of stems to a maximal theoretical number given by the self-thinning law, for a given average diameter. A second approach consists of selecting a reference diameter (10 in., or 25.4 cm) to compare stands of different compositions or diameters. Through such a method, a “stand density index” or SDI can be defined, computed according to Eq. 2.
When compared with the maximum value, the relative density SDI/SDImax ranges from 0 (empty stands) to 1 (self-thinning stands). The intensity of thinning in silvicultural scenarios can be determined by comparing a target SDI with the actual SDI, obtained by a simple inventory.
Yoda et al. (1963) found a similar relationship when comparing average individual plant mass and stand density. Known as the “−3/2 power law,” this relationship has shown good results in analyzing the self-thinning process. Nevertheless, tree mass is more difficult to measure than diameter. Depending on the objective of the studies and the data available, either Reineke’s or Yoda’s law should be used.
The early works undertaken by Reineke (1933) and Yoda et al. (1963) looked for general laws applicable to a high number of species and situations. Some authors confirmed that the slope parameter of Eq. 1 was universal, by using other datasets (Westoby 1984; White 1981). However, as data availability was improved and computer capacity increased, several authors doubted the generality of this parameter. Small differences have been described in parameter values, for example the effect of different species on the slope of Reineke’s self-thinning line (Pretzsch and Biber 2005; Weiskittel et al. 2009) and Yoda’s law (Lonsdale 1990; Hamilton et al. 1995; Shaw 2006; Weller 1987; Zeide 1987).
The differences in slopes have been attributed to intra- and interspecific differences in shade tolerance (Henry and Aarssen 1997; Lonsdale 1990; Shaw 2006; Weiskittel et al. 2009; Zeide 2005) and ability to colonize open spaces (Zeide 1987, 2005). In fact, these are complex biological functions that are very difficult to describe (Henry and Aarssen 1997). Many authors have stated that these parameters should not be universal to reflect the huge diversity in the geometrical shapes of trees in either Reineke’s approach (Pretzsch and Biber 2005; Zeide 2010) or Yoda’s one (Hamilton et al. 1995; Lonsdale 1990; Woodall et al. 2005; Zeide 1987, 2005, 2010).
Some authors assumed that site fertility does not influence the intercept of the self-thinning line, but rather influences the rate at which a stand grows along this line (White 1981). Nevertheless, the influence of some factors such as mineral availability has been detailed on Yoda’s law (Dewar 1993; Morris 2003) in contradiction to the independence of SDI from fertility. In his early approach, Reineke (1933) indicated that an increasing fertility should increase the intercept of the self-thinning line because more trees would survive, but he was not able to demonstrate it. Westoby (1984), Weller (1987), then Shaw (2006) synthesized available results of Yoda’s and Reineke’s laws and noted the difficulty of explaining the influence of fertility with biological interpretations because above- and belowground biomass are affected in a complex way (as shown by Morris 2003). Puettman et al. (1992) included site index as an independent variable for mortality in a broader growth model. Some recent models explicitly include the fertility with a multiplying parameter applied to the general SDI equation (Bi 2001) or by a simple empirical fitting of SDI against nutrient availability (Morris 2003) or site index (Zeide 1987; Weiskittel et al. 2009).
Several authors working on self-thinning equations raised a need for an explicit modeling approach using biological processes (Bi 2001; Enquist and Niklas 2001). In the present paper, we develop a generalized law for self-thinning using a theoretical approach and apply it to inventory data from mixed forests.
2.2 Development of a generalized self-thinning relationship
Let us consider a very simple forest stand. The site in which it grows provides a particular total amount of resources along a given time interval. This amount is assigned the value K. This value represents a limiting resource that may be light, water, nutrients, soil structure, etc. It is necessary to take the available resource as a starting point because this drives the production of vegetative matter, thus overall growth (Berger and Hildenbrandt 2000; Enquist et al. 1998; Enquist and Niklas 2001).
The stand is assumed to be composed of N identical trees. Their common diameter is assigned the value D. It is assumed that the trees are placed homogeneously within the stand. In the case of even-aged plantations, this is a reasonable approach.
Each of these trees uses a quantity of resource, noted k j (j between 1 and N). As all trees are identical, they use the same amount of resource. If this use is assimilation, k j can be assumed to be proportional to the size of the exchange surface of the assimilating organs, which may be either leaves or roots depending on the resource considered.
Another assumption is that allometry exists between the dimension of the assimilating organ through which the resource k j is absorbed and a geometrical variable of the tree such as its diameter D (Berger and Hildenbrandt 2000; Enquist et al. 1998; Pretzsch and Biber 2005; White 1981; Zeide 2010). Equation 3 presents a classical example of such an allometry. The real exchange surface is extremely complex because it is composed of a spatial arrangement of root hairs or leaves. If assimilation was exactly proportional to a volume, the power of allometry would be 3 (Zeide 2010). If it was exactly proportional to a surface, it would be 2. The real geometry of assimilating organs in space is more complex and usually unknown. Thus, the power of allometry is only known to be <3 (Enquist and Niklas 2001; Reynolds and Ford 2005; Pretzsch and Biber 2005; Zeide 1987).
where k j is the individual tree assimilation (j between 1 and N), β is the allometry coefficient, D is the tree diameter, and α the power of the allometric relation (between 0 and 3).
A final assumption is that the stand is self-thinning. This situation corresponds to a maximum use of resources. Thus, the sum of individual assimilations is equal to the total available resource K (Eq. 4).
When applying a logarithm transformation, the relation becomes
This is again the usual mathematical form to represent self-thinning (see Eq. 1). The slope of self-thinning line is −α and the intercept is \( {\log_{{10}}}\left( {\frac{K}{\beta }} \right) \).
Four assumptions have been used until now. They are necessary for the modeling approach and would be reconsidered only if the reasoning is modified.
-
Assumption 1:
K is the maximum resource available, renewed at each step. This is a constant for the short period we consider because demographic and shape changes are negligible within a short period.
-
Assumption 2:
A stand reaches equilibrium in a self-thinning situation, meaning that all of the available resource is used.
-
Assumption 3:
The resource assimilated by a single tree (k j ) depends on the assimilating organs and on competition. It is considered as an allometry of the diameter D, written as β × D α, with α between 0 and 3.
-
Assumption 4:
All trees are homogeneously dispersed within the stand and are identical, i.e., are of the same species, have the same geometry, and have the same age and diameter.
Now let us consider a more general case. A constant total resource is still used (assumption 1), the stand is assumed to be in a self-thinning situation (assumption 2), and an allometry is assumed between diameter and assimilating surface (assumption 3). Assumption 4 on species and diameter homogeneity is, however, modified because it is not the case in reality (Reynolds and Ford 2005; Shaw 2006; Woodall et al. 2005). Now each tree is described by its own species and its own diameter D ij (where i and j are the indices for species and within species, respectively).
Equation 3 is slightly modified as \( {k_{{ij}}} = {\beta_i} \times {D_{{ij}}}^{{\alpha i}} \). The parameters α i and β i are assumed to be unique to each species.
Taking into account these more general situation leads to Eq. 6.
where i is the species (between 1 and I) and j the individual tree within a species (between 1 and n i ).
The equation cannot be simplified further because the diameters are now heterogeneous.
This is a generalized form of the classical self-thinning law (Reineke 1933), also extending developments such as additive SDI (Ducey and Knapp 2010; Long and Daniel 1990), taking into account the effect of tree species, actual diameters, and site fertility.
Each parameter can be interpreted:
-
Parameter K represents site fertility. In this paper, this is a stand-level variable that does not depend on species but only on the immediate environment of each stand. In this paper, we make the assumption that it is constant through the different inventories. This assumption is unrealistic for a very long time period, as shown by Reynolds and Ford (2005). Nevertheless, the modeling approach does not necessarily assume that K is constant. If sufficient data are available to test the influence of a changing resource through time, then Eq. 6 can be changed accordingly.
-
Parameter β depends on species and can be interpreted as the efficiency of resource assimilation.
-
Parameter α i summarizes the geometry of assimilating organs. It is consistent with a fractal dimension, and the value should be between 0 and 3. In Eq. 6, α is assumed to be species-dependent. In fact, α is likely to change with the developmental stage of trees (White 1981; Zeide 2010). A very young tree with a few leaves could have an assimilating surface directly proportional to the length of its stem, thus proportional to a single dimension; α would be close to 1 and increase with age.
Equation 6 is very general and can be applied to any stand for which assumptions H1 to H3 are reasonable, especially the self-thinning situation assumption.
3 Development of an adjustment method
3.1 Issue of data selection
In his early paper, Reineke himself did stress the difficulty of fitting a line to the available data (Reineke 1933). Indeed, even if the stands were very dense, all of them were not a strict self-thinning situation. The author arbitrarily selected the densest stands to perform a graphical regression by hand due to the lack of computing tools. However, other authors have criticized a lack of transparency and objectivity in the method for selecting stands in both Reineke’s and Yoda’s approaches (Bi 2001; Drew and Flewelling 1977; Ducey and Knapp 2010; Hamilton et al. 1995; Lonsdale 1990; Pretzsch and Biber 2005; Puettman et al. 1992; Zeide 1987). Moreover, all stands were pure and even-aged plantations. This raises a problem for applying this method to irregular mixed stands (Ducey and Knapp 2010; Woodall et al. 2005).
3.2 Available data from permanent plots
To calibrate the resource parameter K for each stand and the parameter α for each species, it is necessary to gather successive inventories made on the same site. Permanent plots are a good experimental tool for this purpose (Drew and Flewelling 1977; Puettman et al. 1992).
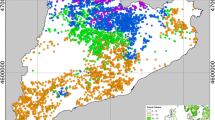
Here, the data available come from a French network of permanent plots currently managed by the laboratory “Laboratoire d’Etudes des Ressources Forêt-Bois” (LERFoB). The network is divided into forests in which one or more sites have been selected (Fig. 1). A site is defined by a homogeneous history and a limited geographical extension.
Available data. Location of French forests included in the dataset. Black dots indicate forests dominated by common beech (F. sylvatica), gray dots are dominated by oaks (Quercus sp.), and white dots are dominated by Norway spruce (P. abies). Each forest is divided into one to four plots, each having several inventories through time (see Table 1). A few major cities are indicated in gray in italics
One to four plots have been established on each site, each plot corresponding to a management option. The dataset is made of 82 plots whose area ranges from 0.2 to 2 ha (Table 1). The details of silvicultural scenarios changed over time in a given plot, but their relative strength (i.e., intensity of thinning) remained constant.
All inventories were performed between 1904 and 1999, each plot having 5 to 20 inventories made at different dates. Inventory files are lists of trees characterized by their diameter and state (alive, dead, thinned, etc.). Eighteen species are present in the dataset, mostly common beech (Fagus sylvatica L.), common oak (Quercus petraea [Mattuschka] Liebl. and Quercus robur L.) and Norway spruce (Picea abies [L.] Karst.).
This dataset is well adapted to study self-thinning relationships because plots with very scarce anthropogenic action are available. We assume that these plots have been very close to the self-thinning situation on at least one date. Even if usual permanent plot networks are placed in managed forests, fortunately, most of the plots reached very high densities through the years in the current dataset. However, it is impossible to determine the exact beginning date of self-thinning. Sometimes, management thinning could have been strong enough to suppress self-thinning situations for a long time. In spite of these difficulties, we chose to keep all data to avoid any subjective selection of the densest plots.
This situation raises questions about the choice of an adjustment method (Shaw 2006; Zhang et al. 2005). Classic statistical methods such as regressions or principal component analysis cannot be accurately applied with such a bias in the sampling. More recent methods called stochastic frontier analysis overcome this issue because all stands can be kept whatever their density (Bi 2001; Weiskittel et al. 2009; Zhang et al. 2005). Unfortunately, these methods are designed for temporary plot data and do not take into account the information provided by several inventories in the same plot. Thus, it is necessary to develop a method able to use permanent plot data and to take as much as possible these uncertainties into account.
3.3 An adjustment adapted to the generalized equation
As detailed above, classical adjustment methods cannot be applied to the present equation and dataset. Here, we present a method developed for this study, among several possible approaches to estimate parameters of the Eq. 6 from experimental data.
These parameters are of two types: two species parameters (α i , β i ) and one stand parameter (K p ), where p is the index associated to the stand. The approach consists of minimizing a distance to the self-thinning situation.
As mentioned above, assumption 2 only concerns extreme self-thinning situations. Uncertainties about the actual situation prevent using Eq. 6 without extension.
For each stand p, the relationship is generalized as an inequality (Eq. 7).
or equivalently
where p is the stand considered, t the time (date of inventories for this stand), i the species (between 1 and I) present in the inventories, and j the individual tree within a species (between 1 and n i ). And where K i,p = K p /β i is a global parameter representing the available resource for each species in the stand p.
Indeed, β i and K p cannot be estimated separately. If any solution were given for those parameters, another equivalent solution would be given by multiplying all these parameters by a same arbitrary positive factor. Only the ratio of β i and K p can be uniquely estimated.
The inequality (Eq. 7) becomes an equality if and only if the stand p is self-thinning at date t. Thus, this quantity can be used to evaluate how far the stand is from self-thinning by comparing its value to 1.
The product of such quantities evaluated for each stand p at each date t can then be used as a global criterion to evaluate how far from self-thinning are the studied stands among all the available dates. Since the data are collected from stands which are about to reach the self-thinning stage of development, our evaluation procedure consists of looking for a set of values for the parameters K i,p and α i that minimizes the criterion (Eq. 8) or, equivalently, its logarithm (Eq. 9).
It should be remarked that, conditionally to α i , the components of this criterion are separable from one stand to another. Each sub-criterion can be minimized separately on K i,p . The optimization procedure uses this property: for a given set of α i , sub-optimizations are processed to determine K i,p . The result is then used to determine a global optimization on α i .
It can be easily demonstrated that during the sub-optimizations, for each stand, the relationship (Eq. 7) will be saturated for at least one date so that in the overall solution, each stand will be considered at the self-thinning limit for at least one date.
The complete optimization is done with R software (version 2.11.0), using optim function (see Appendix), based on the “L-BFGS-B” method (Byrd et al. 1995). This is an optimization procedure for nonlinear continuous functions allowing box constraints on parameters. For example, parameter α is constrained between 0 and 3.
It is possible to estimate the parameter K i,p for any given combination of α i and compute the global criterion presented in Eq. 9. One can remark that in the particular case of pure and even-aged stands, our method is equivalent to find an upper limit for each stand, with the constraint of using a common slope for all forests. As a more general method, the optimization procedure we present here can be used for any number of species.
Since this method does not take into account uncertainties, contrary to usual approaches like regressions or stochastic frontiers (see Section 3.3), the results do not include confidence intervals for the parameters. Thus, we used a bootstrap method. Assuming that the species included in the optimization procedure are present in P stands, a random set of P stands are selected 1,000 times with replacements. The results give an estimate of the distribution of the parameter statistics, from which the approximate 95% confidence intervals can be obtained.
However, the only way to check the consistency of this adjustment method with previous studies is to validate it on pure stands as a preliminary result. Thus, we compared our results with stochastic frontier estimations on pure stands generated from the same dataset. To obtain such data similar to pure stands, all the species other than the targeted ones are gathered in a single virtual species. Each of these two “species” is characterized by an α parameter. A criterion given by Eq. 9 is computed for several sets of values of these α parameters, and the minimum of this criterion indicates optimal α, taken as a result. For the stochastic frontier estimation, we used the R library based on FRONTIER 4.1. See Bi (2001) and Weiskittel et al. (2009) as well as references therein for details on this approach.
4 Results
4.1 Consistency with previous studies on pure stands
The results of stochastic frontier estimations are presented in Table 2 compared with those obtained from the generalized optimization method on pure stands generated from our dataset. The result is displayed as a contour line plot (Fig. 2).
Preliminary results for single species. Global criterion (presented in Eq. 9) for different values of α for oaks (Quercus sp.) (a) against all other species. An optimum region (i.e., minimum in dark gray) is clearly visible. A similar result is obtained for beech (F. sylvatica) (b). On the contrary, spruce (P. abies) (c) and whitebeam (S. aria) (d) do not show optimum value
Different kinds of results show a strong influence of the proportion of the species of interest in the stands.
-
1.
Oak and common beech are well represented in a lot of stands. For these species, an optimum (i.e., minimum) is clearly visible in Fig. 2a, b. The value of parameter α i cannot be interpreted yet as the optimum slightly depends on the value of other species. However, this approach gives good starting parameters for a more precise mixed-species optimization.
-
2.
Contrarily, Norway spruce is only present in plantations in our dataset. A minimum is visible and the other species (a few trees) do not have any influence on the result (Fig. 2c).
-
3.
Opposite results can be obtained with rare species. For example, common whitebeam (Sorbus aria; Fig. 2d) does not have any influence on the result. In other words, an optimization run on whitebeam is unable to determine an optimal value of the α i parameter due to the very small number of trees in the stands.
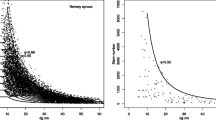
In our modeling, the K i,p parameter is interpreted as a stand fertility parameter for a given species. A good evaluation of the stand fertility is provided by the site index, defined as the dominant height (height of 100 biggest trees per hectare) at a given age, here 100 years. Foresters usually consider that site index is independent of silviculture in dense forests (Lanner 1985).
A relationship exists between this site index at age 100 and the parameter K i,p in Eq. 8 (Fig. 4). The harmonic mean of K i,p (weighted by the number of trees in each species) gives a good idea of the total resource used by the stands.
The linear fitting of this approximated resource to the site index presents a coefficient of determination (R 2) equal to 0.58. The value of R 2 can be considered as good since the parameter K i,p includes both a site effect (quantity of resource) and a species effect (ability to assimilate the resource).
This relationship indicates that the generalized theoretical approach we used is consistent with the behavior of actual mixed forests. Indeed, top height is independent of the diameters used in Eq. 8. To find a relation, even weak, is an incentive to test it on other data.
4.2 Mixed stands
As presented in Section 4.1, mixed stands containing oak and beech can be analyzed in more detail. The results are plotted in four dimensions; among them, three are α parameters (oak, beech, and other species) and a fourth dimension represents the criterion value graphically represented in a grayscale (Fig. 3).
Results for mixed stands of oak and beech. Global criterion (presented in Eq. 9) for different values of parameter α for oak, beech, and all other species. For each combination of α (between 0 and 3 for each species), the corresponding value of criterion is represented by a grayscale color. Optimal (smaller) values are in dark gray, in the center of the figure
A minimum exists for oak and for beech, but the influence of the other species is negligible. This is consistent with our preliminary results showing the negligible influence of rare species. An optimization is then run on data of Quercus and Fagus in mixed forests (65 plots). The bootstrap method samples a random set of 65 stands 1,000 times, with replacements, within the 65 stands including both Quercus and Fagus. The optimum value found for Quercus is 1.76 (95% CI = 1.56–1.99) and the value for Fagus is 1.86 (95% CI = 1.71–2.00).
5 Discussion
5.1 Parameters of the generalized law
Parameter α is constrained between 0 and 3 by assumption 3, consistent with Yoda’s and Reineke’s equations. Indeed, according to Reineke, N is proportional to D −1.605. According to Yoda, tree mass is proportional to N −3/2. Inserting Reineke’s relation into Yoda’s results in tree mass proportional to \( {D^{{ - {1}.{6}0{5}.\left( { - {3}/{2}} \right)}}} = {D^{{{2}.{4}}}} \). Tree mass is related to the mass of assimilating organs; thus, a value of 2.4 between 0 and 3 is consistent with Eq. 3.
The values of parameter α are consistent with those found in earlier literature. The same relative order between species has been found by Pretzsch and Biber (2005), already presented in Table 2. Still, note that a strict comparison is impossible because only pure stands were used by these authors. The same remarks apply to the study of Monserud et al. (2005) (and references therein).
In the generalized law, parameter α is assumed to be unique within species. These values could be applied to any inventory containing oak or beech tree, regardless of their size or species proportion, if they fit to the same range presented in Table 1. This means that the allometry is assumed to be valid for any tree form of a given species. In Reineke’s relationship, this parameter is universal because all trees are assumed to be identical, equal to the mean tree in each stand. Actually, in the generalized law, α is defined as a parameter related to tree architecture; thus, it is likely to change with age and stand density. The main difficulty is to take into account the evolution of tree architecture (Puettman et al. 1992). This could be done with a model of α evolving with age or stand density, but the question of the structure of such a model remains. Here, we kept α constant within each species, but the theoretical framework allows any refinement of this parameter, if adequate data are available.
Another possibility is to introduce variables like height or crown length to better describe tree architecture (Gül et al. 2005). Nevertheless, we focused our work on simple inventories that do not include such variables. This choice has already been detailed by several authors (see Zeide 2010 and references therein). This limitation is a choice to produce a relationship that can be used by managers with a simple inventory.
In Eq. 9, the parameter K i,p is also assumed to be constant through time. This means that the nature of the limiting resource remains as well as its amount during the period of interest. This is obviously wrong for the whole life of a given stand. But the modeling of K i,p raises the same questions as for α. For example, there is no simple method to establish a possible link of K i,p with stand density. A constant parameter has been chosen as a very simple approximation of reality. Again, in the theoretical construct, K i,p breaks down as a specific parameter (β i ) and a site-dependent parameter (K p ); they were gathered for estimation.
Finally, this generalization of usual self-thinning relationships does not claim to be universal. The simple and general assumptions that we make during the theoretical development define clear limits of application and adjustment.
5.2 Adjustment method
The estimation of self-thinning parameters is always hampered by the difficulty to find an upper limit. This issue affects all self-thinning relationships because any stand is below or just above the limit. In the method presented in this paper, the K i,p parameter is adjusted so that the resulting estimated density never takes values above the self-thinning limit. But as for any similar method, our procedure is sensitive to extreme values. However, since K i,p is estimated for each forest, a problematic stand would be moderated by the large number of other stands available.
The method requires that each plot be inventoried several times in order to obtain reasonable estimates of the K i,p parameter. Hence, data for permanent plots are most suitable. It would be possible to use data form temporary plots by grouping plots with assumed common K i,p values. However, such an assumption would be difficult to prove.
The value of parameter α was found to be consistent with its equivalent in the classical relationship. The only difficulties were induced by scarce species. As already pointed out by Ducey and Knapp (2010), such incidental trees are not strongly influencing competition in the stand. In a way, the optimization process excludes species that are not representative of competition induced by density. Despite these limitations, we noted that the generalized self-thinning relationship was adjusted quite easily with the method we use.
Progress has been made when compared with the usual methods because the results are obtained directly from mixed stands, which was not done in a similar way before (Puettman et al. 1992; Weiskittel et al. 2009). Even if this relationship is based on a pure theoretical construct, including a few strong hypotheses, the method resists comparison to real data.
Moreover, a link between site index and parameter K i,p has been found consistently with the theoretical relationship (Fig. 4). It is still an observation, but it is an incentive to elaborate a predictive model of K i,p from site index, as shown by Gül et al. (2005) and earlier developments by Sterba and Monserud (1993). Such a model would need to inspect possible links with other site characteristics, if they are available. Such results are encouraging and could lead to applications for management purposes. For example, the relation with site index could be used to choose plots or inventories in order to get a good statistical sampling of the diversity of forests. Such a sampling could help develop an adjustment method for our generalized self-thinning relationship similar to stochastic frontier analysis on the classical relationship.
Relationship between site index and fertility parameters. Relation between the harmonic mean of species fertility parameters K i,p approximated by the model presented in Eq. 7 and fertility given by the dominant height (reference age, 100 years). A simple linear relationship has been drawn whose R 2 is indicated. Intercept and slope are −22.7 and 1.57, respectively
An inventory giving the distribution of diameters and the site index would be enough to apply this generalized relationship, if species-dependent parameters have been previously estimated on permanent plot data. Thus, the method that we describe would be used for forest management purposes to build a density index that is adapted to mixed stands.
6 Conclusion
Based on theoretical assumptions, we have designed a theoretical self-thinning law for mixed stands. Even if some assumptions can be considered as simplistic compared with the complex behavior of real stands, the relationship fits well the permanent plot data. Pure and mixed stands can be analyzed by our procedure, if target species are sufficiently present in the inventories. An optimization procedure is possible for stands where several inventories are available at different development stages.
With a more detailed analysis of mixed stands of Quercus and Fagus, a relationship to the usual site index was obtained. As fertility is the only parameter that is not based on simple inventory data in the theoretical relationship, there is a hope for a predictive relationship based on site index, as shown by Gül et al. (2005). As permanent plots followed over a long period on non-managed mixed forests are very difficult to find, the results we obtained encourage further investigation on other datasets. If such data exist for species other than Quercus and Fagus, it would be possible to calibrate parameters and validate the link with fertility. Thus, this mixed self-thinning relationship could gain predictive power and be used for management purposes.
References
Berger U, Hildenbrandt H (2000) A new approach to spatially explicit modelling of forest dynamics: spacing, ageing and neighbourhood competition of mangrove trees. Ecol Model 132:287–302
Bi H (2001) The self-thinning surface. For Sci 47:361–370
Byrd RH, Lu P, Nocedal J, Zhu C (1995) A limited memory algorithm for bound constrained optimization. SIAM J Sci Comput 16:1190–1208
Castedo-Dorado F, Crecente-Campo F, Álvarez-Álvarez P, Barrio-Anta M (2009) Development of a stand density management diagram for radiata pine stands including assessment of stand stability. Forestry 82:1–16
Dewar RC (1993) A mechanistic analysis of self-thinning in terms of the carbon balance of trees. Ann Bot 71:147–159
Drew TJ, Flewelling JW (1977) Some recent Japanese theories of yield–density relationships and their application to Monterey pine plantations. For Sci 23:517–534
Ducey MJ, Knapp RA (2010) A stand density index for complex mixed species forests in the northeastern United States. For Ecol Manag 260:1613–1622
Enquist J, Niklas JK (2001) Invariant scaling relations across tree-dominated communities. Nature 410:655–660
Enquist BJ, Brown JH, West GB (1998) Allometric scaling of plant energetics and population density. Nature 385:163–165
Gül AU, Misir M, Misir N, Yavuz H (2005) Calculation of uneven-aged stand structures with the negative exponential diameter distribution and Sterba’s modified competition density rule. For Ecol Manag 214:212–220
Hamilton S, Matthew C, Lemaire G (1995) In defence of the 3/2 boundary rule: a re-evaluation of self-thinning concepts and status. Ann Bot 76:569–577
Henry H, Aarssen L (1997) On the relationship between shade tolerance and shade avoidance strategies in woodland plants. Oikos 80:575–582
Lanner RM (1985) On the insensitivity of height growth to spacing. For Ecol Manag 13:143–148
Long JN, Daniel TW (1990) Assessment of growing stock in uneven-aged stands. West J Appl For 5:93–96
Lonsdale WM (1990) The self-thinning rule: dead or alive? Ecology 71:1373–1388
Mäkelä A, Landsberg J, Ek A, Burk T, Ter-Mikaelian M, Ågren G, Olivier C, Puttonen P (2000) Process-based models for forest ecosystem management: current state of the art and challenges for practical implementation. Tree Physiol 20:89–298
Monserud RA, Ledermann T, Sterba H (2005) Are self-thinning constraints needed in a tree-specific mortality model? For Sci 50:848–858
Morris EC (2003) How does fertility of the substrate affect intraspecific competition? Evidence and synthesis from self-thinning. Ecol Res 18:287–305
Pretzsch H, Biber P (2005) A re-evaluation of Reineke’s rule and stand density index. For Sci 51:304–320
Puettman KJ, Hibbs DE, Hann DW (1992) The dynamics of mixed stands of Alnus rubra and Pseudotsuga menziesii: extension of size-density analysis to species mixture. J Ecol 80:449–458
Reineke LH (1933) Perfecting a stand-density index for even-aged forests. J Agric Res 46:627–638
Reynolds JH, Ford ED (2005) Improving competition representation in theoretical models of self-thinning: a critical review. J Ecol 93:362–372
Shaw JD (2006) Reineke’s stand density index: where are we and where do we go from here? Proceedings of the National Convention of the Society of American Foresters 2005. Society of American Foresters, Bethesda, MD (published on CD)
Sterba H, Monserud RA (1993) The maximum density concept applied to uneven-aged mixed species stands. For Sci 39:432–452
Weiskittel A, Gould P, Temesgen H (2009) Sources of variation in the self-thinning boundary line for three species with varying levels of shade tolerance. For Sci 55:84–93
Weller DE (1987) A reevaluation of the 3/2 power rule of self-thinning. Ecol Monogr 57:23–43
Westoby M (1984) The self-thinning rule. Adv Ecol Res 14:167–225
White J (1981) The allometric interpretation of the self-thinning rule. J Theor Biol 89:475–500
Woodall CW, Miles PD, Vissage JS (2005) Determining maximum stand density index in mixed species stands for strategic-scale stocking assessments. For Ecol Manag 216:367–377
Yoda K, Kira T, Ogawa H, Hozumi K (1963) Self-thinning in overcrowded pure stands pure stands under cultivated and natural conditions. J Biol Osaka City Univ 14:107–129
Zeide B (1987) Analysis of the 3/2 power law of self-thinning. For Sci 33:517–537
Zeide B (2005) How to measure stand density. Trees 19:1–14
Zeide B (2010) Comparison of self-thinning models: an exercise in reasoning. Trees 24:1–10
Zhang L, Bi H, Gove JH, Heath LS (2005) A comparison of alternative methods for estimating the self-thinning boundary line. Can J For Res 35:1507–1514
Acknowledgments
We are grateful to Jean-François Dhôte, François Ningre, Daniel Rittié, Jean-Daniel Bontemps, and people working in the LERFoB laboratory for providing data and for their comments, help, and encouragements. We are also grateful to journal editor and referees for their time and efforts in reviewing the earlier versions of this manuscript.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
Handling Editor: Daniel Auclair
Appendix. Optimization procedure
Appendix. Optimization procedure


Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Rivoire, M., Le Moguedec, G. A generalized self-thinning relationship for multi-species and mixed-size forests. Annals of Forest Science 69, 207–219 (2012). https://doi.org/10.1007/s13595-011-0158-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13595-011-0158-z