Longitudinal modeling of infectious disease

Abstract

When individuals in a community develop an infectious disease, it may quickly spread through personal contacts. Modeling the progression of such a disease is equivalent to modeling a branching process in which an infected person may infect others in a small time interval. It is also possible for some immigrants to enter the community with the disease and thus contribute to an increase in the number of infections. There exist various modeling approaches for dealing with this type of infectious disease data collected over a long period of time. However, there are certain infectious diseases which require very quick remedy by health professionals to prevent it from spreading further due to the dangerous nature of the disease. Such interventions require an understanding of the pattern of the disease in a short period of time. As a result, the spread of such infectious diseases only occur over a short period of time. The modeling of this type of infections that last only for a short period of time across several communities or countries is not, however, adequately discussed in the literature. In this paper, we develop a branching process with immigration to model this type of infectious disease data collected over a short period of time and provide consistent estimates of the parameters involved in the proposed model. We note that the model and inferences exploited in this paper are also applicable to infectious disease data obtained over a long period of time. We discuss a generalization of the proposed model under the assumption that the data may be affected by unobservable random community effects.

1 Introduction

Modeling the spread of infectious diseases is an important epidemiological issue. Since the pioneering work of Kermack and Mckendrick (1927) several mathematical models have been developed for the number of infectives at time t starting at an initial time t = 0. We refer to a recent book edited by Ma and Li (2009) and the references therein for some widely used epidemiological models. See also the epidemic models discussed by Andersson and Britton (2000), Diekmann and Heesterbeek (2000), and Daley and Gani (1999), among others. For example, consider the so-called Kermack and Mckendrick SIS (susceptible-infectives-susceptible) (Ma and Li, 2009, §1.4.2, eqn. (1.22)) dynamic model

$$y(t) = y(0)P(t) + \int_0 ^t \tilde{\beta}S(u)y(u)P(t-u)du, \label{model11.1} $$

(1.1)

where y(t) is the total number of infectives at time t, y(0)P(t) is the number of infectives who were infected at time t = 0 and have not been recovered until time t, P(t − u) is the probability that the individuals who were infectives at time t = u have not been recovered after the time period t − u, and $\tilde{\beta}S(u)y(u)$ is the number of secondary infections during the time period [u, u + du].

Note that the aforementioned models for infectious diseases were developed mainly to deal with infectious disease time series data obtained over a long period of time. For example, one may refer to the weekly mortality data (Choi and Thacker, 1981a, b) for pneumonia and influenza, pooled over 121 cities throughout the United States and covering the 15-year period from 1962 to 1979. In this example, there are 121 communities where mortality data were collected at 52 ×15 = 780 time points. Models have also been developed to deal with infectious disease data collected in the form of a time series of moderate length from a single community. One such example is the data from the October/November 1967 epidemic of respiratory disease in Tristan da Cunha (Shibli et al., 1971), which contains number of infections and number of susceptibles over a period of 16 time points. This type of data can be analyzed by using models similar to the model given in (1.1).

In this paper, we revisit the infectious disease problems modeled by (1.1) and provide an alternative modeling based on a recently developed dynamic model for repeated count data (Sutradhar, 2011, Chapter 6). Note that in the proposed model, we consider that an individual once infected may infect none or a few individuals following a binomial probability distribution where no record of recovery is available. We also note that even though our alternative model can handle infectious disease time series data of long duration that can be analyzed by models similar to that of (1.1), our main objective is to develop models for infectious diseases collected from a large number of independent communities, but over a small period of time. For an example of an infectious disease of this type, one may refer to the Severe Acute Respiratory Syndrome (SARS) epidemic of 2003 which lasted for only a short duration, such as T = 5, 6, or 7 weeks, involving many communities across Asia and secondary cases in large cities in different countries. The modeling of this type of infections that last only for a short period of time across several countries is not, however, adequately discussed in the literature. We remark that our proposed model would be suitable to deal with such longitudinal data. We also note that the inferential techniques we are proposing to develop in this paper based on data for small number of time points is also appropriate for dealing with time series type data obtained over a long period. In this special case, one will simply set the number of communities to one. In fact, it is important to examine whether the inference works for a small number of time points, since it would naturally work better if more time points are considered.

Suppose that K independent communities are at risk of an infectious disease. Also, suppose that at the initial time point, t = 1, y _i1 individuals in the ith (i = 1, ..., K) community developed the disease. It is reasonable to assume that y _i1 follows the Poisson distribution with mean parameter $\mu_{i1} = \mbox{exp}({\bf x}_{i1} ^{\prime} {\boldsymbol\beta})$. That is,

$$ y_{i1} \sim \mbox{Poi}(\mu_{i1} = \mbox{exp}({\bf x}_{i1} ^{\prime} {\boldsymbol\beta})), \label{model1.1} $$

where ${\bf x}_{i1} = (x_{i11}, x_{i12}, \ldots, x_{i1u}, \ldots, x_{i1})^{\prime}$ is a p-dimensional covariate vector representing p demographic and/or socioeconomic characteristics of the ith community such as its age (new or old), population density (low or high), apparent economic status (poor, middle class, or wealthy). In the restricted case, where each of the y _i1 individuals are thought to have infected none or only one individual within a given time interval, one may model the next infected count at time t = 2 as

$$ y_{i2} = \sum\limits_{j=1} ^{y_{i1}} b_j (\rho) + d_{i2}, $$

where b _j (ρ) is a binary variable such that Pr[b _j (ρ) = 1] = ρ and Pr[b _j (ρ) = 0] = 1 − ρ. Here, d _i2 is considered an immigration variable which follows a suitable Poisson distribution, and d _i2 and y _i1 are independent. In general, for t = 1, 2, ..., T, one may write,

$$y_{it} = \sum\limits_{j=1} ^{y_{i,t-1}} b_j (\rho) + d_{it}. \label{model1.2} $$

(1.2)

Beginning with Sutradhar (2003, §4) (see also McKenzie, 1988), this model (1.2) has been used for modeling count data over time which follow an autoregressive, of order 1, type Poisson process. When y _{i,t − 1} is considered as an offspring variable at time t − 1 and d _it is the immigration variable, the model (1.2) represents a branching process with immigration. In a time series context, that is for K = 1 and large T, this model was recently considered by Sutradhar, Oyet, and Gadag (2010) as a special case of a negative binomial branching process with immigration. In the present set up, the binary outcome based model (1.2) is not appropriate. This is because, each of the infected individuals y _{i,t − 1} at time t − 1 may infect none, one, or more than one individuals. Suppose that each of the y _{i,t − 1} patients can infect up to n _t individuals. Then, these y _{i,t − 1} individuals will infect a total of $\sum_{j=1} ^{y_{i,t-1}} B_j (n_t,\rho)$ individuals, where as opposed to (1.2), B _j (n _t ,ρ) is a binomial variable with parameters n _t and ρ such that n _t  = 1 yields the model (1.2). That is,

$$ Pr[B_j (n_t,\rho) = c_j] = \left( \begin{array}{c} n_t \\ c_j \end{array} \right) \rho^{c_j} (1 - \rho)^{n_t - c_j}, $$

for c _j  = 0,1, ..., n _t .

The proposed binomial variable based extended model is discussed in Section 2. A method for consistent estimation of the parameters, namely ${\boldsymbol\beta}$ and ρ, is also given in Section 2. In Section 3, we provide a further generalization under the assumption that apart from community related covariates x _it , the infected counts may also be influenced by an unobservable community effect. Let γ _i represent this latent effect for the ith community. Under the assumption that $\gamma_i \stackrel{iid}{\sim } N(0, \sigma_{\gamma} ^2)$, in Section 3, we develop an estimation method that provides consistent estimates for the parameters ${\boldsymbol\beta}$, ρ, and $\sigma_{\gamma} ^2$.

2 Proposed fixed model for counts over time

Because an infected individual may infect more than one individual in a given time interval, and also because there may be other infected individuals arriving from other communities, we shall model the number of infected persons at time t (t = 2,3, ..., T) as

$$y_{it} = \sum\limits_{j=1} ^{y_{i,t-1}} B_j (n_t,\rho) + d_{it}, \label{model2.1} $$

(2.1)

which accommodates (1.2) with n _t  = 1. In (2.1) we make the following assumptions:

• Assumption 1. $y_{i1} \sim \mbox{Poi}(\mu_{i1} = \mbox{exp}({\bf x}_{i1} ^{\prime} {\boldsymbol\beta}))$.

• Assumption 2. $d_{it} \sim \mbox{Poi}(\mu_{it} - \rho n_t \mu_{i,t-1})$, for t = 2, ..., T with $\mu_{it} = \mbox{exp}({\bf x}_{it} ^{\prime} {\boldsymbol\beta})$, for all t = 1, ...,T.

• Assumption 3. d _it and y _{i,t − 1} are independent for t = 2, ..., T.

Note that the model (2.1) has some similarities with the Kermack and Mckendrick (1927) SIS model given in (1.1). In (2.1), y _i1 is the initial number of infectives in the ith community at initial time t = 1, which is the same as y(0) in (1.1). The dynamic summation in (2.1) is similar to the integral in (1.1). The number of secondary infectives in (2.1) is d _it , whereas $\tilde{\beta}S(u)y(u)$ is the number of secondary infectives in (1.1), and so on.

Now turning to the statistical properties of the model (2.1), it is clear, from Assumption 1 above, that E(Y _i1) = μ _i1. Then, by successive expectation, it follows that for t = 2, ..., T,

$$E(Y_{it}) = \mathop{E}\limits_{y_{i1}} \mathop{E}\limits_{y_{i2}} \cdots \mathop{E}\limits_{y_{i,t-1}} E(Y_{it}| y_{i,t-1}) = \mu_{it} = \mbox{exp}({\bf x}_{it} ^{\prime} {\boldsymbol\beta}). \label{model2.2} $$

(2.2)

Hence, E(Y _it ) = μ _it for all t = 1, 2, ..., T. Next, for t = 2, ..., T one may obtain a recursive relationship for the variance of y _it in terms of the variance of y _{i,t − 1}. To be specific, by using the model (2.1), one writes

$$\begin{array}{lll} var(Y_{it}) & = & E[var(Y_{it}| y_{i,t-1})] + var[E(Y_{it}| y_{i,t-1})] \\[5pt] & = & E[Y_{i,t-1} n_t \rho (1 - \rho) + \mu_{it} - \rho n_t \mu_{i,t-1}]\\[5pt] &&+\, var[Y_{i,t-1} n_t \rho + \mu_{it} - \rho n_t \mu_{i,t-1}]. \end{array}$$

By (2.2), it then follows that for t = 2, ..., T,

$$\begin{array}{lll} var(Y_{it}) & = & n_t \rho (1 - \rho) \mu_{i,t-1} + \mu_{it} - \rho n_t \mu_{i,t-1} + n_t ^2 \rho^2 var(Y_{i,t-1}) \\[5pt] & = & \mu_{it} - n_t \rho^2 \mu_{i,t-1} + n_t ^2 \rho^2 var(Y_{i,t-1}), \\[5pt] & = & \sigma_{i,tt}, \ \ \ \mbox{say}, \label{model2.3} \end{array} $$

(2.3)

with $var(Y_{i1}) = \mu_{i1} = \mbox{exp}({\bf x}_{i1} ^{\prime} {\boldsymbol\beta})$ by Assumption 1. After some algebra, we obtain the following formulas for variances, for all t = 1, 2, ..., T as

$$ \sigma_{i,tt} = \left\{ \begin{array}{ll} \mu_{i1}, & t = 1 \\ \mu_{i2} + \rho^2 n_2(n_2 -1)\mu_{i1} & t = 2 \\ \mu_{it} + \rho^2 n_t (n_t -1) \mu_{i,t-1} + \sum_{l=1} ^{t-2} & t = 3, \ldots, T,\\ \quad \times\left[ \rho^{2(l+1)} n_{t-l}(n_{t-l} - 1) \left( \prod_{j=0} ^{l-1} n_{t-j} ^2 \right) \mu_{i,t-(l+1)} \right], \\ \end{array} \right. \label{model2.4} $$

(2.4)

with n ₁ = 1. Similarly, for lag k = 1, ..., t − 1, because

$$ E(Y_{it}Y_{i,t-k}) = E[Y_{i,t-k} \mathop{E}\limits_{y_{i,t-k+1}} \mathop{E}\limits_{y_{i,t-k+2}} \cdots \mathop{E}\limits_{y_{i,t-1}} E \{ Y_{it}| y_{i,t-1} \}], \label{model2.5} $$

one obtains the covariance between y _it and y _{i,t − k} as

$$cov(Y_{it},Y_{i,t-k}) = \sigma_{it,t-k} = \left( \prod\limits_{l=0} ^{k-1} n_{t-l} \right) \rho^k \sigma_{i,t-k,t-k}, \label{model2.6} $$

(2.5)

where σ _i,tt is given by (2.3). It then follows that the lag k correlation between the infected counts y _it at time t and y _{i,t − k} at time t − k, has the formula

$$corr(Y_{it},Y_{i,t-k}) = \left( \prod\limits_{l=0} ^{k-1} n_{t-l} \right) \rho^k \sqrt{\frac{\sigma_{i,t-k,t-k}}{\sigma_{i,tt}}}. \label{model2.7} $$

(2.6)

Note that when n _t  = 1, for all t = 1, 2, ..., T, the variance of y _it in (2.4) and the correlation between y _it and y _{i,t − k} given in (2.6) reduce to

$$ \sigma_{i,tt} = \mu_{it} \ \mbox{ and } \ corr(Y_{it},Y_{i,t-k}) = \rho^k \sqrt{\frac{ \mu_{i,t-k} }{ \mu_{it} }} \label{model2.8} $$

respectively, which are the same expressions for the binary sum (binomial thinning) based count data model considered by Sutradhar (2010, eqns. (15)–(16), p. 178). Thus, the present binomial sum based count data model (2.1) is an important generalization of the binary sum based count data model discussed by Sutradhar (2010, eqn. (14), p. 178). It is also clear that unlike the existing binomial thinning based count data models, the present model is suitable for modeling the spread of infectious diseases.

3 GQL estimation of the parameters of the infectious disease model (3)

3.1 Estimation of β

Recall from (2.2) that the expectation of the infectious counts y _it in the ith community at time t has the formula $E(Y_{it}) = \mu_{it} = \mbox{exp}({\bf x}_{it} ^{\prime} \boldsymbol{\beta})$ which is a function of $\boldsymbol{\beta}$. Let $\boldsymbol{\mu}_i = (\mu_{i1}, \mu_{i2}, \ldots, \mu_{it}, \ldots, \mu_{iT})^{\prime}$ be the T-dimensional expectation vector of ${\bf y}_i = (y_{i1}, y_{i2}, \ldots, y_{it}, \ldots, y_{iT})^{\prime}$. Following Sutradhar (2010, eqn. (46)), one may then obtain a consistent and efficient estimate of $\boldsymbol{\beta}$ by solving the so-called generalized quasi-likelihood (GQL) estimating equation

$$\sum\limits_{i=1}^K \frac{\partial \boldsymbol{\mu}_i ^{\prime}}{\partial \boldsymbol{\beta}} {\Sigma}_i ^{-1}(\boldsymbol{\beta}, \rho)({\bf y}_i -\boldsymbol{\mu}_i) = {\bf 0}, \label{model3.1} $$

(3.1)

with

$$ {\Sigma}_i ^{-1}(\boldsymbol{\beta}, \rho) = cov({\bf Y}_i) = {\it A}_i ^{1/2} {\it C}_i (\rho) {\it A}_i ^{1/2} $$

where ${\it A}_i = diag[\sigma_{i1}, \ldots, \sigma_{it}, \ldots, \sigma_{iT}]$ and ${\it C}_i$ is the T ×T correlation matrix defined as

$$ {\it C}_i = \left( \begin{array}{cccccc} 1 & \rho_{i12} & \rho_{i13} & \cdots & \cdots & \rho_{i1T} \\ & 1 & \rho_{i23} & \cdots & \cdots & \rho_{i2T} \\ & & \cdots & \cdots & \cdots & \cdots \\ & & & \cdots & \cdots & \cdots \\ & & & & 1 & \rho_{i,T-1,T} \\ & & & & & 1 \end{array} \right) \label{model3.2} $$

with $\rho_{i,t-k,t} = \left( \prod_{l=0} ^{k-1} n_{t-l} \right) \rho^k \sqrt{\frac{\sigma_{i,t-k,t-k}}{\sigma_{i,tt}}}$ by (2.6) for t = 2, ..., T, and k = 1, ..., t  −  1. The GQL estimating equation (3.1) may be solved iteratively by using the Newton–Raphson iterative equation

$$\begin{array}{lll} \hat{\boldsymbol\beta}(r+1) &=& \hat{\boldsymbol\beta}(r) + \left\{ \left[\sum\limits_{i=1} ^K \frac{\partial {\boldsymbol\mu}_i ^{\prime}}{\partial {\boldsymbol\beta}} {\Sigma}_i ^{-1}({\boldsymbol\beta}, \rho) \frac{\partial {\boldsymbol\mu}_i }{\partial {\boldsymbol\beta}} \right]^{-1} \right.\\[6pt] &&\qquad\qquad\left.\times\,\sum\limits_{i=1} ^K \frac{\partial {\boldsymbol\mu}_i ^{\prime}}{\partial {\boldsymbol\beta}} {\Sigma}_i ^{-1}({\boldsymbol\beta}, \rho) ({\bf y}_i -{\boldsymbol\mu}_i) \right\}_{{\boldsymbol\beta} = \hat{\boldsymbol\beta}(r)}, \label{model3.3} \end{array} $$

(3.2)

where $\hat{\boldsymbol\beta}(r)$ is the value of ${\boldsymbol\beta}$ at the rth iteration.

3.2 Estimation of the correlation index parameter ρ

Let S _itt and S _it,t + 1 be the standardized sample variance and the standardized lag 1 sample autocovariance defined as

$$\begin{array}{rll} S_{itt} & = & \sum\limits_{i=1}^K \sum\limits_{t=1} ^T \left( \frac{y_{it} - \mu_{it}} {\sigma_{it}} \right)^2/KT \\[6pt] S_{it,t+1} & = & \sum\limits_{i=1} ^K \sum\limits_{t=1} ^{T-1} \left( \frac{y_{it} - \mu_{it}}{\sigma_{it}} \right) \left.\left( \frac{y_{i,t+1} - \mu_{i,t+1}}{\sigma_{i,t+1}} \right)\right/K(T-1). \end{array}$$

Since

$$ \begin{array}{lll} E(S_{itt}) & = & 1 \\ E(S_{it,t+1}) & = & \rho \sum\limits_{i=1} ^K \sum\limits_{t=1} ^{T-1} n_{t+1} \left. \left( \frac{\sigma_{it}}{\sigma_{i,t+1}} \right) \right/K(T-1), \end{array} $$

one may use the method of moments to obtain a consistent estimator of ρ given by

$$ \hat{\rho} = \left(\frac{S_{it,t+1}}{S_{itt}} \right) \left[\left.\sum\limits_{i=1} ^K \sum\limits_{t=1} ^{T-1} n_{t+1} \left( \frac{\sigma_{it}}{\sigma_{i,t+1}} \right) \right/K(T-1) \right]^{-1}. \label{model3.5} $$

(3.3)

3.3 Forecasting

Once the parameters of the infectious disease model (2.1) have been estimated, one-step ahead forecasts can be obtained for the purpose of planning and control. In this section, we will derive the one-step ahead forecasting function and the variance of the forecast error.

From the model (2.1), it is clear that the conditional mean of Y _it given y _{i,t − 1} is given by

$$E(Y_{it}|y_{i,t-1}) = \mu_{it} + \rho n_t(y_{i,t-1} - \mu_{i,t-1}). \label{model3.6} $$

(3.4)

If we define the l-step ahead forecasting function of y _i,t + l as $y_{i,t}(l) = \hat{y}_{i,t+l} = E(Y_{i,t+l}|y_{i.t+l-1})$, then, from (3.4) the one-step ahead forecasting function can be written as

$$y_{it}(1) = \mu_{i,t+1} + \rho n_{t+1}(y_{it} - \mu_{it}), \label{model3.7} $$

(3.5)

where y _it  = y _it (0) with forecast error

$$e_{it}(1) = y_{i,t+1} - y_{it}(1) = (y_{i,t+1} - \mu_{it}(1)) - \rho n_t(y_{it} - \mu_{it}). \label{model3.8} $$

(3.6)

Using the fact that E[e _it (1) | y _it ] = 0 and that V(Y _i,t + 1|y _it ) = μ _i,t + 1 − ρn _t + 1 μ _it  + y _it n _t + 1 ρ(1 − ρ), one can easily verify that the variance of the one-step ahead forecast error is

$$V[e_{it}(1)] = \mu_{it}(1) - \rho^2 n_t(1) \mu_{it}. \label{model3.9} $$

(3.7)

In Section 3.4, we will examine the performance of the GQL estimation approach [(3.2) and (3.3)] discussed in Sections 3.1 and 3.2 through a simulation study. We will also examine the performance of the forecasting function (3.5).

3.4 A simulation study

3.4.1 Estimation performance of β and ρ

We begin our simulation study by generating data from (2.1) for various combinations of parameter values and simulation design. The parameter values used in the simulation were T = 5, K = 100, ${\boldsymbol\beta}^{\prime} \equiv (0.5,1), (1,1)$, and ${\bf n}^{\prime} = (n_1, n_2, n_3, n_4, n_5) \equiv (1,2,2,2,2), (1,2,2,3,2), (1,2,3,4,2), (1,2,2,2,3)$, (1,2,2,3,3), (1,2,3,4,3). We have used a time dependent covariate vector x _it in order to study the nonstationary case. The components of the covariate vector ${\bf x}_{it} ^{\prime} = (x_{it1}, x_{it2})$ were generated as follows:

$$x_{it1} = \left\{ \begin{array}{rl} -1, & t = 1,2; \; \; i = 1,2, \ldots, \displaystyle\frac{K}{2} \\[6pt] 1, & t = 3,4,5; \; \; i = 1,2, \ldots, \displaystyle\frac{K}{2} \\[6pt] 0, & t = 1; \; \; i = \displaystyle\frac{K}{2}+1, \ldots, K \\[6pt] 0.5, & t = 2,3; \; \; i = \displaystyle\frac{K}{2}+1, \ldots, K \\[6pt] 1, & t = 4,5; \; \; i = \displaystyle\frac{K}{2}+1, \ldots, K \\ \end{array} \right. \label{model3.10} $$

(3.8)

and

$$x_{it2} = \left\{ \begin{array}{cl} \displaystyle\frac{t}{T}, & t = 1,2,3,4,5; \; \; i = 1,2, \ldots, \displaystyle\frac{K}{4} \\[6pt] -1, & t = 1; \; \; i = \displaystyle\frac{K}{4}+1, \ldots, \displaystyle\frac{3K}{4} \\[6pt] 0, & t = 2,3; \; \; i = \displaystyle\frac{K}{4}+1, \ldots, \displaystyle\frac{3K}{4} \\[6pt] 0.5, & t = 4,5; \; \; i = \displaystyle\frac{K}{4}+1, \ldots, \displaystyle\frac{3K}{4} \\[6pt] (0.5 + (t-1)0.5)/T, & t = 1,\ldots,5; \; \; i = \displaystyle\frac{3K}{4}+1, \ldots, K. \\ \end{array} \right. \label{model3.11} $$

(3.9)

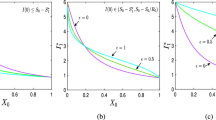
Note that even though we have chosen two covariates hypothetically, they however reflect the time dependent economic (x _it1) and cleanliness (x _it2) conditions of the K communities. For example, the covariate for economic conditions of the communities x _it1 indicates that half of the communities had low income conditions (x _it1 = − 1) at t = 1,2 and subsequently at $t = 3,4 \mbox{ and } 5$, their economic condition improved (x _it1 = 1). The rest of the communities also increasingly did better (x _it1 = 0, 0.5 and 1.0) as time progressed. A similar pattern of improvement in the cleanliness conditions can be observed for the first and fourth quarter of the communities over time and the middle half of the communities also showed improved cleanliness conditions with regard to change in time. The roles of these covariates are highlighted through Figure 1(a), (b) and (c) for time dependent mean, variance, and correlation.

Figure 1

A plot of (a) values of nonstationary mean for t = 1 (solid line); t = 2 (dashed line), t = 3 (dotted line), t = 4 (dotted dashed line); (b) values of nonstationary variance for t = 1 (solid line); t = 2 (dashed line), t = 3 (dotted line), t = 4 (dotted dashed line); and (c) values of nonstationary lag 1 correlation for t = 1 (solid line); t = 2 (dashed line), t = 3 (dotted line); (d) average forecast overlaid on average of longitudinal data; (e) proportion of absolute values of forecast error that are 0 or 1 (solid lines) and > 1 (dashed line); by communities obtained from 1,000 simulations with ρ = 0.5, β = (1, 1)ʹ, nonstationary covariates (3.8)–(3.9) and n ₁ = 1, n ₂ = . . . = n ₅ = 2.

Since the mean of the Poisson random variable d _it given by E(d _it ) = μ _it  − ρn _t μ _{i, t − 1}, must be positive, the values of ρ in our simulation were chosen to satisfy the condition $\rho < \min \left\{\mu_{it}/n_t \mu_{i,t-1}, 1 \right\}$. As a result of the condition on ρ, the data generation process began with the computation of the covariate vector x _it , i = 1, ...,K, t = 1, ..., T which we then used to evaluate the mean of y _it , $\mu_{it} = \exp({\bf x}_{it} ^{\prime} {\boldsymbol\beta})$ for a fixed value of ${\boldsymbol\beta}$, say for instance ${\boldsymbol\beta}^{\prime} = (0.5,1)$. Next, we used the values of μ _it to compute the upper bound for ρ, given by $\rho^* = \frac{\mu_{it}}{n_t \mu_{i,t-1}}$. We then choose ρ = ρ ^* − 0.1 or ρ = ρ ^* − 0.2 as the true value of ρ for the simulation. Once a value of ρ has been chosen, we generated y _i1 and d _it ’s from a Poisson distribution with means μ _i1 and μ _it  − ρn _t μ _{i, t − 1} respectively. The remainder of the observations, namely, y _i2, y _i3, y _i4, y _i5 were then generated from (2.1) for i = 1,2, ..., 100.

Using only the first four observations, y _i1, y _i2, y _i3, y _i4, i = 1,2, ..., 100, the GQL estimate of ${\boldsymbol\beta}$ and the method of moment estimate of ρ were iteratively computed from equations (3.2) and (3.3) respectively. This process was repeated 1,000 times for various combinations of n ₁ = 1, n _t , t = 2,3,4,5, ${\boldsymbol\beta}$, and ρ. The average of the estimated ${\boldsymbol\beta}$, ρ, and their standard errors $s_{\hat{\boldsymbol\beta}}$ and s _ρ over 1,000 simulations are reported in Table 1. The results in Table 1, show that the GQL method performed well in estimating the parameters of the infectious disease model (2.1). For instance, when ${\boldsymbol\beta}^{\prime} = (0.5,1)$, ρ = 0.3, and n ₂ = n ₃ = n ₄ = 2 and n ₅ = 3, the GQL estimate of ${\boldsymbol\beta}$ was (0.501,0.998) and the MM estimate of ρ was 0.292 with standard errors (0.055,0.62) and 0.045 respectively.

Table 1 GQL estimate of ${\boldsymbol\beta}$ and method of moments estimate of ρ and their standard errors obtained from 1,000 simulations.

3.4.2 Forecasting performance

For the purpose of examining the performance of the model (2.1) in forecasting future infections, we used the parameter estimates obtained from using only the first four observations, in Section 3.4.1, and the forecasting function in (3.5) to compute a one-step ahead forecast of the fifth observation, y _i5, i = 1, 2, ..., 100. We also computed the sum of squares of the forecast error (3.6) as well as the variance of the forecast error (3.7). These calculations were repeated 1,000 times for a fixed combination of parameter values. The average sum of squares of the forecast errors and the average variance of the forecast errors, denoted by ASS[e _it (1)] and AV[e _it (1)] respectively are reported in Table 2. From the results in Table 2, we see that the average sum of squares of the forecast errors closely estimates the average variance of the forecast errors irrespective of the combination of parameter values. This is an indication of the satisfactory performance of the estimation of the parameters of the model.

Table 2 Average sum of squared forecast errors and average variance of forecast errors.

In practice, given the data y _it , one may incorrectly assume that ρ = 0 and then estimate only the regression parameter ${\boldsymbol \beta}$. Results not reported here show that this assumption will not affect the GQL estimate of ${\boldsymbol \beta}$. However, the average sum of squares of the forecast errors when the incorrect assumption of ρ = 0 was used, given in Table 2 as ASS0[e _it (1)] shows that this incorrect assumption will significantly inflate the variance of the forecast errors with the percentage of inflation ranging from 18% to 72%. The magnitude of the percentage of inflation appear to increase as the value of ρ increases. For instance when n ₂ = n ₃ = n ₄ = n ₅ = 2, and ${\boldsymbol \beta}^{\prime} = (.5,1)$, if one assumes that ρ = 0 when in fact ρ = 0.5 the average sum of squares of the forecast errors is inflated by approximately 72%; whereas if the true value of ρ were 0.3, the percentage inflation will only be about 30%.

In Figure 1, we have overlaid a graph of the average of the forecast in 1,000 simulations over a scatterplot of the average of the observations y _i5 (Figure 1(a)). The plot shows that the average forecast follows the general pattern of the infections at the fifth time point. In order to assess the accuracy of our forecasts, we have also displayed a graph showing the average of the proportion of the forecast error e _it with absolute deviations 0, 1, and greater than 1. Figure 1(e) shows that deviations of magnitude 0 and 1 appear to be over 50% for the first 25 communities and over 80% for the remaining 75 communities. It is clear from Figure 1(d) that the number of infections for the first 25 communities range from 2.5 to 17.5 approximately. This large spread in the number of infections for the first 25 communities accounts for the 50% deviation of magnitude 0 and 1 in the absolute value of the forecast error for these 25 communities. Graphs showing the nonstationary patterns in the mean μ _it , variance σ _it,t , and the lag 1 correlation ρ _{i,t − 1,t} are also shown in Figure 1. For the purpose of highlighting the differences between the stationary case and the nonstationary case, we constructed similar plots in Figures 2 and 3 for a stationary case obtained from data generated using the covariate components

$$x_{it1} = \left\{ \begin{array}{rl} -0.5, & t = 1,2,3,4,5; \; \; i = 1,2, \ldots, \displaystyle\frac{K}{2} \\[6pt] 0.5, & t = 1,2,3,4,5; \; \; i = \displaystyle\frac{K}{2}+1, \ldots, K \end{array} \right. \label{model3.30} $$

(3.10)

and

$$x_{it2} = \left\{ \begin{array}{cl} 0, & t = 1,2,3,4,5; \; \; i = 1,2, \ldots, \displaystyle\frac{K}{2} \\[6pt] 1, & t = 1,2,3,4,5; \; \; i = \displaystyle\frac{K}{2}+1, \ldots, \displaystyle\frac{3K}{4} \end{array} \right. \label{model3.31} $$

(3.11)

The difference between Figures 2 and 3 is that in Figure 2 the maximum number of individuals that can be infected n _t , t = 1, 2, ..., 5 is time dependent whereas in Figure 3, n _t  = 1, for all t = 1,2,3,4,5.

Figure 2

A plot of (a) values of stationary mean for t = 1, 2, 3, 4; (b) values of nonstationary variance for t = 1 (solid line); t = 2 (dashed line), t = 3 (dotted line), t = 4 (dotted dashed line); and (c) values of nonstationary lag 1 correlation for t = 1 (solid line); t = 2 (dashed line), t = 3 (dotted line); (d) average forecast overlaid on average of longitudinal data; (e) proportion of absolute values of forecast error that are 0 or 1 (solid lines) and > 1 (dashed line); by communities obtained from 1,000 simulations with ρ = 0.3, ${\boldsymbol\beta} =(1,1)^{\prime}$, stationary covariates (3.10)–(3.11) and n ₁ = 1, n ₂ = ... = n ₅ = 2.

Figure 3

A plot of (a) values of stationary mean for t = 1,2,3,4; (b) values of stationary variance for t = 1,2,3,4; (c) values of stationary lag 1 correlation; (d) average forecast overlaid on average of longitudinal data; (e) proportion of absolute values of forecast error that are 0 or 1 (solid lines) and > 1 (dashed line); by communities k = 1,2,...,100 obtained from 1,000 simulations with $\protect\rho =0.8$, ${\boldsymbol\beta } =(1,1)^{\prime }$, stationary covariates (3.10)–(3.11) and n ₁ = n ₂ = ... = n ₅ = 1.

4 Extended model

4.1 Dynamic mixed model

In this section, we account for the fact that aside from the community related covariate x _it , the number of infections generated by the model (2.1) may be influenced by some unobservable community effects. Suppose that for the ith community, $\gamma_i \stackrel{iid}{\sim } N(0, \sigma_{\gamma} ^2)$ is this latent community effect. Then, conditional on the ith community effect γ _i , a dynamic mixed model for the number of infections at time t, t = 2, ...,T, as a generalization of (2.1) can be written as

$$y_{it} \left|_{\gamma_i} \right. = \sum_{j=1} ^{y_{i,t-1}} B_j (n_t,\rho) \left|_{\gamma_i} \right. + d_{it} \left|_{\gamma_i} \right. , \label{model4.1} $$

(4.1)

where,

• Assumption 1. $y_{i1} \left|_{\gamma_i} \right. \sim \mbox{Poi}(\mu_{i1} ^*)$.

• Assumption 2. $d_{it} \left|_{\gamma_i} \right. \sim \mbox{Poi}(\mu_{it} ^* - \rho n_t \mu_{i,t-1} ^*)$, for t = 2, ..., T, where $\mu_{it} ^* = \exp({\bf x}_{it} ^{\prime} {\boldsymbol\beta} + \gamma_i)$, for all t = 1, ...,T.

• Assumption 3. $d_{it} \left|_{\gamma_i} \right.$ and $y_{i,t-1} \left|_{\gamma_i} \right.$ are independent for t = 2, ..., T.

4.1.1 Basic properties of the dynamic mixed model

We note that in the present dynamic mixed model, the conditional means are denoted by $\mu_{it} ^*$ whereas in the fixed model (2.1) the means were denoted by μ _it , free from γ _i . Because of the similarities between the fixed model (2.1) and the mixed model (4.1), following (2.2) and (2.3) or (2.4), the mean and variance of y _it conditional on γ _i can be written as

$$ \begin{array}{lll} &&\mu_{it} ^* = E[Y_{it} \left| {\gamma_i} \right.] = \mbox{exp}({\bf x}_{it} ^{\prime} {\boldsymbol \beta} + \gamma_i), \\ && \sigma_{i,11} ^* = var[Y_{i1} \left| {\gamma_i} \right.] = \mu_{i1} ^*, \label{model4.2} \end{array} $$

(4.2)

and

$$ \sigma_{i,tt} ^* = var[Y_{it} \left| {\gamma_i} \right. ] = n_t \rho (1 - \rho) \mu_{i,t-1} ^* + (\mu_{it}^* - \rho n_t \mu_{i,t-1} ^*) + n_t ^2 \rho^2 var[Y_{i,t-1} \left| {\gamma_i} \right. ], $$

for t = 2, ..., T. Thus,

$$ \sigma_{i,tt} ^* = \left\{ \begin{array}{ll} \mu_{i1} ^*, & t = 1 \\ \mu_{i2} ^* + \rho^2 n_2(n_2 -1)\mu_{i1} ^* & t = 2 \\ \mu_{it} ^* + \rho^2 n_t (n_t -1) \mu_{i,t-1} ^* + \sum_{l=1} ^{t-2} & t = 3, \ldots, T.\\ \quad \times\left[ \rho^{2(l+1)} n_{t-l}(n_{t-l} - 1) \left( \prod_{j=0} ^{l-1} n_{t-j} ^2 \right) \mu_{i,t-(l+1)} ^* \right], \\ \end{array} \right. \label{model4.3} $$

(4.3)

To understand the important properties of the data from the mixed model (4.1) it is now necessary to find the unconditional mean and variance of y _it . They can be found by averaging (4.2) over the distribution of γ _i . More specifically, from (4.2) we obtain

$$\mu_{it} = E(Y_{it}) = \mathop{E}\limits_{\gamma_i} \{ E[Y_{it} \left| {\gamma_i} \right.] \} = \mbox{exp}({\bf x}_{it} ^{\prime} {\boldsymbol \beta} + \sigma_{\gamma} ^2/2), \label{model4.4} $$

(4.4)

and using (4.2) and (4.3) we find that

$$\begin{array}{lll} \sigma_{i,tt} & = & var(Y_{it}) \\ &=& E[var(Y_{it} \left| {\gamma_i} \right. )] + var[E(Y_{it} \left| {\gamma_i} \right. )] \\ & = & \left\{ \begin{array}{ll} \mu_{i1} + \mu_{i1} ^2 [\mbox{exp}(\sigma_{\gamma} ^2) - 1] , & t = 1 \\ \mu_{i2} + \rho^2 n_2(n_2 -1)\mu_{i1} + \mu_{i2} ^2 [\mbox{exp}(\sigma_{\gamma} ^2) - 1] & t = 2 \\ \mu_{it} + \rho^2 n_t (n_t -1) \mu_{i,t-1} + & \\ \sum_{l=1} ^{t-2} \Bigl[ \rho^{2(l+1)} n_{t-l}(n_{t-l} - 1) \\ \quad\qquad \times\left( \prod_{j=0} ^{l-1} n_{t-j} ^2 \right) \mu_{i,t-(l+1)} \Bigr] & t = 3, \ldots, T.\\ \quad + \mu_{it} ^2 [\mbox{exp}(\sigma_{\gamma} ^2) - 1], \end{array} \right. \\ \label{model4.5} \end{array} $$

(4.5)

Regarding the covariance between y _it and y _i,t + k we once again use the similarities between the fixed model (2.1) and the mixed model (4.1) to first write the conditional covariance of y _it and y _i,t + k given γ _i in a form similar to (2.5) as

$$\begin{array}{lll} &&{\kern-36pt} \mbox{Cov}(Y_{it}, Y_{i,t+k} \left| {\gamma_i} \right. ) \\ {\kern-12pt} &=& \left( \prod\limits_{l=1} ^k n_{t+l} \right) \rho^k \sigma_{i,tt} ^*, \; \; t = 1,2, \ldots, T-1, \; \; k = 1,2, \ldots, T-t, \label{model4.6} \end{array} $$

(4.6)

where $\sigma_{i,tt} ^*$ is given by (4.3). We then average (4.6) over the distribution of γ _i and use (4.2) to obtain the expression for the covariance between y _it and y _i,t + k as

$$\begin{array}{lll} \mbox{Cov}(Y_{it}, Y_{i,t+k}) & = & E[\mbox{Cov}(Y_{it}, Y_{i,t+k} \left| {\gamma_i} \right. ) ] + \mbox{Cov}[E(Y_{it}\left| {\gamma_i} \right.), E(Y_{i,t+k} \left| {\gamma_i} \right.)], \\ & = & \left( \prod\limits_{l=1} ^k n_{t+l} \right) \rho^k h_{it}+ \mu_{it} \mu_{i,t+k} [\mbox{exp}(\sigma_{\gamma} ^2) - 1], \\ & = & \sigma_{i,t,t+k}, \ \mbox{ say}, \label{model4.7} \end{array}$$

where μ _it and σ _i,tt are given by (4.4) and (4.5) respectively, and $h_{it} = \sigma_{i,tt} - \mu_{it} ^2 [\mbox{exp}(\sigma_{\gamma} ^2) - 1]$.

We note that when n _t  = 1, for all t = 1, ..., T, the variance of y _it in (4.5) reduces to

$$ \sigma_{i,tt} = \mu_{it} + \mu_{it} ^2 [\mbox{exp}(\sigma_{\gamma} ^2) - 1], $$

which is the variance of a negative binomial random variable. In this case, h _it in (4.7) simplifies to h _it  = μ _it yielding a simplified version of the covariance between y _it and y _i,t + k in (4.7) as

$$ \sigma_{i,t,t+k} = \rho^k \mu_{it} + \mu_{it} \mu_{i,t+k} [\mbox{exp}(\sigma_{\gamma} ^2) - 1]. $$

4.2 Estimation of parameters

The dynamic mixed model (4.1) contains three unknown parameters, namely, ${\boldsymbol \beta}$, ρ, and $\sigma_{\gamma} ^2$. Note that the mean μ _it (4.4) and the variance (4.5) are functions of both β and $\sigma_{\gamma} ^2$, whereas the covariances σ _{i,t,t + k} (4.7) are functions of all three parameters ${\boldsymbol \beta}$, $\sigma_{\gamma} ^2$, and ρ. It is then appropriate to jointly estimate β and $\sigma_{\gamma} ^2$ by exploiting the first and the squared second order responses. Next, for known β and $\sigma_{\gamma} ^2$, we use the method of moments to estimate ρ, where the unbiased moment functions are constructed from the cross products of the responses.

Alternatively, for known $\sigma_{\gamma} ^2$, we may first exploit the first order responses to estimate β. Secondly, for known β, we exploit all second order responses to estimate $\sigma_{\gamma} ^2$. Finally, for known β and $\sigma_{\gamma} ^2$, only pairwise product responses are utilized to estimate ρ. In this section, we follow this alternative approach and solve a GQL estimating equation for the estimation of β for known $\sigma_{\gamma} ^2$. The GQL approach is also used for the estimation of $\sigma_{\gamma} ^2$, whereas the moment approach is used for the estimation of ρ.

4.2.1 Estimation of ${\boldsymbol \beta}$

Recall that ${\boldsymbol \mu}_i ^{\prime} = (\mu_{i1}, \mu_{i2}, \ldots, \mu_{iT})$ is the mean of the response vector ${\bf y}_i ^ {\prime} = (y_{i1}, y_{i2}, \ldots, y_{iT})$. Because ${\Sigma}_i ({\boldsymbol \beta}, \rho, \sigma_{\gamma})$ is the covariance matrix of y _i , it then follows from (3.1) that the GQL estimating equation for ${\boldsymbol\beta}$ has the form

$$ \sum\limits_{i=1} ^K \frac{\partial {\boldsymbol \mu}_i ^{\prime}}{\partial {\boldsymbol \beta}} {\Sigma}_i ^{-1} ({\boldsymbol \beta}, \rho, \sigma_{\gamma}) ({\bf y}_i -{\boldsymbol \mu}_i) = {\bf 0}. $$

Next, because

$$ \frac{\partial {\boldsymbol \mu}_i ^{\prime}}{\partial {\boldsymbol \beta}} = {\it X}_i ^{\prime} {\it U}_i, \; \; \; i = 1,2, \ldots, K, $$

where ${\it X}_i ^{\prime} = ({\bf x}_{i1}, {\bf x}_{i2}, \ldots, {\bf x}_{iT})$ and ${\it U}_i = diag(\mu_{i1}, \mu_{i2}, \ldots, \mu_{iT})$, the GQL estimating equation can be written in the form

$$ \sum\limits_{i=1} ^K {\it X}_i ^{\prime} {\it U}_i {\Sigma}_i ^{-1}({\boldsymbol \beta}, \rho, \sigma_{\gamma})({\bf y}_i -{\boldsymbol \mu}_i) = {\bf 0}, $$

where the diagonal elements and off-diagonal elements of ${\Sigma}_i ({\boldsymbol \beta}, \rho, \sigma_{\gamma}) = cov({\bf Y}_i)$ are given by (4.5) and (4.7) respectively. The GQL estimating equation can now be solved iteratively using the Newton–Raphson iterative procedure, which in this case, is defined by

$$\begin{array}{lll} \hat{\boldsymbol \beta}(r+1) &=& \hat{\boldsymbol \beta}(r) + \left\{ \left[\sum\limits_{i=1} ^K {\it X}_i ^{\prime} {\it U}_i {\it \Sigma}_i ^{-1}({\boldsymbol \beta}, \rho, \sigma_{\gamma}) {\it U}_i ^{\prime} {\it X}_i \right]^{-1}\right.\\[5pt] &&\quad\qquad\quad\left.\times\!\sum\limits_{i=1} ^K \!{\it X}_i ^{\prime} {\it U}_i {\it \Sigma}_i ^{-1}({\boldsymbol \beta}, \rho, \sigma_{\gamma}) ({\bf y}_i -{\boldsymbol \mu}_i) \!\right\}_{{\boldsymbol \beta} = \hat{\boldsymbol \beta}(r)}\!, \label{model4.10} \end{array} $$

(4.7)

where $\hat{\boldsymbol \beta}(r)$ is the value of ${\boldsymbol \beta}$ at the rth iteration.

4.2.2 Estimation of correlation parameter ρ

Similar to the approach in Section 3.2 we define the standardized variance and covariance as

$$\begin{array}{lll} S_{itt} & = & \left.\sum\limits_{i=1} ^K \sum\limits_{t=1} ^T \left( \frac{y_{it} - \mu_{it}} {\sigma_{it}} \right)^2\right/KT \\[5pt] S_{it,t+1} & = & \left.\sum\limits_{i=1} ^K \sum\limits_{t=1} ^{T-1} \left( \frac{y_{it} - \mu_{it}}{\sigma_{it}} \right) \left( \frac{y_{i,t+1} - \mu_{i,t+1}}{\sigma_{i,t+1}} \right)\right/K(T-1). \end{array}$$

For the dynamic mixed model (4.1) we can show that whereas E(S _itt ) = 1, the expectation of the standardized covariance is given by

$$ E(S_{it,t+1}) = \frac{1}{K(T-1)} \sum\limits_{i=1} ^K \sum\limits_{t=1} ^{T-1} \frac{1}{\sigma_{it} \sigma_{i,t+1}} \left\{ n_{t+1} \rho h_{it} + \mu_{it} \mu_{i,t+1} \left[\mbox{exp}({\sigma_{\gamma} ^2}) - 1\right] \right\}. $$

For known ${\boldsymbol \beta}$ and $\sigma_{\gamma} ^2$, using the method of moments, we now solve for ρ in the expression S _it,t + 1/S _itt  = E(S _it,t + 1) to obtain the estimator

$$\hat{\rho} = \frac{ \left\{\frac{S_{it,t+1}}{S_{itt}} - \frac{1}{K(T-1)} \sum\limits_{i=1} ^K \sum\limits_{t=1} ^{T-1} \frac{\mu_{it} \mu_{i,t+1} [\mbox{exp}({\sigma_{\gamma} ^2}) - 1]}{\sigma_{it} \sigma_{i,t+1}} \right\}} {\frac{1}{K(T-1)} \sum\limits_{i=1} ^K \sum\limits_{t=1} ^{T-1} \frac{n_{t+1} h_{it}}{\sigma_{it} \sigma_{i,t+1}}}, \label{model4.11} $$

(4.8)

where $h_{it} = \sigma_{i,tt} - \mu_{it} ^2 [\mbox{exp}(\sigma_{\gamma} ^2) - 1]$.

4.2.3 Estimation of the variance of the latent community effect $\sigma_{\gamma} ^2$

We note that the scale parameter $\sigma_{\gamma} ^2$ is involved in the mean, variance and the covariances between y _it and y _{i, t + k} , for t = 1,2, ..., T, k = 1,2, ..., T − t. However, as first order responses were used for ${\boldsymbol\beta}$ estimation, we will be constructing an unbiased estimating function based on second order responses, where the expectation of these second order responses involve $\sigma_{\gamma} ^2$. Let ${\bf z}_i ^{\prime} = (y_{i1} ^2, y_{i2} ^2, \ldots, y_{iT} ^2, y_{i1} y_{i2}, \ldots, y_{i1} y_{iT}, \ldots, y_{i,T-1} y_{iT})$ and ${\boldsymbol \lambda}_i = E({\bf z}_i)$, i = 1, ...,K with elements

$$ \begin{array}{lll} && \lambda_{itt} = E(y_{it} ^2) = \sigma_{i,tt} + \mu_{it} ^2, \; \; t = 1,2, \dots, T, \\[9pt] && \lambda_{it,t+k} = E(y_{it} y_{i,t+k}) = \sigma_{it,t+k} + \mu_{it} \mu_{i,t+k}, \\[9pt] && k = 1,2, \ldots, T - 1; \; \; t = 1,2,\ldots,T-k, \end{array} \label{model4.12} $$

leading to an unbiased estimating function ${\boldsymbol \lambda}_i - {\bf z}_i$, where μ _it , σ _i,tt , and σ _i,ut are given by (4.4), (4.5), and (4.7) respectively. One can then solve the GQL estimating equation

$$\sum\limits_{i=1} ^K \frac{\partial {\boldsymbol \lambda}_i ^{\prime}}{\partial {\boldsymbol{\sigma}_{\boldsymbol\gamma} ^2}} {\Omega}_i ^{-1}({\boldsymbol\beta}, \rho, \sigma_{\gamma})({\bf z}_i -{\boldsymbol\lambda}_i) = {\bf 0}, \label{model4.13} $$

(4.9)

for $\hat{\sigma}_{\gamma} ^2$, where Ω _i  = Cov(z _i ) and the elements of the vector $\frac{\partial {\boldsymbol\lambda}_i ^{\prime}}{\partial {\boldsymbol\sigma_{\gamma} ^2}}$ are given by

$$\begin{array}{lll} &&\frac{\partial \lambda_{itt}}{\partial {\boldsymbol\sigma_{\gamma} ^2}} = \frac{1}{2} h_{it} + 2 \mu_{it} ^2 \mbox{exp}(\sigma_{\gamma} ^2), \\[9pt] && \frac{\partial \lambda_{it,t+k}}{\partial {\boldsymbol\sigma_{\gamma} ^2}} = \frac{1}{2} \left( \prod\limits_{l=1} ^k \right) h_{it} \rho^k + 2 \mu_{it} \mu_{i,t+k} \mbox{exp}(\sigma_{\gamma} ^2), \\[9pt] && k = 1,2, \ldots, T - 1; \; \; t = 1,2,\ldots,T-k. \end{array}$$

Clearly, computing the matrix Ω _i will require exact second order, third order, and fourth order joint moments of y _it . However, unlike the computation for second order moments, computing third order and fourth order joint moments will require further distributional assumptions, which may not be practical. As a remedy, since the consistency of the estimator is not affected by the weight matrix Ω _i , one can use certain suitable approximations to compute the required third and fourth order joint moments. Two possible approximations that can be used in the computation of the joint higher order moments are: (i) to pretend that the counts y _it are normally distributed with the correct mean (4.4) and variance (4.5), (ii) to pretend that y _it ’s are conditionally independent even if they are correlated. We remark here that the unbiased estimating function ${\boldsymbol\lambda}_i - {\bf z}_i$ is not affected by these approximations. In what follows, we have used the assumption of conditional independence to compute the components of Ω _i .

Now, to begin the computation of the components of Ω _i , we first use the assumption that $\gamma_i \sim N(0, \sigma_{\gamma} ^2)$ to obtain

$$\begin{array}{lll} E[\mbox{exp}(2 \gamma_i)] &=& \mbox{exp}(2 \sigma_{\gamma} ^2), \; \;\\ E[\mbox{exp}(3 \gamma_i)] &=& \mbox{exp}(9 \sigma_{\gamma} ^2/2), \; \mbox{ and } \\ E[\mbox{exp}(4 \gamma_i)] &=& \mbox{exp}(8 \sigma_{\gamma} ^2). \label{model4.14a}\end{array} $$

(4.10)

Then, by taking expectation over γ _i and using (4.10) it can be shown that

$$ \mathop{E}\limits_{\gamma_i} ( \mu_{it} ^{*2} ) = \mu_{it} ^2 \mbox{exp}(\sigma_{\gamma} ^2), \; \; \mathop{E}\limits_{\gamma_i} ( \mu_{it} ^{*3} ) = \mu_{it} ^3 \mbox{exp}(3 \sigma_{\gamma} ^2) \; \mbox{ and } \mathop{E}\limits_{\gamma_i}( \mu_{it} ^{*4} ) = \mu_{it} ^4 \mbox{exp}(6 \sigma_{\gamma} ^2). \label{model4.14b} $$

Under the assumption of conditional independence we can now use the expectation of powers of $\mu_{it} ^*$ in (4.11) to derive second and higher order joint moments of y _it . Specifically, after some algebra, we found that the conditional second and higher order joint moments are given by

$$ \begin{array}{lll} && E(Y_{it} ^2 | \rho = 0) = \mu_{it} + \mu_{it} ^2 \mbox{exp}(\sigma_{\gamma} ^2) \\&& E(Y_{iu} Y_{it} | \rho = 0) = \mu_{iu} \mu_{it} \mbox{exp}(\sigma_{\gamma} ^2) \\&& E(Y_{it} ^4 | \rho = 0) = \mu_{it} + 7 \mu_{it} ^2 \mbox{exp}(\sigma_{\gamma} ^2) + 6 \mu_{it} ^3 \mbox{exp}(3 \sigma_{\gamma} ^2) + \mu_{it} ^4 \mbox{exp}(6 \sigma_{\gamma} ^2), \\&& E(Y_{iu} ^2 Y_{it} ^2 | \rho = 0) = [1 + \{ \mu_{iu} + \mu_{it}\} \mbox{exp}(2 \sigma_{\gamma} ^2) + \mu_{iu} \mu_{it} \mbox{exp}(5 \sigma_{\gamma} ^2)] \mu_{iu} \mu_{it} \mbox{exp}(\sigma_{\gamma} ^2) \\&& E(Y_{iu} ^3 Y_{it} | \rho = 0) = [1 + 3 \mu_{iu} \mbox{exp}(2 \sigma_{\gamma} ^2) + \mu_{iu} ^2 \mbox{exp}(5 \sigma_{\gamma} ^2)] \mu_{iu} \mu_{it} \mbox{exp}(\sigma_{\gamma} ^2) \\&& E(Y_{iu} ^2 Y_{iv} Y_{it} | \rho = 0) = [1 + \mu_{iu} \mbox{exp}(3 \sigma_{\gamma} ^2)] \mu_{iu} \mu_{iv} \mu_{it} \mbox{exp}(3 \sigma_{\gamma} ^2) \\&& E(Y_{iu} Y_{iv} Y_{is} Y_{it} | \rho = 0) = \mu_{iu} \mu_{iv} \mu_{is} \mu_{it} \mbox{exp}(6 \sigma_{\gamma} ^2). \end{array} \label{model4.14} $$

(4.11)

These conditional moments in (4.11) have been used in the computation of the elements of Ω _i needed for estimating the variance of the latent community effect $\sigma_{\gamma} ^2$. For instance,

$$\begin{array}{lll} &&{\kern-24pt} \mbox{Cov}( Y_{iu} ^2 , Y_{iv} Y_{it} | \rho = 0) \\ &&= \left\{ \begin{array}{ll} E(Y_{iu} ^2 Y_{iv} Y_{it} | \rho = 0) & u \neq v \mbox{ and } u \neq t, \\ \quad - E(Y_{iu} ^2 | \rho = 0) E(Y_{iv} Y_{it} | \rho = 0), \\ E(Y_{iu} ^3 Y_{it} | \rho = 0) & u = v \mbox{ and } u \neq t, \\ \quad - E(Y_{iu} ^2 | \rho = 0) E(Y_{iu} Y_{it} | \rho = 0),\\ E(Y_{iu} ^3 Y_{iv} | \rho = 0) & u = t \mbox{ and } u \neq v.\\ \quad - E(Y_{iu} ^2 | \rho = 0) E(Y_{iu} Y_{iv} | \rho = 0), \end{array} \right. \label{model4.16} \end{array}$$

The GQL estimating equation (4.9) can now be solved iteratively for $\sigma_{\gamma} ^2$ using the Newton–Raphson iterative procedure, which in this case, is defined by

$$\begin{array}{lll} \hat{\sigma}_{\gamma} ^2 (r+1) &=& \hat{\sigma}_{\gamma} ^2 (r) + \left\{ \left[\sum\limits_{i=1} ^K \frac{\partial {\boldsymbol\lambda}_i ^{\prime}}{\partial {\boldsymbol\sigma_{\gamma} ^2}} {\Omega}_i ^{-1}({\boldsymbol\beta}, \rho, \sigma_{\gamma}) \frac{\partial {\boldsymbol\lambda}_i }{\partial {\boldsymbol\sigma_{\gamma} ^2}} \right]^{-1}\right.\\ &&\qquad\qquad\quad\left.\times\sum\limits_{i=1} ^K \frac{\partial {\boldsymbol\lambda}_i ^{\prime}}{\partial {\boldsymbol\sigma_{\gamma} ^2}} {\Omega}_i ^{-1}({\boldsymbol\beta}, \rho, \sigma_{\gamma})({\bf z}_i -{\boldsymbol\lambda}_i) \right\}_{\sigma_{\gamma} ^2 = \hat{\sigma}_{\gamma} ^2 (r)}.\\ \label{model4.17} \end{array} $$

(4.12)

4.3 A simulation study

4.3.1 Estimation performance of β, $\sigma_{\gamma} ^2$, and ρ

We observe that the dynamic mixed model has an additional parameter $\sigma_{\gamma} ^2$ as compared to that of the dynamic fixed model discussed in Section 3. The simulation study conducted in Section 3.4.1 showed that the GQL estimation approach performs well in estimating the fixed model parameters ${\boldsymbol\beta}$ and ρ for various selected combinations of ${\bf n}^{\prime} = (n_1, n_2, n_3, n_4)$. In this section, we examine the performance of the GQL approach for estimating the parameters of the extended mixed model including $\sigma_{\gamma} ^2$, the variance component of the latent community effect γ _i . To be specific, the GQL estimates are obtained by solving the GQL estimating equation (4.7) iteratively for ${\boldsymbol\beta}$, and (4.12) for $\sigma_{\gamma} ^2$ and the moment estimating equation (4.8) for ρ.

The data for our study was generated from model (4.1) with covariates previously defined in (3.8) and (3.9) for T = 4, K = 100 and various combinations of the parameter values $\sigma_{\gamma} ^2 \equiv 0.25, 0.5, 0.75$ ${\boldsymbol\beta}^{\prime} \equiv (0.5,1), (1,1)$, and ${\bf n}^{\prime} = (n_1, n_2, n_3, n_4) \equiv (1,2,2,2), (1,2,2,3,), (1,2,3,4,)$. It is clear, from (4.1) that in order to generate the observed longitudinal data y _it , (i = 1,2, ...,K; t = 1,2,..., T), we first had to generate values of the community effect $\gamma_i \sim N(0, \sigma_{\gamma} ^2)$ which are then used in the computation of the conditional mean $\mu_{it} ^* = \mbox{exp}({\bf x}_{it} ^{\prime} {\boldsymbol\beta} + \gamma_i)$ for fixed values of $\sigma_{\gamma} ^2$ and the regression parameter vector ${\boldsymbol\beta}$. We then choose the correlation parameter ρ satisfying the condition $\rho < \min \left\{ \frac{\mu_{it} ^*}{n_t \mu_{i,t-1} ^*}, 1 \right\}$, and generate d _it conditional on γ _i following Assumption 2 under model (4.1). Using the generated values of d _i t and the conditional mean $\mu_{i1} ^*$, the generation of y _i1 and y _it , t = 2, ..., T, and i = 1, ..., K followed directly from Assumption 1 and model (4.1) respectively.

Now, by using y _it and associated x _it , (t = 1,..., T; i = 1,2, ..., K), the method of moments estimate of ρ and the GQL estimates of ${\boldsymbol\beta}$ and $\sigma_{\gamma} ^2$ were computed iteratively from (4.8), (4.7), and (4.12), respectively. The process of data generation and estimation was repeated 1,000 times. The average of the estimated parameters and their standard errors are reported in Table 3. From Table 3, we see that the method of moments and the GQL method perform well in estimating the true values of the parameters. For example, when n ^′ = (1,2,2,3), the parameter values, namely, ρ = .307, ${\boldsymbol\beta}^{\prime} = (.5,1)$ and $\sigma_{\gamma} ^2 = 0.75$ were estimated as $\hat{\rho} = .310$, $\hat{\boldsymbol\beta}^{\prime} = (.510,.989)$, and $\hat{\sigma}_{\gamma} ^2 = 0.755$, respectively, showing that the estimates are very close to their corresponding true values. In a separate example, we took n ^′ = (1,2,3,4) and estimated ρ = .205, ${\boldsymbol\beta}^{\prime} = (1,1)$ and $\sigma_{\gamma} ^2 = 0.25$. The estimates were found to be $\hat{\rho} = .224$, $\hat{\boldsymbol\beta}^{\prime} = (.991,1.035)$, and $\hat{\sigma}_{\gamma} ^2 = 0.229$ which are close to the respective parameter values.

Table 3 GQL estimates of $\sigma_{\gamma} ^2$ and ${\boldsymbol\beta}$ and method of moments estimate of ρ and their standard errors obtained from 1,000 simulations.

5 Concluding remarks

In this paper, we have taken the first step in using branching processes with immigration to model the spread of an infectious disease in communities for the purpose of forecasting future spread and control. Because the model was developed mainly to deal with infectious disease data obtained over a short period of time, we have considered only a small number of time points, such as T = 5, in our simulation studies. This, however does not imply that the proposed methods are applicable only for small T. We have demonstrated that the GQL method performs well in estimating the parameters of the infectious disease model. The results also show that the estimated model can be used to obtain reasonable forecasts of future spread of the disease using the proposed forecasting function. We remark that the lag 1 dynamic models (2.1) and (4.1) show how individuals within communities with infections at time point t − 1 determine the number of new infections at time point t. However, there may be situations, in practice, where an individual who was infected at time point t − k, for k = 1, ..., t − 1, continue to infect others at future time points until he/she is discovered and treated. This higher order lag situation is a subject for future consideration.