1 Introduction

A nanofluid is a fluid that includes nanoparticles. Metals, carbides, carbon nanotubes or metal oxides are the main components of nanoparticles utilized in nanofluids. Nanofluids are beneficial and have a wide variety of applications including as in cells of fuel, powered equipment, controller of temperature, dissipation of heat, heating regime, microelectronic pieces of machines, gas exhausted as from smokestack, etc. [1, 2]. Following the pioneering study of Choi [3], who has conducted a lot of tests in this scope, many analysts worked on nanofluids. Sarkar et al. [4] explained the significance of crossbred nanofluids for augmentation of heat transfer, their applicability in various fields and improvements in recent years. An inclusive review is given for the upcoming hybrid nanofluid challenges. Hayat and Nadeem [5] authorized that in the existence of chemical reaction, source of heat and radiation, the average transmit of heat for hybrid nanoliquid is bigger than nanofluid. The unstable flow of magnetohydrodynamics (MHD) for two mixed kinds of nanoparticles in the fluid with Hall current and thermal radiation impacts in a perpendicular rotating canal was elaborated by Iqbal et al. [6]. CuO and Cu with three diverse forms were utilized to produce the hybrid nanofluid and a closed-shape solution is gained. Chamkha et al. [7] studied the MHD convection of (Al2O3–Cu/Water) with interior heat sink/source in a sloping porous medium. They observed that adding nanoparticles for many Rayleigh numbers leads to a decrease in thermal action and the transfer of heat diminished more in the state of a great volume fraction. EL-Zahar et al. [8] examined mixed convection flux of magneto‑hybrid nanofluids via radiological rotating cylinder. They discovered that the force of drag reduced against the rigid volume fraction. Several recent papers which highlight the significance of hybrid nanoliquid are cited as [9,10,11,12,13].

Non-Newtonian fluids are well-known for their many classical features. With distinguished rheology and intricate nature, scientists are interested in exploring additional fascinating properties of such materials. The liquids of non-Newtonian provide significant contributions to a variety of makings industries, chemical remediation and engineering. Real-world examples of non-Newtonian materials include molten, starch suspension, pharmaceuticals, blood, cosmetics, paints, etc. Such materials characterization is often offered in three forms: differential and integral fluid types and type of rate. Several developed designing implementations have an investigation of the non-Newtonian fluids. This comprises polymer, clay digging for petroleum, food processing and biological gels. Furthermore, the flux of heat transport with non-Newtonian fluids has an important impact on paper manufacture, glass sheet blowing, and hot rolling [14,15,16]. The model of Eyring–Powell which is able to dub the viscosity relaxation theory is one of the non-Newtonian fluid complex models. Fluid of Eyring–Powell includes some features over other fluids of non-Newtonian [17]. The fluid of Eyring–Powell is developed from liquid kinetic theory rather than an experimental relationship. Liquid molecules bond can be any strong or weak according to kinetic theory of fluid. In the paradigm of Eyring–Powell, the bond of a strong molecular corresponds to the rapport of non-Newtonian and the bond of weaker molecular coincides with the Newtonian relation. Consequently, the fluid of Eyring–Powell capable to provide a Newtonian plateau, at high or/and low shear rate, which meaning that it can conquer the quandaries of spriggs liquid paradigm [18] and power law liquid [19]. In a pored channel, the non-Newtonian Eyring–Powell fluid convective flow was investigated numerically and analytically by Nazeer et al. [20, 21]. Comparing to the model of power law Patel and Timol [22] improved the models of Powell–Eyring more important and efficient. However, it was somewhat sophisticated in nature. The magnetic flux of Eyring–Powell liquid over an extending plate was examined numerically by employing a scheme of finite difference by Akbar et al. [23]. Because different equations of non-Newtonian fluid system are, furthermore, tricky than equations of Navier–Stokes, getting solutions to these equations is considerably more difficult, but more significant owing to the simplicity and convenience of the Eyring–Powell paradigm and crucial in chemical engineering processes. Eyring–Powell fluid for MHD and Newtonian heat was elaborated by Hayat et al. [24]. The fluid of Eyring–Powell for transport of mass and heat was examined by Riaz et al. [25]. Hitherto, improving mathematical modeling of liquids of non-Newtonian is critical [26,27,28,29].

Among the most important control elements for the flux of liquid and heat in a high-temperature heat system are radiation parameters. Thermal radiation has an essential impact on the development of steady kit, satellites, nuclear energy plants, turbines of gas, assortment of advanced transformation systems and missiles. Cess [30] was therefore the first investigator to use the perturbation procedure to examine the transfer of heat interplay between free convective and thermal react. Arpaci [31] extended his outstanding work in a perpendicular heat plate to a stagnant beamy gas. Since then, several studies on thermal radiation have been conducted, such as Agbaje et al. [32], who carried out a computational investigation for the unsteady flux in the existence of heat obstetrics and radiation of thermal of Powell–Eyring nanofluid. The outcomes showed that the parameters of thermal radiation and source of heat raised the temperature of fluid and thickness of thermal boundary layer. Abdelhafez et al. [33] checked radiation of thermal with reaction of chemical and yield stress on MHD flux in a pored regime.

In a summary, the non-Newtonian fluid mechanics has obtained prominence in last decennium because of its various experimental applications. The paradigm of non-Newtonian fluid may also be utilized to characterize the exemplary fluid flow properties in industry, such as liquids of biological, oils of motors and liquids of polymeric. A study of the previously mentioned literature, yet, tackles an assortment of shortcomings and limitations. This study purposes to construct a mathematical model for MHD Eyring–Powell hybrid nanofluid mixed convection flux in the presence of thermal radiation and heat source in a pored medium.

2 Mathematical Formulation

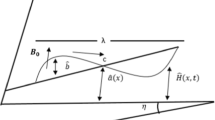
The flux of 2D steady mixed convection flow over a stretched vertical plate was examined. It is supposed that viscous dissipation careless in the equation of energy and the force of body is considered to be truant in the equation of momentum. Hither \(y\)-axis is vertical to \(x\)-axis where the plate is parallel to \(x\)-axis. The components of velocity are \(v\) and \(u\) in \(y\) and \(x\) directions, respectively. Figure 1 shows the system of flow coordinates of the issue and involves model assumption and details.

Fig. 1
figure 1

Problem Schematic Diagram

Full size image

For fluid of Eyring–Powell [34], the stress tensor of Cauchy can be written as

$$ A = - PI + \tau , $$
(1)

where identity \( I\) and pressure \(P\) in Eq. (1). \(\tau\) defined as extra stress tensor and is written by

$$ \tau = \left[ {\mu + \frac{1}{{\delta \dot{\gamma }}}\sinh^{ - 1} \left( {\frac{1}{{c_{1} }}\dot{\gamma }} \right)} \right]A_{1} , $$
(2)

where \(c_{1}\) and \(\delta\) are the fluid parameters, \(\mu\) is the viscidity of dynamic and \(c_{1}\) having (time)−1 dimension. \(\sinh^{ - 1} \left( {\frac{1}{{c_{1} }}\dot{\gamma }} \right)\) is written as

$$ \sinh^{ - 1} \left( {\frac{1}{{c_{1} }}\dot{\gamma }} \right)\tilde{ = }\frac{1}{{c_{1} }}\dot{\gamma } - \frac{1}{6}\left( {\frac{1}{{c_{1} }}\dot{\gamma }} \right)^{3} ,\;{\text{with}}\;\left( {\frac{{\dot{\gamma }}}{{c_{1} }}} \right)^{5} < < < 1 $$

Therefore from Eq. (2),

$$ \tau = \left( {\mu + \frac{1}{{\delta c_{1} }}} \right)A_{1} - \frac{1}{{6\delta c_{1}^{3} }}\left( {\dot{\gamma }} \right)^{2} A_{1} , $$
(3)

Here value of \(\dot{\gamma } = \sqrt {\frac{1}{2}{\text{tr}}A_{1}^{2} }\) and \(A_{1}\) is kinematical tensor and given as \(A_{1} = \nabla V + \left( {\nabla V} \right)^{T}\), with \(V\) is the vector of velocity.

Under the proposition of utilizing approximation of boundary layer and flowing state, the conservation equations that control the hybrid flow are [35]:

$$ \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0, $$
(4)
$$ \begin{aligned} u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} & = \left( {\nu_{hnf} + \frac{1}{{c_{1} \delta \rho_{hnf} }}} \right)\frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{1}{{2\delta c_{1}^{3} \rho_{hnf} }}\left( {\frac{\partial u}{{\partial y}}} \right)^{2} \frac{{\partial^{2} u}}{{\partial y^{2} }} \\ & \quad + \frac{{\left( {\rho \beta } \right)_{hnf} }}{{\rho_{hnf} }}\left( {T - T_{\infty } } \right)g - \frac{{\sigma_{hnf} }}{{\rho_{hnf} }}B_{0}^{2} u - \frac{{\mu_{hnf} }}{{\rho_{hnf} }}\frac{1}{{K_{1} }}u, \\ \end{aligned} $$
(5)
$$ u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }} - \frac{1}{{\left( {\rho c_{p} } \right)_{hnf} }}\frac{{\partial q_{r} }}{\partial y} + \frac{{Q_{0} }}{{\left( {\rho c_{p} } \right)_{hnf} }}\left( {T - T_{\infty } } \right), $$
(6)

and conditions at boundary are:

$$ u = U\left( x \right),\quad v = 0,\quad T = T_{\infty } + \Delta T\left( x \right)\quad {\text{at}}\;y = 0 $$
(7)
$$ u = 0,\quad T = T_{\infty } \quad {\text{at}}\;y \to \infty . $$
(8)

The flux is done by impact of buoyancy and plate continuous stretching. For obtaining solution of non-similar, Eqs. (4)–(8) will subject the non-similar conversions. Non-similarity conversions transform the physical coordinates \(y\), \(x\) into the new coordinates \(\xi\), \(\eta\). \(\xi\) is function of \(x\) only, where \(\eta\) is defined as variables of pseudo-similarity and includes both physical coordinates \(x\) and \(y\). As elaborated by Abdelhafez et al. [36], Table 1 offers the equations of hybrid nanofluid thermophysical features. Further, Table 2 offers the physical features of ethylene glycol (EG), magnetite (Fe3O4) and copper (Cu).

Table 1 Thermophysical features of applied model
Full size table
Table 2 Ehylene glycol, magnetite and copper thermal features
Full size table

The radiant flow of heat \(q_{r}\) is written as [36]:

$$ q_{r} = - \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T^{4} }}{\partial y} $$
(9)

where \(k^{*}\) is the factor of mean absorption and \(\sigma^{*}\) is the fixed of Stefan-Boltzmann. Presuming the distinction of temperature in the flux is \(T^{4}\) and can be extensive in a series of Taylor about \(T_{\infty }\) and disregarding relations of higher order. Hence: \(T^{4} \cong 4T_{\infty }^{3} T - 3T_{\infty }^{4}\). Then \(\frac{{\partial q_{r} }}{\partial y} = - \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} }}\frac{{\partial^{2} T}}{{\partial y^{2} }}\) and Eq. (6) takes the shape:

$$ u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }} - \frac{1}{{\left( {\rho c_{p} } \right)_{hnf} }}\left( { - \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} }}\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) + \frac{{Q_{0} }}{{\left( {\rho c_{p} } \right)_{hnf} }}\left( {T - T_{\infty } } \right), $$
(10)

Let \(\psi\) be stream function and non-similarity and dimensionless variables as,

$$ \psi = \nu_{f} {\text{Re}}^{1/2} f\left( {\eta , \xi } \right),\quad \eta = \frac{y}{x}{\text{Re}}^{1/2} ,\quad \xi = \frac{{Gr_{x} }}{{{\text{Re}}_{x}^{2} }},\quad \theta = \frac{{T - T_{\infty } }}{\Delta T\left( x \right)} $$
(11)

where \({\text{Gr}}_{x} = \frac{{g\beta_{f} \Delta Tx^{3} }}{{\nu^{2} }}\) and \({\text{Re}}_{x} = \frac{Ux}{{\nu_{f} }}\) are Grashof and Reynolds numbers, respectively. \(\alpha = \frac{{k_{hnf} }}{{\left( {\rho c_{p} } \right)_{hnf} }}\) is the thermal diffusivity of the hybrid nanofluid. Forces of buoyancy command the field of flow for higher values of \(\xi\) and forced convection command the field of flow for smaller values of \(\xi\), where \(\rho_{hnf}\), \(\mu_{hnf}\), \(k_{hnf}\), \(\sigma_{hnf}\), \((\rho c_{p} )_{hnf}\) are symbol to density, viscosity of dynamic, conductivity of thermal, electrical conductivity, and capacitance of heat, respectively. The subindexes \(f\), \(nf\), \(hnf\), \(\varphi_{1}\) and \(\varphi_{2}\) refer to EG, nanofluid, hybrid nanofluid, Fe3O4 and Cu concentration of nanoparticles, respectively.

Function of stream is \(\psi\) for which \( v = - \frac{\partial \psi }{{\partial x}}\) and \(u = \frac{\partial \psi }{{\partial y}}\). Continuity equation is satisfied automatically.

Here we expressed the next form of temperature and velocity of the surface:

$$ \Delta T\left( x \right) = T_{0} x^{2} \;{\text{and}}\;U\left( x \right) = U_{0} x. $$

The non-dimensional transformed momentum and energy equations of boundary layer are:

$$ \begin{aligned} & \left( {f^{{\prime}{2}} + \xi f^{\prime}\frac{{\partial f^{\prime}}}{\partial \xi } - ff^{\prime\prime} - \xi f^{\prime\prime}\frac{\partial f}{{\partial \xi }}} \right) = \frac{{\rho_{f} }}{{\rho_{hnf} }}\left( {\varepsilon + \frac{{\mu_{hnf} }}{{\mu_{f} }} - \varepsilon \omega f^{{\prime\prime}{2}} } \right)f^{\prime\prime\prime} \\ & \quad + \frac{{\left( {\rho \beta } \right)_{hnf} /\left( {\rho \beta } \right)_{f} }}{{\rho_{hnf} /\rho_{f} }}\xi \theta - \left( {\frac{{\sigma_{hnf} /\sigma_{f} }}{{\rho_{hnf} /\rho_{f} }}} \right)Mf^{\prime} - \left( {\frac{{\mu_{hnf} /\mu_{f} }}{{\rho_{hnf} /\rho_{f} }}} \right)Kf^{\prime}, \\ \end{aligned} $$
(12)
$$ \xi \left( {\frac{\partial \theta }{{\partial \xi }}f^{\prime} - \frac{\partial f}{{\partial \xi }}\theta^{\prime}} \right) = \frac{1}{\Pr }\left( {\frac{{k_{hnf} /k_{f} }}{{\rho_{hnf} /\rho_{f} }} + \frac{4R}{3}\frac{{\left( {\rho c_{p} } \right)_{f} }}{{(\rho c_{p} )_{hnf} }}} \right)\theta ^{\prime \prime } + \frac{{(\rho c_{p} )_{f} }}{{(\rho c_{p} )_{hnf} }}S\theta + f\theta^{\prime} - 2\theta f^{\prime}, $$
(13)

where \(M = \frac{{\sigma_{f} }}{{\rho_{f} }}\frac{{xB_{0}^{2} }}{U}\) is the magnetic parameter, \(K = \frac{{x\nu_{f} }}{{UK_{1} }}\) is the permeability of porous media, \(\omega = \frac{{\nu_{f}^{2} }}{{2c_{1}^{2} }}\left( {\frac{1}{{x^{4} }}{\text{Re}}_{x}^{3} } \right)\) and \(\varepsilon = \frac{1}{{\nu_{f} \rho_{f} c_{1} \delta }}\), \(\Pr = \frac{{\mu_{f} \left( {c_{p} } \right)_{f} }}{{k_{f} }} \) is the Prandtl number, \(R = \frac{{4\sigma^{*} T_{\infty }^{3} }}{{k^{*} k_{f} }}\) is the thermal radiation, \(S = \frac{{Q_{0} }}{{U_{0} (\rho c_{p} )_{f} }}\) is the heat source/sink.

$$ \begin{aligned} & f\left( {0, \xi } \right) = 0,\quad f^{\prime}\left( {0, \xi } \right) = 1,\quad \theta \left( {0, \xi } \right) = 1\quad {\text{at}}\;y = 0 \\ & f^{\prime}\left( {\infty , \xi } \right) = 0,\quad \theta \left( {\infty , \xi } \right) = 0\quad {\text{at}}\;y \to \infty . \\ \end{aligned} $$
(14)

Parameters of material fluid are offered by \(\varepsilon\) and \(\omega\), prime appears in Eqs. (10)–(12) denotes derivative with respect to \(\eta\). The local Nusselt number \({\text{Nu}}\) and the local coefficient of skin friction are also calculated as:

$$ c_{f} = \frac{{2\tau_{w} \left( x \right)}}{{\rho \left( {U\left( x \right)} \right)^{2} }}, $$
(15)
$$ {\text{Nu}} = \frac{{xq_{w} \left( x \right)}}{{k_{f} \Delta T}}, $$
(16)

where \(\tau_{w} = \left[ {\mu_{hnf} \left( {\frac{\partial u}{{\partial y}}} \right) + \frac{1}{{\delta c_{1} }}\left( {\frac{\partial u}{{\partial y}}} \right) - \frac{1}{{6\delta c_{1}^{3} }}\left( {\frac{\partial u}{{\partial y}}} \right)^{3} } \right]_{y = 0}\), and \(q_{w} = - k_{hnf} \left( {\frac{\partial T}{{\partial y}}} \right)_{y = 0} + \left( {q_{r} } \right)_{y = 0}\).

$$ \left( {\text{Re}} \right)^{1/2} c_{f} = 2\left\{ {\left( {\frac{{\mu_{hnf} }}{{\mu_{f} }} + \varepsilon } \right)f^\prime \prime \left( {0, \xi } \right) - \frac{\varepsilon \omega }{3}\left[ {f^\prime \prime \left( {0, \xi } \right)} \right]^{3} } \right\}, $$
(17)
$$ \left( {\text{Re}} \right)^{ - 1/2} {\text{Nu}} = - \left( {\frac{{k_{hnf} }}{{k_{f} }} + \frac{4}{3}R} \right)\theta ^{\prime }\left( {0,\xi } \right). $$
(18)

3 Computational Procedure

The solutions of nonlinear Eqs. (12)–(14) in locked form are not actually feasible. By using RKF45 with shooting scheme, we can solve this issue with diverse parameters values. \(\Delta \eta = 0.01\) is the size of step. We presumed a convenient value for away field boundary condition in (14), i.e., \(\eta \to \infty\), say \(\eta_{\infty }\).

$$ f^{\prime}\left( {\eta_{\infty } , \xi } \right) = \theta \left( {\eta_{\infty } ,\xi } \right) \to 0 $$
(19)

We settled the attached parameters value in all plots except else stated.

$$ M = 0.5,\;K = 1,\;\varepsilon = 0.1,\;R = 0.1,\;S = 0.02,\;\omega = 0.2,\;\varphi_{1} = 0.02,\;\varphi_{2} = 0.04. $$
(20)

4 Results and Discussion

For studying the influences of nondimensional controlling parameters of Eyring–Powell hybrid nanofluid in a pored medium across a perpendicular extending flat plate, numerical calculations are indicated. A comparison between our results and those previously published to ensure that the method was operating correctly was done; it became evident that our findings agreed with those obtained as in Table 3.

Table 3 Computational values of \(-\theta {^{\prime}}\left(\mathrm{0,0}\right)\) for various \(\mathrm{Pr}\) when \(\omega =R=S=K=M={\varphi }_{1}={\varphi }_{2}=0\)
Full size table

The major motivation of this work is to detect the outcomes of source of heat and radiations on MHD Eyring–Powell hybrid nanoliquid via a vertical plate. The impacts of varying parameters on the temperature, velocity, skin friction and Nusselt number distributions are shown in figures. From Fig. 2, it is perceived that \(f^{\prime}\left( {\eta , \xi } \right)\) is decreased as the decreed magnetic field \(M\) increases. By increasing \(M\), a significant resistance is created between the particles, because of which heat is created in the fluid. A drag force known as the Lorentz force was formed by slapping the magnetic parameter \(M\). It is observed that the temperature is a direct function of \(M\) from Fig. 3. Physically, the increase of magnetic parameter creates resistance to the fluid motion, which automatically grows the thermal rate. Figure 4 illustrates the effect of parameter \(K\) on the profile of velocity and this figure shows that \(f^{\prime}\left( {\eta , \xi } \right)\) and the momentum boundary layer thickness are reduced significantly for the higher values of permeability. The physics of the permeability is that as the amounts of \(K\) increases, so does the resistance to fluid motion and as a consequence the distribution of velocity reduces. Figure 5 demonstrates the influence of \(K\) on \(\theta \left( {\eta , \xi } \right)\). The consequence of upsurging \(K\) values is to grow the thermal field and thereby augmented the thickness of the thermal boundary layer as in Fig. 5. Physically, the hybrid nanoparticles in the fluid cannot execute as readily at greater values of \(K\), this is compensated for by tighter fiber packing, which allows for better heat conduction across the porous medium.

Fig. 2
figure 2

\(f^{\prime}\left( {\eta , \xi } \right)\) versus \(M\)

Full size image
Fig. 3
figure 3

\(\theta \left( {\eta , \xi } \right)\) versus \(M\)

Full size image
Fig. 4
figure 4

\(f^{\prime}\left( {\eta , \xi } \right)\) versus \(K\)

Full size image
Fig. 5
figure 5

\(\theta \left( {\eta , \xi } \right)\) versus \(K\)

Full size image

Figures 6 and 7 explain that \(f^{\prime }\left( {\eta , \xi } \right)\), \(\theta \left( {\eta , \xi } \right)\) and the thickness of the relevant boundary layer are against function with \(R\). This is due to that, the increment in \(R\) produces a tardiness in thermal diffusivity and hence a lowering in the area of the thickness of the thermal boundary layer.

Fig. 6
figure 6

\(f^{\prime}\left( {\eta , \xi } \right)\) versus \(R\)

Full size image
Fig. 7
figure 7

\(\theta \left( {\eta , \xi } \right)\) versus \(R\)

Full size image

The action of parameter \(S\) on \(f^{\prime }\left( {\eta , \xi } \right)\) and \(\theta \left( {\eta , \xi } \right)\) are in Figs. 8 and 9. Perception of Figs. 8 and 9 obviously refers to increase \(S\) values, \(f^{\prime }\left( {\eta , \xi } \right)\) and \(\theta \left( {\eta , \xi } \right)\) upsurge because the thickness of the thermal boundary layer improves (interior heat energy grows) in state of mounting heat source parameter.

Fig. 8
figure 8

\(f^{\prime}\left( {\eta , \xi } \right)\) versus \(S\)

Full size image
Fig. 9
figure 9

\(\theta \left( {\eta , \xi } \right)\) versus \(S\)

Full size image

Figures 10 and 11 explain the diagram of velocity versus different volume fractions of Fe3O4 \(\left( {\varphi_{1} } \right)\) and Cu \(\left( {\varphi_{2} } \right)\), respectively, when \(0 \le \xi \le 1\). Rising volume fraction leads to increment in density and dynamic viscosity of the hybrid nanoliquid. This consequently changes \(f^{\prime }\left( {\eta , \xi } \right)\) and causes reduced generation of momentum as illustrated in these figures. As \(\varphi_{1}\) increases, the distance of intermolecular among simple fluid and hybrid nanoparticles reduced, resulting in increased viscosity and resistance of flow, which causes a decrement in \(\theta \left( {\eta , \xi } \right)\) as indicated in Figs. 12.

Fig. 10
figure 10

\(f^{\prime}\left( {\eta , \xi } \right)\) versus \(\varphi_{1}\)

Full size image
Fig. 11
figure 11

\(f^{\prime}\left( {\eta , \xi } \right)\) versus \(\varphi_{2}\)

Full size image
Fig. 12
figure 12

\(\theta \left( {\eta , \xi } \right)\) versus \(\varphi_{1}\)

Full size image

As noticed in Fig. 13, the temperature is a direct function of the nanoparticles of Cu. This trend is suitable with the reality that nanoparticles of Cu have greater conductivity of thermal than the simple fluid. Computational values of the coefficients of skin friction and heat transport are in Figs. 14 and 15 for different values of \(M\) and \(\xi\). From these figures we realized that for increasing values of \(M\), \(\left( {\text{Re}} \right)^{1/2} c_{f}\) and \(\left( {\text{Re}} \right)^{ - 1/2} {\text{Nu}}\) are improved due to the resistance which caused by Lorentz force, but the against behavior is noticed for increasing \(\xi\).

Fig. 13
figure 13

\(\theta \left( {\eta , \xi } \right)\) versus \(\varphi_{2}\)

Full size image
Fig. 14
figure 14

\({\text{Re}}^{1/2} C_{f}\) versus \(\xi\) with \(M\)

Full size image
Fig. 15
figure 15

\({\text{Re}}^{ - 1/2} {\text{Nu}}\) versus \(\xi\) with \(M\)

Full size image

Figures 16 and 17 deal with the change of \(\left( {\text{Re}} \right)^{1/2} c_{f}\) and \(\left( {\text{Re}} \right)^{ - 1/2} {\text{Nu}}\) in relation to mixed convection parameter for different permeability parameters. It is observed that parameter of permeability has the same action of \(M\) parameter on \(\left( {\text{Re}} \right)^{1/2} c_{f}\) and Nusselt number. Figures 18 and 19 offer the profiles of \(\left( {\text{Re}} \right)^{1/2} c_{f}\) and \(\left( {\text{Re}} \right)^{ - 1/2} {\text{Nu}}\) against \(\xi\) for different thermal radiation parameter. The force of drag and factor of Nusselt raises with rising in \(\xi\) and \(R\) parameters as viewed in Figs. 18 and 19. This is because that the improvement and transport of more heat into the flux, which aids to raise the momentum boundary layer thickness. From Fig. 20 we see that enhancing \(\xi\) and \(S\) parameters leads to improvement in \(\left( {\text{Re}} \right)^{ - 1/2} {\text{Nu}}\).

Fig. 16
figure 16

\({\text{Re}}^{1/2} C_{f}\) versus \(\xi\) with \(K\)

Full size image
Fig. 17
figure 17

\({\text{Re}}^{ - 1/2} {\text{Nu}}\) versus \(\xi\) with \(K\)

Full size image
Fig. 18
figure 18

\({\text{Re}}^{1/2} C_{f}\) versus \(\xi\) with \(R\)

Full size image
Fig. 19
figure 19

\({\text{Re}}^{ - 1/2} {\text{Nu}}\) versus \(\xi\) with \(R\)

Full size image
Fig. 20
figure 20

\({\text{Re}}^{ - 1/2} {\text{Nu}}\) versus \(\xi\) with \(S\)

Full size image

5 Conclusions

This treatise investigates the actions of heat generation and radiative of thermal on flux of mixed convection with magnetic Eyring–Powell hybrid nanofluid in a pored medium. With the aid of non-similarity method which solved by RKF45 with technique of shooting, the results have been obtained. The conclusions gained from the paper are:

  • \(f^{\prime }\left( {\eta , \xi } \right)\) is lowered with increase in parameters values of \(M, K, R, \varphi_{1}\) and \(\varphi_{2}\). But, the against behavior is observed with the heat sink/source.

  • \(\theta \left( {\eta , \xi } \right)\) is upsurged with raise in values of \(M, K, S\) and \(\varphi_{2}\) parameters.

  • The increment in radiation of thermal and nanoparticles amounts of Fe3O4 leads to improve in temperature.

  • With growing magnetic field, permeability of porous media and thermal radiation, drag force reduces.

  • Heat transfer decreases with raising in magnetic field, permeability of porous media and heat source/sink.

  • Increasing thermal radiation, raises Nusselt number coefficient.