1 Introduction

Presently, the heat transfer subject attracts the researches due to the importance in most engineering fields, essentially the heat transport in fluid flow. As polymers production and plastic demands the higher rate of heat transfer for the optimum quality of the product. The usage of nanofluids as an appropriate fluid to improve heat transfer has attracted considerable. Nanofluids are famous for being a modern form of energy transfer and would include small nanosubstances of metal or oxide, like kerosene, water and etc. These modern fluids have higher thermal conductivity than the normal liquid. Nanofluids have wide uses including solar water heating, motor cooling, converter oil refrigeration, electronics equipments cooling, cooling of heat exchanger device, air conditioners, the enhanced heat transfer efficiency of refrigerators, nuclear reactor cooling, space, etc., nanofluids also have many medicinal uses such as medicines delivery and antibacterial. Nanofluids conception was offered by Choi et al. [1] with a view to produce liquids with higher thermal conductivity and heat transport rate. Sheikholeslami and Ganji [2] studied numerically the flux of nanoliquid having copper nanoparticles with united magnetic field impact. Various models have been established to treatise the nanofluid, one of the models of nanofluid is Buongiorno model which are relied by several investigators to examine the nanofluid. The model of Buongiorno nanofluid was used by Khan et al. [3] to scout transfer properties of fluid. He noticed that changing parameter of thermophoretic increases transport of mass and temperature of nanofluid. The effect of thermal radiation by utilizing model of Buongiorno nanofluid on magnetic nanofluid was examined by Ghadikolaei et al. [4]. It was observed that growing parameter of Brownian motion reduces the transfer of mass. Via a permeable surface, the Maxwell nanofluid was investigated numerically in the existence of thermophoresis and Brownian motion by Ahmed et al. [5]. Authors verified that if the convenient nanofluid is utilized, the heat transport feature can be increased. Many investigators [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25] made some modern contributions via different geometries.

Study of the magnetic field influence has significant chemical, physical and engineering applications. The interaction of electro-conducting fluid and magnetic field influences industrial devices like motors, pumps, boundary layer control and magnetohydrodynamic (MHD) generators. The chemical reaction impact on boundary-layer MHD flow of two-phase nanoliquid paradigm above an exponentially extending sheet with heat obstetrics was elaborated by Eid. [26]. The influence of thermal radiation, permeability and Lorentz forces on transport of heat and flow of Casson nanofluid was examined by Kho et al. [27]. They noted that the increment in magnetic and Casson parameters, reduces the velocity and grows the heat transfer. The flow of MHD nanofluid of molybdenum disulfide in a duct was studied by Raza et al. [28]. The unsteady normal convection magneto Couette nanofluid flux with thermal radiation by utilizing two-phase and single-phase nanofluid paradigms for nanofluids was studied numerically [29]. Lahmar et al. [30] discussed the heat transport of squeezing unstable nanoliquid flux under the impacts of sloping MHD and changeable thermal conductivity.

Researchers have often attempted to boost or improve new ways for raising the heat transfer rate, leading to higher performance of heating systems, lower fuel consumption and economical savings. Nowadays, heat transfer by convection within porous materials was commonly studied in various systems. That is due to the broad implementations of transport of heat in porous materials extended from phenomena of transport in biological systems to oil recuperation in the petroleum production. Utilizing porous materials in thermal systems has two advantages. Firstly, the region of transfer of heat is considerably large, essentially raising the heat exchange average. Secondly, a porous regime contributes to disorderly fluid motion through the related pores that greatly improve flow mixing. As an outcome, porous media have gained considerable interest because of their use in heat transport gear in the last few years [31,32,33,34,35,36,37,38,39].

Shear thickening and shear thinning are popular in many manufacturing polymers and such fluid viscosity depends on the rate of shear. The rheology of yield stress is widespread among liquids with shear rate counts on viscosity. Popular examples of such materials are hair cream, ketch up, nail burnish, blood solutions and polymer. Dutta et al. [40] studied the effect of tilt angle on natural convection and yield stress of fluid via a square rod in an annulus of square. Al-Hossainy et al. [41] studied the impact of external yield stress on 3D flow of MHD nanofluid in a porous regime. Sohail et al. [42] analyzed the application of non-Fourier double propagations theories to the flux of the boundary-layer of a yield stress displaying fluid model theoretically and numerically. Kaneeza et al. [43] introduced an improvement in heat energy transfer in yield stress dusty nanofluid and dusty hybrid nanofluid.

Chemical reaction represents sufficient transmit observances of mass and heat in this model. In a revolving regime [44], the impacts of thermal radiation and reaction of chemical on the flux and heat transport of a nanoliquid were studied. The nonlinear flow via an extending plate with react of chemical was examined by Gireesha et al. [45]. They noted that the variation in the system of chemical reaction have contributed to a major divergence in the mass transmit and heat transport. The chemical reaction of the nanoliquid flux of Williamson in a porous regime was demonstrated by Acharya et al. [46] where the influences of Brownian motion, slip condition and thermophoresis were considered. The consequence is that transmit of mass increases at a higher rate of chemical reaction.

One of the most important techniques of heat exchange in industrialization appliances is heat transport, which coats a large section of themes relating to energy. Heat transfer can enhance by porous media and magnetic field in various applications, via supplying great areas in addition to flux blending condensation. And therefore, using porous materials and magnetic field in nanofluids can improve dramatically the different thermal equipment performances. Today, the heat exchangers are crucial ingredients in engineering, science applications and trade. The main reason of this study is to investigate magnetohydrodynamic nanofluid flow via a permeable shrinking cylinder using the Buongiorno's mathematical model. To our knowledge, there is no previously published literature on such model. This paper is discussed in five partitions. Literature on the subject is offered in partition one. In section two, flow descriptions are advanced. The numerical simulation is briefly debated in partition three. Section four contains the discussion of results. Conclusions are offered in partition five. This study will be useful in the processes of water purgation and filtration and in studying movement of water or oil and gas through the cylindrical tanks. The computational results of the dimensionless governing equations have a large significance in geophysics for studying the geomagnetic domain reaction with the liquid in the zone of geothermal.

2 Flow description

2.1 Basic equations

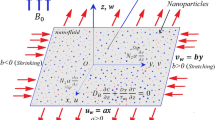
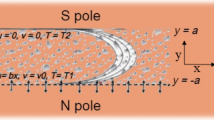
We deem the steady axisymmetric flux of a viscid nanoliquid via a permeable contracting cylinder of radius \(a\). In the existence of thermophoresis and motion of Brownian, transmit of mass and heat transmit are notified. The flux is considered here in the \(x\)-axis direction with the radial coordinate \(r\) in the direction perpendicular to \(x\), as seen in Fig. 1. Extending/contracting velocity \(u_{w} \left( x \right)\) is linear for cylinder. It is supposed that the stationary mass flow velocity is \(v_{w}\), where \(v_{w} < 0\) for injection and \(v_{w} > 0\) for suction of the fluid.

Fig. 1
figure 1

Flow problem diagram

Full size image

Full handling is deemed by assumptions of boundary layer. For these propositions, the controlling equations are (see Ref. [47])

$$ \frac{{\partial \left( {ru} \right)}}{\partial x} + \frac{{\partial \left( {rv} \right)}}{\partial r} = 0 $$
(1)
$$ u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial r}} = \nu \left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{{\partial r}}} \right) - \left( {\frac{{\sigma B_{0}^{2} }}{\rho } + \frac{\nu }{K}} \right)u - \alpha_{0} , $$
(2)
$$ u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial r}} = \alpha \left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{{\partial r}}} \right) + \tau \left[ {D_{B} \frac{\partial C}{{\partial r}}\frac{\partial T}{{\partial r}} + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{{\partial r}}} \right)^{2} } \right] + \frac{1}{{\rho c_{p} }}\frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} }}\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{{Q_{0} }}{{\rho c_{p} }}\left( {T - T_{\infty } } \right), $$
(3)
$$ u\frac{\partial C}{{\partial x}} + v\frac{\partial C}{{\partial r}} = D_{B} \left( {\frac{{\partial^{2} C}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial C}{{\partial r}}} \right) + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{{\partial r}}} \right) - k_{c} \left( {C - C_{\infty } } \right) $$
(4)

with the boundary conditions:

$$\left. {\begin{array}{*{20}l} {\begin{array}{*{20}l} {v = v_{w} ,~u = u_{w} \left( x \right) = \lambda U_{w} \left( x \right),~T = T_{w} ,~D_{B} \frac{{\partial C}}{{\partial r}} + \frac{{D_{T} }}{{T_{\infty } }}\frac{{\partial T}}{{\partial r}} = 0\,{\text{at}}\,~r = a,} \hfill \\ {u \to 0,~T \to T_{\infty } ,~C \to C_{\infty } ~\,{\text{as}}\,~r \to \infty ,} \hfill \\ \end{array} } \hfill \\ \end{array}}\right\}$$
(5)

where \( v\) and \(u\) are the components of velocity along \(r -\) and \(x -\) axes, respectively, \(\alpha_{0}\) is the yield stress parameter, \(\sigma^{*}\) is the Stefan-Boltzmann constant, \(k^{*}\) is the coefficient of mean absorption, \(T\) is the temperature of nanofluid, \(C\) is the volume concentration of nano-particles, \(\left( {C_{\infty } , T_{\infty } } \right)\) are the nanoparticles volume concentration and ambient fluid temperature, \(k\) is the thermal conductivity of the fluid, \(\nu \) is the nanofluid kinematic viscosity, \(\rho\) represents the density, \(D_{T}\) represents the coefficient of thermophoresis diffusion, \( D_{B}\) is the coefficient of Brownian diffusion, \(c_{p}\) represents the specific heat,\( \alpha = k/\rho c_{p}\) symbolizes the thermal diffusivity, \( \left( {\rho c_{p} } \right)_{p}\) is the nano-particles effective heat capacity, \( \left( {\rho c_{p} } \right)_{f}\) represents the fluid heat capacity, \(\tau = \left( {\rho c_{p} } \right)_{p} /\left( {\rho c_{p} } \right)_{f}\) symbolizes the ratio of heat capacity, \(K\) is the permeability of porous media, \(Q_{0}\) is the source/sink of heat, \(k_{c}\) is the chemical reaction and \(\lambda\) is the fixed extending \((\lambda > 0)\) or contracting \((\lambda < 0)\) parameter. Here, we shrinking \((\lambda < 0)\) parameter and we suppose that \(U_{w} \left( x \right) = u_{0} x/l\), where \(u_{0}\) is the characteristic of stationary velocity and \(l\) is the cylinder length characteristic.

Introducing the following similarity variables:

$$ u = \frac{{u_{0} x}}{l}f^{\prime } \left( \eta \right),v = - \frac{a}{r}\sqrt {\frac{{u_{0} \nu }}{l}} f\left( \eta \right),\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\phi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }},\eta = \sqrt {\frac{{u_{0} }}{\nu l}} \left( {\frac{{r^{2} - a^{2} }}{2a}} \right), $$
(6)

where the symbol (′) represents the differentiation with respect to \(\eta\). Replacing the similarity transformations (6) into Eqs. (1) to (4), it is established that the continuity equation is achieved automatically and Eqs. (2)–(4) become:

$$ \left( {1 + 2\alpha_{1} \eta } \right)f^{\prime\prime\prime} + 2\alpha_{1} f^{\prime\prime} + ff^{\prime\prime} - f^{{\prime}{2}} - Mf^{\prime} - K_{p} f^{\prime} - {\Omega } = 0, $$
(7)
$$ \left( {1 + \frac{4}{3}R_{d} } \right)\left( {1 + 2\alpha_{1} \eta } \right)\theta^{\prime\prime} + \alpha_{1} \left( {2 + \frac{4}{3}R_{d} } \right)\theta^{\prime} + Pr\left( {1 + 2\alpha_{1} \eta } \right)\left( {N_{b} \theta^{\prime}\phi^{\prime} + N_{t} \theta^{{\prime}{2}} } \right) + Prf\theta^{^{\prime}} + S\theta = 0 $$
(8)
$$ \left( {1 + 2\alpha_{1} \eta } \right)\phi^{\prime\prime} + 2\alpha_{1} \phi^{^{\prime}} + \frac{{N_{t} }}{{N_{b} }}\left[ {\left( {1 + 2\alpha_{1} \eta } \right)\theta ^{\prime\prime} + 2\alpha_{1} \theta ^{\prime}} \right] + Scf\phi^{\prime} - R_{c} \phi = 0, $$
(9)

subject to:

$$ \left. {\begin{array}{*{20}l} {f\left( 0 \right) = f_{w} ,~f^{\prime}\left( 0 \right) = \lambda ,~\theta \left( 0 \right) = 1,~N_{b} \phi ^{\prime}\left( 0 \right) + N_{t} \theta ^{\prime}\left( 0 \right) = 0,} \hfill \\ {f^{\prime}\left( \infty \right) \to 0,~\theta \left( \infty \right) \to 0,\phi \left( \infty \right) \to 0,} \hfill \\ \end{array} } \right\} $$
(10)

where \(\alpha_{1} = \sqrt {\nu l/a^{2} u_{0} }\) represents the parameter of curvature, \(M = \sigma B_{0}^{2} l/\rho u_{0}\) Symbolizing the magnetic parameter, \(K_{p} = \nu l/Ku_{0}\) is the permeability of porous media, \({\Omega } = \left( {l\alpha_{0} /U_{w} u_{0} } \right)\) is the yield stress parameter, \(Pr = \nu /\alpha\) is the number of Prandtl, \(N_{b} = \tau D_{B} \left( {C_{w} - C_{\infty } } \right)/\nu\) is the parameter of Brownian motion, \(N_{t} = \tau D_{T} \left( {T_{w} - T_{\infty } } \right)/\nu T_{\infty }\) represents the thermophoresis parameter, \(R_{d} = 4\sigma^{*} T_{\infty }^{3} /k^{*} k\) is the nonlinear parameter of thermal radiation and \(S = Q\nu l/ku_{0}\) is the heat source/sink, \({\text{Sc}} = \nu /D_{B}\) represents the number of Schmidt and \(R_{c} = l\nu k_{c} /u_{0} D_{B}\) is the chemical react parameter.

2.2 Physical quantities

The coefficients of local skin friction \(C_{f}\), local Nusselt number \({\text{Nu}}_{x}\) and local Sherwood number are expressed as:

$$ C_{f} = \frac{{\tau_{w} }}{{\rho U_{w}^{2} }}, {\text{Nu}}_{x} = \frac{{xq_{w} }}{{k\left( {T_{w} - T_{\infty } } \right)}}, {\text{Sh}}_{x} = \frac{{xq_{m} }}{{D_{B} \left( {C_{w} - C_{\infty } } \right)}}, $$
(11)

in the \(x -\) oriention of the stretching/shrinking cylinder \(\tau_{w}\) represents the shear stresses or skin frictions, \(q_{m}\) and \(q_{w}\) are the mass and heat fluxes over the cylinder, which are defined as:

$$ \tau_{w} = \mu \left( {\frac{\partial u}{{\partial r}}} \right)_{r = a} , q_{w} = - k\left( {\frac{\partial T}{{\partial r}}} \right)_{r = a} - \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} }}\left( {\frac{\partial T}{{\partial r}}} \right)_{r = 0} , q_{m} = - D_{B} \left( {\frac{\partial C}{{\partial r}}} \right)_{r = a} , $$
(12)

Equation (11) becomes:

$$ {\text{Re}}_{x}^{1/2} C_{f} = f^{\prime\prime}\left( 0 \right), {\text{Re}}_{x}^{ - 1/2} Nu_{x} = - \left( {1 + \frac{4}{3}R_{d} } \right)\theta ^{\prime}\left( 0 \right),{\text{Re}}_{x}^{ - 1/2} Sh_{x} = - \phi ^{\prime}\left( 0 \right) $$
(13)

where \({\text{Re}}_{x} = U_{w} x/\nu\) indicates to the local Reynolds number.

3 Numerical simulation

As previously determined, Eqs. (7)–(9) shapes an extremely nonlinear differential system with their acceptable boundary conditions (10), for facilitating the procedure of solution, the ODEs can be linearized and separated properly to diminish them into a concatenation of subordinate linear subsystems. In accordance with the various simplifying amendments, the acquired subsystems are spatially determined depending on the collocation points of Gauss–Lobatto and then numerically tackled using (SLLM), which Mosta [48] defined more obviously and then Eqs. (7)–(10) become:

$$ a_{1} f_{r + 1}^{\prime \prime \prime } + a_{2} f_{r + 1}^{\prime \prime } + a_{3} f_{r + 1}^{\prime } + a_{4} f_{r + 1} = r_{1} , $$
(14)
$$ b_{1} \theta_{r + 1}^{^{\prime\prime}} + b_{2} \theta_{r + 1}^{^{\prime}} + b_{3} \theta_{r + 1} = r_{2} , $$
(15)
$$ c_{1} \phi_{r + 1}^{^{\prime\prime}} + c_{2} \phi_{r + 1}^{^{\prime}} + c_{3} \phi_{r + 1} = r_{2} , $$
(16)
$$ \left. {\begin{array}{*{20}l} {f_{{r + 1}} \left( 0 \right) = f_{w} ,~f_{{r + 1}}^{'} \left( 0 \right) = \lambda ,~\theta _{{r + 1}} \left( 0 \right) = 1,N_{b} \phi _{{r + 1}}^{'} \left( 0 \right) + N_{t} \theta _{{r + 1}}^{'} \left( 0 \right) = 0,} \hfill \\ {f_{{r + 1}}^{'} \left( \infty \right) \to 0,~\theta _{{r + 1}} \left( \infty \right) \to 0,\phi _{{r + 1}} \left( \infty \right) \to 0,} \hfill \\ \end{array} } \right\} $$
(17)

Where

$$ a_{1} = 1 + 2\alpha_{1} \eta , a_{2} = 2\alpha_{1} + f_{r} , a_{3} = - M - K_{p} , a_{4} = f_{r}^{^{\prime\prime}} , r_{1} = {\Omega } + f_{r} f_{r}^{^{\prime\prime}} , $$
(18)
$$ \left. {\begin{array}{*{20}l} {b_{1} = \left( {1 + \frac{4}{3}R_{d} } \right)\left( {1 + 2\alpha _{1} \eta } \right),~b_{2} = \alpha _{1} \left( {2 + \frac{4}{3}R_{d} } \right) + Pr\left( {1 + 2\alpha _{1} \eta } \right)\left( {N_{b} \phi _{r}^{\prime } + 2N_{t} \theta _{r}^{\prime } } \right) + {\text{Prf}}_{r} ,} \hfill \\ {b_{3} = S,~r_{2} = {\text{Pr}}\left( {1 + 2\alpha _{1} \eta } \right)N_{t} \theta _{r}^{{\prime 2}} ,} \hfill \\ \end{array} } \right\} $$
(19)
$$ c_{1} = \left( {1 + 2\alpha_{1} \eta } \right), c_{2} = 2\alpha_{1} + Scf_{r} , c_{3} = - R_{c} , r_{3} = \frac{{N_{t} }}{{N_{b} }}\left[ {\left( {1 + 2\alpha_{1} \eta } \right)\theta_{r}^{^{\prime\prime}} + 2\alpha_{1} \theta_{r}^{^{\prime}} } \right], $$
(20)

where \(\left( {r + 1} \right)\) and \(r\) subscripts refer to the present and past appreciations, respectively. It must be observed that in all subsequent partitions, unless otherwise shown in the graphical explanations, the values are taken as: \(\alpha_{1} = 0.1, M = 0.5, K_{p} = 5, \Omega = 1, Pr = 1, N_{b} = 0.5, N_{t} = 0.5, R_{d} = 1, S = 0.04, Sc = 1, f_{w} = 2, \lambda = - 0.5, R_{c} = 0.04\).

4 Discussion of results

The system of Eqs. (7)–(9) is solved numerically using (SLLM) with the boundary conditions (10). Different values are utilized for many parameters as seen through graphs. The impacts of heat sink/source, magnetic field, chemical reaction, yield stress, thermal radiation and porous regime permeability are studied in this partition. We have assigned the following values: \(\alpha_{1} = 0.1, M = 0.5, K_{p} = 5, \Omega = 1, Pr = 1, N_{b} = 0.5, N_{t} = 0.5, R_{d} = 1, S = 0.04, Sc = 1, f_{w} = 2, \lambda = - 0.5, R_{c} = 0.04\). To simulate the operation, different amounts of the constant parameters have been taken. The influences of the parameters on the velocity \(f^{\prime}\left( \eta \right)\), temperature \(\theta \left( \eta \right)\), concentration \(\phi \left( \eta \right)\), skin friction \({\text{Re}}_{x}^{1/2} C_{f}\), Nusslet number \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) and number of Sherwood \({\text{Re}}_{x}^{ - 1/2} {\text{Sh}}_{x}\) have been sketched in Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22.

Figure 2 compares drag force \(f^{\prime\prime}\left( 0 \right)\) for changing \(\alpha_{1}\) and \(\lambda\) when \(f_{w} = M = K_{p} = R_{c} = R_{d} = S = {\Omega } = 0\) with Ref. [47]. From this figure, we found that the current results are compatible to assure our computations are validated.

Fig. 2
figure 2

Variation of \(f^{\prime \prime } \left( 0 \right)\) versus \(\lambda\) and \(\alpha_{1}\)

Full size image

In Fig. 3, the influence of parameter of magnetic on \(f^{\prime}\left( \eta \right)\) profile is discussed and it is noted that there is an increment in \(f^{\prime}\left( \eta \right)\) when \(M\) grows. Physically, this is because of the force of Lorentz that supports the fluid flux velocity. In the current case of flux, where \(M\) parameter increases, \(\theta \left( \eta \right)\) diminishes and also the thermal boundary layer thickness as seen in Fig. 4. Temperature impacts magnetism by either weakening or strengthening a magnet's appealing force. A magnet subjected to heat experiences a reduction in its magnetic field as the particles within the magnet are moving at an increasingly faster. It is cleared from Fig. 5 that \(\phi \left( \eta \right)\) and the corresponding boundary layer thickness are decreased as \(M\) increases.

Fig. 3
figure 3

Variation of \(f^{\prime } \left( \eta \right)\) versus \(M\)

Full size image
Fig. 4
figure 4

Variation of \(\theta \left( \eta \right)\) versus \(M\)

Full size image
Fig. 5
figure 5

Variation of \(\phi \left( \eta \right)\) versus \(M\)

Full size image

Figure 6 depicts the effect of \(K_{p}\) on the velocity. It is observed from this figure that \(f^{\prime}\left( \eta \right)\) and the momentum boundary layer thickness increase as \(K_{p}\) increases. Physically, an improvement in the permeability of porous media leads to an enhancement in fluid flow through it. The resistance of the system may be disregarded when the bores of the porous medium be great, where the velocity at the isolated bottom equal to zero and gradually increases as it reaches the free surface and reaches its maximum extent. Figure 7 illustrates the impact of \(K_{p}\) on the temperature and we noticed that as the values of the permeability grow, the temperature and the thermal boundary layer thickness lower. It is noted from Fig. 8 that the concentration is decreased with upsurging \(K_{p}\).

Fig. 6
figure 6

Variation of \(f^{\prime } \left( \eta \right)\) versus \(K_{p}\)

Full size image
Fig. 7
figure 7

Variation of \(\theta \left( \eta \right)\) versus \(K_{p}\)

Full size image
Fig. 8
figure 8

Variation of \(\phi \left( \eta \right)\) versus \(K_{p}\)

Full size image

Figures 9, 10, 11 depict the effectiveness of yield stress parameter on the profiles of \(f^{\prime}\left( \eta \right)\), \(\theta \left( \eta \right)\) and \(\phi \left( \eta \right)\). It is noted that as the amounts of yield stress increases, \(f^{\prime}\left( \eta \right)\) and the corresponding thickness of the boundary layer decay on account of the additional flow resistance. Physically, an increase in the yield stress means that the nanofluid becomes more viscous which in turn decreases the fluid flow rate and increases the nanoparticles concentration as in Figs. 9 and 11, respectively. In Fig. 10, it is observed that increasing values of yield stress, increases the temperature. Physically, the strain rate upsurges by upsurging yield stress, which basically increases the temperature. Also, yield stress is known as the amount energy induced in material to overcome or to avoid yield. This means that increased yield stress leads to an increase in temperature.

Fig. 9
figure 9

Variation of \(f^{\prime } \left( \eta \right)\) versus \(\Omega\)

Full size image
Fig. 10
figure 10

Variation of \(\theta \left( \eta \right)\) versus \(\Omega\)

Full size image
Fig. 11
figure 11

Variation of \(\phi \left( \eta \right)\) versus \(\Omega\)

Full size image

The chemical reaction influence on the profile of concentration is offered in Fig. 12. The boosted values of \(R_{c}\) result in a fluid particles breakthrough near the plate which decreases the concentration and the corresponding boundary layer thickness. Physically, by occurring the chemical reaction, gradually destroying the initial species diffusing in the nanofluid. This in turn, prevents molecular diffusion of the residual species which leads to a decrease in concentration magnitudes and a reduction in concentration boundary layer thickness.

Fig. 12
figure 12

Variation of \(\phi \left( \eta \right)\) versus \(R_{c}\)

Full size image

For improving \(R_{d}\), the reducing of \(\theta \left( \eta \right)\) is offered in Fig. 13. Physically, this is because that an excess in \(R_{d}\) produces a diminish in thermal diffusivity and hence the thermal boundary layer area reduces. Figure 14 presents that when \(R_{d}\) increases, the concentration profile of the nanoparticles reduces initially, whereas against demeanor is noticed when \(\eta > 1.3\). Figure 15 explains that the effect of the parameter \(S\) on the curve of energy. This figure shows that the contours of energy are incremented for increasing amounts of \(S\) because of the reality that additional heat is generated to the liquid.

Fig. 13
figure 13

Variation of \(\theta \left( \eta \right)\) versus \(R_{d}\)

Full size image
Fig. 14
figure 14

Variation of \(\phi \left( \eta \right)\) versus \(R_{d}\)

Full size image
Fig. 15
figure 15

Variation of \(\theta \left( \eta \right)\) versus \(S\)

Full size image

Figures 16, 17, 18 demonstrate that the impact of the parameters of the magnetic field and the permeability of porous media on the curves of \({\text{Re}}_{x}^{1/2} C_{f}\), \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) and \({\text{Re}}_{x}^{ - 1/2} {\text{Sh}}_{x}\), respectively. It is scrutinized from these plots that \({\text{Re}}_{x}^{1/2} C_{f}\), \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) are enhanced when \(M\) and \(K_{p}\) increase as seen in Figs. 16 and 17, respectively. But, Sherwood number \(\left( {{\text{Re}}_{x}^{ - 1/2} {\text{Sh}}_{x} } \right)\) is decreased when the values of \(M\) and \(K_{p}\) increase as shown in Fig. 18.

Fig. 16
figure 16

Variation of \({\text{Re}}_{x}^{1/2} C_{f}\) versus \(M\) and \(K_{p}\)

Full size image
Fig. 17
figure 17

Variation of \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) versus \(M\) and \(K_{p}\)

Full size image
Fig. 18
figure 18

Variation of \({\text{Re}}_{x}^{ - 1/2} {\text{Sh}}_{x}\) versus \(M\) and \(K_{p}\)

Full size image

Figures 19 and 20 represent the distributions of \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) and \({\text{Re}}_{x}^{ - 1/2} {\text{Sh}}_{x}\) for different values of \({\Omega }\) and \(R_{c}\). Increasing values of yield stress \(\left( {\Omega } \right)\) lowers Nusselt number \(\left( {{\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x} } \right)\). Where, enhancing amounts of \(R_{c}\) upsurges local Nusselt number as observed in Fig. 19. Figure 20 shows that Sherwood number is increased by increasing \({\Omega }\) and is decreased by increasing \(R_{c}\) as illustrated in Fig. 20. This means that \({\Omega }\) and \(R_{c}\) parameters have opposite demeanor on heat transfer and mass transfer as displayed in Figs. 19 and 20.

Fig. 19
figure 19

Variation of \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) versus \(\Omega\) and \(R_{c}\)

Full size image
Fig. 20
figure 20

Variation of \({\text{Re}}_{x}^{ - 1/2} {\text{Sh}}_{x}\) versus \(\Omega\) and \(R_{c}\)

Full size image

The Nusselt number \(\left( {{\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x} } \right)\) is enhancemented with increasing \(R_{d}\) parameter, but is reduced with increasing heat absorption/generation parameter as seen in Fig. 21. Figure 22 explains that Sherwood number \(\left( {{\text{Re}}_{x}^{ - 1/2} {\text{Sh}}_{x} } \right)\) is reduced with increasing \(R_{d}\) parameter, but is grown with increasing \(S\) parameter.

Fig. 21
figure 21

Variation of \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) versus \(R_{d}\) and \(S\)

Full size image
Fig. 22
figure 22

Variation of \({\text{Re}}_{x}^{ - 1/2} {\text{Sh}}_{x}\) versus \(R_{d}\) and \(S\)

Full size image

5 Conclusions

This study aims to offer a study for the steady flux of a convective transfer of mass and heat over a shrinking cylinder in a porous regime utilizing Buongiorno's mathematical model. The impact of yield stress, magnetic field, chemical reaction, heat sink/source and thermal radiation is also considered. Therefore, after reviewing of the diagrams, the following concludes:

  • The velocity \(f^{\prime}\left( \eta \right)\) increases by upsurging values of the permeability and magnetic field.

  • The temperature is an increasing function with the raising values of yield stress and heat source parameters. But, the temperature has against trend with the raising amounts of thermal radiation and magnetic field.

  • The improvement of the concentration rate is noticed with the growing amounts of yield stress parameter.

  • As the values of the magnetic field and permeability parameters increases, skin friction coefficient rises.

  • Nusselt number rises with the raising values of magnetic field, permeability of porous media, thermal radiation and chemical reaction. The opposite trend happens with the raising values of yield stress and heat source.

  • Sherwood number has a different behavior compared to Nusselt number with all parameters which are discussed above.

There are several modifications we would make if we were to design this study again. In principle, we would attempt to recruit significantly more situation studies so that we would have a broader selection of options to pursue once our study began in earnest. We would incorporate temperature-dependent viscosity variation into the model of Darcy-Forchheimer model. And also, we can discuss many controlling parameters which have not been studied here as heat sink/source, thermal radiation and Schmidt number.