Mathematical Modeling and MHD Flow of Micropolar Fluid Toward an Exponential Curved Surface: Heat Analysis via Ohmic Heating and Heat Source/Sink

Abstract

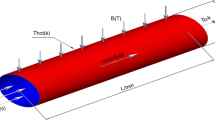
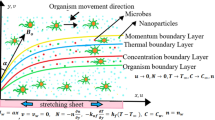
The main goal of the current article analyzed the influence of MHD flow of micropolar fluid via exponentially curved stretching surface. Heat transfer analysis is discussed with the impact of thermal radiation and Joule heating. For mathematical model curvilinear (u, v, r and s) is taken for governing flow problem. Viscous dissipation is also considered. Exponential similarity variables are used to transform partial differential equations to ordinary differential system. (ODEs). Numerical techniques have been used to solve the nonlinear ODEs. Effect of various physical variables like material parameter $(K_{1} = 0.1, 0.2, 0.3, 0.4, 0.5)$, radius of curvature ($\delta = 1,2,3,4,5$), magnetic parameter ($M = 0,0.1, 0.2, 0.3, 0.4$), radiative parameter ($R_{d} = 1.0,2.0,3.0,4.0,5.0$), heat generation parameter (Q = 0, 0.1, 0.2, 0.3, 0.4), surface friction, couple stress and surface temperature on the flow of velocity, temperature field and microrotation velocity has been examined through graphs. A good agreement of the present work has been noticed with a previous published result.

Appendices

Appendix A

$A_{1} = \frac{2}{\xi + \delta },$ $A_{2} = - \frac{1}{{\left( {\xi + \delta } \right)^{2} }} - \frac{{M^{2} }}{{1 + K_{1} }},$ $A_{3} = \frac{1}{{\left( {\xi + \delta } \right)^{3} }} - \frac{{M^{2} }}{{\left( {\xi + \delta } \right)\left( {1 + K_{1} } \right)}},$ $A_{4} = \frac{\delta }{{\left( {\xi + \delta } \right)\left( {1 + K_{1} } \right)}},$ $A_{5} = \frac{\delta }{{\left( {\xi + \delta } \right)^{2} \left( {1 + K_{1} } \right)}},$ $A_{6} = - \frac{\delta }{{\left( {\xi + \delta } \right)^{3} \left( {1 + K_{1} } \right)}},$ $A_{7} = - \frac{3\delta }{{\left( {\xi + \delta } \right)^{2} \left( {1 + K_{1} } \right)}},$ $A_{8} = - \frac{3\delta }{{\left( {\xi + \delta } \right)\left( {1 + K_{1} } \right)}},$ $A_{9} = - \frac{{K_{1} }}{{1 + K_{1} }},$ $A_{10} = - \frac{{K_{1} }}{{\left( {\xi + \delta } \right)\left( {1 + K_{1} } \right)}},$ $A_{11} = \lambda$

$B_{1} = \frac{1}{{\left( {\xi + \delta } \right)}},$ $B_{2} = - \frac{{2K_{1} }}{{\left( {1 + \frac{{K_{1} }}{2}} \right)}},$ $B_{3} = - \frac{{K_{1} }}{{\left( {1 + \frac{{K_{1} }}{2}} \right)}},$ $B_{4} = - \frac{{K_{1} }}{{\left( {\xi + \delta } \right)\left( {1 + \frac{{K_{1} }}{2}} \right)}},$ $B_{5} = \frac{\delta }{{\left( {\xi + \delta } \right)\left( {1 + \frac{{K_{1} }}{2}} \right)}},$ $B_{6} = - \frac{3\delta }{{2\left( {\xi + \delta } \right)\left( {1 + \frac{{K_{1} }}{2}} \right)}},$ $B_{7} = \frac{\delta \Pr }{{\xi + \delta }},$ $B_{8} = - \frac{2\delta \Pr }{{\xi + \delta }},$ $B_{9} = \Pr {\text{Ec}},$ $B_{10} = - \frac{{2\Pr {\text{Ec}}}}{\xi + \delta },$ $B_{11} = \Pr {\text{Ec}}M\left( {\xi + \delta } \right),$ $B_{12} = \Pr Q,$ $B_{13} = \frac{\Pr EC}{{\left( {\xi + \delta } \right)^{2} }}$

Appendix B

Linearize system subject to Newton’s quasi-linearization approach (NQLA)

$$ f_{j}^{{\left( {k + 1} \right)}} = f_{j}^{\left( k \right)} + \delta f_{j}^{\left( k \right)} , u_{j}^{{\left( {k + 1} \right)}} = u_{j}^{\left( k \right)} + \delta u_{j}^{\left( k \right)} , v_{j}^{{\left( {k + 1} \right)}} = v_{j}^{\left( k \right)} + \delta v_{j}^{{\left( {k + 1} \right)}} , w_{j}^{{\left( {k + 1} \right)}} = w_{j}^{\left( k \right)} + \delta w_{j}^{\left( k \right)} , g_{j}^{{\left( {k + 1} \right)}} = g_{j}^{\left( k \right)} + \delta g_{j}^{\left( k \right)} , p_{j}^{{\left( {k + 1} \right)}} = p_{j}^{\left( k \right)} + \delta p_{j}^{\left( k \right)} , \theta_{j}^{{\left( {k + 1} \right)}} = \theta_{j}^{\left( k \right)} + \delta \theta_{j}^{\left( k \right)} , q_{j}^{{\left( {k + 1} \right)}} = q_{j}^{\left( k \right)} + \delta q_{j}^{\left( k \right)} . $$

(i)

$$ \delta f_{j} - \delta f_{j - 1} - \frac{1}{2}h_{j} \left( {\delta u_{j} + \delta u_{j - 1} } \right) = \left( {r_{1} } \right)_{{j - \frac{1}{2}}} , $$

(ii)

$$ \delta u_{j} - \delta u_{j - 1} - \frac{1}{2}h_{j} \left( {\delta v_{j} + \delta v_{j - 1} } \right) = \left( {r_{2} } \right)_{{j - \frac{1}{2}}} , $$

(iii)

$$ \delta v_{j} - \delta v_{j - 1} - \frac{1}{2}h_{j} \left( {\delta w_{j} + \delta w_{j - 1} } \right) = \left( {r_{3} } \right)_{{j - \frac{1}{2}}} , $$

(iv)

$$ \delta g_{j} - \delta g_{j - 1} - \frac{1}{2}h_{j} \left( {\delta p_{j} + \delta p_{j - 1} } \right) = \left( {r_{4} } \right)_{{j - \frac{1}{2}}} , $$

(v)

$$ \delta \theta_{j} - \delta \theta_{j - 1} - \frac{1}{2}h_{j} \left( {\delta q_{j} + \delta q_{j - 1} } \right) = \left( {r_{5} } \right)_{{j - \frac{1}{2}}} , $$

(vi)

$$ \left( {\alpha_{1} } \right)_{j} \delta v_{j} + \left( {\alpha_{2} } \right)_{j} \delta v_{j - 1} + \left( {\alpha_{3} } \right)_{j} \delta f_{j + } \left( {\alpha_{4} } \right)_{j} \delta f_{j - 1} + \left( {\alpha_{5} } \right)_{j} \delta u_{j} + \left( {\alpha_{6} } \right)_{j} \delta u_{j - 1} + \left( {\alpha_{7} } \right)_{j} \delta w_{j} + \left( {\alpha_{8} } \right)_{j} \delta w_{j - 1} + \left( {\alpha_{9} } \right)_{j} \delta p_{j} + \left( {\alpha_{10} } \right)_{j} \delta p_{j - 1} + \left( {\alpha_{11} } \right)_{j} \delta q_{j} + \left( {\alpha_{12} } \right)_{j} \delta q_{j - 1} = \left( {r_{6} } \right)_{{j - \frac{1}{2}}} , $$

(vii)

$$ \left( {\alpha_{21} } \right)_{j} \delta f_{j} + \left( {\alpha_{22} } \right)_{j} \delta f_{j - 1} + \left( {\alpha_{23} } \right)_{j} \delta u_{j + } \left( {\alpha_{24} } \right)_{j} \delta u_{j - 1} + \left( {\alpha_{25} } \right)_{j} \delta g_{j} + \left( {\alpha_{26} } \right)_{j} \delta g_{j - 1} + \left( {\alpha_{27} } \right)_{j} \delta v_{j} + \left( {\alpha_{28} } \right)_{j} \delta v_{j - 1} + \left( {\alpha_{29} } \right)_{j} \delta p_{j} + \left( {\alpha_{30} } \right)_{j} \delta p_{j - 1} = \left( {r_{7} } \right)_{{j - \frac{1}{2}}} , $$

(viii)

$$ \left( {\alpha_{31} } \right)_{j} \delta f_{j} + \left( {\alpha_{32} } \right)_{j} \delta f_{j - 1} + \left( {\alpha_{33} } \right)_{j} \delta u_{j + } \left( {\alpha_{34} } \right)_{j} \delta u_{j - 1} + \left( {\alpha_{35} } \right)_{j} \delta \theta_{j} + \left( {\alpha_{36} } \right)_{j} \delta \theta_{j - 1} + \left( {\alpha_{37} } \right)_{j} \delta v_{j} + \left( {\alpha_{38} } \right)_{j} \delta v_{j - 1} + \left( {\alpha_{39} } \right)_{j} \delta q_{j} + \left( {\alpha_{40} } \right)_{j} \delta q_{j - 1} + \left( {\alpha_{41} } \right)_{j} \delta u_{j} + \left( {\alpha_{42} } \right)_{j} \delta u_{j - 1} + \left( {\alpha_{43} } \right)_{j} \delta \theta_{j} + \left( {\alpha_{44} } \right)_{j} \delta \theta_{j - 1} = \left( {r_{8} } \right)_{{j - \frac{1}{2}}} . $$

(ix)

with

$$ \delta f_{1} = 0, \delta u_{1} = 0, \delta g_{1} = 0, \delta \theta_{1} = 0, \delta v_{J} = 0, \delta w_{J} = 0, \delta g_{J} = 0, \delta \theta_{J} = 0, $$

(x)

where

$$ \left( {r_{1} } \right)_{{j - \frac{1}{2}}} = f_{j - 1} - f_{j} + h_{j} u_{{j - \frac{1}{2}}} , $$

(xi)

$$ \left( {r_{2} } \right)_{{j - \frac{1}{2}}} = u_{j - 1} - u_{j} + h_{j} v_{{j - \frac{1}{2}}} , $$

(xii)

$$ \left( {r_{3} } \right)_{{j - \frac{1}{2}}} = v_{j - 1} - v_{j} + h_{j} w_{{j - \frac{1}{2}}} , $$

( xiii)

$$ \left( {r_{4} } \right)_{{j - \frac{1}{2}}} = g_{j - 1} - g_{j} + h_{j} p_{{j - \frac{1}{2}}} , $$

( xiv)

$$ \left( {r_{5} } \right)_{{j - \frac{1}{2}}} = \theta_{j - 1} - \theta_{j} + h_{j} q_{{j - \frac{1}{2}}} , $$

$$ \begin{aligned} \left( {r_{6} } \right)_{{j - \frac{1}{2}}} & = M_{{{{j}} - \frac{1}{2}}}^{{{{i}} - 1}} - \left\{ {(w_{j} - w_{j - 1} )h_{j}^{ - 1} + A_{1} w_{{j - \frac{1}{2}}} + A_{2} v_{{j - \frac{1}{2}}} + A_{3} u_{{j - \frac{1}{2}}} + A_{4} (fw)_{{j - \frac{1}{2}}} + A_{5} (fv)_{{j - \frac{1}{2}}} } \right. \\ & \quad \left. { + A_{6} (fu)_{{j - \frac{1}{2}}} + A_{7} u_{{j - \frac{1}{2}}}^{2} + A_{8} (uv)_{{j - \frac{1}{2}}} + A_{9} \left( {p_{j} - p_{j - 1} } \right)h_{j} + A_{10} p_{{j - \frac{1}{2}}} + A_{11} q_{{j - \frac{1}{2}}} } \right\}, \\ \end{aligned} $$

(xv)

$$ \left( {r_{7} } \right)_{{j - \frac{1}{2}}} = N_{{{{j}} - \frac{1}{2}}}^{{{{i}} - 1}} - \left\{ {\left( {p_{j} - p_{j - 1 } } \right)h_{j} + B_{1} p_{{j - \frac{1}{2}}} + B_{2} g_{{j - \frac{1}{2}}} + B_{3} v_{{j - \frac{1}{2}}} + B_{4} u_{{j - \frac{1}{2}}} + B_{5} (fp)_{{j - \frac{1}{2}}} + B_{6} (ug)_{{j - \frac{1}{2}}} } \right\}, $$

(xvi)

$$ \left( {r_{8} } \right)_{{j - \frac{1}{2}}} = S_{{{{j}} - \frac{1}{2}}}^{{{{i}} - 1}} - \left\{ {\left( {q_{j} - q_{j - 1 } } \right)h_{j} + B_{1} q_{{j - \frac{1}{2}}} + B_{7} (fq)_{{j - \frac{1}{2}}} + B_{8} (u\theta )_{{j - \frac{1}{2}}} + B_{9} v_{{j - \frac{1}{2}}}^{2} + B_{10} uv_{{j - \frac{1}{2}}} + B_{11} u_{{j - \frac{1}{2}}}^{2} + B_{11} u_{{j - \frac{1}{2}}}^{2} + B_{12} (\theta )_{{j - \frac{1}{2}}} } \right\}, $$

(xvii)

where the coefficients are mathematically addressed as

$$ \left( {\alpha_{1} } \right)_{j} = \left( {\alpha_{2} } \right)_{j} = \frac{{A_{2} }}{2} + \frac{{A_{5} }}{2}f_{{j - \frac{1}{2}}} + \frac{{A_{8} }}{2}u_{{j - \frac{1}{2}}} , $$

$$ \left( {\alpha_{3} } \right)_{j} = \left( {\alpha_{4} } \right)_{j} = \frac{{A_{4} }}{2}w_{{j - \frac{1}{2}}} + \frac{{A_{5} }}{2}v_{{j - \frac{1}{2}}} + \frac{{A_{6} }}{2}u_{{j - \frac{1}{2}}} , $$

$$ \left( {\alpha_{5} } \right)_{j} = \left( {\alpha_{6} } \right)_{j} = \frac{{A_{3} }}{2} + \frac{{A_{6} }}{2}f_{{j - \frac{1}{2}}} + A_{7} u_{{j - \frac{1}{2}}} + \frac{{A_{8} }}{2}v_{{j - \frac{1}{2}}} , $$

$$ \left( {\alpha_{7} } \right)_{j} = \frac{1}{{h_{j} }} + \frac{1}{2}A_{1} + \frac{1}{2}A_{4} f_{{j - \frac{1}{2}}} , $$

$$ \left( {\alpha_{8} } \right)_{j} = - \frac{1}{{h_{j} }} + \frac{1}{2}A_{1} + \frac{1}{2}A_{4} f_{{j - \frac{1}{2}}} , $$

$$ \left( {\alpha_{9} } \right)_{j} = \frac{{A_{9} }}{{h_{j} }} + \frac{{A_{10} }}{2} ,\;\left( {\alpha_{10} } \right)_{j} = - \frac{{A_{9} }}{{h_{j} }} + \frac{{A_{10} }}{2}, $$

$$ \left( {\alpha_{11} } \right)_{j} = \left( {\alpha_{12} } \right)_{j} = A_{11} ,\; \left( {\alpha_{21} } \right)_{j} = \left( {\alpha_{22} } \right)_{j} = \frac{{B_{5} }}{2}p_{{j - \frac{1}{2}}} ,\;\left( {\alpha_{23} } \right)_{j} = \left( {\alpha_{24} } \right)_{j} = \frac{{B_{4} }}{4} + \frac{{B_{6} }}{2}g_{{j - \frac{1}{2}}} , $$

$$ \left( {\alpha_{25} } \right)_{j} = \left( {\alpha_{26} } \right)_{j} = \frac{{B_{2} }}{2} + \frac{{B_{6} }}{2}u_{{j - \frac{1}{2}}} , \left( {\alpha_{27} } \right)_{j} = \left( {\alpha_{28} } \right)_{j} = \frac{{B_{3} }}{2}, $$

$$ \left( {\alpha_{29} } \right)_{j} = \frac{1}{{h_{j} }} + \frac{{B_{1} }}{2} + \frac{{B_{5} }}{2}f_{{j - \frac{1}{2}}} ,\;\left( {\alpha_{30} } \right)_{j} = - \frac{1}{{h_{j} }} + \frac{{B_{1} }}{2} + \frac{{B_{5} }}{2}f_{{j - \frac{1}{2}}} , $$

$$ \left( {\alpha_{31} } \right)_{j} = \left( {\alpha_{32} } \right)_{j} = \frac{{B_{7} }}{2}q_{{j - \frac{1}{2}}} ,\;\left( {\alpha_{33} } \right)_{j} = \left( {\alpha_{34} } \right)_{j} = \frac{{B_{8} }}{2}\theta_{{j - \frac{1}{2}}} + \frac{{B_{10} }}{2}v_{{j - \frac{1}{2}}} + B_{11} u_{{j - \frac{1}{2}}} , $$

$$ \left( {\alpha_{35} } \right)_{j} = \left( {\alpha_{36} } \right)_{j} = \frac{{B_{8} }}{2}u_{{j - \frac{1}{2}}} ,\;\left( {\alpha_{37} } \right)_{j} = \left( {\alpha_{38} } \right)_{j} = \frac{{B_{9} }}{2}v_{{j - \frac{1}{2} }} + \frac{{B_{10} }}{2}u_{{j - \frac{1}{2}}} , $$

$$ \left( {\alpha_{39} } \right)_{j} = \frac{1}{{h_{j} }} + \frac{{B_{1} }}{2} + \frac{{B_{7} }}{2}f_{{j - \frac{1}{2}}} ,\;\left( {\alpha_{40} } \right)_{j} = - \frac{1}{{h_{j} }} + \frac{{B_{1} }}{2} + \frac{{B_{7} }}{2}f_{{j - \frac{1}{2}}} , $$

$$ \left( {\alpha_{41} } \right)_{j} = A_{11} (u)_{{j - \frac{1}{2}}} , \; \left( {\alpha_{42} } \right)_{j} = - (u)_{{j - \frac{1}{2}}} B_{11} $$

$$ \left( {\alpha_{43} } \right)_{j} = B_{12} (\theta )_{{j - \frac{1}{2}}} ,\;\left( {\alpha_{44} } \right)_{j} = - B_{12} (\theta )_{{j - \frac{1}{2}}} $$