Introduction

A nanofluid is a combination of nanoparticles that affects the base fluid’s specific heat, viscosity, and mass permeability. Choi and Eastman (1995) coined the term “nanofluid” to refer to a liquid containing solid particles smaller than 50 nm. Nanofluids have been a popular study topic due to their remarkable thermal characteristics. Nanoparticles are used to cool a wide range of electronics, including welding equipment, high-flux devices, cookers, and light emitting diodes. In recent decades, companies have formed to explore fluid mechanics at the nano and microscale levels. Chakraborty and Panigrahi (2020) investigated the uniformity of nanofluids. Nisar et al. (2020) used the Eyring–Powell model to investigate the role of activation energy in the radiating peristaltic flow of nanofluid. Uddin et al. (2015) investigated the effects of slippage on nanofluid flow across a sheet. Hassan et al. (2018) looked at the features of convection across a wave layer in nanofluid flow. Cui et al. (2022a) studied the thermal properties of nanofluid flow with radiative effects on an inclined stretching surface. Their research dives into the complex dynamics of this particular fluid flow condition, including a thorough examination of the accompanying thermal properties. Zohra et al. (2020) investigated the complicated dynamics of MHD bioconvective slip flow with Stefan blowing impacts on a spinning disk, focusing on the role of nanofluid in their study. Amirsom et al. (2019) investigated the properties of 3-D bioconvection nanofluid flow originating from a biaxial stretched sheet, with a particular emphasis on the role of anisotropic slip in their study. Cui et al. (2022b) investigated the effects of non-similar modeling in their study of forced convection evaluation of nanofluid flow across a stretched sheet. The study looked primarily at the effects of chemical reactions and the generation of heat in this environment. Amjad et al. (2022) investigated the numerical solution for nanofluid flow with magnetic Williamson features on an exponentially extending permeable surface. The study took into account temperature-dependent stiffness and thermal conductivity as well. Khan (2023) investigated the motion of gyrotactic microbes in the setting of altered Eyring–Powell nanofluid flow, including biological convection and nonlinear radiation in their research. Amjad et al. (2023) investigated the numerical behavior of MHD tangent hyperbolic nanofluid flow across an exponentially stretched sheet.

“Bioconvection” refers to fluid convection caused by density fluctuations caused by the joint buoyancy of floating microorganisms. The investigation of bioconvection in nanofluids is beneficial to the development of microfluidic devices. Bioconvection can increase mass transport and blend in microvolumes, making it possible to construct stable nanofluid suspensions. It is used extensively in a variety of domains, including biotechnology, computation in biology, biomechanics, and biological processes. Platt (1961) described bioconvection phenomena in cultures containing self-swimming animals. Hillsdon and Pedley (1996) devised a bioconvection system based on gyrotactic bacterial emulsion. Mutuku and Makinde (2014) investigated hydromagnetic nanofluids and oxytactic microorganisms using a stretchy surface. Researchers (Sheremet et al. 2019; Mansour et al. 2019) investigated (MHD) bioconvection in a square container filled with nanofluids. Nagantran et al. (2021) investigated the heat transmission and bioconvective motion of micropolar fluids in a permeable media. Patil et al. (2023) investigated the flow properties of magnetic bioconvective micropolar nanofluid across a wedge, with a particular emphasis on the role of oxytactic microorganisms. Alqurashi et al. (2023) investigated how melting heat influences the bioconvection movement of micropolar nanofluids over an oscillatory surface. Farooq et al. (2023) conducted a detailed, non-similar investigation of the flow properties of a chemically reactive bioconvective Casson nanofluid across an inclined stretching surface. Arain et al. (2020) investigated the flow structure between two revolving circular plates containing a combination of nanoparticles and gyrotactic bacteria. Farooq and Liu (2023) performed a thorough investigation, concentrating on the distinct study of MHD bioconvective nanofluid flow across a stretched surface. Notably, their work took into account the impact of temperature-dependent viscosity, which added substantial insight to this complex area of research. Waqas et al. (2022) investigated the thermal-convectional movement of magneto-Casson nanofluid via a wedge, taking into account parameters such as microbes that move and the conductivity of heat. Jawad et al. (2021a) investigated the dynamics of MHD bioconvection in Darcy–Forchheimer flow, using Casson nanofluid over a rotating disk and emphasizing entropy optimization. Siddiqui et al. (2021) investigated the bioconvection movement of Casson nanofluid under Darcy–Forchheimer conditions, powered by a spinning and expanding disk. The study also included heat radiation and investigated entropy development in the system. Jawad et al. (2021b) investigated the MHD Darcy–Forchheimer flow of Casson nanofluid induced by a spinning disk. The study took into account thermal radiation and Arrhenius activation energy. Wang and colleagues (2022) performed a numerical simulation to study the hybrid flow of Casson nanofluid in the presence of a magnetic dipole and microorganisms. Wang et al. (2021) studied the erratic thermal transfer of Casson nanofluids flow using the Prabhakar-type modified Mittag–Leffler kernel in their work. Fuzhang et al. (2022) investigated an unstable micropolar nanofluid model across an exponentially extending curved surface, including chemical reactions in their study. Eringen (1966) investigated the theory of micropolar fluids, offering a thorough investigation that adds significant insights to our knowledge of their underlying principles and behaviors.

Micropolar fluid has gained extensive popularity due to its versatile use across various engineering sectors and manufacturing. Eringen (1972) emphasized and expanded on the applications of the micropolar theory to draw numerous researcher’s focus to the micropolar fluids. Patel et al. (2024) conducted a detailed investigation to show how a magnetic field affects the mixing of micropolar nanofluids in inconsistent heat sources and sinks. Studying the micropolar fluid, Soundalgekar and Takhar (1983) discovered that the micro-rotation distribution improves as the coupling constant’s values increase. Motsa and Shateyi (2012) investigated the magnetohydrodynamic micropolar fluid involving a chemical process, Hall ion-slip current, and temperature gradient by taking into account the porous stretching sheet. It was determined that the fluid velocity improves with gradually rising Hall current values. Hsiao (2017) addressed the problem of magnetohydrodynamic (MHD) nanofluid flow near a stretching sheet, taking into account the impacts of viscosity, and he discovered that the heat transfer rate improved as the Prandtl, and Eckert numbers raised. The effects of ferromagnetic and ferrimagnetic past over an extended surface were examined by Ali et al. (2020a). Awati et al. (2024) examined the use of spectral and Haar wavelet collocation methods to address the production of heat and viscous dissipation in micro-polar nanofluids in the context of MHD stagnation point flow. They used a magnetic dipole in conjunction with base fluids made of ethylene glycol and water. Ali et al. (2020b) investigated the effect of several magnetic nanoparticles on heat transmission processes over a stretched sheet while accounting for thermal stratification and slide effects. Aslani et al. (2020) investigated the micropolar Couette flow structure in the presence of magnetic fields. Mishra et al. (2019) used micropolar fluids and porous media to investigate the influence of magnetohydrodynamic (MHD) outflow. Furthermore, Aslani et al. (2021) examined the radiation impacts on micropolar fluids with mass flow. Ramadevi et al. (2020) calculated the free convective flow of a micropolar fluid. Ismail et al. (2020) investigated the MHD flow and heat exchange of a micropolar fluid within a rectangular duct, taking into account the effects of a generated magnetic field and slip boundaries. Patel et al. (2019) investigated the MHD flow of a micropolar nanofluid across a stretching/shrinking sheet while accounting for radiation effects. Turkyilmazoglu (2017) researched and found accurate solutions for the combined convection flow of MHD micropolar fluid induced by a permeable heated/cooled flexible plate.

The impacts of Soret and Dufour were thought to be insignificant in all of these investigations. The connection between fluid flows and driving forces can exhibit a more intricate structure when both heat and mass transfer simultaneously take place within the flowing fluid. In addition to temperature gradients, composition gradients can also produce an energy flux. The Dufour effect, also referred to as the diffusion-thermoeffect, results from an energy flux caused by a concentration gradient. However, the Soret or thermal-diffusion effect also exemplifies how mass flow rate can be produced by thermal gradients. These effects are taken into account in situations where density variations manifest within the fluid flow. In situations where particles are added to a liquid region that has a density lower than the adjacent liquid, both the Soret effect (thermal diffusion) and Dufour effect (diffuse-thermal) can be influenced. These phenomena play a vital role in the integrated process of heat and mass transfer in binary fluid systems that involve gases of moderate molecular weight. This is especially pertinent in the field of chemical processes engineering. Abreu et al. (2006) have discussed boundary layer flows under forced convection, encompassing Soret and Dufour effects, as well as boundary layer flows under free convection. Khan et al. (2023) investigated the complex interaction between heat and mass transportation in a bio-convective reactive flow of nanoparticles. Notably, their research encompassed the subtle qualities of Soret and Dufour, providing new insights into this complicated field of study. Ahmed et al. (2023) thoroughly examined the ramifications of the Soret-Dufour theory, focusing on its function in controlling energy transmission through the bioconvective movement of Maxwell fluid. Bég et al. (2009) used a shooting process in combination with the local non-similarity technique to study heat and mass transport from an inclined surface by mixed convection. This research has practical implications for solar thermal systems. Bhargava et al. (2009) investigated oscillatory MHD heat and mass transmission while accounting for the effects of Soret and Dufour impacts. The study of steady, incompressible non-Newtonian nanofluid circulation across an expanded surface was prompted by the expanding use of non-Newtonian nanofluids in a variety of medical and industrial applications.

Our research focuses on producing one-of-a-kind transformations that address the intricacies of a given situation, notably nanofluid flows and pressure ulcer concerns. The purpose of these changes is to provide accurate and efficient results that will provide useful insights for future studies in this sector. We hope to improve our understanding of the fluid dynamics and thermal factors involved in pressure ulcer development, which will guide advances in preventative and therapeutic measures in the biomedical devices and biomechanics domains. We use the micropolar nanofluid model to evaluate fluid flow, with blood as the main fluid and silver and copper oxide nanoparticles added. The nanofluid model, which takes into account heat production, Soret and Dufour effects, and viscous heating, adheres to Tiwari and Das’ framework (2007). We modify the control system into a non-similar configuration using suitable transformations. MATLAB’s numerical solver (bvp4c) is then used with the local non-similarity approach (LNS) (Minkowycz and Sparrow 1978). Our paper addresses a real-world problem by focusing on how to properly manage non-similar words that arise as a result of similarity transformation. The non-dimensionalization procedure, which uses non-similarity transformations, is based on physics and accountability. According to our literature assessment, our key contribution is to investigate bioconvective MHD micropolar nanofluid on a stretched surface under the impact of Soret and Dufour effects, a topic that has not been investigated previously. Graphical analysis is used to extensively study the impact of dimensionless growth elements on velocity, microrotation, energy, concentration, and microorganism profiles. Furthermore, our research thoroughly investigates the effects of numerous dimensionless factors on both the surface resistance coefficient and thermal characteristics.

Convection differential system flow

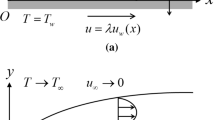
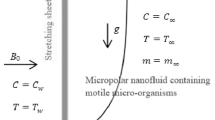
Consider the steady 2-D flow of an incompressible bioconvective micropolar nanofluid, accounting for Soret and Dufour effects. Silver \({\text{Ag}}\) and copper oxide \({\text{CuO}}\) are spread on a stretched sheet inside the base liquid (blood). The stretched fluid velocity \({U}_{w},\) is found on the stretching surface. There is no surrounding velocity, and the ambient temperature inside the boundary layer is equal to \({T}_{\infty }\). The fluid temperature is represented by \(T,\) the concentration of nanoparticles by \(C,\) and the spread of microorganisms by \(n\). The magnetic effect \({B}_{o}\) acts transversely to the fluid flow, resulting in an angle \(\alpha\) along the \(x-\)axis. Furthermore, the analysis considers an array of elements, including heat generation, the Soret and Dufour impacts, and viscous dissipation. Applying the boundary layer and Boussinesq hypotheses, the basic conservation equations for mass, momentum, microrotation, energy, concentration, and microorganisms are given as follows, as cited in Bég et al. (2011); Ahmad et al. 2023). The schematic model depicted in Fig. 1 provides a visual representation of the system.

Fig. 1
figure 1

Physical model and flow configuration

Full size image
$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$
(1)
$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\left(\frac{{\mu }_{nf}+k}{{\rho }_{nf}}\right)\frac{{\partial }^{2}u}{\partial {y}^{2}}-\frac{k}{{\rho }_{nf}}\frac{\partial N}{\partial y}-\frac{{\sigma }_{nf}{B}_{o}^{2}u}{{\rho }_{nf}}{{\text{sin}}}^{2}\left(\alpha \right),$$
(2)
$$u\frac{\partial N}{\partial x}+v\frac{\partial N}{\partial y}=\frac{{\gamma }_{nf}}{j{\rho }_{nf}}\frac{{\partial }^{2}N}{\partial {y}^{2}}-\frac{k}{j{\rho }_{nf}}\left(2N+\frac{\partial u}{\partial y}\right),$$
(3)
$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{{k}_{nf}}{{\left(\rho {C}_{p}\right)}_{nf}}\frac{{\partial }^{2}T}{\partial {y}^{2}}+\left(\frac{{\mu }_{nf}+k}{{\left(\rho {C}_{p}\right)}_{nf}}\right){\left(\frac{\partial u}{\partial y}\right)}^{2}+\frac{{Q}_{o}}{{\left(\rho {C}_{p}\right)}_{nf}}\left(T-{T}_{\infty }\right)+\frac{{D}_{m}{K}_{T}}{{\left(\rho {C}_{p}\right)}_{nf}{C}_{s}}\left({T}_{w}-{T}_{\infty }\right),$$
(4)
$$u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}={D}_{m}\frac{{\partial }^{2}C}{\partial {y}^{2}}-{K}_{o}\left(C-{C}_{\infty }\right)+\frac{{D}_{m}}{{T}_{m}}{K}_{T}\frac{{\partial }^{2}T}{\partial {y}^{2}},$$
(5)
$$u\frac{\partial n}{\partial x}+v\frac{\partial n}{\partial y}={D}_{m}\frac{{\partial }^{2}n}{{\partial y}^{2}}+\frac{b{W}_{c}}{\left({C}_{w}-{C}_{\infty }\right)}\left(\frac{\partial }{\partial y}\left(n\frac{\partial C}{\partial y}\right)\right).$$
(6)

Here, the velocity indices in the \(x\) and \(y-\) directions are represented by \(u\) and \(v\), respectively. \(k,N,{B}_{o},{C}_{p},\gamma ,j,\sigma ,{Q}_{o},{D}_{m},{K}_{T},{C}_{s},{K}_{o},{T}_{m},b,\) and \(n\), is the micro-rotation viscosity, micro-rotation vector, strength of magnetic field, specific heat, spin gradient, electrical conductivity, mass diffusion rate, rate of heat generation or absorption, thermal diffusion coefficient, susceptibility to concentration changes, the chemical response rate constant, the average temperature of the fluid, the chemotaxis rate constant, and the concentration of microorganisms.\({C}_{w},{n}_{w},{T}_{\infty },{C}_{\infty },\) and \({n}_{w}\) represent the nanoparticle concentration, microorganism concentration, free stream temperature, nanoparticle compactness, and microorganism concentration, respectively at the surface. The relevant boundary conditions are given in Ahmad et al. (2023); Waqas et al. 2016).

$$\begin{gathered} u = U_{w} = ax,\;v = v_{w} = 0, N = - n\frac{\partial u}{{\partial y}}, - k_{nf} \frac{\partial T}{{\partial y}} = h_{f} \left( {T - T_{\infty } } \right), C = C_{w} ,n = n_{w} , \;at\; y = 0, \hfill \\ u \to 0,N \to 0,{ }T \to T_{\infty } ,{ }C \to C_{\infty } ,{ }n \to n_{\infty } ,\;{\text{at}}\;\;y \to \infty { } \hfill \\ \end{gathered}$$
(7)

Establishing a non-similar flow by adding a new term, \(\xi (x)\) and \(\eta (x,y)\).

$$\begin{aligned} & \xi = \frac{x}{l},{ }\eta = \sqrt {\frac{c}{{\upsilon_{f} }}} y,{ }u = cx\frac{{\partial f\left( {\xi ,\eta } \right)}}{\partial \eta },{ }v = - \sqrt {\upsilon_{f} c} \left( {\frac{{\partial f\left( {\xi ,\eta } \right)}}{\partial \xi }\xi + f\left( {\xi ,\eta } \right)} \right) \\ & N = cx\sqrt {\frac{c}{{\upsilon_{f} }}} g\left( {\xi ,\eta } \right),{ }\theta \left( {\xi ,\eta } \right) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\varphi \left( {\xi ,\eta } \right) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }},{ }\chi \left( {\xi ,\eta } \right) = \frac{{{\text{n}} - n_{\infty } }}{{n_{w} - n_{\infty } }}, \\ \end{aligned}$$
(8)

By employing Eq. (8), Eq. (1) is fully met following the aforementioned transformation, whereas Eqs. (2) through (6) are transformed as follows:

$$\left( {\frac{{\mu_{nf} }}{{\mu_{f} }} + K} \right)\frac{{\partial^{3} f}}{{\partial \eta^{3} }} - K\frac{\partial g}{{\partial \eta }} - \frac{{\sigma_{nf} }}{{\sigma_{f} }}M\frac{\partial f}{{\partial \eta }}\sin^{2} \left( \alpha \right) - \frac{{\rho_{nf} }}{{\rho_{f} }}\left( {\frac{\partial f}{{\partial \eta }}} \right)^{2} + \frac{{\rho_{nf} }}{{\rho_{f} }}f\frac{{\partial^{2} f}}{{\partial \eta^{2} }} = \frac{{\rho_{nf} }}{{\rho_{f} }}\xi \left( {\frac{\partial f}{{\partial \eta }}\frac{{\partial^{2} f}}{\partial \xi \partial \eta } - \frac{\partial f}{{\partial \xi }}\frac{{\partial^{2} f}}{{\partial \eta^{2} }}} \right),$$
(9)
$$\left( {2\frac{{\mu_{nf} }}{{\mu_{f} }} + K} \right)\frac{{\partial^{2} g}}{{\partial \eta^{2} }} - 2\frac{{\rho_{nf} }}{{\rho_{f} }}\left( {g\frac{\partial f}{{\partial \eta }} - f\frac{\partial g}{{\partial \eta }}} \right) + 2\delta_{B} \left( {2g + \frac{{\partial^{2} f}}{{\partial \eta^{2} }}} \right) = \xi \left( {\frac{\partial f}{{\partial \eta }}\frac{\partial g}{{\partial \xi }} - \frac{\partial f}{{\partial \xi }}\frac{\partial g}{{\partial \eta }}} \right),$$
(10)
$$\frac{{k_{nf} }}{{k_{f} }}\frac{{\partial^{2} \theta }}{{\partial \eta^{2} }} + \Pr \left( {\xi^{2} \left( {\frac{{\mu_{nf} }}{{\mu_{f} }} + K} \right)Ec\left( {\frac{{\partial^{2} f}}{{\partial \eta^{2} }}} \right)^{2} + Q\theta + {\text{Du}}\frac{{\partial^{2} \phi }}{{\partial \eta^{2} }} + \frac{{\left( {\rho C_{p} } \right)_{nf} }}{{\left( {\rho C_{p} } \right)_{f} }}f\frac{\partial \theta }{{\partial \eta }}} \right) = \xi \Pr \left( {\frac{\partial f}{{\partial \eta }}\frac{\partial \theta }{{\partial \xi }} - \frac{\partial f}{{\partial \xi }}\frac{\partial \theta }{{\partial \eta }}} \right),$$
(11)
$$\frac{{\partial^{2} \varphi }}{{\partial \eta^{2} }} + S_{{\text{c}}} \left( {f\frac{\partial \varphi }{{\partial \eta }} - K_{r} \varphi + S_{{\text{r}}} \frac{{\partial^{2} \theta }}{{\partial \eta^{2} }}} \right) = \xi S_{{\text{c}}} \left( {\frac{\partial f}{{\partial \eta }}\frac{\partial \varphi }{{\partial \xi }} - \frac{\partial f}{{\partial \xi }}\frac{\partial \varphi }{{\partial \eta }}} \right),$$
(12)
$$\frac{{\partial^{2} \chi }}{{\partial \eta^{2} }} + {\text{Pe}}\left( {\frac{{\partial^{2} \varphi }}{{\partial \eta^{2} }}\left( {\chi + \delta_{1} } \right) + \frac{\partial \chi }{{\partial \eta }}\frac{\partial \varphi }{{\partial \eta }}} \right) + f{\text{Le}}\frac{\partial \chi }{{\partial \eta }} = \xi {\text{Le}}\left( {\frac{\partial f}{{\partial \eta }}\frac{\partial \chi }{{\partial \xi }} - \frac{\partial f}{{\partial \xi }}\frac{\partial \chi }{{\partial \eta }}} \right).$$
(13)

The related boundary conditions are outlined below,

$$\begin{aligned} & {\text{at}}\;\;\eta = 0,{ }\frac{\partial f}{{\partial \eta }}\left( {\xi ,0} \right) = 1,f\left( {\xi ,0} \right) + \xi \frac{\partial f}{{\partial \xi }}\left( {\xi ,0} \right) = 0,g\left( {\xi ,0} \right) = - n\frac{{\partial^{2} f}}{{\partial \eta^{2} }}\left( {\xi ,0} \right), \\ & \frac{{k_{nf} }}{{k_{f} }}\frac{\partial \theta }{{\partial \eta }}\left( {\xi ,0} \right) = B_{i} \left( {1 - \theta } \right),\varphi \left( {\xi ,0} \right) = 1,\chi \left( {\xi ,0} \right) = 1, \\ & {\text{as }}\eta \to \infty ,\frac{\partial f}{{\partial \eta }}\left( {\xi ,{ }\infty } \right) \to 0, g\left( {\xi ,\infty } \right) \to 0, \;\theta \left( {\xi ,\infty } \right) = 0, \varphi \left( {\xi ,\infty } \right) \to 0,{ }\chi \left( {\xi ,\infty } \right) \to 0. \\ \end{aligned}$$
(14)

The parameters utilized in Eqs. (9) to (13) are specified as:

$$\begin{aligned} K = & \frac{k}{{\mu_{f} }}, M = \frac{{\sigma B_{0}^{2} }}{{c\rho_{f} }},\delta_{B} = \frac{k}{{jc\rho_{f} }},\Pr = \frac{{\nu_{f} \left( {\rho C_{p} } \right)_{f} }}{{k_{f} }},Ec = \frac{{a^{2} l^{2} }}{{\left( {c_{p} } \right)_{f} \left( {T_{w} - T_{\infty } } \right)}},Q = \frac{{Q_{0} }}{{c(\rho C_{Pf} }}, \\ {\text{Du}} = & \frac{{D_{m} K_{T} \left( {C_{w} - C_{\infty } } \right)}}{{\nu C_{s} \left( {\rho C_{p} } \right)_{f} \left( {T_{w} - T_{\infty } } \right)}},S_{{\text{c}}} = \frac{\nu }{{D_{m} }},S_{{\text{r}}} = \frac{{D_{m} K_{T} }}{{\nu T_{m} }}\frac{{T_{w} - T_{\infty } }}{{C_{w} - C_{\infty } }},{\text{Pe}} = \frac{{bW_{c} }}{{D_{m} }},\delta_{1} = \frac{{n_{\infty } }}{{n_{w} - n_{\infty } }}, \;{\text{and}}\;{\text{Le}} = \frac{\nu }{{D_{m} }}, \\ \end{aligned}$$

where \(K, {\text{Pr}}, M, {S}_{c}, {\delta }_{B,} Ec, Q,\mathrm{ Du}, {S}_{r}, {\text{Pe}}, {\delta }_{1},\) and \(Le\) are material parameter, Prandlt number, magnetic field parameter, Schmidt number, microorganism parameter, Eckert number, heat source, Dufour effect, Soret number, Peclet number, microorganism difference parameter, and Lewis number.

A list of relevant physical quantities is provided in the (Waqas et al. 2016).

$$\begin{aligned} C_{f} = & \frac{{\tau_{w} }}{{\rho_{f} U^{2}_{W} }},{\text{Nu}} = \frac{{xq_{w} }}{{k_{f} \left( {T_{w} - T_{\infty } } \right)}},\tau_{w} = \left( {\left( {\mu_{nf} + \alpha } \right)\frac{\partial u}{{\partial y}} + \alpha N} \right)_{y = 0} , \\ q_{w} = & \left( {k_{nf} \frac{\partial T}{{\partial y}}} \right)_{y = 0} . \\ \end{aligned}$$
(15)

where \({C}_{f}, {\text{Nu}}, {\tau }_{w},\) and \({q}_{w}\) are the drag coefficient, Nusselt number, surface shear stress, and surface flux. Dimensionless forms of Eq. (15) are.

$${C}_{f}{({{\text{Re}}}_{x})}^\frac{1}{2} = \left(\frac{{\mu }_{nf}}{{\mu }_{f}}+(1-n)K\right)\frac{{\partial }^{2}f}{\partial {\eta }^{2}}\left(\xi ,0\right), {{\text{Nu}}}_{x}({{{\text{Re}}}_{x})}^\frac{1}{2}=\xi \frac{\partial \theta }{\partial \eta }\left(\xi ,0\right).$$
(16)

Local non-similarity method

Suppose that at the first level of truncation, the terms \(\xi <<1\). The right parts of Eqs. (9)–(13) are equal to zero. Thus, the modified system of equations takes the form.

$$\frac{{\rho }_{f}}{{\rho }_{nf}}\left(\left(\frac{{\mu }_{nf}}{{\mu }_{f}}+K\right){f}^{{\prime}{\prime}{\prime}}-{{\text{Kg}}}^{\prime}-\frac{{\sigma }_{nf}}{{\sigma }_{f}}{f}^{\prime}M{{\text{sin}}}^{2}\left(\alpha \right)\right)-{\left({f}^{\prime}\right)}^{2}+f{f}^{{\prime}{\prime}}=0,$$
(17)
$$\left(2\frac{{\mu }_{nf}}{{\mu }_{f}}+K\right){g}^{{\prime}{\prime}}-2\frac{{\rho }_{nf}}{{\rho }_{f}}\left(g{f}^{\prime}-f{g}^{\prime}\right)+2{\delta }_{B}\left(2g+{f}^{{\prime}{\prime}}\right)=0,$$
(18)
$$\frac{{k}_{nf}}{{k}_{f}}{\theta }^{\mathrm{^{\prime}}\mathrm{^{\prime}}}+{\text{Pr}}\left({\xi }^{2}\left(\frac{{\mu }_{nf}}{{\mu }_{f}}+K\right){\text{Ec}}{\left({f}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\right)}^{2}+Q\theta +{\text{Du}}{\phi }^{\mathrm{^{\prime}}\mathrm{^{\prime}}}+\frac{{\left(\rho {C}_{p}\right)}_{nf}}{{\left(\rho {C}_{p}\right)}_{f}}f{\theta }^{\mathrm{^{\prime}}}\right)=0,$$
(19)
$${\varphi }^{{\prime}{\prime}}+{S}_{c}\left(f{\varphi }^{\prime}-{K}_{r}\varphi +{S}_{r}{\theta }^{{\prime}{\prime}}\right)=0,$$
(20)
$${\chi }^{\mathrm{^{\prime}}\mathrm{^{\prime}}}+Pe\left({\varphi }^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(\chi +{\delta }_{1}\right)+{\chi }^{\mathrm{^{\prime}}}{\varphi }^{\mathrm{^{\prime}}}\right)+f{\text{Le}}{\chi }^{\mathrm{^{\prime}}}=0.$$
(21)

Corresponding boundary conditions are:

$$\begin{aligned} & f\left( \eta \right) = 0, f^{\prime}\left( \eta \right) = 1, \frac{{k_{nf} }}{{k_{f} }}\theta^{\prime}\left( \eta \right) = B_{i} \left( {1 - \theta \left( \eta \right)} \right), g\left( \eta \right) = - nf^{\prime\prime}\left( \eta \right),\varphi \left( \eta \right) = 1, \\ & \chi \left( \eta \right) = 1, \;{\text{at}}\; \eta = 0, \\ & f^{\prime}\left( \eta \right) \to 0, g\left( \eta \right) \to 0, \theta \left( \eta \right) \to 0, \theta \left( \eta \right) \to 0, \varphi \left( \eta \right) \to 0, \chi \left( \eta \right) \to 0,\; {\text{as}}\; \eta \to \infty \\ \end{aligned}$$
(22)

To attain a second-order truncation, it is crucial to differentiate Eqs. (9) to (13) with respect to \(\xi\) and introduce new functions.

The relations described below are introduced to reach the second level of truncation:

$$\frac{\partial f}{\partial \xi }=p, \frac{\partial g}{\partial \xi }=q, \frac{\partial \theta }{\partial \xi }=r, \frac{\partial \varphi }{\partial \xi }=s, \frac{\partial \chi }{\partial \xi }=t {\text{and}}\frac{\partial p}{\partial \xi }=\frac{\partial q}{\partial \xi }=\frac{\partial r}{\partial \xi }=\frac{\partial s}{\partial \xi }=\frac{\partial t}{\partial \xi }=0$$
(23)

In light of this, the second iteration of LNS is

$$\left( {\frac{{\mu_{nf} }}{{\mu_{f} }} + K} \right)p^{\prime \prime \prime } \frac{{\rho_{nf} }}{{\rho_{f} }}\left( {3f^{\prime } p^{\prime } - 2pf^{\prime \prime } - fp^{\prime \prime } + \xi \left( {p^{\prime 2} - pp^{\prime } } \right)} \right) + Kq^{\prime } + \frac{{\sigma_{nf} }}{{\sigma_{f} }}Mp^{\prime } \sin^{2} \left( \alpha \right),$$
(24)
$$\left( {2\frac{{\mu_{nf} }}{{\mu_{f} }} + K} \right)q^{\prime\prime} = 2\frac{{\rho_{nf} }}{{\rho_{f} }}\left( {qf^{\prime} - fq^{\prime} + gp^{\prime} - pg^{\prime}} \right) - 2\delta_{B} \left( {2q + p^{\prime\prime}} \right) + \left( {f^{\prime}q - pg^{\prime}} \right) + \xi \left( {p^{\prime}q - pq^{\prime}} \right),$$
(25)
$$\frac{{k_{nf} }}{{k_{f} }}r^{\prime\prime} = \Pr \left( {\left( {f^{\prime}r - p\theta^{\prime}} \right) + \xi \left( {rp^{\prime} - pr^{\prime}} \right) - 2\xi^{2} \left( {\frac{{\mu_{nf} }}{{\mu_{f} }} + Ec} \right)f^{\prime\prime}p^{\prime\prime} - {\text{Qr}} - {\text{Du}}s^{\prime\prime} - \frac{{\left( {\rho C_{p} } \right)_{nf} }}{{\left( {\rho C_{p} } \right)_{f} }}\left( {p\theta^{\prime} + fr^{\prime}} \right)} \right),$$
(26)
$${s}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}={\text{Sc}}\left(\xi \left({p}^{\mathrm{^{\prime}}}s+p{s}^{\mathrm{^{\prime}}}\right)-A\left(p\phi +sf\right)-2p{\phi }^{\mathrm{^{\prime}}}-f{s}^{\mathrm{^{\prime}}}+{f}^{\mathrm{^{\prime}}}s\right),$$
(27)
$${t}^{{\prime}{\prime}}={\text{Le}}\left(p{\chi }^{\prime}+{f}^{\prime}{t}^{\prime}-{f}^{\prime}t+p{\chi }^{\prime}\right)-{\text{Pe}}\left({s}^{{\prime}{\prime}}\left(\chi +{\delta }_{1}\right)+{\phi }^{{\prime}{\prime}}t+{t}{\prime}{\phi }{\prime}+{\chi }{\prime}{s}{\prime}\right).$$
(28)

Associated boundaries are,

At \(\eta =0,\)

$$\begin{aligned} p^{\prime}\left( {\xi ,0} \right) = & 0, p\left( {\xi ,0} \right) = 0, q\left( {\xi ,0} \right) = - np^{\prime\prime}\left( {\xi ,0} \right), \\ s\left( {\xi ,0} \right) = & 0,t\left( {\xi ,0} \right) = 0, \frac{{k_{nf} }}{{k_{f} }}r^{\prime}\left( {\xi ,0} \right) = B_{i} \left( {1 - r\left( {\xi ,0} \right)} \right), \\ \end{aligned}$$
(29)

At \(\eta \to \infty ,\)

$${p}{\prime}\left(\xi ,\infty \right)\to 0, q\left(\xi ,\infty \right)\to 0, r\left(\xi ,\infty \right)\to 0, s\left(\xi ,\infty \right)\to 0, t\left(\xi ,\infty \right)\to 0.$$
(30)

Table 1 and Table 2 lists the nanoparticles and base fluids thermophysical properties.

Table 1 Thermophysical features of nanofluid (Bég et al. 2009)
Full size table
Table 2 Nanoparticles thermophysical properties in the presence of the base fluid
Full size table

The impacts of the dimensionless parameters \(K\) and \(M\) on the local skin friction coefficients are shown in Table 3. It has been found that as \(K\) and \(M\) are increased, the local skin friction coefficient also rises.

Table 3 \({{\text{Re}}}^\frac{1}{2}{C}_{f}\) for \({\text{CuO}}\) and \({\text{Ag}}\) against distinct value of \(K\) and \(M,\) with \({\text{Pr}}=21.\)
Full size table

Table 4 shows the local Nusselt number estimates for distinct \(K, Q,\) and \(Ec\) parameters. The local Nusselt number increases as the estimations of \(K, {\text{and}} Q\) are increase, while decreased by enhancing values of \(Ec\).

Table 4 \({{\text{Re}}}^\frac{1}{2}{\text{Nu}}\) for \({\text{CuO}}\) and \({\text{Ag}}\) via distinct values of \(K, Q,\) and \({\text{Ec}}\), with \({\text{Pr}}=21.\)
Full size table

Table 5 presents a comparison between the findings of the current study and those reported in existing literature.

Table 5 Comparison of \(-{\theta }{\prime}(0)\) with distinct values of \({\text{Pr}}\) when \(Q={\text{Ec}}=M={K}_{r}={\text{Du}}={S}_{{\text{c}}}={S}_{{\text{r}}}=0,\) and \(\xi =0.3\)
Full size table

Findings and discussion

Graphs have been generated to elucidate the physical interpretation of this section, demonstrating the behavior of various dimensionless physical parameters concerning velocity, microrotation, temperature, concentration, and microorganism profiles. Every graph provides a contrast between two nanofluids, \({\text{CuO}}\) + blood and \({\text{Ag}}\) + blood.

Figure 2 depicts the impact of material parameters \((K)\) on the velocity profile. An increase correlates to a fall in the velocity profile, indicating that the fluid speed has decreased. This complicated connection is attributable to the interplay of rotating degrees of freedom inside a micropolar fluid, particularly when exposed to an inclinational magnetic field. The inclined magnetic field causes directional variations that influence the alignment and intensity of magnetic forces acting on the micropolar nanofluid. The increased rotational degrees of freedom associated with rising \(K\) values interact with the inclined magnetic field, resulting in a subtle change in fluid dynamics. The magnetic field’s influence, along with an increase in fluid flow resistance. As a result, the combined interaction of \(K\) and the inclined magnetic field results in a reduced velocity profile, affording full insights into the subtle processes governing the behavior of micropolar Fig. 3 shows how \(K\) influences the micro-rotation profile. As kk grows, the fluid becomes more resistant to compression, allowing it to hold its form more effectively. This higher fluid stiffness may result in an increased micro-rotation profile, suggesting that fluid particles spin more as they move through the system. It is critical to understand that the influence on the micro-rotation profile is linked to other parameters such as fluid thickness and system geometry.

Fig. 2
figure 2

Variation in the velocity profile for \(K,\) when \(\alpha ={60}^{^\circ }\)

Full size image
Fig. 3
figure 3

Variation in the micro-rotation profile for \(K\)

Full size image

The impact of the magnetic field is combined with a rise in fluid flow impedance. As a result, the combined interaction of \(K\) with the inclined magnetic field results in a decreased velocity profile, offering comprehensive insights into the intricate mechanisms driving the behavior of micropolar. Figure 3 illustrates how \(K\) affects the micro-rotation profile. As \(K\) increases, the fluid becomes more resistant to compression, allowing it to better maintain its shape. This higher fluid stiffness may cause a change in the micro-rotation profile, implying that fluid particles spin more as they pass through the system. It is crucial to note that the micro-rotation profile is influenced by other characteristics such as fluid thickness and system geometry. Understanding this dynamic is critical since variations in \(K\) can have a variety of implications on fluid behavior. This knowledge enables us to comprehend changes in the micro-rotation profile and serves as a foundation for investigating the larger dynamics of fluid mechanics. Figure 4 shows that when the material parameter increases, so does the temperature profile. This relationship is due to the nature of the bio-convective micropolar fluid, which experiences quicker flow as the material parameter value increases. The higher fluid speed caused by the rising parameter value helps to a better temperature profile. This implies that when the micropolar fluid experiences more rotational motion and bio-convection, it produces more kinetic energy, allowing for more effective heat transmission. Consequently, the system’s temperature profile improves with greater material parameter values. Importantly, this connection reveals the complicated dynamics inside the bio-convective micropolar fluid and gives vital insights into how changes in material parameters impact the system's thermal properties.

Fig. 4
figure 4

Variation in the temperature profile for \(K\)

Full size image

By increasing the value of the magnetic field parameter \((M)\), the velocity profile increases. In the examination of an inclined \((M)\), Fig. 5 gains significance by unraveling the intricate dynamics of bioconvective micropolar fluids. This particular fluid system, characterized by a blend of biological elements and micropolar attributes, undergoes notable changes when exposed to \(M\), especially those with an inclined orientation. The study underscores the complex interplay between the fluid’s velocity profile and the spatial orientation of the magnetic field, offering a more comprehensive perspective on the underlying dynamics. Figure 5, functioning as a visual tool, vividly illustrates this complex interplay. It shows how adjustments in \(M\) strength within an inclined configuration lead to distinct shifts in the velocity profile.

Fig. 5
figure 5

Variation in the velocity profile for \(M,\) when \(\alpha ={60}^{^\circ }\)

Full size image

By raising the value of the magnetic field parameter \((M)\), the velocity profile rises. Figure 5 is significant in the investigation of an inclination because it reveals the complicated dynamics of bioconvective micropolar fluids. This fluid system, which is characterized by a combination of biological components and micropolar properties, alters significantly when subjected to, particularly those with an inclined orientation. The work emphasizes the complicated interplay between the fluid's velocity profile and the spatial direction of the magnetic field, providing a more complete understanding of the underlying dynamics. Figure 5, which serves as a visual aid, vividly depicts this complicated interaction. It demonstrates how changes in strength within an inclined design cause unique modifications in the velocity profile. Fluid speed fluctuations across distinct spatial sites are controlled not just by changes in magnetic field intensity, but also by the magnetic field’s spatial inclination. This element of the study emphasizes the need to address \(M\) orientation while studying the behavior of bioconvective micropolar fluids. Essentially, the findings underscore the need to widen our understanding of fluid dynamics by investigating the impact of magnetic fields in other directions. By providing light on the complicated link between inclined magnetic fields and the velocity distribution of bioconvective micropolar fluids, this study provides a deeper awareness of how magnetic forces impact the changing behavior of these complicated fluid systems.

Figures 6, 7 and 8 an show the impacts of \({\text{Ec}}, Q,\) and \({\text{Du}}\) on the temperature profile. In bioconvective micropolar fluid flow, changes in the Eckert number \(({\text{Ec}})\) and heat source \((Q)\) have a significant impact on the system’s behavior. The Eckert number, a dimensionless quantity that describes the connection between a fluid’s thermal diffusivity and viscosity, is an important factor. An increase in the Eckert number, as shown in Fig. 6, indicates an improvement in the fluid’s heat conduction capabilities, meaning greater efficiency in heat transmission within the system. Concurrently, as seen in Fig. 7, the heat source \((Q)\) is critical for estimating the fluid’s temperature. An increase in the heat source adds energy to the fluid, resulting in a greater temperature profile. When both the \({\text{Ec}}\) and the \(Q\) increase at the same time, the greater heat conduction capabilities of the higher Ec combine with the increased energy input of the higher \(Q\). This combined impact promotes more effective heat transmission, resulting in a lower overall temperature profile inside the bioconvective micropolar fluid. Essentially, the combination of a higher Eckert number and a higher heat source generates an environment in which the fluid’s heat-conducting capacity is improved, resulting in a more effective heat transfer process and a consequent drop in the temperature profile across the fluid. As a result, the heat transmission mechanism improves, and temperature differences in the fluid are reduced. In contrast, as the Dufour effect \(({\text{Du}})\) increases, significant changes occur inside the system, as seen in Fig. 8. The temperature differential becomes more acute, and particle movement accelerates. This increased particle activity raises the temperature profile of the fluid. The technique includes particles moving to higher-temperature locations, transmitting heat and generating an overall temperature increase in those places. Furthermore, the intensity of the temperature gradient has a significant influence on the fluid’s stability.

Fig. 6
figure 6

Variation in the temperature profile for \({\text{Ec}}\)

Full size image
Fig. 7
figure 7

Variation in the temperature profile for \(Q\)

Full size image
Fig. 8
figure 8

Variation in the temperature profile for \({\text{Du}}\)

Full size image

As the gradient gets more prominent, the fluid’s stability decreases, resulting in more obvious convective patterns. As a result, heat is transferred more effectively from the bottom to the top of the liquid, resulting in a higher temperature profile throughout the fluid. To summarize, an augmentation in the triggers a cascade of processes in which larger temperature gradients, enhanced particle movement, and better convective patterns all lead to an elevated temperature profile inside the fluid.

Figures 9 and 10 show how \({\text{Sc}}\) and \({\text{Sr}}\) alter the concentration profile. When the Schmidt number \(({\text{Sc}})\) grows, the rate of molecular diffusion increases, causing dramatic changes in the fluid’s concentration profile. This modification makes the concentration profile more visible, resulting in a more intense and evenly dispersed pattern as solute diffusion becomes more prominent. Increased molecular diffusion promotes a more effective mixing of solutes within the fluid, resulting in a changed concentration profile with heightened steepness and uniform distribution. An increase in the Soret effect \(({\text{Sr}})\), as seen in Fig. 10, reduces the concentration profile. This event can be related to increased \({\text{Sr}},\) which causes particles to migrate to places with greater temperatures. In the case of a bioconvective micropolar fluid containing temperature-sensitive microorganisms, the increased Soret effect causes these microorganisms to travel to higher-temperature zones. As a result, microbe migration to high-temperature locations results in a lower concentration profile throughout the fluid.

Fig. 9
figure 9

Variation in the concentration profile for \({\text{Sc}}\)

Full size image
Fig. 10
figure 10

Variation in the concentration profile for\(\mathrm{ Sr}\)

Full size image

Figures 11 and 12 show the influence of \({\text{Pe}}\) and \({\text{Le}}\) on microbes profile. By increasing the Peclet number \(({\text{Pe}}),\) the fluid flow rate exceeds the rate of microbial growth, resulting in a decrease in the microorganism profile. This drop happens when the increased fluid flow moves microbes away from their areas of growth, resulting in a lower concentration in those places. The increase promotes fluid flow over microbial development, altering the spatial dispersion of microorganisms inside the system. About Fig. 12, a rise in the Lewis number \(({\text{Le}})\) correlates to an expansion of the microorganisms profile. In the complex world of bioconvective microfluid systems, an increased \(Le\) indicates a higher preponderance of thermal dispersion over mass diffusion. This change has the potential to cause the production of buoyant heat plumes, which will drive microorganisms upward and contribute to an enhanced microorganism profile. The enhanced \(Le\) emphasizes the importance of heat diffusion in determining the distribution of microbes inside the bioconvective microfluid system, highlighting the intricate connection between the motion of fluids and biological activities.

Fig. 11
figure 11

Variation in the microorganism profile for\(\mathrm{ Pe}\)

Full size image
Fig. 12
figure 12

Variation in the microorganism profile for \({\text{Le}}\)

Full size image

Here are Fig. 2 through 12, by setting \(\xi =K=0.3, \alpha ={60}^{\circ }, M=2.5, Q={B}_{i}=0.6,{\delta }_{B}=0.5, {\text{Pr}}=21, {\text{Ec}}=2.2,{\text{Du}}=0.2, {S}_{c}=0.4{, S}_{{\text{r}}}=0.2, {\text{Le}}=0.5, {\text{Pe}}=0.3.\)

Conclusion

The present work investigates non-similarity in bioconvective micropolar nanofluid flow over stretched surfaces, taking into account elements such as Soret and Dufour effects, viscous dissipation, and heat source. The complex governing system is modeled using the LNS approach and MATLAB’s bvp4c module. The main conclusions of this study are as follows:

  • The interplay of rotating degrees of freedom in a micropolar fluid, particularly under an inclined magnetic field, causes an increase in material parameters \((K)\) to correspond with a lower velocity profile. This interaction produces increased fluid flow resistance and a lower velocity profile. Furthermore, raising the magnetic field \((M)\) value improves the velocity profile and reveals complicated dynamics in bioconvective micropolar fluids.

  • Increasing \(K\) increases fluid resistance, which preserves form and may enhance micro-rotation. The stiffness effect is closely connected to fluid thickness and system structure, impacting a wide range of fluid behaviors. Understanding this interaction is critical for interpreting micro-rotation fluctuations and investigating larger dynamics in fluid mechanics.

  • Increasing the material parameter \((K)\) speeds up the bio-convective micropolar fluid, resulting in a better temperature profile. Raising both the Eckert number \(({\text{Ec}})\) and heat source \((Q)\) simultaneously results in a more effective heat transfer process and a lower overall temperature profile. Furthermore, a greater Dufour effect \(({\text{Du}})\) exacerbates temperature gradients and particle mobility, raising the fluid’s temperature profile.

  • Increasing the Schmidt number \(({\text{Sc}})\) increases molecular diffusion, resulting in a uniform distribution of solutes in fluids. This effective mixing results in a changed concentration profile with increased steepness and uniform distribution. An increased Soret effect \(({\text{Sr}})\), on the other hand, causes particles to move to higher-temperature locations, affecting temperature-sensitive bacteria in bioconvective micropolar fluids in particular.

  • Increasing the Peclet number \(({\text{Pe}})\) reduces microorganisms by accelerating fluid flow and moving them away from growing zones. In contrast, an increasing Lewis number \(({\text{Le}})\) broadens the microbe profile in bioconvective microfluid systems, stressing the importance of heat diffusion over mass diffusion.

  • Increasing the material parameters and magnetic field intensity improves the drag coefficient.

  • Elevating the heat source and material parameter raises the local Nusselt number while decreasing the Eckert number.

  • This work is supported by a comparative analysis that confirms earlier findings.

  • This work offers valuable information for future developments in medical device design and patient care, especially in addressing wound healing and enhancing comfort in pressure ulcer treatment.