An Efficient Method to Calculate the Aggregated Isotopic Distribution and Exact Center-Masses

Abstract

In this article, we present a computation- and memory-efficient method to calculate the probabilities of occurrence and exact center-masses of the aggregated isotopic distribution of a molecule. The method uses fundamental mathematical properties of polynomials given by the Newton-Girard theorem and Viete’s formulae. The calculation is based on the atomic composition of the molecule and the natural abundances of the elemental isotopes in normal terrestrial matter. To evaluate the performance of the proposed method, which we named BRAIN, we compare it with the results obtained from five existing software packages (IsoPro, Mercury, Emass, NeutronCluster, and IsoDalton) for 10 biomolecules. Additionally, we compare the computed mass centers with the results obtained by calculating, and subsequently aggregating, the fine isotopic distribution for two of the exemplary biomolecules. The algorithm will be made available as a Bioconductor package in R, and is also available upon request.

1 Introduction

The isotopic distribution is an important, but often forgotten, concept in the field of mass spectrometry (MS). Yet, it is particularly useful for the interpretation of the complex patterns observed in mass spectral data. For example, a peptide molecule visualized by MS should exhibit a characteristic signal in the form of series of regularly spaced peaks of a specific profile. The profile is related to the isotopic distribution of the peptide. Prior knowledge about the distribution can thus be used to develop strategies for searching for the profile in the spectra and, hence, for efficient processing of the spectral information [2–6]. Another application can be found in the field of metabolomics. For example, a comparison of the observed pattern of peaks in a mass spectrum with a set of hypothesized isotopic distributions from moieties with a similar mass as the observed molecule can be used to construct a confidence score for the identification.

The isotopic distribution reflects the number and probabilities of occurrence of different isotopic variants of a molecule. The occurrence probabilities are reflected in the mass spectrum by the relative heights of the series of peaks related to the molecule; whilst the different variants result from the fact that there are different isotopes of chemical elements.

Every isotopic variant of a molecule has, in principle, a different mass¹. However, if we ignore the small deviations of the masses from integer values, we can define aggregated isotopic variants of a molecule, with masses differing approximately by 1 Da. The aggregated isotopic distribution provides the number and occurrence probabilities for the aggregated isotopic variants. In fact, given the finite resolution of mass spectrometers, the profile of peak heights observed in a spectrum for a molecule is directly related to the aggregated isotopic distribution.

The calculation of the (aggregated) isotopic distribution for a molecule of a known atomic composition is thus a relevant and important problem. Several methods have already been proposed to this aim. In the early sixties of the 20th century, Biemann suggested a step-wise procedure [7]. In the late seventies, Yamamoto and McCloskey [8], and Brownawell and Fillippo [9] argued that for large molecules, the isotopic distribution could be easily obtained by symbolically expanding a polynomial function. Later in the eighties, Yergey and colleagues [10, 11] generalized the concept of polynomial expansion to a multinomial expansion. In the nineties, Rockwood and co-workers propagated the use of the convolution [12]. An overview of the different procedures to calculate isotopic distributions has been recently provided by Valkenborg et al. [13].

A vital element in the calculation of aggregated isotopic distributions is the assignment of the center-masses to the aggregated isotope variants. To this aim, the center-mass is calculated as a probability-weighted sum of the masses of the isotopic variants that contribute to an aggregated variant, as defined by Roussis and Proulx [14]. The accuracy of this mass calculation depends on the number of isotopic variants accounted for. Rockwood et al. [15] solved this problem by a linear transformation based on the average mass and standard deviation of the isotopic distribution to acquire semi-accurate masses. In a later paper, Rockwood and colleagues focused on the accurate mass calculation of a pre-selected aggregated isotope variant [16, 17]. Another solution to aforementioned problem was proposed by Olson and Yergey [18], who developed the idea of using equatransneutronic isotopes. The method, however, induces some error in the mass assignments of the aggregated isotope variants. To overcome this inaccuracy, Olson and Yergey proposed to estimate the error and to account for it in the calculation of the center-masses.

In this manuscript, we present an alternate, computation- and memory-efficient method to calculate the probabilities of occurrence and exact center-masses of the aggregated isotopic distribution of a molecule. The calculation is based on the atomic composition of the molecule and the natural abundances of stable elemental isotopes in normal terrestrial matter [19]. Note that this excludes unstable radio-isotopes, and that our use of the term “exact center-masses” is conditional on this assumption. Our method, which we name BRAIN (Baffling Recursive Algorithm for Isotopic distributioN calculations), allows computing the exact center-masses because it accumulates the mass information along a recursive calculation of the aggregated isotopic distribution. The algorithm will be made available as a Bioconductor package [1], and is also available upon request.

To evaluate the performance of the proposed method, we compare it to the results obtained from five existing packages (IsoPro [20], Mercury [15], Emass [16], NeutronCluster [18], and IsoDalton [21]) for 10 biomolecules. Additionally, we compare the computed exact mass-centers with the results obtained by the calculation of the fine isotopic distribution and subsequent aggregation of this distribution by the method of Roussis and Proulx [14] for two of the 10 exemplary biomolecules.

For the purposes of the current manuscript, we restrict the calculation of the isotopic distribution to molecules containing only carbon (C), nitrogen (N), hydrogen (H), oxygen (O), and sulphur (S), unless specified otherwise. The most-abundant (and lightest) isotopes for the latter elements are ¹²  C, ¹ H, ¹⁴  N, ¹⁶ O, and ³² S. A molecule composed out of only these elemental isotopes is called the monoisotopic variant. In addition, we only consider stable isotopes, that is, the isotopes just mentioned, together with ¹³  C, ² H, ¹⁵  N, ¹⁷ O, ¹⁸ O, ³³ S, ³⁴ S, and ³⁶ S. Extending the presented algorithm to molecules containing other poly-isotopic elements is straightforward.

2 Methods

Yamamoto et al. [8] and Brownawell et al. [9] argued that for large molecules, the isotopic forms could be easily obtained by symbolically expanding a polynomial function. In the case of proteins or peptides with a composition C _v H _w N _x O _y S _z , this polynomial takes the following form:

$$ \begin{gathered} {\left( {^{{12}}C{ +^{{13}}}C} \right)^v} \times {\left( {^1H{ +^2}H} \right)^w} \times {\left( {^{{14}}N{ +^{{15}}}N} \right)^x} \times \hfill \\ {\left( {^{{16}}O{ +^{{17}}}O{ +^{{18}}}O} \right)^y} \times {\left( {^{{32}}S{ +^{{33}}}S{ +^{{34}}}S{ +^{{36}}}S} \right)^z}\;. \hfill \\ \end{gathered} $$

(1)

Symbolic expansion of Equation (1) results in many product terms, which correspond to different isotopic variants of a molecule. By substituting the probabilities of occurrence for ¹² C,¹³ C,…,³⁶ S from Table 1 in each term, the prevalence of the variants of the peptide could be obtained.

Table 1 List of Stable Isotopes for Carbon, Hydrogen, Nitrogen, Oxygen, and Sulphur. Source: IUPAC 1997 Standard [19]

Given that the deviations of the masses of the isotopes of C, N, H, O, and S from integer values are different (see Table 1), every isotopic variant of a molecule has, in principle, a different mass. By ignoring the small deviations, we obtain the aggregated isotopic variants, with masses differing by approximately 1 Da. The aggregated variants are represented in the expansion of Equation (1) by multiple product terms. To identify these components more explicitly, we introduce in Equation (1) an indicator variable I. The introduction explicitly expresses the calculation of the isotopic distribution in terms of the additional neutron content, i.e., as an aggregated isotopic distribution. The modified form of Equation (1) is given as follows:

$$ \begin{aligned} Q\left( {I;v,w,x,y,z} \right) = \mathop{{\left( {{P_{{{C_{{12}}}}}}{I^0} + {P_{{{C_{{13}}}}}}{I^1}} \right)}}\nolimits^v \times \mathop{{\left( {{P_{{{H_1}}}}{I^0} + {P_{{{H_2}}}}{I^1}} \right)}}\nolimits^w \times \mathop{{\left( {{P_{{{N_{{14}}}}}}{I^0} + {P_{{{N_{{15}}}}}}{I^1}} \right)}}\nolimits^x \times \\ \mathop{{\left( {{P_{{{O_{{16}}}}}}{I^0} + {P_{{{O_{{17}}}}}}{I^1} + {P_{{{O_{{18}}}}}}{I^2}} \right)}}\nolimits^y \times \mathop{{\left( {{P_{{{S_{{32}}}}}}{I^0} + {P_{{{S_{{33}}}}}}{I^1} + {P_{{{S_{{34}}}}}}{I^2} + {P_{{{S_{{36}}}}}}{I^4}} \right)}}\nolimits^z \;, \\ \end{aligned} $$

(2)

where ${P_{{{C_{{12}}}}}},{P_{{{C_{{13}}}}}}, \ldots, {P_{{{S_{{36}}}}}}$ represent the natural abundances (probabilities of occurrence) of the isotopes of carbon, hydrogen, nitrogen, oxygen, and sulphur in normal terrestrial matter, as displayed in Table 1. Note that the power of the symbolic indicator I represents the additional neutron content (or discrete mass shift) with respect to the monoisotopic variant. This indicator serves a book keeping-device to keep track of the different aggregated isotopic variants.

It should be stressed that Equation (2) makes abstraction of the mass information, as the aggregated isotopic variants are presented by their additional neutron count. Later in the manuscript we discuss how the exact center-masses can be calculated.

In what follows, we will also be referring to the following, abbreviated form of Equation (2):

$$ Q\left( {I;v,w,x,y,z} \right) = {\left\{ {{Q_C}(I)} \right\}^v} \times {\left\{ {{Q_H}(I)} \right\}^w} \times {\left\{ {{Q_N}(I)} \right\}^x} \times {\left\{ {{Q_O}(I)} \right\}^y} \times {\left\{ {{Q_S}(I)} \right\}^z}\;, $$

(3)

with ${Q_C}(I) = \left( {{P_{{{C_{{12}}}}}}{I^0} + {P_{{{C_{{13}}}}}}{I^1}} \right)$, etc.

Generally, the expansion of the polynomial in Equation (2) can be written as

$$ Q\left( {I;v,w,x,y,z} \right) \equiv \sum\limits_{{j = 0}}^n \,{q_j}{I^j}\;, $$

(4)

where n = v + w + x + 2y + 4z is a function of the atomic composition of the molecule. The coefficient q _j represents the occurrence probability of the j-th aggregated isotopic variant of the molecule. Hence, the problem of calculating the aggregated isotopic distribution may be reformulated as the problem of finding values of the coefficients q ₀, q ₁,…q _n of the expanded polynomial in Equation (4).

To clarify the role of the polynomial in Equation (2), consider a very simple example of ozone (O ₃). For this molecule, the polynomial takes the following form:

$$ Q(I;0,0,0,3,0) = \mathop{{\left( {{P_{{{O_{{16}}}}}}{I^0} + {P_{{{O_{{17}}}}}}{I^1} + {P_{{{O_{{18}}}}}}{I^2}} \right)}}\nolimits^3 = {\{ {Q_O}(I)\}^3} = \sum\limits_{{j = 0}}^6 \,{q_j}{I^j}\;, $$

(5)

where the coefficients q ₀,…q ₆ are the result of expanding Equation (5):

$$ \begin{array}{*{20}{c}} {{q_{0}} = P_{{{O_{{16}}}}}^{3},\quad {q_{1}} = 3P_{{{O_{{16}}}}}^{2}{P_{{{O_{{17}}}}}},\quad {q_{2}} = 3P_{{{O_{{16}}}}}^{2}{P_{{{O_{{18}}}}}} + 3{P_{{{O_{{16}}}}}}P_{{{O_{{17}}}}}^{2},\quad {q_{3}} = P_{{{O_{{17}}}}}^{3} + 6{P_{{{O_{{16}}}}}}{P_{{{O_{{17}}}}}}{P_{{{O_{{18}}}}}},} \hfill \\ {{q_{4}} = 3P_{{{O_{{17}}}}}^{2}{P_{{{O_{{18}}}}}} + 3{P_{{{O_{{16}}}}}}P_{{{O_{{18}}}}}^{2},\quad {q_{5}} = 3{P_{{{O_{{17}}}}}}P_{{{O_{{18}}}}}^{2},\quad {q_{6}} = P_{{{O_{{18}}}}}^{3}.} \hfill \\ \end{array}$$

(6)

Thus, the coefficients indeed provide the probabilities of occurrence of aggregated isotopic variants with masses differing from the monoisotopic one by a specified integer number of mass units. In particular, q ₀ gives the occurrence probability of the monoisotopic variant of O ₃.

Note that, even for this seemingly simple example, the form of the coefficients is already quite complex. They are obtained by summing the occurrence probabilities of all isotope variants with exactly j additional neutrons, compared with the monoisotopic variant. In a general case, however, such a naive approach to the calculation of the values of the coefficients is numerically not feasible.

Rockwood [12] proposed to approach the problem of the calculation of the coefficients by using the Fast Fourier Transform. The approach is numerically efficient and has been widely used. In what follows, we outline an alternate method by using the properties of the elementary symmetric polynomials and power sums of the roots of the polynomial in Equation (2).

2.1 The New Method for Calculating the Aggregated Isotopic Distribution

By applying the Newton-Girard theorem and Viete’s formulae [22], we can express the coefficients q _j in the following recursive form:

$$ {q_j} = - \frac{1}{j}\sum\limits_{{l = 1}}^j \,{q_{{j - l}}}{\psi_l}, $$

(7)

where Ψ _l is a linear combination of the (−l)-th power of the roots of Q _C (I), Q _H (I), Q _N (I), Q _O (I), and Q _S (I), defined in Equation (3). More specifically, for C, H, and N, the roots become equal to

$$ \begin{array}{*{20}{c}} {{r_{C}} = - \frac{{{P_{{{C_{{12}}}}}}}}{{{P_{{{C_{{13}}}}}}}},} \hfill & {{r_{H}} = - \frac{{{P_{{{H_{1}}}}}}}{{{P_{{{H_{2}}}}}}},} \hfill & {{\text{and}}} \hfill & {{r_{N}} = - \frac{{{P_{{{N_{{14}}}}}}}}{{{P_{{{N_{{15}}}}}}}}} \hfill \\ \end{array} . $$

(8)

The roots of Q _O (I) are conjugate complex numbers r _O and $\mathop{{\bar{r}}}\nolimits_O$, defined as follows:

$$ {r_{O}} = \frac{{ - {P_{{{O_{{17}}}}}} + \sqrt {{P_{{{O_{{17}}}}}^{2} - 4{P_{{{O_{{16}}}}}}{P_{{{O_{{18}}}}}}}} }}{{2{P_{{{O_{{18}}}}}}}},\;{\overline r _{O}} = \frac{{ - {P_{{{O_{{17}}}}}} - \sqrt {{P_{{{O_{{17}}}}}^{2} - 4{P_{{{O_{{16}}}}}}{P_{{{O_{{18}}}}}}}} }}{{2{P_{{{O_{{18}}}}}}}}. $$

(9)

The roots of Q _S (I), a fourth-order polynomial, are less trivial, but can be expressed in a closed form. The expression is not very transparent, though; it can also be calculated using numerical root finding methods. There are two pairs of complex and conjugate roots of Q _S (I), which we will denote by $\left( {{r_{{S,1}}},\mathop{{\bar{r}}}\nolimits_{{S,1}} } \right)$ and $\left( {{r_{{S,2}}},\mathop{{\bar{r}}}\nolimits_{{S,2}} } \right)$.

Using the roots defined above, the coefficients Ψ _l can be expressed in general as follows:

$$ {\psi_l} = v{\left( {{r_C}} \right)^{{ - l}}} + w{\left( {{r_H}} \right)^{{ - l}}} + x{\left( {{r_N}} \right)^{{ - l}}} + y{\left( {{r_O}} \right)^{{ - l}}} + y{\left( {\mathop{{\bar{r}}}\nolimits_O } \right)^{{ - l}}} + z{\left( {{r_{{S,1}}}} \right)^{{ - l}}} + z{\left( {\mathop{{\bar{r}}}\nolimits_{{S,1}} } \right)^{{ - l}}} + z{\left( {{r_{{S,2}}}} \right)^{{ - l}}} + z{\left( {\mathop{{\bar{r}}}\nolimits_{{S,2}} } \right)^{{ - l}}}. $$

(10)

Note that the sum of powers for conjugate complex numbers r and $\bar{r}$ can be written as

$$ {r^{{ - l}}} + \mathop{{\bar{r}}}\nolimits^{{ - l}} = |r{|^{{ - l}}}cos\left\{ { - l\varphi (r)} \right\}, $$

(11)

where $|r|$ and φ(r) indicate the modulus and argument of r and $\bar{r}$, respectively. From Equation (11) it follows that the sum on the right-hand side of Equation (10) can be simplified by replacing the sum of the powers of the conjugate roots of oxygen and sulphur by their reduced forms.

As it was already noted, Equation (7) is recursive. To start the recursion, we need to compute the value of the coefficient q ₀. In this case, the computation is trivial, as q ₀ corresponds to the probability of occurrence of the monoisotopic variant. As pointed out by Beynon [23], the probability that no heavy isotopes would occur in a peptide of composition C _v H _w N _x O _y S _z is

$$ {q_0} = P_{{{C_{{12}}}}}^v \times P_{{{H_1}}}^w \times P_{{{N_{{14}}}}}^x \times P_{{{O_{{16}}}}}^y \times P_{{{S_{{32}}}}}^z. $$

(12)

After having computed q ₀, we can use Equation (7) to compute q ₁, q ₂, etc.

Let us consider an example. For propane C ₃ H ₈, the polynomial in Equation (2) assumes the following form:

$$ Q\left( {I;3,8,0,0,0} \right) = \mathop{{\left( {{P_{{{C_{{12}}}}}}{I^0} + {P_{{{C_{{13}}}}}}{I^1}} \right)}}\nolimits^3 \times \mathop{{\left( {{P_{{{H_1}}}}{I^0} + {P_{{{H_2}}}}{I^1}} \right)}}\nolimits^8 = {\left\{ {{Q_C}(I)} \right\}^3}{\left\{ {{Q_H}(I)} \right\}^8} = \sum\limits_{{j = 0}}^{{11}} \,{q_j}{I^j}. $$

Following Equation (12), the probability of occurrence of the monoisotopic variant (see Table 1) is given by

$$ {q_0} = P_{{{C_{{12}}}}}^3 \times P_{{{H_1}}}^8 = {0.9893^3} \times {0.999885^8} = 0.967352. $$

From Equation (7), the probability of occurrence of the first aggregated isotopic variant is obtained as q ₁ = –q ₀ × Ψ ₁, where, according to Equation (10),

$$ {\psi_1} = 3 \times r_C^{{ - 1}} + 8 \times r_H^{{ - 1}} = 3 \times \mathop{{\left( { - \frac{{0.9893}}{{0.0107}}} \right)}}\nolimits^{{ - 1}} + 8 \times \mathop{{\left( { - \frac{{0.999885}}{{0.000115}}} \right)}}\nolimits^{{ - 1}} = - 0.033367. $$

Hence, ${q_1} = - {q_0} \times {\psi_1} = - 0.967352 \times \left( { - 0.033367} \right) = 0.032278$. Thus, the probability of occurrence of an isotopic variant heavier by approximately 1 mass unit than the monoisotopic one is equal to 0.032278.

Next, we have ${q_2} = - \left( {{q_0} \times {\psi_2} + {q_1} \times {\psi_1}} \right)/2$, where

$$ {\psi_2} = 3 \times r_C^{{ - 2}} + 8 \times r_H^{{ - 2}} = 3 \times \mathop{{\left( { - \frac{{0.9893}}{{0.0107}}} \right)}}\nolimits^{{ - 2}} + 8 \times \mathop{{\left( { - \frac{{0.999885}}{{0.000115}}} \right)}}\nolimits^{{ - 2}} = 0.000351. $$

It follows that ${q_2} = - \left( {0.967352 \times 0.000351 + 0.032278 \times \left( { - 0.033367} \right)} \right)/2 = 0.000369$. This procedure is repeated up to q ₁₁. The resulting aggregated isotopic distribution of propane is as follows:

$$ \begin{array}{*{20}{c}} {{q_{0}} = 0.967352,} & {{q_{1}} = 0.032278,} & {{q_{2}} = 0.000369,} & {{q_{3}} = 1.55 \times {{10}^{{ - 6}}},} \\ {{q_{4}} = 1.25 \times {{10}^{{ - 9}}},} & {{q_{5}} = 4.83 \times {{10}^{{ - 13}}},} & {{q_{6}} = 1.09 \times {{10}^{{ - 16}}},} & {{q_{7}} = 1.54 \times {{10}^{{ - 20}}},} \\ {{q_{8}} = 1.40 \times {{10}^{{ - 24}}},} & {{q_{9}} = 8.01 \times {{10}^{{ - 29}}},} & {{q_{{10}}} = 2.62 \times {{10}^{{ - 33}}},} & {{q_{{11}}} = 2.26 \times {{10}^{{ - 38}}}} \\ \end{array} $$

A few comments are worth giving here.

• It can be observed that the complexity of calculations depends primarily on the number of different chemical elements present in the molecule (for peptides: C, H, N, O, S). It does not depend on the numbers of atoms for each element present in the molecule, but on the number of the aggregated isotopic variants, for which computations are required. In practice, one would stop the computations when the value of q _j falls below a particular (very small) threshold or when a preset percentage of the isotopic distribution is covered. Alternately, the computation of a fixed number of the q _j coefficients might be of interest.

• The method is very memory-efficient. In particular, it requires the storage of the mono-isotopic variant and only two variables, namely, q _j and Ψ _l , for each desired aggregated isotopic variant. Hence, calculating the first, e.g., 100 aggregated isotopic variants, require only 201 numbers to be stored.

• It is possible to reduce the number of computations by computing in advance the roots and their powers (by using the logarithmic transformation for improved numerical stability) needed to compute the coefficients Ψ _l and storing them for consecutive calculation steps.

• For chemical elements with more than four isotopic variants, a closed form solution of the roots is in general infeasible (the Abel-Ruffini theorem). The roots can be calculated by using numerical root-finding methods, such as the Newton-Raphson or Dandelin-Graeffe method. Again, the computed roots and their powers can be stored for further calculations.

• The value of Ψ _l may be easily calculated by using vectorization and recursive formulae. For instance, because ${b^{{ - l}}} = {b^{{ - 1}}}{b^{{ - \left( {l - 1} \right)}}}$, if we have already calculated Ψ ₁,Ψ ₂,…,Ψ _(l−1), we can use the values to calculate Ψ _l .

In the next section we show how the method can be used to compute the center-masses of the aggregated isotopic variants.

2.2 The New Method for Calculating the Center-Masses of the Aggregated Isotopic Variants

As discussed by Roussis and Proulx [14], the center-mass $\mathop{{\bar{m}}}\nolimits_j$ of the j-th aggregated variant is calculated as a probability-weighted sum of masses of the contributing isotopic variants:

$$ \mathop{{\bar{m}}}\nolimits_j = \frac{{\sum\nolimits_k \,{m_{{jk}}}{p_{{jk}}}}}{{\sum\nolimits_k \,{p_{{jk}}}}}, $$

(13)

where p _jk and m _jk denote, respectively, the probability of occurrence and the mass of the k-th isotopic variant contributing to the j-th aggregated variant. Note that the sum in the denominator of the fraction at the right-hand side of Equation (13) is the occurrence probability of the j-th aggregated isotopic variant. Thus, Σ _k p _jk is equal to q _j and can be computed by the methods outlined in the Introduction section.

It is obvious that accurate computations of the center-masses can only be achieved if all the isotopic variants contributing to the particular aggregated one are considered. Again, computations for all individual isotopic variants are in general not feasible due to the combinatorial explosion of the number of the variants for large molecules. However, we can circumvent this exhaustive method of calculation by resorting to the use of the Newton-Girard theorem and Viete’s formulae.

To this aim, we first consider the following polynomial:

$$ U\left( {I;v,w,x,y,z} \right) = \sum\limits_j \,\left( {\sum\limits_k \,{m_{{jk}}}{p_{{jk}}}} \right){I^j} \equiv \sum\limits_j \,q_j^{ \star }{I^j}. $$

(14)

Note that we are interested in the coefficients $q_j^{ \star } \equiv \sum\nolimits_k \,{m_{{jk}}}{p_{{jk}}}$, which correspond to the numerator of the fraction at the right-hand side of Equation (13).

In order to obtain information about $q_j^{ \star }$, we define a new polynomial by adding an additional indicator variable K to the polynomial in Equation (2):

$$ \begin{array}{*{20}{c}} {{Q^{ * }}\left( {I,K;v,w,x,y,z} \right) = } \hfill \\ {\mathop{{\left( {{P_{{{C_{{12}}}}}}{K^{{{M_{{{C_{{12}}}}}}}}}{I^{0}} + {P_{{{C_{{13}}}}}}{K^{{{M_{{{C_{{13}}}}}}}}}{I^{1}}} \right)}}\nolimits^{v} \times \mathop{{\left( {{P_{{{H_{1}}}}}{K^{{{M_{{{H_{1}}}}}}}}{I^{0}} + {P_{{{H_{2}}}}}{K^{{{M_{{{H_{2}}}}}}}}{I^{1}}} \right)}}\nolimits^{w} \times } \hfill \\ {\mathop{{\left( {{P_{{{N_{{14}}}}}}{K^{{{M_{{{N_{{14}}}}}}}}}{I^{0}} + {P_{{{N_{{15}}}}}}{K^{{{M_{{{N_{{15}}}}}}}}}{I^{1}}} \right)}}\nolimits^{x} \times \mathop{{\left( {{P_{{{O_{{16}}}}}}{K^{{{M_{{{O_{{16}}}}}}}}}{I^{0}} + {P_{{{O_{{17}}}}}}{K^{{{M_{{{O_{{17}}}}}}}}}{I^{1}} + {P_{{{O_{{18}}}}}}{K^{{{M_{{{O_{{18}}}}}}}}}{I^{2}}} \right)}}\nolimits^{y} \times } \hfill \\ {\mathop{{\left( {{P_{{{S_{{32}}}}}}{K^{{{M_{{{S_{{32}}}}}}}}}{I^{0}} + {P_{{{S_{{33}}}}}}{K^{{{M_{{{S_{{33}}}}}}}}}{I^{1}} + {P_{{{S_{{34}}}}}}{K^{{{M_{{{S_{{34}}}}}}}}}{I^{2}} + {P_{{{S_{{36}}}}}}{K^{{{M_{{{S_{{36}}}}}}}}}{I^{4}}} \right)}}\nolimits^{z} } \hfill \\ \end{array} $$

(15)

where M _C12, M _C13, .., M _S36 represent the masses of the isotopes of carbon, hydrogen, nitrogen, oxygen, and sulphur in normal terrestrial matter, as displayed in Table 1. The indicator variable K acts as a tracking device for the masses.

By using argumentation similar to the one used in a prior section, we can express the polynomial in Equation (15) as follows:

$$ {Q^{ * }}\left( {I,K;v,w,x,y,z} \right) \equiv \sum\limits_{j} \left( {\sum\limits_{k} {p_{{jk}}}{K^{{{m_{{jk}}}}}}} \right){I^{j}}. $$

(16)

We will use Q ^*(I, K; v, w, y, z) to obtain the polynomial U(I; v, w, x, y, z) from Equation (14). To this aim, we differentiate Q ^*(I, K; v, w, y, z) with respect to K:

$$ \frac{\partial }{{\partial K}}{Q^{ * }}\left( {I,K;v,w,x,y,z} \right) = \sum\limits_{j} \left( {\sum\limits_{k} {m_{{jk}}}{p_{{jk}}}{K^{{{m_{{jk}}} - 1}}}} \right){I^{j}}. $$

(17)

Then, by setting K = 1 in Equation (17), we obtain:

$$ \begin{array}{*{20}{c}} {U(I;v,w,x,y,z) = } \hfill \\ {v{Q}\left( {I;v - 1,w,x,y,z} \right)\left( {{P_{{{C_{{12}}}}}}{M_{{{C_{{12}}}}}} + {P_{{{C_{{13}}}}}}{M_{{{C_{{13}}}}}}{I^{1}}} \right)} \hfill \\ \end{array} $$

(18)

$$ + w{Q}\left( {I;v,w - 1,x,y,z} \right)\left( {{P_{{{H_{1}}}}}{M_{{{H_{1}}}}} + {P_{{{H_{2}}}}}{M_{{{H_{2}}}}}{I^{1}}} \right) $$

(19)

$$ + x{Q}\left( {I;v,w,x - 1,y,z} \right)\left( {{P_{{{N_{{14}}}}}}{M_{{{N_{{14}}}}}} + {P_{{{N_{{15}}}}}}{M_{{{N_{{15}}}}}}{I^{1}}} \right) $$

(20)

$$ + y{Q}\left( {I;v,w,x,y - 1,z} \right)\left( {{P_{{{O_{{16}}}}}}{M_{{{O_{{16}}}}}} + {P_{{{O_{{17}}}}}}{M_{{{O_{{17}}}}}}{I^{1}} + {P_{{{O_{{18}}}}}}{M_{{{O_{{18}}}}}}{I^{2}}} \right) $$

(21)

$$ + z{Q}\left( {I;v,w,x,y,z - 1} \right) \times $$

(22)

$$ \left( {{P_{{{S_{{32}}}}}}{M_{{{S_{{32}}}}}} + {P_{{{S_{{33}}}}}}{M_{{{S_{{33}}}}}}{I^1} + {P_{{{S_{{34}}}}}}{M_{{{S_{{34}}}}}}{I^2} + {P_{{{S_{{36}}}}}}{M_{{{S_{{36}}}}}}{I^4}} \right)\;.$$

(23)

By using the method outlined in the section about The New Method for Calculating the Aggregated Isotopic Distribution, we can compute the coefficient q _j (i.e., the occurrence probability of the j-th aggregated isotopic variant) separately for each of the Q(·) polynomials, present in Equations (18–23). Consequently, we can compute the coefficients of the five polynomials included in the sum on the right-hand side of Equations (18–23). By adding the coefficients corresponding to I ^j for the five polynomials, we obtain $q_j^{ \star }$ for Equation (14). Finally, the centered mass for the j-th aggregated isotopic variant is obtained from Equation (13) as $q_j^{ \star }/{q_j}$.

3 Results and Discussion

We compared our method, named BRAIN, with five other algorithms. All methods were used to compare the aggregated isotopic distribution of 10 biomolecules shown in Table 2. The 10 biomolecules are the same as those used in the paper of Olson and Yergey [18]. The size of the molecules ranges from considerably small to very large.

Table 2 List of Selected Biomolecules

3.1 Compared Algorithms

The five packages considered in our comparison with BRAIN are IsoPro, Mercury, Emass, NeutronCluster, and IsoDalton.

IsoPro [20] is an implementation of the multinomial expansion method proposed by Yergey [10]. Mercury contains an implementation of the convolution method of Rockwood and Van Orden [15]. Emass calculates the masses and intensities of isotopic peaks by the linear transformation of Rockwood and Haimi [16]. NeutronCluster uses the equatransneutronic isotopes proposed by Olson and Yergey [18]. IsoDalton [21] efficiently calculates the fine isotopic distribution by means of dynamic programming. Latter outcome can be used as an intermediate step to retrieve the aggregated isotopic structure of a biomolecule.

For large molecules, the implementations of IsoPro and IsoDalton become computationally inefficient in terms of the memory usage and computation time. Because of this limitation, we report for these two methods the masses for the first seven and first five biomolecules, respectively.

All the algorithms were used with their default parameter settings, except of IsoPro and NeutronCluster. For the former the permutation threshold was set to 10⁻⁶, while for the latter the required ion current coverage was changed to 0.999. As four out of the five algorithms use different values for the atomic masses and abundances of the isotopes (see Table S1 in the appendix), we have changed the abundances and masses to the values used by IsoDalton, which correspond to the IUPAC 1997 standard [19] as displayed in Table 1.

All the algorithms, except of NeutronCluster, have been run on a Dell Latitude E6500 with an Intel dual core P8400 2.26 GHz and 4 GB RAM. NeutronCluster has been run on an Apple MacBook with 4 GB RAM, due to technical incompatibilities with the BigFloat and BigInt packages of Perl on a Windows operating system (personal communication with Olson and Yergey).

3.2 Results of the Comparison

Table 3 presents the comparison of the mass of the first peak returned by BRAIN and by the other selected algorithms with the theoretical monoisotopic mass of the molecules presented in Table 2. The theoretical monoisotopic mass was simply computed as follows:

$$ Monoisotopic\;mass = v{M_{{{C_{{12}}}}}} + w{M_{{{H_1}}}} + x{M_{{{N_{{14}}}}}} + y{M_{{{O_{{16}}}}}} + z{M_{{{S_{{32}}}}}}, $$

(24)

assuming that the atomic composition of the molecule is of the form C _v H _w N _x O _y S _z . In the remainder of this manuscript, we use the term "peak" to indicate the aggregated isotopic variant and not a variant of the isotopic fine structure as calculated via IsoDalton.

Table 3 Differences Between the Monoisotopic Mass According to [8] (see Table 2) and the Mass of the First Returned Peak by the Algorithm. Negative Values Correspond to Higher Reported Masses

Negative values in Table 3 indicate that the mass of the first returned peak is higher than the monoisotopic mass. As BRAIN’s algorithm uses the same formula for the calculation of the monoisotopic mass as Equation (24), there is no difference between the reported and theoretical monoisotopic mass for BRAIN. For NeutronCluster, awkwardly, there is a considerably large difference for molecule no. 4. The returned monoisotopic mass of the molecule is identical to the mass reported in the paper of Olson and Yergey [18]. All other monoisotopic masses returned by NeutronCluster are identical to the ones calculated by Equation (24).

For the first four molecules, the mass of the returned first peak is the same or close to the monoisotopic-variant mass in the case of Emass and IsoPro. Starting from molecule no. 5, the difference between the monoisotopic and the returned mass increases. To put these results in perspective, it is worth noting that for large molecules, e.g., (5)–(10) in Table 2, the probability of occurrence of the monoisotopic variants is very small, <10⁻¹⁰. In practice, such small values fall below the detection limits of a mass spectrometer and will go unnoticed. Therefore, one can argue that returning isotopic variants with such low probabilities is not meaningful. It can happen that some of the non-reported peaks were actually calculated inside the compared programs, but were not reported due to a reporting threshold built into the method. In our method, we have chosen to return all aggregated isotope variants regardless of their probability of occurrence.

For Mercury, the first returned peaks have masses that are lower than the monoisotopic mass in the case of small biomolecules. A possible explanation for this behavior could be the numerical imprecisions of the (discrete) Fast Fourier Transform, e.g., distortion of the signal due to aliasing. This could be fixed by a slight modification of the computer code to widen the calculation window. Generally, peaks with lower masses than the monoisotopic one should just be ignored.

For larger molecules, the masses returned for the first peaks by Emass and IsoPro are higher than the theoretical monoisotopic mass. This is probably the result of pruning techniques applied by these methods. Note that this is also the case for Mercury.

Although IsoDalton calculates the fine structure of the isotopic distribution, there are slight differences between the returned and theoretical monoisotopic mass. These differences can possibly be explained by the fact that in the calculations presented in Table 3, the “exact_probability” module has been used, as was advised by Snider (personal communication), instead of the “exact_mass” module. The latter results in more accurate estimates for the masses, but is less accurate for the average aggregated mass and its corresponding expected peak abundance.

To check the overall accuracy of the computation of an aggregated isotopic distribution, we considered the theoretical average mass of the molecules presented in Table 2. The average mass is computed according to the following definition:

$$ \begin{aligned} {\text{Average}}\;{\text{mass}}\; = v{M_{{{C_{{12}}}}}} \times {P_{{{C_{{12}}}}}} + v{M_{{{C_{{13}}}}}} \times {P_{{{C_{{13}}}}}} \\ + w{M_{{{H_1}}}} \times {P_{{{H_1}}}} + w{M_{{{H_2}}}} \times {P_{{{H_2}}}} \\ + x{M_{{{N_{{14}}}}}} \times {P_{{{N_{{14}}}}}} + x{M_{{{N_{{15}}}}}} \times {P_{{{N_{{15}}}}}} \\ + y{M_{{{O_{{16}}}}}} \times {P_{{{O_{{16}}}}}} + y{M_{{{O_{{17}}}}}} \times {P_{{{O_{{17}}}}}} + y{M_{{{O_{{18}}}}}} \times {P_{{{O_{{18}}}}}} \\ + z{M_{{{S_{{32}}}}}} \times {P_{{{S_{{32}}}}}} + z{M_{{{S_{{33}}}}}} \times {P_{{{S_{{33}}}}}} + z{M_{{{S_{{34}}}}}} \times {P_{{{S_{{34}}}}}} + z{M_{{{S_{{36}}}}}} \times {P_{{{S_{{36}}}}}}. \\ \end{aligned} $$

(25)

Table 4 presents the results of the comparison of the theoretical average mass, as computed in Equation (25), and the weighted average based upon the predicted masses and occurrence probabilities for all peaks returned by a particular algorithm. There is virtually no difference between the two average values for BRAIN and for Emass. Somewhat larger, but small deviations are obtained for IsoDalton. The differences are larger for Mercury and NeutronCluster, and they increase as the molecules become larger. IsoPro is unexpectedly the least accurate method in our comparison; the large differences are most likely a side effect of the pruning step, which removes low probability variants during the calculation. Pruning is a necessity to calculate the isotope fine structure for large molecules in order to maintain the computational complexity and memory usage within limits.

Table 4 Difference Between the Theoretical (see Table 2) and Calculated (Using all returned peaks) Average Mass. Negative Values Correspond to Higher Calculated Masses. The Values in Parentheses are the Relative Differences in ppb

It is worth mentioning that when the results in Table 4 are viewed in relative terms, all of the reported numbers are quite satisfactory. The reported differences between Emass, Mercury, NeutronCluster, and IsoDalton are in fact not measurable with the accuracy available in the current generation of mass spectrometers.

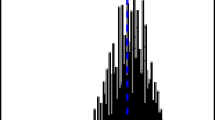
The differences observed in Table 4 are mainly due to the fact that every algorithm returns a different number of peaks (i.e., aggregated isotopic variants), with a different first and last reported peak. Figure 1 illustrates how the methods perform in the tail of the distribution for molecule no. 5 from Table 2. The figure shows three vertical lines for each method, indicating the mass of the first reported peak, the average mass, and the last reported peak. In other words, the representation in Figure 1 can be seen as the coverage of the isotopic distribution by a particular method. Note that the lines indicating the mass of the first reported peak for BRAIN, NeutronCluster, and IsoDalton overlap with the line corresponding to the theoretical monoisotopic mass, in agreement with the results presented in Table 3. Similarly, the lines indicating the average mass practically overlap with the line corresponding to the theoretical average mass for BRAIN, Emass, IsoDalton, Mercury, and NeutronCluster, in agreement with the results presented in Table 4. A clear difference can be observed in the mass of the last reported peak. IsoPro and NeutronCluster report a peak with the smallest mass, followed by Mercury, Emass, IsoDalton, and BRAIN. Depending on the shape of the true aggregated isotopic distribution, the different number and location of the reported peaks may lead to a difference between the value of the average mass computed for a particular algorithm and the theoretical value, obtained from Equation (25). For the case presented in Figure 1, the difference is small, though visible for IsoPro.

Figure 1

The calculated aggregated isotopic distribution of human intrinsic factor. (The height of the lines have no meaning, they are only chosen to facilitate the interpretation of the graph.)

As mentioned in the Methods section, for BRAIN, the calculations can be stopped when the computed occurrence probabilities become too small or when the required number of aggregated isotopic variants has been reached. The latter number can be heuristically obtained. For this purpose, we propose the following rule of thumb: compute the difference between the theoretical monoisotopic mass and the theoretical average mass, multiply this number by two, and subsequently round it to the nearest integer greater than or equal to the multiplied difference. For instance, for the molecule no. 10 in Table 2, the heavy chain of the human dynein protein, this method gives 664 as the number of the aggregated isotopic variants to be included in the calculations. Note, however, that the method may return a too small number for smaller molecules. For instance, in the case of the molecule no. 1 in Table 2, angiotensin II, the obtained number is equal to 2. For such small molecules, the minimal number of peaks should be four or five. As already mentioned before, schemes based on the percentage coverage of the isotopic distribution can also be used.

The number of isotopic variants used in the computation of the average masses in Table 4 and the corresponding computation time for our method are listed in Table 5. Increasing the number of the requested variants influences the computation time, but the effect is minor. Comparison of the computation time of BRAIN with the other algorithms is difficult, as the methods are implemented using different softwares on different platforms. In general terms, Emass and Mercury are faster than our method, but the differences are negligible small. It is worth noting, however, that BRAIN is now operated by an interpreted language. We believe that a compiled version of BRAIN will be as fast as Emass and Mercury.

Table 5 Requested Number of Aggregated Isotopic Variants and the Associated Computation time for BRAIN. The Calculations were Performed in Matlab

The results presented in Table 4 already indicate the proper functioning of BRAIN. If the calculation of the occurrence probabilities and/or center-masses were wrong, then the average masses of the molecules would deviate from their theoretical values. In order to further investigate the accuracy of the calculations for our method in more detail, we computed the isotopic distribution for the molecules no. 1 (angiotensin II) and 2 (bovine insulin) from Table 2 by considering all possible isotopic variants, while using an implementation of the multinomial expansion [10]. From the obtained result we derived the aggregated isotopic distribution. Tables 6 and 7 present the center-masses and occurrence probabilities for the first 50 aggregated isotopic variants for angiotensin II and bovine insulin, respectively. We can confirm that BRAIN provides exactly the same masses and occurrence probabilities for these aggregated isotopic variants.

Table 6 The First 50 Aggregated Isotopic Variants for Angiotensin II

Table 7 The First 50 Aggregated Isotopic Variants for Bovine Insulin

As mentioned previously, for large molecules, the occurrence probabilities for the monoisotopic and (several) consecutive aggregated isotopic variants can be very small. In that case, given that the recursive relationship Equation (7) implies starting the calculations from the monoisotopic variant, the computations of these initial probabilities can be affected by the level of the available numerical precision. As seen from the results presented in Table 4, these numerical precision issues do not influence the calculations for the meaningful region of the aggregated isotopic distribution, i.e., for the aggregated isotopic variants with non-negligible occurrence probabilities. However, for extremely large molecules this does not hold. These molecules have abundances for the mono-isotopic and consecutive peaks that are extremely small (i.e., ≪10⁻¹⁰⁰). As these molecules are exceptional and difficult to measure with the accuracy available in the current generation of mass spectrometers, we can ignore this numerical issue.

The method we propose is predominantly conceived for calculating the aggregated isotopic distribution. From a practical point of view, ignoring the isotopic fine structure is not a serious limitation. This is because for large molecules such as (e.g., intact proteins) the resolution in MS does not allow for observing the fine structure of aggregated isotopic variants. For large molecules, the calculation of exact center-masses of aggregated variants becomes fundamental, and the calculation is taken care of by our method. When information about the isotopic fine structure is required, other methods proposed in (e.g., [24], [25], [26], or [21]) can be used. If the molecule is not too large, the multinomial expansion [10] can be applied to infer the isotopic fine structure.

4 Conclusions

The proposed BRAIN method allows a fast computation of the aggregated isotopic distribution. It provides the correct values of the occurrence probabilities of various aggregated isotopic variants and the center-masses. In terms of speed and accuracy, BRAIN yields results comparable to those obtained by existing algorithms like Emass, but is more memory-efficient and simpler to implement. The BRAIN method will be made available within the Bioconductor package in R.