FormalPara Key Points

The time courses of both the in vitro dissolution rate and in vivo absorption rate of a prolonged-release ketamine dosage form could be well described by a sum of two inverse Gaussian functions.

This modeling reveals more details of the absorption process. The information obtained from the in vitro dissolution rate profile can be useful in estimating bioavailability.

1 Introduction

Oral administration of ketamine is of special interest due to the formation of the secondary metabolite 2,6-hydroxynorketamine via presystemic metabolism. Thus, low doses of a newly developed prolonged-release ketamine dosage form (PR-ketamine) led to high plasma concentrations of the potential analgesic/antidepressant 2R,6R- and 2S,6S-hydroxynorketamine [1]. Given these advantages of oral ketamine administration, the goal of this study was to investigate the in vitro-in vivo correlation (IVIVC) for these PR-ketamine tablets. One goal was to assess how well the oral data can be fitted when the input function is represented by the vitro dissolution rate followed by a delay process [2]. The latter can stand for the absorption process or gastrointestinal transport. Furthermore, assuming that the shape of the in vivo input rate curve is identical to that of the in vitro dissolution rate, leaving only bioavailability as an unknown parameter, it was tested whether bioavailability can be predicted from the oral data with only one sampling point per subject. Finally, it will be shown that while intestinal absorption appears dissolution limited, calculation of the input rate of ketamine to the systemic circulation reveals more details of the absorption process.

2 Materials and Methods

2.1 Model

2.1.1 In Vitro Dissolution

Denoting the amount of drug released up to time t by Ad(t), the normalized in vitro dissolution profile is given by Fd(t) = Ad(t)/Ad(∞). A linear combination of two inverse Gaussian distributions (2IG) has been proved useful in modeling dissolution profiles of extended release tablets [3] (Eq. 1):

$$F_{d} \left( t \right) \, = pF_{{{1}d}} \left( t \right) \, + \, \left( {{1} - p} \right)F_{{{2}d}} \left( t \right)$$
(1)

where 0 < p < 1 and Fid (i = 1,2) are cumulative distribution functions of the IG, which can be expressed in terms of the standard normal distribution Φ as Eq. 2:

$$F_{id} (t) = \Phi \left( {\sqrt {\frac{{MT_{id} }}{{RD_{id}^{2} t}}\left( {\frac{t}{{MT_{i} }} - 1} \right)} } \right) + e^{{2/RD^{2} }} \Phi \left( { - \sqrt {\frac{{MT_{{_{id} }}}}{{RD_{{^{id} }}^{2} t}}\left( {\frac{t}{{MT_{id} }} + 1} \right)} } \right)$$
(2)

with \(\Phi (x) = (1/\sqrt {2\pi } \int_{ - \infty }^{x} {e^{{ - u^{2} /2}} } du\).

Fd(t) represents a two-point distribution with probability p of outcome F1d with parameters MT1d, \(RD_{1d}^{2}\) and probability (1 − p) of outcome F2d with parameters MT2d, \(RD_{2d}^{2}\), where the IG with the longer MDT accounts for the tail part of the dissolution data. The mean dissolution time is then given by Eq. 3:

$$MDT = pMT_{1d} + \left( {1 - p} \right)MT_{2d}$$
(3)

The dissolution rate, dFd/dt = fd(t), is then obtained as Eq. 4:

$$f_{d} \left( t \right) \, = pf_{1d} \left( t \right) + \left( {1 - p} \right)f_{2d} (t)$$
(4)

fid(t) denotes the ith IG density function (Eq. 5):

$$f_{id} (t) = \sqrt {\frac{{MT_{id} }}{{2\pi RD_{id}^{2} t^{3} }}} \exp \left[ { - \frac{{(t - MT_{id} )^{2} }}{{2RD_{id}^{2} MT_{id} t}}} \right]$$
(5)

With these parameters, the normalized dissolution rate fd(t) could be calculated (Eqs. 4 and 5). The fractional dissolution rate function is defined as Eq. 6:

$$k_{d} (t) = \frac{{f_{d} (t)}}{{1 - F_{d} (t)}}$$
(6)

and has been proved useful for the assessment of the dissolution process [4].

2.1.2 In Vivo Input Function

The same kind of function (Eqs. 4 and 5) was used previously to describe the absorption (or input) rate of drugs into the systemic circulation (central compartment) after administration of extended release formulations [5, 6] (Eq. 7):

$$I(t) = DFf_{a} (t) = DF(pf_{1a} (t) + (1 - p)f_{2a} (t))$$
(7)

where D is dose, F denotes bioavailability and fa(t) is the normalized input rate. Note that the fractional input rate (defined analogously to Eq. 6) provides important guidance for selection of appropriate input rate models [6].

Like in Eq. 3, the mean input time is given by Eq. 8:

$$MIT = pMT_{1a} + \, \left( {1 - p} \right)MT_{2a}$$
(8)

Assuming that the input rate in vivo is determined by the dissolution rate in vitro, a time delay in drug release after ingestion has to be considered in linking the input rate with the dissolution rate, for example, a delay due to gastric emptying or the absorption process. As proposed by Yu and Amidon [7], we used a transit compartment model to characterize this delay (Fig. 1). The estimated optimal number of transit compartments was four. The mean delay in absorption onset, MTk, is given in terms of the rate constant k as MTk = 4/k. Thus, with this model we predicted the absorption rate fa(t) (or I(t)) of the drug from the dissolution rate of the tablet, fd(t).

Fig. 1
figure 1

Pharmacokinetic model of ketamine absorption after a prolonged-release tablet, illustrating the direct estimation of the input rate, I(t) [via fa(t)] and the reduced model based on the delayed in vitro dissolution rate, fd(t).

Full size image

3 Data Analysis

All fittings were done using the software package ADAPT 5 [8]. The maximum likelihood expectation maximization (MLEM) program available in ADAPT 5 provides estimates of the population mean and inter-subject variability as well as of the individual subject parameters (conditional means). We assumed log-normally distributed model parameters and that the measurement error has a standard deviation that is a linear function of the measured quantity. ‘Goodness of fit’ was assessed using the Akaike information criterion (AIC) and by plotting the predicted versus the measured responses.

3.1 In Vitro Dissolution Rate

The PR-ketamine tablets consisted of sugar spheres coated with ketamine hydrochloride (multi-unit pallets) surrounded by a sustained-release membrane of water-insoluble ethyl cellulose polymer embedded in a hydrogel-forming polymer. Dissolution of ketamine hydrochloride tablets was conducted in 1000 ml 0.1N HCL at 37 °C using the USP apparatus 1 at 100 rpm with six replicates. The amount of released R/S-ketamine was measured using a validated achiral LC−MS/MS method (data on file of the producer, Develco Pharma Schweiz AG, Pratteln, Switzerland). The dissolution parameters, MT1d, \(RD_{1d}^{2}\), MT2d, \(RD_{2d}^{2}\) and p, were estimated by fitting Eq. 2 to the in vitro dissolution data of the 20 mg PR-ketamine tablets using a population approach in which the six data sets (replicates) were analyzed simultaneously.

3.2 In Vivo Input Rate

The in vivo input parameters have been previously estimated in 15 healthy volunteers after intravenous and oral dosing of 20 mg PR-ketamine tablets using a population approach [5]. The linear range for serum measurements was 0.5–200 ng/ml. For details of the clinical study and the analytical method (liquid chromatography-tandem mass spectrometry), see Hasan et al [1]. In short, the data after intravenous injection were first fitted using a three-compartment disposition model (Fig. 1); then, holding the estimated parameters fixed, the parameters of the input function I(t) (Eq. 6), i.e., F, MT1a, \(RD_{1a}^{2}\), MT2a, \(RD_{2a}^{2}\) and p, were estimated for the R-enantiomer after oral administration of PR-ketamine tablets. Note that there was no significant difference in the bioavailability between the R- and S-enantiomer [1, 5]. These parameters were used to calculate the normalized input rate in vivo, fa(t) (Eq. 7). Note that the IVIVC is illustrated here only for R-ketamine since there were no significant differences in the input functions of the R- and S-enantiomer.

3.3 Dissolution Rate and Delay Process

Instead of estimating the F, MT1a, \(RD_{1a}^{2}\), MT2a, \(RD_{2a}^{2}\) and pa when fitting the oral data with the full model [5], the parameters were estimated in the same way with the difference that the dissolution parameters, MT1d, \(RD_{1d}^{2}\), MT2d, \(RD_{2d}^{2}\) and pd, were fixed in all subjects, only estimating the delay parameter k and bioavailability F (Fig. 1). This means that instead of the six parameters in Eq. 6, only two parameters, F and k, were estimated.

Based on the mean parameter estimates of the dissolution profile (from the six replicates) the time course of dissolution rate (Eqs. 4 and 5) and fractional release rate (Eq. 6), respectively, were simulated using the simulation module of ADAPT 5. Likewise, curves of the normalized input rates of 20 mg PR-ketamine tablets were simulated for the full model (parameters MT1a, \(RD_{1a}^{2}\), MT2a, \(RD_{2a}^{2}\) and pa) and the delay model (parameter k with fixed dissolution parameters MT1d, \(RD_{1d}^{2}\), MT2d, \(RD_{2d}^{2}\) and pd).

3.4 One-point Sampling Strategy

The question arises whether the information obtained from the in vitro dissolution process could be used to develop a one-point sampling method for approximate estimation of bioavailability, F, when otherwise nothing is known of the time course of oral plasma concentration after oral administration. If the normalized in vivo input rate and the in vitro dissolution rate curves have the same shape, the time course of the input rate is defined by that of dissolution rate after a vertical shift by the factor F. We selected the plasma concentration sampled near the maximum of the in vitro dissolution rate, in this case at t = 5h (Fig. 4). The data (one point per subject) were fitted as described above, but using the dissolution rate, i.e., only one parameter, F, was estimated.

4 Results

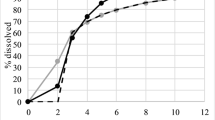
The simultaneous fit of the 2IG model (Eq. 2) to the in vitro dissolution data measured for six PR-ketamine tablets (20 mg) is demonstrated in Fig. 2, with predicted population mean curve and open circles representing the observed data. The inset shows the fraction absorbed in vivo against the fraction dissolved in vitro. Fits of concentration versus time plots for oral administration of PR-ketamine tablets are illustrated in Fig. 3. The fit obtained with delay time model using fixed dissolution parameters (k and F as adjustable parameters) is compared with that of the full 2IG-absorption model (parameters F, MT1a, \(RD_{1a}^{2}\), MT2a, \(RD_{2a}^{2}\) and p); both fits are demonstrated by the plotting of model-predicted concentration-time curves together with the medians of the observed data. (For the quality of fit obtained with the 2IG-model, see also [5]). The estimated parameters are listed in Table 1. Despite the lower quality of fit of the delay time model (higher AIC), the estimated bioavailability was only 2% lower. Figure 4 compares the mean dissolution rate in vitro calculated from the in vitro dissolution curve (Fig. 2) with the mean input rates in vivo corresponding to the two different input models, i.e., the fits shown in Fig. 3. The input rate curve calculated from the parameters of the delay time model represents the dissolution rate shifted by a delay time of 0.36 h. The real input rate obtained by the full model shows a characteristic double peak (Fig. 4). The difference between the dissolution rate in vitro and the input rate in vivo becomes particularly visible in the plots of the fractional rates (Fig. 5). In contrast to the real input rate, which is characterized by a nonmonotonic fractional rate curve, dissolution rate and input rate predicted by the delay time model belong to the class of monotonically increasing fractional rate [4, 6]. Both the mean absorption time, MIT, and the relative dispersion of the absorption time distribution, \(RD_{{{\text{input}}}}^{2}\), exceed the corresponding parameters of the in vitro dissolution process, MDT and \(RD_{{{\text{diss}}}}^{2}\) (Table 1). Furthermore, \(RD_{{{\text{input}}}}^{2}\) increases linearly with MAT (r = 0.64, p < 0.05), starting at a value near that for \(RD_{{{\text{diss}}}}^{2}\).

Fig. 2
figure 2

In vitro release profile data of 20 mg PR-ketamine tablets (six replicates) simultaneously fitted by the 2IG model (Eq. 1) with population mean curve and percent absorbed vs. percent dissolved plot in the inset.

Full size image
Fig. 3
figure 3

Average concentration-time curve for R-ketamine after administration of 20 mg PR-ketamine as predicted with the full model (a) and the delay model (b), with the medians of R-ketamine data (open circles). The curves were simulated using the population mean parameter estimates.

Full size image
Table 1 Mean dissolution time in vitro and pharmacokinetic absorption parameters of prolonged-release ketamin 20 mg (R-enantiomere) in 15 healthy human subjects
Full size table
Fig. 4
figure 4

Normalized dissolution rate and input rate functions, showing the in vitro dissolution rate (a), the input rate predicted by the delay model (b) and the input rate calculated with the full model (c). The curves were simulated using the population mean parameter estimates of the input function.

Full size image
Fig. 5
figure 5

Fractional rates (cf. Eq. 6) corresponding to the in vitro dissolution rate (a) and in vivo input rate (b).

Full size image

Interestingly, the one-point method gave a reasonable prediction of bioavailability; the approximate estimate was 14% lower (Table 1).

5 Discussion

IVIVCs play a key role in the development of oral drug formulations [9]. For PR-ketamine, we found a nearly perfect correlation (IVIVC at level A) (Fig. 2). However, in contrast to the typical application of IVIVC for predicting plasma concentration-time profiles in bioequivalence testing [9], our goal here was to discuss the usefulness of the dissolution profile when data of only one oral formulation are available (together with the accompanying intravenous data). In other words, we only ask to which extent the absorption rate profile of a ketamine formulation can be predicted by in vitro dissolution data. For a review of the general problem of bioavailability prediction, see Ref. [10].

To more clearly reveal the differences between in vitro dissolution and in vivo absorption, we compared the performance of the complete input model (six adjustable parameters, F, MT1a, \(RD_{1a}^{2}\), MT2a, \(RD_{2a}^{2}\) and p) with the delayed dissolution rate, i.e., the simple delay time model (two adjustable parameters, F and k, holding MT1d, \(RD_{1d}^{2}\), MT2d, \(RD_{2d}^{2}\) and pd fixed). In contrast to the full model, the delay time model (i.e., the IVIVC predicted curve) fails to fit the peak of the curve (Fig. 3); furthermore, its AIC value is much lower (Table 1). Figure 4 shows the characteristic differences in the input rates. The delay time model produces a shifted dissolution curve that matches the curve obtained with the full model in the ascending phase but not in the peak region: contrary to the bimodal curve of the full model, the delay time model produces an unimodal curve. When comparing the corresponding fractional rates, these differences become even more clear (Fig. 4). In contrast to the monotonically increasing fractional input rate of the dissolution and delay time model (i.e., this property of the dissolution rate is preserved under the delay-time operation), the fractional input rate of the complete input model is nonmonotonic; thus, the input rate belongs to a different class of functions [4, 6]. This fact restricts the selection of input models: models characterized by an increasing fractional input rate (i.e., a log-concave input rate curve) as the as first-order absorption model, a gamma density function (chain of transit compartments) as well as the Weibull model are not suitable in this case [6]. Interestingly, the in vitro dissolution rate nearly matches the in vivo input rate (Fig. 4); as expected, the fit with the reduced model (with only two adjustable parameters) was worse than that with the 2IG-input model (AIC = − 113 versus − 173), but the estimated bioavailability was not much different (F =12.2% versus 12.4%). Using only one sample at t = 5 h (one-point method), the estimated F value was only 14% lower than that obtained by fitting the complete data set (19 samples per subject). This is however not a proof of concept, but rather is a suggestion for further study.

The fact that the mean input time, MIT, was about 1 h higher than the mean dissolution time in vitro, MDT, shows that the increase in input time is only partly due to the delayed initial rise in the input rate. That the spread of the input/absorption time distribution (\(RD_{{{\text{input}}}}^{2}\) = 0.528) exceeds that of the dissolution time distribution (\(RD_{{{\text{diss}}}}^{2}\) = 0.388), and that \(RD_{{{\text{input}}}}^{2}\) increases linearly with MIT, may be explained by the heterogeneity of absorption during intestinal transit. Notably, the present analysis reveals information about the absorption process, which remains hidden in conventional IVIVC studies. Thus, the bimodal pattern of input rate (Fig. 4) may indicate absorption in two regions of the intestinal tract. Given the similarity to the input rates observed for the p-glycoprotein substrates talinolol [11] and trospium chloride [12] as well as the information on ketamine transporters [13, 14], it appears likely that absorption occurs from the distal parts of the small intestine and the colon. However, such an explanation remains speculative at this stage.

6 Conclusions

A comparison of the in vivo input rate with in vitro dissolution rate reveals more details about the absorption process compared to the conventional correlation of dissolved and absorbed amounts. If absorption is dissolution-limited, the information given by the in vitro dissolution rate could be used to predict bioavailability by one-point sampling.