Mixed Market Structure and R &D: A Differential Game Approach

Abstract

We consider a dynamic model of an industry consisting of a few large firms, which can manipulate the market outcome, and a mass of small enterprises, each of which has a negligible impact on the market. The production costs of the respective firms depend on the stock of knowledge capital, which accumulates over time through research and development (R &D) investment made by large firms. The model is a variant of the differential game of voluntary provision of public goods, but in contrast to previous studies, we focus on the interaction between market competition and dynamic game outcomes. We derive both open-loop and Markov-perfect Nash equilibria. There exists a unique open-loop Nash equilibrium. By contrast, depending on the parameters of the model, there can be two linear Markov-perfect Nash equilibria. We also examine the short- and long-run effects of a change in the number of large firms. An increase in the number of large firms unambiguously harms both types of firms in the short run but may benefit them in the long run. In the open-loop Nash equilibrium, the relationship between the number of large firms and the steady-state stock of knowledge capital is inverted-U shaped. Concerning the Markov-perfect Nash equilibria, the effect of increased competition from large firms depends on the specific feedback strategy chosen in equilibrium.

1 Introduction

Innovation is the major engine of economic growth and development because it improves product quality, enhances productivity, and reduces production costs. Firms engage in research and development (R &D) activities to create innovative technologies, and some of these technologies are of high public interest; examples include the smart grid, wireless technology, renewable energy, and open-source software development. Thus, firms’ R &D investment in such technologies can be interpreted as voluntary provision of public goods.

Not all firms engage in R &D activities. Klette and Kortum [24] provide a number of stylized facts on the properties of firm innovation. Among other findings, they provide the following evidence: productivity and R &D are positively associated across firms; R &D increases in proportion to sales; and the distribution of R &D intensity is highly skewed, with a considerable fraction of firms reporting zero R &D.

Many industries also consist of a configuration of different types of firms. Specifically, they consist of a few large firms, which are able to manipulate the market, and a host of small businesses, each of which has a negligible impact on the market. Although standard theories of imperfect competition, which consider either oligopoly or monopolistic competition models, do not reflect the nature of such industries, recent studies consider models that capture such mixed markets. Shimomura and Thisse [37] develop a general equilibrium model of a mixture of oligopoly and monopolistic competition under constant-elasticity-of-substitution (CES) preferences. Parenti [32] and Pan and Hanazono [31] develop a model with quadratic preferences and a multiproduct-firm oligopoly, in which each large firm produces a range of varieties and strategically chooses both the product range and the quantity of each variety, while each small firm only produces one variety of product.¹ In these studies, the conditions under which there is a mixed market equilibrium are identified, and they examine the impacts of large firms’ entry into the market.

In this paper, we consider a dynamic model of an industry consisting of a few large firms (i.e., oligopolists), which can manipulate the market outcome, and a host of small enterprises, each of which has a negligible impact on the market, as in Shimomura and Thisse [37], Parenti [32], and Pan and Hanazono [31]. The production costs of the respective firms depend on the stock of knowledge capital, which accumulates over time through voluntary investments made only by the oligopolists. The knowledge capital has the character of a public good, and the contribution to public-good accumulation can be interpreted as investment in cost-reducing R &D, which requires large investment costs; thus, we assume that small firms find it difficult to make investment, and only the oligopolists make R &D investment.

Using the abovementioned model, we investigate how large (i.e., oligopolistic) and small firms interact. Specifically, we address how the stock of knowledge capital affects large and small firms’ equilibrium outputs, prices, and profits, and what the equilibrium outcomes of the dynamic game of R &D investment by large firms are. We derive an open-loop Nash equilibrium (OLNE), in which the large firms choose their investment strategies as a simple time path at the beginning of the game and commit themselves to maintaining the pre-announced paths for the entire duration of the game, and a Markov-perfect Nash equilibrium (MPNE), in which the large firms choose their investment strategies as a feedback decision rule dependent on the stock of knowledge capital. We identify the following properties of the temporary equilibrium and the dynamic equilibrium. First, the output of each type of firms in the temporary market equilibrium may be decreasing in the stock of knowledge capital. However, the large firms make R &D investment only if their temporary equilibrium outputs are increasing in the knowledge stock. Second, there exists a unique OLNE, and the large firms’ equilibrium investment is increasing in the knowledge stock. Third, there are two possible equilibria for a linear MPNE, both of which are positively dependent on the knowledge stock, and depending on the parameters of the model, either of the two or both become an equilibrium outcome.

There is evidence of a considerable disparity in R &D performance across countries (see, e.g., [18]). A number of studies in different fields of economics including macroeconomics (e.g., [26]) and economic history (e.g., [29]) have sought to explain this fact. The possibility of multiple Nash equilibria derived in our model can provide an explanation for this fact.

In the economics of innovation, there has been interest in the relationship between the degree of competition and innovation. There are two conventional views; one is that less competition enhances innovation because of monopoly rents, yielding intensive R &D [35], and the other is the opposite view that a competitive firm has a greater incentive to innovate than a monopolist [3]. Recent studies identify a nonmonotonic relationship between the ferocity of competition and R &D activities.² Aghion et al. [1] find strong evidence of an inverted-U shaped relationship using UK panel data and develop a model that explains this relationship. Hashmi [21] reexamines the inverted-U relationship by using US data. By contrast, Flath [14] shows a U-shaped relationship between competition and innovation using Japanese data, and Matsumura et al. [27] develop a theoretical model that is consistent with this finding.

We address the relationship between competition and innovation in our model by examining how a change in the number of oligopolists affects the economy. We consider both short-run effects, that is, the effects under a constant stock of knowledge capital, and long-run effects, that is, the effects when the stock of knowledge capital is endogenously determined. The findings reveal that an increase in the number of large firms unambiguously reduces the outputs of both types of firms in the short run. In addition, under certain conditions, increased competition among large firms has a positive effect on these firms’ investment in a given stock of knowledge capital in the OLNE. This means that increased competition among large firms has a negative effect on the short-run profits of large and small firms. In the long run, however, the relationship between the number of large firms and the steady-state stock of knowledge capital in the OLNE is shown to be inverted-U shaped. Concerning the MPNEs, the effect of an increase in the number of large firms depends on the specific feedback strategy chosen in equilibrium; for example, increased competition among large firms may have a negative effect on these firms’ investment in a given stock of knowledge capital and thus may benefit large firms in the short run.

The model that we use in this paper is a variant of the dynamic game of voluntary provision of public goods analyzed by Fershtman and Nitzan [13], Wirl [40], Itaya and Shimomura [22], Yanase [41], Benchekroun and Long [6], Fujiwara and Matsueda [15], and Battaglini et al. [5], in which private agents voluntarily contribute to a public good, the stock of which accumulates over time and affects the agents’ utility.³ In contrast to these studies, in which the private agents’ objective function is exogenously determined and no market competition is considered, we focus on the interaction between market competition and dynamic game outcomes.

A noteworthy result obtained in this study is that along the dynamic equilibrium, the large firms’ investment is increasing in the stock of knowledge capital. The key to this finding is that in the present model the large firms’ instantaneous payoff is convex rather than concave in the stock of knowledge capital, meaning that the marginal benefit from knowledge accumulation is increasing. Thus, our model is in common with the existing studies [4, 12, 20] that examine optimal investment problems for a single firm with the instantaneous payoff exhibiting “increasing returns.” In other words, this study can be interpreted as an extension of these studies to an environment in which multiple firms make investment for the accumulation of common capital stock.

The present study is also related to a large body of literature on cost-reducing R &D under oligopoly (e.g., [8, 11, 23, 33]). However, these papers consider a two-stage game in which the R &D effort is made only once, and the R &D investment game is virtually static in nature. Lambertini and Mantovani [25] consider a differential game model in which oligopolists have an infinite horizon and the marginal costs are state variables that decrease over time due to the oligopolists’ R &D investments. In addition to the difference in the structure of the model, our model differs from that of Lambertini and Mantovani [25] in that we consider not only oligopolists but also small firms that completely free-ride on the oligopolists’ R &D efforts and the interaction between different types of firms in a market is examined.⁴

The remainder of this paper is organized as follows. In Sect. 2, we establish our model, characterize the respective firms’ optimization problems, and derive the temporary equilibrium for a given stock of knowledge capital. Sections 3 and 4 derive the OLNE and the MPNE, respectively, of the differential game of R &D investment by large firms. In each equilibrium, we examine the effects of a change in the number of oligopolists on the equilibrium outcomes. Section 5 discusses how robust the results obtained from the basic model are under different assumptions. Section 6 concludes the paper.

2 The Model

2.1 Basic Setups

We consider an industry that produces horizontally differentiated products. In this industry, there are $m\ge 2$ large firms, indexed by $i=1,\ldots ,m$, and a continuum of small firms. The collection of small firms is called the fringe. Let $\eta >0$ denote the measure of this continuum. Small firms are indexed by $\omega$, where $\omega \in \left[ 0,\eta \right]$. We assume that both m and $\eta$ are exogenous. In other words, unlike in the conventional monopolistic competition model, there is no entry or exit of small firms. We will relax this assumption later.

The large firms recognize that their behavior affects the aggregate variables (e.g., the price index specified later) in the economy. Since all firms produce horizontally differentiated products, small firms face a downward-sloping demand curve for their respective products. However, they are assumed to take the price index as given. Each firm’s marginal cost of production is dependent on a common pool of knowledge, and the stock of knowledge accumulates over time due to large firms’ investment.

2.1.1 Preferences and Demand

The utility function of the representative consumer is assumed to be quasilinear and quadratic, represented as a single-product version of that considered in Parenti [32] and Pan and Hanazono [31]⁵:

$$\begin{aligned}&u (\textbf{x},y(\omega ),h_0; \omega \in [0,\eta ]) \nonumber \\&\quad = \alpha \left[ \sum _{i=1}^m x_i + \int _0^{\eta } y(\omega )d\omega \right] -\frac{1-\gamma }{2} \left[ \sum _{i=1}^m x_i^2 + \int _0^{\eta } y(\omega )^2 d\omega \right] \nonumber \\&\qquad -\frac{\gamma }{2} \left[ \sum _{i=1}^m x_i + \int _0^{\eta } y(\omega )d\omega \right] ^2 +h_0, \end{aligned}$$

(1)

where $\textbf{x}=(x_1,\ldots ,x_m)$ denotes the vector of consumption of differentiated goods produced by large firms, $y(\omega )$ is the consumption of a differentiated good produced by a small firm $\omega$, $h_0$ is the consumption of a homogeneous good (assumed to be the numeraire), the parameter $\alpha >0$ is assumed to be sufficiently large, and the parameter $\gamma \in (0,1)$ represents the degree of substitutability among differentiated goods; the higher the parameter $\gamma$ is, the greater the substitutability among these goods.

The consumer’s budget constraint is given by

$$\begin{aligned} \sum _{i=1}^m p_i x_i + \int _0^{\eta } q(\omega ) y(\omega ) d \omega + h_0 = I, \end{aligned}$$

(2)

where $p_i$ denotes the price of a differentiated good produced by a large firm i, $q(\omega )$ is the price of a differentiated good produced by a small firm $\omega$, and I is the consumer’s income.

The representative consumer maximizes (1) subject to (2). The first-order conditions for utility maximization are represented as follows:

$$\begin{aligned} p_i= & {} \alpha -(1-\gamma )x_i-\gamma Q, \quad i=1,\ldots ,m, \end{aligned}$$

(3)

$$\begin{aligned} q(\omega )= & {} \alpha -(1-\gamma )y(\omega )-\gamma Q, \quad \omega \in [0,\eta ], \end{aligned}$$

(4)

where

$$\begin{aligned} Q \equiv \sum _{i=1}^m x_i + \int _0^{\eta } y(\omega )d\omega \end{aligned}$$

(5)

is the sum of the outputs of all firms, i.e., the industry output.

Equations (3) and (4) define the inverse demand functions for the respective differentiated goods. In the polar case where $\gamma =0$, the volume of industry output has no effect on the demand curve that each firm faces. In the opposite polar case where $\gamma =1$, consumers regard all varieties as perfect substitutes, and they can only be sold at the same price.

Summing (3) over $i=1,\ldots ,m$ and integrating (4) over $\omega \in [0,\eta ]$, we obtain

$$\begin{aligned} \sum _{i=1}^{m}p_{i}= & {} m\alpha -(1-\gamma )X-\gamma mQ, \end{aligned}$$

(6)

$$\begin{aligned} \int _{0}^{\eta }q(\omega )d\omega= & {} \eta \alpha -(1-\gamma )Y-\gamma \eta Q, \end{aligned}$$

(7)

where $X\equiv \sum _{i=1}^m x_i$ and $Y\equiv \int _{0}^{\eta }y(\omega )d\omega$ denote the total output of large firms and the fringe output, respectively. Adding (6) and (7) and using (5), we obtain the relationship between the (market-clearing) price index P and the industry output, Q:

$$\begin{aligned} P \equiv \sum _{i=1}^m p_{i}+\int _{0}^{\eta }q(\omega )d\omega =(m+\eta )\alpha -\left[ 1+(m+\eta -1)\gamma \right] Q. \end{aligned}$$

(8)

That is, in equilibrium,

$$\begin{aligned} Q=\frac{(m+\eta )\alpha -P}{1+(m+\eta -1)\gamma } \end{aligned}$$

holds.

2.1.2 Knowledge Capital

The large firms conduct R &D activities, which constitute a common pool of knowledge. Let us denote the stock of the knowledge capital at time t by K(t), which accumulates over time according to the following differential equation:

$$\begin{aligned} {\dot{K}}(t)=\sum _{i=1}^m k_i(t) -\delta K(t), \end{aligned}$$

(9)

where $k_i(t)$ denotes the R &D investment by large firm i at time t and the parameter $\delta >0$ represents the depreciation rate of the stock.⁶

An increase in the stock of the knowledge capital benefits all firms in the industry in the form of process innovations. That is, the unit costs of both large and small firms are decreasing in K. We assume that all large firms and all small firms, respectively, have identical technologies. The unit cost of a representative large firm is denoted by $\sigma (K)\ge 0$, and that of a representative small firm is denoted by $\tau (K)\ge 0$.⁷

2.2 Temporary Equilibrium

At any point in time, given K, the firms know their unit cost of production (i.e., $\sigma (K)$ for the large firms and $\tau (K)$ for the small firms). We make the following assumption on $\sigma (K)$ and $\tau (K)$.

Assumption 1

The unit cost of small firms is never lower than that of large firms:

$$\begin{aligned} \sigma (K)\le \tau (K) \quad \text { for all }K\ge 0. \end{aligned}$$

Assumption 2

The unit cost functions are of the following piecewise linear form:

$$\begin{aligned} \sigma (K)= {\left\{ \begin{array}{ll} \overline{\sigma }-\sigma _{0}K &{} \text {for }0\le K\le \overline{\sigma }/\sigma _{0} \\ 0 &{} \text {for }K\ge \overline{\sigma }/\sigma _{0}, \end{array}\right. } \\ \tau (K)= {\left\{ \begin{array}{ll} \overline{\tau }-\tau _{0}K &{} \text {for }0\le K\le \overline{\tau }/\tau _{0} \\ 0 &{} \text {for }K\ge \overline{\tau }/\tau _{0}, \end{array}\right. } \end{aligned}$$

where $\overline{\sigma }$, $\sigma _{0}$, $\overline{\tau }$, and $\tau _{0}$ are all positive parameters.

Remark 1

Under the piecewise linear specification in Assumption 2, to also satisfy Assumption 1, it is necessary to impose two restrictions on parameter values, namely (i) $\overline{\sigma }\le \overline{\tau }$ and (ii) $\overline{\sigma }/\sigma _{0}\le \overline{\tau }/\tau _{0}$. Note that given the first restriction, the second restriction is automatically satisfied if $\sigma _{0}\ge \tau _{0}$, but it can also be satisfied even in the case where $\sigma _{0}-\tau _{0}<0$ as long as this difference is not too great.

In what follows, we admit two cases: case A, where $\sigma _{0}>\tau _{0}$ holds (i.e., for all $K\in (0,\overline{\sigma }/\sigma _{0})$, a marginal increase in K reduces the unit cost of large firms by more than it reduces the unit cost of small firms), and case B, where $\sigma _{0}\le \tau _{0}$ holds (i.e., for all $K\in (0,\overline{\sigma }/\sigma _{0})$, a marginal increase in K reduces the unit cost of large firms by less than it reduces the unit cost of small firms).

2.2.1 Cournot Behavior

We assume that firms make decisions on their output, taking the output of other firms as given. Once the outputs are placed on the market, the prices are determined endogenously by the market clearing condition, equating the quantities supplied (the outputs) and consumer demand.

2.2.2 Large Firms

When a large firm i determines its output to maximize its profit, it accounts for the fact that, given the outputs of other large firms and small firms, any increase in its output will increase industry output

$$\begin{aligned} Q=Y+x_{i}+\sum _{j\ne i}x_{j}\equiv Y+X_{-i}+x_{i}\equiv Q_{-i}+x_{i}, \end{aligned}$$

and that this in turn will affect its market clearing price $p_{i}=\alpha -(1-\gamma )x_{i}-\gamma Q=(\alpha -\gamma Q_{-i})-x_{i}\equiv p_{i}(x_{i},Q_{-i})$, where

$$\begin{aligned} \frac{\partial p_{i}}{\partial x_{i}}=-1, \quad \frac{\partial p_{i}}{\partial Q_{-i}}=-\gamma . \end{aligned}$$

The profit of a large firm i is therefore given by

$$\begin{aligned} \pi _{i}^{L}=\left[ p_{i}(x_{i},Q_{-i})-\sigma (K)\right] x_{i}-c(k_{i}), \end{aligned}$$

(10)

where $c(k_{i})$ is the cost of R &D investment $k_{i}$. Firm i chooses $x_{i}$ to maximize (10). The first-order condition for profit maximization is

$$\begin{aligned} x_{i}\frac{\partial p_{i}}{\partial x_{i}}+p_{i}(x_{i},Q_{-i})-\sigma _{i}(K)=0, \quad \text {or} \quad \left[ \alpha -\sigma (K)-\gamma (Y+X_{-i})\right] -2x_{i}=0. \end{aligned}$$

(11)

Substituting (11) into (10) yields firm i’s maximized profit as follows:

$$\begin{aligned} \pi _{i}^{L}= -\frac{\partial p_{i}}{\partial x_{i}} (x_{i}^{*})^{2}-c(k_{i})=(x_{i}^{*})^{2}-c(k_{i}), \end{aligned}$$

(12)

where $x_i^*$ denotes the profit-maximizing output.

We assume symmetry among the respective types of firms, so that in a Cournot equilibrium among large firms, i.e., $x_i=x$ for $i=1,\ldots ,m$. This means that $X_{-i}=(m-1)x$, and thus condition (11) yields

$$\begin{aligned} \alpha -\sigma (K)-\gamma (\eta y+m x)-(2-\gamma )x=0. \end{aligned}$$

(13)

2.2.3 Small Firms

Since the members of the fringe also produce differentiated varieties, the price $q(\omega )$ at which fringe firm $\omega$ can sell its entire output, $y(\omega )$, also depends on both $y(\omega )$ and the industry output, Q: $q(\omega )=\alpha -(1-\gamma )y(\omega )-\gamma Q\equiv f(y(\omega ),Q)$, with

$$\begin{aligned} \frac{\partial f(y(\omega ),Q)}{\partial y(\omega )}=-(1-\gamma ), \quad \frac{\partial f(y(\omega ),Q)}{\partial Q}=-\gamma . \end{aligned}$$

We assume that each of the small firms perceives that its output $y(\omega )$ has no impact on Y and hence no impact on Q. Thus, each small firm perceives that its profit function is

$$\begin{aligned} \pi ^{S}(\omega ) = \left[ q(\omega )-\tau (K)\right] y(\omega ) =\left[ f(y(\omega ),Q)-\tau (K)\right] y(\omega ), \end{aligned}$$

(14)

where Q is taken as given. The first-order condition for profit maximization is

$$\begin{aligned} y(\omega ) \frac{\partial f}{\partial y(\omega )} +\left[ f(y(\omega ),Q)-\tau (K)\right] =0, \quad \text {or} \quad \alpha -\gamma Q-\tau (K) -2(1-\gamma )y(\omega )=0.\nonumber \\ \end{aligned}$$

(15)

From (14) and (15), the maximized profit of a representative small firm is

$$\begin{aligned} \pi ^{S}(\omega )= -\frac{\partial f}{\partial y(\omega )} \left[ y^{*}(\omega )\right] ^2 =(1-\gamma )\left[ y^{*}(\omega )\right] ^{2}, \end{aligned}$$

(16)

where $y^{*}(\omega )$ denotes the profit-maximizing output.

In a symmetric equilibrium, $y(\omega )=y$ for $\omega \in [0,\eta ]$ and $Y=\eta y$ hold. Thus, condition (15) becomes

$$\begin{aligned} \alpha -\gamma (\eta y+m x)-\tau (K) -2(1-\gamma )y=0. \end{aligned}$$

(17)

2.2.4 Equilibrium

Using (13) and (17), we can solve for the equilibrium outputs of the large and small firms:

$$\begin{aligned} x= & {} \frac{1}{\Gamma }\left[ 2(1-\gamma )\alpha +\gamma \eta \tau (K)-(\gamma \eta +2(1-\gamma ))\sigma (K)\right] \equiv x^*(K), \end{aligned}$$

(18)

$$\begin{aligned} y= & {} \frac{1}{\Gamma }\left[ (2-\gamma )\alpha +\gamma m\sigma (K)-(\gamma m+2-\gamma )\tau (K)\right] \equiv y^*(K), \end{aligned}$$

(19)

where $\Gamma \equiv 2(1-\gamma )(2-\gamma )+\gamma \left[ 2(1-\gamma )m+(2-\gamma )\eta \right] >0$. We assume that $\alpha$ is large enough that $x^*(K)>0$ and $y^*(K)>0$ for all K.

2.3 Comparative Statics of Temporary Equilibrium

2.3.1 Effects of a Change in K

From (18) and (19), we obtain the following comparative statics results for varying the value of K in the interval $\left[ 0,\overline{\sigma }/\sigma _{0}\right]$:

$$\begin{aligned} \frac{dx^*(K)}{dK}= & {} \frac{1}{\Gamma } \left[ (\gamma \eta +2(1-\gamma ))\sigma _{0}-\gamma \eta \tau _{0}\right] , \end{aligned}$$

(20)

$$\begin{aligned} \frac{dy^*(K)}{dK}= & {} \frac{1}{\Gamma } \left[ (\gamma m+2-\gamma )\tau _{0}-\gamma m\sigma _{0}\right] . \end{aligned}$$

(21)

What do these results say about the response of large firms’ output to an increase in K? In case A, where $\sigma _{0}\ge \tau _{0}$ (the increase in K reduces large firms’ unit cost by at least as much as it reduces small firms’ unit cost), a large firm’s temporary equilibrium output increases in response to a marginal increase in K for all $K\in \left[ 0, \overline{\sigma }/\sigma _{0}\right)$. In contrast, in case B, where $\sigma _{0}<\tau _{0}$, a large firm’s temporary equilibrium output is decreasing in K provided that the following additional inequality holds: $\tau _{0}>\sigma _{0}\left[ 1+2(1-\gamma )( \gamma \eta ) ^{-1}\right]$.

For small firms, in case A, where $\sigma _{0}\ge \tau _{0}$, its temporary equilibrium output decreases in response to a marginal increase in K for all $K\in \left[ 0, \overline{\sigma }/\sigma _{0}\right)$ provided that the following additional inequality holds: $\sigma _{0}>\tau _{0}\left[ 1+(2-\gamma )(\gamma m)^{-1}\right]$. In case B, where $\sigma _{0}<\tau _{0}$, a small firm’s temporary equilibrium output increases when there is a marginal increase in K for all $K\in \left[ 0, \overline{\sigma }/\sigma _{0}\right) .$

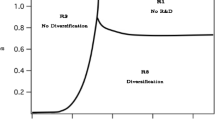
Figure 1 summarizes the abovementioned comparative statics results, where the parameter $\sigma _{0}$ is measured along the horizontal axis, while the parameter $\tau _{0}$ is measured along the vertical axis. In the upper region where $\tau _{0}>\sigma _{0}\left[ 1+2(1-\gamma )(\gamma \eta ) ^{-1}\right]$, we have $dx^{*}(K)/dK<0$ and $dy^{*}(K)/dK>0$, which implies, via (12) and (16), that an increase in K is harmful to large firms. From this fact, we conjecture that no large firm will want to invest in K if $(\sigma _{0},\tau _{0})$ is in this region. It will be verified that this conjecture is correct.

Fig. 1

Signs of $dx^*(K)/dK$ and $dy^*(K)/dK$ for $K< {\bar{\sigma }}/\sigma _0$

For $K \in [{\bar{\sigma }}/\sigma _0,{\bar{\tau }}/\tau _0]$, the comparative statics results for varying K are

$$\begin{aligned} \frac{dx^*(K)}{dK}=-\frac{\gamma \eta \tau _0}{\Gamma }<0, \quad \frac{dy^*(K)}{dK}=\frac{(\gamma m+2-\gamma )\tau _0}{\Gamma }>0. \end{aligned}$$

As $\sigma (K)=0<\tau (K)$ and $\tau '(K)<0$ in this case, an increase in K induces a decrease only in small firms’ marginal costs. Thus, the small firms increase their respective outputs. This has a negative effect on each large firm’s marginal revenue. In response to this, the large firms reduce their respective outputs.

Finally, for $K>{\bar{\tau }}/\tau _0$, $\sigma (K)=\tau (K)=0$ holds, and thus,

$$\begin{aligned} \frac{dx^*(K)}{dK}=\frac{dy^*(K)}{dK}=0. \end{aligned}$$

Remark 2

If there are no small firms, each large firm’s output in the symmetric equilibrium is derived as

$$\begin{aligned} x^*(K)=\frac{\alpha -\sigma (K)}{2+(m-1)\gamma }. \end{aligned}$$

Thus, $dx^*(K)/dK>0$ holds.

2.3.2 Effects of a Change in m

From (18) and (19), we obtain the following comparative statics results for varying the value of m:

$$\begin{aligned} \frac{\partial x^*(K)}{\partial m}= & {} -\frac{2\gamma (1-\gamma )x^*(K)}{\Gamma }<0, \end{aligned}$$

(22)

$$\begin{aligned} \frac{\partial y^*(K)}{\partial m}= & {} -\frac{\gamma (2-\gamma )x^*(K)}{\Gamma }<0. \end{aligned}$$

(23)

Therefore, an increase in m reduces the temporary equilibrium outputs for both types of firms. In light of (16), the small firms’ temporary equilibrium profits also decrease.

Proposition 1

More competition among large firms (i.e., an increase in m) reduces the temporary equilibrium outputs of both large and small firms. Thus, the small firms unambiguously become worse off from the increased competition among large firms in the short run.

Intuitively, since each firm produces an imperfectly substitutable good, the more competitive environment (i.e., an increase in m) implies lower product prices. Thus, each firm, whether large or small, has an incentive to decrease its output.

Let us denote the industry output in the temporary equilibrium by $Q^*(K)= m x^*(K)+\eta y^*(K)$. Then, an increase in m reduces each large firm’s market share:

$$\begin{aligned} \frac{\partial \left[ x^*(K)/Q^*(K)\right] }{\partial m} =-\frac{2(1-\gamma )\left[ \alpha -\sigma (K)\right] x^*(K)}{Q^*(K)^2 \Gamma }<0. \end{aligned}$$

(24)

For given outputs x and y, an increase in m has a positive effect on the industry output Q, and this positive effect dominates the negative effects on the respective firms outputs (i.e., $\partial x^*(K)/\partial m<0$ and $\partial y^*(K)/\partial m<0$). In other words, increased competition among large firms increases the industry output in the temporary equilibrium. Since $x^*(K)$ decreases and $Q^*(K)$ increases, each large firm’s market share decreases.

Equations (22) and (23) also indicate that if $\gamma \rightarrow 0$ or $\gamma \rightarrow 1$, any changes in m do not affect the large firms’ equilibrium output. Intuitively, $\gamma \rightarrow 0$ means that all goods become independent, and $\gamma \rightarrow 1$ means that all goods become homogeneous. In the case where all goods become independent, each firm supplies its product in a monopolistic way. This means that the number of firms does not affect the respective firms’ behavior or, thus, their profit-maximizing outputs. In the case where all goods become homogeneous, each small firm cannot exercise its monopoly power over its own product, which means that the firm’s profit-maximization condition is to equalize the price to the marginal cost (see also (15)), or $\alpha -Q=\tau (K)$. This condition solves the equilibrium level of Q, which is independent of m. With this fact and the large firms’ profit-maximization condition (13), where $\eta y+mx=Q$, the Cournot equilibrium output of each large firm is also independent of m.⁸

2.4 R &D Investment

The large firms make R &D investment by considering the accumulation of knowledge capital, (9). Thus, each large firm’s objective is to maximize the discounted sum of its profits $V_i= \int _0^{\infty } e^{-rt} \pi _i^L(t) dt$, $i=1,\ldots ,m$, where $r>0$ denotes the discount rate assumed to be common to all firms. In light of (12), $V_i$ can be rewritten as

$$\begin{aligned} V_i= \int _0^{\infty } e^{-rt} \left[ x^*(K(t))^2-c(k_i(t)) \right] dt. \end{aligned}$$

(25)

A large firm determines its investment, $k_i(t) \ge 0$, for $t \in [0,\infty )$ to maximize (25) subject to the dynamics of knowledge capital (9).

We make the following assumption on the cost function of R &D investment.

Assumption 3

The cost function of the R &D investment is of the following quadratic form:

$$\begin{aligned} c(k_i)=\frac{\beta }{2}k_i^2, \quad \beta >0. \end{aligned}$$

In the following sections, we consider two types of the large firms’ investment strategies and corresponding Nash equilibrium concepts. One is an open-loop Nash equilibrium (OLNE), in which the large firms choose open-loop strategies, that is, their investment strategies are a simple time path at the beginning of the game, and commit themselves to maintaining the pre-announced paths for the entire duration of the game. The other equilibrium concept is a feedback or Markov-perfect Nash equilibrium (MPNE), in which the large firms choose feedback strategies; that is, their investment strategies are a decision rule dependent on the stock K.

3 Dynamic Equilibrium in Open-Loop Strategies

In this section, we consider a situation in which the large firms use open-loop strategies for R &D investment.⁹ Formally, in the OLNE, a large firm i chooses the time path of its investment $\left\{ k_i(t)\right\} _{t=0}^{\infty }$ to maximize (25) subject to (9), taking the time path of other firms’ investment, $\left\{ k_j(t)\right\} _{t=0}^{\infty }$, $j\ne i$, as given. Since this strategy concept requires that the large firms can commit themselves to particular strategy paths at the beginning of the game, we assume that the commitment is credible.

Let us define the current-value Hamiltonian as follows:

$$\begin{aligned} H_i = x^*(K)^2-\frac{\beta }{2}k_i^2+\lambda _i \left[ k_i+\sum _{j\ne i}k_j -\delta K \right] , \end{aligned}$$

where the costate variable $\lambda _i$ represents the shadow value of the knowledge stock K. The necessary conditions are as follows:

$$\begin{aligned}{} & {} \frac{\partial H_{i}}{\partial k_{i}}=-\beta k_{i}+\lambda _{i}\le 0\text { ( }=0\text { if }k_{i}>0)\text {.} \end{aligned}$$

(26)

$$\begin{aligned}{} & {} {\dot{\lambda }}_{i} =r\lambda _{i}-\frac{\partial H_{i}}{\partial K} =(r+\delta )\lambda _{i}-2x^*(K)\frac{dx^{*}(K)}{dK}, \end{aligned}$$

(27)

$$\begin{aligned}{} & {} \lim _{t\rightarrow \infty }e^{-rt}\lambda (t)K(t)=0. \end{aligned}$$

(28)

In light of Assumption 2, the equilibrium output of each large firm, (18), can be rewritten as $x^*(K)=\overline{\xi }+\xi _{0}K$, where

$$\begin{aligned} \overline{\xi }\equiv \frac{2(1-\gamma )\alpha +\gamma \eta \overline{\tau }-(\gamma \eta +2(1-\gamma ))\overline{\sigma }}{\Gamma }, \quad \xi _{0}\equiv \frac{(\gamma \eta +2(1-\gamma ))\sigma _{0}-\gamma \eta \tau _{0}}{ \Gamma }. \end{aligned}$$

Because $\alpha$ is large, $\overline{\xi }>0$, while $\xi _{0}$ can have either sign, as illustrated in Fig. 1. However, the following lemma holds when $\xi _{0}\le 0$.

Lemma 1

For each large firm, it is never optimal to make investment if $dx^*(K)/dK=\xi _0\le 0$.

Proof

See Appendix A. $\square$

In what follows, we focus on the case in which $\xi _0>0$ so that the large firms choose positive levels of R &D investment. From (26), it holds that ${\dot{\lambda }}_i=\beta {\dot{k}}_i$. Thus, the adjoint equation (27) in a symmetric OLNE can be rewritten as

$$\begin{aligned} {\dot{k}} = (r+\delta )k - \frac{2\xi _0}{\beta }\left( \overline{\xi }+\xi _{0}K\right) \end{aligned}$$

(29)

for $K \le {\bar{\sigma }}/\sigma _0$. For $K > {\bar{\sigma }}/\sigma _0$, $dx^*(K)/dK<0$, and thus $k=0$. In addition, in the symmetric equilibrium, (9) can be rewritten as

$$\begin{aligned} {\dot{K}}=mk-\delta K. \end{aligned}$$

(30)

3.1 Existence and Stability of Steady State

The dynamic path of the symmetric OLNE is characterized by the system of linear differential equations (29) and (30). A steady state of this dynamic system can be diagrammatically expressed as an intersection of the ${\dot{k}}=0$ and ${\dot{K}}=0$ loci in a (K, k) plane. From (30), the ${\dot{K}}=0$ locus satisfies $k=(\delta /m)K$. Above this locus (i.e., $k>(\delta /m)K$), ${\dot{K}}>0$ holds, and below this locus (i.e., $k<(\delta /m)K$), ${\dot{K}}<0$ holds. From (29), the ${\dot{k}}=0$ locus satisfies

$$\begin{aligned} k= {\left\{ \begin{array}{ll} \displaystyle \frac{2\xi _0({\bar{\xi }}+\xi _0 K)}{\beta (r+\delta )} &{} \text {for} \quad K \le {\bar{\sigma }}/\sigma _0, \\ 0 &{} \text {for} \quad K > {\bar{\sigma }}/\sigma _0. \end{array}\right. } \end{aligned}$$

Thus, for $K \le {\bar{\sigma }}/\sigma _0$, the ${\dot{k}}=0$ locus has a positive slope:

$$\begin{aligned} \left. \frac{dk}{dK}\right| _{{\dot{k}}=0} =\frac{2\xi _0^2}{\beta (r+\delta )} >0. \end{aligned}$$

Moreover, above this locus (i.e., $k>2\xi _0({\bar{\xi }}+\xi _0)/[\beta (r+\delta )]$), ${\dot{k}}>0$ holds, and below this locus (i.e., $k<2\xi _0({\bar{\xi }}+\xi _0)/[\beta (r+\delta )]$), ${\dot{k}}<0$ holds. Since $2\xi _0{\bar{\xi }}>0$ holds by assumption, there exists a unique interior steady state if the slope of the ${\dot{K}}=0$ locus is steeper than that of the ${\dot{k}}=0$ locus, i.e.,

$$\begin{aligned} \frac{2\xi _0^2}{\beta (r+\delta )}<\frac{\delta }{m}, \end{aligned}$$

(31)

and the level of k at which $K={\bar{\sigma }}/\sigma _0$ satisfying ${\dot{K}}=0$ is larger than the level of k that satisfies ${\dot{k}}=0$, i.e.,

$$\begin{aligned} \frac{2\xi _0 ({\bar{\xi }}+\xi _0{\bar{\sigma }}/\sigma _0)}{\beta (r+\delta )}<\frac{\delta {\bar{\sigma }}}{m \sigma _0}. \end{aligned}$$

(32)

Note, however, that if condition (32) is satisfied, condition (31) is also satisfied. See Fig. 2, which also shows that the steady state is a saddle point.

Proposition 2

Suppose that $\xi _0>0$ and that condition (32) is satisfied. Then, there exists a unique OLNE that achieves the steady-state stock of the knowledge capital

$$\begin{aligned} K^*=\frac{2m \xi _0 {\bar{\xi }}}{\beta (r+\delta )\delta -2m \xi _0^2}. \end{aligned}$$

(33)

The steady state is saddle-point stable.

Fig. 2

The equilibrium path and the steady state of an OLNE

3.2 Feedback Representation of OLNE

Let us focus on the case in which $K_0 <{\bar{s}}/s_0$. Solving the system of linear differential equations (29) and (30), it follows that

$$\begin{aligned} K(t)= & {} \left( K_0-K^*\right) e^{\frac{r-\sqrt{r^2-4\Delta }}{2}t}+K^*, \end{aligned}$$

(34)

$$\begin{aligned} k(t)= & {} \frac{1}{m}\left( \frac{r-\sqrt{r^2-4\Delta }}{2}+\delta \right) \left( K_0-K^*\right) e^{\frac{r-\sqrt{r^2-4\Delta }}{2}t} +\frac{\delta }{m}K^*, \end{aligned}$$

(35)

where $\Delta \equiv -(r+\delta )\delta +2\xi _0^2 m/\beta$, the sign of which is, in light of (31), negative.¹⁰

From (34) and (35), we obtain the feedback representation of the OLNE investment level:

$$\begin{aligned} k(t)= \frac{r+2\delta -\sqrt{r^2-4\Delta }}{2m}K(t) -\frac{r-\sqrt{r^2-4\Delta }}{2m}K^* \equiv k^{OL}(K(t)). \end{aligned}$$

(36)

Since $r+2\delta -\sqrt{r^2-4\Delta }>0$, we obtain the positive sign for $dk^{OL}/dK$, which is also indicated by arrows towards the steady-state point in Fig. 2.¹¹

Proposition 3

Along the OLNE path, each oligopolist’s investment level is increasing in the stock of the knowledge capital.

Proposition 3 has the following important implication. From (25), we observe that the instantaneous payoff is increasing and convex in the knowledge stock k, meaning that the marginal benefit is increasing rather than decreasing. Thus, the greater the stock of knowledge, the more each large firm’s investment level. This finding is similar to the one obtained by Dechert [12], Barucci [4], and Hartl and Kort [20], who consider optimal investment problems for a single firm with the instantaneous profit being nonconcave in the capita stock.¹²

It should be noted that a steady state with a positive and finite level of knowledge stock exists only if the parameter $\beta$ is not too small. For each large firm, both the marginal cost of investment, which is equal to $\beta k$, and the marginal benefit are increasing. Suppose that an equilibrium path starting from $K(0)<K^*$. Given the property that k is increasing in the knowledge capital, if $\beta$ is sufficiently large, the marginal cost of investment increases along the equilibrium path and the gap between the marginal benefit and marginal cost becomes smaller as K increases. However, if $\beta$ is very small, the marginal cost of investment does not increase sufficiently along the equilibrium path, and the gap between the marginal benefit and marginal cost continues to expand. This result is also similar to the ones obtained in the models with a single firm,¹³

3.3 Effects of a Change in m

In this subsection, we examine how the degree of competition among large firms affects these firms’ investment levels and the knowledge stock. We first examine the effect on each firm’s equilibrium investment for a given stock of knowledge, and then we proceed to the effects on the steady-state levels of the knowledge stock and investment.

3.3.1 Effect on the Equilibrium Investment Level

The feedback representation of the equilibrium investment (36) can be rewritten as $k^{OL}(K)=A^o K + B^o$, where

$$\begin{aligned} A^o \equiv \frac{r+2\delta -\sqrt{(r+2\delta )^2-\frac{8\xi _0^2 m}{\beta }}}{2m}> 0, \quad B^o \equiv \frac{\sqrt{(r+2\delta )^2-\frac{8\xi _0^2 m}{\beta }}-r}{\beta (r+\delta )\delta -2m \xi _0^2}\xi _0 {\bar{\xi }}>0. \end{aligned}$$

The sign of $\partial A^o/\partial m$ can be calculated as

$$\begin{aligned} \frac{\partial A^o}{\partial m}= \frac{4\left( -\xi _0+2\frac{\partial \xi _0}{\partial m}m\right) \xi _0 m +\beta (r+2\delta )\left[ r+2\delta -\sqrt{(r+2\delta )^2-\frac{8\xi _0^2 m}{\beta }}\right] }{2m^2\beta \sqrt{(r+2\delta )^2-\frac{8\xi _0^2 m}{\beta }}}, \end{aligned}$$

where the first term in the numerator is negative (recall (22) and that $x^*(K)={\bar{\xi }}+\xi _0 K$) while the second term is positive. The sign of $\partial B^o/\partial m$ can be calculated as

$$\begin{aligned} \frac{\partial B^o}{\partial m}&= \frac{\sqrt{(r+2\delta )^2-\frac{8\xi _0^2 m}{\beta }}-r}{\beta (r+\delta )\delta -2m \xi _0^2} \left( \frac{\partial \xi _0}{\partial m} {\bar{\xi }} +\xi _0 \frac{\partial {\bar{\xi }}}{\partial m} \right) \\&\quad +\frac{2\xi _0^2 {\bar{\xi }} \left[ r^2+2r\delta +2\delta ^2-\frac{4\xi _0^2 m}{\beta } -r\sqrt{(r+2\delta )^2-\frac{8\xi _0^2 m}{\beta }} \right] }{\left[ \beta (r+\delta )\delta -2m \xi _0^2\right] ^2\sqrt{(r+2\delta )^2-\frac{8\xi _0^2 m}{\beta }}} \left( \xi _0+2\frac{\partial \xi _0}{\partial m}m\right) , \end{aligned}$$

where the first term is negative but the second term is ambiguous in sign. Therefore, the signs of $\partial A^o/\partial m$ and $\partial B^o/\partial m$ are generally ambiguous. However, in special cases, we can determine the signs of $\partial A^o/\partial m$ and $\partial B^o/\partial m$.

Proposition 4

Increased competition among large firms has a positive effect on each large firm’s investment level for a given stock of knowledge K in the OLNE if $\gamma$ is close to 0 or 1.

Proof

See Appendix A. $\square$

$\gamma =0$ means that all goods are independent, and $\gamma =1$ means that all goods are homogeneous. As we have shown that in these polar cases, the number of large firms does not affect their equilibrium outputs, increased competition among large firms does not affect their profits. Moreover, for a given investment level k, an increase in m means a larger level of total investment, which leads to a larger stock of knowledge in the future. Anticipating the reduction in the marginal cost $\sigma (K)$ in response to an increase in K, the large firms have an incentive to make more investment in each moment.

In the general case where the firms produce imperfectly substitutable goods (i.e., where $\gamma$ takes intermediate values), however, increased competition has a negative effect on profits, which discourages large firms from investing. Therefore, the effect on the oligopolists’ investment levels is ambiguous.

From Propositions 1 and 4, we obtain the following corollary.

Corollary 1

Increased competition among large firms has a negative effect on the large firms’ short-run profits in the OLNE if $\gamma$ is close to 0 or 1.

Thus, if the large firms use the open-loop strategy, increased competition among large firms is harmful to both large and small firms in the short run under certain conditions.

3.3.2 Effect on the Steady-State Stock of Knowledge Capital

We proceed to the long-run effects of a change in m on the steady-state levels of the stock of knowledge capital. From (22) and (33), the effect of a change in m on $K^*$ can be calculated as follows:

$$\begin{aligned} \frac{\partial K^*}{\partial m} = \frac{2\xi _0{\bar{\xi }}\beta (r+\delta )\delta \left[ 2(1-\gamma )(2-\gamma ) -2\gamma (1-\gamma )m+\gamma (2-\gamma )\eta \right] }{\left[ \beta (r+\delta )\delta -2m \xi _0^2\right] ^2\Gamma }, \end{aligned}$$

(37)

the sign of which depends on the sign of the terms in the square brackets in the numerator.¹⁴ With the restriction that $m<\beta (r+\delta )\delta /(2\xi _0^2)$, we obtain the following proposition.

Proposition 5

Let ${\bar{m}}\equiv (2-\gamma )[2(1-\gamma )+\gamma \eta ]/[2\gamma (1-\gamma )]$. If $m<\min \left\{ \frac{\beta (r+\delta )\delta }{2\xi _0^2},{\bar{m}}\right\}$ (resp. ${\bar{m}}<m<\frac{\beta (r+\delta )\delta }{2\xi _0^2}$), increased competition among the large firms induces an increase (resp. a decrease) in the steady-state stock of the knowledge capital in the OLNE.

Intuitively, an increase in m has two effects that work in opposite directions. On the one hand, it makes the ${\dot{K}}=0$ locus flatter, meaning that for a given level of R &D investment by each oligopolist, the total investment becomes larger as does the steady-state level of the knowledge capital. On the other hand, the increase in m also causes a downward shift in the ${\dot{k}}=0$ locus because the oligopolists’ output and profits become smaller and they have less incentive to invest. If there are relatively few large firms, competition is not severe, meaning that the latter effect is dominated by the former, and thus, an increase in m increases $K^*$. By contrast, if the number of firms is sufficiently large, the latter effect dominates the former, yielding a negative effect of increased competition on the steady-state stock of knowledge.

3.3.3 Effects on the Steady-State Outputs

Since the stock of knowledge capital is endogenously determined, the long-run effects of a change in the number of oligopolists on the steady-state outputs should account for the change in the steady-state stock of knowledge capital $K^*$:

$$\begin{aligned} \frac{dx^*(K^{**})}{d m} = \frac{\partial x^*(K^{*})}{\partial m} +\frac{dx^*(K^{*})}{dK}\frac{\partial K^{*}}{\partial m}, \end{aligned}$$

(38)

and the effect on the long-run equilibrium output of each small firm is

$$\begin{aligned} \frac{dy^*(K^{*})}{d m} = \frac{\partial y(K^{*})}{\partial m} +\frac{dy^*(K^{**})}{dK}\frac{\partial K^{*}}{\partial m}. \end{aligned}$$

(39)

We focus on the case in which the large firms choose positive investment levels, which requires that $dx^*(K^{*})/dK>0$. Thus, if the steady-state stock of knowledge capital is decreasing in m, (38) indicates that the long-run effect of increased competition on the large firms’ output is the same as the short-run effect. However, as shown by Proposition 5, $\partial K^{*}/\partial m$ can take either sign, and thus, the long- and short-run effects on the large firms’ output can differ.

Regarding the long-run effect on small firms’ output, $dy^*(K^{*})/dK$ can take either sign, as illustrated in Fig. 1. Therefore, while increased competition among large firms has a negative effect on the small firms’ output and, thus, profit in the short run, it can be true that its long-run effect is beneficial for the small firms.

We have shown that increased competition among large firms reduces each large firm’s market share in the temporary equilibrium (see (24)). Again, as $\partial K^*/\partial m$ can have either sign, the long-run effect of increased competition on large firm’s market share is indeterminate.

4 Dynamic Equilibrium in Feedback Strategies

We proceed to the case in which the oligopolists choose their investment strategies based on the feedback decision rule, that is, k is dependent on time t and the current state K. However, since none of the functions or parameters of the problem directly depend on time and the time horizon is infinite, the problem is stationary and thus, we consider stationary Markov-perfect strategies, which depend only on K.

4.1 Nash Equilibrium Conditions

To characterize the stationary MPNE, let us define the Hamilton–Jacobi–Bellman (HJB) equation of each oligopolist as follows:

$$\begin{aligned} rV_i(K)= \max _{k_i} \left\{ [x^*(K)]^2-\frac{\beta }{2}k_i^2 +V_i'(K)\left[ k_i+\sum _{j \ne i}k_j(K) -\delta K \right] \right\} , \quad i=1,\ldots ,m,\nonumber \\ \end{aligned}$$

(40)

where $k_j(K)$ is rival firm j’s feedback strategy. The first-order condition for optimal investment is

$$\begin{aligned} -\beta k_i^* + V_i'(K) \le 0 \; (=0 \; \text {if} \; k_i^*>0). \end{aligned}$$

(41)

Lemma 2

Assume that $\xi _0 \le 0$, and thus, $dx^{*}(K)/dK \le 0$ for all $K>0$. Then, the following strategy profiles represent a MPNE:

$$\begin{aligned} \text { for all }i\text {, }k_{i}^{*}(K)=0\text { for all }K\ge 0. \end{aligned}$$

Proof

See Appendix A. $\square$

Therefore, in what follows, we focus on the case in which $\xi _0>0$. From the first-order condition (41) that holds with equality, firm i’s optimal investment can be expressed as a function of K: $k_i=k_i(K)$. We focus on a symmetric equilibrium, that is, $k_i(K)=k(K)$, $i=1,\ldots ,m$.

Given symmetry, the HJB equation (40) can be rewritten as

$$\begin{aligned} rV(K)=[x^*(K)]^2-\frac{\beta }{2}k(K)^2+V'(K)\left[ m k(K)-\delta K\right] . \end{aligned}$$

(42)

Differentiating (42) and substituting $V'(K)=\beta k(K)$ and $V''(K)=\beta k'(K)$, it follows that

$$\begin{aligned} k'(K)=\frac{(r+\delta )\beta k(K)-2x^*(K)\frac{dx^{*}(K)}{dK}}{\beta \left[ (2m-1)k(K)-\delta K\right] }. \end{aligned}$$

(43)

4.2 Linear Markov-Perfect Nash Equilibrium

We focus on the stock of the knowledge capital that satisfies $K<{\bar{\sigma }}/\sigma _0$ and assume that the oligopolists use linear feedback strategies, that is, the equilibrium investment k(K) is a linear function of K.

Let us denote $k(K)=AK+B$, where A and B are parameters to be determined. In light of $x^*(K)={\bar{\xi }}+\xi _0 K$, (43) can be rewritten as

$$\begin{aligned} A=\frac{(r+\delta )\beta (AK+B)-2\xi _0({\bar{\xi }}+\xi _0 K)}{\beta \left[ (2m-1)(AK+B)-\delta K\right] }, \end{aligned}$$

(44)

and the parameters A and B must satisfy this equation for any $K \in [0,{\bar{\sigma }}/\sigma _0)$. There are two pairs of candidates, $(A^+,B^+)$ and $(A^-,B^-)$, for the parameters that satisfy (44):

$$\begin{aligned} A^+\equiv \frac{r+2\delta + \sqrt{(r+2\delta )^2-8(2m-1)\xi _0^2/\beta }}{2(2m-1)}, \quad B^+\equiv \frac{2\xi _0{\bar{\xi }}}{\beta [(r+\delta )-(2m-1)A^+]}; \\ A^-\equiv \frac{r+2\delta - \sqrt{(r+2\delta )^2-8(2m-1)\xi _0^2/\beta }}{2(2m-1)}, \quad B^-\equiv \frac{2\xi _0{\bar{\xi }}}{\beta [(r+\delta )-(2m-1)A^-]}. \end{aligned}$$

The equilibrium investment level must be real valued, which requires that $(r+2\delta )^2-8(2m-1)\xi _0^2/\beta \ge 0$. It also should be nonnegative for any $K \in [0,{\bar{\sigma }}/\sigma _0)$, meaning that $B \ge 0$. Moreover, the stability of the steady state must be satisfied, which requires $mA<\delta$ (see (A8) in Appendix A). Inspecting these conditions, we obtain the following proposition that characterizes the linear MPNE.

Proposition 6

Suppose that $\delta >r$.

• 1. There exists a unique linear MPNE, $k^{LM}(K)=A^{-}K+B^{-}$, if any one of the following conditions is satisfied:

  • (a) $m< \delta /(\delta -r)$ and $\beta > 2\,m^2 \xi _0^2/(mr+\delta )\delta$; or

  • (b) $m\ge \delta /(\delta -r)$ and $\beta \ge 2(2\,m-1)\xi _0^2/(r+\delta )\delta$.

• 2. There exist multiple linear MPNEs, $k^{LM}(K) \in \left\{ A^{+}K+B^{+}, A^{-}K+B^{-}\right\}$, if any one of the following conditions is satisfied:

  • (a) $m< \delta /(\delta -r)$ and $2\,m^2 \xi _0^2/(mr+\delta )\delta \ge \beta \ge 8(2\,m-1)\xi _0^2/(r+2\delta )^2$; or

  • (b) $m\ge \delta /(\delta -r)$ and $2(2\,m-1)\xi _0^2/(r+\delta )\delta > \beta \ge 8(2\,m-1)\xi _0^2/(r+2\delta )^2$.

The equilibrium feedback investment levels are positively related to the stock of knowledge capital.

Proof

See Appendix A. $\square$

Proposition 6 indicates that contrary to the linear-quadratic differential game of voluntary provision of public goods studied in Fershtman and Nitzan [13] and following papers, where the linear feedback strategy yields a unique MPNE, the present dynamic game can yield multiple linear MPNEs. Moreover, we can verify that $A^+>A^->0$; that is, both linear feedback equilibria feature investment by the large firms that is increasing in the stock of knowledge capital (see also Fig. 3).

Fig. 3

Linear MPNEs and steady states

The driving force that derives the results contrary to the previous studies is, as discussed in Sect. 3.2, the fact that the marginal benefit of knowledge capital is increasing. The existing differential game models of voluntary provision of public goods assume that the benefit function is strictly concave, meaning that the marginal benefit of public good stock is decreasing. In the linear-quadratic specification, there are two candidates for feedback investment strategies; one that is increasing in the stock and the other that is decreasing in the stock. To guarantee the stability of the steady state, only the feedback strategy that is decreasing in the stock should be chosen as a linear MPNE. By contrast, in the present model, both of the two candidates for linear MPNEs are increasing in K. Moreover, depending on the parameter values (see the discussion below), both of them can satisfy the stability of the steady state.

Let us define the steady-state stock of knowledge capital corresponding to each linear MPNE as follows:

$$\begin{aligned} K^{+}=\frac{mB^{+}}{\delta -m A^{+}}, \quad K^{-}=\frac{mB^{-}}{\delta -m A^{-}}. \end{aligned}$$

(45)

Comparing the two steady-state stocks, we obtain the following inequality:

$$\begin{aligned} K^{+}-K^{-} =\frac{\sqrt{(r+2\delta )^2-8(2m-1)\xi _0^2/\beta }}{2m-1}(m-1)\delta > 0. \end{aligned}$$

(46)

That is, the linear MPNE with a higher feedback effect achieves a higher steady-state stock of knowledge capital.

Figure 4 illustrates the parameter configurations for the possible linear MPNE(s).¹⁵ As shown in Fig. 4, the linear MPNE does not exist for sufficiently small values of $\beta$, and only $k(K)=A^- K+B^-$ is chosen as a unique MPNE if $\beta$ is sufficiently large. For intermediate values of $\beta$, we have multiple equilibria, i.e., both $k(K)=A^+ K+B^+$ and $k(K)=A^- K+B^-$ are chosen as the linear MPNEs. In addition, for an intermediate value of $\beta$, the unique MPNE $k(K)=A^- K+B^-$ is more likely to exist for smaller values of m even though there can be multiple MPNEs for larger values of m.

Fig. 4

Parameter configurations and linear MPNE

From Fig. 4 and (46), we obtain the following result as a corollary to Proposition 6.

Corollary 2

The smaller the number of large firms m, and/or the higher the marginal investment cost parameter $\beta$, the more likely is the existence of a unique linear MPNE, which is the one that has a smaller feedback effect and achieves a lower steady-state stock of knowledge capital.

Intuitively, Corollary 2, which presents the condition(s) for whether multiple MPNEs or a unique MPNE with the lower feedback effect can be obtained, can be explained as follows. It can be verified that $A^+$ is increasing in $\beta$ and $A^-$ is decreasing in $\beta$. Thus, higher values for $\beta$ means that the slope of the investment function k(K) in Fig. 3 becomes steeper for the one with a larger feedback effect (i.e., $k'(K)=A^+$), whereas it becomes flatter for the one with a smaller feedback effect (i.e., $k'(K)=A^-$). If $\beta$ is sufficiently high, the investment function with a larger feedback effect, $k(K)=A^+ K+B^+$, cannot intersect the steady-state line ${\dot{K}}=0$, and only the investment function with a smaller feedback effect can be achieved as a unique linear MPNE. As discussed in Sect. 3.2, each large firm’s marginal cost of investment and the marginal benefit of knowledge capital accumulation are both increasing. Because of the positive sign of $k'(K)$, an increase in K causes a higher investment of each large firm. However, since the large firms use feedback strategies, each firm recognizes the increase in not only its own investment but also all other large firms’ investments. This feedback effect causes each firm’s anticipation of a higher knowledge stock and thus the greater marginal benefit in the future. A higher value of $\beta$ means a higher marginal cost, but the strong feedback effect (in the case of $k'(K)=A^+$) makes the marginal benefit outweigh the marginal cost. Accordingly, the gap between the marginal benefit and marginal cost continues to expand along the equilibrium path with the larger feedback effect.

As for the effects of the number of large firms m, an increase in m leads to a greater (smaller) free-riding effect because each firm needs to make less (more) investment in order to achieve a certain level of total investment. Thus, for larger values of m, anticipating that the other large firms will free ride on its investment, each large firm’s marginal benefit from knowledge accumulation becomes smaller. This means that even for the equilibrium investment rule with a larger feedback effect, there is more possibility of narrowing the gap between the marginal benefit and marginal cost as K rises. However, for smaller values of m, the opposite can occur; the gap between the marginal benefit and marginal cost widens for the case of larger feedback effect and thus, only the linear MPNE with a smaller feedback effect can be chosen.

The total mass of small firms, $\eta$, affects the parameter configurations for possible linear MPNE(s) via $\xi _0=dx^*(K)/dK$. As

$$\begin{aligned} \frac{\partial \xi _0}{\partial \eta }= \frac{2\gamma (1-\gamma )\left[ \gamma m \sigma _0-(2-\gamma +\gamma m)\tau _0\right] }{\Gamma ^2}, \end{aligned}$$

(47)

an increase in $\eta$ causes upward (downward) shifts in all the boundary curves in Fig. 4 if $\gamma m \sigma _0-(2-\gamma +\gamma m)\tau _0>0 (<0)$. Moreover, as demonstrated in Appendix B, the area for the multiple MPNEs expands (shrinks) if $\gamma m \sigma _0-(2-\gamma +\gamma m)\tau _0>0(<0)$. As shown in Fig. 1, when $\gamma m \sigma _0-(2-\gamma +\gamma m)\tau _0>0(<0)$, the sign of $dy^{*}(K)/dK$ is negative (positive). It therefore follows that if small firms’ temporary equilibrium output is decreasing in the knowledge stock, it is more likely that either no MPNE or multiple MPNEs exist. Intuitively, as small firms do not make R &D investment, an increase in $\eta$ means more free riders. However, if $dy^{*}(K)/dK<0$, the small firms decrease their outputs, which has a positive effect on large firms’ outputs. In this case, the presence of more small firms leads to an increase in the marginal benefit of knowledge capital for large firms. If $\beta$ and thus the marginal cost of investment $\beta k$ is sufficiently small, its gap with the marginal benefit cannot narrow even if the large firms choose the investment strategy with a smaller feedback effect, and accordingly there is no MPNE. If there is a unique linear MPNE, which comes with a smaller feedback effect, under an intermediate value of $\beta$, an increase in $\eta$ can provide the large firms more opportunity to choose the investment strategy with a larger feedback effect.

4.3 Effects of a Change in m

4.3.1 Effects on the Equilibrium Investment Level

Let us begin with the effect of a change in m on the linear MPNE investment for given knowledge stock K. This effect can be obtained by calculating $\partial A/\partial m$ and $\partial B/\partial m$ for $(A,B)\in \{(A^+,B^+), (A^-,B^-)\}$. Although the signs of these derivatives are generally ambiguous, the signs can be determinate if $\gamma$ is close to 0 or 1. Specifically, we obtain the following proposition.

Proposition 7

Suppose that $\gamma$ is close to 0 or 1. If the linear MPNE is $k^{LM}(K)=A^+ K +B^+$, increased competition among large firms has a negative effect on these firms’ investment for a given K. If the linear MPNE is $k^{LM}(K)=A^- K +B^-$, the opposite holds (i.e., the effect is positive).

Proof

See Appendix A. $\square$

Intuitively, even when the large firms use feedback strategies, if the feedback effect is not very large, the properties of the MPNE are qualitatively similar to those of the OLNE. That is, if $\gamma$ is close to 0 or 1, increased competition does not affect their profits, and an increase in m gives the large firms an incentive to make more investment because it leads to an increase in K and thus more benefits for these firms in the future. However, as the large firms use feedback strategies, the increase in the number of contributors to the knowledge capital as a public good enhances the accumulation of knowledge stock even if each contributor does not change its contribution level. In other words, each large firm as an individual contributor has an incentive to free ride on other firms’ contributions. This dynamic free-rider incentive reduces the large firm’s investment when m becomes larger, and this incentive outweighs the aforementioned positive effect of an increase in m on k if the feedback effect is sufficiently large.

Since the large firms’ equilibrium output is decreasing in m as demonstrated in Proposition 1, their short-run profit is decreasing in m if $k^{LM}(K)$ is increasing in m. Then, in light of Proposition 7, the following corollary is established.

Corollary 3

Increased competition among the large firms reduces their short-run profit if $\gamma$ is close to 0 or 1 and if these firms’ linear feedback strategy is $k^{LM}(K)=A^{-}K+B^{-}$.

The linear MPNE $k^{LM}(K)=A^{-}K+B^{-}$ has a similar property to the OLNE regarding the short-run effect of increased competition. However, if the large firms’ feedback strategy is $k^{LM}(K)=A^{+}K+B^{+}$, the result is reversed; increased competition among large firms induces less investment, spending a smaller amount of resource cost for investment. In this case, while increased competition is harmful to small firms, it may benefit large firms.

4.3.2 Effect on the Steady-State Stock of Knowledge Capital

From (45), the effect of a change in m on the steady-state stock of knowledge capital in each linear MPNE is derived as follows:

$$\begin{aligned} \frac{\partial K^{+}}{\partial m}= & {} \frac{B^{+}}{(\delta -mA^{+})^2} \left( \delta +m^2 \frac{\partial A^{+}}{\partial m}\right) +\frac{m}{\delta -mA^{+}}\frac{\partial B^{+}}{\partial m}, \end{aligned}$$

(48)

$$\begin{aligned} \frac{\partial K^{-}}{\partial m}= & {} \frac{B^{-}}{(\delta -mA^{-})^2} \left( \delta +m^2 \frac{\partial A^{-}}{\partial m}\right) +\frac{m}{\delta -mA^{-}}\frac{\partial B^{-}}{\partial m}. \end{aligned}$$

(49)

Although the signs of the above equations are generally ambiguous, we may obtain the comparative static results in the limiting case in which $\gamma$ is close to 0 or 1. In this case, for the feedback solution $k(K)=A^- K +B^-$, both $A^-$ and $B^-$ are increasing in m. Therefore, $\partial K^{-}/\partial m>0$.

Proposition 8

Suppose that $\gamma$ is close to 0 or 1. If the linear MPNE is $k(K)=A^- K +B^-$, increased competition among large firms has a positive effect on the steady-state stock of knowledge capital.

However, $K^{+}$ can be decreasing in m; then, increased competition may reduce the steady-state stock of knowledge capital.

4.3.3 Effects on the Steady-State Outputs

As in the analysis of ONLE, the long-run effects of increased competition among large firms on the steady-state outputs can be expressed by (38) and (39), with $K^*$ being replaced by $K^{+}$ or $K^{-}$. A similar discussion can apply; although an increase in m reduces both large and small firms’ output for a given stock of knowledge capital, the knowledge capital itself is endogenously determined in the long run and can change in either way in response to a change in m. Thus, the long-run effects of increased competition on the equilibrium outputs of the respective firms and the large firm’s market share can differ from the short-run effects.

5 Discussion

5.1 Degree of Market Competition

We have considered the degree of market competition in terms of the number of large firms, m. However, there are also small firms, the total mass of which is $\eta$. As only large firms can invest in R &D, the effects of a change in the degree of market competition on equilibrium outcomes may vary between the case of a change in m and that of a change in $\eta$. In what follows, we examine the effects of a change in $\eta$.

From (18) and (19), we can verify that an increase in $\eta$ reduces the temporary equilibrium outputs for both types of firms if $\gamma \in (0,1)$:

$$\begin{aligned} \frac{\partial x^*(K)}{\partial \eta } =-\frac{2\gamma (1-\gamma )y^*(K)}{\Gamma }<0, \quad \frac{\partial y^*(K)}{\partial \eta } =-\frac{\gamma (2-\gamma )y^*(K)}{\Gamma }<0. \end{aligned}$$

(50)

Thus, Proposition 1 remains valid if we consider an increased competition among small firms.

We next consider the effects on the equilibrium investment rules and the steady-state knowledge stocks.¹⁶ As in the analysis of the effects of a change in m, we focus on the case where $\gamma$ is close 0 or 1. As shown by (50), the large firms’ temporary equilibrium outputs are independent of $\eta$ if $\gamma =0$ (i.e., all goods are independent) or $\gamma =1$ (i.e., all goods are homogeneous). This means that increased competition among small firms does not affect the large firms’ profits. In addition, as only large firms make R &D investment, the number of small firms is irrelevant to the dynamics of knowledge capital. Therefore, if $\gamma$ is close 0 or 1, no matter which type of strategy (i.e., open-loop or feedback) the large firms use, a change in the number of small firms has negligible effects on the large firms’ equilibrium investment levels and the steady-state knowledge stock.

As an extension of this exercise, we may examine the effect of a change in the relative number of large and small firms. That is, suppose that the total number of firms, $m+\eta$, is constant, and consider a change in the market structure such that there are more large firms relative to small firms: $d\eta =-dm<0$. Focusing again on the case where $\gamma$ is close to 0 or 1, Propositions 4, 5, 7, and 8 indicate that an increase in the ratio of large firms in the industry increases the large firms’ investment and the steady-state knowledge stock in the OLNE or the linear MPNE with a smaller feedback effect.

5.2 Assumptions on the Small Firms’ Behavior

We have assumed that the total number of small firms is exogenously given and thus there is no entry or exit of these firms. We have also assumed that only large firms make R &D investment In what follows, we discuss how our finding change under alternative assumptions.

5.2.1 Free Entry of Small Firms

Suppose that small firms have to pay fixed costs of entry, f, and produce their products in every period. Then, the free-entry condition of small firms becomes $(1-\gamma )[y^*(K)]^2=f$, where $y^*(K)$ is given by (19). From this free-entry condition, the number of small firms, $\eta$, is determined and it depends on knowledge capital. Let us denote it by $\eta (K)$. Substituting $\eta =\eta (K)$ into (18), we obtain (see Appendix C.2 for details):

$$\begin{aligned} x^*(K)= \frac{2 \sqrt{(1-\gamma ) f}+\sigma (K)-\tau (K)}{2-\gamma }, \end{aligned}$$

(51)

which is independent of m.

Given the assumption that $\sigma (K)$ and $\tau (K)$ are linear in K, we can derive the OLNE and linear MPNE(s) in the same manner as in the basic model, where the parameters ${\bar{\xi }}$ and $\xi _0$ of the temporary equilibrium output, $x^*(K)={\bar{\xi }}+\xi _0 K$, are now given by

$$\begin{aligned} {\bar{\xi }}\equiv \frac{2\sqrt{(1-\gamma )f}+{\bar{\tau }}-{\bar{\sigma }}}{2-\gamma }, \quad \xi _0\equiv \frac{\sigma _0-\tau _0}{2-\gamma }. \end{aligned}$$

We focus on the case in which $\sigma _0>\tau _0$ so that $dx^*(K)/dK>0$ and the large firms have an incentive to make R &D investment. Propositions 2, 3, and 6 remain valid. Moreover, as the claims in Propositions 4 and 7 are those under the case in which $x^*(K)$ is independent of m, these propositions are also valid in the present model. That is, under free entry of small firms, increased competition among large firms enhances each large firm’s investment for a given knowledge stock if these firms use the open-loop strategy or the linear feedback strategy with a smaller feedback effect. However, if the large firms use the linear feedback strategy with a larger feedback effect, increased competition discourages the investment.

5.2.2 R &D Investment by Small Firms

Since there is a continuum of small firms, each small firm is negligible and the interaction between any two small firms is zero. Although the aggregate market conditions, which are represented by Q, P, and K in this paper, affect any single firm, each small firm considers that any changes in its output or investment do not affect the aggregate variables. This fact implies that if we consider a situation in which the small firms make R &D investment, these firms would choose no investment.

6 Conclusion

This paper developed a dynamic game model of a mixed market with large firms, which conduct R &D investment for knowledge accumulation, and small firms, which are free-riders on the benefits from the knowledge accumulation in the form of a reduction in marginal costs. The presence of free-riding by small firms can make the large firms’ temporary equilibrium outputs decreasing in the stock of knowledge capital for certain parameter configurations. However, in such a case, the large firms have no incentive to make R &D investment. Focusing on the case where the large firms choose positive levels of R &D investment, we demonstrated that a unique OLNE exists while multiple linear MPNEs may exist, and irrespective of the type of equilibrium strategy, the investment levels positively depend on the stock of knowledge capital. We also examined the effects of a change in the number of large firms, which can be interpreted as the degree of competitiveness among these firms. We showed that increased competition among large firms reduces the temporary equilibrium outputs but can increase the steady-state knowledge stock, depending on the strategies chosen by the large firms. We also demonstrated that increased competition may lead to opposite results between the OLNE and linear MPNE. As mentioned in Introduction, there has been mixed empirical evidence concerning the relationship between competitiveness and innovation. Our theoretical results on the relationship between the number of large firms and the equilibrium R &D levels and the steady-state stock of knowledge capital may explain such complex empirical results.

Throughout this paper, we have assumed that both large and small firms determine their outputs simultaneously at each moment in time. However, as large firms are more advantaged than small firms, the large firms may act as Stackelberg leaders. The analysis of sequential moves in the determination of output would be an interesting extension of the present model. In addition, to assess the effects of the degree of competitiveness, we focused on a change in the number of firms. However, there are alternative measures of competitiveness. As discussed in Vives [39], we could also consider a change in the degree of substitutability among products ($\gamma$ in this paper), and it would be interesting to see how the effects of a change in $\gamma$ can differ from the effects of a change in the number of firms. These extensions are left for future research.

Appendices

Appendix A: Proofs

Proof of Lemma 1

If $dx^*(K)/dK\le 0$, (27) indicates that $\lambda _i$ increases over time at a rate higher than r. This means, however, that the transversality condition (28) is violated. The only solution that is consistent with the optimality conditions is $k_i(t)=0$ for all $t \in [0,\infty )$. $\square$

Proof of Proposition 4

From (22), $\partial \xi _0/\partial m=-2\gamma (1-\gamma )\xi _0/\Gamma$, which approaches zero if $\gamma \rightarrow 0$ or $\gamma \rightarrow 1$. Then, the numerator of $\partial A^o/\partial m$ is simplified to $\beta f(m)$, where

$$\begin{aligned} f(m)\equiv (r+2\delta )^2-\frac{4\xi _0^2 m}{\beta } -(r+2\delta )\sqrt{(r+2\delta )^2-\frac{8\xi _0^2 m}{\beta }}. \end{aligned}$$

Note that $\xi _0$ is independent of m. From the definition of $\Delta$, m should be less than $\beta (r+\delta )\delta /(2\xi _0^2)$. Evaluating f(m) at this upper bound, it follows that $f\left( \frac{\beta (r+\delta )\delta }{2\xi _0^2}\right) =2\delta ^2$. In addition, it holds that $f(0)=0$ and

$$\begin{aligned} f'(m)=\frac{4\xi _0^2}{\beta }\left[ \frac{r+2\delta }{\sqrt{(r+2\delta )^2-\frac{8\xi _0^2 m}{\beta }}}-1\right] >0. \end{aligned}$$

Thus, $f(m)>0$ for $m<\beta (r+\delta )\delta /(2\xi _0^2)$. Since the denominator of $\partial A^o/\partial m$ is positive, we can conclude that $\partial A^o/\partial m>0$ for $m<\beta (r+\delta )\delta /(2\xi _0^2)$ if $\gamma \rightarrow 0$ or $\gamma \rightarrow 1$.

With regard to $\partial B^o/\partial m$ when $\gamma \rightarrow 0$ or $\gamma \rightarrow 1$, the first term of $\partial B^o/\partial m$ approaches zero because both $\partial \xi _0/\partial m$ and $\partial {\bar{\xi }}/\partial m$ approach zero. Therefore, the sign of $\partial B^o/\partial m$ depends on the sign of

$$\begin{aligned} g(m)\equiv r^2+2r\delta +2\delta ^2-\frac{4\xi _0^2 m}{\beta }-r\sqrt{(r+2\delta )^2-\frac{8\xi _0^2 m}{\beta }}. \end{aligned}$$

Again, m should be less than $\beta (r+\delta )\delta /(2\xi _0^2)$, and it holds that $g\left( \frac{\beta (r+\delta )\delta }{2\xi _0^2}\right) =0$. It can also be verified that $g(0)=2\delta ^2$ and

$$\begin{aligned} g'(m)=\frac{4\xi _0^2}{\beta }\left[ \frac{r}{\sqrt{(r+2\delta )^2-\frac{8\xi _0^2 m}{\beta }}}-1\right] <0. \end{aligned}$$

Thus, $g(m)>0$ for $m<\beta (r+\delta )\delta /(2\xi _0^2)$.

To summarize, we obtain $\partial A^o/\partial m>0$ and $\partial B^o/\partial m>0$ if $\gamma \rightarrow 0$ or $\gamma \rightarrow 1$. Hence, in each case, for a given K, $k^{OL}(K)=A^o K + B^o$ is increasing in m. $\square$

Proof of Lemma 2

Suppose that firm 1 believes that all other large firms $j=2,3,\ldots ,m$ adopt the strategy $k_{j}^{*}(K)=0$ for all $K\ge 0.$ Then, firm 1 faces the following optimal control problem:

$$\begin{aligned} \max _{k_{1}(t)}\int _{0}^{\infty }e^{-rt}\left[ \pi _{1}(K(t))-\frac{\beta }{2} k_{1}^{2}(t)\right] dt \end{aligned}$$

subject to $k_{1}(t)\ge 0$ and

$$\begin{aligned} {\dot{K}}(t)=k_{1}(t)-\delta K(t), \end{aligned}$$

where $\pi _{1}(K(t))=\left[ x^{*}(K(t))\right] ^{2}$. Since

$$\begin{aligned} \frac{dx^{*}(K)}{dK}= {\left\{ \begin{array}{ll} \xi _{0}\le 0 &{} \text {if }K\in \left( 0,\overline{\sigma }/\sigma _{0}\right) \\ \frac{-\gamma \eta \tau _{0}}{\Delta }<0 &{} \text {if }K\in \left( \overline{\sigma }/\sigma _{0},\overline{\tau }/\tau _{0}\right) \\ 0 &{} \text {if }K>\overline{\tau }/\tau _{0}, \end{array}\right. } \end{aligned}$$

(A1)

it holds that $d\pi _{1}/dK=2x^{*}(K(t))dx^{*}/dK\le 0$.

The current-value Hamiltonian for this dynamic optimization problem is

$$\begin{aligned} H_{1}=\left[ \pi _{1}(K(t))-\frac{\beta }{2}k_{1}^{2}(t)\right] +\lambda _{1}(t) \left[ k_{1}(t)-\delta K(t)\right] . \end{aligned}$$

The optimality conditions are

$$\begin{aligned} \frac{\partial H_{1}}{\partial k_{1}(t)}=-\beta k_{1}^{*}(t)+\lambda _{1}(t)\le 0\text {, }k_{1}^{*}(t)\ge 0\text {, }k_{1}^{*}(t)\left[ \lambda _{1}(t)-\beta k_{1}^{*}(t)\right] =0 \end{aligned}$$

(A2)

and

$$\begin{aligned} {\dot{\lambda }}(t)=(r+\delta )\lambda (t)-\frac{d\pi _{1}}{dK} \end{aligned}$$

(A3)

in addition to the transversality condition. However, from (A1) and (A3), ${\dot{\lambda }}(t)\ge (r+\delta )\lambda (t)$ holds. Thus, if $\lambda (t)$ is ever positive, then

$$\begin{aligned} \lim _{t\rightarrow \infty }e^{-rt}\lambda (t)>0, \end{aligned}$$

which violates the transversality condition. We conclude that along the optimal path, we must have $\lambda (t)\le 0$ for all t. In particular, the path such that $\lambda (t)=0$ identically and $k^{*}(t)=0$ identically is optimal. $\square$

Proof of Proposition 6

As the parameters A and B must satisfy (44) for any $K \in [0,{\bar{\sigma }}/\sigma _0)$, the following system of equations must hold:

$$\begin{aligned}{} & {} K-\text {term:} \quad \beta (2m-1)A^2 -\beta (r+2\delta )A+2\xi _0^2=0, \end{aligned}$$

(A4)

$$\begin{aligned}{} & {} \text {Constant term:} \quad \beta [(2m-1)A-(r+\delta )]B+2\xi _0{\bar{\xi }}=0. \end{aligned}$$

(A5)

Solving (A4) for A, we have

$$\begin{aligned} A=\frac{r+2\delta \pm \sqrt{(r+2\delta )^2-8(2m-1)\xi _0^2/\beta }}{2(2m-1)}. \end{aligned}$$

Since A should be real, we have to assume that $(r+2\delta )^2-8(2m-1)\xi _0^2/\beta \ge 0$, or equivalently,

$$\begin{aligned} \beta \ge \frac{8(2m-1)}{(r+2\delta )^2}\xi _0^2. \end{aligned}$$

(A6)

This condition also indicates that, although there are two candidates for A, both of them must be positive. In other words, if the oligopolists use feedback strategies, the feedback decision rules are such that their investment levels are positively dependent on the stock of knowledge.

Solving (A5) for B, we have

$$\begin{aligned} B= \frac{2\xi _0{\bar{\xi }}}{\beta [(r+\delta )-(2m-1)A]}. \end{aligned}$$

Since $k(K) \ge 0$ for all K, B should be nonnegative.

The steady-state stock of knowledge capital in a linear MPNE is derived as follows:

$$\begin{aligned} {\dot{K}}=m(AK+B)-\delta K=0 \quad \Rightarrow \quad K^{**}=\frac{mB}{\delta -mA}. \end{aligned}$$

(A7)

The steady-state solution must also satisfy the following stability condition:

$$\begin{aligned} \left. \frac{d{\dot{K}}}{dK}\right| _{K=K^{**}}=mA-\delta <0. \end{aligned}$$

(A8)

Therefore, under the parameter restriction (A6), the parameters of the economy must satisfy $mA<\delta$ and $B>0$.

Between the two candidates for the values of A and B that satisfy (44), we begin with a larger value of $A^+$:

$$\begin{aligned} A^{+} \equiv \frac{r+2\delta + \sqrt{(r+2\delta )^2-8(2m-1)\xi _0^2/\beta }}{2(2m-1)}, \quad B^+ \equiv \frac{2\xi _0{\bar{\xi }}}{\beta [(r+\delta )-(2m-1)A^+]}. \end{aligned}$$

We will identify under what parameter values $A^{+}$ and $B^+$ can constitute a linear MPNE. In this case, the stability condition (A8) can be rewritten as follows:

$$\begin{aligned} \frac{m(r+2\delta ) + m\sqrt{(r+2\delta )^2-8(2m-1)\xi _0^2/\beta }}{2(2m-1)}-\delta <0, \end{aligned}$$

which is satisfied if and only if¹⁷

$$\begin{aligned} 2(m-1)\delta>mr \quad \Leftrightarrow \quad m >\frac{2\delta }{2\delta -r} \end{aligned}$$

(A9)

and

$$\begin{aligned} \frac{2 m^2}{(mr+\delta ) \delta }\xi _0^2 > \beta . \end{aligned}$$

(A10)

Since $\xi _0>0$, $B^+\ge 0$ holds iff $r+\delta -(2\,m-1)A^{+}=[r-\sqrt{(r+2\delta )^2-8(2\,m-1)\xi _0^2/\beta }]/2\ge 0$. This inequality is satisfied if and only if

$$\begin{aligned} \frac{2(2m-1)}{(r+\delta )}\xi _0^2 \ge \beta . \end{aligned}$$

(A11)

Note that if $\delta >r$, $2\delta /(2\delta -r)<2$ holds. In this case, under the assumption that $m\ge 2$, the stability condition (A10) is always satisfied. Therefore, $A^{+}$ and $B^+$ can constitute a candidate for a linear MPNE if the parameters satisfy (A9),

$$\begin{aligned} \frac{2m^2}{(mr+\delta )\delta }\xi _0^2 > \beta \ge \frac{8(2m-1)}{(r+2\delta )^2}\xi _0^2, \end{aligned}$$

(A12)

and

$$\begin{aligned} \frac{2(2m-1)}{(r+\delta )\delta }\xi _0^2 \ge \beta \ge \frac{8(2m-1)}{(r+2\delta )^2}\xi _0^2. \end{aligned}$$

(A13)

Since $m^2(r+2\delta )^2-4(2\,m-1)(mr+\delta )\delta =[mr-2(m-1)\delta ]^2 >0$, the left-hand side of inequality (A12) is always larger than the right-hand side. Additionally, since $(r+2\delta )^2-4(r+\delta )\delta =r^2>0$, the left-hand side of inequality (A13) is always larger than the right-hand side. Comparing the left-hand sides of inequalities (A12) and (A13), it follows that

$$\begin{aligned} \frac{2m^2}{(mr+\delta )\delta }- \frac{2(2m-1)}{(r+\delta )\delta } =\frac{2(m-1)[(m-1)\delta -mr]}{(mr+\delta )(r+\delta )\delta }. \end{aligned}$$

As $m \ge 2$, if $(m-1)\delta \ge mr$, or equivalently,

$$\begin{aligned} m\ge \frac{\delta }{\delta -r}, \end{aligned}$$

(A14)

the left-hand side of (A12) is not smaller than the left-hand side of (A13). Since m should be a positive number, $\delta >r$ must hold. In this case, the stability condition (A9) is satisfied and thus a pair of conditions (A13) and (A14) ensures the existence of the linear MPNE with $(A,B)=(A^{+},B^+)$. By contrast, if

$$\begin{aligned} m<\frac{\delta }{\delta -r}, \end{aligned}$$

(A15)

the left-hand side of (A13) is larger than the left-hand side of (A12). In this case, a pair of conditions (A12) and (A15) ensures the existence of the linear MPNE with $(A,B)=(A^{+},B^+)$. Thus, we obtain the following lemma.

Lemma 3

Suppose that $\delta >r$. Then, a linear MPNE $k^{LM}(K)=A^+ K+ B^+$ exists if either a pair of conditions (A13) and (A14) or a pair of conditions (A12) and (A15) is satisfied.

We next consider the smaller value of A and the corresponding value of B that satisfy (44):

$$\begin{aligned} A^- \equiv \frac{r+2\delta - \sqrt{(r+2\delta )^2-8(2m-1)\xi _0^2/\beta }}{2(2m-1)}, \quad B^- \equiv \frac{2\xi _0{\bar{\xi }}}{\beta [(r+\delta )-(2m-1)A^-]}. \end{aligned}$$

The stability condition (A8) can be rewritten as follows:

$$\begin{aligned} \frac{m(r+2\delta ) - m\sqrt{(r+2\delta )^2-8(2m-1)\xi _0^2/\beta }}{2(2m-1)}-\delta <0 \\ \Leftrightarrow \quad m\sqrt{(r+2\delta )^2-8(2m-1)\xi _0^2/\beta }>mr -2(m-1)\delta . \end{aligned}$$

We have shown that if $\delta >r$, $mr -2(m-1)\delta <0$. Thus, the above condition is always satisfied if the condition for A to be a real number, (A6), is satisfied. $B^-\ge 0$ holds if and only if $r+\delta -(2m-1)A^- \ge 0$, which is always satisfied because

$$\begin{aligned} r+\delta -(2m-1)A^-= \frac{r+ \sqrt{(r+2\delta )^2-8(2m-1)\xi _0^2/\beta }}{2}>0. \end{aligned}$$

To summarize, we obtain the following lemma regarding the existence of the linear MPNE with $(A,B)=(A^-,B^-)$.

Lemma 4

Suppose that $\delta >r$. Then, a linear MPNE $k^{LM}(K)=A^- K+ B^-$ exists only if condition (A6) is satisfied.

From Lemmas 3 and 4, we obtain the statement of Proposition 6. Clearly, both $A^+$ and $A^-$ are positive; the linear feedback equilibrium investment is increasing in K in both cases. $\square$

Proof of Proposition 7

Consider a linear MPNE with a larger feedback effect, that is, $k^{LM}(K)=A^+ K+ B^+$. The effect of a change in m on $A^+$ is as follows:

$$\begin{aligned} \frac{\partial A^+}{\partial m} {=} \frac{4(2m-1)\xi _0\left[ \xi _0{-}(2m-1)\frac{\partial \xi _0}{\partial m}\right] {-}\beta (r+2\delta )\left[ r+2\delta {+}\sqrt{(r+2\delta )^2{-}8(2m-1)\xi _0^2/\beta }\right] }{(2m-1)^2 \beta \sqrt{(r+2\delta )^2{-}8(2m-1)\xi _0^2/\beta }}.\nonumber \\ \end{aligned}$$

(A16)

Since both terms in the numerator of (A16) are positive, the sign of $\partial A^+/\partial m$ is generally ambiguous. However, if $\gamma \rightarrow 0$ or 1, the sign is unambiguously negative:

$$\begin{aligned} \frac{\partial A^+}{\partial m}= \frac{4(2m-1)\xi _0^2-\beta (r+2\delta )^2 -\beta (r+2\delta ) \sqrt{(r+2\delta )^2-8(2m-1)\xi _0^2/\beta }}{(2m-1)^2 \beta \sqrt{(r+2\delta )^2-8(2m-1)\xi _0^2/\beta }}<0. \end{aligned}$$

This is because it must hold that $(r+2\delta )^2\ge 8(2\,m-1)\xi _0^2/\beta >4(2\,m-1)\xi _0^2/\beta$.

The effect on $B^+$ is derived as follows:

$$\begin{aligned} \frac{\partial B^+}{\partial m} \!=\! \frac{2\left\{ \left( \xi _0\frac{\partial \xi _0}{\partial m} \!+\!{\bar{\xi }}\frac{\partial {\bar{\xi }}}{\partial m}\right) \left[ r\!+\!\delta \!-\!(2m-1)A^{+}\right] \!+\!\xi _0{\bar{\xi }} \left[ (2m\!-\!1)\frac{\partial A^{+}}{\partial m}\!+\!2A^{+}\right] \right\} }{\beta \left[ r\!+\!\delta \!-\!(2m-1)A^{+}\right] ^2}, \end{aligned}$$

(A17)

which is generally ambiguous in sign. However, if $\gamma \rightarrow 0$ or 1, (A17) can be reduced to

$$\begin{aligned} \frac{\partial B^+}{\partial m} = \frac{2\xi _0{\bar{\xi }} \left[ (2m-1)\frac{\partial A^{+}}{\partial m}+2A^{+}\right] }{\beta \left[ r+\delta -(2m-1)A^{+}\right] ^2}, \end{aligned}$$

where

$$\begin{aligned} (2m-1)\frac{\partial A^+}{\partial m} +2A^{+} = -\frac{4(2m-1)\xi _0^2}{(2m-1)\beta \sqrt{(r+2\delta )^2-8(2m-1)\xi _0^2/\beta }}<0. \end{aligned}$$

Thus, given $\xi _0>0$, $\partial B^+/\partial m<0$.

To summarize, we have

$$\begin{aligned} \frac{\partial k^{LM}(K)}{\partial m} =\frac{\partial A^+}{\partial m}K +\frac{\partial B^+}{\partial m}<0 \end{aligned}$$

(A18)

if $\gamma$ approaches 0 or 1.

We next consider the linear MPNE investment with a smaller feedback effect, $k^{LM}(K)=A^- K +B^-$. The effect on $A^-$ is as follows:

$$\begin{aligned} \frac{\partial A^{-}}{\partial m} {=} \frac{\beta (r+2\delta )\left[ r+2\delta {-}\sqrt{(r+2\delta )^2{-}8(2m-1)\xi _0^2/\beta }\right] {-}4(2m-1)\xi _0\left[ \xi _0{-}(2m-1)\frac{\partial \xi _0}{\partial m}\right] }{(2m-1)^2 \beta \sqrt{(r+2\delta )^2{-}8(2m-1)\xi _0^2/\beta }}.\nonumber \\ \end{aligned}$$

(A19)

If $\gamma \rightarrow 0$ or 1, (A19) can be rewritten as

$$\begin{aligned} \frac{\partial A^{-}}{\partial m} = \frac{\beta (r+2\delta )^2-4(2m-1)\xi _0^2 -\beta (r+2\delta )\sqrt{(r+2\delta )^2-8(2m-1)\xi _0^2/\beta }}{(2m-1)^2 \beta \sqrt{(r+2\delta )^2-8(2m-1)\xi _0^2/\beta }}. \end{aligned}$$

Since $\beta (r+2\delta )^2-4(2m-1)\xi _0^2>0$ and

$$\begin{aligned}{} & {} \left[ \beta (r+2\delta )^2-4(2m-1)\xi _0^2\right] ^2-\left[ \beta (r+2\delta )\sqrt{(r+2\delta )^2-8(2m-1)\xi _0^2/\beta }\right] ^2\\{} & {} \quad =16(2m-1)^2 \xi _0^4>0, \end{aligned}$$

it holds that $\partial A^{-}/\partial m>0$.

The effect on $B^-$ is as follows:

$$\begin{aligned} \frac{\partial B^{-}}{\partial m} = \frac{2\left\{ \left( \xi _0\frac{\partial \xi _0}{\partial m} +{\bar{\xi }}\frac{\partial {\bar{\xi }}}{\partial m}\right) \left[ r+\delta -(2m-1)A^{-}\right] +\xi _0{\bar{\xi }} \left[ (2m-1)\frac{\partial A^{-}}{\partial m}+2A^{-}\right] \right\} }{\beta \left[ r+\delta -(2m-1)A^{-}\right] ^2}.\nonumber \\ \end{aligned}$$

(A20)

If $\gamma \rightarrow 0$ or 1, it follows that

$$\begin{aligned} \frac{\partial B^{-}}{\partial m} = \frac{2\xi _0{\bar{\xi }} \left[ (2m-1)\frac{\partial A^{-}}{\partial m}+2A^{-}\right] }{\beta \left[ r+\delta -(2m-1)A^{-}\right] ^2}, \end{aligned}$$

where

$$\begin{aligned} (2m-1)\frac{\partial A^-}{\partial m} +2A^{-} = \frac{4(2m-1)\xi _0^2}{(2m-1)\beta \sqrt{(r+2\delta )^2-8(2m-1)\xi _0^2/\beta }}>0. \end{aligned}$$

Thus, given $\xi _0>0$, it holds that $\partial B^{-}/\partial m>0$.

To summarize, it holds that

$$\begin{aligned} \frac{\partial k^{LM}(K)}{\partial m} =\frac{\partial A^-}{\partial m}K +\frac{\partial B^-}{\partial m}>0 \end{aligned}$$

(A21)

if $\gamma$ approaches 0 or 1. $\square$

Appendix B: Supplement to Fig. 4

Let us define

$$\begin{aligned} F_1(m,\eta )= & {} \frac{2 (2 m-1) \left\{ \left[ \gamma \eta +2 (1-\gamma )\right] \sigma _0 -\gamma \eta \tau _0\right\} ^2}{(r+\delta )\delta \left\{ 2 (1-\gamma )(2-\gamma )+\gamma \left[ 2(1-\gamma )m+(2-\gamma )\eta \right] \right\} ^2}, \end{aligned}$$

(B1)

$$\begin{aligned} F_2(m,\eta )= & {} \frac{2 m^2 \left\{ \left[ \gamma \eta +2 (1-\gamma )\right] \sigma _0 -\gamma \eta \tau _0\right\} ^2}{(m r+\delta )\delta \left\{ 2 (1-\gamma )(2-\gamma )+\gamma \left[ 2(1-\gamma )m+(2-\gamma )\eta \right] \right\} ^2}, \end{aligned}$$

(B2)

$$\begin{aligned} F_3(m,\eta )= & {} \frac{8 (2m-1) \left\{ \left[ \gamma \eta +2 (1-\gamma )\right] \sigma _0 -\gamma \eta \tau _0\right\} ^2}{(r+2 \delta )^2 \left\{ 2 (1-\gamma )(2-\gamma )+\gamma \left[ 2(1-\gamma )m+(2-\gamma )\eta \right] \right\} ^2}. \end{aligned}$$

(B3)

Clearly, it holds that for any $\eta >0$, $F_1(1/2,\eta )=F_3(1/2,\eta )=0$, $F_2(0,\eta )=0$, $F_1(0,\eta )<0$, and $F_3(0,\eta )<0$. In addition,

$$\begin{aligned} \frac{F_1(m,\eta )}{F_3(m,\eta )}=\frac{(r+2\delta )^2}{4(r+\delta )\delta }=\frac{r^2+4(r+\delta )\delta }{4(r+\delta )\delta }>1 \end{aligned}$$

and thus, $F_1(m,\eta )>F_3(m,\eta )$ for any $(m,\eta )\in {\mathbb {R}}_+^2$.

The graph of $F_1(m,\eta )$ with respect to m has the following properties. Since

$$\begin{aligned} \frac{\partial F_1}{\partial m}= & {} \frac{4\left[ 2(1-\gamma )(2-m\gamma )+(2-\gamma )\gamma \eta \right] \left\{ \left[ \gamma \eta +2 (1-\gamma )\right] \sigma _0 -\gamma \eta \tau _0\right\} ^2}{(r+\delta )\delta \left\{ 2 (1-\gamma )(2-\gamma )+\gamma \left[ 2(1-\gamma )m+(2-\gamma )\eta \right] \right\} ^3}, \\ \frac{\partial ^2 F_1}{\partial m^2}= & {} {-}\frac{16(1-\gamma )\gamma \left\{ (1-\gamma )\left[ 8-(2m+1)\gamma \right] {+}2(2-\gamma )\gamma \eta \right\} \left\{ \left[ \gamma \eta +2 (1-\gamma )\right] \sigma _0 {-}\gamma \eta \tau _0\right\} ^2}{(r+\delta )\delta \left\{ 2 (1-\gamma )(2-\gamma ){+}\gamma \left[ 2(1-\gamma )m+(2-\gamma )\eta \right] \right\} ^4}, \end{aligned}$$

$\partial F_1/\partial m$ is positive (negative) for $m<{\tilde{m}}$ ($m>{\tilde{m}}$) and $\partial ^2 F_1/\partial m^2$ is negative (positive) for $m<\tilde{{\tilde{m}}}$ ($m>\tilde{{\tilde{m}}}$), where

$$\begin{aligned} {\tilde{m}}\equiv \frac{4(1-\gamma )+(2-\gamma )\gamma \eta }{2(1-\gamma )\gamma }, \quad \tilde{{\tilde{m}}}\equiv \frac{(8-\gamma )(1-\gamma )+2(2-\gamma )\gamma \eta }{2(1-\gamma )\gamma }. \end{aligned}$$

The graph of $F_3(m,\eta )$ with respect to m has the same properties. Clearly, ${\tilde{m}}<\tilde{{\tilde{m}}}$ holds. We can also verify that ${\tilde{m}}>2$. To summarize, $F_1(m,\eta )$ and $F_3(m,\eta )$ are increasing and concave in m for $2\le m<{\tilde{m}}$, decreasing and concave in m for ${\tilde{m}}<m<\tilde{{\tilde{m}}}$, and decreasing and convex in m for $\tilde{{\tilde{m}}}<m$. Figure 5 (a) illustrates the graphs of $F_1(m,\eta )$ and $F_3(m,\eta )$.

Fig. 5

Graphs of $F_1(m,\eta )$, $F_2(m,\eta )$, and $F_3(m)$

As for the graph of $F_2(m,\eta )$ with respect to m, we obtain the following properties. Since

$$\begin{aligned} \frac{F_1(m,\eta )}{F_2(m,\eta )}=\frac{(2m-1)(mr+\delta )}{m^2(r+\delta )} =\frac{(m-1) \left[ \delta +m (r-\delta )\right] }{m^2 (\delta +r)}+1, \end{aligned}$$

$F_1(m,\eta )>F_2(m,\eta )$ if $m<\delta /(\delta -r)$ and vice versa. In addition,

$$\begin{aligned} \frac{F_2(m,\eta )}{F_3(m,\eta )} =\frac{m^2(r+2\delta )^2}{4(2m-1)(mr+\delta )\delta } =\frac{\left[ m r-2 \delta (m-1)\right] ^2}{4(2m-1)(mr+\delta )\delta }+1>1 \end{aligned}$$

and thus, $F_2(m,\eta )>F_3(m,\eta )$ for any $(m,\eta )\in {\mathbb {R}}_+^2$. Differentiating $F_2(m,\eta )$ with respect to m yields

$$\begin{aligned} \frac{\partial F_2}{\partial m} {=}\frac{2m\left\{ (2-\gamma )(mr+2\delta )\left[ 2(1-\gamma ){+}\gamma \eta \right] {-}2(1-\gamma )\gamma m^2 r\right\} \left\{ \left[ \gamma \eta {+}2 (1-\gamma )\right] \sigma _0 {-}\gamma \eta \tau _0\right\} ^2}{(mr+\delta )^2 \delta \left\{ 2 (1-\gamma )(2-\gamma )+\gamma \left[ 2(1-\gamma )m{+}(2-\gamma )\eta \right] \right\} ^3}, \end{aligned}$$

which is positive (negative) if and only if

$$\begin{aligned} m<(>) \frac{(2-\gamma )\left[ 2(1-\gamma )+\gamma \eta \right] }{4\gamma (1-\gamma )} \left\{ 1+\sqrt{1+\frac{16\gamma (1-\gamma )\delta }{(2-\gamma )\left[ 2(1-\gamma )+\gamma \eta \right] r}}\right\} . \end{aligned}$$

In addition, it can be verified that evaluated at $m=0$, $\partial F_2/\partial m=0$ and $\partial ^2 F_2/\partial m^2>0$. Thus, the graph of $F_2(m,\eta )$ can be depicted as in Fig. 5 (b).

Since $F_1(m,\eta )$, $F_2(m,\eta )$, and $F_3(m,\eta )$ are proportional to $\xi _0^2$, whether these functions are increasing in $\eta$ depends on the sign of $\partial \xi _0/\partial \eta$. As shown by (47), $\partial \xi _0/\partial \eta >0$ if $\gamma m \sigma _0-(2-\gamma +\gamma m)\tau _0>0$ and vice versa. In addition,

$$\begin{aligned}{} & {} \frac{\partial F_1(m,\eta )}{\partial \eta }-\frac{\partial F_3(m,\eta )}{\partial \eta } =\frac{4 (2 m-1) r^2}{\delta (r+\delta ) (r+2 \delta )^2} \xi _0 \frac{\partial \xi _0}{\partial \eta }, \\{} & {} \frac{\partial F_2(m,\eta )}{\partial \eta }-\frac{\partial F_3(m,\eta )}{\partial \eta } =\frac{4 \left[ 2 \delta +m (r-2 \delta )\right] ^2}{\delta (r+2 \delta )^2 (mr+ \delta )} \xi _0 \frac{\partial \xi _0}{\partial \eta } \end{aligned}$$

and thus, both the difference between $F_1(m,\eta )$ and $F_3(m,\eta )$ and the difference between $F_2(m,\eta )$ and $F_3(m,\eta )$ are positive (negative) if and only if $\partial \xi _0/\partial \eta >0(<0)$. To summarize, an increase in $\eta$ widens (narrows) the area in which there are multiple MPNEs in Fig. 4 if $\gamma m \sigma _0-(2-\gamma +\gamma m)\tau _0>0 (<0)$.

Appendix C: Supplement to Sect. 5

1.1 C.1 Effects of a Change in $\eta$ on Equilibrium Investments and Steady-State Knowledge Stock

We begin with an OLNE, the equilibrium investment rule in which is given by $k^{OL}(K)=A^o K +B^o$. As

$$\begin{aligned} \frac{\partial A^o}{\partial \eta } =\frac{4\xi _0}{\beta \sqrt{(r+2\delta )^2-\frac{8m\xi _0^2}{\beta }}}\frac{\partial \xi _0}{\partial \eta }, \end{aligned}$$

(C1)

the sign of $\partial A^o/\partial \eta$ is the same as that of $\partial \xi _0/\partial \eta$. The effect of a change in $\eta$ on the constant term $B^o$ is as follows:

$$\begin{aligned} \frac{\partial B^o}{\partial \eta }&= \frac{\sqrt{(r+2\delta )^2-\frac{8m\xi _0^2}{\beta }}-r}{\beta (r+\delta )\delta -2m\xi _0^2} \left( \frac{\partial \xi _0}{\partial \eta }{\bar{\xi }} +\xi _0\frac{\partial {\bar{\xi }}}{\partial \eta }\right) \nonumber \\&\quad +4m\xi _0^2{\bar{\xi }} \frac{\beta (r^2+2\delta r+2\delta ^2)-4m\xi _0^2-r\beta \sqrt{(r+2\delta )^2-\frac{8m\xi _0^2}{\beta }}}{\beta \sqrt{(r+2\delta )^2-\frac{8m\xi _0^2}{\beta }}\left[ \beta (r+\delta )\delta -2m\xi _0^2\right] ^2} \frac{\partial \xi _0}{\partial \eta }. \end{aligned}$$

(C2)

The sign of (C2) is generally ambiguous.

We next consider linear MPNE(s). For the effect on the feedback term, $A^+$ or $A^-$, we have the following results:

$$\begin{aligned} \frac{\partial A^+}{\partial \eta }= & {} -\frac{4\xi _0}{\beta \sqrt{(r+2\delta )^2-\frac{8(2m-1)}{\beta }\xi _0^2}}\frac{\partial \xi _0}{\partial \eta }, \end{aligned}$$

(C3)

$$\begin{aligned} \frac{\partial A^-}{\partial \eta }= & {} \frac{4\xi _0}{\beta \sqrt{(r+2\delta )^2-\frac{8(2m-1)}{\beta }\xi _0^2}}\frac{\partial \xi _0}{\partial \eta }. \end{aligned}$$

(C4)

Thus, the sign of $\partial A^-/\partial \eta$ is the same as that of $\partial \xi _0/\partial \eta$, but the sign of $\partial A^+/\partial \eta$ is opposite to that of $\partial \xi _0/\partial \eta$. For the effect on the constant term, it follows that

$$\begin{aligned} \frac{\partial B^+}{\partial \eta }= & {} 2 \frac{\left( \frac{\partial \xi _0}{\partial \eta }{\bar{\xi }}+\xi _0\frac{\partial {\bar{\xi }}}{\partial \eta }\right) \left[ r+\delta -(2m-1)A^+\right] +\xi _0{\bar{\xi }}(2m-1)\frac{\partial A^+}{\partial \eta }}{\beta \left[ r+\delta -(2m-1)A^+\right] ^2}, \end{aligned}$$

(C5)

$$\begin{aligned} \frac{\partial B^-}{\partial \eta }= & {} 2 \frac{\left( \frac{\partial \xi _0}{\partial \eta }{\bar{\xi }}+\xi _0\frac{\partial {\bar{\xi }}}{\partial \eta }\right) \left[ r+\delta -(2m-1)A^-\right] +\xi _0{\bar{\xi }}(2m-1)\frac{\partial A^-}{\partial \eta }}{\beta \left[ r+\delta -(2m-1)A^-\right] ^2}. \end{aligned}$$

(C6)

Again, the signs of (C5) and (C6) are generally ambiguous.

If $\gamma =0$ or $\gamma =1$, we have $\partial {\bar{\xi }}/\partial \eta =\partial \xi _0/\partial \eta =0$. In this case, (C1), (C2), (C3), (C4), (C5), and (C6) are all equal to zero.

1.2 C.2 Derivation of (51)

Substituting (19) into the free-entry condition $(1-\gamma )[y^*(K)]^2=f$ derives the equilibrium mass of small firms as follows:

$$\begin{aligned} \eta (K){=} \frac{(2-\gamma )\alpha {+}\gamma m \sigma (K){-}(\gamma m{+}2-\gamma )\tau (K)}{\gamma (2-\gamma )}\sqrt{\frac{1-\gamma }{f}} {-}\frac{2(1-\gamma )(2-\gamma +\gamma m)}{\gamma (2-\gamma )}.\nonumber \\ \end{aligned}$$

(C7)

Substituting (C7) into (18) and rearranging terms, we obtain (51).