Introduction

Nanofluid transport phenomena have received extensive attention in the past decade or so, following seminal studies by researchers at the Argonne Energy Laboratory in Illinois, USA, in the 1990s (Eastman et al. 2004). Although initially interests in nanofluids were directed at thermal enhancement in transport engineering (automotive, aerospace etc.), applications have significantly diversified in the past decade. New areas in which nanofluids have been deployed include bioconvection in microbial fuel cells (Bég et al. 2013a), electronics cooling (Townsend and Christianson 2009), building physics and contamination control (Kulkarni et al. 2009), pharmacological administration mechanisms (Mody et al. 2013), peristaltic pumps for diabetic treatments (Bég and Tripathi 2012) and solar collectors (Rana et al. 2013a). Experimental works have been complemented in recent years by numerous theoretical and computational simulations. The latter have deployed an extensive range of sophisticated algorithms. Rashidi et al. (2012) used the homotopy analysis method (HAM) and Mathematica symbolic software to analyze coating flows of a vertical cylinder with nanofluids. Rashidi et al. (2013) studied the Von Karman swirl flow of a nanofluid with entropy generation using differential transform methods. Bég et al. (2013b) studied both single and two-phase nanofluid dynamics in circular conduits using finite volume numerical codes. Although nanofluids have largely been simulated as Newtonian fluids, their rheological properties have been established for some time. Important experimental confirmation of nanofluid rheology has been made by Chen et al. (2007) for ethylene glycol-based titania nanofluids. Kedzierski et al. (2010) described the results of a significant series of colloidal dispersions collected as part of the International Nanofluid Property Benchmark Exercise (INPBE). They considered the rheology of seven different fluids that include dispersions of metal-oxide nanoparticles in water, and in synthetic oil, elaborating on the effects of particle shape and concentration on the viscosity of these same nanofluids and benchmarking computations with classical theories on suspension rheology. Further significant studies exploring the non-Newtonian characteristics of nanofluids include Anoop et al. (2009) who considered agglomeration. Kim et al. (2011) showed that rod-like alumina nanoparticles have a sol- or weakly flocculated gel-structure depending on particle concentration and that thermal conductivity rate is enhanced with concentration and is markedly faster in the sol state than in the weakly flocculated gel state. They also observed that when the nanofluid becomes a strongly flocculated gel thermal conductivity remains almost the same as the pure liquid value and that Brownian motion is the key mechanism contributing to enhancing thermal conductivity.

As with Newtonian nanofluid dynamics, non-Newtonian modeling of nanofluid transport phenomena has also attracted significant attention very recently. A diverse range of rheological models have been implemented to simulate different flow characteristics of nanofluid suspensions including Oswald–DeWaele power-law models, viscoelastic models and micro-morphic models. These studies have revealed many interesting features of non-Newtonian nanofluids. Sheu (2011) employed an Oldroyd-B viscoelastic model to study nanofluid convection in a horizontal layer of a saturated porous medium. Goyal and Bhargava (2013) used the Reiner-Rivlin second order rheological model to simulate the effect of velocity slip boundary condition on the flow and heat transfer of non-Newtonian nanofluid over a stretching sheet. They employed a finite element algorithm and examined Brownian motion and thermophoresis effects also. Gorla and Kumari (2012) utilized the Eringen micromorphic model in their analysis of mixed convection non-Newtonian nanofluid flow from a nonlinearly stretching sheet. Hojjat et al. (2012) conducted both analytical and experimental studies of frictional pressure drop of non-Newtonian nanofluids flowing through a horizontal circular tube in both the laminar and the turbulent regimes, for three different types of oxide nanoparticles, γ-Al2O3, CuO, and TiO2, were used for the preparation of nanofluids. They observed that improved heat transfer coefficients are achieved with nanofluids without requiring an increase in the pressure drop. Uddin et al. (2013a) utilized Maple quadrature and a power-law rheological model to investigate nanofluid boundary layer flow in porous media with heat source effects. He et al. (2012) considered laminar forced convective heat transfer of dilute liquid suspensions of nanoparticles (nanofluids) in a straight pipe. Using high shear mixing and ultrasonication methods, they observed that the non-Newtonian character of nanofluids influences the overall thermal enhancement. Estellé et al. (2013) performed experiments on the steady-state rheological behaviour of carbon nanotube (CNT) water-based nanofluid and considered the influence of a controlled pre-shear history on the viscosity. They examined both the effect of the influence of stress rate during pre-shear and the effect of resting time before viscosity measurement, and demonstrated that CNT water-based nanofluid behaves as a viscoelastic media at low shear rate and as a shear-thinning fluid at higher shear rates, with the observed behaviour being a function of shear history due to the breakdown in the structural network of nanofluid agglomerates. It is also observed that the nanofluid can reform at rest. Ellahi et al. (2012) studied analytically using a homotopy method, the fully-developed flow of an incompressible, thermodynamically-compatible non-Newtonian third-grade nanofluid in coaxial cylinders, employing the Reynolds and Vogel variable viscosity models. Akbar and Nadeem (2013) implemented the Eyring-Prandtl rheological fluid model to study peristaltic nanofluid transport in a diverging tube. They used a homotopy perturbation technique to compute the effects of Brownian motion and thermophoresis on velocity, temperature, nanoparticle, and pressure gradient under five different peristaltic waves. Very recently Bég (2013a) used a Lattice Boltzmann method to simulate nanofluid transport in elliptical tubes with the Eringen microstretch model, examining deformability of suspending nanoparticles and gyratory motions of micro-elements. Further studies of nano-rheological flows include Susrutha et al. (2012) who examined experimentally the behaviour of gold-nanofluids with poly (vinylidene fluoride) molecules and Hojjat et al. (2011) who studied power-law nanofluid thermal convection in tubes.

Recently great progress has also been made in a new generation of magnetic nanofluids which provide very desirable features in materials processing, energy applications and also medical engineering. Nkurikiyimfura et al. (2011) have described the excellent thermal and flow control characteristics of magnetic nanofluids which respond to magnetic fields. Such fluids offer many rich problems for mathematical modeling since they amalgamate nanofluid dynamics with the established field of magnetohydrodynamics (MHD). Finite element simulations of the heat and mass transfer characteristics of transient magneto-nanofluid flows in rotating manufacturing processes were reported by Rana et al. (2013b). Ferdows et al. (2013) used Maple software to study the effects of radiative heat transfer on unsteady MHD nanofluid transport from a stretching surface in high-temperature materials processing. Boundary layer flow of magnetic nanofluid with buoyancy forces was examined by Hamad et al. (2011). The most popular mathematical model for boundary layer flows of nanofluids is the Kuznetsov and Nield (2010) theory which incorporates Brownian motion and thermophoresis effects. This model has been implemented successfully in increasingly more complex multi-physical nanofluid problems. For example, Bég et al. (2012) investigated nanofluid transport phenomena in porous media from a sphere using homotopy methods and the Kuznetsov–Nield model.

The above studies have all assumed the no-slip condition at the wall. However in various industrial processes, slip effects can arise at the boundary of pipes, walls, curved surfaces etc. A frequently adopted approach in simulating slip phenomena is the Navier velocity slip condition. Thermal slip may also arise. Recent studies on hydrodynamic slip include the article by Wang (2007) who developed analytical solutions for stagnating Newtonian flows on a cylindrical body. Uddin et al. (2012a) used Lie algebra to derive similarity solutions for double-diffusive convective boundary layer flows with slip. Prasad et al. (2013) used the Keller box finite difference method to simulate numerically the heat transfer in boundary layer slip flow of Casson non-Newtonian fluid from a cylinder. Bég et al. (2011a) employed the network electro-thermal simulation code (PSPICE) to study magneto-convective Von Karman slip flow with radiative heat transfer and slip effects. Hamad et al. (2013) analyzed the composite heat and mass transfer in boundary layer flow with variable diffusivity and hydrodynamic slip and thermal convective boundary conditions. Tripathi et al. (2012) studied the rhythmic flow of Oldroyd-B fractional viscoelastic fluids with wall slip effects. Several studies have also addressed nanofluid slip flows. Uddin et al. (2012b) and Bég (2013b) have studied computationally the magneto-convective Sakiadis nanofluid slip flow with heat source effects. Yang et al. (2012) have considered wall mass flux and slip effect on nanofluid convection from a porous two-dimensional wedge configuration.

In the present work, we extend the work of Andersson and Bech (1992) to analyze the transport of non-Newtonian nanofluids from a linear stretching surface with a hydrodynamic slip boundary condition. A linear group of transformation has been used to develop similarity variables for the two-point boundary value problem. Numerical solutions are obtained with both Maple quadrature and also the Nakamura implicit finite difference technique, showing excellent correlation. Further validation is achieved with simpler models from the published literature. The effect of the emerging thermophysical parameters dictating transport characteristics, on the dimensionless axial velocity, temperature and nanoparticle volume fraction are elaborated in detail. To the authors’ best knowledge, the present problem has not been communicated thus far in the literature and has important applications in nano-technological materials processing.

Governing equations

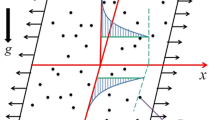
Consider the two-dimensional \((\bar{x},\bar{y})\) steady-state MHD boundary layer slip flow of a an electrically-conducting non-Newtonian power law nanofluid from a heated porous stretching sheet. The nanofluid is assumed to be single phase, in thermal equilibrium and there is a slip velocity between base fluid and particles. The nanoparticles are assumed to have uniform shape and size. The coordinate system and flow regime are illustrated in Fig. 1. Thermophysical properties are assumed to be invariant. A transverse magnetic field of constant strength is imposed in the \(\bar{y}\)-direction. Hall current and Alfven wave effects are neglected as are magnetic induction and Ohmic dissipation. The sheet surface is also assumed to be non-conducting. The governing flow field equations in dimensional form are obtained by combining the models of Andersson and Bech (1992) and Makinde and Aziz (2011):

$$\frac{{\partial \bar{u}}}{{\partial \bar{x}}} + \frac{{\partial \bar{v}}}{{\partial \bar{y}}} = 0,$$
(1)
$$\bar{u}\frac{{\partial \bar{u}}}{{\partial \bar{x}}} + \bar{v}\frac{{\partial \bar{u}}}{{\partial \bar{y}}} = - \frac{K}{\rho }\frac{\partial }{{\partial \bar{y}}}\left( { - \frac{{\partial \bar{u}}}{{\partial \bar{y}}}} \right)^{n}\,-\,\frac{{\sigma B_{0}^{2} }}{\rho }\bar{u},$$
(2)
$$\bar{u}\frac{\partial T}{{\partial \bar{x}}} + \bar{v}\frac{\partial T}{{\partial \bar{y}}} = \alpha \frac{{\partial^{2} T}}{{\partial \bar{y}^{2} }}\,+\,\tau D_{\text{B}} \frac{\partial T}{{\partial \bar{y}}}\frac{\partial C}{{\partial \bar{y}}}\,+\,\tau \left( {\frac{{D_{\text{T}} }}{{T_{\infty } }}} \right){\left(\frac{\partial T}{{\partial \bar{y}}}\right)}^{2},$$
(3)
$$\bar{u}\frac{\partial C}{{\partial \bar{x}}} + \bar{v}\frac{\partial C}{{\partial \bar{y}}} = D_{\text{B}} \frac{{\partial^{2} C}}{{\partial \bar{y}^{2} }}\,+\,\left( {\frac{{D_{\text{T}} }}{{T_{\infty } }}} \right)\frac{{\partial^{2} T}}{{\partial \bar{y}^{2} }},$$
(4)

where \(\alpha = \frac{K}{{(\rho c_{\text{p}} )_{\text{f}} }}\) is the thermal diffusivity of the fluid and \(\tau = \frac{{(\rho c)_{\text{p}} }}{{(\rho c)_{\text{f}} }}\) is the ratio of heat capacities, and all other terms are defined in the notation section. The boundary conditions at the wall (sheet) and in the free stream are prescribed thus:

$$\begin{gathered} \bar{u} = \bar{u}_{\text{w}} + \bar{u}_{\text{slip}} = U_{\text{r}} \left( {\frac{{\bar{x}}}{L}} \right) + N_{1} \nu \left( { - \frac{{\partial \bar{u}}}{\partial y}} \right)^{n - 1} \left( {\frac{{\partial \bar{u}}}{\partial y}} \right),v = \bar{v}(\bar{x}),T = T_{\text{w}} ,C = C_{\text{w}} \quad {\rm at} \, y = 0, \hfill \\ \bar{u} \to 0,T \to T_{\infty } ,C \to C_{\infty } \quad {\rm as} \, y \to \infty . \hfill \\ \end{gathered}$$
(5)

Here Ur is a reference velocity, L is the characteristic of length, and N1 is the slip factor having the dimension (seconds/metres). It needs to be mentioned that for the non-Newtonian power law model, the case of N < 1 is associated with shear-thinning fluids (pseudoplastic fluids), n = 1 corresponds to Newtonian fluids and n > 1 applies to the case of shear-thickening (dilatant).

Fig. 1
figure 1

Coordinate system and flow model

Full size image

Non-dimensionalization

Express the governing equations into dimensionless using following dimensionless boundary layer variables:

$$\bar{x} = \frac{x}{L},\bar{y} = \frac{x}{L}Re_{L}^{{\frac{1}{n + 1}}} ,u = \frac{{\bar{u}}}{{U_{\text{r}} }},v = \frac{{\bar{v}}}{L}Re_{L}^{{\frac{1}{n + 1}}} ,\theta = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }},\phi = \frac{{C - C_{\infty } }}{{C_{\text{w}} - C_{\infty } }}.$$
(6)

We introduce also a stream functions ψ is defined by:

$$u = \frac{\partial \psi }{\partial y},{\,}- v = - \frac{\partial \psi }{\partial x}.$$
(7)

The normalized transformed partial differential conservation equations are thereby reduced to:

$$\frac{\partial \psi }{\partial y}\frac{{\partial^{2} \psi }}{\partial x\partial y}\,-\,\frac{\partial \psi }{\partial x}\frac{{\partial^{2} \psi }}{{\partial y^{2} }}\,-\,n\left( { - \frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{n - 1} \frac{{\partial^{2} \psi }}{{\partial y^{3} }}\,+\,M\frac{\partial \psi }{\partial y} = 0,$$
(8)
$$\frac{\partial \psi }{\partial y}\frac{\partial \theta }{\partial x}\,-\,\frac{\partial \psi }{\partial x}\frac{\partial \theta }{\partial y}\,-\,\frac{1}{{Pr_{L} }}\frac{{\partial^{2} \theta }}{{\partial y^{2} }}\,-\,Nb_{L} \frac{\partial \theta }{\partial y}\frac{\partial \phi }{\partial y}\,-\,Nt_{L} \left( {\frac{\partial \theta }{\partial y}} \right)^{2}\,=\,0,$$
(9)
$$\frac{\partial \psi }{\partial y}\frac{\partial \phi }{\partial x}\,-\,\frac{\partial \psi }{\partial x}\frac{\partial \phi }{\partial y}\,-\,\frac{1}{{Le_{L} }}\frac{{\partial^{2} \phi }}{{\partial y^{2} }}\,-\,\frac{1}{{Le_{L} }}\frac{{Nt_{L} }}{{Nb_{L} }}\frac{{\partial^{2} \theta }}{{\partial y^{2} }}\,=\,0,$$
(10)

The transformed boundary conditions assume the form:

$$\begin{aligned} \frac{\partial \psi }{\partial y} &= x + \frac{{N_{1} \nu }}{{L^{n} }}U_{\text{r}}^{n - 1} Re_{L}^{{\frac{n}{n + 1}}} \left( { - \frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{n - 1} \left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right),\frac{\partial \psi }{\partial x} = {\text{fw}}_{L},\quad \theta = \psi = 1\quad{\text{ at }}y = 0, \\ \frac{\partial \psi }{\partial y} &= \theta = \psi = 0\quad{\text{ as }}y \to \infty . \\ \end{aligned}$$
(11)

In Eqs. (8)–(11), the parameters M, Re L , Pr L , Nb L , Nt L , Le L , fw L denote the magnetic body force parameter, uniform Reynolds number, uniform Prandtl number, uniform Brownian motion parameter, uniform thermophoresis parameter, uniform Lewis number and uniform suction, respectively, and are defined as

$$\begin{aligned} M &= \frac{{\sigma B_{0}^{2} L}}{{\rho cU_{\text{r}} }},\;Re_{L} = \frac{{\rho L^{n} U_{\text{r}}^{2 - n} }}{K},\;Pr_{L} = \frac{{U_{\text{r}} L}}{\alpha }\left( {\frac{{\rho L^{n} U_{\text{r}}^{2 - n} }}{k}} \right)^{{ - \frac{2}{n + 1}}} ,Nb_{L} = \tau D_{\text{B}} \Updelta C\left( {\frac{{U_{\text{r}}^{{\frac{3 - 3n}{2}}} L^{{\frac{n - 1}{2}}} \rho }}{K}} \right)^{{\frac{2}{n + 1}}} , \\ Nt_{L} &= \frac{{\tau D_{\text{T}} \Updelta T}}{{T_{\infty } }}\left( {\frac{{\rho U_{\text{r}}^{{\frac{3 - 3n}{2}}} }}{K}} \right)^{{^{{\frac{2}{n + 1}}} }},\;Le_{L} = \frac{{LU_{\text{r}} }}{{D_{\text{B}} }}\left( {\frac{{\rho L^{n} U_{\text{r}}^{2 - n} }}{K}} \right)^{{ - \frac{2}{n + 1}}} ,{\text{fw}}_{L} = \frac{{v_{\text{w}} Re_{L}^{1/(n + 1)} }}{{U_{\text{r}} }} \\ \end{aligned}$$
(12)

where K is the consistency coefficient of the nano-rheological fluid.

Applications of linear group of transformations

The governing partial differential Eqs. (8)–(10) with the boundary conditions (11) comprise a strongly coupled nonlinear boundary value problem. Totally analytical solutions for such a system are intractable. Additionally numerical solutions of these equations are complicated and computationally expensive. Similarity solutions have been demonstrated to provide an excellent mechanism for further transforming boundary value problems and reducing computational costs, while retaining essentially the physical accuracy of mathematical models. We therefore now implement a group theoretical method which combines the independent two variables (x, y) into a single independent variable (η) and reduce the governing partial differential equations into ordinary differential equations. For this purpose we scale all independent and dependent variables as:

$$\Upgamma :x^{*} = xA^{{\alpha_{1} }},\;y^{*} = yA^{{\alpha_{2} }},\;\psi^{*} = \psi A^{{\alpha_{3} }},\;\theta^{*} = \theta A^{{\alpha_{4} }},\;\phi^{*} = \psi A^{{\alpha_{5} }} ,$$
(13)

where A(α i , i = 1, 2, 3…, 5) are all arbitrary real constants. We seek the values of α i such that the form of Eqs. (8)–(11) is invariant under the transformations in (13). Substituting new variables in Eq. (13) into Eqs. (8)–(11), equating powers of A (to confirm the invariance of the Eqs. (8)–(11) under this group of transformations), we have, following Hansen (1964) and Shang (2010):

$$\begin{aligned} &2\alpha_{3} - 2\alpha_{2} - \alpha_{1} = (n - 1)\alpha_{3} - 2(n - 1)\alpha_{2} + \alpha_{3} - 3\alpha_{2} = \alpha_{3} - \alpha_{2} , \\ &\alpha_{4} + \alpha_{3} - \alpha_{2} - \alpha_{1} = \alpha_{4} - 2\alpha_{2} = \alpha_{4} + \alpha_{5} - 2\alpha_{2} = 2\alpha_{4} - 2\alpha_{2} , \\ &\alpha_{4} + \alpha_{3} - \alpha_{2} - \alpha_{1} = \alpha_{5} - 2\alpha_{2} = \alpha_{4} - 2\alpha_{2} , \\ \end{aligned}$$
(14)

solving the linear system defined by Eq. (14), we arrive in due course at:

$$\alpha_{1} = \frac{n + 1}{2n}\alpha_{3} ,\alpha_{2} = \frac{n - 1}{2n}\alpha_{3} ,\alpha_{4} = \alpha_{5} = 0.$$
(15)

Here at least one of α ≠ 0 (i = 1, 2, 3, 4, 5)-if all α i  = 0, this group method is invalidated, as further elaborated by Hansen (1964). Next, we seek “absolute invariants” under this elected group of transformations. Absolute invariants are the functions possessing the same form before and after the transformation. It is apparent from Eqs. (13) and (15) that:

$$\frac{y}{{x^{{\frac{n - 1}{2n}}} }} = \frac{{y^{*} }}{{x^{{\frac{n - 1}{2n}}} }}.$$
(16)

This combination of variables is therefore invariant under the present group of transformations and consequently, it constitutes an absolute invariant. We denote this functional form by:

$$\eta = \frac{y}{{x^{{\frac{n - 1}{2n}}} }} = \frac{{y^{*} }}{{x^{{\frac{n - 1}{2n}}} }}.$$
(17)

By the same argument, other absolute invariants are readily yielded:

$$\psi = x^{{\frac{2n}{n + 1}}} f(\eta ),\theta = \theta (\eta ),\phi = \phi (\eta ).$$
(18)

Here η is the similarity independent variable, f(η), θ(η), ϕ(η) are the dimensionless stream function, temperature and nanoparticle concentration functions, respectively. Using Eqs. (17) and (18), it emerges that Eqs. (8)–(11) may be written as the following “local similarity” ordinary differential equations:

Momentum conservation

$$n\left( { - f^{\prime \prime} } \right)^{n - 1} f^{\prime \prime \prime}\,+\,\frac{2n}{n + 1}ff^{\prime \prime} - f^{\prime 2} - Mf^{\prime} = 0,$$
(19)

Energy conservation

$$\frac{1}{{Pr_{x} }}\theta^{\prime \prime}\,+\,Nb_{x} \theta^{\prime} \phi^{\prime}\,+\,Nt_{x} \theta^{\prime 2}\,+\,\frac{2n}{n + 1}f\theta^{\prime} = 0,$$
(20)

Species (Nanoparticle concentration) conservation

$$\frac{1}{{Le_{x} }}\phi^{\prime \prime}\,+\,\frac{1}{{Le_{x} }}\frac{{Nt_{x} }}{{Nb{}_{x}}}\theta^{\prime \prime}\,+\,\frac{2n}{n + 1}f\phi ^{\prime} = 0.$$
(21)

The final forms of the wall and edge boundary layer conditions associated with the Eqs. (19)–(21) now become

$$f^{\prime} (0) = 1 + a_{x} \left[ { - f^{\prime \prime} (0)} \right]^{n - 1} f^{\prime \prime} (0),\;f(0) = fw_{x},\;\theta (0) = \phi (0) = 1,\;f^{\prime} (\infty) = \theta (\infty ) = \phi (\infty ) = 0.$$
(22)

Here \(Pr_{x} = Pr_{L} x^{{\frac{2n - 2}{n + 1}}}\) is the local Prandtl number, \(Nb_{x} = Nb_{L} x^{{\frac{2 - 2n}{n + 1}}}\) is the local Brownian motion parameter, \(Nt_{x} = Nt_{L} x^{{\frac{2 - 2n}{n + 1}}}\) is the local thermophoresis parameter, \(Le_{x} = Le_{L} x^{{\frac{2 - 2n}{n + 1}}}\) is the local Lewis number, \(a_{x} = \frac{{N_{1} \nu }}{{L^{n} }}U_{\text{r}}^{n - 1} Re_{L}^{{\frac{n}{n + 1}}} x^{{\frac{n - 1}{n + 1}}}\) is the local momentum slip parameter and \({\text{fw}}_{x} = {\text{fw}}_{L} \frac{n + 1}{2n}x^{{\frac{1 - n}{1 + n}}}\) is the local lateral mass flux (wall suction/injection) parameter. In adopting local similarity solutions, we have deployed a subscript x. This subscript (·) x is now dropped for brevity when referring to the local dimensionless numbers hereafter.

It interesting to note that the transformed local similarity model developed reduces exactly to the Newtonian nanofluid transport model of Makinde and Aziz (2011) and also to that of Noghrebadi et al. (2012) for n = 1 (Newtonian fluids), M = 0 (vanishing magnetic field), fw = 0 (solid wall, i.e., suction/injection absent) and no wall momentum slip. (a = 0) Furthermore the current model retracts to that of Andersson and Bech (1992) for the impermeable wall case (fw = 0) with nanofluid characteristics neglected (i.e., Eq. (21) dropped and Nb = Nt = 0) and with no wall slip (a = 0) Finally the model presented by Xu and Liao (2009) is retrieved in absence of magnetohydrodynamic, species diffusion (nanoparticle) and momentum slip effects. These cases therefore provide excellent benchmarks for validating the numerical solutions developed for the present more general boundary value problem.

Physical quantities

Since our motivation is nano-technological materials processing, a number of engineering design quantities are of great interest. These are the local friction factor, \(C_{{{\text{f}}_{{\bar{x}}} }}\), the local Nusselt number, \(Nu{}_{{\bar{x}}}\) and the local Sherwood number, \(Sh{}_{{\bar{x}}}\) respectively. Physically, \(C_{{{\text{f}}_{{\bar{x}}} }}\) represents the wall shear stress, \(Nu{}_{{\bar{x}}}\) defines the heat transfer rate and \(Sh{}_{{\bar{x}}}\) designates nanoparticle volume fraction gradient (wall species diffusion rate). These quantities can be calculated from the following relations:

$$C_{{{\text{f}}_{{\bar{x}}} }} = \frac{2K}{{\rho \bar{u}_{\text{w}}^{2} }}\left( { - \frac{{\partial \bar{u}}}{{\partial \bar{y}}}} \right)_{{\bar{y} = 0}}^{n},\;Nu_{{\bar{x}}} = \frac{{ - \bar{x}}}{{T_{\text{w}} - T_{\infty } }}\left( {\frac{\partial T}{{\partial \bar{y}}}} \right)_{{\bar{y} = 0}},\;Sh_{{\bar{x}}} = \frac{{ - \bar{x}}}{{C_{\text{w}} - C_{\infty } }}\left( {\frac{\partial C}{{\partial \bar{y}}}} \right)_{{\bar{y} = 0}}^{{}} .$$
(23)

Using Eqs. (6), (17) and (18), we obtain:

$$C_{{{\text{f}}_{{\bar{x}}} }} Re_{{\bar{x}}}^{{\frac{1}{n + 1}}} = 2\left[ {f^{\prime \prime} (0)} \right]^{n},\;Nu_{{\bar{x}}} Re_{{\bar{x}}}^{{ - \frac{1}{n + 1}}} = - \theta '(0),\;Sh_{{\bar{x}}} Re_{{\bar{x}}}^{{ - \frac{1}{n + 1}}} = - \phi^{\prime} (0),$$
(24)

where \(Re_{{\bar{x}}} = \frac{{\bar{u}_{\text{w}} \bar{x}}}{\nu }\) is the local Reynolds number. It is pertinent to highlight that the local skin friction factor, local Nusselt number and local Sherwood number are directly proportional to the numerical values of [−2f″(0)]n, −θ′(0) and \(- \phi \prime (0)\) respectively. In the parlance of Kuznetsov and Nield (2010), \(Nu_{{\bar{x}}} Re_{{\bar{x}}}^{{ - \frac{1}{n + 1}}}\) and \(Sh_{{\bar{x}}} Re_{{\bar{x}}}^{{ - \frac{1}{n + 1}}}\) may be referred as the reduced local Nusselt number, Nur, and reduced local Sherwood number, Shr, for non-Newtonian nanofluids, and are represented by −θ′(0) and \(- \phi \prime (0)\), respectively.

Numerical solutions with maple quadrature

Equations (19)–(21) subject to the boundary conditions (22) have been solved using Runge–Kutta–Fehlberg fourth-fifth order numerical method provided in the symbolic computer software Maple 14. Thermophysical problem solving with Maple has been addressed succinctly in the monograph of Aziz (2010). Maple has become increasingly popular in the 21st century and has been deployed by the authors to resolve many highly coupled, nonlinear thermomechanics problems. These include bioconvection flows as elaborated by Uddin et al. (2013b, c), viscoelastic channel flows reader as examined by Bég and Makinde (2011), hydromagnetic entropy problems in hybrid aerospace propulsion as studied by Makinde and Bég (2010) and thermoelasticity of functional graded materials as described by Tounsi et al. (2013). In the current problem, the asymptotic boundary conditions given in Eq. (22) are replaced by a finite value in the range 15–20 depending on the parameters values. The choice of ηmax must be selected judiciously to ensure that all numerical solutions approached to the asymptotic values correctly. The selection of sufficiently large value for ηmax is imperative for maintaining desired accuracy in boundary layer flows, and is a common pitfall encountered in numerous studies.

Validation with Nakamura difference scheme

The seventh order nonlinear boundary value problem defined by Eqs. (19)–(21), with boundary conditions (22), has also been solved with the exceptionally efficient implicit Nakamura Tridiagonal finite difference Method (NTM) (Nakamura 1994). The NANONAK code has been developed to implement the Nakamura method for nonlinear nano-rheological flow problems. As with other difference schemes, a reduction in the higher order differential equations, is also fundamental to this method. It is also particularly effective at simulating highly nonlinear flows as characterized by nanofluids and also non-Newtonian fluids. The application of Nakamura’s method (and numerous other computational algorithms) to nonlinear magnetofluid dynamics problems has been presented very recently by Bég (2012). NTM works well for both one-dimensional (ordinary differential) similar and two-dimensional (partial differential) non-similar flows. NTM entails a combination of the following aspects.

  • The flow domain for the convection field is discretized using an equi-spaced finite difference mesh in the η direction.

  • The partial derivatives for f, θ, ϕ, with respect to η are evaluated by central difference approximations.

  • A single iteration loop based on the method of successive substitution is utilized due to the high nonlinearity of the momentum, energy and species (nanoparticle) conservation equations.

  • The finite difference discretized equations are solved as a linear second order boundary value problem of the ordinary differential equation type on the η domain.

For the energy and species conservation Eqs. (20), (21) which are second order equations, only a direct substitution is needed. However a reduction is required for the momentum Eq. (19) which is of third order. Setting:

$$P = f^{\prime}$$
(25a)
$$Q = \theta$$
(25b)
$$R = \phi$$
(25c)

The Eqs. (19)–(21) then assume the form:Nakamura momentum equation

$$A_{1} P^{\prime \prime} + B_{1} P^{\prime} + C_{1} P = S_{1}$$
(26)

Nakamura energy equation

$$A_{2} Q^{\prime \prime} + B_{2} Q^{\prime} + C_{2} Q = S_{2}$$
(27)

Nakamura species (nanoparticle diffusion) equation

$$A_{3} R^{\prime \prime} + B_{3} R^{\prime} + C_{3} R = S_{3}$$
(28)

where Ai=1…3, Bi=1…3, Ci=1…3 are the Nakamura matrix coefficients, Si=1…3 are the Nakamura source terms containing a mixture of variables and derivatives associated with the lead variable. The Nakamura Eqs. (26)–(28) are transformed to finite difference equations and these are formulated as a “tridiagonal” system which is solved iteratively.

Results and discussion

Prior to describing full numerical solutions to the present problem, we validate the Maple solutions via selected comparisons with previous studies and furthermore with the NANONAK code. We compare the value of −f″(0) with asymptotic solutions of Andersson and Bech (1992) and homotopy solutions of Xu and Laio (2009) for non-Newtonian fluid in Table 1. Table 2 shows comparison of −f″(0) for various magnetic parameters (M) and rheological power-law index (n) again with Andersson and Bech (1992) and the NANONAK solutions. The numerical results for −θ′(0) computed by Maple 14 are additionally benchmarked with those reported by Grubka and Bobba (1985), Chen (1998) and Ishak (2010) for Newtonian fluids, as presented in Table 3. In all cases we have found very close agreement is achieved and thus great confidence is assured in the accuracy of the Maple numerical results to be reported subsequently. Tables 4 and 5 also document the direct comparison of Maple 14 solutions with NANONAK and once again very close correlation is achieved, further testifying to the validity of the Maple computations.

Table 1 Comparison of −f″(0) for various n when M = 0, a = 0, fw = 0
Full size table
Table 2 Comparison of −f″(0) for various M and n when a = 0, fw = 0
Full size table
Table 3 Comparison of −θ′(0) with published results for various Pr
Full size table
Table 4 Comparison of −f″(0) between Maple and NANONAK for various M and n when a = 0, fw = 0
Full size table
Table 5 Comparison of −θ′(0) between Maple and NANONAK for various Pr
Full size table

Figures 2a–c, 3, 4, 5, 6a, b document the graphical computations for non-Newtonian power-law nanofluid flow characteristics, i.e., dimensionless axial velocity, temperature and nanoparticle concentration for the effects of the dictating thermophysical parameters. Figure 2a–c depict the influence of linear momentum slip (a), mass transfer velocity (fw) and magnetic field (M) on velocity profiles with transverse coordinate (η) for the pseudoplastic cases (n = 0.5) and also n = 1 (Newtonian fluids).

Fig. 2
figure 2

Effects of a momentum slip, b lateral mass flux and c magnetic field on the dimensionless velocity profiles, for pseudoplastic and Newtonian nanofluids

Full size image
Fig. 3
figure 3

Effects of a momentum slip, b lateral mass flux and c magnetic field on the dimensionless temperature profiles, for pseudoplastic and Newtonian nanofluids

Full size image
Fig. 4
figure 4

Effects of a thermophoresis, b Brownian motion and c Prandtl number on the dimensionless temperature profiles, for pseudoplastic and Newtonian nanofluids

Full size image
Fig. 5
figure 5

Effects of a momentum slip, b lateral mass flux and c thermophoresis on the dimensionless concentration profiles, for pseudoplastic and Newtonian nanofluids

Full size image
Fig. 6
figure 6

Effects of a Brownian motion and b Lewis number on the dimensionless concentration profiles, for pseudoplastic and Newtonian nanofluids

Full size image

Inspection of Fig. 2a–c, indicates that the velocity profiles are larger for a pseudoplastic fluid than for Newtonian fluid. Evidently with lower rheological index (n), the viscosity of the nanofluid is depressed and the boundary layer flow is accelerated. Since dilatant fluids are relatively rarely encountered in materials processing, the case of n > 1 is not examined here. Velocity is also found to decrease with increasing parameter momentum slip (Fig. 2a), wall mass flux (Fig. 2b) and magnetic parameter (Fig. 2c). Increased momentum slip (Fig. 2a) imparts a retarding effect to the flow at the wall and this influences the entire flow through the boundary layer, transverse to the wall. With increased mass flux into the sheet regime via the wall (fw < 0, i.e., injection), the boundary layer flow is significantly accelerated, as observed in Fig. 2b. The converse behaviour accompanies increasing mass flux our of the boundary layer (fw > 0, i.e., suction). Evidently the suction effect induces greater adherence to the wall of the fluid regime and this also increases momentum boundary layer thickness. With greater injection, the momentum boost results in a reduction in momentum boundary layer thickness. These computations concur with many previous studies in transpiring boundary layer flows of nanofluids (Rashidi et al. 2013; Goyal and Bhargava 2013; Rana et al. 2013b; Ferdows et al. 2013; Hamad et al. 2011). The case of the impervious sheet, i.e., solid wall (fw = 0) naturally falls between the injection and suction cases. With an increase in magnetic parameter, there is an escalation in magnitude of the Lorentzian hydromagnetic drag force. This very clearly acts to depress velocity magnitudes (Fig. 2c) and even though the magnetic body force is only a linear term [−Mf′ in Eq. (18)] it exerts a very dramatic effect on the flow. Hydrodynamic (momentum) boundary layer thickness is therefore sizeably decreased with increasing values of M. In all three Fig. 2a–c, asymptotically smooth convergence of computations is achieved into the freestream.

Figure 3a–c present the response of temperature profiles, again for both pseudoplastic (n = 0.5) and Newtonian (n = 1) fluids, for a variation in momentum slip, wall mass flux and magnetic parameter. Temperatures are markedly elevated with pseudoplastic fluids compared with Newtonian fluids. Increasing momentum slip significantly increases the temperature magnitudes throughout the boundary layer regime and therefore enhances thermal boundary layer thickness (Fig. 3a). The presence of injection (fw < 0) as elaborated earlier, aids momentum development, i.e., viscous diffusion. This will also serve to encourage thermal diffusion leading to manifestly higher temperatures than for the suction case (fw > 0) which will depress temperatures (Fig. 3b). Injection therefore elevates thermal boundary layer thickness whereas suction decreases it. A similar observation has been reported by Makinde and Aziz (2011) and Rana et al. (2013a), who have also noted, as in the present case, that despite the strong influence of suction in decelerating the flow (and the corresponding cooling of the boundary layer), there is never any flow reversal (velocities are sustained as positive). The Lorentz force magnetohydrodynamic drag generated by the imposition of transverse magnetic field, has the tendency to not only slow down the flow but achieves this at the expense of increasing temperature (Fig. 3c). The supplementary kinetic energy necessary for dragging the magnetic nanofluid against the action of the magnetic field, even at relatively low values of M, is dissipated as thermal energy in the boundary layer. As elucidated by Bég et al. (2011b) this is characteristic of boundary layer hydromagnetics and reproduces the famous “Rossow results”. The overall effect is to boost the temperature. Clearly for the non-conducting case, temperatures will be minimized as magnetic field will vanish. Moreover for the pseudoplastic nanofluid case, temperatures are the highest achieved with the infliction of a magnetic field, and evidently this is beneficial in the synthesis of electro-conductive nanopolymers, as highlighted in the recent theoretical studies by Rana et al. (2013b), Ferdows et al. (2013), and further emphasized in the experimental study of Crainic et al. (2003).

Figure 4a–c depict the evolution of temperature fields with a variation in thermophoresis number (Nt), Brownian motion parameter (Nb) and Prandtl number (Pr), respectively, in all cases for both Newtonian and pseudoplastic nanofluids. A consistent response is not observed in all the temperature profiles with rheological index, as computed in earlier graphs. In Fig. 4a, b, temperatures are maximized for the pseudoplastic case (n = 0.5), whereas in Fig. 4b they are greatest for the Newtonian fluid. Clearly in Fig. 4b, since Brownian motion effect is being varied, this parameter has a complex interaction with the thermal field, which alters the familiar response computed in other figures. Both an increase in Nt and Nb result in a substantial accentuation in temperatures (Fig. 4a, b respectively). This will therefore be accompanied with a significant increase in thermal boundary layer thickness. Thermophoresis relates to increasing nanoparticle deposition on the sheet surface in the direction of a decreasing temperature gradient. As such, the nanofluid temperature is elevated by this enhancement in particle migration, a trend also observed by numerous experimental studies including Eastman et al. (2004) and many theoretical simulations including Kuznetsov and Nield (2010). Within the framework of the Kuznetsov–Nield theory, a nanofluid behaves significantly more as a viscous fluid rather than the conventional solid–fluid mixtures in which relatively larger particles with micrometer or millimeter orders are suspended. Nevertheless, since the nanofluid is a two-phase fluid in nature and has some common features with solid–fluid mixtures, it does exhibit similar shear characteristics. The enhanced heat transfer by the nanofluid may result from either the fact that the suspended particles increase the thermal conductivity of the two-phase mixture or owing to chaotic movement of ultrafine particles accelerating energy exchange process in the fluid. However much needs to be resolved in elucidating more explicitly the exact mechanisms for the contribution of suspended particles to thermal enhancement, and in this regard the micro-structure of the nanofluid (whether Newtonian or non-Newtonian) may provide a more robust fluid dynamical framework. Indeed this has been explored by Gorla and Kumari (2012) with the Eringen micropolar model, and most recently by Bég (2013a) using the Eringen micro-stretch model with greater degrees of freedom of micro-elements. These studies have revealed that the gyratory motions of micro-elements containing the nanoparticles exert a significant influence on thermal transport, and capture features which are basically not realizable even in rheological nanofluid models which neglect microstructural properties. Although the present power-law model would indicate that thermal conductivity is boosted in the nanofluid, it is not possible to analyze whether the spin of nanoparticles is also a contributory factor. It is envisaged therefore that the “microstructural” rheological models of Eringen (2001) which have been reviewed comprehensively in computational micropolar transport modeling by Bég et al. (2011c) will also be deployed for stretching sheet magneto-nanofluid dynamics as explored in the near future. Figure 4c demonstrates that a rise in Prandtl number (Pr) effectively suppresses the nanofluid temperatures. Temperature is however for both Newtonian and non-Newtonian nanofluids, reduced markedly with an increase in Pr. Pr defines the ratio of momentum diffusivity to thermal diffusivity for a given nanofluid. With lower Pr nanofluids, heat diffuses faster than momentum (the energy diffusion rate exceeds the viscous diffusion rate) and vice versa for higher Pr fluids. With an increase in Pr, temperatures will therefore fall, i.e., the nanofluid boundary layer regime will be cooled as observed in Fig. 4c. Larger Pr values correspond to a thinner thermal boundary layer thickness and more uniform temperature distributions across the boundary layer. Smaller Pr nanofluids possess higher thermal conductivities so that heat can diffuse away from the vertical plate faster than for higher Pr fluids (low Pr fluids correspond to thicker boundary layers). We finally note that for the Newtonian case with maximum Pr (=6.8) temperature plummets very sharply from the sheet surface and assumes very low values very quickly. At the other extreme, with the lowest value of Pr (=0.72) a very gentle decay (monotonic descent) is observed from the wall to the free stream.

Figure 5a–c depicts the variation of nanoparticle concentration profiles (ϕ) for Newtonian and pseudoplastic nanofluids, with different values of the momentum slip (a), lateral mass flux (fw) and thermophoresis (Nt) parameters. In all the figures greater concentration magnitudes are attained with pseudoplastic fluids than Newtonian fluids. The concentration profiles increases with increasing wall slip and thermophoresis and furthermore are also enhanced with greater injection at the sheet surface. Enhanced migration of suspended nanoparticles via the mechanisms of thermophoresis, increases energy exchange rates in the fluid and simultaneously assists in nanoparticle diffusion, leading to greater values of (ϕ). The dispersion of nanoparticles will not only successfully heat the boundary layer and augment heat transfer rate from the nanofluid to the wall, but will also enhance concentration (species) boundary layer thicknesses.

Finally Fig. 6a, b, illustrates the nanoparticle concentration distributions with a variation in Brownian motion parameter (Nb) and Lewis number (Le), again for both Newtonian and pseudoplastic nanofluids. The general pattern observed in most of the computations described in earlier figures is confirmed in Fig. 6a, b, namely, that pseudoplastic fluids achieve greater concentration magnitudes relative to Newtonian nanofluids. As indicated in many studies including Kuznetsov and Nield (2010) for Newtonian nanofluids, Sheu (2011) for viscoelastic nanofluids and Uddin et al. (2013a) for power-law nanofluids, an increase in Brownian motion parameter effectively depresses nanoparticle concentrations in the nanofluid regime. This is attributable to the enhanced mass transfer to the sheet wall from the main body of the nanofluid (boundary layer) with increasing Brownian motion. Among others, Rana et al. (2013a, b) have demonstrated that the Brownian motion of nanoparticles achieves thermal conductivity enhancement either by way of a direct effect owing to nanoparticles that transport heat or alternatively via an indirect contribution due to micro-convection of fluid surrounding individual nanoparticles. For larger nanoparticles (and in the present study all nanoparticles in the nanofluid possess consistent sizes) Brownian motion is weakened so that Nb has lower values—this aids in species diffusion from the wall to the nanofluid and elevates nanoparticle concentration values. The exact opposite is manifested with higher Nb values. As anticipated the Brownian motion parameter causes a substantial modification in nanoparticle species distributions throughout the boundary layer regime. An even more dramatic effect is induced on the nanoparticle concentrations, via an increase in the Lewis number (Fig. 6b). This dimensionless number signifies the ratio of thermal diffusivity to mass diffusivity in the nanofluid. It is used to characterize fluid flows where there is simultaneous heat and mass transfer by convection. Le also expresses the ratio of the Schmidt number to the Prandtl number. For Le = 1, both heat and nanoparticle species will diffuse at the same rate. For Le < 1, heat will diffuse more slowly than nanoparticle species and vice versa for Le > 1. For the cases examined here, Le ≥ 1, i.e., thermal diffusion rate substantially exceeds the mass fraction (species) diffusionrate. Inspection of Fig. 6b shows that nanoparticle concentration is clearly also suppressed with an increase in Le. As in all the other graphs, asymptotically smooth results are achieved in the free stream, testifying to the prescription of an adequately large value for infinity in the Maple code.

Conclusions

A laminar transport model has been developed for hydromagnetic nanofluid rheological flow from a stretching permeable sheet subjected to a transverse magnetic field, as a model of nano-magnetic materials processing. Slip effects have been incorporated in the model at the wall (sheet surface) via a Navier momentum slip parameter. Via a suitable group of Lie algebra transformations, the nonlinear two-point boundary value problem has been normalized and formulated as a system of coupled, multi-degree, multi-order nonlinear ordinary differential equations with physically justifiable boundary conditions. Both Maple 14 shooting quadrature and an implicit finite difference algorithm (Nakamura’s method) have been implemented to obtain comprehensive numerical solutions. Additionally the Maple 14 and Nakamura solutions (NANONAK code) have been validated against each other, showing excellent correlation and furthermore have been benchmarked against published works, again achieving exceptionally close agreement. The present solutions obtained have indicated that:

  1. 1.

    Increasing momentum slip parameter decelerates the boundary layer flow (reduces velocities) whereas it generally strongly increases temperatures and nanoparticle concentration values.

  2. 2.

    With increasing wall injection, velocity, temperature and concentration are generally enhanced with the converse behaviour observed with increasing wall suction.

  3. 3.

    Increasing magnetic field parameter markedly decelerates the flow (due to the Lorentzian retarding effect), increases momentum boundary layer thickness and moreover induces a noteworthy elevation in temperatures and thermal boundary layer thickness.

  4. 4.

    Increasing thermophoresis parameter boosts both the temperatures and nanoparticle concentration magnitudes throughout the boundary layer regime.

  5. 5.

    Increasing Brownian motion parameter enhances temperatures strongly whereas it markedly depresses nanoparticle concentration values.

  6. 6.

    Increasing Prandtl number substantially reduces temperatures.

  7. 7.

    Increasing Lewis numbers significantly stifles nanoparticle concentration values.

  8. 8.

    Generally the flow is accelerated, temperatures increased and nanoparticle concentrations boosted for pseudoplastic nanofluids with the converse for Newtonian nanofluids.

The present simulations have been confined to steady-state flows and neglected micro-structural rheological characteristics in nanofluids. Future studies will address both transient effects and utilize a variety of thermo-micromorphic constitutive models, and will be communicated imminently. Furthermore to generalize the study of electro-conductive nanopolymers, future analyses will also address electrical field effects (Bég et al. 2013c).