Effect of aggregation on thermal conductivity and viscosity of nanofluids

Abstract

Nanofluids have drawn large attention because they exhibit anomalous behaviour in their thermo physical properties. There has been an enormous innovation in heat transfer applications of these fluids especially to industrial sectors including transportation, power generation, cooling, thermal therapy for cancer treatment, etc. In the present work, we have studied the anomalous increase in the thermal conductivity and viscosity of nanofluids by taking clustering as one of the causes. It is assumed that the nanoparticles may aggregate on dispersion. Few of these nanoparticles may just touch each other, whereas others may do so along with interfacial layer developed around them (analogous to porous media). The variation in thermal conductivity has been studied with particle concentration, concentration of aggregates and thickness of interfacial layer. The concept of aggregation and equivalent volume fraction has also been used in Kreiger and Dougherty (K-D) model to study the viscosity of nanofluids. The obtained results for thermal conductivity agree well with the available experimental results when the effect of different types of clusters is taken into account. Viscosity increases with the increase in particle aggregate (r_a) and is found to match well for r_a = 3r at low concentration.

Introduction

The ongoing miniaturization of electronic devices, increasing globalisation, increased operating speeds demand more innovative and superior coolants and thus inspire intensive research efforts to explore this area. Application of modern nanotechnology results in a new class of heat transfer fluids termed as “nanofluids”. The term nanofluid was first coined by Choi and Eastman (1995) and these fluids are engineered by dispersing nanoparticles (metallic, oxide nanoparticles, nanofibres and carbon nanotubes) in traditional heat transfer fluids to boost the fluid conductivity.

These nanofluids have advantages over millimetre or micro-sized particles due to the issues of possible sedimentation, clogging, erosion, and excessive pumping power. The use of nanofluids in heat exchangers can produce significant energy and cost savings (Wen et al. 2009). More exotic applications occur in biomedical engineering and medicine in terms of optimal nanodrug delivery (Shawgo et al. 2002) and implantable nanothermal therapeutical devices. During the last decade nanofluid has become focus of research because of the enhanced thermal conductivity that characterizes the strength of heat conduction (Wang and Fan 2010; Choi 2009; Fan and Wang 2011). Developing such effective nanofluids depends very much on the depth of understanding of the involved mechanisms responsible for the significant enhancement of thermal conductivity. However, there is still a lack of agreement even among various experimental results reported by labs worldwide and hence eventually among different proposed theories.

The proposed mechanisms for the explanation of thermal conductivity typically fall into two categories: static and dynamic. Static mechanisms assume that the nanoparticles are stationary in base fluids and mainly focus on factors such as interfacial layer at the particle–liquid interface and particle aggregation, while the dynamic mechanisms include particle Brownian motion and convection in base fluids. There are various classical models which explain the enhancement in the thermal conductivity of nanofluids (Maxwell 1873; Hamilton and Crosser 1962; Masuda et al. 1993; Pak and Cho 1998; Lee et al. 1999; Eastman et al. 2001; Xie et al. 2002; Kwak and Kim 2005; Chon et al. 2005). Recent studies have suggested that nanoparticle aggregation is a dominant mechanism for the experimentally observed thermal conductivity of nanofluids (Hong et al. 2006; Keblinski et al. 2008; Nan et al. 2003; Prasher et al. 2006; Wang et al. 2003). The authors have earlier proposed a model (Gaganpreet and Srivastava 2011) wherein the cluster formation of nanoparticles was taken into account with interfacial layers around them. In addition to the thermal properties, rheological properties of complex fluids are also important parameters in many industrial processes which often affect the final quality of product.

Attempts to understand the viscosity of nanofluids is still sparse as compared with the thermal conductivity literature. There are few models available in literature for colloidal suspensions. Commonly used models predict the effective viscosity of these suspensions (Einstein 1906; Krieger and Dougherty 1959). For high concentration, Einstein model was generalised by Brinkman (1952). Effective nanofluid viscosity models have also been proposed by considering the Brownian motion of nanoparticles (Masoumi et al. 2009). Experimental results have been reported for the effect of aggregation on nanoparticle viscosity of nanofluids (Duan et al. 2011; Chen et al. 2007a, b).

In the present model, a new parameter α₂ as the weight factor has been incorporated into the model which allows us to take into account the formation of different kinds of clusters in the nanofluid which play significant role in conductivity mechanism of heat in nanofluids as well as viscosity.

Theoretical modelling for thermal conductivity

Here, we make use of the involved static mechanisms. It is assumed that there are two paths of heat flow through the suspension: one through the medium and the other by aggregating particles. Aggregating nanoparticles form clusters which may differ in their formation. It is proposed that some clusters may form when the nanoparticles just touch each other with an interfacial layer around them while others are formed without any interfacial layer around them. Also, the nanoparticles inside the fluid no longer retain their original shape but deviate slightly from sphericity which, in turn, enhances their surface properties. This is supported by the experimental evidences provided by the TEM images (Premkumar and Geckeler 2006; Lee et al. 2008) of CuO and Al₂O₃ particles. These particles may take some irregular shape due to coagulation, particle adhesion to wall of the vessel and agglomeration. It may also be due to induced charges if the charged nanoparticles are considered.

However, for the present case, we take the deviated shape of nanoparticles to be prolate spheroid to reduce the mathematical complexity. The overall heat transfer of the system for one-dimensional heat flow may be expressed as

$$ q = q_{\text{m}} + q_{\text{c}} + q_{\text{il}} $$

(1)

where the subscripts m and c denote quantities for medium and clusters, respectively, consisting of nanoparticles without interfacial layer and il for clusters of particles with interfacial layer. After dispersion in the base fluid, there is formation of interfacial layer around the nanoparticles, which may consist of atoms more ordered than that of bulk liquid as shown in Fig. 1. Hence, thermal conductivity of this ordered layer is expected to be higher than that of bulk liquid modifying its thermo physical properties (Lee 2006; Keblinski et al. 2002; Wang et al. 2003; Yu and Choi 2003; Xue 2003). Nanoparticle with nanolayer developed around them can be termed as equivalent nanoparticles suspended in the base fluid (Yu and Choi 2003). The thermal conductivity of the equivalent particles can be expressed using the concept of effective medium theory (Schwartz et al. 1995) as:

Fig. 1

Schematic cross section of nanofluid after dispersion of nano-sized particle in base fluid. a Well-dispersed prolate-shaped nanoparticle with nanolayer around them which deviates from the spherical shape with no overlapping. b Morphological structure aggregate of few nanoparticles inside the fluid

$$ k_{pe} = \frac{{\left[ {2\left( {1 - \sigma } \right) + \left( {1 + \delta_{maj} } \right)\left( {1 + \delta_{\min } } \right)^{2} \left( {1 + 2\sigma } \right)} \right]\sigma k_{p} }}{{\left[ {\left( {\sigma - 1} \right) + \left( {1 + \delta_{maj} } \right)\left( {1 + \delta_{\min } } \right)^{2} \left( {1 + 2\sigma } \right)} \right]}}, $$

(2)

where $\sigma = k_{lr} /k_{p}$ is the ratio of thermal conductivities of interfacial layer to that of the nanoparticle, respectively. Due to these equivalent nanoparticles, volume fraction ϕ of nanoparticles get modified and results in equivalent volume fraction given by

$$ \phi_{m} = \phi \left( {1 + \delta_{maj} } \right)\left( {1 + \delta_{\min } } \right)^{2} , $$

(3)

$$ {\text{Here,}}\quad \delta_{maj} = \frac{h}{a}, \quad \delta_{\min } = \frac{h}{b} $$

(4)

where h is the nanolayer thickness, a and b are the semi major and minor axis of prolate spheroid nanoparticle. The effective thermal conductivity for the medium due to these equivalent nanoparticles for low volume concentration (Maxwell 1954).

$$ K_{m} = \frac{{k_{pe} + 2k_{f} + 2\left( {k_{pe} - k_{f} } \right)\phi_{m} }}{{k_{pe} + 2k_{l} - \left( {k_{pe} - k_{f} } \right)\phi_{m} }}k_{f} . $$

(5)

Following Feng et al. (2007), theoretical formalism has been developed for aggregation structure formed by the prolate-shaped nanoparticles based on the fact that thermal conductivity increases because of aggregating nanoparticles. The particles are generally taken to be in small volume fraction so that the chance of agglomeration is very low (Gharagozloo and Goodson 2010). However, with lapse of time they start forming aggregate structures as shown in Fig. 1b.

Cluster formed by nanoparticles occupy more space than the individual nanoparticles that makes up the cluster as these are porous in nature. The effective volume concentration of aggregates is larger than that of nanoparticles making up the cluster because there is interspace between the aggregated nanoparticles (Feng et al. 2007). Aggregating model has contribution due to two parts: one due to coherent base fluid and the other due to the contribution from one-fourth of column of length 2(b + h) as shown in Fig 2.

Fig. 2

One dimensional heat flow through network consisting of infinitesimal layers of thickness dx

Thus the total volume fraction ϕ _c corresponds to one-fourth of column in the aggregation model as shown in Fig. 2 with the dotted line. Thus, the total volume of the quarter of column is

$$ \phi_{c} = \phi_{m} + \phi_{cf} = 1.5\phi_{m} . $$

(6)

Here, ϕ _cf is the volume fraction of base fluid inside the column. Thus, the upper limit of porosity is ϕ _m  = 2/3. As ϕ _m  → 2/3, the aggregation model contains only a one-fourth column of length 2(b + h) and all the particles are in touching state. In this way the aggregation model can be approximately used to describe a cluster. The effective thermal conductivity, K_il of the aggregation model is

$$ K_{\text{il}} = \left( {1 - 1.5\phi_{\text{m}} } \right)k_{\text{f}} + 1.5\phi_{\text{m}} k_{\text{cl}} . $$

(7)

Here, K_cl is the effective thermal conductivity of a quarter of a column. For the one-dimensional heat flow model, application of thermal electrical analog for the thermal conductivity for touching model has been evaluated as shown in Fig. 2. T₁ and T₂ are the temperatures of the top and bottom surfaces of aggregation column, respectively. The thermal resistance of the layer is in series with infinitesimal thickness dx for each layer. Let dr_p1, dr_p2, dr_bf, and dr_t, be the thermal resistances of upper and bottom part of equivalent particle, of the base fluid and of the total resistance, respectively. The detailed formulation of thermal conductivity of prolate spheroid nanoparticles is given in (Gaganpreet and Srivastava 2011). Nanoparticle is prolate ellipsoidal in shape with the nanolayer thickness h that makes the semi major axis A = a + h and semi minor axis B = b + h (along y and z directions). Here dr_p1, dr_p2, dr_bf are connected in series and hence the total thermal resistance of an infinitesimal layer is given by

$$ \begin{gathered} {\text{d}}r_{\text{t}} = {\text{d}}r_{p1} + {\text{d}}r_{p2} + {\text{d}}r_{\text{bf}} \\ = \frac{{4\left[ {k_{\text{p}} (1 - \gamma \sin \vartheta } \right]}}{{k_{\text{f}} k_{\text{p}} Ad\vartheta }} \\ \end{gathered} $$

(8)

Here $\gamma = 1 - k_{f} /k_{pe}$ and it is a positive fraction. Since the infinitesimal layers are in parallel, the total resistance of the quarter column is

$$ \frac{1}{{R_{\text{t}} }} = \frac{{k_{\text{f}} }}{4}\int\limits_{0}^{2\pi } {\frac{{{\text{d}}\vartheta }}{1 - \gamma \sin \vartheta }} . $$

(9)

Since $\gamma$ is less than 1, the integrand is analytic or finite for all $\vartheta.$ Being rational function, it is single-valued and we can carry out the above integration using calculus of residues. Since the conductivity enhancement in the parallel mode can be much larger than that of series mode, it corresponds to a geometric configuration that allows the most efficient way of heat propagation

$$ \frac{1}{{R_{t} }} = \frac{{\pi k_{\text{f}} A}}{{2\sqrt {\left( {1 - \gamma^{2} } \right)} }}. $$

(10)

Using the Fourier law of heat conduction, the effective thermal conductivity of quarter of column k_cl is obtained to be

$$ k_{\text{cl}} = \frac{{4k_{f} }}{{\sqrt {1 - \gamma^{2} } }}. $$

(11)

Thus, the effective thermal conductivity of the equivalent nanoparticles defined by the formation of clusters is given by

$$ K_{\text{il}} = \left( {1 - 1.5\phi_{\text{m}} } \right)k_{\text{f}} + \frac{{6\phi_{\text{m}} }}{{\sqrt {\left( {1 - \gamma^{2} } \right)} }}k_{{{\text{f}}.}} $$

(12)

Now let us consider the contribution to the thermal conductivity of nanofluids from the aggregates formed by the particles without interfacial layer. The effective stagnant thermal conductivity of spatially porous media of solid cubes with thermal resistance is shown in Fig 3.

Fig. 3

Aggregation structure of porous cluster formed by particles without interfacial layer around them

The thermal conductivity of these clusters in nanofluids is given by (Hsu et al. 1995)

$$ \begin{gathered} k_{\text{ce}} = \left[ {\left( {1 - \varsigma_{r}^{2} - 2\varsigma_{c} \varsigma_{r} + 2\varsigma_{c} \varsigma_{r}^{2} } \right) + \frac{{\varsigma_{c}^{2} \varsigma_{r}^{2} }}{\lambda }} \right. \\ + \left. {\frac{{\varsigma_{r}^{2} - \varsigma_{c}^{2} \varsigma_{r}^{2} }}{{1 - \varsigma_{r} + \varsigma_{r} \lambda }} + \frac{{2\left( {\varsigma_{c} \varsigma_{r} - \varsigma_{c} \varsigma_{r}^{2} } \right)}}{{1 - \varsigma_{c} \varsigma_{r} + \varsigma_{c} \varsigma_{r} \lambda }}} \right]K_{\text{f}} \\ \end{gathered} $$

(13)

where $\lambda = k_{f} /k_{p}$ is the ratio of thermal conductivities of fluids and particles, respectively. Effective volume fraction of porous cluster in the fluid is

$$ \phi_{\text{ce}} = \phi /\left( {\left( {1 - 3\varsigma_{c}^{2} } \right)\varsigma_{r}^{3} + 3\varsigma_{c}^{2} \varsigma_{r}^{2} } \right). $$

(14)

Here, $\varsigma_{r} = r/l$ is the ratio of nanoparticle radius to length of unit cell and $\varsigma_{c} = c/r$ ratio of width of thermal resistance to the nanoparticle radius. The parameter $\varsigma_{r}$ and $\varsigma_{c}$ describe the compactness and perfectness of contact between the nanoparticles in the cluster, respectively. Figure 3 shows the picture of the porous clusters formed by the cubes (Jie et al. 2006). A higher value of $\varsigma_{r}$ implies that the nanoparticles aggregate more loosely. A higher value of $\varsigma_{c}$ implies the smaller contact resistance between the nanoparticles in the cluster. If nanoparticles without interfacial layer agglomerate to form clusters the thermal conductivity has the following form (Jie et al. 2006).

$$ K_{c} = \left[ {\frac{{k_{\text{ce}} + 2k_{\text{f}} + 2\left( {k_{\text{ce}} - k_{\text{f}} } \right)\phi_{\text{ce}} }}{{k_{\text{ce}} + 2k_{\text{f}} - \left( {k_{\text{ce}} - k_{\text{f}} } \right)\phi_{\text{ce}} }}} \right]k_{\text{f}} . $$

(15)

Depending on the weight factor α₁ which is the ratio of aggregating particles to all nanoparticles and α₂ the weight factor which allows both types of cluster consisting of particles with and without interfacial layer between them, the dimensionless effective thermal conductivity can be approximated by

$$ \frac{{K_{\text{eff}} }}{{k_{\text{f}} }} = \left( {1 - \alpha_{1} } \right)K_{\text{m}} + \alpha_{2} \alpha_{1} K_{c} + \left( {1 - \alpha_{2} } \right)\alpha_{1} K_{\text{il}} . $$

(16)

For calculations, we took $\alpha_{1} = \phi_{m}$ and $\alpha_{2}$ as varying parameters.

Effective viscosity of nanofluids

Using the concept of equivalent particle volume fraction and the aggregation formation of nanoparticles (Chen et al. 2007a, b), we use the Kreiger and Dougherty (K-D) model (Krieger and Dougherty 1959) to determine the effective viscosity as

$$ \frac{{\mu_{eff} }}{{\mu_{f} }} = \left( {1 - \frac{{\phi_{a} }}{{\phi_{m} }}} \right)^{{ - \left[ \eta \right]\phi_{md} }} . $$

(17)

Here [η] is the intrinsic viscosity with a value of 2.5 for hard spherical particles. ϕ _md is the volume fraction of densely packed spheres, ϕ _a is the volume fraction of aggregates, expressed as

$$ \phi_{a} = \phi \left( {\frac{{r_{\text{a}} }}{r}} \right)^{{3 - d_{f} }} . $$

(18)

r_a is the radius of aggregates, r is the nominal radius of particle, d_f is the fractal dimension of aggregates and is the volume fraction of the well-dispersed individual particle. However, gets modified due to the formation of interfacial layer around spherical nanoparticles as.

$$ \phi_{\text{me}} = \phi \left( {1 + \frac{h}{r}} \right)^{3} . $$

(19)

Here, r is the radius of nanoparticles. Therefore, ϕ_me = ϕ_a and Eq. (17) is used to find out the effective viscosity of nanofluids.

Results and discussion

Using Eqs. (15) and (16), the thermal conductivity of nanofluids of Al₂O₃-water nanofluid has been plotted as function of particle volume concentration and is shown in Fig. 4. The parameters for Al₂O₃-water are k_p = 46.0(W/m–K), k_f = 0.604 (W/m–K), r = 30.2 nm, k_lr = 2k_f, c = 8 nm, l = 31 nm, h = 2 nm, eccentricity e = 0.04.

Fig. 4

Variation of the effective thermal conductivity of Al₂O₃-water system with particle volume concentration

The graph shows that the thermal conductivity of nanofluids significantly increases with increase in particle volume concentration. The graphs have been drawn for α₂ = 0.1 and 0.2. Our results compare well with available experimental results (Xie et al. 2002) for α₂ = 0.2. This value of α₂ gives the measure of the type of cluster formation. These results have also been compared with those reported by Feng et al. (2007). Figure 5 depicts the plot of effective thermal conductivity for Al₂O₃-ethylene glycol system with k_p = 46.0(W/m–K), k_f = 0.258(W/m–K), r = 13 nm, k_lr = 1.5k_f, c = 3 nm, l = 14 nm, h = 1 nm and eccentricity e = 0.04.

Fig. 5

Variation of effective thermal conductivity with particle volume concentration at r = 13 nm for Al₂O₃-ethylene glycol nanofluid

Some research workers have also pointed out that the thermal conductivity of fluid decreases with increase in concentration of aggregation in the fluid (Jie et al. 2006; Karthikeyan et al. 2008). This is understandable as one expects that the aggregation of nanoparticles leading to large size clusters would eventually sediment down to the bottom of nanofluids rather than participating in the enhancement process of thermal conductivity of nanofluids.

Viscosity of nanofluids

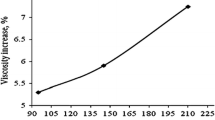
For viscosity of nanofluids, we used Eq. (17) to plot relative viscosity as function of volume concentration for TiO₂-deionised water (DIW) as shown in Fig. 6. Size of aggregates have been chosen to be r_a = 3r, 4r, and 5r. Results have been compared with those reported by Murshed et al. (2008).

Fig. 6

Effective viscosity as function of volume concentration at different size of particle aggregates r_a

The graph of relative viscosity of TiO₂-DIW nanofluid as a function of particle size has been depicted in Fig. 7. The graph corresponds to ϕ = 0.016 and interfacial thickness h = 1 nm and 2 nm. When we compare with the experimental result of Murshed et al. (2008), we find that the results match well with h = 2 nm for particle size 15 nm. Thus, we conclude that the interfacial layer formed around 15-nm-sized particle is roughly of thickness h = 2 nm.

Fig. 7

Relative viscosity of TiO₂ –DIW nanofluid as function of particle size at φ = 0.016, r_a = 4r for h = 1 nm and 2 nm

Conclusions

In the present study, the effective thermal conductivity and relative viscosity has been investigated theoretically as a function of particle volume concentrations, particle size, and concentration of aggregate nanoparticles. We focussed on static mechanism i.e., aggregation of nanoparticle formation inside the fluid. The obtained result matches well with the available experimental results to a great extent for thermal conductivity as concentration of α₂ aggregation increases. This new proposed model gives better results than the earlier model formulated by the authors (Gaganpreet and Srivastava 2011) in which only the concept of clusters of nanoparticles with interfacial layers was used, whereas in the present model, a new aspect α₂ as the weight factor has been incorporated into the model. Hence, we can conclude that formation of different kinds of clusters play important role in conductivity mechanism of heat in nanofluids. Relative viscosity of nanofluids has been predicted with the modified K-D equation which matches well the available data for TiO₂-DIW spherical nanoparticles with an aggregate size of r_a = 3r. As this size of nanoparticle aggregates is increased, the viscosity is found to increase at much faster rate and show a behaviour which is almost independent of the nanofluid volume fraction.