Introduction

Formation resistivity factor is an important petrophysical property that has been widely used for reservoir characterization. Cementation factor, the \(m\) exponent in Archie's law, is a crucial parameter in the estimation of water saturation (\(S_{w}\)) of reservoir rocks (Archie 1942). The value of the cement factor is strongly influenced by the pressure and temperature conditions of the reservoir, size of the pore throat, secondary porosity, electrical conductivity of water, lithology, mineralogy, specific surface area, tortuosity factor, packing index, and degree of cementation (Winsauer et al. 1952; Wardlaw 1980; Ransom 1984; Salem 1993a; Elias and Steagall 1996; Abedini et al. 2011; August et al. 2022; Rashid et al. 2022; Wan Bakar et al. 2022). Therefore, it has become an area of interest to lower the uncertainties associated with cementation factor estimation by demonstrating the impact of different parameters (Winsauer et al. 1952; Wyllie and Gregory 1953; Hill and Milburn 1956; Towle 1962; Helander and Campbell 1966; Waxman and Thomas 1972; Jackson et al. 1978; Biella 1981; Wong et al. 1984; Givens 1987; Brown 1988; Donaldson and Siddiqui 1989; Salem 1993b; Huang et al. 2019; Tan et al. 2020; Zheng et al. 2022).

Laboratory measurement through special core analysis (SCAL) represents the most accurate approach to the quantification of cementation factor. Although several alternative empirical equations have been presented in the literature for determining \(m\), these equations may not capture the effects of geological settings other than the ones on which basis they have been originally developed (Kadhim et al. 2013). Al-Ofi et al. (2022) generated artificial continuous logs of Archie’s parameters by interpreting downhole dielectric logs. Rock classification has been introduced in different studies as a workaround for improving the estimation of cementation factor. For instance, Saner et al. (1996) pointed out that discrimination of electro-facies in reservoir is necessary to obtain accurate values of \(m\). Focke and Munn (1987) attempted to reduce the scattering of electrical data by classifying them into four groups based on permeability and presented independent correlations to relate \(m\) to porosity for different groups. Rezaee et al. (2007) extended the flow zone indicator (FZI) technique of Amaefule et al. (1993) and defined current zone indicator (CZI) to classify samples into electrical flow units (EFUs) and hence predict changes in cementation factor, tortuosity, and water saturation. Recently, Soleymanzadeh et al. (2018) presented electrical quality index (EQI), in analogy with reservoir quality index (RQI), as a clustering criterion for electrical rock typing. Through the conventional EQI method, samples are manually categorized into distinct electrical rock types (ERTs), with each ERT characterized by a specific range of EQI. Soleymanzadeh et al. (2018) stated that the EQI method is a proper alternative approach for estimating cementation factor given that this factor is affected mainly by the electrical properties of reservoir rock. It should be mentioned that conventional EQI-based electrical rock typing is time-consuming and sometimes too complicated for large datasets. To overcome this challenge, machine learning (ML)-assisted solutions seem to be promising.

ML methods have recently gained tremendous attention in the petroleum industry where they offered valuable cost-efficient and computationally affordable results for complex subsurface engineering problems. These methods have been already applied to many complex problems encountered in reservoir engineering (Ertekin and Sun 2019), such as water saturation estimation (Helle and Bhatt 2002), history matching (Foroud et al. 2014; Shahkarami et al. 2014), estimation of dew-point pressure (Ahmadi et al. 2014), reservoir characterization (Jamalian et al. 2018), rock typing (Mohammadian et al. 2022; Muoghalu 2022), etc. However, very limited research has been done to optimize existing methods of cementation factor estimation using ML models. The present work investigates some of these ML methods which were used for determination of cementation factor in literature. Then, a ML-assisted enhanced version of EQI methodology is introduced and evaluated. The proposed hybrid model is capable of clustering electrical core data into proper ERTs and providing a fair estimation of cementation factor for each sample.

Background

ML-assisted methods for cementation factor estimation

ML is picking up pace in the petroleum industry due to its high computational efficiency and strong learning abilities (Tariq et al. 2021). ML models have shown high potential to improve conventional reservoir engineering methods. As discussed earlier, cementation factor estimation has been investigated to address its significant uncertainty. However, very few ML models have been developed to study the cementation factor of rocks. Mardi et al. (2012) used artificial neural network (ANN) to determine water saturation in a limestone formation. They also calculated variations of cementation factor and saturation exponent across pay zone. Kadhim et al. (2015) found ANN very efficient and fast in modeling the cementation factor on the basis of petrophysical properties such as average porosity, average permeability, and average formation resistivity factor. Anifowose et al. (2017) trained robust ML models with a large log dataset containing six basic logs to predict the \(m\) for un-cored reservoir sections. Later on, Anifowose et al. (2019) extended their previous work and conducted a feature selection technique to choose the best optimal subset of input logs that are nonlinearly related to \(m\), rather than using all available logs. Mahmoodpour et al. (2021) proposed a model for cementation factor prediction using ANN, particle swarm optimization (PSO) algorithm, and genetic programming (GP) algorithm. The complementary information and results of the aforementioned applications of ML models on cementation factor estimation are expressed in detail in Table 1.

Table 1 Different studies on the application of ML in estimation of cementation factor
Full size table

EQI concept

Rock typing is described as the method of dividing reservoir rocks into distinct classes on the basis of particular parameter(s) to capture the reservoir heterogeneity. This process has been extensively applied for reservoir assessment (Abedini et al. 2011). Capillary-based method and petrophysical static rock typing (PSRT) are two common rock typing techniques that work based on drainage capillary pressure curves and water saturation above free water level, respectively (Purcell 1949; Archie 1952; Skalinski and Kenter, 2013, 2014; Roque et al. 2017; Mirzaei-Paiaman et al. 2018; Mirzaei-Paiaman et al. 2019; Liu et al. 2020). Recently, petrophysical dynamic rock typing (PDRT), based on fluid flow behavior, and petrophysical pseudo-static rock typing (PPSRT), based on imbibition capillary pressure similarities, were introduced by Mirzaei-Paiaman et al. (2018) and Mirzaei-Paiaman and Ghanbarian (2021), respectively. Moreover, electrical rock typing has been practiced by defining the CZI (Rezaee et al. 2007) and EQI (Soleymanzadeh et al. 2018) as new parameters for categorizing rocks based on electrical properties.

Using the analogy of rock capacity for transmitting electricity and fluid, Soleymanzadeh et al. (2018) developed a new procedure for electrical rock typing, which can be used for the estimation of \(m\). They introduced EQI (Eq. (1)) as a criterion to categorize rocks into separate ERTs.

$${\text{EQI}} = \sqrt {\frac{{\sigma_{{\text{o}}} }}{\varphi }\frac{1}{{\sigma_{{\text{w}}} }}} = \sqrt {\frac{1}{F\varphi }} ;\, F = \sigma_{{\text{w}}} /\sigma_{{\text{o}}}$$
(1)

where \(\varphi\) denotes porosity and \(F\) is formation resistivity factor. In this equation, \(\sigma_{{\text{w}}}\) and \(\sigma_{{\text{o}}}\) are conductivities of water and rock upon full saturation with the same water, respectively. Soleymanzadeh et al. (2018) declared that rocks with similar EQIs exhibit similar electrical quality and hence represent a particular electrical rock type. Later on, acknowledging the variable level of water saturation along hydrocarbon zone, dynamic electrical rock typing (DERT) was developed by Soleymanzadeh et al. (2021a, b) for the prediction of saturation exponent (\(n\)) at un-cored depths. Kolah-kaj et al. (2021) investigated the effect of pressure on ERTs. Besides, some efforts have been made to predict consequential porous media properties based on the concept of EQI (Soleymanzadeh, Kolah-kaj, et al. 2021, 2022).

Materials and methodology

Dataset

Performance of an ML model is largely controlled by the quality and quantity of the used training data. Herein, a high-quality dataset from the literature (Glover 2016) was used to train and test the developed models. The data included a total of 3554 carbonate and sandstone samples collected from 11 reservoirs. Statistics of the parameters included in the dataset are listed in Table 2, with probability density of the data depicted in Fig. 1 using kernel density estimate (KDE) plot.

Table 2 Statistics of the studied dataset
Full size table
Fig. 1
figure 1

a Distribution of porosity for carbonate and sandstone samples, and b distribution of formation resistivity factor for carbonate and sandstone samples

Full size image

The dataset covers a total of 2193 carbonate and 1361 sandstone samples with porosities in the ranges of 0.023–0.453 and 0.038–0.280 for carbonate and sandstone samples, respectively. Measured values of formation resistivity factor were available for all samples, which varied from 5.791 to 1603.523 for carbonates and from 8.650 to 743.426 for sandstones. Porosity and formation resistivity factor of the rock samples fell in the ranges of 0.023–0.453 and 5.791–1603.522, respectively.

Modeling

As previously discussed, the EQI technique categorizes samples into different ERTs based on their EQI values, representing a 1-dimensional clustering problem by definition of unsupervised learning (modeling the underlying structure of data using unlabeled training data) (Sathya and Abraham 2013). In order to gain a better understanding of the clustering concept and choose the proper algorithm, some basic definitions must be clarified.

There are two types of clustering: hard and soft (or fuzzy). In hard clustering, each item is completely assigned to a specific cluster; however, fuzzy clustering deals with the probabilities of the existence (i.e., degree of membership) of an item in different clusters. Xu and Tian (2015) presented an inclusive review of various clustering approaches that suit different data distributions. The four most common approaches included centroid-based, density-based, distribution-based, and hierarchical clustering. Centroid-based clustering represents each cluster with its centroid vector (e.g., k-means algorithm) (MacQueen 1967; Lloyd 1982). In density-based clustering, clusters occur in dense regions and are separated by contiguous low-density areas (e.g., DBSCANFootnote 1 algorithm) (Ester et al. 1996). Distribution-based clustering considers data with multiple distributions (e.g., Gaussian mixture model, GMM) (Rasmussen 1999). Finally, hierarchical clustering categorizes data into different levels of a cluster tree, (e.g., BIRCHFootnote 2 algorithm) (Zhang et al. 1996).

In this study, the GMM, a distribution-based fuzzy clustering algorithm, was used to automate the originally manual EQI method. GMM is a parametric probability density function expressed as the weighted sum of the density of the Gaussian components. It is mainly used as a clustering technique on continuous unlabeled data. The probability is given through a mixture of M Gaussians, as in Eq. (2).

$$p\left( x \right) = \mathop \sum \limits_{i = 1}^{M} w_{i} \times g\left( {x|\mu_{i} ,\Sigma_{i} } \right)$$
(2)

where \(x\) is a D-dimensional continuous-valued data vector, \(\mu_{i}\) is a mean vector, \(\Sigma_{i}\) is the covariance matrix specifying the spread and orientation of the distribution, \(w_{i}\) is the Gaussian weight, and \(g(x|\mu_{i} ,\Sigma_{i} ), i = 1, . . . , M\) are the component Gaussian densities. The density of each component is a D-variate Gaussian function (Eq. (3)).

$$g\left( {x|\mu_{i} ,\Sigma_{i} } \right) = \frac{1}{{\left( {2\pi } \right)^{D/2} |\Sigma_{i} |^{1/2} }} \exp \left( { - \frac{1}{2}\left( {x - \mu_{i} } \right)^{^{\prime}} \mathop \sum \limits_{i}^{ - 1} \left( {x - \mu_{i} } \right)} \right)$$
(3)

GMM enables performing soft assignments, which makes more sense in the automation of electrical rock typing. The reason is that hydrocarbon reservoirs exhibit natural heterogeneities, and coring operation is performed in very limited depth intervals of a reservoir, introducing a large amount of uncertainty into reservoir evaluations. Therefore, it is better to consider the probability of a sample being in a cluster rather than hardly assigning them to a specific cluster. Furthermore, GMM is flexible in cluster shapes, where the covariance matrix finds its use case in providing unconstrained covariance structures. Hence, clusters can emerge into elongated elliptical, rather than spherical, boundaries in the case of k-means. Such flexibility helps achieve ERTs with parallel trendlines on a log–log plot of \(F\) versus \(\varphi\) on the basis of the EQI method. Additionally, GMM is robust to outliers and provides good results for anomaly detection.

Evaluation metrics are helpful for obtaining the best representative model for the data at hand and describing its performance. Clustering validation is challenging since there is no actual target to be compared. Accordingly, a customized evaluation approach was established based on the EQI methodology.

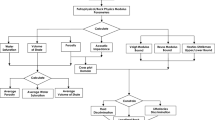
The flowchart in Fig. 2 represents the workflow of the hybrid EQI-GMM model. In this process, first, the dataset, including data on formation resistivity factor and porosity of each sample, was preprocessed and EQI values were calculated for each sample. Next, GMM algorithm was initiated with minimum number of clusters and “tied” covariance type (i.e., clusters have the same arbitrary shape). Results were checked to detect empty clusters, if any. Then, variances of tuning parameters and coefficients of determination (\(R^{2}\) s) were calculated after applying Archie’s equation to each cluster. These variances were then examined to see whether they are below a pre-defined threshold. In case of having empty cluster(s) or variance(s) exceeding the threshold, the model was returned to GMM initialization step to proceed with a new number of clusters. Finally, any cluster with less than two samples or poor tuning parameter and R2 was withdrawn as an outlier.

Fig. 2
figure 2

Flowchart of the proposed EQI-based clustering model

Full size image

By increasing the number of clusters, number of samples in each cluster decreases. Eventually, the values of tuning parameters and R2s got closer to 1. Therefore, a threshold had to be defined to prevent the overfitting of the model. Note that this threshold might vary for different datasets.

According to relevant literature, two information criteria, i.e., Schwarz's Bayesian Criterion (BIC) and Akaike Information Criterion (AIC) have been commonly used to determine the most efficient number of clusters (Akaike et al. 1973; Schwarz 1978). These criteria are defined in Eqs. (4) and (5).

$${\text{AIC}} = - 2\sum\limits_{i = 1}^{k} {L_{i} + 2k}$$
(4)
$${\text{BIC}} = - 2\sum\limits_{i = 1}^{k} {L_{i} + k\ln N}$$
(5)

where \(k\) is the number of parameters for k-cluster solution, \(L_{i}\) is the log-likelihood of cluster \(i\) in it, and \(N\) is the number of data points. The results of these criteria were also examined to see if they meet EQI criterion.

Finally, mean absolute error (MAE), mean squared error (MSE), and root mean squared error (RMSE) were used to evaluate prediction accuracy of cementation factor estimation, as defined in Eqs. (6), (7), and (8), respectively.

$${\text{MAE}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| {y_{i} - \hat{y}} \right|}$$
(6)
$${\text{MSE}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {y_{i} - \hat{y}} \right)^{2} }$$
(7)
$${\text{RMSE}} = \sqrt {{\text{MSE}}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {y_{i} - \hat{y}} \right)^{2} } }$$
(8)

where \(\hat{y}\) is the predicted value of \(y\),\(\overline{y}\) is the mean value of \(y\), and \(N\) is the total number of data points.

Results and discussion

Traditionally, the values of \(F\) were plotted versus \(\varphi\) for all samples without considering their electrical conductivity. Then, \(m\) was obtained from the slope of the trendlines shown in Fig. 3, where the fitted Archie’s equation and the corresponding \(R^{2}\) are reported for both sandstone and carbonate samples. The trendlines suggest a fixed value of cementation factor for all samples, i.e., 0.681 and 1.887 for carbonate and sandstone datasets, respectively. Clearly, poor determination coefficients show that this approach cannot precisely estimate the cementation factor. ML-assisted electrical rock typing was applied as an alternative method to overcome this issue.

Fig. 3
figure 3

Applying traditional Archie’s law on training datasets referring to a carbonate and b sandstone samples, respectively

Full size image

In order to implement the ML technique mentioned above, GMM was utilized to cluster datasets into distinct classes with similar electrical properties. To do so, EQI was calculated for each sample from Eq. (1), and the data were randomly split into training and testing subsets. Statistics of the subsets are listed in Table 3.

Table 3 Statistics of training and testing subsets
Full size table

GMM clustering model selection concerns the covariance type and the number of components. BIC and AIC were calculated by varying the number of clusters from 2 to 200 to specify the number of components. These well-known information criteria adjust the model likelihood and avoid over-fitting. Scikit-learn's GMM includes built-in methods that compute both criteria. The minimum value of each criterion indicates the optimal number of clusters. As shown in Figs. 4 and 5, the minimum values suggest 8 (based on AIC) and 5 (based on BIC) as optimum number of clusters for carbonate samples and 3 (based on both AIC and BIC) for sandstone samples.

Fig. 4
figure 4

Calculated BIC and AIC for different numbers of components from 2 to 200 with tied covariance type for carbonate samples

Full size image
Fig. 5
figure 5

Calculated BIC and AIC for different numbers of components from 2 and 200 with tied covariance type for sandstone samples

Full size image

Table 4 lists three models initiated by 8, 5, and 3 components and the results of applying Archie’s equation on each cluster in these models. This table also shows the cardinality (number of samples in a cluster) and EQI range for each cluster. Analyzing these clusters based on the EQI concept demonstrates poor tunning parameters and small values of R2. Although some ERTs are acceptable due to their high determination coefficient, some provide quite weak correlations with a large cardinality.

Table 4 Results of EQI technique for different ERTs (Models 1 and 2: AIC and BIC for carbonates, respectively, Models 3: AIC and BIC for sandstones)
Full size table

Since neither AIC nor BIC could lead us toward optimum number of clusters, the hybrid EQI-GMM model was employed. Setting the threshold at 0.001, results for the training subsets are demonstrated in Tables 5 and 6 for carbonate and sandstone samples, respectively. The three last columns of these tables indicate a linear correlation relating cementation factor to porosity for each ERT, which provides for high determination coefficients, based on Soleymanzadeh et al. (2018) work.

Table 5 Results of EQI technique for 44 ERTs generated by EQI-GMM model on training data from carbonate samples
Full size table
Table 6 Results of EQI technique for 65 ERTs generated by EQI-GMM model on training data from sandstone samples
Full size table

ERT 65 in Table 6 was removed from the sandstone training set as an outlier as it contained less than three samples. The rest of the ERTs remained intact since they properly satisfied the model criteria. As mentioned earlier, Soleymanzadeh et al. (2018) considered a step size in their manual electrical rock typing procedure; however, evaluation of the EQI ranges in Tables 5 and 6 shows that there is no need to specify any step size for the EQI technique to determine the ERTs.

Figures 6 and 7 illustrate log–log plots of formation resistivity factor versus porosity for each ERT together with the corresponding trendline. Clearly, the proposed approach could properly classify the electrical data into different clusters with parallel negative-slope (~ − 1) trendlines, as expected.

Fig. 6
figure 6

Log–log plot of formation resistivity factor versus porosity for 44 ERTs with corresponding trendlines on training data from carbonate samples

Full size image
Fig. 7
figure 7

Log–log plot of formation resistivity factor versus porosity for 64 ERTs with corresponding trendlines on training data from sandstone samples

Full size image

In Fig. 8, the tortuosity factor (\(a\)) is plotted versus average EQI for each ERT on a logarithmic scale. The descending trends with high determination coefficients show that more tortuous rocks exhibit lower electrical transmittance (i.e., lower EQI) because of longer current paths. For carbonate samples, \(a\) changes from 1.576 to 63.817 with an average and a median of 13.346 and 7.570, respectively. On the other hand, for sandstone samples, \(a\) varies from 2.077 to 57.286 with an average and a median of 9.561 and 6.331, respectively. The fact that carbonate rocks are more heterogeneous than sandstones, justifies the wider range of tortuosity factors obtained for the carbonates.

Fig. 8
figure 8

Log–log plot of a versus average EQI for each ERT: a sandstones, b carbonates

Full size image

To evaluate the accuracy of the proposed clustering technique, Archie’s equation \(\left(F = {\raise0.7ex\hbox{$a$} \!\mathord{\left/ {\vphantom {a {\varphi^{m} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\varphi^{m} }$}} ;a = 1\right)\) was used to calculate the actual cementation factor for each sample in the testing subsets. Using statistical methods, the predicted cementation factor by EQI-GMM was compared to the output of Archie’s law (Table 7). As is evident, EQI-GMM predictions are associated with significantly low levels of error while Archie’s law fails to produce accurate estimations.

Table 7 Evaluation report for testing data
Full size table

A graphical comparison of cementation factor predictions between the proposed model and traditional Archie’s law is demonstrated in Figs. 9 and 10. On these graphs, the \(y = x\) line was plotted to provide a better insight into the model performance. The figure highlights high percent errors (i.e., 65.575% for carbonates and 9.313% for sandstones) of Archie’s law for both lithologies, while the proposed EQI-based clustering model produced much lower percent errors (i.e., 0.507% for carbonates and 0.241% for sandstones), as depicted by the closeness of the results to the \(y = x\) line (Figs. 9b and 10b).

Fig. 9
figure 9

Cross plot of predicted cementation factor by a Archie’s law and b the proposed EQI-based clustering model versus actual values for testing data from carbonate samples

Full size image
Fig. 10
figure 10

Cross plot of predicted cementation factor by a Archie’s law and b the proposed EQI-based clustering model versus actual values for testing data from sandstone samples

Full size image

For some samples in the test dataset, no ERT could be assigned as they did not follow the electrical patterns characterizing any of the identified ERTs. Indeed, their electrically identical rocks were situated in un-cored sections of the well profile, highlighting a challenge of data limitation.

Summary and conclusions

Gaussian mixture model (GMM), as a powerful probability clustering algorithm, was utilized to conduct electrical rock typing on carbonate and sandstone samples based on electrical quality index (EQI). The following conclusions were drawn accordingly:

  • Two common clustering criteria, namely Schwarz's Bayesian Criterion and the Akaike Information Criterion, failed to determine optimum number of electrical rock types (ERTs).

  • A hybrid EQI-GMM model was developed to estimate the optimum number of ERTs.

  • The proposed EQI-GMM model turned out to be much faster and more efficient than manual EQI methodology.

  • EQI-GMM model gives more accurate predictions of cementation factor, as compared to those obtained from traditional Archie’s law.

  • Considering EQI ranges for different ERTs, the need for a step size for electrical rock typing was eliminated.

  • The tortuosity factor was found to be inversely related to average EQI for each ERT and varies in a wider range for carbonates because of their higher heterogeneity.