Rock typing and uncertainty assessment in geological and petrophysical properties by integrating electrofacies, hydraulic flow units, and geostatistical techniques in the Kangan gas field, Zagros basin

Abstract

The structural complexities of hydrocarbon reservoirs make it difficult to correlate geological and petrophysical properties. A successful field development depends on accurately mapping the spatial distributions of reservoir key parameters. In this study, we present results on rock type analysis, estimation, and uncertainty evaluation of geological and petrophysical data of 33 wells in one of the south Iranian gas fields. This paper is divided into two parts. In the first part, we used a reservoir rock classification theme based on identifying electrofacies (EFs) and hydraulic flow units by analyzing both log and core data. In the second part of the paper, we performed estimation, uncertainty evaluation, and assessment of the porosity–thickness relationship of the high-quality EFs using geostatistical techniques. We used sequential simulation schemes to map the spatial distributions of porosity and thickness of the high-quality EFs across the field. Using probabilistic approaches, the generated multiple realizations were used to quantify the local and spatial uncertainties. Variogram analysis showed that property distributions had a higher continuity and minimum variance in the NW–SE direction. Based on spatial uncertainty analysis, we found that the indicator-based sequential simulated maps exhibited less spatial uncertainty. Furthermore, the obtained probability maps indicated that the SE part of the study area is more suitable for drilling and production scenarios.

Introduction

Exploration and production of oil and gas are costly processes that include high risk due mainly to incomplete knowledge about the complex structure of underground resources. Due to the requirement for increasing and/or maintaining production from the conventional reservoirs and finding new techniques for developing unconventional resources, it is of great importance to employ methods to effectively and efficiently characterize the underground resources. In reservoir characterization, it is essential to create accurate maps of reservoir structures to be used to simulate dynamic events such as enhanced oil recovery processes. Geostatistical techniques are commonly used to effectively generate geological and petrophysical property maps and determine local and spatial uncertainties as a result of using limited sample data in property estimation (Evans Annan et al. 2019). Geostatistics originated in the work of D.G. Krige in the early 1950s in the field of mining engineering (Krige 1951). The Krige’s technique was expanded and formulized by the French engineer George Matheron (Matheron 1962). From the 1980s, geostatistical techniques were introduced and used in the petroleum industry, wherein their main goal was to provide a more realistic model of reservoir heterogeneity (Wilson et al. 2011) and hence improve reservoir simulation forecasts. It should be noted that the geostatistical techniques can only be efficient with enough input data points. It is hard to define enough data points, but it is generally suggested that it should not be less than 10 or 15 for highly anisotropic data sets (Zelenika et al. 2013).

Despite being commonly and widely used in various applications, a question may arise about the degree to which the geostatistical tools provide a reliable reservoir description. To answer this question, we should be aware of the limitations of the major geostatistical methods. Kriging estimation, a common geostatistical method, is a smooth interpolation, which is locally accurate but globally inaccurate (Zhao et al. 2005), and as a result, it cannot generate basic statistics of input data and also cannot include details of spatial pattern (Juang et al. 2004). Another disadvantage of kriging estimation is that the smoothing effect depends on local data configuration. The closer it is to the data locations, the smaller the smoothing effect. As a consequence, kriging maps should not be used for applications that are sensitive to the presence of extreme values (Goovaerts 1999; Zhao et al. 2005). An error variance provided by the kriging estimation is also often used as a measure to ensure the accuracy of the kriging estimate (Goovaerts 1999), and thus, it is a typical measure of local uncertainty (Zhao et al. 2005). To alleviate the disadvantages of kriging in uncertainty assessment, nonlinear kriging approaches, for example, Indicator Kriging (IK) have been used to assess uncertainty (Goovaerts 2001). The uncertainty of IK estimation is based only on spatial data variation observed at sampled locations. In addition, the cumulative distribution function (CDF) obtained by IK provides a measure of local uncertainty at one single location. It is worth mentioning that a sequence of single point CDFs does not provide any criteria for spatial (multi-point) uncertainty (Goovaerts 2001; Juang et al. 2004). Beyond kriging estimation, conditional geostatistical simulations, e.g., Gaussian sequential simulation (SGS) and sequential indicator simulation (SIS), can eliminate the smoothing effect of kriging estimates and evaluate the uncertainty of estimation (de Souza and Costa 2013; Juang et al. 2004; Lv and Liu 2019; Wang et al. 2020a, b; Zhao et al. 2005). SGS assumes that data must be normally distributed (Juang et al. 2004; Wang et al. 2020a, b), which limits its application to data sets with high skewness. In contrast to SGS, there is no particular constraint concerning the actual data distribution when SIS is used (Huang et al. 2016; Juang et al. 2004; Y. Wang et al. 2020a, b).

Over the last two decades, several studies have investigated distributions of geological and physical properties of underground and surface formations, particularly petroleum reservoirs and soils, using geostatistical techniques (Juang et al. 2004; Lv and Liu 2019; Normando et al. 2022; Pawar et al. 2001; Ren et al. 2019; Wang et al. 2020a, b). Zelenika et al. (2013) used data from the Lower Pontian sandstone reservoir to prepare maps of porosity and thickness distributions using the simulation methods. Their results showed that the maps showed a distinct sedimentological feature. Geostatistical modeling and data analysis approaches such as histogram analysis and scatter plot have been undertaken by Zhao et al. (2014) to determine the spatial structure of reservoir properties. They obtained maps of reservoir properties using kriging and cokriging, SGS, and Markov model 2 (Journel 1999) methods. Their results show that the anisotropic variogram provided better spatial relationship interpretations than the isotropic one. By comparing the estimation and simulation techniques, they found that the simulation approach could well reflect the reservoir's intrinsic properties in terms of the associated extreme values. In another study, Ilozobhie et al. (2015) analyzed the porosity distribution of part of Bornu basin by kriging and cokriging methods using oil well log data. They found that the study area's north-eastern part depicted a well-developed sand region for hydrocarbon accumulation. They also noticed that the southern regions of the area have low porosity distribution. Zelenika (2017) used IK and SIS to map the porosity of a reservoir in the Sava Depression. The input dataset was divided into six classes based on appropriate cutoff values. They found that the kriging results and the probability maps strongly depended on the number of cutoffs. The IK maps showed the probability that a mapped variable was lower than a certain cutoff while the SIS results showed a reverse trend. Evans Annan et al. (2019) used geostatistical methods to analyze the distributions of thickness, porosity, and permeability of a reservoir in the Jubilee oilfield. They used kriging estimation, SIS, and SGS to generate 3D spatial-based maps for the properties. Their results showed that porosity, permeability, and thickness were distributed uniformly at the center toward the northeast direction of the reservoir. The geostatistical methods were used by Hosseini et al. (2019) to analyze spatial pattern of the porosity and permeability, presenting the direction of anisotropy for each variable and describing the variation of these parameters in a gas reservoir of the Khangiran gas field. They used kriging and SGS to get the property maps across the whole reservoir. They concluded that the kriging tended to smooth out estimates while the SGS method revealed much more details. They then used cross-validation for model validation and concluded that SGS models had a better match with the actual data than the match obtained by the kriging models.

A few studies have reported integrated approaches for the simultaneous use of geology and reservoir engineering to effectively characterize petroleum reservoirs. A combined use of EFs determination and geostatistical simulation for building spatial models of reservoir EFs were reported by Kiaei et al. (2015). Sacchi et al. (2016) proposed a novel method to integrate basin-scale data into reservoir models. They used forward stratigraphic modeling and quantitatively investigated the uncertainty of reserve estimation. In a study, Ren et al. (2019) developed a 3D high-resolution reservoir model of a heavy oil-rich field in China. They combined geostatistical modeling with stratigraphic correlation, log interpretation, core data, lithology assessment, and sedimentary facies analysis. They classified petrofacies units of a well based on core data and compared them with four sets of well logs, EH, SP, RT, GR (see the Nomenclature section for the meanings of the symbols and abbreviations). They developed an artificial neural network to predict petrofacies at uncored wells. In another study, Wang et al. (2020a, b) assessed the spatial distribution of thickness, porosity, and saturation of gas hydrate-bearing layers by integrating lithofacies constraints and geostatistical inversion. They analyzed spatial variations of the properties and made recommendations on the well development for hydrate production testing. Recently, a workflow for general geostatistical significance which supports subsurface applications was proposed by Salazar and Pyrcz (2021). They extensively used mathematical statistics to investigate significant measures for assessing spatial structures. In the well-log discipline, Mirhashemi et al. (2022) have used geostatistics to estimate petrophysical logs. They have shown that the combined geostatistics with the petrophysical relations provided accurate and applied tools to estimate missing logs. Very recently, Normando et al. (2022) reported research that integrated various reservoir data of an oil field in Brazil, including geological, geophysical, petrophysical, and engineering data, to generate a reservoir model using geostatistics. They found that integrating the reliable data using geostatistical methods could provide a sound geological model whose large-scale properties, such as original volume in place, matched those obtained from other techniques.

Because of the current demand in petroleum engineering to put more emphasis on integrating geology and engineering aspects in reservoir studies than on implementing individual reservoir disciplines, it is required to adopt a systematic approach when evaluating the physical properties of reservoir rocks. Despite extensive research into the physical properties of hydrocarbon reservoirs over the years, accurately mapping and assessing the spatial distribution and uncertainties of geological and petrophysical parameters, particularly in complex carbonate reservoirs, remains a substantial challenge. This is because effective mapping methods, such as geostatistical tools, require careful handling in oil and gas fields where data availability is limited. Furthermore, the results obtained must be analyzed with due consideration for the varying reservoir rock types and zones. This paper should be viewed in the context of these challenges, aiming to underscore the importance of characterizing reservoir zones and facies before embarking on the stochastic simulation of reservoir properties. In a previous study (Karimian Torghabeh et al. 2022), we identified and distinguished different electrofacies (EFs) and hydraulic flow units (HFUs) within two gas-bearing formations of the Kangan gas field in southern Iran, utilizing well-log and core data. The objective of this paper is to assess the local and spatial uncertainties and the relationship between two critical parameters, namely, porosity and the thickness of EFs exhibiting the best reservoir quality, using information derived from stochastic conditional simulations. This paper begins with a concise presentation of the geological context within the study area. Subsequently, it provides a comprehensive examination of the data sources, the methodologies employed for determining EFs and HFUs, geostatistical simulations, and the evaluation of uncertainties. This is followed by the presentation of results, discussion, and the conclusions drawn from this research. The insights from this study offer valuable contributions to the development and enhanced production of the study field and similar oil and gas reservoirs.

Geology of study area

In this study, data from the Kangan gas field were used. Details of the geology of the field were described in our previous paper (Karimian Torghabeh et al. 2022). In this paper, a brief description of the studied geological formations is given. The Kangan field is one of the largest gas fields globally, located in southern Iran (Fig. 1a) and has two main reservoirs, the Kangan and Dalan formations (Fig. 1b). The Dalan formation is made up of carbonate and evaporitic rocks with frequent lithological and faciological variations (Motiei 2003). As shown in Fig. 1b, the Dalan Formation is stratigraphically subdivided into three members from top to base: Upper Dalan, Nar, and Lower Dalan. The detailed descriptions of these geological units were given in (Karimian Torghabeh et al. 2022). The Kangan formation is a carbonate-evaporate succession and is subdivided into four reservoir units, as denoted by Ka1- to Ka-4 in Fig. 1b. The Kangan formation exhibits three distinct facies, clean carbonate facies, principal shale and clay facies, and evaporate carbonate facies (Szabo and Kheradpir 1978).

Fig. 1

a Location of the Kangan gas field in southern Iran (adapted and modified from (Faraji et al. 2017)), b the Cenozoic to the Paleozoic stratigraphic column of the Zagros region and main reservoirs of the Dalan and Kangan Formations (adapted and modified from (Insalaco et al. 2006) and (Enayati-Bidgoli et al. 2014a, b))

Methods

Figure 2 shows a workflow adopted in this study to stochastically assess the petrophysical properties of a carbonate gas reservoir. It describes an integrated approach covering both the geological and physical aspects of the properties. The workflow suggests a three-phase sequence for assessing uncertainty and correlating geological and petrophysical properties of reservoir rocks. The first part is data collection and quality control. It is obvious that incomplete data produces inaccuracy and uncertainty in the next stages of reservoir characterization and modeling. Key to the effectiveness of the stochastic methods is identifying the best-quality reservoir zones by integrating the well-log and core data (the middle stage shown in Fig. 2). Statistical and probabilistic analyses are extensively used in all parts of the proposed plan. The proposed workflow is described in detail in the following sections.

Fig. 2

Proposed workflow from data collection to determining the best-quality reservoir zone and stochastic simulation. The arrows are used to relate the tasks and milestones

Data collection

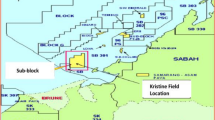
A suite of petrophysical well log data was taken from 33 wells in the Kangan gas field. The locations of wells in this field are shown in Fig. 3. The data included density log (RHOB), neutron log (NPHI), sonic log (DT), and gamma-ray log (GR). As reported in our previous paper (Karimian Torghabeh et al. 2022), the log data were used to determine EFs of the field's formations and the one with the best reservoir quality was selected for further geostatistical investigation. In addition, the available core data, including core porosity and permeability, of one well was utilized to determine the HFUs (Karimian Torghabeh et al. 2022). Table 1 shows the basic statistical parameters of the core data obtained from 490 core samples. The average neutron-log porosity and thickness of the best EFs were used for uncertainty assessment using geostatistical simulation.

Fig. 3

Underground contour and location maps of wells in the study area

Table 1 Basic statistical information of the core data

Methods for identification EFs and HFUs

Identification and separation of different zones and rock types are of great importance in understanding and analyzing production from a reservoir. Electrofacies (Efs) are a set of log responses that diagnose and distinguish a specific layer from other layers. To determine EFs, log data should be clustered to separate pay zone segments and achieve field-level matching (i.e., scale-up log data). The basis of cluster analysis is finding similarities between data in accordance with the properties found in the data and grouping similar data into clusters (Karimian Torghabeh et al. 2014). In our previous study (Karimian Torghabeh et al. 2022), all available log data (RHOB, NPHI, DT, and GR) were used to determine EFs in the Kangan field. In particular, we employed the multi-resolution graph-based clustering (MRGC) method to define the optimal number of clusters and separate different layers and zones. The MRGC method has been successfully applied to permeability prediction and hydraulic flow unit determination (Khoshbakht and Mohammadnia 2012; Nouri-Taleghani et al. 2015). In this method, log data are characterized by the kernel representative and neighborhood indices. Small data groups, called absorption bands, are formed based on these two indicators, differing in shape, size, density, and separation ratio. These absorption bands are separated by boundaries and eventually, in a growing process, combine with larger groups, which are defined as electrofacies. The MRGC method was applied using the Paradigm™ Geolog v7.4 software.

Apart from identifying electrofacies, other methods have been used to separate reservoir formations into distinct classes. Efficient divisions of reservoir formations into specific layers with the same storage capacity and fluid flow efficiency are crucial, particularly for complex carbonate reservoirs. One of the most effective methods uses the concept of hydraulic flow units (HFUs). We previously used and tested several methods to discriminate different HFUs in the field (Karimian Torghabeh et al. 2022). In this study, we used and adopted the results based on the concept of flow zone indicator and reservoir quality index using the core data. Details of equations and the method used for identifying HFUs were given in (Karimian Torghabeh et al. 2022).

Geostatistical modeling methods

This section briefly introduces the geostatistical tools used in this study to evaluate the uncertainty associated with the spatial distributions of porosity and thickness of the high-quality EFs in the study area. All the geostatistical calculations were performed using the Stanford Geostatistical Modeling Software (SGeMS v2.1) package (Remy et al. 2009).

Variogram

A semivariogram (commonly referred to as the variogram) is a basic tool for quantifying spatial variability between sample data. The main purpose of using a variogram is to identify data variability with respect to the distance between sample points. Mathematically, semivariogram, denoted by γ, is calculated by the following expression (Kelkar et al. 2002):

$$\gamma \left( {\varvec{L}} \right) = \frac{1}{2n}\sum\limits_{i = 1}^{n} {\left[ {X\left( {{\varvec{r}}_{i} } \right) - X\left( {{\varvec{r}}_{i} + {\varvec{L}}} \right)} \right]^{2} },$$

(1)

where X(r_i) and X(r_i + L) are sample data values at locations r_i and r_i + L, respectively, separated by a vector L (called lag distance), and n is the number of sample pairs. In Eq. (1), vectors are represented by bold letters. Olea (2006) proposed a multistep practical approach to variogram modeling. The goal here is to determine the characteristic parameters of a semivariogram (range, sill, and nugget) using experimentally calculated semivariogram data and a curve-fitting approach.

Kriging

Kriging is a linear estimation technique to estimate a value at unsampled locations based on the minimization of variance and unbiased conditions (Delfiner et al. 1983). There are several kriging techniques, including simple kriging, ordinary kriging, cokriging, universal kriging, and indicator kriging (Deutsch 2002). The ordinary kriged estimator, denoted by X^*, at an unsampled location r₀ is calculated by:

$$X^{*} \left( {{\varvec{r}}_{0} } \right) = \sum\limits_{i = 1}^{n} {\lambda_{i} X\left( {{\varvec{r}}_{i} } \right)},$$

(2)

where X(r_i) is the sample value at location r_i and λ_i is the weight assigned to the sample X(r_i). The weights λ_i are solutions of a system of linear equations according to the kriging estimation criteria (Kelkar et al. 2002).

Indicator kriging

Indicator kriging is applied to variables that are binary indicators of the occurrence of an event. In indicator kriging, the conditioning data X(r_i) is transformed into indicator data using an indicator function I(r_i,x_t), at desired cutoff values x_t, defined by:

$$I\left( {{\varvec{r}}_{i} ,x_{t} } \right) = \left\{ \begin{gathered} 1, \, X\left( {{\varvec{r}}_{i} } \right) \le x_{t} \hfill \\ 0,{\text{ otherwise}} \hfill \\ \end{gathered} \right. \, t = 1,...,k.$$

(3)

To express the spatial structure of the indicator variables, the semivariogram given by Eq. (1) should be updated for the indicator variables obtained by Eq. (3).

Sequential Gaussian simulation (SGS)

The kriging technique produces a single best guess of the unknown at the unsampled location. Due to the essence of the kriging method, the kriging map gives a smooth estimate and eliminates local variability; hence it cannot be identical to reality due to limited sample data (Caers 2005). Kriging is also locally accurate regardless of the global map of estimates. However, unlike kriging, stochastic simulation gives a globally accurate map of the reservoir heterogeneity, and more importantly, it provides a basis for examining uncertainty. SGS is a common geostatistical technique for property modeling and has been widely used to estimate the spatial distributions of geometric and petrophysical properties of subsurface structures, including thickness, porosity, and permeability in particular (Deutsch 2002). In this technique, it is assumed that all distributions are Gaussian. In practice, most samples obtained from the field are not Gaussian. So, it is required to transform all the original sample values into standard normal values. In SGS, the estimate of the central cell given the neighboring data is provided by a Gaussian distribution constructed by the kriging mean and kriging variance of the corresponding estimate using neighboring data. Note that a random path is first defined that loops over all the grid cells, and the previously simulated values are used in the kriging estimate of the next location. Once the simulation is completed, all simulated values are transformed back into the original data histogram. (Caers 2005).

Sequential indicator simulation (SIS)

Sequential indicator simulation (SIS) is another common geostatistical tool for developing variograms, mapping, and generating high-resolution models (Novak Zelenika & Malvić, 2011). In SIS, the probability of the grid cell value given the neighboring values is calculated using kriging. The conditioning data is first transformed into the indicator codes using appropriate cutoff values. The experimental semivariograms of the indicator data are then calculated. The conditional cumulative distribution functions are constructed based on a random path at unsampled locations. The kriging is used to estimate the probability of the grid cell values being less than the given cutoff values in the indicator kriging estimator (Lin et al. 2016). Similar to SGS, the previously simulated values are used in the kriging estimate of the next location.

Determination of local and spatial uncertainties

Multiple realizations of the unknown value provided by the sequential simulation schemes represent a model of the uncertainty of the original variable (Caers 2011; Oliveira et al. 2017). Quantification of uncertainty makes it possible to assess the risk associated with any decisions that may be made based on the distribution maps of the variables. Regarding the uncertainty of a variable associated at a single location r₀ (local uncertainty), the probability that the unknown variable X^*(r₀) at r₀ is greater than a threshold x_t is denoted by P[X^*(r₀) > x_t], which can be computed by (Zhao et al. 2005):

$$P\left[ {X^{*} \left( {{\varvec{r}}_{0} } \right) > x_{t} } \right] = \frac{{n\left( {{\varvec{r}}_{0} } \right)}}{N},$$

(4)

where N is the number of generated realizations, and n(r₀) is the number of realizations in which the simulated values generated by the SIS exceed the threshold x_t in each of the N realizations.

A probability map obtained by Eq. (4) can only give a measure of local (single location) uncertainty and cannot ensure the reliability of spatial mapping uncertainty at several locations simultaneously (Juang et al. 2004). Therefore, it is also essential to assess the probability that multiple locations are all above or below a threshold. This type of uncertainty is called the spatial or multi-local uncertainty (Goovaerts 2001) and can be used to evaluate the confidence level or reliability of areas determined by P[X^*(r₀) > x_t] at a given critical probability p_c (Wang et al. 2020a, b). Assume that for a given threshold x_t and critical probability p_c, an area determined by P[X^*(r₀) > x_t] ≥ p_c is denoted by A. Suppose there are m locations, r₁,r₂,…,r_m, in area A, the joint probability of the variable at m locations, all being greater than the threshold x_t can be calculated by (Zhao et al. 2005):

$$P\left[ {X\left( {{\varvec{r}}_{1} } \right) > x_{{\text{t}}} ,X\left( {{\varvec{r}}_{2} } \right) > x_{{\text{t}}} ,...,X\left( {{\varvec{r}}_{m} } \right) > x_{{\text{t}}} } \right] = \frac{{n\left( {{\varvec{r}}_{1} ,{\varvec{r}}_{2} ,...,{\varvec{r}}_{m} } \right)}}{N},$$

(5)

where n(r₁, r₂,…, r_m) is the number of realizations that have all simulated values of m locations in area A are greater than the threshold x_t in each of the N realizations.

Results

Determination of EFs and HFUs

Details of the results used for EFs and HFUs determination were given in our previous paper (Karimian Torghabeh et al. 2022). Here, a brief description is provided in order to elucidate the role of rock typing for further geostatistical mapping and uncertainty analysis. Four types of log data, namely RHOB, NPHI, DT, and GR, were utilized to identify EFs (see the Nomenclature section for the meanings of the symbols and abbreviations). The selection of well-log data was guided by previous research aimed at identifying facies characteristics (Correia and Schiozer 2016; Enayati‐Bidgoli et al. 2014a, b; Ghadami et al. 2015; Jafarzadeh et al. 2019; Torghabeh et al. 2014). In the first place, the EFs model was built in the base well. After validating the results for this well, the model was propagated to all wells in the field. Considering 4 and 18 as the minimum and the maximum number of clusters, three models with 9, 13, and 16 clusters were generated. By examining and merging similar clusters, the 16-cluster model resulted in five EFs with distinct lithology and reservoir quality. Figure 4 provides information on the dominant minerals comprising the electrofacies of the formations and boxplots of the effective porosity of each electrofacies. It was found that EF-4 has considerably larger porosity values than other electrofacies, while EF-5 has the lowest porosity and reservoir quality, comprising mainly of shale.

Fig. 4

Information of mineralogy and boxplots of the effective porosity of electrofacies of the Dalan and Kangan formations

Regarding hydraulic flow units (HFUs), the method based on the concept of flow zone indicator and reservoir quality index discriminated six HFUs with the average porosity values reported in Table 2 (Karimian Torghabeh et al. 2022). Figure 5 illustrates examples of the distributions of EFs and HFUs against depth in one of the wells of the field. Each color spectrum represents specific EFs and HFUs with different lithology, petrophysical properties, and reservoir quality. The results of EFs accompanied by the HFUs findings showed that EF-4, with high effective porosity and low shale volume, exhibited the best reservoir quality with high production potential in Kangan 3 and Upper Dalan 4 formations (Fig. 1).

Table 2 Average porosity values for each HFU (Karimian Torghabeh et al. 2022)

Fig. 5

Distributions of EFs and HFUs in a well of the Kangan field. This figure shows that the EFs in some places contain several different flow units. Low reservoir quality HFUs that include HFUs 1, 2, and some fraction 3 correspond to the low core porosity and permeability values in the left column

Accuracy of the reservoir classification scheme

The validity of the reservoir clustering strategy, through EFs analysis using the MRGC technique and HFUs determination (Wu et al. 2020), is closely linked to the drilling depth and the specific formations encountered during drilling. It is essential to consider the depth of drilling, the formations penetrated, and the availability of relevant logging and drilling data to assess the reliability of the information. When drilling encompasses all the formations, the uncertainty associated with the available data tends to decrease. The classifications performed rely on three primary types of data: logging data, drilling data, and core data. Deeper wells provide more comprehensive data, including extensive logging information, leading to increased data reliability. The reservoir classification heavily depends on the available data. Most of the wells under study have been drilled through two distinct formations, ensuring data availability for these specific formations. This study's significance lies in its continuity with a prior investigation (Karimian Torghabeh et al. 2022), in which a zone with a high reservoir quality was identified. Utilizing geostatistics and averaging log data, we are able to pinpoint the optimal geographical location within this zone. Consequently, we have identified a region with both geographical and zonal advantages, promising a higher potential for production.

Data used for geostatistical simulation and uncertainty assessment

In this study, SGS and SIS were used to generate multiple realizations of porosity and thickness of the obtained high-quality EFs (EF-4 in Fig. 5) using 33 wells data (refer to Fig. 3 for a location map of the wells). Porosity data were collected from neutron logs which are available in all the wells. At each well, the neutron-log porosity values were arithmetically averaged over the high-quality EFs thickness to estimate the average porosity at that location. The thickness of high-quality EFs was determined from analysis of the log data clustering by Geolog software. Descriptive statistics and histograms of porosity and thickness of high-quality EFs data are presented in Table 3 and Fig. 6, respectively.

Table 3 Basic descriptive statistical parameters of porosity and thickness of the high-quality EFs data

Fig. 6

Histograms of the porosity and thickness of the high-quality EFs data

Mapping of porosity and thickness distributions using SGS

Variogram analysis

Since the porosity and thickness used in this study were not normal data, the first step was to transform the data into standard normal distributions. Then, experimental anisotropic semivariograms were estimated on the transformed data in four directions with 45° angular increments and a directional tolerance of ± 40° for porosity (Fig. 7) and thickness (Fig. 8). The variogram model parameters are summarized in Table 4. The nugget-to-sill ratio is commonly used as a criterion to define the automatic spatial dependence of a variable (Cambardella et al. 1994; Qu et al. 2013). Ratio values below 25% and above 75% represent strong and weak spatial dependencies, respectively, while ratios between 25 and 75% show moderate spatial dependence. The nugget-to-sill ratio for porosity in the directions of 45°, 90°, and 180° indicates moderate spatial dependency, but spatial dependence is weak at 135°, which has a nugget-to-sill ratio above 75%. For thickness, the nugget-to-sill ratio for directions of 45° and 90° is equal to zero, indicating strong spatial dependencies and moderate spatial dependencies are observed in 135° and 180° directions. The variograms of porosity and thickness data show maximum continuity at 135° with estimated ranges (correlation lengths) of 11,000 m and 12,000 m for porosity and thickness, respectively. From Figs. 7 and 8, it is apparent that the direction of 45° shows the minimum spatial correlation lengths of 750 m and 850 m for porosity and thickness, respectively.

Fig. 7

Experimental semivariograms and variogram models for standard normal transformed data of the porosity in four directions: a 45°, b 90°, c 135°, and d 180°

Fig. 8

Experimental semivariograms and variogram models for standard normal transformed data of the thickness in four directions: a 45°, b 90°, c 135°, and d 180°

Table 4 Parameters of theoretical models for standard normal transformed data of the porosity and thickness fitted to experimental semivariograms in four directions

SGS simulation results

Two hundred realizations for each variable (porosity and thickness of the high-quality electrofacies) were generated using SGS using a gridblock size of 25 × 25 m. A total of 240,000 grid nodes were simulated. The simulation was performed using the ordinary kriging (OK) estimator and the variogram parameters given in Table 4. Four randomly selected SGS realizations are displayed for each variable in Figs. 9 and 10. It is worth noting that all the realizations created by the simulation are equally likely to happen. The colorbars alongside the realizations in Figs. 9 and 10 show the SGS-calculated porosity and thickness values of high-quality electrofacies, respectively. It is noted that the rectangular dots in these figures denote the sample points corresponding to the well locations (Fig. 3). The sample porosity and thickness data at each location are represented by the average neutron-log porosity and thickness of the best EFs at the respective well. The obtained realizations indicated that the estimates respected the sample points to a certain extent, albeit with some degree of dispersion.

Fig. 9

Four randomly selected SGS realizations for the porosity, in percentage, of high-quality electrofacies (The colorbar displays the porosity values in percentage)

Fig. 10

Four randomly selected SGS realizations for the thickness, in meters, of high-quality electrofacies (The colorbar displays the thickness values in meters)

Mapping of porosity and thickness distributions using SIS

Variogram analysis

In this study, four cutoffs were used to perform the indicator transformation of porosity and thickness. The cutoff values were set at 20.42 m (20th percentile), 22.5 m (40th percentile), 24.8 m (60th percentile), and 27.5 m (80th percentile) for thickness data and set at 0.074, 0.091, 0.094, and 0.099 for porosity data based on average porosity obtained for HFUs (Table 2). The calculated experimental omnidirectional (isotropic) semivariograms for all the cutoff values for porosity and thickness are shown in Figs. 11 and 12, respectively. The variogram model parameters are summarized in Table 5. The nugget-to-sill ratio for all cutoff values of porosity and thickness is between 25 and 75%, indicating moderate spatial dependencies of these variables.

Fig. 11

Semivariogram of the indicator codes of the porosity obtained by cutoff values of a 0.074, b 0.091, c 0.094, and d 0.099

Fig. 12

Semivariogram of the indicator codes of the thickness obtained by cutoff values of (a) 20.42 m, b, 22.5 m, c, 24.8 m, and d 27.5 m

Table 5 Parameters of theoretical models for indicator transformed data of the porosity and thickness fitted to experimental semivariograms for four cutoffs

SIS simulation results

Based on the variogram parameters (Table 5), two hundred realizations for porosity and thickness of high-quality EFs were generated using SIS using a gridblock size of 25 × 25 m. Figures 13 and 14 display four randomly selected SIS realizations for porosity and thickness, respectively, including the rectangular dots as the sample points. Similar to SGS maps, each SIS realization represents a possible spatial distribution of porosity and thickness without a smoothing effect. Figures 13 and 14 clearly demonstrate that the SIS realizations differ considerably from the SGS maps (Figs. 9 and 10), indicating a substantial level of dispersion.

Fig. 13

Four randomly selected SIS realizations for the porosity of the high-quality electrofacies (The colorbar displays the porosity values in percentage)

Fig. 14

Four randomly selected SIS realizations for the thickness of the high-quality electrofacies (The colorbar displays the thickness values in meters)

Assessment of spatial distributions of porosity and thickness

The map of conditional means (E-type estimates), calculated by averaging over all the realizations generated by the SGS and SIS methods, is a useful method to illustrate the global spatial pattern of the variable and nearly converges into a kriged map when the number of realizations is high (Qu et al. 2013; Wang et al. 2020a, b). Figures 15 and 16 illustrate the E-type estimates of porosity and thickness, respectively, obtained by the SGS, and SIS approaches. Like the kriging methods, the E-type estimates provide much smoother maps than the stochastic simulation maps shown in Figs. 9, 10, 13, and 14. This smoothing effect usually causes high values to be underestimated, and low values to be overestimated and generally does not represent local variabilities (Lark and Webster 2006; Qu et al. 2013). In addition, similar trends can be seen in Figs. 15 and 16, so that the southeast to middle part has high porosity and thickness values, and the middle to northwest parts of the study area have low porosity and thickness values. A comparison between the histograms of the E-type estimates calculated by the stochastic simulation methods and the OK method is shown in Fig. 17. The summary statistics of the E-type estimates and the kriging method are also reported in Fig. 17.

Fig. 15

E-type estimates of the porosity (in percentage) calculated by a SGS and b SIS methods

Fig. 16

E-type estimates of the thickness (in meters) calculated by a SGS and b SIS methods

Fig. 17

Comparison of histograms of the porosity maps (a–c) and the thickness maps (d–f). (a, d) E-type estimates calculated by SGS, (b, e) E-type estimates calculated by SIS, and (c, f) OK maps

Figure 18 shows the conditional variance maps of porosity and thickness calculated from the SGS and SIS methods. In the diagonal regions of the field from the northwestern to the southeastern parts of the study area, less certainty was observed in the SIS estimated data, as evidenced by the conditional variance maps. Regarding the SGS results, the least and most uncertain were observed near the sampled and unsampled areas, respectively. This finding is not necessarily true for the SIS results, where regions with a relatively high uncertainty near the sampled locations were found. The regions with high uncertainty require additional sampling.

Fig. 18

(a, b) Conditional variance maps for the porosity (in percentage) calculated by the SGS and SIS methods, respectively. (c, d) Conditional variance maps for the thickness (in meters) calculated by the SGS and SIS methods, respectively

Assessment of local and spatial uncertainty

In this study, Eq. (4) was used to evaluate the local uncertainty of porosity and thickness at any unsampled locations using the SGS and SIS methods. In this regard, proper thresholds were chosen for porosity and thickness to calculate the probability of being higher than the given thresholds. Regarding porosity, 0.07 and 0.075, values close to the mean and median of sample data, were chosen as threshold values. For thickness, a high thickness threshold equal to 27.5 m (80th percentile) and a low threshold equal to 21 (between 20 and 40th percentiles) were selected to calculate the probability of thickness values that is larger than a specific threshold value. The resulting probability maps (the conditional cumulative distribution function, ccdf) for 200 realizations obtained by the SGS and SIS methods are shown in Figs. 19 and 20. The probability maps simply represent the high and low probability of areas with the desired porosity and thickness values. Figure 19 illustrates those areas with porosity and thickness greater than the corresponding threshold values are mainly located in the southeast of the study area.

Fig. 19

(a, b) Probability maps for the porosity being greater than 0.075 from the SGS and SIS methods, respectively. (c, d) Probability maps for the thickness being greater than 27.5 m from the SGS and SIS methods, respectively

Fig. 20

(a, b) Probability maps for the porosity being greater than 0.07 from the SGS and SIS methods, respectively. (c, d) Probability maps for the thickness being greater than 21 m from the SGS and SIS methods, respectively

The probability maps based on SGS and SIS only represent local uncertainty (uncertainty at a single point) and cannot show multi-point spatial uncertainty (Goovaerts 2001; Zhao et al. 2005). Alternatively, the joint probability, defined by Eq. (5), obtained from the realizations generated by the SGS and SIS methods, can be used to evaluate the spatial uncertainty. In this study, 0.96, 0.98, and 0.99 were adopted as critical probability (p_c) thresholds to calculate the corresponding joint probability (Table 6). It is expected that the joint probability increases as the critical probability increases. Furthermore, the uncertainty obtained by the SGS and SIS was found to be different. Based on the SGS data, if the given p_c is 0.96, the joint probability will be only 0.005 for porosity for 915 simulated locations in the areas obtained by P[X^*(r₀) > 0.075] ≥ 0.96, and the joint probability of thickness will be 0.02 for 919 simulated locations in the areas obtained by P[X^*(r₀) > 27.5] ≥ 0.96. This means that only 1 out of 200 porosity realizations and 4 out of 200 thickness realizations, porosity and thickness of the simulated locations are all greater than the respective thresholds. With increasing the critical probability, the joint probability increases, which indicates that the spatial uncertainty becomes smaller. Regarding the SIS method, the joint probability values for both variables are higher in different critical probabilities than those from the SGS method. This means that the spatial uncertainty obtained from the SIS data is significantly lower than that of the SGS method.

Table 6 Evaluation of spatial uncertainty of areas where porosity and thickness are greater than 7.5% and 27.5, respectively, based on joint probability under different critical probability

Discussion

Verification of the geostatistical inference results

In this paper, we employed geostatistical-based approaches to forecast the spatial distribution patterns of porosity and strata thickness using well data. As previously mentioned, the porosity data for each well were computed by averaging the neutron-log porosity readings from that specific well, while the thickness data were obtained through the analysis of log data clustering. The findings led to the conclusion that the porosity in the southeastern direction of the study area exhibits a superior quality. An intriguing point that may be raised here pertains to the substantiating evidence for the conclusions drawn from the geostatistical analysis presented in this study. In our prior work (Karimian Torghabeh et al. 2022), we conducted a thorough comparison between core data and well-log information. This analysis demonstrated a strong correlation between the well-log data and core-derived information. The relationship was not limited to a single well but was consistent across multiple wells, validating the use of average log data for geostatistical investigations. Therefore, it can be concluded that the conclusions drawn from well-log data are substantiated by core and drilling data.

Using stochastic simulation data to find a correlation between porosity and thickness of the high-quality electrofacies

The simulated data gathered in this study provide a sound basis to explore the possible correlation between porosity and thickness. Figure 21 shows the distribution of thickness of the high-quality EFs as a function of porosity based on simulation data. The red line in Fig. 21 gives a moving average of the relationship between thickness and porosity. As expected, the data shows a strong correlation between thickness and porosity. A linear trend can be observed for most parts of the graph given in Fig. 21. The intermediate to highly porous regions have high thicknesses. In contrast, lower-thickness zones are concentrated in the low-porosity rocks.

Fig. 21

Relationship between thickness and porosity of the high-quality Efs; the points give a scatter plot of the local porosity and thickness, and the line provides a moving average of the relationship between them

Summary and conclusions

Accurate characterizations of production zones and spatial distributions of geological and petrophysical parameters are challenging issues in oil and gas field development. In this study, we conducted a survey of reservoir characteristics of a carbonate reservoir from an important field (Kangan gas field, Iran). First, suitable cluster well logs were used (i.e., gamma-ray, neutron, sonic, and density) along with core porosity–permeability data to determine EFs and HFUs in this field. Then we evaluated the spatial distributions, the local and spatial uncertainties, and the relationship between two key parameters of porosity and thickness of EFs with the best reservoir quality using the kriging and stochastic conditional simulations (i.e., SGS and SIS). Several key findings can be summarized as follows:

• The multi-resolution graph-based clustering (MRGC) method was applied to log data and determined five EFs in the field. In addition, the flow zone indicator (FZI) method was applied using the available core data and identified six distinct HFUs. Electrofacies#4 (EF-4) with high effective porosity, low shale volume, and a high-quality flow unit were considered the best reservoir quality with high production potential in Kangan 3 and Upper Dalan 4 formations of the field.

• The variogram analysis showed that the porosity and thickness of the high-quality EFs (i.e., EF-4) exhibited a higher continuity and minimum variance in the NW–SE direction.

• Assessment of the local uncertainty denoted that the areas with porosity greater than the threshold value of 0.075 (values close to the mean and median of sample data) and thickness greater than the threshold value of 27.5 m (80% percentile) were mainly located in the southeast of the study area.

• The spatial uncertainty obtained from the SIS data was significantly lower than that of the SGS method.

• Overall, a positive linear relationship was found between the porosity and thickness of the high-quality EFs of the field such that the intermediate to high porous zones corresponded to high thicknesses and vice versa.

As a final remark, It is worth noting the practical implications of the results derived from this study. When it comes to assessing reservoir uncertainty, it is essential to evaluate both static factors, such as facies and reservoir parameters, and dynamic properties, like capillary pressure and relative permeability. This research offers valuable insights into the reservoir, facilitating the identification of high-quality zones for targeted well perforation, thereby increasing production rates and optimizing enhanced oil recovery techniques. Moreover, the probability map generated can assist in identifying cost-effective drilling locations for wells. Additionally, the spatial uncertainty assessment proves invaluable in determining the reliability of designated areas for oil and gas field development. For instance, based on the probability maps obtained in this study, it is advisable to prioritize drilling and production activities in the southeastern part of the study area.