Introduction

To enhance oil and gas production capacity and fulfill the world's energy needs, wells are explored with recent drilling methods such as extended reach wells, deep water wells, and slim holes to meet energy consumption demand. However, the challenge of such drilling methods is to maintain the pressure induced by drilling fluid in the annulus within the operating window (the pore and fracture pressure) (Erge et al. 2016).

An efficient hydraulics program associated with an explored well results from an accurate prediction of pressure loss of drilling fluid in the annular space. Among problems that can be caused by a wrong estimation of pressure loss of drilling fluid are a wrong selection of drilling pump, hole cleaning problems which may induce an obstruction of the annulus, stuck of the drill string, excessive torque, and drag, etc.

The cleaning process during drilling operation mainly depends on pressure loss and velocity distribution of drilling fluid in the annulus between the drill string and casing (Ofei et al. 2015). Therefore, a good understanding of the influence of different parameters (inner cylinder motion, eccentricity, and flow rate of drilling fluid) on the pressure loss and velocity profiles is required to avoid problems during drilling operations.

Among early studies of non-Newtonian fluid (Sutterby Model) flowing through an eccentric annular geometry is that of Mitsuishi and Aoyagi (1974), where they used the variational method to solve the continuity and motion equations in bipolar coordinates. They validated their calculated results against experimental data obtained from the experimental setup. The authors used hydrogen bubbles as a tracer to obtain the distribution of non-Newtonian fluid velocity within different annulus regions. They found that pressure loss of non-Newtonian fluids diminishes with the increase in the eccentricity, whereas fluids with high non-Newtonian behavior present a gradual decrease in pressure loss. They also noticed the appearance of a secondary flow in the wide part of the annular geometry for non-Newtonian fluid.

Based on the experimental and numerical investigations, Nouar et al. (1987) examined the presence of the inner cylinder rotation on the axial and tangential velocity profiles of Ostwald-de Waele fluid in a concentric annular geometry for both laminar and turbulent flow regimes. They found that rotation of the inner cylinder causes a deformation of the axial velocity profile. They attributed this deformation to the increase in the shear rate provoked by the rotation of the inner cylinder. Later, Naimi et al. (1990) extended the work of Nouar et al. (1987) using the same flow loop system. They found that the tangential velocity profile exhibits an inflection point in the middle region of the annulus, which is explained by the appearance of the Taylor vortices in the annular space for the laminar regime. The authors reported that this inflection point is well observed for low flow rates and high-speed rotation of the inner cylinder. Nouar et al. (1998) numerically solved the continuity, momentum, and energy equations where they validated their numerical results with experimental data obtained from the experimental flow loop. They deduced that the inner cylinder rotation is found to reduce the velocity gradient near the outer pipe. Furthermore, they observed a decrease in the plug region until its disappearance when the inner cylinder rotation increases.

Nouri et al. (1993) carried out an experimental study of Newtonian and non-Newtonian (Ostwald-de Waele) fluids using an experimental flow loop with a concentric and eccentric annulus in the absence of the inner cylinder rotation. The laser doppler velocimeter was used to measure the velocity in different radial positions of the annulus. Results indicated that the increment of the eccentricity up to 1 causes a decrease of 22.5% in the flow resistance compared to the concentric annular geometry for the Newtonian fluid in a turbulent regime. Moreover, the authors found that the flat region of the axial velocity of the non-Newtonian fluid was situated in the middle of the annular geometry where the maximum velocities are 1.45, 1.33, and 1.27 times greater than the bulk velocities for the Reynolds numbers 1150, 6200 and 9600, respectively. Using the same flow loop, Nouri and Whitelaw (1994) conducted an experimental study on the same fluid, considering the rotation of the inner cylinder for a concentric annulus. They concluded that the inner cylinder rotation decreases the maximum axial velocity with 13.5% and 5% for the Newtonian and Ostwald-de Waele fluids, respectively, compared to those cases where rotation of the inner cylinder was not considered. Furthermore, the rotation speed increase from 0 to 300 rpm tends to make the axial velocity profile flatter for the power-law fluid. Nouri and Whitelaw (1997) extended their experimental investigation by considering the eccentricity of the inner cylinder. They found that the tangential velocity values of the non-Newtonian fluid in the middle of the widest region of the eccentric annulus are 2.6 times higher than those of the Newtonian fluid. Moreover, a secondary flow (counter-rotating swirl) was also observed in the wide part of the annular geometry for the power-law fluid.

Escudier and Gouldson (1995) experimentally investigated the influence of the inner cylinder rotation on pressure loss and distribution of the axial and tangential velocity profiles of Newtonian and non-Newtonian (Cross model) fluids flowing through a concentric annular geometry. In this work, it was observed that the inner cylinder rotation has an obvious effect on the axial velocity profile at low Reynolds numbers. Conversely, a marginal impact of the inner cylinder rotation on pressure loss of Newtonian and non-Newtonian fluids for the turbulent regime was reported. Escudier et al. (2000) solved the continuity and momentum equations using the finite volume method for a Newtonian fluid flowing through an eccentric annulus in the laminar regime. They reported that the inner cylinder rotation significantly affected the axial velocity profile, where two peaks in the axial velocity were recorded for high eccentricity values at high cylinder rotation speeds. Later, Escudier et al. (2002) continued their numerical study to investigate the effect of the inner cylinder rotation on the flow of non-Newtonian fluid (power-law model) using the finite volume approach. A decrease in the dimensionless hydraulic resistance (the Reynolds number times the friction factor) was reported when the axial flow dominates the flow; however, for the flow where rotation is dominated, the dimensionless hydraulic resistance was increased due to the high shear stress on the outer cylinder. Furthermore, the authors found that for high shear-thinning fluid (\(n=0.2\)), the secondary flow (recirculation flow) in the wide part of the annulus was disappeared entirely in contrast to the Ostwald-de Waele fluids with high flow behavior index (\(n\)), including Newtonian fluid (\(n=1\)).

Meuric et al. (1998) solved the continuity and momentum equations using the finite element method for yield power-law fluid (Herschel–Bulkley fluid) in an eccentric annular geometry with the rotation of the inner cylinder. Their results showed that the increment of the rotation speed causes an increase in the axial volumetric flow rate for the concentric annular geometry, while a reverse trend was stated for the eccentric one.

The Finite Element Method (FEM) and Finite Difference Method (FDM) are applied by Lockett (1992) to investigate the flow of Newtonian and non-Newtonian fluids through a concentric and eccentric annulus. Lockett (1992) analyzed the flow in terms of Taylor vortices, where the rheological properties are considered for a wide range of operation conditions. Besides, transportation of cuttings was evaluated in the presence of Taylor vortices.

The flow of drilling fluid in a slim hole was analyzed by Roberto Ribeiro (1994) using the Finite Element Method for power-law fluids flowing in a concentric and eccentric annulus with and without rotation of the inner cylinder, respectively. The study revealed that both rotation of the inner cylinder and eccentricity induce a decrease in pressure loss gradient of power-law fluid. Moreover, the author found that the drill string’s dynamic motions should be considered to get closer to the real case of drilling fluids circulation.

Another numerical work was carried out by Laruccia (1995), where the analysis is divided into two parts: (a) yield power-law fluid flow through an annular geometry, (b) cuttings transportation in inclined wells. In the first part, Laruccia (1995) studied the influence of the inner cylinder rotation, eccentricity, and yield stress on fluid velocity distribution in the annular gap using 2D and 3D contours. For the second part, two correlations were developed to estimate the critical conditions of cuttings transportation in inclined wellbores.

In the experimental and numerical work of Bicalho et al. (2016), it was shown that the tangential velocity profile of yield power-law fluid where the inner cylinder makes an orbital motion behaves differently. However, they did not consider the rotation of the inner cylinder around its central axis. Furthermore, it was found that eccentricity causes a decrease in pressure loss contrary to the numerical investigation of GhasemiKafrudi and Hashemabadi (2016) where they found that pressure loss amplifies with the increment of the eccentricity in the presence of cuttings. Pang et al. (2019) conducted simulation studies on the influence of the inner cylinder orbital motion on cuttings transport using the commercial code ANSYS-Fluent. It was found that the cleaning process is significantly enhanced when the inner cylinder makes both pure rotation and orbital motion.

Recently, Ferroudji et al. (2019) and Ferroudji et al. (2020) analyzed the presence of the inner cylinder orbital motion on pressure drop of non-Newtonian fluids flowing in an annular geometry where they defined the orbital motion of the inner cylinder as the rotation of the inner cylinder around its central axis, as well as, around the central axis of the outer cylinder, simultaneously. They concluded that the orbital motion can enhance the erosion effect of cuttings bed, which improves the cleaning process; however, they did not consider the torque induced on the drill pipe when the orbital motion occurs.

In the present work, extensive simulation runs were carried out using the commercial code ANSYS-Fluent 17.0 to study the influence of different parameters (orbital motion speed, eccentricity, diameter ratio, and flow behavior index) on the distribution of the axial and tangential velocity profiles of non-Newtonian fluid (Ostwald-de Waele fluid) flowing through an eccentric annulus which can be considered as a part of the novelty of this work since most of the previous studies modeled the orbital motion as the rotation of the inner cylinder around the axis of the outer one without considering self-rotation around its axis. Furthermore, the impact of these parameters on the fluid homogeneity in the annulus is evaluated in terms of the maximum velocity ratio of the narrow and wide regions, which can be considered as new tests for the orbital motion case according to the open literature. Moreover, torque induced on the drill pipe for both pure and orbital motions is discussed. It is worthy of mentioning that this study is limited only to the orbital motion case; however, there are various motions and configurations of the drill string that can be observed in a real drilling operation, including buckling motion, chaotic motion, etc. It is revealed that the axial velocity component of the Ostwald-de Waele fluid is improved by the orbital motion for all studied cases, in particular for high speeds and high values of eccentricity, where this effect resulted in a better homogeneity of the axial velocity in the annulus as compared to the pure rotation case. On the other hand, it is found that high torque induced by orbital motion could be reduced by increasing the fluid velocity.

Materials and methods

Physical model

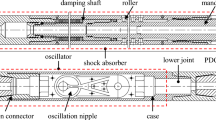
The model simulates the flow of non-Newtonian fluid (Ostwald-de Waele) through an annular space, which is bounded by the outer cylinder (casing) and the inner cylinder (drill pipe). The inner cylinder makes an orbital motion which is considered as a combination of a rotation around its own central axis and rotation around the central axis of the outer cylinder when it is not in the concentric position. According to the findings of Avila et al. (2008), the orbital motion begins to appear when the rotation of the inner cylinder is within the range of 80–110 rpm. Thus, it is assumed that the orbital motion speed increases with pure rotation speed, simultaneously, as shown in Fig. 1.

Fig. 1
figure 1

Orbital motion of the inner cylinder

Full size image

The geometry characteristics and fluid properties adopted in this study are summarized in Table 1.

Table 1 Annulus and fluid characteristics
Full size table

Mathematical model

The flow of the non-Newtonian fluid in the annular space can be considered as an incompressible, fully developed, steady, and isothermal in a laminar regime which can be modeled in the cylindrical coordinates (\(r\), \(\theta \), \(z\)) by the continuity and momentum equations, as follows (Holzmann 2016):

$$ \frac{1}{r}\frac{{\partial \left( {rv_{r} } \right)}}{\partial r} + \frac{1}{r}\frac{{\partial \left( {v_{\theta } } \right)}}{\partial \theta } + \frac{{\partial \left( {v_{z} } \right)}}{\partial z} = 0 $$
(1)
$$ \rho \left( {\frac{{\partial v_{r} }}{\partial t} + v_{r} \frac{{\partial v_{r} }}{\partial r} + \frac{{v_{\theta } }}{r}\frac{{\partial v_{r} }}{\partial \theta } + v_{z} \frac{{\partial v_{r} }}{\partial z} - \frac{{v_{\theta }^{2} }}{r}} \right) = - \frac{\partial P}{{\partial r}} - \left( {\frac{1}{r}\frac{{\partial \left( {r\tau_{rr} } \right)}}{\partial r} + \frac{1}{r}\frac{{\partial (\tau_{\theta r} )}}{\partial \theta } + \frac{{\partial \left( {\tau_{zr} } \right)}}{\partial z} - \frac{{\tau_{\theta \theta } }}{r}} \right) + \rho g_{r} $$
(2)
$$ \rho \left( {\frac{{\partial v_{\theta } }}{\partial t} + v_{r} \frac{{\partial v_{\theta } }}{\partial r} + \frac{{v_{\theta } }}{r}\frac{{\partial v_{\theta } }}{\partial \theta } + v_{z} \frac{{\partial v_{\theta } }}{\partial z} + \frac{{v_{r} v_{\theta } }}{r}} \right) = - \frac{1}{r}\frac{\partial P}{{\partial \theta }} - \left( {\frac{1}{{r^{2} }}\frac{{\partial \left( {r^{2} \tau_{r\theta } } \right)}}{\partial r} + \frac{1}{r}\frac{{\partial \left( {\tau_{\theta \theta } } \right)}}{\partial \theta } + \frac{{\partial (\tau_{z\theta } )}}{\partial z} + \frac{{\tau_{\theta r} - \tau_{r\theta } }}{r}} \right) + \rho g_{\theta } $$
(3)
$$ \rho \left( {\frac{{\partial v_{z} }}{\partial t} + v_{r} \frac{{\partial v_{z} }}{\partial r} + \frac{{v_{\theta } }}{r}\frac{{\partial v_{z} }}{\partial \theta } + v_{z} \frac{{\partial v_{z} }}{\partial z}} \right) = - \frac{\partial P}{{\partial \theta }} - \left( {\frac{1}{r}\frac{{\partial \left( {r\tau_{rz} } \right)}}{\partial r} + \frac{1}{r}\frac{{\partial \left( {\tau_{\theta z} } \right)}}{\partial \theta } + \frac{{\partial \left( {\tau_{zz} } \right)}}{\partial z}} \right) + \rho g_{z} $$
(4)

where \({v}_{r}\),\({v}_{\theta }\) and \({v}_{z}\) are the velocity components, \(\tau \) denotes the stress tensor, \(P\) is the pressure, \(g\) is the gravity, ρ is the density.

Moreover, in the previous studies, various models are considered to model the relationship between shear stress and velocity gradient of drilling fluids, such as Newtonian model, Power-law model, Yield power-law model (Epelle and Gerogiorgis 2017; Pang et al. 2019; Rasul et al. 2020; Qureshi et al. 2021; Moukhametov et al. 2021). In this investigation, the power-law rheological behavior is used to establish this relationship through the following expression:

$$ \tau = K\left( {\dot{\gamma }} \right)^{n} $$
(5)

where \(K\) is the consistency index, \(\dot{\gamma }\) is the shear rate, and \(n\) is the flow behavior index.

The eccentricity can be defined as the ratio of the offset distance of the inner cylinder from the concentric position to the maximum offset distance, which is expressed as follows:

$$ E = \frac{2\delta }{{D_{o} - D_{i} }} $$
(6)

where \(\delta \) is the offset distance between the centers of the inner and outer cylinders, \({D}_{i}\) and \({D}_{o}\) stand for the diameter of the inner and outer cylinder.

Madlener et al. (2009) presented a relationship to calculate the Reynolds number of a power-law fluid in annular geometry as follows:

$$ R_{e} = \frac{{\rho D_{h}^{n} u^{2 - n} }}{{K\left( {\frac{3n + 1}{{4n}}} \right)^{n} 8^{n - 1} }} $$
(7)

where \(u\) is the bulk velocity and \({D}_{h}\) is the hydraulic diameter which is calculated as:

$$ D_{h} = D_{o} - D_{i} $$
(8)

On the other hand, the torque along the axial axis is evaluated based on the following relationship (Fluent 2009):

$$ M_{z} = \overrightarrow {{e_{z} }} .\vec{M} $$
(9)

where \(\overrightarrow{{e}_{z}}\) is the vector of a unit of the axial direction and \(\overrightarrow{M}\) is the total torque applied on the inner cylinder. The total moment is calculated, as follows:

$$ \vec{M} = \vec{r} \times \overrightarrow {{F_{p} }} + \vec{r} \times \overrightarrow {{F_{v} }} $$
(10)

where \(\overrightarrow{{F}_{p}}\) is the force vector of pressure, \(\overrightarrow{{F}_{v}}\) is the force vector of viscosity, \(\overrightarrow{r}\) is the moment vector.

Numerical model strategy

In the present analysis, the pure rotation case is considered as a reference to evaluate the impact of the orbital motion on the flow of drilling fluid during drilling operations where the annular geometry is meshed into 1.2 × 106 and 1.76 × 106 elements for pure rotation and orbital motion cases, respectively. Initially, a grid independence study is carried out where the number of elements is chosen to ensure that the calculated outputs are not affected by the adopted meshes, as well as, to maintain the number of elements as low as possible to optimize computational time. The grid independence, in this case, is evaluated from the perspective of axial velocity, tangential velocity, strain rate distribution, and pressure drop gradient, as can be seen in Figs. 2, 3, and 4.

Fig. 2
figure 2

Grid independence study for pure rotation case with a fully eccentric annulus (\(U=0.5\) m/s and 200 rpm). a Axial velocity. b Tangential velocity. c Strain rate

Full size image
Fig. 3
figure 3

Grid independence study for orbital motion case with a fully eccentric annulus (\(U=0.5\) m/s and 200 rpm). a Axial velocity. b Tangential velocity. c Strain rate

Full size image
Fig. 4
figure 4

Grid independence study for both orbital motion and pure rotation cases with a fully eccentric annulus (3 m/s and 200 rpm)

Full size image

Besides, the regions near walls are refined, allowing reliable results and capturing a high gradient of outputs. On the other hand, the sliding mesh technique is employed to model the orbital motion of the inner cylinder in which the annular geometry is split into three regions: the inner and middle regions, which are affected by pure rotation and orbital motion, respectively, and the outer region in which the fluid is considered to be static. These regions are connected through two interfaces where the nodes of each boundary zone are not shared with the other one, as can be seen in Fig. 5. Also, the right side of this Figure depicts in 3D the discretization of the annular domain for the orbital motion case where the annular geometry is divided into three regions with different colors.

Fig. 5
figure 5

Regions of the annular geometry when the inner cylinder makes an orbital motion

Full size image

Aside from that, since the sliding mesh approach is considered to model the orbital motion of the inner cylinder, the built cell zones (inner, middle, and outer regions in this case) will rotate relative to each other through the interfaces, i.e., the inner region rotates with respect to the middle region and the latter in turn rotates with respect to the outer region. The rotating regions slide relative to the other ones in discrete steps when the calculation is in progress. Additionally, node alignment through the interfaces is not required, as the rotation occurs (Fluent 2009).

Moreover, displacement of drilling fluid through an annular geometry can be analyzed by considering flow in the wide and narrow regions of the annulus and flow characteristics in these regions is considered as a key factor to understand the impact of the orbital motion on cuttings deposition in the lower side (narrow region). Based on that, Fig. 6 depicts the plans (wide and narrow plans for both orbital motion and pure rotation cases) where the velocity and dynamic viscosity are calculated.

Fig. 6
figure 6

Sections where velocity and dynamic viscosity are obtained

Full size image

The calculation process of FLUENT® initially consists of calculating the current time step until the convergence criterion is satisfied, then the position of the inner and middle regions will be updated automatically according to the angular speed of the orbital motion. The case file of each time step is saved for all flow time to store the mesh rotation at various positions. Thus, it was necessary to perform this study using transient formulation.

The numerical simulations are performed utilizing the SIMPLE (Semi-Implicit Method for Pressure Linked Equations) algorithm, where a guessed velocity is used to determine the convective fluxes per unit mass through cell faces. Moreover, the momentum equations are solved based on a guessed pressure field, and then the continuity equation is employed to deduce the pressure correction equation to calculate the corrected pressure field, where the latter is utilized to update the velocity and pressure (Versteeg and Malalasekera 2007).

The discretization of pressure is carried out with PRESTO! (PREssure STaggering Option) where the discrete continuity balance for a staggered control volume about the face to compute the staggered pressure is employed for this scheme. Also, comparable accuracy can be obtained for tetrahedral, triangular, and hybrid meshes (Fluent 2009). Besides, this scheme is adopted since it is suitable for high-speed rotating flows, as well as, highly swirling flows.

On the other hand, the first-order scheme is employed for momentum equations since the second-order scheme may induce convergence challenges for certain flow situations. Even though the second-order scheme presents better accuracy than the first-order scheme, the latter is preferred to avoid calculation instabilities since it results in a reasonable accuracy (Fluent 2011). In this study, and based on a preliminary test, the time step of 10–4 is adopted, which allowed attaining a convergence (continuity and velocity residuals) from 10–4 to 10–5 for all simulations. This convergence level can be considered a sufficient criterion to obtain accurate results (Fluent 2011).

Boundary conditions

For the boundary conditions, a uniform velocity of the fluid is applied at the inlet, while pressure outlet type is adopted at the outlet where the latter is placed to assure that the fully developed flow is reached along the axis of the annulus to avoid entry effects. Furthermore, the inner and outer cylinders are kept stationary since the orbital motion of this study is obtained through rotation of the inner region around the central axis of the inner pipe coupled to rotation of the middle region around the central axis of the outer cylinder. Besides, a no-slip condition is applied to the walls of the outer and inner cylinders.

Results and discussion

Validation

According to the open literature, there is a lack of experiential data regarding velocity profiles of non-Newtonian fluids in an annular space with an orbital motion of the inner cylinder. For that, the outputs of this study are validated against the experimental work of Nouri and Whitelaw (1997), where the inner cylinder makes only pure rotation. However, the developed mesh for the orbital motion case can be employed to check its validity for the rotational case where only the region influenced by the rotation of the inner cylinder (region “a” of Fig. 5) makes a pure rotation around its central axis. Figure 7 indicates that the obtained results are in good matching with the experiential data in which the average error of the tangential velocity is 11.5%; however, for the axial velocity, the average error is estimated as 13.2% and 8.3% for 0 rpm and 300 rpm, respectively.

Fig. 7
figure 7

Comparison of the obtained results against the experiential data of Nouri and Whitelaw (Ferroudji et al. 2019) for an eccentric annulus with rotation of the inner cylinder

Full size image

Radial distribution of axial velocity

Distribution of the axial and tangential velocity profiles of drilling fluid in an annular geometry can be considered as indicating parameters for preferential regions of flow that can be caused by the appearance of the orbital motion where this behavior is evaluated for various values of orbital motion angular speeds, eccentricity, flow behavior index, and diameter ratio. Moreover, viscosity profiles can explain the behavior of the obtained results of velocity. On the other hand, homogeneity of the considered fluid is characterized by calculating the maximum value of the axial velocity ratio in the narrow and wide regions, which are considered new tests for the orbital motion case according to the open literature. In addition to that, the generated torque on the inner cylinder is studied for the orbital motion case and compared with the pure-rotation one.

Effects of pure rotation and orbital motion

The effect of the inner cylinder rotation and orbital motion speed on the radial distribution of the axial velocity of the non-Newtonian fluid in the eccentric annular space (\(E=0.5\)) flowing with a constant bulk velocity (0.5 m/s) is depicted in Fig. 8. The increase in the rotation speed from 100 to 400 rpm results in a raise of 275% of the maximum of the axial velocity in the narrow gap of the annular geometry, while an increase of 300% is recorded for the orbital motion case where the latter is 70% to 140% higher than rotation case for all angular speeds. This finding confirms the beneficial effect when orbital motion takes place rather than the only rotational motion of the inner cylinder on the axial velocity, which would help to avoid the formation of the cuttings deposition. The beneficial impact of the orbital motion on cuttings removal is also reported by Ozbayoglu et al. (2008). However, for the large gap of the eccentric annulus, the maximum value of the axial velocity diminishes with the rotation of the inner cylinder, where this trend is more pronounced for the orbital motion case due to the enhancement of the rotational flow in this region. Bicalho et al. (2016) observed the same influence of the orbital motion, even though their definition of orbital motion is different from the present study.

Fig. 8
figure 8

Effect of pure rotation and orbital motion speed on the radial distribution of the axial velocity (\(E=0.5\), \(n=0.52\), \(\kappa =0.5\))

Full size image

Effect of cylinder eccentricity

Figure 9 indicates the axial velocity distribution of the non-Newtonian fluid for both rotation and orbital motion cases when the eccentricity increments from (\(E=0.2\)) to (\(E=0.8\)). As can be seen, the eccentricity increases the maximum of the axial velocity in the wide gap of the eccentric annulus, while the opposite trend is observed for the narrow gap. This effect can be attributed to the increase and decrease in the resistance to flow in the narrow and wide gaps of the annular geometry, respectively. Moreover, since the eccentricity intensifies the orbital motion of the inner cylinder, a slight effect is found for the eccentric annulus (\(E=0.2\)); however, as the eccentricity increases (from \(E=0.2\) to \(E=0.8\)), the axial velocity distribution is influenced by the orbital motion of the inner cylinder, especially for the narrow gap of the annular geometry where a dramatic increase of 450% is stated. These findings confirm that once the orbital motion of drill pipe takes place, deposition of cuttings can be easily removed by the enhanced axial flow at high eccentric levels.

Fig. 9
figure 9

Effect of eccentricity on the radial distribution of the axial velocity (200 rpm, \(n=0.52\), \(\kappa =0.5\))

Full size image

Effect of flow behavior index

The effect of flow behavior index on the radial distribution of the axial velocity in the narrow and wide gaps of the eccentric annulus is illustrated in Fig. 10. As the flow behavior index decreases, thus becoming more shear-thinning, the axial velocity profile becomes flatter in the middle of the wide gap clearance of the eccentric annulus. Conversely, the decrease in the flow behavior index in the presence of high resistance to flow in the narrow gap results in a considerable increase in the axial velocity to satisfy the mass conservation in the entire annulus. A flatter velocity profile enhances better sweep efficiency of the drilled cuttings near the walls of the wellbore. This observation may confirm the necessity to use drilling fluids with shear-thinning behavior to enhance the cuttings cleaning out from the lower side of the annulus, particularly in the presence of the orbital motion.

Fig. 10
figure 10

Effect of flow behavior index on the radial distribution of the axial velocity (200 rpm, \(E=0.5\), \(\kappa =0.5\))

Full size image

Effect of diameter ratio

Figure 11 shows the impact of the diameter ratio on the Ostwald-de Waele axial velocity profiles in the eccentric annular geometry for both rotation and orbital motion situations. When the inner cylinder makes an orbital motion, the axial velocity profile behaves similarly to the rotation case where the increment of the diameter ratio increases and decreases the maximum value of the axial velocity for the wide and narrow gaps of the eccentric annulus, respectively. The evolution of the resistance to flow from the narrow gap to the wide gap is the reason behind such behavior, and the same observation is made by Ofei et al. (2015) for the rotation case. Moreover, the increase in the diameter ratio acts in the same way as the increase in the eccentricity in which this effect diminishes till \(\kappa =0.8\) where the orbital motion has a slight impact on the axial velocity profile. Therefore, the axial flow in narrow wells would not be highly influenced by the orbital motion; nonetheless, the orbital motion could be seen to enhance much flow in the narrow gap of the eccentric annulus with smaller diameter ratios.

Fig. 11
figure 11

Effect of diameter ratio on the radial distribution of the axial velocity (200 rpm, \(E=0.5\), \(n=0.52\))

Full size image

Radial distribution of tangential velocity

Effects of pure rotation and orbital motion

Figure 12 depicts the difference in the tangential velocity profiles caused by the rotation and orbital motion of the inner cylinder. For the rotation case, the tangential velocity is increased by around 300% in the vicinity of the inner cylinder when the rotation speed increases from 100 to 400 rpm. On the other hand, for the orbital motion case, this increase is evaluated to be 300% of the tangential velocity near the inner cylinder in the narrow gap of the eccentric annulus, which is 150% higher than the rotation case. This effect is less pronounced for the wide gap of the eccentric annular geometry near the inner cylinder. This effect can be explained by the fact that for the orbital motion case, the inner cylinder makes two motions at the same time causing a significant increment in the tangential velocity, in particular in the narrow gap of the annulus. This enhancement of the tangential velocity for the orbital motion case can improve erosion of cuttings bed.

Fig. 12
figure 12

Effect of pure rotation and orbital motion speed on the radial distribution of the tangential velocity (\(E=0.5\), \(n=0.52\), \(\kappa =0.5\))

Full size image

Effect of cylinder eccentricity

Figure 13 exemplifies how the tangential velocity behaves with eccentricity in the wide and narrow gaps of the eccentric annulus with a constant angular speed of 200 rpm for both rotation and orbital motion cases. When the inner cylinder makes only rotational motion, eccentricity does not affect the tangential velocity near the inner cylinder. Also, it is worth mentioning that the characteristic inflection point of the tangential velocity profile in the narrow gap disappears when the eccentricity reaches a certain high level. On the other side, negative values of the tangential velocity are observed in the vicinity of the outer cylinder in the wide gap, indicating the occurrence of a fully developed secondary flow for the eccentric annulus (\(E=0.8\)). For the orbital motion case, the tangential velocity profiles indicate that the orbital motion of the drill pipe may play a vital role in the cuttings transport process due to enhancement of the tangential velocity inducing an effective erosive impact in the lower region of the annulus, particularly for high eccentricities where cuttings are transported in the wide gap since the axial flow is enhanced for such conditions of eccentricity.

Fig. 13
figure 13

Effect of eccentricity on the radial distribution of the tangential velocity (200 rpm, \(n=0.52\), \(\kappa =0.5\))

Full size image

Effect of flow behavior index

Figure 14 presents the radial distribution of the tangential velocity profiles of the non-Newtonian fluid in the wide and narrow gaps of the eccentric annulus when the inner cylinder rotates and makes an orbital motion with a constant angular speed of 200 rpm. As observed, the main effect induced by high shear-thinning phenomena is the appearance of the Ostwald-de Waele characteristic shape of the tangential velocity profile (also called inflection point) where this effect is more prominent when the flow behavior index reaches (\(n=0.2\)). This behavior is more evident in the wide gap of the eccentric annular geometry. Moreover, an obvious improvement of the tangential velocity is stated when the inner cylinder makes an orbital motion, particularly in the narrow gap of the eccentric annulus.

Fig. 14
figure 14

Effect of flow behavior index on the radial distribution of the tangential velocity (200 rpm, \(E=0.5\), \(\kappa =0.5\))

Full size image

Effect of diameter ratio

Distribution of the tangential velocity profiles in the wide and narrow gaps of the eccentric annulus when the diameter ratio increases from \(\kappa =0.2\) to \(\kappa =0.8\) at a constant angular speed of rotation and orbital motion of the inner cylinder are illustrated in Fig. 15. As the diameter ratio increases, the orbital motion of the inner pipe induces a dramatic increase in the tangential velocity near the inner cylinder, especially for the narrow gap. On the other hand, the tangential velocity induced by pure rotation produces a similar effect in the eccentric annulus’s wide and narrow gaps.

Fig. 15
figure 15

Effect of diameter ratio on the radial distribution of the tangential velocity (200 rpm, \(E=0.5\), \(n=0.52\))

Full size image

Valuable points can be concluded from these profiles of tangential velocity. For all considered scenarios, the orbital motion results in a considerable increase in the tangential velocity of the Ostwald-de Waele fluid, indicating that an important rotational flow occurs, especially for high angular speeds. This claim is supported by 3D visualization of streamlines where the flow of the power-law fluid in the annulus is dominated by an essential rotational flow generated by the orbital motion of the inner cylinder. In contrast, for the pure rotation case, the rotational flow is stated only in the vicinity of the inner cylinder, as can be observed in Figs. 16 and 17. Thus, the turbulent flow might occur even before the transition to the turbulent flow in the presence of an important rotational flow (Marken et al. 1992). Also, it is revealed from these Figures that the fluid stagnation in the lower side of the eccentric annulus is eliminated by the orbital motion and the overall velocity field of the Ostwald-de Waele fluid is enhanced in this part of the annulus. Moreover, the orbital motion of the inner cylinder prevents the secondary flow from taking place in the wide gap of the annular geometry, thereby avoiding complicated flow patterns that may affect the annulus's pressure loss.

Fig. 16
figure 16

Evolution of streamlines and fluid velocity for pure rotation case (200 rpm, \(E=0.5\))

Full size image
Fig. 17
figure 17

Evolution of streamlines and fluid velocity for orbital motion case (200 rpm, \(E=0.5\))

Full size image

On the other hand, the geometry parameters (eccentricity and diameter ratio) almost act in the same way on the radial distribution of axial and tangential velocity profiles for both rotation and orbital motion cases at a constant angular speed.

Dynamic viscosity profile

Figure 18 presents a complementary explanation of the behavior of the axial velocity profiles in the narrow and wide gaps of the eccentric annulus (\(E=0.5\)) as the angular speed increases from 100 to 300 rpm, with the fluid velocity of 0.3 m/s. It is observed that the dynamic viscosity peak in the middle of the annulus narrow gap is decreased by 88% and 80% for orbital motion and rotation cases, respectively. This again confirms the effect of orbital motion on the improvement of the axial flow due to the reduction in the viscosity in this region induced by the increase in the shear rate, especially near the inner cylinder.

Fig. 18
figure 18

Effect of pure rotation and orbital motion speed on the dynamic viscosity profiles (\(E=0.5\), \(n=0.52\), \(\kappa =0.5\))

Full size image

Maximum velocity ratio

It is well known that the eccentricity of the inner cylinder causes a stagnation region of fluid flow in the lower region of the annulus, which affects the homogeneity of the axial velocity in the entire annulus, and therefore accumulation of cuttings might be enhanced in this region. For that, the effect of the orbital motion of the inner cylinder on the homogeneity of the Ostwald-de Waele fluid is considered since the orbital motion radius is directly related to the eccentricity.

The homogeneity of the Ostwald-de Waele fluid is evaluated in terms of the ratio of the maximum axial velocities in the wide and narrow gaps, as exemplified in Fig. 19. Figure 19a indicates that the increment of the inner cylinder rotation up to 400 rpm allows the maximum axial velocity in the wide gap to be 3 times higher than the maximum axial velocity in the narrow gap, while they are almost similar for the orbital motion case due to the vanishment of the stagnation region by the mechanical agitation induced by orbital motion of the inner cylinder. Figure 19b shows that when the inner cylinder makes a rotational motion, the wide and narrow maximum velocities ratio increases exponentially with eccentricity. However, intensification of the orbital motion (increase in the eccentricity) reduces the value of the ratio of the maximum velocities to be around 12. Furthermore, the orbital motion case shows better performance in homogenizing the axial velocity through the eccentric annulus. However, this performance is enhanced as the power-law index increases (the Ostwald-de Waele fluid gets closer to the Newtonian behavior). This trend could be attributed to the shear-thinning character at low values of the power-law index in which the axial velocity is no longer affected by the inner cylinder motion as indicated in Fig. 19c. Besides, The orbital motion has a positive influence on the homogeneity of the non-Newtonian fluid in the eccentric annulus; however, this effect is reduced as the diameter ratio raises where the ratio of the maximum velocities in the wide and narrow gaps shows an increase from 1 to 9 and from 5 to 14 for the orbital and rotational motions, respectively, as shown in Fig. 19d. This would explain the efficacity of carrying of cuttings when the drill string makes an orbital motion.

Fig. 19
figure 19

Evolution of the wide and narrow max velocities ratio. a Effect of pure rotation and orbital motion speed (\(E=0.5\), \(n=0.52\), \(\kappa =0.5\)). b Effect of eccentricity (200 rpm, \(n=0.52\), \(\kappa =0.5\)). c Effect of flow behavior index (200 rpm, \(E=0.5\), \(\kappa =0.5\)). d Effect of diameter ratio (200 rpm, \(E=0.5\), \(n=0.52\))

Full size image

Effect on torque

Effect of eccentricity

Figure 20 illustrates the effect of eccentricity (\(E=0.2-0.8\)) on the torque applied on the inner cylinder during its motion. As shown in this Figure, the increase in pure rotation speed induces a higher torque on the inner cylinder, particularly for the eccentricity range of \(E=0.2-0.6\), as shown in Fig. 20a–c. The torque, however, diminishes for the eccentric annulus \(E=0.8\) as can be seen in Fig. 20d where this effect is observed for all angular speeds of pure rotation of the inner cylinder. A reduction in the viscous force is the most likely explanation since the pressure force is not affected as much as in the concentric annulus (pressure loss gradient of a power-law fluid flow through a concentric annulus is almost two times higher than the fully eccentric annulus). On the contrary, as the eccentricity increases from \(E=0.2\) to \(E=0.8\) with increasing the angular speed of orbital motion, an exponential increment of torque on the inner cylinder is recorded, particularly for the angular speed of 400 rpm.

Fig. 20
figure 20

Effect of eccentricity on the torque applied on the inner cylinder induced by rotation and orbital motion (\(U=0.5\) m/s, \(\kappa =0.5\)). a \(E=0.2\). b \(E=0.4\). c \(E=0.6\). d \(E=0.8\)

Full size image

Effect of diameter ratio

The effect of the diameter ratio (\(\kappa =0.2-0.8\)) on the torque applied on the inner cylinder during its motion is presented in Fig. 21. A linear and a significant increase in torque are observed when the diameter ratio increases for rotational and orbital motions, respectively. The origin of this effect could be attributed to the pressure force exerted by the fluid on the inner cylinder during its orbital motion.

Fig. 21
figure 21

Effect of diameter ratio on the torque applied on the inner cylinder induced by rotation and orbital motion (\(U=0.5\) m/s, \(E=0.5\)). a \(\kappa =0.2\). b \(\kappa =0.4\). c \(\kappa =0.6\). d \(\kappa =0.8\)

Full size image

Effect of fluid velocity

Figure 22 shows the recorded torque when the non-Newtonian fluid velocity increases from \(U=0.5\) m/s to \(U=2\) m/s for various angular speeds. As shown, the torque applied on the inner cylinder is almost unaffected by the increment in the fluid velocity for the rotation case when the angular speed increases. However, there is an unexpected torque reduction for the orbital motion case as the fluid velocity increases. This reduction is estimated at 4.3%, 25%, 35%, and 40% for the angular speeds of 100 rpm, 200 rpm, 300 rpm, and 400 rpm, respectively. Therefore, incrementing the fluid velocity could reduce the torque applied on the inner cylinder in the presence of orbital motion. However, more studies are required to verify the origin of this effect.

Fig. 22
figure 22

Effect of fluid flow velocity on the torque applied on the inner cylinder induced by rotation and orbital motion (\(E=0.5\), \(\kappa =0.5\)). a \(U=0.5\) m/s. b \(U=1\) m/s. c \(U=1.5\) m/s. d \(U=2\) m/s

Full size image

Conclusions

In this paper, the sliding mesh approach is applied to study the influence of the orbital motion of the inner cylinder (pure rotation around its own axis and its rotation around the central axis of the outer cylinder) on the radial distribution of the axial and tangential velocities and the dynamic viscosity of the non-Newtonian (Ostwald-de Waele) fluid flow through an eccentric annular geometry in the laminar regime for various orbital angular speeds, eccentricities, flow behavior indexes, and diameter ratios. In addition to that, the homogeneity of the power-law fluid in the presence of the orbital motion is analyzed by calculating the ratio of the maximum and minimum values of the axial velocity in the annulus. Moreover, a comparison of the induced torque on the inner cylinder between orbital motion and rotational motion cases is carried out. The following can be concluded from this work:

  • Geometry parameters (eccentricity and diameter ratio) almost act in the same way on the radial distribution of the axial and tangential velocity profiles for both rotation and orbital motion cases at a constant angular speed.

  • The orbital motion of the inner cylinder prevents the secondary flow from appearing in the annulus's wide gap, thus avoiding complicated flow patterns which may affect pressure loss in the annulus.

  • The orbital motion enhances the Ostwald-de Waele fluid's axial flow through the annular geometry for all considered parameters of this study, particularly for high angular speeds and high eccentricity levels. This trend is confirmed again by the 3D visualization of streamlines in the annular geometry.

  • Orbital motion positively influences the homogeneity of the axial velocity of the non-Newtonian fluid in the eccentric annulus as compared to the pure rotation case, especially for high eccentricities.

  • In the presence of the orbital motion, the increase in the fluid velocity could reduce the torque applied on the inner cylinder.