A general regression neural network model offers reliable prediction of CO₂ minimum miscibility pressure

Abstract

This study introduces a general regression neural network (GRNN) model consisting of a one-pass learning algorithm with a parallel structure for estimating the minimum miscibility pressure (MMP) of crude oil as a function of crude oil composition and temperature. The GRNN model was trained with 91 samples and was successfully validated with a blind testing data set of 22 samples. The MMP for six of these data samples was experimentally measured at the Petroleum Fluid Research Centre at Kuwait University. The remaining data consisted of experimental MMP data collected from the literature. The GRNN model was used to estimate the MMP from the training data set with an average absolute error of 0.2 %. The GRNN model was used to predict the MMP for the blind test data set with an average absolute error of 3.3 %. The precision of the introduced model and models in the literature was evaluated by comparing the predicted MMP values with the measured MMP values and using training and testing data sets. The GRNN model significantly outperformed the prominent models that have been published in the literature and commonly used for estimating MMP. The use of the GRNN model was reliable over a large range of crude oil compositions, impurities, and temperature conditions. The GRNN model provides a cost-effective alternative for estimating the MMP, which is commonly, measured using experimental displacement procedures that are costly and time consuming. The results provided in this study support the use of artificial neural networks for predicting the MMP of CO₂.

Introduction

Enhanced oil recovery (EOR) using carbon dioxide injection can increase the oil production of a reservoir to beyond what it is typically achievable from primary recovery. Compared to other enhanced oil recovery methods, supercritical CO₂ potentially enters zones that have not been previously invaded by water and releases trapped oil. However, a fraction of the injected CO₂ remains stored underground, which is beneficial for the environment. EOR can be achieved using CO₂ injection through two processes, miscible and immiscible displacement, which depend on the reservoir pressure, temperature, and crude oil composition (Andrei et al. 2010). In the 1950s, when CO₂ injection began as an oil recovery method, the immiscible process was emphasized as an alternative recovery scheme for reservoirs where water-based recovery techniques were inefficient (Jarrell et al. 2002). CO₂ flooding is one of the most widely used methods for medium and light oil recovery in sandstone and carbonate reservoirs (Moritis 2006; Alvarado and Manrique 2010). Throughout the last five decades, extensive laboratory studies, numerical simulations and field applications of CO₂ flooding processes have been reported (Burke et al. 1990; Grigg and Schecter 1997; Idem and Ibrahim 2002; Moritis 2006; Chukwudeme and Hamouda 2009; Alvarado and Manrique 2010).

Interest in implementing CO₂ injection as a miscible enhanced oil recovery technique has increased since 1970s (Mungan 1981). CO₂ lowers the interfacial tension (IFT) and enhances mobility by reducing oil viscosity and causing oil swelling (Simon et al. 1978; Green and Willhite 1998).

Previous research indicated that CO₂ achieves miscibility through multiple contacts with the crude oil in a reservoir (Jarrell et al. 2002). In multi-contact miscibility, the composition of the displacing or displaced fluids is continuously altered. In vaporizing drive by CO₂, miscibility is obtained by vaporizing the light hydrocarbon components into the driving gas. Relative to natural gas and N₂, CO₂ miscibility occurs at a lower pressure. Miscible displacement is characterized by the absence of a phase boundary or interface between the displaced and displacing fluids (Benham et al. 1960). Two fluids are miscible when all mixtures of the two fluids remain in a single phase without any interfaces. In this case, no interfacial tension occurs between the fluids (Stalkup 1983).

Importance of MMP for CO₂ injection

Miscible displacement is only achieved at pressures greater than a certain minimum. The successful design and implementation of a miscible gas injection project depend on the accurate determination of the MMP, which is the lowest possible operating pressure at which the gas can miscibly displace oil.

MMP is also defined as the lowest pressure at which a distinct point of maximum curvature exits in a plot of oil recovery versus pressure. When the maximum curvature point is not obvious, the 95 % oil recovery, which corresponds to 1.2 PV of injected solvent, is used to define the MMP (Lake 1989). A very good oil recovery is guaranteed if the reservoir pressure is greater than the minimum miscibility pressure. MMP is a function of temperature and crude oil properties (Mungan 1981). MMP is an important design factor in the selection of candidate reservoirs for gas injection in which miscible recovery occurs.

MMP is often experimentally estimated using published correlations or modeled using equations of state. Equation-of-state (EOS) calculations are generally conducted by simplifying multicomponent systems into a light component (C₁), intermediate pseudo-component (C₂–C₆), and heavy pseudo-component (C₇₊). An EOS is used to generate the two-phase region (if it exists) for the resulting ternary composition. The critical point and limiting tie line of the mixture are estimated by extrapolating the near-critical data or estimating directly using an EOS (Ahmed 1997). The MMP is generally estimated using this critical region and the solvent/oil compositional data. The EOS technique is plagued by the inaccuracy of gas and liquid data near the plait-point region. These gas and liquid equilibrium data are often experimental and are time consuming to determine.

Experimental techniques for measuring MMP

Experimental determination of the MMP can be performed using the following typical methods.

• Slim-tube test (Yellig and Metcalfe 1980)

• Micro slim-tube test (Kechut et al. 1999)

• Rising bubble apparatus (Christiansen and Haines 1987)

• Single bubble injection technique (Srivastava and Huang 1998)

• Vanishing interfacial tension methods (Rao 1997)

• Vapor liquid equilibrium-interfacial tension test (Kechut et al. 1999)

• Vapor density of injected gas versus pressure (Harmon and Grigg 1986)

• High-pressure visual sapphire cell (Hagen and Kossak 1986)

• “PVT multi-contact experiments (Thomas et al. 1994)”

The slim-tube method is potentially the primary technique used to determine MMP under reservoir conditions. Slim-tube experiments involve the displacement of live oil from the slim tube by injecting gas at a constant temperature (Thomas et al. 1994). A hybrid slim-tube experimental approach was developed to determine the MMP using a displacement test and the analysis time of the hybrid slim tube was one-tenth shorter than the conventional slim-tube (Kechut et al. 1999). The rising bubble apparatus (RBA) involves injecting a small bubble of gas at the base of a live oil column (Srivastava and Huang 1998). The RBA for MMP was further extended to single bubble injection techniques that estimate MMP by averaging the pressures of bubble disappearance at the bottom and top of the rising bubble column (Srivastava and Huang 1998). To overcome most of the disadvantages in conventional approaches (slim-tube and RBA), a relatively new method, with an elaborative experimental set up but simple technique, was developed by Rao in 1997, called the vanishing interfacial technique (VIT). A prototype of vapor–liquid equilibrium-interfacial tension (VLE-IT) apparatus, proposed by Kechut et al. (1999), is used to measure the interfacial tension (IFT) between the injected gas and oil at a definite temperature, and desired pressures. The plot of IFT values versus pressure is extrapolated to zero IFT. The miscibility of the injected gas and oil is evaluated according to the vanishing IFT between the two phases. The vapor density method is a dynamic test that directly measures the ability of the injected gas to extract intermediate components from the crude oil. The measurements are conducted in a constant-volume visual PVT cell. In addition to measuring the upper-phase density, the volume of the liquid (lower phase) is monitored to help determine the MMP (Harmon and Grigg 1986). A high-pressure visual cell composed of sapphire was developed to determine the minimum dynamic miscibility pressures (MDMP) by visual observations of gas droplets that pass through the reservoir fluid (Hagen and Kossak 1986). In the Multi-Contact experimental method (Thomas et al. 1994), discrete mixtures of displaced and displacing fluids are combined to determine the MMP.

Correlations used for estimating MMP

Many correlations that relate the MMP to the physical properties of the oil and the displacing gas have been proposed to facilitate screening procedures and to understand the miscible displacement process. The pure CO₂ miscibility pressure was correlated with the temperature, C₅₊ molecular weight, volatile oil fraction, and intermediate oil fraction (Alston et al. 1985). These correlations were also used for impure CO₂ gas streams by including an injection gas critical property function.

The original correlation of Alston et al. (1985) is given by

$$ {\text{MMP}} = 6.056 \times 10^{ - 6} \times (1.8T_{\text{R}} + 32)^{1.06} \times ({\text{Mw}}_{{{\text{C}}_{5 + } }} )^{1.78} \times (X_{\text{vol}} /X_{\text{int}} )^{0.136} $$

(1)

In the above equation, MMP is in KPa and T _R is in °C. To complete all calculations and analyses in field units, Eq. (1) has been re-arranged and is provided in the “Appendix”.

A correlation (Cronquist 1978) was developed by regression fitting 58 data points. The tested oil gravity varied from 23.7° to 44° API. The reservoir temperature varied from 71 to 248 °F, and the experimental MMP varied from 1073 to 5000 psi. The original correlation (Cronquist 1978) is provided below.

$$ {\text{MMP}} = 0.11027 \times \left( {1.8 \, T_{\text{R}} + 32} \right)^{Y} $$

(2)

In the above notation, MMP is in KPa and T _R is in °C. In Eq. (2), the exponent Y is given by

$$ Y = 0.744206\; + \;0.0011038\; \times \;{\text{Mw}}_{{{\text{C}}_{5 + } }} + 0.0015279\; \times \;{\text{vol}} $$

(3)

To complete all calculations and analyses in field units, Eq. (2) has been re-arranged and is provided in the “Appendix”.

A correlation that used temperature as the independent variable and included a bubble point pressure correction was developed and presented in graphical form by Yellig and Metcalfe (1980). If the oil bubble point pressure exceeded the estimated MMP, the miscibility pressure was set to the bubble point pressure of the oil. Later on, Yellig and Metcalfe (1980) work was given in an equation form by Tarek Ahmed (1997) and is given as follows:

$$ {\text{MMP}}\; = \;12.6472\,\; + \;\,0.015531\,\, \times \;\left( {1.8 \, \,T_{\text{R}} + 32} \right) + 1.24192\; \times \;10^{ - 4} \; \times \;\left( {1.8 \, \,T_{\text{R}} + 32} \right)^{2} {{ - 716.9427} \mathord{\left/ {\vphantom {{ - 716.9427} {\left( {1.8 \, \,T_{\text{R}} + 32} \right)}}} \right. \kern-0pt} {\left( {1.8 \, \,T_{\text{R}} + 32} \right)}} $$

(4)

In the above equation, MMP is in KPa and T _R is in °C. To complete all calculations and analyses in field units, Eq. (4) has been re-arranged and is provided in the “Appendix”.

Originally, Eq. (5) was used by Newitt et al. (1956) to estimate CO₂ vapor pressure. Later on, in 1984 it was claimed that effects of oil composition on MMP are small at low temperatures (Orr and Jensen 1984). Thus, the vapor pressure at low temperatures may be a good estimate of MMP. It was suggested that the vapor pressure curve of CO₂ can be extrapolated and compared with the minimum miscibility pressure to estimate the MMP for low temperature reservoirs (T < 120 °F). This correlation, referred to as Orr and Jensen (1984) correlation, is given as follows:

$$ {\text{MMP}} = 0.10386 \times \exp \;\left( {10.91 - \frac{2015}{{255.372 + 0.5556 \times \left( {1.8\, \, T_{\text{R}} + 32} \right)}}} \right) , $$

(5)

where MMP is in KPa and T _R is in °C. To complete all calculations and analyses in field units, Eq. (5) has been re-arranged and is provided in the “Appendix”.

A generalized correlation (Glaso 1985) was presented for predicting the MMP required for the multi-contact miscible displacement of reservoir fluids by hydrocarbons, CO₂, or N₂ gas. The original correlation (Glaso 1985) is provided below.

When C₂₋₆ > 18 – mole %

$$ {\text{MMP}} = 5.58657 - 0.02347739 \times {\text{Mw}}_{{{\text{C}}_{7 + } }} + (1.1725 \times 10^{ - 11} {\text{Mw}}_{{{\text{C}}_{7 + } }}^{3.73} \times e^{{786.8 \times {\text{Mw}}_{{{\text{C}}_{7 + } }}^{ - 1.058} }} ) \times (1.8T_{\text{R}} + 32) $$

(6)

where MMP is in KPa and T_R is in °C.When C₂₋₆ < 18 – mole %

$$ {\text{MMP}} = 20.33 - 0.02347739 \times {\text{Mw}}_{{{\text{C}}7 + }} + \left( {1.1725 \times 10^{ - 11} \times {\text{Mw}}_{{{\text{C}}7 + }}^{3.73} \times e^{{786.8 \times {\text{MW}}_{{{\text{C}}7 + }}^{ - 1.058} }} } \right) \times \left( {1.8 \, T_{\text{R}} + 32} \right) - 0.836 \times {\text{C}}_{2 - 6} \, $$

(7)

where MMP is in KPa and T _R is in °C. To complete all calculations and analyses in field units, Eqs. (6) and (7) have been re-arranged and are provided in the “Appendix”.

The above correlations are easy to implement and can be accommodated by simple hand calculations. However, none of these correlations is credible enough to use for the final project design. For screening purposes, these correlations provide a fair guess depending on the data used (Yurkiw and Flock 1994). The success of these correlations is usually limited by the composition and temperature ranges for which they were developed. The objective of this study is to develop a reliable empirical model for predicting the CO₂–oil minimum miscibility pressure using GRNN.

Discussion

Data acquisition

Six fluid samples were collected from various reservoirs in the Middle East. Prior to conducting miscibility studies to determine the MMP of these six fluid samples, detailed and extensive fluid characterization was performed at the General Facility Laboratory in the College of Engineering and Petroleum at Kuwait University. A mercury-free PVT cell was used to determine the thermo-physical properties of the reservoir fluids. Detailed fluid analysis, including the measurement of critical properties, density, viscosity, and molecular weight, was accomplished in our laboratory utilizing a Crude Oil Analyzer that was equipped with a liquid chromatograph for C₃₆₊ measurements and a gas chromatograph for C₁₂₊ measurements.

To determine the MMP data, six multiple contact experiments were performed at various reservoir temperature and pressure conditions. Pure CO₂ was used as the injecting gas. A series of single cell, multiple-contact experiments were conducted. Here, a reservoir fluid sample was loaded into a pressure–volume–temperature (PVT) cell. Next, a sample of pure CO₂ was introduced before allowing the cell to equilibrate at the desired pressure. At this stage, the phase volumes were measured and the equilibrium gas phase was collected in a gas pycnometer before analyzing with a gas chromatograph. Meanwhile, a small liquid sample at equilibrium was collected in a liquid pycnometer and was analyzed using the Liquid Chromatograph. This procedure was repeated again with a new dose of CO₂.

Typically, approximately seven stages or contacts were performed during each experiment. At a certain point, it is observed that both equilibrated phase (liquid and gas) densities converged to the same values, which corresponded to the K values as they approached unity. This result implies that both phases become indistinguishable and the boundary between them cannot be ascertained. At this point, the pressure of the system is recorded and is considered as the MMP.

In addition to the six MMP values measured in our laboratory, MMP data for 107 case studies that were measured using the slim tube, RBA and multi-contact techniques were collected from the published literature (Holm and Josendal 1974; Yellig and Metcalfe 1980; Alston et al. 1985; Glaso 1985; Sebastian et al. 1985; Holm 1987; Zuo et al. 1993; Ahmed 1997; Alomair et al. 2012). The entire data set consisted of 113 samples is given in Table 1. The MMP values were tabulated from these data as a function of crude oil composition, temperature, molecular weights of Mw₅₊ and Mw₇₊, and concentrations of CO₂, H₂S, and N₂.

Table 1 Data set used for GRNN model development

Data description

This research was based on 113 crude samples for which the MMP values were measured as a function of composition (C₁, C₂, C₃, C₄, C₅, C₆, C₇₊), molecular weight (Mw₅₊, Mw₇₊), temperature, and concentrations of CO₂, H₂S, and N₂. Sample histograms for some of these parameters are shown in Figs. 1, 2, 3, 4, 5, 6. Both MMP and temperature appear to have bimodal distributions (Figs. 1, 2). The molar composition data for C₁, C₂, C₃, C₄, C₅, C₆, and C₇₊ exhibited nearly normal distributions. An example histogram for C₄ is shown in Fig. 3. In addition, the molecular weights for the C₅₊ and C₇₊ pseudo-components appear to be nearly normally distributed (Figs. 4, 5). Generally, the molar concentrations of CO₂, H₂S, and N₂ were positively skewed. An example histogram for CO₂ is shown in Fig. 6. As shown in Table 2, the data set tabulated in Table 1 features few statistical variations in magnitude between the variables. For example, the measured MMP values and the H₂S concentrations vary by three orders of magnitude. Consequently, all variables were standardized to vary within the same order of magnitude (from −1 to +1). The dependent and independent variables were transformed into standardized values using the following equation:

$$ \overline{Z} = - 1 + 2\left[ {\frac{Z - L}{H - L}} \right] $$

(8)

where $\overline{Z}$ is the standardized variable value, Z is the variable value, L is the lowest value of a particular variable, and H is the highest value of a particular variable

Fig. 1

Frequency histogram of the minimum miscibility pressure (in psi)

Fig. 2

Frequency histogram for temperature (°F)

Fig. 3

Frequency histogram for the C₄ molar composition

Fig. 4

Frequency histogram for the molecular weights of the C₅₊ pseudo-component

Fig. 5

Frequency histogram for the molecular weights of the C₇₊ pseudo-component

Fig. 6

Frequency histogram for the molar composition of CO₂

Table 2 Statistical summary of the data used to develop the GRNN model

The standardized molar compositions of C₁, C₂, C₃, C₄, C₅, C₆, and C₇₊, the molar concentrations of CO₂, H₂S, and N₂, the molecular weights (Mw₅₊, Mw₇₊), and the temperature were used as input vectors in the GRNN model. The standardized MMP values correspond with the values of the GRNN model output as described below.

GRNN model algorithm

The general regression neural network (GRNN) performs non-linear regressions when the target variables are continuous. This regression analysis requires that the functional form that mimics the data behavior be estimated. In a multi-dimensional problem, it is difficult to choose this function, which is the main shortcoming of non-linear regression analysis. In contrast, the GRNN algorithm (Specht 1991) successfully overcomes this drawback because it does not require an assumed functional form. The GRNN establishes a functional relationship between the dependent and target variables based on the probability density function of the training data. X in our analysis corresponds to the set of input parameters, described earlier. The random variable Y assumes the value of MMP. An estimate of the pdf (Dai et al. 2010) is given by

$$ f(X,Y) = \frac{1}{{2\pi^{{\left( {\frac{p + 1}{2}} \right)}} \sigma^{{\left( {p + 1} \right)}} }} \cdot \frac{1}{n}\sum\limits_{i = 1}^{n} {\exp \left( { - \frac{{D_{i}^{2} }}{{2\sigma^{2} }}} \right) \cdot \exp \left[ { - \frac{{\left( {Y - Y^{i} } \right)^{2} }}{{2\sigma^{2} }}} \right]} $$

(9)

where,

σ is the smoothing factor

n is the number of training vectors

p is the dimension of the vector X

Y ⁱ is the output target value for the ith training vector

$D_{i}^{2}$ is the distance between X and the ith training sample X _i , and is given by

$$ D_{i}^{2} = \sum\limits_{i = 1}^{p} {\left( {X_{j} - X_{ij} } \right)^{2} } $$

(10)

Using a nonparametric estimator of the joint probability density function f(x, y), general regressions acquire an estimate $\hat{Y}$ for the conditional mean of a target random variable Y, when given an input vector of a random variable (X). The class of consistent estimators proposed by Parzen (1962) was used for this purpose. For sample values of X _i and Y _i , the following function was used to estimate the mean of the target random variable ($\hat{Y}\left( X \right)$):

$$ \mathop Y\limits^{ \wedge } \left( X \right) = \frac{{\sum\limits_{i = 1}^{n} {Y_{i} \exp \left( { - \frac{{D_{i}^{2} }}{{2\sigma^{2} }}} \right)} }}{{\sum\limits_{i = 1}^{n} {\exp \left( { - \frac{{D_{i}^{2} }}{{2\sigma^{2} }}} \right)} }} $$

(11)

Equation (11) shows that the general regression is a weighted average of all observed values of Y _i , which are weighted exponentially according to their Euclidean distance from X. For very large standard deviations or a smoothing factor of σ, $\hat{Y}\left( X \right)$ converges to the mean of the observed value of Y _i (Specht 1991). In general regression networks, σ is the only important computing parameter that must be optimized (Huang and Williamson 1994). For very large values of n, it is necessary to group observations into a smaller number of clusters to obtain an efficient general regression. The cluster version of a general regression is given as follows:

$$ \mathop Y\limits^{ \wedge } \left( X \right) = \frac{{\sum\limits_{i = 1}^{m} {A_{i} \exp \left( { - \frac{{D_{i}^{2} }}{{2\sigma^{2} }}} \right)} }}{{\sum\limits_{i = 1}^{m} {B_{i} \exp \left( { - \frac{{D_{i}^{2} }}{{2\sigma^{2} }}} \right)} }} $$

(12)

In the above equation, parameters A _i and B _i are given by

$$ A_{i} \left( k \right) = A_{i} \left( {k - 1} \right) + Y_{j} $$

(13)

and

$$ B_{i} \left( k \right) = B_{i} \left( {k - 1} \right) + 1 $$

(14)

where

m is the number of clusters

k is the number of observations

A _i and B _i are the sum of the Y values and number of observations grouped into cluster i.

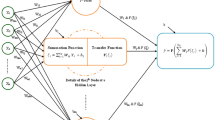
The A _i and B _i coefficients are determined in one pass using the observed samples. A commonly adapted clustering technique consists of arbitrarily setting a single radius, r. When scrolling through the data, the first data point is taken as the first cluster center. If the successive data point has a distance of less than r from this cluster center, the cluster center is updated using Eqs. (13) and (14). Otherwise, the successive data point becomes an additional cluster center (Al-Dousari and Garrouch 2013). The GRNN built based on Eq. (8) through Eq. (12) consists of the following four layers (Fig. 7).

Fig. 7

General regression neural network architecture

a. An input layer The number of neurons in the input layer is equal to the number of independent variables. Values for these neurons are standardized by subtracting the lowest variable value and dividing by the variable range, as shown in Eq. (8). The input neurons feed these standardized values to each of the neurons in the hidden layer (Fig. 7).

b. A hidden layer This layer associates one neuron for each row in the training data set matrix. The neuron stores the values of the independent variables for a particular row with the corresponding dependent variable values. During training, the GRNN calculates the Euclidean distances for each input neuron of the input vector (X). The distances from each input neuron are fed with a smoothing factor into a nonlinear exponential activation function, as specified by equation Eq. (12). The resulting value is passed to the neurons in the summation layer (Fig. 7).

c. A summation layer Next, neurons of the summation layer execute the dot product between the weighted A and B coefficients in Eq. (13) and Eq. (14) and the activation results from the input neurons. The summation layer consists of two neurons: a denominator summation unit neuron and a numerator summation unit neuron. The denominator summation unit neuron sums the weight values that arrive from each of the hidden neurons. The numerator summation unit neuron sums the weight values that are multiplied by the actual dependent value for each hidden neuron (Huang and Williamson 1994).

d. An output layer This layer divides the values accumulated in the numerator summation neuron unit by the values accumulated in the denominator summation neuron unit. The resulting values are presented as the predicted output value. The weights of the hidden layer neurons represent cluster centers of a multidimensional space. A and B coefficients related with these clusters are taken as the weights that connect the summation layer and the hidden layer (Huang and Williamson 1994). The smoothing factor is perhaps the most prominent computing parameter for the GRNN’s paradigm (Huang and Williamson 1994).

The optimum σ for a GRNN built from a training data set is approximated using an initial guess. Next, the sum squared error (SSE) is calculated for the training data set. This process is repeated by varying σ by a fixed increment. After using a series of trials for σ, the smoothing factor associated with the smallest SSE is used to represent the optimum σ for the training data set. The process of optimizing σ is a default built-in process in NeuroShell toolbox which was used in this study (Ward and Sherald 2006; Al-Dousari and Garrouch 2013).

GRNN model training and validation

An input file, consisting of 113 vectors with 14 attributes, has been downloaded into NeuroShell database (Ward and Sherald 2006; Al-Dousari and Garrouch 2013). NeuroShell randomly splits the data file into a training data set that consists of 80 % of the data (91 vectors), and a blind test data set consisting of the remaining 20 % of the data (22 vectors), used for validation purposes.

Figure 8 compares the estimated MMP using the GRNN model and the MMP values measured experimentally for the training data set. With an average absolute error of approximately 0.2 %, the network appears to mimic the physical relationships between the MMP and the remaining variables. However, this statement is not confirmed unless the model performs well for estimating MMP for the blind test data set. Figure 9 compares the estimated MMP values that resulted from the GRNN model and were measured experimentally for the testing data set. The GRNN model prediction of MMP appears to be very reasonable, yielding an average absolute error of approximately 3.3 %. The GRNN model performance was compared with the MMP correlations (Alston et al. 1985; Cronquist 1978; Orr and Jensen 1984; Glaso 1985). Figures 10, 11, 12, 13, and 14 compare the MMP values predicted by the above models against the experimentally measured MMP values that were determined from the training data set. According to these figures, the predicted MMP values from these correlations are generally unreliable. Table 3 summarizes the average absolute error for these correlations and the GRNN model for the training and testing data sets. The GRNN model prediction is more precise than the other previously mentioned literature correlation methods. The maximum average absolute error when using these correlations varies from approximately 32 to 94 %, which indicates that these predictions are often unreliable. The maximum absolute average error when using the GRNN model on the same data set was approximately 6 %. These results were confirmed by the blind test data set (Table 3). The maximum average absolute error that was obtained using the GRNN model for the testing data set was approximately 12 %.

Fig. 8

Comparing the MMP values using the GRNN to MMP data values measured experimentally for the training data set

Fig. 9

Comparing the MMP values using the GRNN to MMP data values measured experimentally for the testing data set

Fig. 10

Comparing the MMP values estimated when using the Alston et al. (1985) model to the MMP data values measured experimentally for the training data set

Fig. 11

Comparing the MMP values estimated using the Cronquist (1978) model to the MMP data values measured experimentally for the training data set

Fig. 12

Comparing the MMP values estimated using the Yellig and Metcalfe (1980) model to the MMP data values measured experimentally for the training data set

Fig. 13

Comparing the MMP values estimated using the Orr and Jessen (1984) model to the MMP data values measured experimentally for the training data set

Fig. 14

Comparing the MMP values estimated using the Glaso (1985) model to the MMP data values measured experimentally for the training data set

Table 3 Average error between the measured data and the predicted data using the GRNN and other models. Results are compared for the training and blind test data sets

The reliabilities of each of the literature correlations that were discussed earlier were evaluated using the blind testing and training data sets. The calculation results are summarized in Table 3 with the minimum error, maximum error, average absolute error, and standard deviation of the error for each correlation. Among the literature correlations that were used, Glaso (1985) correlation yielded the best results (Table 3). Figures 15 and 16 compare the average absolute errors between the correlation (Glaso 1985) and the GRNN model predictions for the training and testing data sets, respectively. From these figures, the GRNN model outperformed the model (Glaso 1985) by a reasonable margin. However, the correlation (Glaso 1985) presented better prediction accuracy than the other correlations because it accounted for additional effects on the CO₂ MMP that resulted from the presence of intermediate components in the reservoir oil. In contrast, west Texas oils-based correlations (Yellig and Metcalfe 1980) that included the temperature effects showed the poor performance and may be explained by the dependency of the MMP values on variables that were not included in the correlation. These variables consist of the molecular weight of C₅₊, the oil intermediate fraction, and the paraffinicity. The poor performance model (Orr and Jensen 1984) was likely related to the temperature variations of the data, which vastly exceeded the correlation range of 120 °F. The model (Alston et al. 1985) provided the least adequate predictions, potentially because the correlation was not suitable for flue gas streams that contain N₂.

Fig. 15

Comparing the performance of the GRNN model to the Glaso (1985) model for estimating the MMP data using the training data set

Fig. 16

Comparing the performance of the GRNN model to the Glaso (1985) model for estimating the MMP data using the testing data set

Conclusions

This manuscript introduces a general regression neural network (GRNN) model for estimating the minimum miscibility pressure (MMP) required for the multi-contact miscible displacement of reservoir fluids by CO₂ injection. The model input consists of the reservoir temperature (°F), molecular weight of pentane plus (Mw₅₊), molecular weight of heptane plus (Mw₇₊), mole percent of methane in the crude oil sample, molar percentage of the intermediates (C₂ through C₆) in the oil sample, and the molar percentages of the non-hydrocarbons (CO₂, N₂ and H₂S). The MMP values that are predicted using the GRNN model are compared to experimental data from laboratory tests and MMP data collected from the literature. The GRNN model was able to generalize the training data set results to a new data set that was unseen by the network during training. The GRNN has a parallel structure where the learning is not iterative (i.e., onefold learning going from the input slab to the output slab). This structure allows these networks to learn fast. In addition to fast learning, the GRNN is efficient for noisy data and performs accurately with light data sets.

Five correlations for predicting MMP that were proposed by a number of investigators were used to predict the MMP for the same data sets that were used by the GRNN model. The GRNN model significantly outperformed all these correlations.

Appendix

See Table 4.

Table 4 .