Introduction

The excessive population growth, limited surface water resources, and excessive operation of aquifers have imposed serious damages to Iran’s natural resources in the past decades. In addition to the severe drop in the water level of aquifers, agricultural, industrial and urban activities impose various pollutants on aquifers, that in order to prevent the continued decrease in quantity and quality, management of operation and protection of groundwater should be placed as a principle and basis in the country’s planning. With the expansion of settlement in areas where there is no surface water or its amount is low, the use of groundwater resources as a safe alternative was considered. So in some areas, groundwater is considered the only source of water supply. Therefore, for better planning and optimal use of groundwater resources, strategies should be utilized to accurately forecast groundwater level (GWL) variations, especially in dry and low water years. In order to evaluate the effects of development on groundwater, both from a quantitative and qualitative point of view, mathematical and computer simulation of these resources is considered a powerful tool for the optimal use of these resources. Recently, many mathematical and computer techniques have been considered for simulating the hydraulic behavior of groundwater resources and predicting GWL fluctuations. Studying the progress of numerical models displays that a series of different parameters such as boundary and environmental conditions, physical and hydraulic properties of the aquifer, river sections and wetted surface, aquifer hydraulic parameters, the way of distribution and extraction of water in the plain, parameters of aquifer recharge, topographical factors and geology, etc., are effective in simulating GWL changes (Fleckenstein et al. 2010; Luo and Sophocleous 2011; Zampieri et al. 2012). Many of these models, such as MODFLOW and GMS, are developed based on finite difference numerical methods, and in various research works, they require the definition and preparation of many input data and maps based on a specific standard (Larsen et al. 2000; Toddand kenneth 2001; Yanxun et al. 2011; Irawan et al. 2011; Lachaal et al. 2012; azizpour et al. (2021, 2022); Poursaeid et al. (2020, 2021, 2022); Yosefvand and Shabanlou (2020); Malekzadeh et al. (2019a,b)). In such structures, checking climatic parameters such as temperature and precipitation on the entire system and predicting GWL variations in the coming years under the influence of these parameters using mathematical modeling makes the matter more complicated and extracting valid results in this field requires much time and money (Klove et al. 2014; Shrestha et al. 2016; Lemieux et al. 2015; Panda et al. 2012; Erturk et al. 2014). Due to the undeniable connection between surface and groundwater, the utilization of integrated models and the investigation of the interaction effect of surface and groundwater withdrawal on the changes in the aquifer level have attracted the attention of researchers, which requires adding new information and variables related to surface and groundwater (Fleckenstein et al. 2010; Graham et al. 2015; Ramírez-Hernández et al. 2013; Xie et al. 2016 ).

In some research works, in order to predict GWLs in the whole plain, the connection of surface and groundwater models has been carried out based on the recreation of saturated and unsaturated zones. The unsaturated zone is the boundary between the earth’s surface and the groundwater level. The most highlighted advantage of the recreation of saturated and unsaturated areas of the soil in the surface and groundwater linked model is that it is able to calculate the exchange between surface and groundwater in different time intervals and places. This method works based on the complete hydroclimatology water budget in each region. But due to the need for a wide range of data and complex maps, it is not possible to implement this method in many aquifers (Zeinali et al. 2020a, 2020b). Simulation methods are able to analyze problems related to unified systems of surface and groundwater resources that have complex relations and equations. Therefore, there is a need for one or more powerful simulation tools that can express complex systems in accordance with existing reality and make the user able to participate in the model construction in order to increase confidence in the modeling process, and these models are usually expensive (Hu et al. 2016; Ivkovic 2009; Pahar and Dhar 2014; Bayesteh and Azari 2021).

Real system details and its behavior may be much more complicated than what is configurated in the model. If the studied system is simplified more than required, we might not be able to obtain the required information from the model (Bear 2010).

Hence, it is very important to replace simple and reliable methods that require little information and, at the same time, with very little time and cost, have accurate results compared to numerical methods and mathematical models (Hafezparast Mavadat and Marabi, 2021; Hafezparast and Marabi, 2021; Fatemi and Parvini 2022). Some of these models use a combination of stochastic methods and artificial intelligence (Moeeni et al. 2017a, 2017b; Malekpour and Tabari 2020).

Therefore, it is very important to replace simple and reliable methods that require a small amount of information and at the same time have accurate results with very little time and cost compared to numerical methods and mathematical models. In most of these methods, the prediction of GWLs without using simulation models is usually a series of averages and does not provide a distribution map for the plain, but they are able to predict GWL variations in less time and with high accuracy (Guzman et al. 2019; Nadiri et al. 2019; Soltani and Azari, 2022). In recent years, along with stochastic methods (Ebtehajet al. 2020; Zeynoddin et al. 2020; Azari et al. 2021), artificial intelligence-based methods such as GMDH, ELM, ORELM and hybrid methods have been widely used for hydroclimatological parameters such as temperature, precipitation, river flow and water level changes of surface reservoirs and GWL have been used (Ebtehaj et al. 2016; Zeynoddin et al. 2018; Soltani et al. 2021; Esmaeili et al. 2021).

Reviewing previous studies proves that the majority of mathematical models used in each watershed require the definition of new boundary conditions and information and maps related to that area, and practically applying the model requires its adaptation to the specific conditions of the studied area. Due to the large volume of required statistics and information, as well as the need to carry out the calibration and verification process in these models, which is a very time-consuming and complex process, the use of an alternative method that can be used with the same accuracy and in less time compared to mathematical models is very important to predict GWL fluctuations using insignificant data. In many plains, there is not enough information for hydraulic analysis and system simulation of groundwater resources to predict the GWL or it is not accurate enough. The objective of this paper is to employ the artificial intelligence tool as an alternative tool and compare it with the results of the numerical model to predict the GWL fluctuations. In this regard, hybrid methods such as the GA-ANN, GA-ICA and ELM and ORELM methods are used and their results are compared with the GMS numerical model.

Materials and methods

Study area

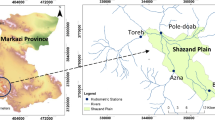
The under study area is the Sonqor plain in western Iran, located 100 km northwest of Kermanshah (Fig. 1). The Sonqor plain is one of the fertile plains in Kermanshah province, whose demands are supplied by both systems (i.e., surface and groundwater). Part of the water required for the plain is supplied by the Soleimanshah Dam and the rest is supplied by 278 deep wells drilled south and west of the plain. One of the problems that can always be proposed is to study the role of extraction wells in draining and reducing river discharge, especially in the southern parts of the plain. If a high hydraulic gradient is created between the river water level and the groundwater level due to the decrease in the level in the southern and western parts of the aquifer, the river leakage rate to the aquifer increases. The provision of part of the needs of the region by Soleimanshah Dam and the infiltration of surface water into the aquifer in the northern regions of the plain has faced the interaction of rivers and aquifers in this region with complications. Therefore, providing a dynamic model to calculate the interaction of the river and aquifer and the amount of recharge or discharge of the river and aquifer in different reaches of the river is very important. In this research, to ensure the ability of such models, their performance is evaluated in comparison with valid mathematical models such as GMS.

Fig. 1
figure 1

Location of study area for building a numerical model and artificial intelligence modeling

Full size image

Groundwater model construction

By considering the general groundwater flow direction in the whole Sonqor plain, for gridding, a 250 × 250 m mesh networking is considered. Therefore, the model gridding is made with 2596 cells (44 rows and 59 columns) with distances of 250 m including 908 active cells and 1688 inactive cells. The general head boundary package is utilized in this research to recreate the inflow and outflow boundaries of the study area, in which the inflow or outflow is impacted by the hydraulic gradient at the boundary and the conductance of the boundary cell. The use of the General Head Boundary package makes it is possible to simulate the input and output boundary flows at the plain borders more accurately. This method intelligently uses water level fluctuations at boundaries and boundary cell conductivity to predict inlet and outlet flows. By employing the geophysical sections and log information of wells, a map of the plain bedrock is prepared. The DEM map of the plain is also used for specifying the upper bound of the layer in the groundwater model. However, in the GMS model, the WELL package is used to reproduce existing wells within Songor plain (278 wells) and well cells are specified. One of the most influencing factors in the groundwater model is recharge. Groundwater recharge is usually different in various parts because of various characteristics of geology, pedology, vegetation, precipitation intensity and land slope. In the GMS model, the RCH package is implemented for considering recharge. The zoning method is used to approximate aquifer hydrodynamic parameters. Zoning of the region is conducted for hydraulic conductivity and specific yield according to the drilling log of observational, extraction and piezometric wells and also geophysical sections prepared from the region. Based on the soil type and sediments of each area, the initial amounts of hydraulic conductivity and specific yield are approximated. Eventually, after the calibration process, the optimal value of hydraulic conductivity and specific yield are taken into account for each zone. In the groundwater simulation step, after calibration and validation tests of the model and ensuring its exactness, the final zoning of the model main variables (i.e., hydraulic conductivity and specific yield) is prepared to make the model allow to reproduce the GWL changes for six successive years, because all data necessary for six years (October 2009 to September 2015) are available.

Artificial intelligence models

As discussed, in order to save time and avoid processing a large amount of information and considering the complexities of mathematical models, in this study, in addition to the GMS numerical model, artificial intelligence-based models are also used to predict the GWL fluctuations in the Sonqor plain. First, to draw the GWL variations in the whole plain, the water level data set of 10 piezometers located in the Sonqor plain is used to obtain the groundwater unit hydrograph of the plain in a statistical period of 306 months (October 1993 to March 2019). Water level fluctuations in these piezometers, groundwater unit hydrograph and rainfall during the study period are shown in Fig. 2.

Fig. 2
figure 2

a Fluctuations of GWL in each of the piezometers in the plain b Thiessen polygons and weight of each piezometer c unit hydrograph of groundwater (m) and rainfall (mm) in the whole study period in the plain

Full size image

The groundwater unit hydrograph of is drawn after depicting the Thiessen Polygons in GIS environment and obtaining the weight of each piezometer. After adjusting the required information, the GA-ANN and ICA-ANN hybrid models and ELM and ORELM models are used to predict the GWL in the whole plain. To this end, the parameters of the groundwater unit hydrograph (UH) and precipitation (P) in the previous months and with different delays are considered as model inputs and the GWL values in the current month are considered as the model outputs. By considering 70% of the data as the train data and 30% of the data as the test data, the best structure of the model with different number of inputs with the minimum error rate and the maximum correlation coefficient with the observed data is obtained. To select the best model, the RMSE, NRMSE, NASH and R statistical indices are used, which are shown in Eqs. (1)–(4). Finally, the Taylor diagram is used to ensure the correct selection of the superior model. This diagram introduces the best model with the lowest simulation error based on three indicators including the standard deviation, correlation coefficient and RMSE.

$${\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} (X_{i}^{{{\text{obs}}}} - X_{i}^{{{\text{sim}}}} )^{2} }$$
(1)
$${\text{NRMSE}} = \frac{{{\text{RMSE}}}}{{\left( {X_{{{\text{Max}}}}^{{{\text{obs}}}} - X_{{{\text{Min}}}}^{{{\text{obs}}}} } \right)}}$$
(2)
$${\text{NSE}} = 1 - \mathop \sum \limits_{i = 1}^{n} (X_{i}^{{{\text{obs}}}} - X_{i}^{{{\text{sim}}}} )^{2} /\mathop \sum \limits_{i = 1}^{n} (X_{i}^{{{\text{obs}}}} - X_{{{\text{Mean}}}}^{{{\text{obs}}}} )^{2}$$
(3)
$$R = \left( {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {X_{i}^{{{\text{obs}}}} - X_{{{\text{Mean}}}}^{{{\text{obs}}}} } \right)\left( {X_{i}^{{{\text{sim}}}} - X_{{{\text{Mean}}}}^{{{\text{sim}}}} } \right)}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{n} \left( {X_{i}^{{{\text{obs}}}} - X_{{{\text{Mean}}}}^{{{\text{obs}}}} } \right)^{2} } \mathop \sum \nolimits_{i = 1}^{n} \left( {X_{i}^{sim} - X_{{{\text{Mean}}}}^{{{\text{sim}}}} } \right)^{2} }}} \right)$$
(4)

where \(X_{i}^{{{\text{obs}}}}\) is the ith observed data, \(X_{i}^{{{\text{sim}}}}\) is the ith simulated data, \(X_{{{\text{Mean}}}}^{{{\text{obs}}}}\) and \(X_{{{\text{Mean}}}}^{{{\text{sim}}}}\) are the mean of observed and simulated data, and n is the total number of observations.

Extreme Learning Machine

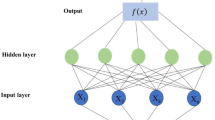
The extreme learning machine (ELM) is a single-layer feed-forward neural network extended by Huang and siew (2004); Huang et al. (2006). The ELM specifies the input weights randomly and the output weights analytically. The general structure of this algorithm is presented in Fig. 2a. The only difference between the ELM and single-layer feed-forward neural network (SLFFNN) is not using bias for the output neuron. Neurons of the input layer are connected with all hidden layer neurons. The activation function (AF) of hidden neurons can be a piecewise continuous function, while it is linear for the output layer neuron. The ELM model uses different algorithms to calculate weights and biases, which results in a significant reduction in network training time. The mathematical description of the single-layer feed-forward neural network with n number of hidden nodes is expressed as follows:

$$f_{n} \left( x \right) = \mathop \sum \limits_{i = 1}^{n} \beta_{i} G(a_{i} ,b_{i} , x)$$
(5)

where βi represents the weight between the ith hidden node and the output node \(a_{i} \in R^{n}\) and bi are the training factors of hidden nodes and G(ai, bi, x) denotes the ith node output for the input x. The AF g(x) (which has different types) for the additive hidden node G(ai, bi, x) can be rewritten as follows:

$$G\left( {a_{i} , b_{i} , x} \right) = g\left( {a_{i} .x + b_{i} } \right)$$
(6)

AFs are employed to calculate the response output of neurons. Once a set of weighted input signal is applied, AFs are used to obtain the response. The nonlinear AF of ELM that have been investigated in this study include the step function (hardlim), sigmoid (sig), sinusoidal (sin), triangular bias (tribas) and radial bias (radbas), which are shown in Fig. 3.

Fig. 3
figure 3

a Structure of ELM network b Various activation functions (AFs) in ELM model

Full size image

The activation of hidden layer neurons for each training sample in an ELM network with the j neurons in the hidden layer, i input neurons and k training samples is calculated from the following equation:

$$H_{jk} = g\left( {\sum \left( {W_{ji} X_{ik} } \right) + B_{j} } \right)$$
(7)

where g(.) can be any continuous nonlinear AF, Wji is the weight of ith input neuron and jth is the hidden layer neuron, Bj is the bias of the jth hidden layer neuron, Xik is the input of the input neuron for the kth training sample and Hik is the activation matrix of the jth neuron of the hidden layer for the kth training sample, so that the activation of all hidden layer neurons for the samples employed in training is provided by this matrix. In this matrix, j and k represent column and row, respectively. The matrix H is expressed as the matrix of the output hidden layer of the neural network. Weights between neurons of the hidden layer and the output layer are applied using the least square fit for target values in the training mode versus outputs of hidden layer neurons for each training example, in which its mathematical equivalent is expressed as

$$H\beta = T$$
(8)
$$\beta = \left( {\beta_{1} , \ldots , \beta_{j} } \right)_{j \times l}$$
(9)

where β represents the weight between the output layer and hidden layer neurons and T is the vector displaying objective values for training samples which is described by Eq. (10):

$$T = (T_{1} , \ldots ,T_{k} )_{k \times 1}$$
(10)

Finally, weights can be calculated by Eq. (11):

$$\beta = H\prime T$$
(11)

where

$$H(\tilde{a},\tilde{b},\tilde{x})\;\left[ {\begin{array}{*{20}l} {G(a_{1} ,b_{1} ,x_{1} )} \hfill & \cdots \hfill & {G(a_{L} ,b_{L} ,x_{L} )} \hfill \\ {G(a_{1} ,b_{1} ,x_{N} )} \hfill & \cdots \hfill & {G(a_{L} ,b_{L} ,x_{N} )} \hfill \\ \end{array} } \right]_{N \times L}$$
(12)
$$\beta = \left[ {\begin{array}{*{20}c} {\beta_{1}^{T} } \\ \vdots \\ {\beta_{L}^{T} } \\ \end{array} } \right]_{L \times M} \quad {\text{and}}\quad T = \left[ {\begin{array}{*{20}c} {T_{1}^{T} } \\ \vdots \\ {T_{L}^{T} } \\ \end{array} } \right]_{L \times M}$$
(13)

where \(\tilde{a} = a_{1} , \ldots .,a_{L} ;\;\tilde{b} = b_{1} , \ldots .,b_{L} ;\;\tilde{x} = x_{1} , \ldots .,x_{L}\), β is the vector of weight between hidden layer neurons and \(H\prime\) denotes the Moore–Penrose pseudo-inverse of the matrix H. T represents the vector of weight between training samples. According to the explanations given, it is concluded that the ELM training consists of two steps: the first step, randomly assigning weights and biases to hidden layer neurons and calculating the hidden layer output of the matrix H, and the second step, calculating output weights by employing the Moore–Penrose pseudo-inverse of the matrix H and target values for different training samples. The training process to find the hidden layer matrix (H) is fast, so that it has a higher speed than the common iteration-based algorithms such as Lunberg-Marquardt, which does not include any type of nonlinear optimization procedure. Thus, the network training time is significantly reduced (Huang et al. 2006).

Outlier robust extreme learning machine (ORELM)

In order to work with models based on artificial intelligence, there are always outlier data, and because the existence of such samples in many cases is related to the nature of the problem, it is not possible to eliminate them. Therefore, it contains a percentage of the total training error (e). In order to deal with such data, the presence of outliers is specified by sparsity. Zhang and Luo (2015) knowing that the utilization of l0-norm reflects sparsity better than l2-norm, to calculate the output weight matrix (β), instead of using l2-norm, considered the training error (e) in such a way to be sparse.

$$\mathop {\min }\limits_{\beta } \,C\left\| e \right\|\,_{0} + \left\| \beta \right\|_{2}^{2} \quad {\text{subject}}\,{\text{to}}\,\,y - H\beta = e$$
(14)
$$\beta = [\beta_{1} ,...,\beta_{N} ]^{T}$$

(β) is the matrix of output weights (\({\text{w}}_{{\text{o}}}\) or is the same \({\text{ w}}_{{{\text{output}}}}\)).

(or in some sources, it is written in this way (\({\text{w}}_{{\text{o}}}\))):

)\(min_{{{\text{w0}}}} Ce_{0} + w_{02}^{2} subject to T - Hw_{0}\)).

The above relation is a non-convex programming problem. One of the easiest ways to solve this problem is to write it as a tractable convex relaxation form without loss of the sparsity characteristic. The sparse term is obtained using l1-norm. Replacing \(l_{{\text{0 - norm}}}\) with \(l_{{\text{1 - norm}}}\) not only leads to the minimization of convexity (decreasing the error function) but also guarantees the existence of sparsity characteristics or the existence of limit events (rare data).

$$\mathop {\min }\limits_{\beta } \,\left\| e \right\|\,_{1} + \frac{1}{C}\left\| \beta \right\|_{2}^{2} \quad {\text{subject}}\,{\text{to}}\,\,y - H\beta = e$$
(15)

The above equation is a constrained convex optimization problem so that it completely adapts the appropriate domain of the augmented Lagrangian (AL) multiplier approach.

$$L_{\mu } (e,\beta ,\lambda ) = \left\| e \right\|_{1} + \frac{1}{C}\left\| \beta \right\|_{2}^{2} + \lambda^{2} (y - H\beta - e) + \frac{\mu }{2}\left\| {y - H\beta - e} \right\|_{2}^{2}$$
(16)

where \(\mu = 2N/\left\| {\mathbf{y}} \right\|_{1}\) represents the penalty parameter and \(\lambda \in R^{n}\) is the Lagrangian multiplier vector. The optimal response (e,β) and the Lagrangian multiplier vector (λ) are obtained via the minimization of the following function through the iteration process:

$$\left\{ \begin{gathered} (e_{k + 1} ,\beta_{k + 1} ) = \arg \,\,\mathop {\min }\limits_{e,\beta } L_{\mu } (e,\beta ,\lambda )\,\,\,\,\,\,\,\,\,\,\,\,(a) \hfill \\ \lambda_{k + 1} = \lambda_{k} + \mu (y - H\beta_{k + 1} - e_{k + 1} )\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(b) \hfill \\ \end{gathered} \right\}$$
(17)

GA-ANN and ICA-ANN hybrid models

One of the simplest and most efficient proposed methods for the design of neural networks is the multilayer perceptron (MLP) model, which contains an input layer, one or more hidden layers, and an output layer. In this structure, all the neurons of one layer are linked to all the neurons of the next layer. This arrangement forms a network with complete connections. Unlike single-layer perceptron neural networks, multilayer networks can be used to train nonlinear problems and also problems with multiple decisions. If the data set has m features, then in the neural networks, the input layer also has m neurons, and hence, the need for n W weights to be multiplied by the inputs. Data set characteristics are independent variables that affect the output or dependent variable. Also, having n neurons in the hidden layer, you need n sets of weights (W1, W2,…, Wn) to be able to multiply the weights in X inputs. To accurately predict the output of the model, the weights of the network in all layers should be modified and their optimal values should be obtained. In order to train the network and modify the weights until a meaningful error is reached, there are many methods. One of the effective methods in this field is to combine the MILP model with the optimization algorithm in the form of a hybrid model. The GA-ANN and ICA-ANN hybrid models are used in this research. In the structure of these models, optimal weights are obtained via the genetic optimization and colonial competition algorithms. The target function in these models is to minimize the RMSE value. The generation and correction of weights in the model structure continue until the minimum error is reached, and the number of iterations of the algorithm is adjusted accordingly.

Results and discussion

Numerical simulation results

Prior to linking both models (i.e., surface and groundwater), the groundwater model is calibrated and verified for the model main variables, namely hydraulic conductivity and specific yield. At this stage, the RMSE index is used for the statistical comparison of the calculated and observed values of the GWL at the location of the observational wells in the Sonqor plain. The results of this investigation in Fig. 4 show that the value of this index in the steady-state model is around 0.65. The results of the calibration and verification of the groundwater model in the transient state during 6 years from October 2009 to September 2015 (Fig. 5) indicate that the model can accurately predict the changes in the GWL due to the stresses applied to it so that considering all simulation months, the value of RMSE is around 0.42. Figure 5 shows the box plot related to the values of average, minimum and maximum groundwater level simulation error in different months in the whole plain area.

Fig. 4
figure 4

Components of prepared numerical model and GWL in the plain for steady state

Full size image
Fig.5
figure 5

Values of mean absolute error for GWL in MODFLOW model in transient state during period a calibration b verification

Full size image

Prediction of GWL based on artificial intelligence

In this study, the methods based on artificial neural networks are used to predict the GWL time series in comparison with complex numerical models with massive data volumes such as GMS, so that the possibility of replacing these methods with complex models can be assessed. This is very important for the place where the favorable conditions for the use of complex numerical models are not established or where there is not enough information so that GWL variations can be predicted with great accuracy based on a very small number of inputs. According to the objectives of this research, in all artificial intelligence methods and hybrid models, monthly data of precipitation and GWL in the past months (t-1, t-2, t-3, t-6, t-12, t-24) are used as input data to the model. Using rainfall data as an input to artificial intelligence model reduces the prediction accuracy of these models. Because in the study area, groundwater level fluctuations relative to rainfall are delayed, and in different months and in different years, the amount of this delay is different and an acceptable equation cannot be fitted. Because a large area of the north of the region is affected by the boundary currents of other aquifers that affect the groundwater level of the plain. The output of the model is the data of the GWL of the plain (groundwater unit hydrograph) in the current month (t), which is extracted based on the observed data in the piezometers. To predict the GWL variations in the Sonqor plain, the performance of these models is evaluated based on the RMSE, NRMSE, NASH and R indices.

To better compare the results, the number of repetitions in all methods was considered to be about 20,000 repetitions. ORELM and ELM methods were faster than other methods in this field.

The best results obtained from the implementation of each of these models are given in Table 1. Based on this table, the ORELM is more accurate than other models in the train and test stages, considering all the indices. After that, the ELM model is in the second place in terms of prediction accuracy. Figure 6 shows the scatter points around the Y = X line and the squared value of the correlation coefficient for choosing the best artificial intelligence model in the modeling test stage for each of the GA-ANN, ICA-ANN, ELM and ORELM models. The more regular and closer scattering of points around the Y = X line in the ORELM model also indicates the greater exactness of this model in comparison with other models. Based on this, the time series of the predicted values of the GWL based on the superior model (ORELM) compared to the observed data in the training and testing stages is shown in Fig. 7. In most studies, the ORELM model is more accurate than other models. But this method cannot be generalized to all data and to all plains and water resources issues. For each problem and for each data type, these models must be re-tested and evaluated. The technique of deleting out of range data can also be used in other models.

Table 1 performance evaluation of GA-ANN, ICA-ANN, ELM and ORELM models in predicting GWL based on statistical indices in the train and test stages
Full size table
Fig. 6
figure 6

Graphic representation of scatter points around the Y = X line and the squared value of the correlation coefficient for choosing the best artificial intelligence model in the modeling test stage

Full size image
Fig. 7
figure 7

Time series of predicted values of GWL based on the superior model (ORELM) compared to the observed data in training and testing phases

Full size image

.Choosing the best model based on Taylor diagram

To ensure the proper selection of the superior model, the Taylor diagram is used. Figure 8 shows the Taylor diagram for choosing the best method among the GA-ANN, ICA-ANN, ELM and ORELM methods for predicting the GWL in the plain.

Fig. 8
figure 8

Taylor diagram for choosing the best artificial intelligence model in modeling test phase

Full size image

The distance of the points created for each method from the observed point equals centered RMSE. Thus, a model that is compatible with observed values is a set of simulated amounts that have a coefficient of determination of 1 and have a similar standard deviation with observed values (Zeynoddin et al. 2018).

In this diagram, point A represents the observed data of the GWL and the evaluation results of the above-mentioned models are shown by points B, C, D and E, respectively. This diagram examines the exactness of various methods by utilizing correlation coefficient and standard deviation indices. This figure compares the efficiency of the GA-ANN, ICA-ANN, ELM and ORELN methods with the proposed method to evaluate the exactness of the forecasts made. The distance of each point considered for various models (B, C, D and E) from the observed point (A) is considered as a comparison reference. Therefore, a model consistent with observed values is a set of points that have a correlation coefficient close to 1 and have a standard deviation similar to observed values (Zeynoddin et al. 2018).

The outcomes of the evaluation of the methods using the Taylor diagram show that the GA-ANN, ICA-ANN and ELN methods (points B, C and D) are less accurate in predicting the GWL based on the unit hydrograph of the plain, while the ORELM method (point E) differs relatively little from the observed values. Therefore, the closest point to the reference point is related to the ORELM method (point E). Therefore, based on this, the ORELM method has higher accuracy than other methods for predicting the GWL.

The results of using the ORELM artificial intelligence model show that this method is able to predict the GWL in the statistical period of 306 months with the lowest amount of error in the train and test stages. So that the value of RMSE in this method is 0.37 and 0.42 in the two stages of train and test, respectively. The value of RMSE in the numerical model of GMS considering the transient period of 6 years is about 0.42, which shows that the ORELM model does not require too much data and without using the complex process of modeling based on the governing equations and with spending much less time can predict GWL variations correctly and with great accuracy. It should be noted that the length of the simulation period in the GMS model is about 72 months due to the need for a large amount of information and related maps and the lack of sufficient information. However, in the artificial intelligence models, due to the fact that they only use the information of precipitation and the GWL recorded by piezometers, based on the availability of data, the length of the forecast period is considered to be 306 months.

Conclusion

The possibility of predicting the GWL for a long-term period based on a very small amount of information compared to numerical models and only using piezometric data and precipitation information is one of the most important achievements of this study. In this case, there is no need for meteorological parameters, soil, geology, layering and geophysical information, logs of exploitation wells, information on water extraction from wells, springs and aqueducts, surface and underground water interaction data, and without the need for complex maps and software and without spending much time and money for the calibration and verification of mathematical models, the groundwater level is predicted based on the artificial intelligence methods. This is of great help to experts in the water resources sector in basins that lack statistics or aquifers that lack basic information and accurate maps, or plains that are faced with widespread statistical deficiencies. Because by using artificial intelligence models, very valuable management information regarding the prediction of GWL fluctuations in dry and wet years can be obtained with very little time and cost. The evaluation of the performance of the artificial intelligence models (GA-ANN, ICA-ANN, ELM and ORELN) in the Sonqor plain showed that these models are very accurate in predicting the GWL fluctuations compared to the GMS numerical model. Among these models, the ORELM model had the highest accuracy with the RMSE values of 0.37 and 0.42 in the two phases of train and test. The Taylor diagram also confirmed this result by using more error criteria, so that the ORELM model can be introduced with high confidence as the best artificial intelligence model for predicting the GWL in the Sonqor plain. Considering the importance of knowing the GWL variations as one of the most important parameters of the water budget, the artificial intelligence models used in this research can be recommended, especially for areas without basic statistics or in situations where it is not possible to use mathematical models. Based on the obtained results, the models developed in this research can be proposed for other study areas with the integrated operation approach of the river and aquifer like the Sonqor plain. In this case, without the need for complex relationships and equations to examine the effect of surface and groundwater interaction and only based on piezometric information and precipitation data, it is possible to predict the GWL in the study area in dry and wet periods with great accuracy.