Introduction

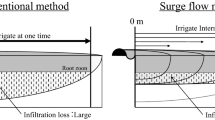
Concerning the arid circumstances in Iran and un-usability of forced irrigation in all circumstances, a rise in the competence of superficial irrigation is vital. Optimum development of superficial irrigation approaches is one of the operative stages to accomplish this determination. Commonly, the superficial irrigation development approaches or systems for computation of the advance period (a significant component in development) can be considered into the subsequent groups: Group one is the modest approaches such as the SCS technique. Reddy and Clyma (1981) and Reddy and Apolayo (1991) used the SCS equation for optimum development of channels and measured the entire irrigation expenditure as the goal meaning. But, findings displayed that this technique led to significant errors in calculating the progressive period (Shayannejad et al. 2022; Ostad-Ali-Askari et al. 2017a; Ostad-Ali-Askari and Shayannejad 2020, 2021a, b; Vanani et al. 2017; Valiantzas 2001a; Banti et al. 2011). Group 2 is the arithmetical approaches such as the kinematic wave, zero inertia and dynamic wave mockups. These approaches are compound and similarly cannot calculate the advance period obviously (Ostad-Ali-Askari et al. 2017b; Fatahi Nafchi et al. 2021a, b, 2022a, b; Ostad-Ali-Askari 2022; Abdollahi et al. 2021; Talebmorad et al. 2020, 2021; Salehi-Hafshejani et al. 2019; Strelkoff and Katopodes 1977). Strelkoff and Katopodes (1977) and Elliott et al. (1982) applied the zero inertia mockups for calculating the advance period. The optimal circumstances and alternate-furrow fertigation powerfully decrease water and nitrate losses compared with conservative channel irrigation. The simulation–optimization prototypical is a valuable instrument for mitigation of the ecological impression of channel irrigation (Ebrahimian et al. 2013a, b; Pais et al. 2010). Ostad-Ali-Askari and Shayannejad (2015a, b) stated that input flexibles of a precise prototypical model were active parameters on profound filtration, for example, bed gradient, inflow degree and coefficients of soil infiltration. These flexibles were measured in 16 ranches of Zayandehrood basin. Comparison of assessed and measured deep filtration displayed that the error of prototypical was 1.73%. Gonc et al. (2011) stated that assuming water and shortage irrigation were normally problematic in financial terms; thus, it is essential to support the agriculturalists. The water current of superficial irrigation exhibits a main characteristic which is the presence of wet-dry border (Eslamian et al. 2018a, b; Derakhshannia et al. 2020; Pirnazar et al. 2018; Ostad-Ali-Askari  et al. 2018a, b, 2019, 2020; Ostad-Ali-Askari and Shayannejad 2021c; Golian et al. 2020; Albert et al. 2011; Hosseini et al. 2014). In mathematical simulation, owing to the anti-diffusion distinctive of the coarseness term of the Saint–Venant equations, wet-dry border of the superficial current can impact the constancy of momentum preservation equation and decrease the simulation correctness of reiterative coupled samples (Javadinejad et al. 2018, 2019a, b, 2021; Dong et al. 2013; Fenoglio et al. 2007). Group 3 is the volume balance model. In this prototypical model, the superficial and subsurface form features during the advance step are presumed to be constant. Similarly, this prototypical model depends on the normal depth. Walker and Skogerboe (1987) stated that the volume balance model is more suitable for advance calculation. Operators of volume balance model need to be conscious that indeterminate superficial volume designs can lead to possibly large volume balance errors. Therefore, these consequences require to be interpreted sensibly (Bautista et al. 2012). None of the above-declared approaches appears suitable for the development of the optimum channel irrigation, since these approaches cannot calculate the advance time obviously and exactly (Raeisi-Vanani et al. 2015). Optimum development requires an accurate equation for obvious calculation of the advance time and applying in the goal function (Soltani-Todeshki et al. 2015). In this article, the overall essential cost for once irrigation including the workforce cost, water, channels and ditch excavation has been measured as the goal meaning which should be minimized. Noticeably, the workforce cost is a function of the irrigation time which is contingent on the advance period. In this investigation, the equation was recommended by Valiantzas (2001b) applied for the calculation of the advance time. This is an obvious equation for the calculation of the advance time. Valiantzas equation gained depends on the consequences of the zero inertia prototypical with high accuracy.

Methodology

In prototypical expansion for irrigation of a part of quantified farm land through the channel, it must be separated into a number of irrigation sets (Ns). Each irrigation segment comprises a number of channels which are concomitantly irrigated. The plan of irrigation sets for better comprehends of symbols and the technique of this article are shown in Fig. 1.

Fig. 1
figure 1

Furrow irrigation arrangement

Full size image

where Nsl is the total number of irrigation sets in the way of channels; Nsw is the total number of irrigation sets in the way of vertical to channels; Lf is the length of the ranch in meters (in the way of channels); Wf is the width of the ranch in meters (in the way of vertical channels); Q0 is the influx current degree to each channel (m3/min); Qt is the total obtainable current degree (m3/min); L is the length of each channel (m); Nfs is the number of channels/each irrigation set; and W is the width of each channel (m). Concerning Fig. 1, Eqs. 1–4 can be obtained as follows:

$$N_{{{\text{sl}}}} = \frac{{L_{{\text{f}}} }}{L}$$
(1)
$$N_{{{\text{fs}}}} = \frac{{Q_{{\text{t}}} }}{{Q_{0} }}$$
(2)
$$N_{{{\text{sw}}}} = \frac{{W_{{\text{f}}} }}{{W \cdot N_{{{\text{fs}}}} }}$$
(3)
$$N_{{\text{s}}} = N_{{{\text{s1}}}} \cdot N_{{{\text{sw}}}}$$
(4)

Substituting Eqs. 1, 2 and 3 in Eq. 4, Eq. 5 can be obtained:

$$N_{{\text{s}}} = \frac{{W_{{\text{f}}} \cdot L_{{\text{f}}} \cdot Q_{0} }}{{L \cdot W \cdot Q_{{\text{t}}} }}$$
(5)

Costs of the channel irrigation can be separated into four portions that are explicated in the following.

Water cost

Water cost is calculated by increasing the compulsory water volume and the value of unit volume of water (m3) as Eq. 6:

$$C_{{{\text{tw}}}} = Q_{{\text{t}}} \cdot T_{{{\text{co}}}} \cdot N_{{\text{s}}} \cdot C_{{\text{w}}}$$
(6)

where Ctw is the cost of the compulsory water for one time irrigation of the whole farmhouse (Rials); Cw is the price of water volume unit (Rials/m3); and Tco is the cutoff time (min). By substituting Eq. 5 and Eq. 6, Eq. 7 can be obtained:

$$C_{{{\text{tw}}}} = \frac{{T_{{{\text{co}}}} \cdot Q_{0} \cdot L_{{\text{f}}} \cdot W_{{\text{f}}} \cdot C_{{\text{w}}} }}{w \cdot l}$$
(7)

Workforce cost

This cost is attained by increasing the compulsory period for irrigating the whole farm and the employees cost in the unit of time given in Eq. 8:

$$C_{{{\text{tl}}}} = T_{{{\text{co}}}} \cdot N_{{\text{s}}} \cdot C_{1}$$
(8)

where Ctl is the workforce compulsory expenditure for one time irrigation of the whole homestead (Rials) and C1 is the workforce cost for unit of time (Rials/min). By substituting Eq. 5 and Eq. 8, Eq. 9 can be obtained:

$$C_{tl} = \frac{{T_{co} .Q_{0} .L_{f} .W_{f} .C_{1} }}{w.l.o}$$
(9)

Furrow digging cost

The channel excavating cost is obtained by increasing the total length of channels and the excavation cost of their length unit which concerns the whole of increasing season. For one time irrigation, it must separate to the number of irrigation proceedings as Eq. 10:

$$C_{{{\text{tw}}}} = \frac{{L_{{\text{f}}} \cdot W_{{\text{f}}} \cdot C_{{\text{w}}} }}{{w \cdot N_{{\text{i}}} }}$$
(10)

where Ctf is the cost of channel digging for one time irrigation of the entire ranch (Rials), Cf is the cost of excavating channel length unit (Rials/m) and Ni is the number of irrigation proceedings throughout the rising season. The above-mentioned cost is not a purpose of advance flexibles such as the influx degree and the channel length. So, its value is persistent and is not significant in the scheming of the optimization and only involves in calculating the total of the costs.

Cost of digging the head ditch

According to Fig. 1, for numerous irrigation sets, a head ditch is excavated at end of upriver of channels. Cost of these channels is calculated by increasing their total length to the excavation cost of length unit. Comparable to the preceding piece, this cost should be separated by the number of irrigation procedures given in Eq. 11:

$$C_{{{\text{td}}}} = \frac{{N_{{{\text{s1}}}} \cdot W_{{\text{f}}} \cdot C_{{\text{d}}} }}{{N_{{\text{i}}} }}$$
(11)

where Ctd is the cost of excavating the irrigation rivers for one time irrigation of the whole farm (Rials) and Cd is the disbursement of excavating the length unit of stream (Rials/m). By substituting Eq. 1 and Eq. 11, Eq. 12 can be attained:

$$C_{{{\text{td}}}} = \frac{{N_{{{\text{s1}}}} \cdot W_{{\text{f}}} \cdot C_{{\text{d}}} }}{{L \cdot N_{{\text{i}}} }}$$
(12)

Total cost for one time irrigating is calculated with Eq. 13:

$$C_{{\text{t}}} = \frac{{T_{{{\text{co}}}} \cdot Q_{0} \cdot L_{{\text{f}}} \cdot W_{{\text{f}}} }}{w \cdot l}\left( {C_{{\text{w}}} + \frac{{C_{1} }}{{Q_{{\text{t}}} }}} \right) + \frac{{w_{{\text{f}}} \cdot L_{{\text{f}}} }}{{N_{{\text{i}}} }}\left( {\frac{{C_{{\text{f}}} }}{w} + \frac{{c_{{\text{d}}} }}{L}} \right)$$
(13)

where Ct is the total irrigation cost for one time irrigation of the farm (Rials). An equation comparable to Eq. 13 was planned by Valiantzas (2001a, b). Equation 13 designates that the total cost is contingent on three flexibles including Q0, Tco and L. Tco can be written as a function of the 2 other flexibles. So, Eq. 14 can be obtained:

$$T_{{{\text{co}}}} = T_{1} + T_{{\text{r}}}$$
(14)

where Tl is the advance time (min) and Tr is the consumption chance time (min). To calculate Tr, any penetration equation can be applied. For the Kostiakov equation, calculation is as follows (Eqs. 15 and 16):

$$Z = K \cdot T^{ \propto }$$
(15)
$$T_{{\text{r}}} = \left( {\frac{{Z_{{\text{r}}} }}{K}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \propto }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$ \propto $}}}}$$
(16)

where Z is the depth of the infiltrated water (m), T is the filtration time (min), Zr is the net irrigation condition (m) and K and α are the permeation coefficients of the Kostiakov equation. To calculate T1, an obvious and detailed equation should be applied. So, optimization of Eq. 13 can be completed. For this determination, Eq. 17 that was planned by Valiantzas (2001a, b) is applied:

$$T_{1} = \frac{{\left( {1 + 0.15 \propto } \right) \cdot L \cdot A_{0} }}{{Q_{0} + \left( {\sigma_{{\text{Z}}} \cdot K \cdot L/Q_{0} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\left( {1 - \propto } \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( {1 - \propto } \right)}$}}}} }}$$
(17)

where A0 is the part of cross segment at the end of upriver of the channel (m2) and σz is the subsurface current form feature. This quantity is calculated from Eq. 18:

$$\sigma_{{\text{Z}}} = \frac{{ \propto \cdot \pi \cdot \left( {1 - \propto } \right)}}{{{\text{Sin}}\left( { \propto \cdot \pi } \right)}}$$
(18)

A0 value is calculated using the Manning equation, and the channel form coefficients are calculated using Eq. 19:

$$A_{0} = \left( {\frac{{N^{2} Q_{0}^{2} }}{{3600S_{0} \cdot \rho_{1} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\rho^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\rho^{2} }$}}}}$$
(19)

where N is the Manning’s coarseness coefficient, S0 is the channel bed gradient (m/m) and ρ1 and ρ2 are the channel form factors. These factors, regarding the Manning equation, are calculated as Eq. 20:

$$A \cdot R^{4/3} = \rho_{1} A^{{\rho_{2} }}$$
(20)

where A is the current cross segment (m2) and R is the hydraulic radius (m). Finally, by substituting Eqs. 4, 16 and 17 in Eq. 13, Eq. 21 can be obtained, where Ct is a function of the two flexibles of Q0 and L0. Equation 21 can be written as follows:

$$C_{{\text{t}}} = f\left( {Q_{0} ,L} \right)$$
(21)

To calculate these two flexibles, Eq. 21 should be improved.

Findings and discussion

The purpose of applying the optimization technique in channel project is initially variation of Eq. 21 that does not find the flexibles overtly. Furthermore, the optimization technique delivers the opportunity for retaining the numerical solution methods using the processer. The technique for applying this technique is clarified in the following. An optimization technique includes the subsequent four portions:

  1. I.

    Choice flexibles: These flexibles are unidentified and should be quantified by the optimization.

  2. II.

    Choice flexibles of the optimization prototypical in the investigation are Q0 and L.

  3. III.

    Parameters: These flexibles are recognized. These parameters are all the flexibles remaining in Eq. 21, excluding the choice ones. Equation 21 is united with Eqs. 13, 14, 15, 16, 17, 18 and 19 that have many recognized flexibles.

  4. IV.

    Goal function: Eq. 21 displays the association among the enhanced quantities with the choice-pleasing flexibles in the procedure of a precise purpose.

  5. V.

    Boundaries: Some of the optimization approaches are controlled. Thus, the choice-captivating flexibles call limitations. In this investigation, the subsequent limitations are applied for the choice-taking flexibles:

    $$L > 0, Q_{0} \le Q_{{{\text{max}}}}$$

In these circumstances, Qmax is the maximum influx rate to the channel which does not cause corrosion. SCS has been proposed in Eq. 22 for calculating it (m3/min):

$$Q_{{{\text{max}}}} = \frac{0.00036}{{S_{0} }}$$
(22)

Applying the above four portions, optimization is achieved in the subsequent stages:

  1. 1.

    Main standards are expected for the result flexibles:

    \(X_{1} = \left[ {\begin{array}{*{20}c} {Q_{0}^{1} } \\ {L^{1} } \\ \end{array} } \right]\).

  2. 2.

    An assuming way of \(S_{1} = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right]\) is measured whose original standards for the result flexibles are assessed as follows:

    \(X_{2} = \left[ {\begin{array}{*{20}c} {Q_{0}^{2} } \\ {L^{2} } \\ \end{array} } \right]\) = \(X_{1} + \lambda_{1} \cdot S_{1}\) (23).

  3. 3.

    Over employing X2 in the goal meaning and equal its imitative to zero, λ1 is projected and by substituting it in Eq. 23, X2 value is calculated.

  4. 4.

    X3 value is calculated by Eq. 24:

    $$X_{3} = 2X_{2} - X_{1}$$
    (24)
  5. 5.

    Providing f (X3) < f (X2), the aforementioned steps are recurrent. Then, the S1 way should be altered as follows:

    $$S_{1} = X_{2} - X_{1}$$
    (25)
  6. 6.

    Calculations are repeated with the novel S1 until the smallest point of the goal meaning is accomplished. All the declared calculations are achieved using LINGO, and lastly, L and Q values and the least costs are calculated. Then, applying Eq. 14 and with the subsequent calculation, the irrigation competence can be calculated:

    $$E_{{\text{a}}} = \frac{{Z_{{\text{r}}} \cdot W \cdot L}}{{Q_{{\text{o}}} \cdot T_{{{\text{co}}}} }} \times 100$$
    (26)

In the above calculation, E is the irrigation competence fraction. According to Eq. 13 along with minimization of C1, Qo. Tco, irrigation competence in Eq. 26, will be maximized. Momentarily, the technique that was clarified in this paper led to scheming of influx degree to the channel, channel distance, irrigation period (period) and irrigation competence depending on expenditure minimization and irrigation competence enlargement. In the other words, optimum channel strategy has been gained. For instance, the subsequent statistics for channel enhanced preparation have been introduced into the optimization:

Zr = 0.1 m, Qt = 9.48 m3/min, 0.0016, a = 0.762, Ni = 7, n = 0.04, S0 = 0.001, 1 ρ = 0.3269, 2 ρ = 2.734, Wf = 100 m, Lf = 1000 m, C1 = 60 Rials/min, Cf = 100 Rials/m, Cd = 200 Rials/m, Cw = 20 Rials/m3.

Consequences of the optimizations prototypical are given as follows:

L = 100 m, Q0 = 0.0498 m3/min, Tco = 312 min, Ea = 48.7% and Ct = 2,450,000 Rials.

Conclusion

In the existing education, the least irrigation cost and extreme irrigation competence were obtained for the influx degree of 0.0498 (m3/min) and length of 100 (m) for the channel. So, in the goal meaning, a calculation should be measured for calculating the water advance period in a clear and detailed way. Since none of the meticulous approaches applied for advance channel irrigation like zero inertia calculate the advance time plainly, consequently in this investigation the Valiantzas calculation has been applied which has been assumed from the consequences of the zero inertia prototypical. In the goal purpose, in addition to the preparation flexibles, soil features, furrow and net irrigation condition have been included. So, the project flexibles and irrigation competence can be calculated for each kind of soil and precise herbal. An example of this project has been offered in this education. According to the above current degree, by increasing or declining the channel length, the irrigation competence declines and its cost rises. The gradient of cost and irrigation changes relative to the channel length has optimum facts that are exposed in Fig. 2. Correspondingly, the gradient of cost and irrigation productivity qualified to influx degree can be strained for a channel in the length of 100 m. In this circumstance, by increasing or diminishing the influx degree, irrigation cost rises and irrigation competence declines. According to the conclusions, a channel length of 190 m is attained which is meaningfully dissimilar to the present-day study conclusions. In the stated tables, the channel length is a purpose of depth of irrigation water and bed gradient of the channel and soil quality. Other channel properties have not been measured. According to Fig. 2, irrigation competence is 32%, for a channel length of 190 m. The succeeding explanations endorse: The optimum channel project bends can be drawn for diversity of soils and channels for numerous standards of net irrigation necessities. The problem of low irrigation can be simply implanted into this technique. For this determination, it is expected that filtration at the end of the channel is less than the net irrigation condition.

Fig. 2
figure 2

Sample of cost and irrigation efficiency variations related to length of furrow

Full size image