Introduction

Bridge scour is the result of the erosive action of flowing water, excavating and carrying away material from the bed and banks of streams and from around the piers and abutments of bridges (Richardson and Davis 2001). The scour is accountable for about 60% of bridge failures (Lagasse et al. 1997), resulting in loss of lives and huge economic losses. Designing the bridge foundation safely needs an accurate estimation of scour depth; underestimation may lead to bridge failure, while overestimation will lead to excessive construction costs (Azamathulla and Ghani 2010).

Pier scour attracted significant research interest for more than a century now, and numerous studies on this subject were published. Much of this research dealt with laboratory model studies of local scour. In this context, several reviews summarized equations for pier scour depths in Breusers et al. (1977), Dey (1997), and Melville and Sutherland (1988). However, these equations are often suitable only for conditions similar to those under which they were developed. Moreover, this empirical approach suffers from its associated simplified conditions and scale effects. When applying the existing empirical equations for predicting bridge pier scour to field cases, the scour depths are overpredicted (Babaeyan-Koopaei and Valentine 1999). This means increased construction and maintenance costs as the foundation levels are required to be deeper than it should be.

Soft computing tools gained importance in many fields as they differ from conventional hard computing in many ways, such as their robustness, low solution cost, and tolerance to imprecision (Chuan-Yi et al. 2013). Artificial intelligence methods, such as artificial neural networks (ANNs), adaptive neuro-fuzzy inference systems (ANFIS), genetic programming (GP), and linear genetic programming (LGP), are now widely used to predict scour around hydraulic structures and bridge piers. The American Society of Civil Engineers Task Committee (2000) reported the application of ANNs in different fields of hydrology. Deo et al. (2008) used GP to predict scour depth downstream of spillways. Azamathulla et al. (2008a, b) used ANNs and GP to determine scour depth downstream of ski-jump buckets. Guven et al. (2009) applied LGP for predicting scour depth at circular piles. ANFIS and genetic expression programming were used by Azamathulla et al. (2009a, b) to estimate scour below flip buckets. For scour below a submerged pipeline, Azamathulla et al. (2011) employed the LGP model. Najafzadeh and Barani (2011) compared the group method of data handling-based GP and the back-propagation system to predict scour depth around bridge piers.

Different from traditional physically based analytical or empirical approaches, this study investigates the utility of artificial intelligence modeling tools in predicting scour depth around bridge piers. The main objective of this research was to further enhance the available inductive modeling tools for predicting bridge scour by developing ANFIS and GP-based models for pier scour prediction utilizing available laboratory and field data and comparing their performance with several well-known bridge pier regression-based models. The already existing equations used in this study are Modified Laursen by Neill (1964), Shen et al. (1969), The Colorado State University (1975), Jain and Fischer (1979), Kothyari et al. (1992), Modified Froehlich by Fischenich and Landers (1999), and Richardson and Davis (2001). A further objective of this research was to find out which of the existing formulae works for the Nile River and how well the newly developed formula performs. Thus, the applicability of the GP model, provided that it yielded better prediction results, to large-scale models and field data was verified via applying the developed GP model to the case of Imbaba Bridge, Giza, Egypt.

Proposed artificial intelligence networks

Genetic programming (GP) and ANFIS being recently the most widely used branches of soft computing in hydraulic engineering were employed in this research as an alternative tool in the prediction of local scour around bridge piers.

Adaptive neuro-fuzzy inference system

The ANFIS is a hybrid scheme which uses the learning capability of the ANN to derive the fuzzy if–then rules with appropriate membership functions worked out from the training pairs, leading finally to the inference (Tay and Zhang 1999). The difference between the common neural network and the ANFIS is that while the former captures the underlying dependency in the form of the trained connection weights, the latter does so by establishing the fuzzy language rules (Azamathulla et al. 2009a, b). The input in ANFIS is first converted into fuzzy membership functions, which are combined together and, after following an averaging process, used to obtain the output membership functions and finally the desired output (Mousavi et al. 2007).

The configuration of an adaptive network performs a static node function on its incoming signals to generate a single node output, and each node function is a parameterized function with modifiable parameters (Navneet et al. 2015). Thus, a trial-and-error method, where a range of different shapes, numbers, and types of membership functions, as well as various parameters used as input data, should be followed toward identifying the optimal ANFIS architecture.

Genetic programming

Genetic programming (GP) is an extension of John Holland’s genetic algorithms (GAs) proposed by Koza (1992). The major difference between GP and GAs is that the variable parse tree structure of GP replaces the fixed gene structure of GAs (Chuan-Yi et al. 2013). Genetic programming uses four steps to solve problems:

  1. 1.

    Generate an initial population of random compositions of the functions and terminals of the problem (computer programs).

  2. 2.

    Execute each program in the population and assign it a fitness value according to how well it solves the problem.

  3. 3.

    Create a new population of computer programs.

  4. (a)

    Copy the best existing programs.

  5. (b)

    Create new computer programs by mutation.

  6. (c)

    Create new computer programs by crossover.

  7. 4.

    The best computer program that appeared in any generation, the best-so-far solution, is designated as the result of genetic programming (Koza 1992).

Based on the natural selection obtained by way of the evolutionary process, GP produces an optimal function set (formula). The use of this flexible coding system allows the algorithm to perform structural optimization (Chuan-Yi et al. 2013). This can be useful in solving many engineering problems. In the development of the GP model, the terminal set, functional set, fitness function, algorithm control parameters, and termination criterion are defined (Koza 1992). The first three components determine the algorithm search space, whereas the last two components affect the quality and speed of the search.

Pier scour parameters

The equilibrium local scour depth (ds) around a pier (Fig. 1) in a steady flow over a bed of uniform and non-cohesive sediment depends on numerous parameters including flow, fluid, sediment characteristics, and pier geometry. The factors affecting the magnitude of the local scour depth at piers are stated in Bateni et al. (2007) as follows: velocity of the approach flow, depth of flow, width of the pier, length of the pier if skewed to flow, size and gradation of bed material, angle of attack, and bed configuration.

Fig. 1
figure 1

Flow and local scour at bridge pier (Bateni et al. 2007)

Full size image

Local scour depth at piers is a function of the following decision variables:

$$d_{\text{s}} = f\left( {U, Y, \rho , \rho_{\text{s}} , g, D, L, d_{50} , \sigma , \alpha } \right),$$
(1)

where U is the approach velocity, Y is the approach flow depth, ρ is the mass density of water, ρs is the mass density of sediment, g is the acceleration due to gravity, d50 is the particle mean diameter, D is the pier width, L is the length of the pier, σ is the standard deviation of grain size distribution, α is the opening ratio (= (B − D)/B), and B is the channel width. However, the influence of the Reynolds number Re is insignificant for a turbulent flow over rough beds (Melville and Coleman 2000). Considering uniform sediments, dimensional analysis of the variables in Eq. (1) reduces it to five dimensionless parameters as follows:

$$\frac{{d_{\text{s}} }}{D} = f\left( {F_{\text{r}} , \frac{Y}{D}, \frac{D}{{d_{50} }}, \sigma , \alpha } \right),$$
(2)

where Fr is the Froude number. These five parameters were used as decision variables in the development of the GP model.

Conventional regression models

Most of the pier scour prediction formulae available in the literature are based on conventional regression methods and most overpredict pier scour, resulting in an uneconomical bridge foundation design. In this section, a list is made of the bridge pier scour equations used in this study. In all the formulae listed below, it was assumed that the flow angle of the attack is negligible and that the pier shape is rectangular. Chang (1988) reported that the scour depth of circular piers is 90% of that for rectangular piers and 80% of that for sharp-nosed piers. It was also assumed that the effect of the flow angle of attack and the circular shape of the pier will mutually cancel each other. This is done because of the lack of information about these factors in the data.

The Modified Laursen by Neill (1964) equation

Neill (1964) used Laursen and Toch’s (1956) design curve to obtain the following explicit formula for the scour depth:

$$\frac{{d_{\text{s}} }}{D} = 1.35\left( {\frac{Y}{D}} \right)^{0.30} ,$$
(3)

where ds is the equilibrium scour depth, D is the obstruction width (or pier width), and Y is the approach water depth. This equation does not include the Froude number or in other words the velocity of the attacking stream.

Shen et al. (1969) formula

Shen et al. (1969) used the Froude number in their scour depth prediction in addition to the pier width as given as follows:

$$\frac{{d_{\text{s}} }}{D} = 3.4 \left( {F_{\text{r}} } \right)^{2/3} \left( {\frac{Y}{D}} \right)^{1/3},$$
(4)

where Fr is the Froude number and the other variables are as defined before.

The Colorado State University (CSU) formula (1975)

This equation is developed as a best fit to the data (laboratory) available at the time. The formula is given as:

$$\frac{{d_{\text{s}} }}{Y} = 2.2 \left( {F_{\text{r}} } \right)^{0.43} \left( {\frac{D}{Y}} \right)^{0.65} .$$
(5)

The CSU (1975) formula is similar in form to Shen et al. (1969) equation. Later on, correction factors were added for the effects of flow angle, pier shape, and bed conditions.

Jain and Fischer (1979) equations

Jain and Fischer (1979) developed a set of equations based on laboratory data. For (Fr − Fc) > 0.2, the formula reads as:

$$\frac{{d_{\text{s}} }}{D} = 2.0 \left( {F_{\text{r}} - F_{\text{c}} } \right)^{0.25} \left( {\frac{Y}{D}} \right)^{0.50} ,$$
(6)

where Fc is the critical Froude number. For (Fr − Fc) < 0.2, the formula is:

$$\frac{{d_{\text{s}} }}{D} = 1.84 \left( {F_{\text{r}} } \right)^{0.25} \left( {\frac{Y}{D}} \right)^{0.30} .$$
(7)

Kothyari et al. (1992) formula

Kothyari et al. (1992) developed the following equation:

$$\frac{{d_{\text{s}} }}{D} = 0.66 \left( {\frac{D}{d}} \right)^{ - 0.25} \left( {\frac{Y}{D}} \right)^{0.16} \left( {F_{\text{r}} } \right)^{0.40} \alpha^{ - 0.30} .$$
(8)

Modified Froelich by Fischenich and Landers (1999) formula

Fischenich and Landers (1999) modified Froelich’s (1988) equations for live-bed scour at bridge crossings as:

$$\frac{{d_{\text{s}} }}{Y} = 2 \left( {\frac{\theta }{90}} \right)^{0.13} \left( {F_{\text{r}} } \right)^{0.61} \left( {\frac{D}{Y}} \right)^{0.43} + 1,$$
(9)

where \(\theta\) is the angle of flow attack (°). This equation does include a safety factor (+ 1.0) that accounts for contraction scour in most cases. To compare this formula with other formulae, this factor will not be considered, as only local bridge pier scour is considered herein.

Richardson and Davis (2001) formula

Originally, this formula was presented in HEC-18 (Richardson and Davis 2001) and was recently used by Mohamed et al. (2005) for comparison with other regression-based equations.

$$\frac{{d_{\text{s}} }}{D} = 2 K_{\text{s}} K_{\theta } \left( {F_{\text{r}} } \right)^{0.43} \left( {\frac{D}{Y}} \right)^{0.65} .$$
(10)

Different values for Ks and Kθ are reported by Simons and Senturk (1992).

Development of ANFIS and GP models

The experimental results of the laboratory study were used in training and testing sets of the proposed ANFIS and GP models. The data sets that were used were collected from the studies of Chabert and Engeldinger (1956), Verstappen (1978), Walker (1978), Melville and Chiew (1999), Mohamed et al. (2006) and Beg (2013). A total number of 150 datasets were collected. From the total 150 test sets, 110 sets were selected randomly for the training and the remaining 40 sets were used for validating the proposed two models. Table 1 presents the ranges of various parameters used in developing the two models. After training and validating the models, the field data (170 data sets) collected by Mueller and Wagner (2005) was employed to verify the developed models (Table 1).

Table 1 Ranges of data used in the development of ANFIS and GP models
Full size table

ANFIS model

The ANFIS model was established using the MATLAB fuzzy logic toolbox. First, all data and input parameters were utilized in search of the best performing ANFIS structure. This involves running models (22 models) with various types of membership functions and the number of membership functions for each input parameter.

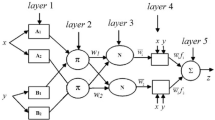
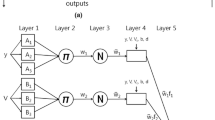
The ANFIS model network includes five layers and works according to Takagi and Sugeno (1985) as follows: In the first layer, let x and y be the typical input values fed at the two input nodes, which will then transform those values to the membership functions (say bell-shaped) and give the output as follows: note in general, w = output from a node; l = membership function, Ai, Bi = fuzzy sets associated with nodes x, y.

$$\mu_{Ai} \left( x \right) = \frac{1}{{1 + \left( {\left( {x - C_{1} } \right)/a_{1} } \right)^{{2b_{1} }} }} ,$$
(11)

where a1, b1, and c1 = changeable premise parameters. Similar computations are carried out for the input of y to obtain \(\mu_{Bi} \left( y \right)\). The membership functions are thereafter multiplied in the second layer, e.g.,

$$W_{i} = \mu_{Ai} \left( x \right) \cdot \mu_{Bi} \left( y \right)\quad \left( {i = 1,2} \right) .$$
(12)

Such products or firing strengths are then averaged in the third layer. Nodes of the fourth layer use the above ratio as a weighting factor, and using fuzzy if–then rules produces the output as below: (An example of the if–then rule is: If x is A1 and y is B1 then f1= p1x + q1y + r1.)

$$W_{i} \left( {{\text{avg}} .} \right)f_{i} = W_{i} \left( {{\text{avg}} .} \right) \times \left( {p_{1} x + q_{1} y + r_{1} } \right),$$
(13)

where p, q, r = changeable consequent parameters. The final network output f is produced by the node of the fifth layer as a summation of all incoming signals, exemplified in Eq. (13).

For imparting faster training and adjusting the network parameters to the above network, a two-step process is used. In the first step, the premise parameters are kept fixed and the information is propagated forward in the network to layer 4, where a least-squares estimator identifies the consequent parameters. In the second step, the backward pass, the consequent parameters are held fixed while the error is propagated, and the premise parameters are modified using the gradient descent.

It was realized that using three or more membership functions not only results in overtraining, but also is exponentially more costly in time required to train the model (e.g., the time required for training the model with four membership functions per input was 50 times greater than for the model employing only three). The optimum value of the cluster radius was determined by the trial-and-error method based on the criterion of the maximum correlation coefficient and minimum root-mean-square error. An optimum value of 0.58 was realized for the cluster radius, for which the optimum number of rules obtained was 6. Thus, using two membership functions per input, subtractive clustering with six rules, and testing for different types of membership functions ranging from triangular to sigmoid, the Gaussian was found to obtain the best accuracy, with good generalization ability. The prediction of the ANFIS model versus the actual experimental values for the training and testing sets is shown in Figs. 2 and 3.

Fig. 2
figure 2

ANFIS- and GP-predicted values of ds/D versus measured values for training sets

Full size image
Fig. 3
figure 3

ANFIS- and GP-predicted values of ds/D versus measured values for testing sets

Full size image

GP model

In this study, the GP model for scour depth prediction was developed using the epochX, a powerful Java software computing package. The function set consisted of eight basic arithmetic operators (+, −, × , ÷, √, log, exp, and power) and constants. The terminal set included five fundamental groups of hydraulic parameters of ds, as expressed in Eq. (14). The terminal set encompasses the dimensionless relationships obtained from the variables influencing ds, as expressed by Eq. (2).

$$\frac{{d_{\text{s}} }}{D} = f\left( {F_{\text{r}} , \frac{Y}{D}, \frac{D}{{d_{50} }}, \sigma , \alpha } \right) = f\left( {X_{1} , X_{2} , X_{3} , X_{4} , X_{5} } \right).$$
(14)

In this study, the operations of crossover and mutation were selected as 0.30–0.70 and 0.01–0.10, respectively. The population size considered was 500–1000 members. The total number of generations was 1000–10,000, and the maximum depth of the parse tree structure was allowed during 20–25 generations. The restriction in the maximum depth of the parse tree structure is aimed at achieving a balanced accuracy of the solutions and the parsimony problem in GP. The parsimony problem indicates the diverging growth of population size without an associated increase in fitness during the process of obtaining best-fit optima. The fitness function was the sum of absolute differences (SAD= Σ Pi − mi) between the measured values and the estimated values present in the database. The program was run for a number of generations and was stopped when there was no improvement in fitness function value or coefficient of determination. The optimum result found through the GP development and program was obtained when the population size was 700 members with a total of 5500 generations having crossover 0.6 and mutation 0.05. The prediction of the proposed GP formula versus the actual experimental values for the training and testing sets is shown in Figs. 2 and 3. It is a common result that the predictions of training sets are slightly better than the results for the testing sets. These figures show that the proposed GP formula can learn very well the nonlinear relationship between parameters and also provide high generalization capacity. The generated prediction formula of GP for ds/D is given in Eq. (15) as follows:

$$\frac{{d_{\text{s}} }}{D} = \frac{D}{{d_{50} }} \left[ {0.61 - F_{\text{r}} - \left( {\frac{D}{{d_{50} }}} \right)\left( {\frac{Y}{\alpha D}} \right)^{2} } \right]^{{\log \left( {\frac{{\frac{D}{{d_{50} }}}}{{F_{\text{r}} }}} \right)^{0.20} }} \left[ {\frac{{F_{r}^{2.2} \left( {\frac{{\frac{D}{{d_{50} }}}}{3.82}} \right)}}{{\left( {\alpha \frac{D}{{d_{50} }}} \right)^{{\log \left( {\frac{{\frac{D}{{d_{50} }}}}{{F_{\text{r}} }}} \right)}} }}} \right] - \left( {\frac{D}{{d_{50} }}} \right)^{2} \left( {\sigma - 1} \right).$$
(15)

Results and discussion

The comparison of ds/D predicted using the ANFIS model and Eq. (15) derived from the GP model with that predicted using empirical equations proposed by various researchers is presented in Figs. 4, 5, 6, 7, 8, 9, and 10 and in Table 2. For this comparison, the experimental data given in Table 1 are used. The performance of these formulas is validated in terms of the common statistical measures of the root-mean-square error (RMSE), mean absolute percentage error (MAPE), and correlation coefficient (R). The results indicated that the GP model (Eq. 15) has a superior performance to the ANFIS model and the empirical pier scour equations furnished in "Conventional regression models" section for all the experimental data considered. The values of RMSE, MAPE, and R for the proposed GP formula considering all data (Table 2) are 0.29, 19.85%, and 0.89, respectively, which are better than those of other equations in this study. The equations of Richardson and Davis (2001) and The Colorado State University (1975) resulted in larger errors than did the other equations.

Fig. 4
figure 4

ANFIS- and GP-predicted values of ds/D versus Modified Laursen (1964) values

Full size image
Fig. 5
figure 5

ANFIS- and GP-predicted values of ds/D versus Shen et al. (1969) values

Full size image
Fig. 6
figure 6

ANFIS- and GP-predicted values of ds/D versus CSU (1975) values

Full size image
Fig. 7
figure 7

ANFIS- and GP-predicted values of ds/D versus Jain and Fischer (1979) values

Full size image
Fig. 8
figure 8

ANFIS- and GP-predicted values of ds/D versus Kothyari et al. (1992) values

Full size image
Fig. 9
figure 9

ANFIS- and GP-predicted values of ds/D versus Modified Froelich (1999) values

Full size image
Fig. 10
figure 10

ANFIS- and GP-predicted values of ds/D versus Richardson and Davis (2001) values

Full size image
Table 2 Statistical parameters of pier scour models
Full size table

A comparison between the proposed GP equation (Eq. 15), ANFIS model results, and all other pier scour equations (Table 2) for different ranges of D/d50 and Y/D was carried out. For all ranges of D/d50 and Y/D, the proposed GP performance gives the best results that are quantitatively reflected in all statistical parameters, i.e., RMSE, MAPE, and R. GP followed by ANFIS outperforms in high-value predictions for the conditions of D/d50 > 100, D/d50≦ 40, Y/D > 2, Y/D ≦ 1, compared to all other traditional equations. It should be noted that GP is more effective at extreme ranges of D/d50 and Y/D.

The results confirmed that none of the conventional regression equations give acceptable results, as reflected in higher RMSE and MAPE and lower R for D/d50 ≦ 100. At D/d50 > 100, only the equation by Kothyari et al. (1992) gave good results. Also, for dimensionless approaching flow depth Y/D < 1, the equation of Kothyari et al. (1992) performed well, as reflected in lower RMSE and MAPE. However, at 1 < Y/D, all of them gave reasonable results because the depth was difficult to measure for this range. The comparison of ANFIS and GP performance with other empirical equations presented in Figs. 4, 5, 6, 7, 8, 9, and 10 illustrates that the pier scour equations of Modified Froelich by Fischenich and Landers (1999) and Richardson and Davis (2001) over-estimated scour depth (Figs. 9, 10) because these formulas are based on high safety factors and envelop curves to data. Therefore, the correlation coefficient R for these two equations is lower in some selected ranges of D/d50 and Y/D, indicating poor performance. However, the equation of Shen et al. (1969) overpredicted the scour depth to some extent (Fig. 5) but performed well under the conditions of D/d50 > 100, 0 < Y/D ≤ 1. Contrary to this, the equations of Jain and Fischer (1979) under-predicted the scour depth at some ranges (Fig. 7). Furthermore, the equation of Kothyari et al. (1992) has an advantage over the other equations, as it is based on a large data range, which was used for regression analysis, but with minimal R in some selected ranges. The correlation coefficient R is lower, showing that there is a wide variation in the prediction of scour depth.

The robustness of ANFIS and GP was further verified and evaluated with the field data of (Mueller and Wagner 2005), which were not used in developing the ANFIS and GP models. Table 2 furnishes details of the data. The RMSE, MAPE, and R values using the ANFIS and GP models for these data are listed in Table 2. The statistical parameters show that the prediction performance of both ANFIS and GP is satisfactory. Hence, the two models can be used with a wide range of data because the data of Mueller and Wagner (2005) consist of large-scale pier models. Figure 11 shows the comparison of scour depth as predicted by the GP and ANFIS models and respective field data.

Fig. 11
figure 11

ANFIS- and GP-predicted values of ds/D versus field data values

Full size image

The relatively inferior performance of the regression-based models further strengthens the notion that such models are not always suitable for effectively predicting bridge pier scour depth.

GP model application to Imbaba Bridge, Egypt

According to the results discussed above, the GP model proved to provide a better prediction of the local scour depth around bridge piers other than the ANFIS model and other empirical formulas. Hence, it is used to investigate the local scour around bridge piers for the Nile River conditions. In Egypt, many investigators have worked on this important subject, but most have built their findings on laboratory data that have simplified conditions and scale effects. Therefore, the developed GP equation was employed to predict the local scour around the piers of the Imbaba Bridge. The results of the GP equation were then compared to those revealed by the seven regression equations illustrated earlier in "Conventional regression models" section.

Imbaba Bridge is located several kilometers upstream of the Delta Barrages (km 946 from HAD) north of Cairo. Imbaba Bridge is located in the backwater curve of Delta Barrage from about 150 years (HRI 1992). This bridge is a steel one, with two levels: one for railway and the other for roadway. It has seven piers; the second pier from the left bank is circular with 10.6 m diameter, and the other six piers are rectangular with 15 m length and 3.6 m width having rounded noses (Fig. 12). The scour holes of Imbaba Bridge have been going under detailed monitoring programs by The Hydraulics Research Institute (HRI) since 1981. The deep scour hole lies 97 m from the left bank and 32 m downstream of the centerline of the bridge with a bottom elevation of − 8.30 m (HRI 1992). Also, the mean velocity is not larger than 0.8 m/s since the bridge construction (HRI 1992). The monitoring programs revealed that the scour holes at Imbaba Bridge and are stable under current flow conditions after HAD (HRI 1997). This is because the peak flood flows released from HAD are dramatically reduced after its completion in 1968. Therefore, these scour holes are believed to be resulting from very large historic flows occurred before HAD. Table 3 shows the field data used in scour depth prediction at different piers of Imbaba Bridge.

Fig. 12
figure 12

View of Imbaba Bridge, Giza, Egypt

Full size image
Table 3 Field data of local scour depth at Imbaba Bridge, Egypt (HRI 1992)
Full size table

The sediment specific gravity is taken as 2.65, sediment porosity of 0.4, and bed material angle of repose of 300. In applying Jain and Fischer (1979) formula, a mean sediment diameter of 0.00017 m and D90 of 0.00035 m were taken from 1962 data (El-Motassem 1985) and the bed characteristics were fine sand as reported by HRI (1992). In this study, it was decided to investigate the worst condition (clear water scour). Table 4 illustrates the results of the local scour estimation for the six piers provided that Pier No. 7 was not included due to its location in a shallow area above the minimum water level.

Table 4 Predicted local scour at Imbaba Bridge, Egypt
Full size table

The results of this table indicated that the GP equation gives very close local scour depth values to those of field measurements followed by Kothyari et al. (1992) and then Modified Froelich by Fischenich and Landers (1999). This coincides with the results of the statistical analysis presented in Table 2. Also, Table 4 shows that both Modified Laursen by Neill (1964) and Jain and Fischer (1979) overpredicted the scour depth compared to other regression equations. Table 5 demonstrates the accuracy of the developed GP equation in predicting the local scour depth for the Nile River conditions at Imbaba Bridge. The table shows that the percentage error of the derived GP equation in predicting the local scour depth around the piers of Imbaba Bridge varies between 2 and 9% with an average error of 6%.

Table 5 Accuracy of GP equation for Nile River conditions at Imbaba Bridge, Egypt
Full size table

Conclusions

This paper investigated the use of both ANFIS and GP-based inductive models for predicting relative bridge pier scour depth utilizing previously collected laboratory and field data, and their performance was compared with regression-based models. The following conclusions were drawn from this study:

  • The developed GP formula as given in Eq. (15) for the prediction of pier scour depth showed better agreement with experimental results than did the ANFIS model and the other regression equations considered in this study.

  • The proposed GP formula has a higher and more stable accuracy (smaller errors and greater R) in all ranges of pier scour parameters than the other empirical equations. The other equations work well only in some selected ranges of these conditions.

  • The study also validates the promise of ANFIS and GP as effective modeling tools for applications in hydraulic modeling.

  • The developed GP equation herein, Eq. (15), yielded very good agreement (6% average error) with field data than other existing empirical equations when applied to Imbaba Bridge Giza, Egypt. Thus, the GP equation is quite convenient for scour prediction in the Nile River conditions. For further studies, it is recommended to test the developed GP equation with several field data of Egyptian bridges such as El-Tahrir Bridge, El-Menyia Bridge, and Kafr El-Zayat Bridge.