Introduction

Heavy metals are the major environmental problem with a global concern. Heavy metals are determined, non-biodegradable and known to have detrimental effects on the health of living systems, hence the need for removing it from the wastewater. Nickel is one of the non-biodegradable toxic heavy metals present in wastewater. Nickel is generally present in the effluents of industrial production processes such as mining, painting, steam electric power generation, galvanization, smelting, dye manufacturing, battery manufacturing and metal finishing (Al-Qodah 2006). The permissible limit of nickel in industrial wastewaters is 2.0 mg/L by WHO guidelines, and the concentration of Ni(II) in industrial wastewaters ranges from 3.40 to 900 mg/L (MINAS pollution control acts 2001). Therefore, it is essential to remove Ni(II) from industrial wastewaters before discharging them into the environment. A number of technologies are available with varying degrees of success to control water pollution, such as coagulation, froth flotation, filtration, ion exchange, aerobic and anaerobic treatment, advanced oxidation processes, solvent extraction, adsorption, electrolysis, microbial reduction and activated sludge (Raval et al. 2016). However, most of them require multi-step processing and their use is restricted because of limited removal efficiency, sensitive operating conditions and cost factor.

Biosorption process is considered as a desirable method because of its convenience, easy handling, lower operating costs and high efficiency in removing heavy metals from dilute solutions even at low concentrations. Heavy metals can be removed by agro-industrial waste products due to their low cost and bulk availability. Recently, potential biosorbents such as non-living biomass of plant wood, roots, leaves, bark (Vinod et al. 2010) and grape stalk waste (Villaescusa et al. 2004) have been used for the treatment of aqueous solutions of Ni(II).

In recent years, A. barbadensis Miller (Aloe vera) has increasingly been used as a raw material in food, pharmaceutical and cosmetic industries due to its medicinal properties. Fresh Aloe vera leaves are used to obtain bitter yellow latex from a peripheral sheath, called Aloe vera sap, and a mucilaginous gel from parenchymatous tissue. After processing of fresh Aloe vera leaves, about 65% of the biomass is left as a residue (Boghani et al. 2012).

The objectives of this research are to investigate the removal of Ni(II) from simulated aqueous solution by using A. barbadensis Miller leaves (ABL) residue powder as biosorbent. The effects of various process parameters such as pH, adsorbent dose, initial metal ion concentration, contact time and temperature on the removal of Ni(II) were investigated. Biosorption equilibria, kinetics and thermodynamic parameters were also evaluated, and besides, interference of other metals ions on the removal behaviour was also investigated.

Materials and methods

All chemicals used in this study were of analytical reagents grade, unless otherwise stated.

Preparation of adsorbent

Biosorption experiments were carried out using aqueous solutions containing Ni(II) in the form of Ni (NO3)2·6H2O. The standard stock solution of 1000 mg/L was prepared by dissolving 4.9538 g in one litre of double-distilled water. The initial pH of the solution was adjusted using 0.1 M HCl/0.1 M NaOH. The final concentrations of metal ions were analysed using atomic absorption spectrophotometer (AAS 4141), ECIL, India, at a wavelength of 217 nm using an air–acetylene flame.

Preparation of biosorbent

The A. barbadensis Miller leaves (ABL) residue was collected from a nearby industry (Juneja Ayurveda and Herbal Industry, Karol Bagh, New Delhi) and washed twice with distilled water to remove dust and other impurities. The washed leaves were steam-heated at high pressure (15 psig) for 20 min using a pressure cooker, further pressed and washed with distilled water to remove colour and then dried in an oven at 80 °C for 24 h. The dried residue was pulverized using a grinder and sieved to 100 mesh sizes (150 µm). The dried material was stored in airtight bottles for further use as biosorbent.

Biosorption study

Batch biosorption experiments were carried out for removal of Ni(II) by mixing known weights (1 g) of biosorbent with 100 mL of Ni(II) solution in the concentration range of 20–200 mg/L (freshly prepared from the stock solution). The suspension of neutral pH 7 was prepared with phosphate buffer. The mixture was shaken on an orbital shaker at 150 rpm for 180 for equilibration studies. After equilibration time, the biosorbent was separated by filtrations and the residual concentration of Ni(II) in the filtrates was determined by atomic absorption spectrophotometer (AAS).

Biosorption capacity of Ni(II) (qe) and percentage of biosorption were calculated according to the following general equations:

$$q_{e} = \frac{{\left( {C_{0} - C_{e} } \right)V}}{M},$$
(1)
$$\% \, {\text{of Removal }} = \frac{{\left( { C_0 {-} C_e} \right) }}{C_0} \times 100,$$
(2)

where qe is the amount of Ni(II) adsorbed on the biosorbent (mg/g); C0 and Ce represent the initial and equilibrium concentrations of Ni(II) (mg/L), respectively; V is the volume of Ni(II) solution (ml); M is the amount of biosorbents (g). Experiments were carried out in triplicate, and mean value was reported.

Results and discussion

Characterization of biosorbent

Zeta potential

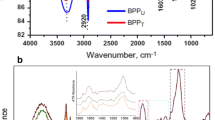
The zeta potential describes the charge behaviour at the solid–liquid interface. The surface charge at the interface between a solid material and an aqueous phase was measured. The adsorbent was characterized by measuring the zeta potential using a cylindrical cell of Surpass Electrokinetic Analyser (Anton Paar) at room temperature and different pH values. The result is reported in Fig. 1a with a net zero charge near pH 4.2, meaning that the surface of prepared biosorbent has negative charge above this pH value.

Fig. 1
figure 1

a pH of zero point charge of ABL and SEM images of ABL b-I before biosorption and b-II after biosorption

Full size image

Surface morphology

Scanning electron microscopy (SEM) was used to investigate the metal interaction with the biosorbent before and after biosorption [Fig. 1b-I, b-II]. The micrograph before biosorption revealed an irregular and porous surface. After biosorption of Ni(II), the pores were filled with adsorbate ions on the surface of the biosorbent (Fig. 1b-I). It clearly indicates the presence of new shiny bulky particles and layers in metal-loaded adsorbent which are absent for the native adsorbent (Fig. 1b-II).

BET surface area and pore volume

The specific surface area of the biosorbent was determined by the Brunauer, Emmett and Teller (BET) method, using surface area analyser (Sorptomatic, 1990 Series, Thermo Finnigan, Italy) using the nitrogen gas. The physico-chemical characteristics of the biosorbent determined using standard methods are summarized in Table 1.

Table 1 Physico-chemical characteristics of biosorbent
Full size table

Effect of operational parameters

Effect of pH

pH is the most important parameter affecting the solubility of metal ions, concentration of counter ions on the functional groups of the biosorbent and the degree of ionization of the adsorbate during reaction. The studies were carried out to obtain optimum pH or the adsorption of nickel (II) using 1 g of biosorbent in 100 ml solution of 100 mg/L of nickel (II) concentration adjusted to different pH values from 1.0 to 10. The solutions after equilibration were centrifuged. The filtrates were tested for Ni(II) concentrations by AAS. Figure 2a shows the effect of pH on adsorption of Ni(II) ion. Maximum removal of 42.2% was achieved at pH 7, and at lower pH values, nickel removal was inhibited, possibly because of the competition between hydrogen and nickel ions on the sorption site. With an apparent dominance of hydrogen ions in the solution, these ions seem to restrict due to the repulsive force (Yipmantin et al. 2011). At pH > 8, precipitations started, and hence, higher pH was not selected for the present study. Biosorption of nickel ions was maximum at pH=7. This is possibly due to the precipitations of Ni(II) ions as a result of hydroxide anions forming nickel hydroxide precipitate. The results were obtained for the biosorption of nickel (II) on the powder ABL at pH 7. Further experiments were conducted at the same pH.

Fig. 2
figure 2

Effect of parameters behaviour. a Effect of pH, b effect of dose, c effect of initial concentration, d effect of temperature, e effect of contact time

Full size image
Table 2 Adsorption isotherm constants for adsorption of Ni(II) on ABL
Full size table

Effect of ABL dose

The dependence of Ni(II) biosorption on biosorbent dose was studied by varying the amount of ABL from 0.2 to 2.0 g while keeping the volume 100 mL, concentration of metal ion 100 ppm, pH 7 and constant contact time 180 min. The uptake of metal increased from 25.6 to 60.2% with an increase in ABL dose up to 0.6 g to 2 g (Fig. 2b) and finally attains a steady value. An increase in biosorption percentage with an increase in biosorbent dose may be attributed to the availability of more sorption sites present on the surface of the biosorbent (Thirumavalavan et al. 2011). Hence, 1 g/L biosorbent was taken as the optimum.

Effect of contact time

Contact time is one of the most important parameters for the successful use of the ABL for a practical application. It has been observed that biosorption rate increased from 18.9 to 42.8% with an increase in contact time from 15 to 300 min. Maximum Ni(II) removal was achieved up to 180 min and thereafter remained constant as shown in Fig. 2c. This may be due to the fact that initially for biosorption the large number of vacant sites was available, which slowed down later due to exhaustion of remaining surface sites and repulsive force between solute molecule and bulk phase (Saravanane et al. 2002).

Effect of initial metal ion concentration

The effect of initial metal concentration on the biosorption experiment is shown in Fig. 2d. It was observed that biosorption of Ni(II) decreased from 56.5% to 38.3% with an increase in metal concentration from 20 to 200 mg/L. At a higher concentration, most of the Ni(II) is left unabsorbed due to saturation of biosorption sites. As the ratio of adsorptive surface to ion concentration decreased with increasing metal ion concentration, metal ion removal was reduced. At low initial concentration of metal ions, more binding sites are available. But as the concentration increased, the number of ions competing for available binding sites in the biomass increased (Gupta and Mohapatra 2003).

Effect of temperature

The effect of temperature was studied in the temperature range 20–60 °C at pH 7 (Fig. 2e). It was found that uptake capacity decreased with an increase in temperature, which was probably related to increased solubility of nickel hydroxide at higher temperatures. The value of sorption rate constant slightly decreased between 40 and 60 °C and above 40° very much decreased. This is mainly due to the decreased surface activity, suggesting that adsorption between nickel and biosorption is an exothermic process. This variation in removal of nickel seems due to the enhancement of relative escaping tendencies of the metal ions from aqueous phase to the bulk and consequent reduction in the boundary layer thickness. The decrease in the removal at increasing temperatures can also be attributed to the increased solubility of metal at relatively higher temperatures (Arief et al. 2008).

Adsorption isotherm

An adsorption isotherm expresses the functional equilibrium distribution of adsorption with different concentrations of adsorbate in solution at constant temperature. These isotherms are generally used to establish the relationship between the amount of metal ion adsorbed and its equilibrium concentration in solution. They also help provide vital information to understand the mechanism of the adsorption process. (Ncibi 2008)

A number of isotherms have been developed to describe equilibrium relationships. In this study, the Langmuir, Freundlich isotherm, Brunauer–Emmett–Teller (BET), D–R isotherm and Temkin isotherms were applied to the experimental data.

The Langmuir model (Langmuir 1916) is based on the assumption that the maximum adsorption occurs when a saturated monolayer of solute molecules is present on the adsorbent surface, the energy of adsorption is constant and there is no migration of adsorbate molecules in the surface plane. The Langmuir isotherm is given by

$$\frac{1}{{q_{e} }} = \frac{1}{{q_{m } K_{L} C_{e} }} + \frac{1}{{q_{m} }},$$
(3)

where Ce is the equilibrium concentration in solution (mg/L) and qm and KL are the Langmuir constants, representing the maximum adsorption capacity for the solid phase loading and the energy constant related to the heat of adsorption, respectively.

Separation factor

Langmuir isotherm can be characterized by a dimensionless constant called separation factor (RL) (Webber and Chakkravorti 1974) as shown by the following equation:

$$R_{L} = \frac{1}{{1 + K_{L }\, C_{0} }} ,$$
(4)

where C0 (mg/L) is the initial concentration and KL = (L/mg) is Langmuir constant. The value of RL indicates the shape of the isotherm to be either linear (RL = 1), unfavourable (RL > 1), favourable (0 < RL < 1) or irreversible (RL = 0). The RL values were in the range of 0.05 to 0.005, which is less than unity, indicating that the adsorption of Ni(II) into this process is a favourable process and thus ABL is a good adsorbent for Ni(II).

The values of RL for the studied system at different initial concentrations were found to be in between 0 and 1, which indicates favourable adsorption of nickel onto the adsorbent.

The Freundlich isotherm model (Freundlich 1906) is an empirical relationship describing the adsorption of solutes from a liquid to a solid surface and assumes that different sites with several adsorption energies are involved. Freundlich adsorption isotherm is the relationship between the amounts of nickel adsorbed per unit mass of adsorbent, qe, and the concentration of the nickel at equilibrium, Ce.

$$\log q_e = \log K_{f} + \frac{1}{{n_{f} }}\log C_e,$$
(5)

where Kf and 1/n are the Freundlich constants, the characteristics of the system. Kf and n are the indicators of the adsorption capacity and adsorption intensity, respectively, as shown in Fig. 3b.

Fig. 3
figure 3

Isotherm of adsorption of Ni(II). a Langmuir, b Freundlich, c Temkin, d Dubinin–Radushkevich, e BET [initial Ni(II) conc. = 20–200 mg/L; pH = 7.0; ABL dose = 1 g; temperature = 303 °C]

Full size image

Temkin isotherm

This model assumes that heat of adsorption (function of temperature) of all molecules in the layer would decrease linearly rather than logarithmic with coverage (Tempkin and Pyzhev 1940). The adsorption potential of adsorbent to adsorbate can be tested by applying Temkin isotherm model (Eq. 6). This equation is supposed that the coverage increases. The linear form of Temkin is as follows:

$$q_{e } = \left( { {\raise0.7ex\hbox{${RT}$} \!\mathord{\left/ {\vphantom {{RT} {b_{T } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${b_{T } }$}}} \right)\ln K_{T } + \left( { {\raise0.7ex\hbox{${RT}$} \!\mathord{\left/ {\vphantom {{RT} {b_{T } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${b_{T } }$}}} \right)lnC_{e} ,$$
(6)

where R is the common gas constant (0.008314 kJ/mol/K), T is the absolute temperature (K), 1/bT is the Temkin constant related to the heat of adsorption (KJ/mol) which indicates the adsorption potential (intensity) of the adsorbent and KT (L/g) is the Temkin constant related to the adsorption capacity.

Dubinin–Radushkevich (D–R) isotherm model

To calculate the biosorption energy, D–R model is used to calculate the adsorption energy. It is generally applied to express the adsorption mechanism (Gunay and Arslankaya 2007). This isotherm does not assume constant adsorption potential or homogeneous surface for the adsorbent. Thus, the D–R linear form can be applied on both homogenous and heterogonous surfaces.

$$\ln q_{e} = \ln q_{m } - \beta \varepsilon^{2} ,$$
(7)

where β is a constant related to the mean free energy of adsorption, qm (mg/g) is the theoretical saturation capacity based on D–R isotherm and ε is the Polanyi potential. ε can be calculated from Eq. (8):

$$\varepsilon = RT\ln \left( {1 + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {C_{e} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${C_{e} }$}}} \right),$$
(8)

where R (J/mol/K) is the gas constant and T (K) is the absolute temperature

Mean energy of adsorption (Ea)

Applying D–R isotherm model for the adsorption data of Ni(II) into bioadsorbent allows to calculate the mean energy of adsorption (Ea) from the value of β according to the following relation:

$$\varvec{E}_{\varvec{a}} = \frac{1}{{\left( {2{\varvec{\upbeta}}} \right)^1/2 }}.$$
(9)

The numerical value of Ea was calculated as 0.158 kJ/mol. According to the literature (Dubinin 1960), this adsorption energy is independent of the temperature but varies depending on the nature of the adsorbent and adsorbate. The magnitude of Ea provides information on the nature of the sorption process, i.e. whether it is chemical or physical, with values in the range Ea = 1–8 kJ/mol corresponding to physical adsorption and in the range 9–16 kJ/mol to chemisorption. Ea value less than 8 kJ/mol as indicated by our results shows that the adsorption process of nickel on bioadsorbent follows physical adsorption.

While the value of Ea in the range of 1–8 kJ/mol indicates physical adsorption process, that above 8 indicates chemisorption.

BET isotherm

The BET isotherm (Bruanuer et al. 1938) is a theoretical equation applied widely in gas–solid equilibrium systems. It was developed to derive multilayer adsorption systems with relative pressure ranges from 0.05 to 1.50 corresponding to a monolayer coverage lying between 0.50 and 1.50. This isotherm has been applied in liquid–solid interface and is given in its linear form in (10)

$$\frac{{C_{e} }}{{q_{e} }} \left[ { C_{s} - C_{e} } \right] = \frac{1}{{q_{{s C_{B} }} }} + \left[ { \frac{{C_{B} - 1}}{{q_{{s C_{B} }} }}} \right]\frac{{C_{e} }}{{C_{s} }} ,$$
(10)

where CB (L/mg) is the BET adsorption isotherm, Cs (mg/L) is the adsorbate monolayer saturation concentration and qs (mg/g) is the theoretical isotherm saturation capacity. This isotherm was applied by a linear plot of Ce/qe[Cs− Ce] versus Ce/Cs shown in Fig. 3e, and the BET isotherm parameters are given in Table 2.

Table 3 Kinetics parameters for the removal of Ni(II)
Full size table

Biosorption kinetics

The study of the adsorption kinetics is the main factor for designing an appropriate adsorption system and quantifying the changes in bioadsorption with time, requires that an appropriate kinetic model is used. The values of various kinetics parameters are given in Table 3. The kinetics of metal biosorption governs the rate, which determines the residence time and is one of the important characteristics defining the efficiency of biosorbent. (Chang et al. 2004). The bioadsorption kinetics can be controlled by several independent processes which could act in series or in parallel, such as external mass transfer, bulk diffusion, chemisorptions and intraparticle diffusion. This Elovich equation and Weber and Morris intraparticle diffusion model were applied in the description of the kinetics of bioadsorption (Fig. 4).

Fig. 4
figure 4

Kinetic model for Ni(II) adsorption. a Pseudo-first-order, b pseudo-second order, c Bangham, d intraparticle diffusion, e Elovich models [initial Ni(II) conc. = 100 mg/L; contact time = 15–300 min]

Full size image

Pseudo-first-order model: The pseudo-first-order rate expression based on solid capacity is the most widely used rate equation for assigning the biosorption rate of an adsorbate from a liquid phase and is known as the Lagergren rate equation.

It is represented as:

$$\log \left( {q_{e } - q_{t} } \right) = \log q_{e} - \frac{{K_{1} t}}{2.303} ,$$
(11)

where qe (mq/g) and qt (mg/g) are the adsorption capacity at equilibrium and time t, respectively, and K1 is the rate constant of the pseudo-first-order bioadsorption. The plot of log (qe− qt) versus t gives K1 and qe from the slope and the intercept, respectively.

Pseudo-second-order model

The pseudo-second-order kinetic expression was developed by (Lagergran and Venska 1898) to describe the adsorption of metal ions onto adsorbents. The rate expression is represented as:

$$\frac{t}{{q_{t} }} = \frac{1}{{K_{2 } q_{e}^{2} }} + \frac{t}{{q_{e} }},$$
(12)

where qe and qt (mg/g) are the biosorption capacities at equilibrium and time t, respectively, and k2 (g/mg’’min”1) is the rate constant for the pseudo-second-order adsorption reaction.

The value of qe and k2 can be calculated from the linear plot of Eq. (12). The initial bioadsorption rate can be obtained as q/t, when t approaches zero. This is expressed as

$$h = K_{2 } q_{e}^{2} ,$$

where h is the initial adsorption rate and is expressed in mg/g/min

Bangham’s equation

The Bangham model of adsorption kinetic studies is used to test whether the pore diffusion is the only rate controlling step. The model can be represented by the following equation (O. Abdelwaha 2007):

$$\log \left[ {\log \left\{ {\frac{{c_{b } }}{{C_{b } - q_{t } M}}} \right\}} \right] = \log \left\{ {\frac{{K_{0 } M}}{2.303 V}} \right\} + 6\log \left( {\text{t}} \right),$$
(13)

where Cb (mg/L) is the amount of initial adsorbate in the liquid phase, qt (mg/g) is the concentration of solute in the solid phase at any time t (min), M (g) is the amount of bioadsorbent, V (L) is the volume of solution used and Ko(L/g) and ϭ (< 1) are the Bangham’s equation parameters.

Intraparticle diffusion model

The Weber’s diffusion mode (Weber and Morris 1963) is the most commonly used technique for identifying the mechanism involved in the bioadsorption process. During the process of bioadsorption, the transportation of the adsorbate particles to the surface of the adsorbent surface takes place in several steps. The adsorption process may be controlled by film or external surface diffusion, pore diffusion, surface diffusion and adsorption on the pore surface or a combination of one or more steps. In a rapidly stirred batch process, the diffusive mass transfer can be related by an apparent diffusion coefficient which will fit experimental adsorption rate data. Usually, a process is diffusion controlled if its rate is dependent on the rate at which the components diffuse towards each other. The Weber’s diffusion model is expressed as

$$q_{t} = K_{ip} t^{1/2} + I,$$
(14)

where q (mg/g) is the concentration of adsorbate in the solid phase at time t (min) and kip (mg.g’ min) is the intraparticle diffusion rate constant. A linear plot of qt versus t1/2 shows I as the intercept which gives an idea of the thickness of the boundary layer on the bioadsorbent surface. The larger the value of I, the greater the boundary layer effect.

Elovich kinetic model

The Elovich kinetic mode (Chien and Clayton 1980) is based on chemisorption phenomena. It is expressed as

$$q = \frac{{{ \ln }\left( {a\omega } \right)}}{\omega } + \frac{1}{\omega } lnt,$$
(15)

where q (mg/g) is the adsorbate in the solid phase at time t (min), a is the initial adsorption rate (mg/g min) and ω is the related to the extent of surface coverage and activation energy for chemisorption. From the linear plot of Eq. (15), the values of a and ω can be evaluated as intercept and slope of the straight line.

Bioadsorption thermodynamics

Thermodynamics are essential in adsorption studies as temperature is directly related to the kinetic energy of metal ions in the solution. In general, increasing temperature increases the diffusion rate of the metal ions into the biosorbent. In this study, experiments were carried out at different temperatures, viz. 293, 303, 313, 323 and 333 K for the bioadsorption of initial Ni(II) ion concentration (100 mg/L) on ABL at their respective optimal values of pH, ABL dose and equilibrium time. A change in temperature affects the thermodynamic parameters, viz. thermodynamic parameters such as free energy (∆G°), enthalpy (∆H°) and entropy (∆S°). A change in biosorption can be evaluated from the following equations:

$$\Delta G{^\circ } = - RT\, lnK_{d} ,$$
(16)

where R is the gas constant (8.314 J/mol/K), T is the temperature (K) and Kd is the equilibrium constant. The value of Kd was calculated using Eq. 22

$$K_{d } = \frac{{q_{e} }}{{C_{e} }} ,$$
(17)
$$ln K_{d} = \frac{{\Delta S{^\circ }}}{R} - \frac{{\Delta H{^\circ }}}{RT} ,$$
(18)

where qe and Ce are the equilibrium concentrations of metal ions on the biosorbent and in the solution, respectively.

The Gibbs free energy (ΔG°) for the adsorption of Ni(II) onto biomass at all temperatures was obtained from Eq. 16 and is presented in Table 4. The values of ΔH° and ΔS° were calculated from the slope and intercept of the plot log Kd against 1/T from Eq. (18) van’t Hoff plot and are also listed in order to support that physical adsorption is the predominant mechanism; the values of activation energy (Ea) and sticking probability (S*) were calculated from the experimental data. They were calculated using modified Arrhenius-type equation related to surface coverage (θ) as follows (Huang and Cheng 1997):

Table 4 Thermodynamic parameters for biosorption of Ni(II) on ABL
Full size table
$$\theta = \left( { 1 - \frac{{C_{e} }}{{C_{i} }}} \right),$$
(19)
$$S^{*} = \left( { 1 - \theta } \right)e^{{\frac{{ - E_{a} }}{RT}}} .$$
(20)

The sticking probability, S*, is a function of the adsorbate/adsorbent system under consideration but must satisfy the condition 0 < S* < 1 and is dependent on the temperature of the system. The values of Ea and S* can be calculated from slope and intercept of the plot of ln(1 − θ) versus 1/T, respectively (Fig. 5), and are listed in Table 4.

Fig. 5
figure 5

Van’t Hoff plots for Ni(II) (a) and modified Arrhenius plots for Ni(II) (b)

Full size image

Table 4 shows that the reaction is spontaneous in nature as ∆Go values are negative at all the temperature studied. The negative value of ∆H° (− 7.58 kJ/mol)) confirms that the bioadsorption is exothermic in nature. The positive value of ∆S° (0.011 kJ/mol) reflects the affinity of the adsorbents for the Ni(II) ions. The values of Ea was found to be − 3.17 kJ/mol for the adsorption of Ni(II)) onto biomass. The positive value of Ea indicates the exothermic nature of the adsorption process which is in accordance with the positive values of ΔH°. (Chegrouche et al. 2009)

Fig. 6
figure 6

Interference studies of the biosorption of Ni2+

Full size image

The result as given in Table 4 indicates that the probability of the Ni(II) ions to stick on surface of biomass is very high as S* ≪ 1, and these values confirm that the sorption process is physisorption (Ho et al. 2004).

Interference study

The sorption of metal ions in the presence of other common ions may be affected due to competition for the sorption sites (Malik et al. 2005). Mg2+ and Ca2+ on the sorption of Ni(II) at optimum conditions were investigated. Nickel without interference recorded 60.2% adsorption to ABL biomass. However, it reduced to 59.4  when calcium or magnesium ions were present at 40 ppm. It is evident that the presence of the ions in the adsorbate solution practically did not affect the extent of adsorption (Fig. 6). A higher concentration level of interfering ions may, however, adversely affect the adsorption capacity of ABL. 10, 20, 30, or 40 ppm concentration of Mg2+ or Ca2+ ion in 100 ml of 100 ppm Ni(II) ion solution  was interacted with 1.0 g biosorbent dose at pH 7, 303 K, 150 rpm.

Conclusion

Aloe barbadensis Miller leaves (ABL) biomass was selected for studying biosorption due to the possibility of utilizing a waste biomass to eradicate the metal pollution. Optimum pH of adsorption was found to be 7. Freundlich isotherm is the best fitted model with adsorption capacity of 10 mg/g. Pseudo-second order was fitted in kinetic studies. According to thermodynamic studies, negative value of Gibb’s free energy and enthalpy signifies the spontaneity and exothermic nature of the adsorption process. Not much more effect of interference of cations of other metal ions at different concentrations was found on biosorption potential of Ni(II) ions. Sticking probability (S* ≤ 1) indicates that ABL biosorbent is the excellent biosorbent for the removal of Ni(II) ions from solution.

The outcome of this study shall help in designing the biosorbers used in the industry for removal of Ni(II) ions from their effluents. Moreover, the use of Aloe vera leaves waste shall minimize the use of activated carbons, which are usually obtained from wood, thus protecting our environment.