Introduction

Water consumption in Taiwan has increased significantly in recent years. The Water Resources Agency and the Taiwan Water Corporation have raised certain issues regarding the quantity and quality of water. According to statistical data, the island’s average annual rainfall is approximately 2515 mm. Despite its abundance, rainfall is unevenly distributed in terms of both time and space. Because of the island’s steep natural terrain, short river flows, and geological weaknesses, the majority of rainwater flows out to sea before it can be harnessed for public use. Thus, reservoirs are an essential means of realizing effective water usage. From the viewpoint of water resource management, both the availability and quality of water are a concern.

One of the water resources of the Nanhua Reservoir is the discharge of the Cishan River, which is diverted through a tunnel from the Chiahsien Weir. The majority of water diversion occurs during the annual wet period, from June to October, which is also the typhoon season. Because of the adverse effect of soil degradation in the upstream catchment area, heavy rainstorms rapidly and significantly increase the Cishan River discharge; they also increase the sand content and turbidity. If this flow is allowed to persist and enter the Nanhua Reservoir, the level of reservoir sediment will undoubtedly increase, potentially shortening the lifespan of the reservoir and creating problems for the operation of the Nanhua water-treatment plant.

This study examines the relevant hydrological data variables that influence water turbidity in the Chiahsien Weir. A unique group method of data handling (GMDH) multilayer algorithm is used to deduce the relationship between groups of input variables and output functions. The result is combined into a suitable set of higher-order nonlinear equations that engender a simple turbidity-forecasting model. This enables the prediction of water turbidity, and provides pertinent reference turbidity information for the Chiahsien Weir water diversion operation.

Methodology

The GMDH algorithm introduced by Ivakhnenko (1968) is a heuristic self-organization process that establishes an input–output relationship within a complex system. It utilizes a multilayered conceptual structure, similar to a feed-forward multilayer neural network. Ikeda et al. (1976) added a recursive procedure to the GMDH algorithm to utilize updated observation data and to modify parameters within the nodes of each layer, enabling time-variable modeling. They subsequently applied the enhanced model to the prediction of daily river flows. Tamura and Kondo (1980) utilized the prediction of sum-of-squares or Akaikes’s information criterion as parameter selection indicators. Because the algorithm can easily generate high-level nonlinear terms, this nonlinear dynamic system can be well defined; however, its practicality would be seriously reduced. In response, Yoshimura et al. (1982) improved the model with a stepwise regressive procedure, returning the complex final system to a low-level nonlinear system, thereby increasing its applicability.

The GMDH algorithm enables the automatic selection of input variables during model construction, as well as a hierarchical polynomial regression of necessary complexity (Farlow 1984). Specific functional dependence between the input and output variables is unnecessary, as the dependence has been incorporated into the modeling structure. The GMDH algorithm has been applied in various fields, e.g., weather modeling, pattern recognition, physiological experiments, cybernetics, medical science, education, ecology, safety science, economics, and hydraulic field engineering systems (Lebow et al. 1984; Ivakhnenko et al. 1994; Kondo et al. 1999; Chang and Hwang 1999; Sarycheva 2003; Pavel and Miroslav 2003; Hwang et al. 2009; Tsai et al. 2009; Najafzadeh et al. 2013, 2014, 2015; Najafzadeh 2015). Nevertheless, few studies have explored turbidity modeling.

GMDH algorithm

The GMDH algorithm is a kind of feed-forward network, normally classified as a special type of neutral network. The model’s underlying concept resembles animal evolution or plant breeding, as it adheres to the principle of natural selection. The multilayer criteria preserve superior networks for successive generations, eventually yielding an optimal network. This network (equation) more closely describes the physical phenomena that the model is intended to simulate. The self-organization algorithm can be classified as GMDH, SGMDH (stepwise regressive GMDH), and recursive/sequential GMDH. These model types are described below.

In the GMDH algorithm, the general connection between input and output variables is expressed by the Volterra functional series of the Kolmogorov–Gabor polynomial (Madala and Ivakhnenko 1994):

$$y(t) = a_{0} + \sum\limits_{i = 1}^{m} {a_{i} x_{i} } + \sum\limits_{i = 1}^{m} {} \sum\limits_{j = 1}^{m} {a_{ij} x_{i} x_{j} } + \sum\limits_{i = 1}^{m} {} \sum\limits_{j = 1}^{m} {} \sum\limits_{k = 1}^{m} {a_{ijk} x_{i} x_{j} x_{k} } + ..,$$
(1)

where y(t) is the output variable, X(x 1,x 2,…,x m ) is the vector of input variables, and A(a 1,a 2,…,a m ) gives the vector coefficients or weights.

The GMDH model based on heuristic self-organization was developed to overcome the complexity of large-dimensional problems. It first pairs variables that might affect the system, and sets a default threshold to eliminate variables that cannot achieve a certain level of performance. This procedure describes a self-organization algorithm; it is a fundamental concept of derivative hierarchical multilevel models. The GMDH was built according to the following steps:

Step 1: Divide the original data into training and test sets

The original data are separated into training and test sets. The training data are used to estimate certain characteristics of the nonlinear system, and the test data are then applied to determine the complete set of characteristics.

Step 2: Generate combinations of input variables in each layer

All combinations of r input variables are generated for each layer. The number of combinations is given by:

$${\text{C}}_{r}^{m} = \frac{m!}{{r!\left( {m - r} \right)!}}\;\;,$$
(2)

where m is the number of input variables and r is usually set to two (Ivakhnenko 1971).

Step 3: Optimization principle for elements in each layer

Optimum partial descriptions of the nonlinear system are calculated by applying regression analysis to the training data. The optimum standard uses the root mean square (RMS) as an index to screen out underperforming elements in each layer. RMS is defined as:

$$r_{i} = \left[ {\frac{{\sum\nolimits_{t = 1}^{n} {\left( {y(t) - Z_{i}^{k} (t)} \right)^{2} } }}{{\sum\nolimits_{t = 1}^{n} {\left( {y(t)} \right)^{2} } }}} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} ,$$
(3)

where r i is the RMS, t = 1, 2,…n, n represents the length of the measurement data, y(t) is the measured value at moment t; and Z k i (t) is the output value of element i in layer k.

Step 4: Stopping rule for multilayer structure generation

By comparing the index value of the current (competent) layer with that of the next layer to be generated, further layers are prevented from being developed if the index value does not improve or falls below a certain objective default value; otherwise, Steps 2 and 3 are repeated until the value matches the limited condition set above.

After the above steps have been completed, all competent elements in each layer are recombined as an optimum high-level nonlinear equation. This is utilized as the final model for turbidity forecasting.

Stepwise regressive GMDH algorithm

The process of the stepwise regressive GMDH algorithm is very similar to that of the original GMDH algorithm. The key difference is that the least-squares method is replaced by a stepwise regressive procedure in Step 2. This procedure evaluates the optimum forward state, and determines whether it is more accurate than the next variable to be introduced. If so, it is incorporated into the model; otherwise, it is deleted to ensure the most precise simplified system equation. The assessment method employs the F-test for statistical analysis.

Recursive/sequential GMDH algorithm

Because of real-world time-variable characteristics, the system should respond to situations in real time. If the measured input data conceal the errors, or if the system is affected by human or natural factors, model parameters may no longer be applicable to the circumstances. The model forecasts will deviate and affect the overall precision of the model. To resolve this, the forecast model is revised using a recursive structure, thus allowing the system parameters to be modified in real time. This procedure can improve the forecast accuracy. In the GMDH algorithm, each progressive output element is composed of two prior elements with six parameters in a two-dimensional second-order equation. Thus, the system has an n-set of data, and the parameters (\(\theta\)) of the newly composed equations of each layer are forecast as \(Y_{n} = X_{n} \times \theta\). When the n + 1 data point is added, the system parameter \(\theta\) can be updated to \(\theta^{*}\) according to:

$$\theta_{n + 1}^{*} = (X_{n + 1}^{t} X_{n + 1} )^{ - 1} X_{n + 1}^{t} Y_{n + 1} .$$
(4)

Upon completion of the recursive procedure, the system parameters can be adjusted to ensure model optimality.

Establishment and assessment of the turbidity forecast model

Establishment of a turbidity-forecasting model

We now apply self-organizing nonlinear models for GMDH and SGMDH. The GMDH turbidity forecast model is developed according to the procedure described below. Figure 1 presents a flowchart of turbidity forecasting.

  1. 1.

    Obtain turbidity-related historical data, such as turbidity, rainfall, and discharge, at specific stations.

  2. 2.

    Select the input variables.

    1. (1)

      Assume the output variable is Y, which represents the forecast turbidity.

    2. (2)

      Assume the input variables are X 1, X 2, X 3,…, X m , which represent turbidity, rainfall, discharge, and so on.

    3. (3)

      Establish a nonlinear equation Y = f (X 1, X 2,…, X m ).

  3. 3.

    Determine the optimum number of modeling data and variable combinations to establish a forecast model through trial-and-error.

  4. 4.

    Establish an input–output relationship with both the GMDH and SGMDH algorithms; derive the model layer-by-layer until optimality is achieved, and then return, layer-by-layer, to the inertial input layer to establish a GMDH or SGMDH forecast equation.

  5. 5.

    Input the variables and begin model forecasting.

  6. 6.

    Output the forecast results.

  7. 7.

    Consider whether there is a temporal impact. If so, a recursive/sequential structure is necessary.

  8. 8.

    Generate a final optimum turbidity-forecasting model.

Fig. 1
figure 1

Flowchart of GMDH/SGMDH turbidity-forecasting model construction

Full size image

Based on the previous step, the output variable of the forecasting model is the turbidity MUD(t) at time t, where t represents the time period. The input variables are the daily turbidity T(t−1) ~ T(t−m) for the period 1 ~ m, daily rainfall R(t−1) ~ R(t−n) for the period 1 ~ n, and daily discharge of the Cishan River Q(t−1) ~ Q(t−k) for the period 1 ~ k. The forecast relation is presented below:

$${\text{MUD}}(t )= F(T(t - 1),T(t - 2), \ldots ,T(t - m),R(t - 1),R(t - 2), \, \ldots ,R(t - n),Q(t - 1), \, Q(t - 2), \ldots ,Q(t - k)).$$
(5)

Model efficiency evaluation

The model can be evaluated by comparing its predictions to the measured values. The efficiency of the model is evaluated using the root mean square error (RMSE) and the coefficient of correlation (CC):

$${\text{RMSE}} = \sqrt {\frac{{\sum\nolimits_{T = 1}^{N} {\left( {X_{T} - \hat{X}_{T} } \right)^{2} } }}{N}}$$
(6)
$${\text{CC}} = \frac{{\sum\nolimits_{T = 1}^{N} {\left( {X_{T} - \bar{X}} \right)\left( {\hat{X}_{T} - \bar{\hat{X}}} \right)} }}{{\sqrt {\sum\nolimits_{T = 1}^{N} {\left( {X_{T} - \bar{X}} \right)^{2} } \sum\nolimits_{T = 1}^{N} {\left( {\hat{X}_{T} - \bar{\hat{X}}} \right)^{2} } } }},$$
(7)

where \(X_{T}\) is the observed value, \(\hat{X}_{T}\) is the predicted value, \(\bar{X}\) is the mean observed value, \(\bar{\hat{X}}\) is the mean predicted value, and N represents the total number of observations in the data set. RMSE values approaching 0 and CC values approaching 1 signify better forecast performance.

Case studies

In this section, we compare the results given by our forecast model with real-world data. We first describe the study area and the data set used for comparison; then, we present the forecast results and evaluate the model’s performance.

Study area description

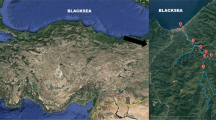
Nanhua Reservoir is located 40 km northeast of Tainan, Taiwan, and approximately 15 km south of the Tseng-Wen Reservoir. Its catchment area is approximately 104 km2. Figure 2 illustrates the reservoir location.

Fig. 2
figure 2

Position of the study area (Nanhua Reservoir)

Full size image

Chiahsien Weir is located in Kaohsiung County, near the Cishan River in Jiashian Township, approximately 450 m upstream of the Jiashian Bridge. The weir is part of the over-basin diversion project of Nanhua Reservoir. Figure 3 presents the site layout. Excess water from the Cishan River is mainly diverted into the Nanhua Reservoir during the wet season. According to reports by the Water Resources Agency and the Taiwan Water Corporation, the Nanhua Reservoir is seriously sediment-impacted. Over-basin diversion has been reported to be the most likely cause of increases in the reservoir sediment level.

Fig. 3
figure 3

Photograph of the Chiahsien Weir

Full size image

Selection of research data

This paper explores turbidity changes in the Nanhua Reservoir prior to over-basin diversion (i.e., turbidity changes at the diversion tunnel entrance of the Chiahsien Weir). Numerous variables, such as storms, human activities, and complex natural processes, affect turbidity. These influencing factors closely match the nonlinear structural model of the GMDH algorithm.

Those factors that have the greatest impact on turbidity were utilized as input parameters. Thus, turbidity, rainfall, and discharge were chosen as the domain input parameters. The turbidity at the entrance to the diversion tunnel of the Chiahsien Weir was selected as the main parameter. Rainfall data from the Jiashian rainfall station (the only rainfall station upstream of the diversion channel) and Cishan River discharge data were used as secondary parameters. Using the aforementioned nonlinear system, a predictive turbidity model was built, calibrated, and verified.

GMDH and SGMDH calibrated result comparison

Selection of best algorithm

In the early stages of modeling, the GMDH and SGMDH algorithms were subjected to a trial-and-error procedure. This was intended to select the best algorithm and, finally, to obtain the optimum self-organizing nonlinear system for turbidity forecasting. The best performance results were analyzed by comparing the RMSE and CC given by different data sets and variable combinations. We used historical data from 2000 to 2008, as presented in Table 1. The SGMDH model gave better results in 2000, 2001, 2007, and 2008. The performance in the other years substantiates the assertion that the GMDH model generates better results, and so, this became the preferred model. The algorithm for all hierarchical regression parameters is shown in Table 2. The model was built over four levels, and the variable combinations differed between each level. As can be seen from the table, GMDH remains the best algorithm for computing the average RMSE over an 8-year period. The turbidity data from early 2004 displayed some abnormalities, which led to increased modeling errors. Table 1 presents the modeling results for turbidity data following these abnormal readings; these were not included in the averaging procedure. Eventually, the GMDH algorithm was selected as the most appropriate algorithm for this research.

$$\begin{aligned} Z_{9}^{1} &= \, 16.62866 + 0.5386Q(t - 1) - 0.00147R(t - 1) + 0.31608Q(t - 1)^{2} - 0.00088R(t - 1)^{2} + 0.002Q(t - 1)R(t - 1) \hfill \\ Z_{10}^{1} &= \, 3.60373 + 0.92624T(t - 4) - 0.00036T(t - 3) + 0.50314T(t - 4)^{2} + 0.00275T(t - 3)^{2} - 0.00903T(t - 4)T(t - 3) \hfill \\ Z_{5}^{1} &= \, 0.29692Q(t - 1) + 1.04566Q(t - 1)^{2} + 0.00148T(t - 4)^{2} + 0.0117Q(t - 1)T(t - 4) \hfill \\ Z_{8}^{1} &= \, 24.90101 + 0.08174Q(t - 1) - 0.00022T(t - 1) + 0.42458Q(t - 1)^{2} - 0.0026T(t - 1)^{2} + 0.00479Q(t - 1)T(t - 1) \hfill \\ Z_{2}^{2} &= \, - 4.5464 + 1.64904(Z_{9}^{1} ) - 0.0072(Z_{10}^{1} ) - 0.8618(Z_{9}^{1} )^{2} + 0.00757(Z_{10}^{1} )^{2} + 0.0028(Z_{9}^{1} )(Z_{10}^{1} ) \hfill \\ Z_{3}^{2} &= \, 6.8366 + 1.20849(Z_{9}^{1} ) + 0.0015(Z_{5}^{1} ) - 0.78898(Z_{9}^{1} )^{2} + 0.01028(Z_{5}^{1} )^{2} - 0.00896(Z_{9}^{1} )(Z_{5}^{1} ) \hfill \\ Z_{4}^{2} &= \, 20.20312 + 0.22685(Z_{8}^{1} ) + 0.0034(Z_{10}^{1} ) - 0.22952(Z_{8}^{1} )^{2} + 0.00681(Z_{10}^{1} )^{2} - 0.00292(Z_{8}^{1} )(Z_{10}^{1} ) \hfill \\ Z_{4}^{3} &= \, - 4.75467 + 2.95573(Z_{4}^{2} ) - 0.0161(Z_{3}^{2} ) - 1.83673(Z_{4}^{2} )^{2} + 0.00561(Z_{3}^{2} )^{2} + 0.01(Z_{4}^{2} )(Z_{3}^{2} ) \hfill \\ Z_{2}^{3} &= \, 20.80679 + 1.7062(Z_{2}^{2} ) - 0.00304(Z_{3}^{2} ) - 1.54077(Z_{2}^{2} )^{2} + 0.01046(Z_{3}^{2} )^{2} - 0.00323(Z_{2}^{2} )(Z_{3}^{2} ) \hfill \\ Z_{1}^{4} &= \, 16.08485 - 1.98537(Z_{2}^{3} ) + 0.03366(Z_{4}^{3} ) + 2.35709(Z_{2}^{3} )^{2} + 0.0026(Z_{4}^{3} )^{2} - 0.0336(Z_{2}^{3} )(Z_{4}^{3} )]. \hfill \\ \end{aligned}$$
(8)
Table 1 Comparison of evaluation indicators of GMDH and SGMDH forecast efficiency
Full size table
Table 2 Regression parameters of all segments by GMDH method
Full size table

Choices of modeling data length and variable combinations

The modeling data length and variable combinations were obtained through a trial-and-error procedure, with a series of combinations of input variables. To develop the model, a sequential data length of 20, 30, 40, 50, 60, and 70 (days) was first introduced (taking into consideration simultaneous data integrity under no residual conditions). The optimum modeling data length differed annually, as can be determined from Table 3 by comparing the aforementioned assessment indicators between the trial-and-error procedures. The optimum data length is 70 in most cases, although it is 60 in 2003 and 2008, and 40 in 2006. According to the analysis results, a modeling data length of 70 is most appropriate for turbidity forecasting. Table 4 shows the results for the optimum modeling data lengths and variable combinations.

Table 3 Calibration RMSE results (NTU) of the best annual forecast model given by trial-and-error
Full size table
Table 4 The best annual input variables
Full size table

Turbidity forecasting

Permissible errors

We adopted the safety concepts applied in general engineering construction projects, allowing a maximum error range of only 10 %. The Taiwan Water Corporation is able to treat water with a turbidity of up to 500 NTU. As such, 50 NTU (10 % of 500 NTU) was chosen as the index of turbidity prediction accuracy. According to standard normal distribution and confidence interval calculations, the results for each year were between 51–66 NTU. An error of only 50 NTU is more restrictive, and was, thus, used as the study threshold.

Verification and analysis of forecast results

Errors between the forecast and actual observations were verified using the best yearly forecast models. Figure 4 indicates that almost all errors were within the 50 NTU threshold. The GMDH turbidity prediction model could forecast levels for up to 10 days, after which the prediction became too uncertain to be trusted for modeling data lengths; so, only 20–70 days were selected.

Fig. 4
figure 4

Predicted errors between observation and forecast values at the Chiahsien Weir

Full size image

Best forecast model

The best yearly forecast model could be utilized for the overall turbidity forecasting of other years (e.g., the next occurrence of the same type of storm event). Table 5 presents the RMSE range, revealing that the RMSE in 2006 was comparatively small. Thus, the 2006 model was used to forecast water turbidity in 2007. This gave an RMSE value of 93.137 NTU, a slightly higher error. However, when the 2006 model was used to predict turbidity for other years, the results were generally within the required confidence interval (Fig. 5). If the predicted values were beyond the error range, a recursive algorithm could be introduced to reduce the prediction error. The 2006 turbidity prediction model was selected as the best predictive model because of its ability to predict turbidity within the acceptable error range and required confidence interval.

Table 5 Comparison of RMSE (NTU) value of annual forecast
Full size table
Fig. 5
figure 5

Predicted errors in the forecasted annual turbidity values using the 2006 model

Full size image

Recursive/sequential turbidity forecast model

The recursive/sequential GMDH algorithm incorporates temporal variability once the variance between the predicted and newly observed turbidity exceeds an acceptable range at a certain time. This newly observed value is then added to the model, with previous data being deleted to maintain the same data length. The updated forecasting model then retains its accuracy for later turbidity forecasts. If the updated forecast model does not produce valid output, the steps for adding newly observed values are repeated to enable the system to auto-adjust. Using these procedures, the actual turbidity trend can be observed over any given time period.

In this example, the 2002 model was used to predict the turbidity in 2003, as shown at the top of Fig. 6. Data from the initial 70 days were used to begin model construction, followed by 10-day predictions. However, the results for day 71 already exhibited a large error. Using recursive model calculations, the predicted value for day 71 was discarded, and instead, the measured turbidity value was included. Thus, the original 1st day datum was discarded, the data set was kept at 70 days, and the model was rebuilt to continue 10-day forecast predictions. As shown in the middle of Fig. 6, the predicted values recovered their original accuracy. However, 11 days after the prediction model was rebuilt, the turbidity prediction error for day 81 was excessively large (beyond the acceptable threshold). Thus, GMDH recursive computing was again used to reduce the error. The measured turbidity datum for day 82 was then included for analysis, and its forecast value was discarded. Meanwhile, the original data for the first 12 days were discarded, and the remaining 70 days’ data set was utilized for model reconstruction. Again, a recursive structure was applied. As illustrated in the bottom part of Fig. 6, the accuracy of the predicted values was maintained. In principle, using the 10-day prediction as a guide, when the prediction error was within the acceptable range, the forecasts could continue. Whenever an updated turbidity datum was added for recursive calculation, the RMSE value of the prior model decreased, meaning that the deletion of the earliest old datum is more significant than adding the updated one, i.e., no specific recursive computing procedure should be carried out in this step.

Fig. 6
figure 6

Forecasted 2003 turbidity values using the regressive 2002 model

Full size image

Conclusion

Turbidity is the most important index for public water supply. High turbidity inflow causes harassment on treatment of public water supply, even bringing the need to cut off the water supply. To avoid high turbidity water inflow, it is important to strengthen the catchment’s conservation, protect the water resources territory, and predict the inflow turbidity concentration before the treatment operation.

A local historical turbidity, rainfall, and discharge database was constructed to develop a turbidity prediction model based on the GMDH algorithm. The results from a cross-validation revealed that GMDH was more appropriate than SGMDH for this case study. The majority of predictive turbidity values were within a confidence interval of 90 % or approaching 90 %. Using the recursive GMDH algorithm, the model can be modified to generate better predictions and improve forecast accuracy. The test results indicate that this turbidity prediction model is feasible and reliable for turbidity forecasting. Even with complex environmental factors, the model remains applicable.