Skip to main content
SpringerLink
Log in

Analytical solution of a modified single item continuous production inventory model under constant deterioration, goal levels and penalties

  • Theoretical Article
  • Published:
OPSEARCH Aims and scope Submit manuscript

Abstract

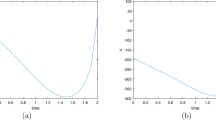
The paper tries to modify the existing single-item continuous inventory production management model with constant deterioration, goal levels and penalties under the addition of quadratic salvage term and product term in the expression of the objective function to make the model more general and meaningful. The model is solved by applying Pontryagin’s maximum principle. The solution reduces to the solution of a pair of ordinary differential equations, one for the state variable and the other one for the co-state variable. The latter equation is solved by a change of variables, where the function expressing the salvage term takes part directly. This makes the inclusion of salvage term indispensable in solving such inventory control problems. Once the co-state variable is obtained, it is used to give optimal control. Finally, using this expression of optimal control, the optimal inventory level is obtained by solving the corresponding state equation. Now the solutions of optimal control and also of the inventory are obtained under a special choice of parameters with constant, linear and quadratic demands separately. In each case, the graphical solution is shown separately, and its interpretation is given accordingly. Lastly, a proper sensitivity analysis of the model is also carried out.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Data availability

The data which are used for numerical verification of the proposed model, will be provided as per requirement.

References

  1. Harris, F. W.: How many parts to make at once. Operations Research. Vol. 38, No. 6 (Nov. Dec., 1990), pp. 947–950. Reprinted from Factory, The Magazine of Management, Volume 10, Number 2. (1913)

  2. Taft, E.W.: Formulas for exact and approximate evaluation–handling cost of jigs and interest charges of product manufactured included. The Iron Age 101(5), 1410–1412 (1918)

    Google Scholar 

  3. Nahmias, S.: Perishable inventory theory: A review. Oper. Res. 30(4), 680–708 (1982)

    Article  MathSciNet  CAS  PubMed  Google Scholar 

  4. Raafat, F.: Survey of literature on continuously deteriorating inventory models. J Oper Res Soc 42, 27–37 (1991)

    Article  Google Scholar 

  5. Goyal, S.K., Giri, B.C.: Recent trends in modeling of deteriorating inventory. Eur. J. Oper. Res. 134(1), 1–16 (2001)

    Article  MathSciNet  Google Scholar 

  6. Nestorenko, T., Morkunas, M., Peliova, J., Volkov, A., Balezentis, T., Streimkiene, D.: A new model for determining the EOQ under changing price parameters and reordering time. Symmetry 12(9), 1512 (2020)

    Article  ADS  Google Scholar 

  7. Alfares, H.K., Ghaithan, A.M.: EOQ and EPQ production-inventory models with variable holding cost: state-of-the-art review. Arab. J. Sci. Eng. 44, 1737–1755 (2019)

    Article  Google Scholar 

  8. Thinakaran, N., Jayaprakas, J., Elanchezhian, C.: Survey on inventory model of EOQ & EPQ with partial backorder problems. Mater Today: Proc 16, 629–635 (2019)

    Google Scholar 

  9. Tsao, Y.C., Putri, R.P.F.R., Zhang, C., Linh, V.T.: Optimal pricing and ordering policies for perishable products under advance-cash-credit payment scheme. J Ind Eng Int 15, 131–146 (2019)

    Article  Google Scholar 

  10. Utama, D. M., Santoso, I., Hendrawan, Y., & Dania, W. A. P.: Integrated procurement-production inventory model in supply chain: A systematic review. Operations Research Perspectives, 100221. (2022)

  11. Chow, G.C.: Analysis and control of dynamic economic systems. John Wiley & Sons, New York (1975)

    Google Scholar 

  12. Aronna. M.S.: “On the pontryagin maximum principle - 15 th international young researchers workshop on geometry, mechanics and control.” Escola de Matemática Aplicada, Fundação Getúlio Vargas (FGV EMAp) Rio de Janeiro, Brazil. (2020)

  13. Ignaciuk, P.: Discrete inventory control in systems with perishable goods–a time-delay system perspective. IET Control Theory Appl. 8(1), 11–21 (2014)

    Article  MathSciNet  Google Scholar 

  14. Salama, Y.: Optimal control of a simple manufacturing system with restarting costs. Oper. Res. Lett. 26(1), 9–16 (2000)

    Article  MathSciNet  Google Scholar 

  15. Riddalls, C.E., Bennett, S.: The optimal control of batched production and its effect on demand amplification. Int. J. Prod. Econ. 72(2), 159–168 (2001)

    Article  Google Scholar 

  16. Zhang, Q., Yin, G.G., Boukas, E.K.: Optimal control of a marketing-production system. IEEE Trans. Autom. Control 46(3), 416–427 (2001)

    Article  MathSciNet  Google Scholar 

  17. Khmelnitsky, E., Gerchak, Y.: Optimal control approach to production systems with inventory-level-dependent demand. IEEE Trans. Autom. Control 47(2), 289–292 (2002)

    Article  MathSciNet  Google Scholar 

  18. Bounkhel, M., Tadj, L.: Optimal control of deteriorating production inventory systems. APPS 7, 30–45 (2005)

    MathSciNet  Google Scholar 

  19. Tadj, L., Messaoud, B.: Optimal control of production inventory systems with deteriorating items and dynamic costs. Appl Math E-Notes 8, 194–202 (2008)

    MathSciNet  Google Scholar 

  20. El-Gohary, A., Tadj, L., Al-Rasheedi, A.F.: Using optimal control to adjust the production rate of a deteriorating inventory system. J Taibah Univ Sci 2(1), 69–77 (2009)

    Article  Google Scholar 

  21. Baten, M.A., Kamil, A.A.: An optimal control approach to inventory-production systems with Weibull distributed deterioration. J. Math. Stat. 5(3), 206 (2009)

    Article  MathSciNet  Google Scholar 

  22. Chaudhary, K., Singh, Y., Jha, P.C.: Optimal control policy of a production and inventory system for multi-product in segmented market. Ratio Math 25(1), 29–46 (2013)

    Google Scholar 

  23. Zaher, H., Zaki, T.T.: Optimal control theory to solve production inventory system in supply chain management. J Math Res 6(4), 109 (2014)

    Article  Google Scholar 

  24. Bhattacharya, D.K.: On multi-item inventory. Eur. J. Oper. Res. 162(3), 786–791 (2005)

    Article  MathSciNet  Google Scholar 

  25. El-Gohary, A., Elsayed, A.: Optimal control of a multi-item inventory model. Int Math Forum 27(3), 1295–1312 (2008)

    MathSciNet  Google Scholar 

  26. Wang, Y., & Xu, L.: Dynamics and control on a discrete multi-inventory system. Journal of Control Science and Engineering, 2019, https://doi.org/10.1155/2019/6926342.

  27. Sivashankari, C.K., Panayappan, S.: A production inventory model for deteriorating items with growth of demand and shortages. Int J Ope Res 24(4), 441–460 (2015)

    Article  MathSciNet  Google Scholar 

  28. Sivashankari, C.K.: Production inventory model with deteriorating items with constant, linear and quadratic holding cost-a comparative study. Int J Oper Res 27(4), 589–609 (2016)

    Article  MathSciNet  Google Scholar 

  29. Majumder, P., Bera, U.K., Maiti, M.: An EPQ model of deteriorating substitute items under trade credit policy. Int J Ope Res 34(2), 161–212 (2019)

    Article  MathSciNet  Google Scholar 

  30. Moghadam, M.R.S., Kamalabadi, I.N., Karbasian, B.: Joint pricing and inventory control modelling for obsolescent products: a case study of the telecom industry. Int J Appl Dec Sci 12(4), 375–401 (2019)

    Google Scholar 

  31. Singhal, S., Singh, S.R.: Supply chain system for time and quality dependent decaying items with multiple market demand and volume flexibility. Int J Oper Res 31(2), 245–261 (2018)

    Article  MathSciNet  Google Scholar 

  32. Dari, S., Sani, B.: An EPQ model for delayed deteriorating items with quadratic demand and linear holding cost. Opsearch 57, 46–72 (2020)

    Article  MathSciNet  Google Scholar 

  33. Malumfashi, M. L., Ismail, M. T., Rahman, A., Sani, D., & Ali, M. K. M. (2021). An EPQ model for delayed deteriorating items with variable production rate, two-phase demand rates and shortages. In Modelling, Simulation and Applications of Complex Systems: CoSMoS 2019, Penang, Malaysia, April 8–11, 2019 (pp. 381–403). Springer Singapore.

  34. Rout, C., Kumar, R.S., Chakraborty, D., Goswami, A.: An EPQ model for deteriorating items with imperfect production, inspection errors, rework and shortages: a type-2 fuzzy approach. Opsearch 56, 657–688 (2019)

    Article  MathSciNet  Google Scholar 

  35. Rahaman, M., Mondal, S.P., Alam, S., De, S.K., Ahmadian, A.: Study of a fuzzy production inventory model with deterioration under marxian principle. Int. J. Fuzzy Syst. 24(4), 2092–2106 (2022)

    Article  Google Scholar 

  36. Rahaman, M., Mondal, S. P., Alam, S. (2021). Artificial neural network for solving the inventory control problem in fuzzy environments. In Artificial Neural Network Applications in Business and Engineering (pp. 126–143). IGI Global.

Download references

Acknowledgements

The authors express their sincere thanks to the editor and the anonymous reviewers for their valuable and constructive comments and suggestions leading to a significant improvement of the manuscript.

Funding

None.

Author information

Authors and Affiliations

  1. Department of Basic Science & Humanities, Narula Institute of Technology, Kolkata, West Bengal, 700109, India

    Debopriya Dey

  2. Department of Mathematics, National Institute of Technology, Durgapur, West Bengal, 713209, India

    Debopriya Dey & Samarjit Kar

  3. Department of Pure Mathematics, University of Calcutta, Kolkata, West Bengal, India

    Dilip Kumar Bhattacharya

  4. Department of Graphical Systems, Vilnius Gediminas Technical University, Vilnius, Lithuania

    Samarjit Kar

Authors
  1. Debopriya Dey
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Samarjit Kar
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dilip Kumar Bhattacharya
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

DD Conceptualization, Methodology, Model Analysis and Writing original draft. SK Investigation, Formal Analysis, Writing and Supervision. DKB Model validation, Review and Editing, Over all Supervision. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Samarjit Kar.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests regarding the publication of this paper or personal relationships that could have appeared to influence the work reported in this paper.

Ethics approval and consent to participate

This article does not contain any studies with human participants or animals performed by any of the authors.

Consent for publication

Not Applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dey, D., Kar, S. & Bhattacharya, D.K. Analytical solution of a modified single item continuous production inventory model under constant deterioration, goal levels and penalties. OPSEARCH 61, 399–420 (2024). https://doi.org/10.1007/s12597-023-00700-w

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12597-023-00700-w

Keywords

Search

Navigation