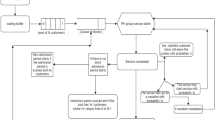
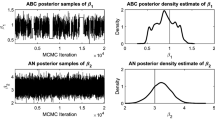
Appendix
1.1 Derivation of joint and marginal posterior distributions of m, \(\rho _1\) and \(\rho _2\) under different prior
Beta Prior
$$\begin{aligned}&\pi _1(\rho _1,\rho _2,m|x) = \frac{\prod _{i=1}^{m}p(x_i)\pi _1(\rho _1) \cdot \prod _{i=m+1}^{n}p(x_i)\pi _1(\rho _2)}{ \sum _{m=1}^{n-1}\int _{0}^{1} \int _{0}^{1} \left[ \prod _{i=1}^{m}p(x_i)\pi _1(\rho _1) \cdot \prod _{i=m+1}^{n}p(x_i)\pi _1(\rho _2) \right] d{\rho _1} d{\rho _2} } \\&\quad = \frac{ \frac{ \rho _1^{S_{m}+a_1-1} (1-\rho _1)^{m+b_1-1}}{{\mathscr {B}}(a_1, b_1 )} \cdot \frac{ \rho _2^{S_{n-m}+a_2-1} (1-\rho _2)^{n-m+b_2-1} }{{\mathscr {B}}(a_2, b_2 )} }{ \sum _{m=1}^{n-1} \int _{\rho _1} \int _{\rho _2} \frac{ \rho _1^{S_{m}+a_1-1} (1-\rho _1)^{m+b_1-1}}{{\mathscr {B}}(a_1, b_1 )} \cdot \frac{ \rho _2^{S_{n-m}+a_2-1} (1-\rho _2)^{n-m+b_2-1} }{{\mathscr {B}}(a_2, b_2 )} d\rho _1 d\rho _2 } \\&\quad = \frac{ \rho _1^{S_{m}+a_1-1} (1-\rho _1)^{m+b_1-1} \cdot \rho _2^{S_{n-m}+a_2-1} (1-\rho _2)^{n-m+b_2-1} }{ \sum _{m=1}^{n-1} \int _{0}^{1} \rho _1^{S_{m}+a_1-1} (1-\rho _1)^{m+b_1-1} d\rho _1 \cdot \int _{0}^{1}\rho _2^{S_{n-m}+a_2-1} (1-\rho _2)^{n-m+b_2-1} d\rho _2 } \\&\quad = \frac{ \rho _1^{S_{m}+a_1-1} (1-\rho _1)^{m+b_1-1} \cdot \rho _2^{S_{n-m}+a_2-1} (1-\rho _2)^{n-m+b_2-1} }{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 ) } \end{aligned}$$
$$\begin{aligned} \pi _1(m|x)&= \int _{0}^{1} \int _{0}^{1} \pi _1(\rho _1,\rho _2,m|x) d\rho _1 d\rho _2 \\&= \frac{\int _{0}^{1} \rho _1^{S_{m}+a_1-1} (1-\rho _1)^{m+b_1-1} d\rho _1 \cdot \int _{0}^{1}\rho _2^{S_{n-m}+a_2-1} (1-\rho _2)^{n-m+b_2-1}d\rho _2}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \\&= \frac{ {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \\ \pi _1(\rho _1|x)&= \sum _{m=1}^{n-1} \int _{0}^{1} \pi _1(\rho _1,\rho _2,m|x)d\rho _2 \\&=\frac{\sum _{m=1}^{n-1} \left( \int _{0}^{1} \rho _2^{S_{n-m}+a_2-1} (1-\rho _2)^{n-m+b_2-1} d\rho _2 \right) \cdot \rho _1^{S_{m}+a_1-1} (1-\rho _1)^{m+b_1-1} }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \\&= \frac{ {\sum _{m=1}^{n-1} {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \rho _1^{S_{m}+a_1-1} (1-\rho _1)^{m+b_1-1} }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \\ \pi _1(\rho _2|x)&= \sum _{m=1}^{n-1} \int _{0}^{1} \pi _1(\rho _1,\rho _2,m|x)d\rho _1 \\&=\frac{\sum _{m=1}^{n-1} \left( \int _{0}^{1} \rho _1^{S_{m}+a_1-1} (1-\rho _1)^{m+b_1-1} d\rho _1\right) \cdot \rho _2^{S_{n-m}+a_2-1} (1-\rho _2)^{n-m+b_2-1}}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \\&=\frac{\sum _{m=1}^{n-1}{\mathscr {B}}( S_{m}+a_1, m+b_1 ) \rho _1^{S_{n-m}+a_2-1} (1-\rho _1)^{n-m+b_2-1} }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \end{aligned}$$
Truncated Uniform Prior
$$\begin{aligned} \pi _2(\rho _1,\rho _2,m|x)&= \frac{\prod _{i=1}^{m}p(x_i)\pi _2(\rho _1) \cdot \prod _{i=m+1}^{n}p(x_i)\pi _2(\rho _2)}{\sum _{m=1}^{n-1}\int _{c_1}^{d_1} \int _{c_2}^{d_2} \left[ \prod _{i=1}^{m}p(x_i)\pi _2(\rho _1)\cdot \prod _{i=m+1}^{n}p(x_i)\pi _2(\rho _2) \right] d{\rho _1} d{\rho _2}} \\&= \frac{ \rho _1^{S_{m}} (1-\rho _1)^{m} \cdot \rho _2^{S_{n-m}} (1-\rho _2)^{n-m} }{ \sum _{m=1}^{n-1} \int _{0}^{1} \rho _1^{S_{m}} (1-\rho _1)^{m} d\rho _1 \cdot \int _{0}^{1} \rho _2^{S_{n-m}} (1-\rho _2)^{n-m} d\rho _2 } \\&= \frac{\rho _1^{S_{m}} (1-\rho _1)^{m} ~\rho _2^{S_{n-m}} (1-\rho _2)^{n-m}}{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 )} \\ \pi _2(m|x)&= \int _{c_1}^{d_1} \int _{c_2}^{d_2} \pi _2(\rho _1,\rho _2,m|x) d\rho _1 d\rho _2 \\&= \frac{ \int _{c_1}^{d_1} \rho _1^{S_{m}} (1-\rho _1)^{m}d\rho _1 \cdot \int _{c_2}^{d_2}\rho _2^{S_{n-m}} (1-\rho _2)^{n-m} d\rho _2 }{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 )} \\&= \frac{ {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 ) }{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 ) } \\ \pi _2(\rho _1|x)&= \sum _{m=1}^{n-1} \int _{c_2}^{d_2} \pi _2(\rho _1,\rho _2,m|x)d\rho _2 \\&= \frac{\sum _{m=1}^{n-1} \left( \int _{c_2}^{d_2} \rho _2^{S_{n-m}} (1-\rho _2)^{n-m} d\rho _2\right) \cdot \rho _1^{S_{m}} (1-\rho _1)^{m} }{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 ) } \\&= \frac{ { {\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 ) }} \rho _1^{S_{m}} (1-\rho _1)^{m} }{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 ) } \\ \pi _2(\rho _2|x)&= \sum _{m=1}^{n-1} \int _{c_1}^{d_1} \pi _2(\rho _1,\rho _2,m|x)d\rho _1 \\&= \frac{\sum _{m=1}^{n-1}\left( \int _{c_1}^{d_1} \rho _1^{S_{m}} (1-\rho _1)^{m}d\rho _1 \right) \cdot \rho _2^{S_{n-m}} (1-\rho _2)^{n-m}}{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 ) } \\&= \frac{ {\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) } \rho _2^{S_{n-m}} (1-\rho _2)^{n-m} }{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 ) } \end{aligned}$$
Quasi Prior
$$\begin{aligned} \pi _3(\rho _1,\rho _2,m|x)&= \frac{\prod _{i=1}^{m}p(x_i)\pi _3(\rho _1)\cdot \prod _{i=m+1}^{n}p(x_i)\pi _3(\rho _2)}{\sum _{m=1}^{n-1}\int _{\rho _1} \int _{\rho _2} \left[ \prod _{i=1}^{m}p(x_i)\pi _3(\rho _1) \cdot \prod _{i=m+1}^{n}p(x_i)\pi _3(\rho _2) \right] d{\rho _1} d{\rho _2}} \\&= \frac{ \rho _1^{S_{m}-\alpha _1} (1-\rho _1)^{m} \rho _2^{S_{n-m}-\alpha _2} (1-\rho _2)^{n-m} }{ \sum _{m=1}^{n-1} \int _{01}^{1}\rho _1^{S_{m}-\alpha _1} (1-\rho _1)^{m} d\rho _1 \cdot \int _{0}^{1}\rho _2^{S_{n-m}-\alpha _2} (1-\rho _2)^{n-m}d\rho _2 } \\&= \frac{ \rho _1^{S_{m}-\alpha _1} (1-\rho _1)^{m} \rho _2^{S_{n-m}-\alpha _2} (1-\rho _2)^{n-m} }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )} \\ \pi _3(m|x)&= \int _{0}^{1} \int _{0}^{1} \pi _3(\rho _1,\rho _2,m|x) d\rho _1 d\rho _2 \\&=\frac{\int _{0}^{1} \rho _1^{S_{m}-\alpha _1} (1-\rho _1)^{m} d\rho _1 \cdot \int _{0}^{1}\rho _2^{S_{n-m}-\alpha _2} (1-\rho _2)^{n-m} d\rho _2}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 ) } \\&= \frac{ {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 ) }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 ) } \\ \pi _3(\rho _1|x)&= \sum _{m=1}^{n-1} \int _{0}^{1} \pi _3(\rho _1,\rho _2,m|x)d\rho _2 \\&= \frac{\sum _{m=1}^{n-1} \left( \int _{0}^{1} \rho _2^{S_{n-m}-\alpha _2} (1-\rho _2)^{n-m} d\rho _2\right) \cdot \rho _1^{S_{m}-\alpha _1} (1-\rho _1)^{m}}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )} \\&= \frac{ {\sum _{m=1}^{n-1} {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 ) } \rho _1^{S_{m}-\alpha _1} (1-\rho _1)^{m} }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )} \\ \pi _3(\rho _2|x)&= \sum _{m=1}^{n-1} \int _{0}^{1} \pi _3(\rho _1,\rho _2,m|x)d\rho _1 \\&=\frac{ \sum _{m=1}^{n-1} \left( \int _{0}^{1} \rho _1^{S_{m}-\alpha _1} (1-\rho _1)^{m}d\rho _1\right) \cdot \rho _2^{S_{n-m}-\alpha _2} (1-\rho _2)^{n-m}}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )} \\&=\frac{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 )\rho _2^{S_{n-m}-\alpha _2} (1-\rho _2)^{n-m} }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 ) } \end{aligned}$$
Jeffreys Prior
$$\begin{aligned} \pi _4(\rho _1,\rho _2,m|x)&= \frac{\prod _{i=1}^{m}p(x_i)\pi _4(\rho _1)\cdot \prod _{i=m+1}^{n}p(x_i)\pi _4(\rho _2)}{\sum _{m=1}^{n-1}\int _{\rho _1} \int _{\rho _2} \left[ \prod _{i=1}^{m}p(x_i)\pi _4(\rho _1) \cdot \prod _{i=m+1}^{n}p(x_i)\pi _4(\rho _2)\right] d{\rho _1} d{\rho _2}} \\&=\frac{\rho _1^{S_{m}+1/2-1} (1-\rho _1)^{m -1} \rho _2^{S_{n-m}+1/2-1} (1-\rho _2)^{n-m -1} }{ \sum _{m=1}^{n-1} \int _{0}^{1}\rho _1^{S_{m}+1/2-1} (1-\rho _1)^{m -1}d\rho _1 \cdot \int _{0}^{1}\rho _2^{S_{n-m}+1/2-1} (1-\rho _2)^{n-m -1}d\rho _2 } \\&= \frac{ \rho _1^{S_{m}+1/2-1} (1-\rho _1)^{m -1} \rho _2^{S_{n-m}+1/2-1} (1-\rho _2)^{n-m -1}}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \\ \pi _4(m|x)&= \int _{0}^{1} \int _{0}^{1} \pi _4(\rho _1,\rho _2,m|x) d\rho _1 d\rho _2 \\&= \frac{\int _{0}^{1} \rho _1^{S_{m}+1/2-1} (1-\rho _1)^{m -1} d\rho _1 \cdot \int _{0}^{1}\rho _2^{S_{n-m}+1/2-1} (1-\rho _2)^{n-m -1} d\rho _2 }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \\&= \frac{ {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \\ \pi _4(\rho _1|x)&= \sum _{m=1}^{n-1} \int _{0}^{1} \pi _4(\rho _1,\rho _2,m|x)d\rho _2 \\&= \frac{\sum _{m=1}^{n-1} \left( \int _{0}^{1} \rho _2^{S_{n-m}+1/2-1} (1-\rho _2)^{n-m -1} d\rho _2 \right) \cdot \rho _1^{S_{m}+1/2-1} (1-\rho _1)^{m -1}}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \\&= \frac{ {\sum _{m=1}^{n-1} {\mathscr {B}}( S_{n-m}+1/2, n-m )} \rho _1^{S_{m}+1/2-1} (1-\rho _1)^{m -1} }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \\ \pi _4(\rho _2|x)&= \sum _{m=1}^{n-1} \int _{0}^{1} \pi _4(\rho _1,\rho _2,m|x)d\rho _1 \\&= \frac{\sum _{m=1}^{n-1} \left( \int _{0}^{1} \rho _1^{S_{m}+1/2-1} (1-\rho _1)^{m -1} d\rho _1 \right) \cdot \rho _2^{S_{n-m}+1/2-1} (1-\rho _2)^{n-m -1}}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \\&=\frac{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) \rho _2^{S_{n-m}+1/2-1} (1-\rho _2)^{n-m-1} }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \end{aligned}$$
1.2 Derivation of Bayesian estimators of m, \(\rho _1\) and \(\rho _2\) under different loss functions
1.3 Squared error loss function (SELF)
Beta Prior
$$\begin{aligned} {\widehat{m}}^B_{BS}&= E(m|x) = \sum _{m=1}^{n-1} m~\pi _1(m|x)\\&= \frac{ \sum _{m=1}^{n-1} m ~{\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \\ {\widehat{\rho }}^B_{1BS}&= E(\rho _1|x) = \int _{0}^{1} \rho _1~\pi _1(\rho _1|x) d\rho _1 \\&= \frac{ {\sum _{m=1}^{n-1} {\mathscr {B}}(S_{n-m}+a_2, n-m+b_2)} \cdot \int _{0}^{1} \rho _1^{S_{m}+a_1} (1-\rho _1)^{m+b_1-1} d\rho _1 }{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \\&= \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1+1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \\ {\widehat{\rho }}^B_{2BS}&= E(\rho _2|x) = \int _{0}^{1} \rho _2~\pi _1(\rho _2|x) d\rho _2\\&= \frac{ {\sum _{m=1}^{n-1} {\mathscr {B}}(S_{m}+a_1, m+b_1)} \cdot \int _{0}^{1} \rho _2^{S_{n-m}+a_2} (1-\rho _2)^{n-m+b_2-1} d\rho _2 }{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \\&= \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2+1, n-m+b_2 )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \end{aligned}$$
Truncated Uniform Prior
$$\begin{aligned} {\widehat{m}}^T_{BS}&= E(m|x) = \sum _{m=1}^{n-1} m~\pi _2(m|x) \\&= \frac{ \sum _{m=1}^{n-1} m ~{\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 )}{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 )} \\ {\widehat{\rho }}^T_{1BS}&= E(\rho _1|x) = \int _{c_1}^{d_1} \rho _1~\pi _2(\rho _1|x) d\rho _1 \\&= \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}_{(c_2, d_2)}(S_{n-m} +1, n-m+1) \cdot \int _{c_1}^{d_1} \rho _1^{S_{m} +1} (1-\rho _1)^{m} d\rho _1 }{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} (S_{m}+1, m+1) {\mathscr {B}}_(c_2, d_2) ( S_{n-m} +1, n-m+1 ) } \\&= \frac{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +2, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 )}{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 ) } \\ {\widehat{\rho }}^T_{2BS}&= E(\rho _2|x) = \int _{c_2}^{d_2} \rho _2~\pi _2(\rho _2|x) d\rho _2 \\&= \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} (S_{m}+1, m+1) \cdot \int _{c_2}^{d_2} \rho _2^{S_{n-m}+1} (1-\rho _2)^{n-m} d\rho _2 }{ \sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 ) } \\&= \frac{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +2, n-m+1 )}{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 ) } \end{aligned}$$
Quasi Prior
$$\begin{aligned} {\widehat{m}}^Q_{BS}&= E(m|x) = \sum _{m=1}^{n-1} m~\pi _3(m|x) \\&= \frac{ \sum _{m=1}^{n-1} m ~{\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 ) } \\ {\widehat{\rho }}^Q_{1BS}&= E(\rho _1|x) = \int _{0}^{1} \rho _1~\pi _3(\rho _1|x) d\rho _1 \\&= \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}(S_{n-m}-\alpha _2+1, n-m+1) \cdot \int _{0}^{1} \rho _1^{S_{m}-\alpha _1 +1} (1-\rho _1)^{m} d\rho _1 }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )} \\&= \frac{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+2, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )} \\ {\widehat{\rho }}^Q_{2BS}&= E(\rho _2|x) = \int _{0}^{1} \rho _2~\pi _3(\rho _2|x) d\rho _2 \\&= \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}(S_{m}-\alpha _1+1, m+1) \cdot \int _{0}^{1} \rho _2^{S_{n-m}-\alpha _2+1} (1-\rho _2)^{n-m} d\rho _2 }{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 ) } \\&= \frac{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+2, n-m+1 )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )} \end{aligned}$$
Jeffreys Prior
$$\begin{aligned} {\widehat{m}}^J_{BS}&= E(m|x) = \sum _{m=1}^{n-1} m~\pi _1(m|x) \\&= \frac{ \sum _{m=1}^{n-1} m ~{\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \\ {\widehat{\rho }}^J_{1BS}&= E(\rho _1|x) = \int _{0}^{1} \rho _1~\pi _1(\rho _1|x) d\rho _1 \\&= \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}(S_{n-m}+1/2, n-m) \cdot \int _{0}^{1} \rho _1^{S_{m}+3/2-1} (1-\rho _1)^{m -1} d\rho _1 }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \\&= \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+3/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \\ {\widehat{\rho }}^J_{2BS}&= E(\rho _2|x) = \int _{0}^{1} \rho _2~\pi _1(\rho _2|x) d\rho _2 \\&= \frac{\sum _{m=1}^{n-1} {\mathscr {B}}(S_{m}+1/2, m) \cdot \int _{0}^{1} \rho _2^{S_{n-m}+3/2-1} (1-\rho _2)^{n-m-1} d\rho _2}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \\&= \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+3/2, n-m )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \end{aligned}$$
1.4 Precautionary loss function (PLF)
Beta Prior
$$\begin{aligned} {\widehat{m}}^B_{BP}&= \left[ E(m^2|x)\right] ^{\frac{1}{2}} = \left[ \sum _{m=1}^{n-1} m^2 ~\pi _1(m|x) \right] ^{\frac{1}{2}} \\&= \left[ \frac{ \sum _{m=1}^{n-1} m^2 ~{\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \right] ^{\frac{1}{2}} \\ {\widehat{\rho }}^B_{1BP}&= \left[ E(\rho ^2_1|x)\right] ^{\frac{1}{2}} = \left[ \int _{0}^{1} \rho _1^2 ~\pi _1(\rho _1|x) d\rho _1 \right] ^{\frac{1}{2}} \\&=\left[ \frac{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 ) \cdot \int _{0}^{1} \rho _1^{S_{m}+a_1+1} (1-\rho _1)^{m+b_1-1} d\rho _1 }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \right] ^{\frac{1}{2}} \\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1+2, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \right] ^{\frac{1}{2}} \\ {\widehat{\rho }}^B_{2BP}&=\left[ E(\rho _2^2|x)\right] ^{\frac{1}{2}} = \left[ \int _{0}^{1} \rho _2^2 ~\pi _1(\rho _2|x) d\rho _2 \right] ^{\frac{1}{2}} \\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}(S_{m}+a_1, m+b_1)\cdot \int _{0}^{1} \rho _2^{S_{n-m}+a_2+1} (1-\rho _2)^{n-m+b_2-1} d\rho _2 }{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \right] ^{\frac{1}{2} } \\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2+2, n-m+b_2 )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \right] ^{\frac{1}{2}} \end{aligned}$$
Truncated Uniform Prior
$$\begin{aligned} {\widehat{m}}^T_{BP}&= \left[ E(m^2|x)\right] ^{\frac{1}{2}} = \left[ \sum _{m=1}^{n-1} m^2 ~\pi _2(m|x) \right] ^{\frac{1}{2}} \\&= \left[ \frac{ \sum _{m=1}^{n-1} m^2 ~{\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 )}{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 )} \right] ^{\frac{1}{2}} \\ {\widehat{\rho }}^T_{1BP}&= \left[ E(\rho ^2_1|x)\right] ^{\frac{1}{2}} = \left[ \int _{c_1}^{d_1} \rho _1^2 ~\pi _2(\rho _1|x) d\rho _1 \right] ^{\frac{1}{2}} \\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 )\cdot \int _{c_1}^{d_1} \rho _1^{S_{m} +2} (1-\rho _1)^{m} d\rho _1 }{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 ) } \right] ^{\frac{1}{2}} \\&= \left[ \frac{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +3, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 )}{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 ) } \right] ^{\frac{1}{2}} \\ {\widehat{\rho }}^T_{2BP}&= \left[ E(\rho ^2_2|x)\right] ^{\frac{1}{2}} =\left[ \int _{c_2}^{d_2} \rho _2^2 ~\pi _2(\rho _2|x) d\rho _2 \right] ^{\frac{1}{2}} \\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} (S_{m}+1, m+1) \cdot \int _{c_2}^{d_2} \rho _2^{S_{n-m}+2} (1-\rho _2)^{n-m} d\rho _2 }{ \sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} (S_{m}+1, m+1) {\mathscr {B}}_{(c_2, d_2)} (S_{n-m}+1, n-m+1)} \right] ^{\frac{1}{2}} \\&=\left[ \frac{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +3, n-m+1 )}{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 ) } \right] ^{\frac{1}{2}} \end{aligned}$$
Quasi Prior
$$\begin{aligned} {\widehat{m}}^Q_{BP}&= \left[ E(m^2|x)\right] ^{\frac{1}{2}} =\left[ \sum _{m=1}^{n-1} m^2 ~\pi _3(m|x) \right] ^{\frac{1}{2}} \\&=\left[ \frac{ \sum _{m=1}^{n-1} m^2 ~ {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 ) }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )} \right] ^{\frac{1}{2}} \\ {\widehat{\rho }}^Q_{1BP}&= \left[ E(\rho ^2_1|x)\right] ^{\frac{1}{2}} = \left[ \int _{0}^{1} \rho _1^2 ~\pi _3(\rho _1|x) d\rho _1 \right] ^{\frac{1}{2}} \\&= \left[ \frac{ {\sum _{m=1}^{n-1} {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 ) } \cdot \int _{0}^{1} \rho _1^{S_{m}-\alpha _1 +2} (1-\rho _1)^{m} d\rho _1 }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )} \right] ^{\frac{1}{2}} \\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+3, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )} \right] ^{\frac{1}{2}} \\ {\widehat{\rho }}^Q_{2BP}&=\left[ E(\rho _2^2|x)\right] ^{\frac{1}{2}} = \left[ \int _{0}^{1} \rho _2^2 ~\pi _3(\rho _2|x) d\rho _2 \right] ^{\frac{1}{2}} \\&=\left[ \frac{\sum _{m=1}^{n-1} {\mathscr {B}}(S_{m}-\alpha _1+1, m+1)\cdot \int _{0}^{1} \rho _2^{S_{n-m}-\alpha _2+2} (1-\rho _2)^{n-m} d\rho _2 }{ \sum _{m=1}^{n-1} {\mathscr {B}}(S_{m}-\alpha _1+1, m+1) {\mathscr {B}}(S_{n-m}-\alpha _2+1, n-m+1) }\right] ^{\frac{1}{2}} \\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+3, n-m+1 )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )} \right] ^{\frac{1}{2}} \end{aligned}$$
Jeffreys Prior
$$\begin{aligned} {\widehat{m}}^J_{BP}&= \left[ E(m^2|x)\right] ^{\frac{1}{2}} = \left[ \sum _{m=1}^{n-1} m^2 ~ \pi _4(m|x) \right] ^{\frac{1}{2}} \\&= \left[ \frac{ \sum _{m=1}^{n-1} m^2 ~{\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \right] ^{\frac{1}{2}} \\ {\widehat{\rho }}^J_{1BP}&= \left[ E(\rho ^2_1|x)\right] ^{\frac{1}{2}}= \left[ \int _{0}^{1} \rho _1^2 ~\pi _4(\rho _1|x) d\rho _1 \right] ^{\frac{1}{2}} \\&= \left[ \frac{ {\sum _{m=1}^{n-1} {\mathscr {B}}( S_{n-m}+1/2, n-m )} \cdot \int _{0}^{1} \rho _1^{S_{m}+5/2-1} (1-\rho _1)^{m -1} d\rho _1 }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \right] ^{\frac{1}{2}} \\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+5/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \right] ^{\frac{1}{2}} \\ {\widehat{\rho }}^J_{2BP}&=\left[ E(\rho ^2_1|x)\right] ^{\frac{1}{2}} =\left[ \int _{0}^{1} \rho _1^2 ~\pi _4(\rho _1|x) d\rho _1 \right] ^{\frac{1}{2}} \\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}(S_{m}+1/2, m) \cdot \int _{0}^{1} \rho _2^{S_{n-m}+5/2-1} (1-\rho _2)^{n-m-1} d\rho _2 }{ \sum _{m=1}^{n-1} {\mathscr {B}}(S_{m}+1/2, m) {\mathscr {B}}(S_{n-m}+1/2, n-m )} \right] ^{\frac{1}{2}}\\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+5/2, n-m )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \right] ^{\frac{1}{2}} \end{aligned}$$
1.5 General entropy loss function (GELF)
Beta Prior
$$\begin{aligned} {\widehat{m}}^B_{BE}&= \left[ E(m^{-\gamma }|x)\right] ^{-\frac{1}{\gamma }} = \left[ \sum _{m=1}^{n-1} m^{-\gamma } ~\pi _1(m|x) \right] ^{-\frac{1}{\gamma }} \\&= \left[ \frac{ \sum _{m=1}^{n-1} m^{-\gamma } ~{\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \right] ^{-\frac{1}{\gamma }} \\ {\widehat{\rho }}^B_{1BE}&= \left[ E(\rho _1^{-\gamma }|x)\right] ^{-\frac{1}{\gamma }} = \left[ \int _{0}^{1} \rho _1^{-\gamma } ~\pi _1(\rho _1|x) d\rho _1 \right] ^{-\frac{1}{\gamma }} \\&= \left[ \frac{ {\sum _{m=1}^{n-1} {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \cdot \int _{0}^{1} \rho _1^{S_{m}+a_1-\gamma -1} (1-\rho _1)^{m+b_1-1} d\rho _1 }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \right] ^{-\frac{1}{\gamma }} \\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1-\gamma , m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \right] ^{-\frac{1}{\gamma }} \\ {\widehat{\rho }}^B_{2BE}&=\left[ E(\rho _2^{-\gamma }|x)\right] ^{-\frac{1}{\gamma }} = \left[ \int _{0}^{1} \rho _2^{-\gamma }~\pi _1(\rho _2|x) d\rho _2 \right] ^{-\frac{1}{\gamma }} \\&= \left[ \frac{\sum _{m=1}^{n-1} {\mathscr {B}}(S_{m}+a_1, m+b_1) \cdot \int _{0}^{1} \rho _2^{S_{n-m}+a_2-\gamma -1} (1-\rho _2)^{n-m+b_2-1} d\rho _2 }{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \right] ^{-\frac{1}{\gamma }} \\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2-\gamma , n-m+b_2 )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+a_1, m+b_1 ) {\mathscr {B}}( S_{n-m}+a_2, n-m+b_2 )} \right] ^{-\frac{1}{\gamma }} \end{aligned}$$
Truncated Uniform Prior
$$\begin{aligned} {\widehat{m}}^T_{BE}&= \left[ E(m^{-\gamma }|x)\right] ^{-\frac{1}{\gamma }} = \left[ \sum _{m=1}^{n-1} m^{-\gamma } ~\pi _2(m|x) \right] ^{-\frac{1}{\gamma }} \\&= \left[ \frac{ \sum _{m=1}^{n-1} m^{-\gamma } ~{\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 )}{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 )} \right] ^{-\frac{1}{\gamma }} \\ {\widehat{\rho }}^T_{1BE}&= \left[ E(\rho _1^{-\gamma }|x)\right] ^{-\frac{1}{\gamma }} =\left[ \int _{c_1}^{d_1} \rho _1^{-\gamma } ~\pi _2(\rho _1|x) d\rho _1 \right] ^{-\frac{1}{\gamma }} \\&= \left[ \frac{ {\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 )} \cdot \int _{c_1}^{d_1} \rho _1^{S_{m} - \gamma } (1-\rho _1)^{m} d\rho _1 }{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 ) } \right] ^{-\frac{1}{\gamma }} \\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} -\gamma +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 ) }{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 )} \right] ^{-\frac{1}{\gamma }} \\ {\widehat{\rho }}^T_{2BE}&= \left[ E(\rho _2^{-\gamma }|x)\right] ^{-\frac{1}{\gamma }} = \left[ \int _{c_2}^{d_2} \rho _2^{-\gamma } ~\pi _2(\rho _2|x) d\rho _2 \right] ^{-\frac{1}{\gamma }} \\&=\left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m}+1, m+1) \cdot \int _{c_2}^{d_2} \rho _2^{S_{n-m}-\gamma } (1-\rho _2)^{n-m} d\rho _2 }{ \sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1)} \right] ^{-\frac{1}{\gamma }} \\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m}+1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} -\gamma +1, n-m+1 ) }{\sum _{m=1}^{n-1} {\mathscr {B}}_{(c_1, d_1)} ( S_{m} +1, m+1 ) {\mathscr {B}}_{(c_2, d_2)} ( S_{n-m} +1, n-m+1 )} \right] ^{-\frac{1}{\gamma }} \end{aligned}$$
Quasi Prior
$$\begin{aligned} {\widehat{m}}^Q_{BE}&= \left[ E(m^{-\gamma }|x)\right] ^{-\frac{1}{\gamma }} = \left[ \sum _{m=1}^{n-1} m^{-\gamma } ~\pi _3(m|x) \right] ^{-\frac{1}{\gamma }} \\&= \left[ \frac{ \sum _{m=1}^{n-1} m^{-\gamma } ~{\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 ) }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )} \right] ^{-\frac{1}{\gamma }} \\ {\widehat{\rho }}^Q_{1BE}&=\left[ E(\rho _1^{-\gamma }|x)\right] ^{-\frac{1}{\gamma }} = \left[ \int _{0}^{1} \rho ^{-\gamma } ~\pi _3(\rho _1|x) d\rho _1 \right] ^{-\frac{1}{\gamma }} \\&= \left[ \frac{ {\sum _{m=1}^{n-1} {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 ) } \cdot \int _{0}^{1} \rho _1^{S_{m}-\alpha _1 - \gamma } (1-\rho _1)^{m} d\rho _1 }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )} \right] ^{-\frac{1}{\gamma }} \\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1-\gamma +1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 ) }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 ) } \right] ^{-\frac{1}{\gamma }} \\ {\widehat{\rho }}^Q_{2BE}&= \left[ E(\rho _2^{-\gamma }|x)\right] ^{-\frac{1}{\gamma }} = \left[ \int _{0}^{1} \rho _2^{-\gamma } ~\pi _3(\rho _2|x) d\rho _2 \right] ^{-\frac{1}{\gamma }} \\&=\left[ \frac{\sum _{m=1}^{n-1} {\mathscr {B}}(S_{m}-\alpha _1+1, m+1) \cdot \int _{0}^{1} \rho _2^{S_{n-m}-\alpha _2-\gamma } (1-\rho _2)^{m}d\rho _2 }{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )} \right] ^{-\frac{1}{\gamma }} \\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2-\gamma +1, n-m+1 )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\alpha _1+1, m+1 ) {\mathscr {B}}( S_{n-m}-\alpha _2+1, n-m+1 )} \right] ^{-\frac{1}{\gamma }} \end{aligned}$$
Jeffreys Prior
$$\begin{aligned} {\widehat{m}}^J_{BE}&= \left[ E(m^{-\gamma }|x)\right] ^{-\frac{1}{\gamma }} = \left[ \sum _{m=1}^{n-1} m^{-\gamma } ~\pi _4(m|x) \right] ^{-\frac{1}{\gamma }} \\&= \left[ \frac{ \sum _{m=1}^{n-1} m^{-\gamma } ~{\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \right] ^{-\frac{1}{\gamma }} \\ {\widehat{\rho }}^J_{1BE}&= \left[ E(\rho _1^{-\gamma }|x)\right] ^{-\frac{1}{\gamma }} = \left[ \int _{0}^{1} \rho _1^{-\gamma } ~\pi _4(\rho _1|x) d\rho _1 \right] ^{-\frac{1}{\gamma }} \\&= \left[ \frac{ {\sum _{m=1}^{n-1} {\mathscr {B}}( S_{n-m}+1/2, n-m )} \cdot \int _{0}^{1} \rho _1^{S_{m}-\gamma +1/2-1} (1-\rho _1)^{m -1} d \rho _1}{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \right] ^{- \frac{1}{\gamma }} \\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}-\gamma +1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m ) }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \right] ^{-\frac{1}{\gamma }} \\ {\widehat{\rho }}^J_{2BE}&= \left[ E(\rho _2^{-\gamma }|x)\right] ^{-\frac{1}{\gamma }} =\left[ \int _{0}^{1} \rho _2^{-\gamma } ~\pi _4(\rho _2|x) d\rho _2 \right] ^{-\frac{1}{\gamma }} \\&= \left[ \frac{\sum _{m=1}^{n-1}{\mathscr {B}}(S_{m}+1/2, m) \cdot \int _{0}^{1} \rho _2^{S_{n-m}-\gamma +1/2-1} (1-\rho _2)^{n-m-1} d\rho _2 }{ \sum _{m=1}^{n-1}{\mathscr {B}}(S_{m}+1/2, m) {\mathscr {B}}(S_{n-m}+1/2, n-m )} \right] ^{-\frac{1}{\gamma }} \\&= \left[ \frac{ \sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}-\gamma +1/2, n-m ) }{\sum _{m=1}^{n-1} {\mathscr {B}}( S_{m}+1/2, m ) {\mathscr {B}}( S_{n-m}+1/2, n-m )} \right] ^{-\frac{1}{\gamma }} \end{aligned}$$