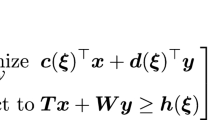Abstract
Since its introduction in the early 2000s, robust optimization with budget uncertainty has received a lot of attention. This is due to the intuitive construction of the uncertainty sets and the existence of a compact robust reformulation for (mixed-integer) linear programs. However, despite its compactness, the reformulation performs poorly when solving robust integer problems due to its weak linear relaxation. To overcome the problems arising from the weak formulation, we propose a bilinear formulation for robust binary programming, which is as strong as theoretically possible. From this bilinear formulation, we derive strong linear formulations as well as structural properties for robust binary optimization problems, which we use within a tailored branch and bound algorithm. We test our algorithm’s performance together with other approaches from the literature on a diverse set of “robustified” real-world instances from the MIPLIB 2017. Our computational study, which is the first to compare many sophisticated approaches on a broad set of instances, shows that our algorithm outperforms existing approaches by far. Furthermore, we show that the fundamental structural properties proven in this paper can be used to substantially improve the approaches from the literature. This highlights the relevance of our findings, not only for the tested algorithms, but also for future research on robust optimization. To encourage the use of our algorithms for solving robust optimization problems and our instances for benchmarking, we make all materials freely available online.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Dealing with uncertainties is inevitable when considering real-world optimization problems. A classical approach to include uncertainties into the optimization process is robust optimization, where different realizations of the uncertain parameters are modeled via an uncertainty set. A robust optimal solution remains feasible for all considered scenarios in the uncertainty set and minimizes the worst-case cost occurring under these scenarios. The concept was first introduced by Soyster [40] in the early 1970s, was later considered for combinatorial optimization problems and discrete uncertainty sets by Kouvelis and Yu [30] in the 1990s, and was analyzed in detail by Ben-Tal and Nemirovski [10,11,12] and Bertsimas and Sim [15, 16] at the beginning of this century. An overview on robust optimization is given in [9, 13, 21]. The approach by Bertsimas and Sim has proven to be the most popular, with the introductory paper [16] being the most cited document on robust optimization in the literature databases Scopus and Web of Science (search for robust optimization in title, keywords, and abstract). The approach’s popularity is primarily based on the intuitive definition of the uncertainty set and the existence of a compact reformulation for the robust counterpart. However, instances from practice can still pose a considerable challenge for modern MILP solvers, even if the non-robust problem is relatively easy to solve, as observed e.g. by Kuhnke et al. [31]. In this paper, we address this challenge by studying the structure of robust binary problems and proposing a new branch and bound algorithm. Thereby, we restrict ourselves to problems with uncertain objective functions. However, most of our results carry over to general robust optimization.
We start by formally defining a standard, so called nominal, binary program
with an objective vector \(c\in {\mathbb {R}}^{n}\), a constraint matrix \(A\in {\mathbb {R}}^{m\times n}\), and a right-hand side \(b\in {\mathbb {R}}^{m}\). Instead of assuming the objective coefficients \(c_{i}\) to be certain, we consider uncertain coefficients \(c'_{i}\) that lie in an interval \(c'_{i}\in \left[ c_{i},c_{i}+{\hat{c}}_{i}\right] \) and can deviate from their nominal value \(c_{i}\) by up to the deviation \({\hat{c}}_{i}\). In the worst-case, all coefficients \(c_{i}'\) are equal to their maximum value \(c_{i}+{\hat{c}}_{i}\), as this maximizes the optimal solution value. However, for practical problems it is in general very unlikely that all coefficients deviate to their maximum value. Bertsimas and Sim [16] propose a robust counterpart to \(\text {NOM}\), with an adjustable level of conservatism, by defining a budget \(\varGamma \in \left[ 0,n\right] \) on the set of considered uncertain scenarios. For this robust counterpart, we do not consider all scenarios, but only those in which at most \(\left\lfloor \varGamma \right\rfloor \) coefficients \(c_{i}'\) deviate to their maximum \(c_{i}+{\hat{c}}_{i}\) and one coefficient deviates by a fraction of \(\left( \varGamma -\left\lfloor \varGamma \right\rfloor \right) \). The robust counterpart can be written as
with \(\left[ n\right] :=\left\{ 1,\ldots ,n\right\} \). The above problem is non-linear and thus impractical, but can be reformulated by dualizing the inner maximization problem, as shown by Bertsimas and Sim [16]. This results in the compact robust problem
with
Unfortunately, solving \(\text {ROB}\) as an MILP may require much more time than solving the nominal problem \(\text {NOM}\). For example, we observed in our computational study that Gurobi [26] already struggles to solve robust knapsack instances with only 100 items within a time limit of an hour (see Sect. 8.5). This is because the integrality gap of the formulation \({\mathscr {P}}^{\text {ROB}}\) may be arbitrarily large, even if the integrality gap of the corresponding nominal problem is zero (see Sect. 2). This is problematic, since a large integrality gap implies that optimal solutions to the linear relaxation are most likely far from being integer feasible, i.e., many variables that should be integer take fractional values. However, primal heuristics in MILP solvers, like the feasibility pump [19], perform better for solutions that are nearly integer feasible. Furthermore, even if we find an optimal solution, we probably have to spend much more time proving that it is indeed optimal.
There exist several approaches and studies in the literature on how to solve \(\text {ROB}\) in practice. Bertsimas et al. [14] as well as Fischetti and Monaci [20] evaluate whether it is more efficient to solve \(\text {ROB}\) over the compact reformulation \({\mathscr {P}}^{\text {ROB}}\) or using a separation approach over an alternative formulation with exponentially many inequalities, all of which correspond to a scenario from the uncertainty set. Although the alternative formulation is exponentially large, it is theoretically as strong, or weak respectively, as the compact reformulation. Atamtürk [5] addresses the issue of the weak formulation \({\mathscr {P}}^{\text {ROB}}\) and proposes four different strong, although considerably larger, formulations for solving \(\text {ROB}\). Atamtürk even proves that the strongest of the four formulations describes the convex hull of the set of robust solutions if the linear relaxation
is the convex hull of the set of nominal solutions. Another approach for solving \(\text {ROB}\) is to resort to its nominal counterpart. Bertsimas and Sim [15] show that there always exists an optimal solution \(\left( x,p,z\right) \) to \(\text {ROB}\) such that \(z\in \left\{ {\hat{c}}_{0},{\hat{c}}_{1},\ldots ,{\hat{c}}_{n}\right\} \), with \({\hat{c}}_{0}=0\). Note that the ideal choice for \(p_{i}\) is always \(\left( {\hat{c}}_{i}-z\right) ^{+}x_{i}\), with \(\left( a\right) ^{+}:=\max \left\{ a,0\right\} \) for \(a\in {\mathbb {R}}\). When fixing \(z\in \left\{ {\hat{c}}_{0},{\hat{c}}_{1},\ldots ,{\hat{c}}_{n}\right\} ,\) the term \(\left( {\hat{c}}_{i}-z\right) ^{+}x_{i}\) becomes linear, and thus \(\text {ROB}\) can be written as an instance of its nominal counterpart
Hence, solving \(\text {ROB}\) reduces to solving up to \(\left| \left\{ {\hat{c}}_{0},{\hat{c}}_{1},\ldots ,{\hat{c}}_{n}\right\} \right| \le n+1\) nominal subproblems \(\text {NOS}\left( z\right) \), implying that the robust counterpart of polynomially solvable nominal problems is again polynomially solvable. However, if the number of distinct deviations \(\left| \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \right| \) is large then solving all nominal subproblems may require too much time. Hence, it is beneficial to discard as many non-optimal choices for z as possible. For \(\varGamma \in {\mathbb {Z}}\), Álvarez-Miranda et al. [4] as well as Park and Lee [38] showed independently that there exists a subset \({\mathscr {Z}}\subseteq \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \) containing an optimal choice for z with \(\left| {\mathscr {Z}}\right| \le n+2-\varGamma \), or \(\left| {\mathscr {Z}}\right| \le n+1-\varGamma \) respectively. This result was later improved by Lee and Kwon [33], who prove that \({\mathscr {Z}}\) can be chosen such that \(\left| {\mathscr {Z}}\right| \le \left\lceil \frac{n-\varGamma }{2}\right\rceil +1\) holds. Hansknecht et al. [27] propose a divide and conquer approach for the robust shortest path problem that also aims to reduce the number of nominal subproblems to be solved. Their algorithm, which can as well be used to solve general problems \(\text {ROB}\), successively divides the set of deviations \(\left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \) into intervals and chooses in each iteration a value z from the most promising interval for solving the nominal subproblem \(\text {NOS}\left( z\right) \). After each iteration, given the optimal objective values of the previously considered subproblems, non-optimal choices of z are identified and discarded by using a relation between the optimal objective values of \(\text {NOS}\left( z\right) \) for different z.
Roughly summarized, there are two general directions for solving \(\text {ROB}\) in the literature: strong formulations on the one hand and fixing z on the other hand. In this paper, we take a middle course between these directions by proposing a branch and bound algorithm that combines restrictions on z with strong formulations. The general idea of the branch and bound paradigm, which was first proposed by Land and Doig [32], for solving general optimization problems \(\min \left\{ v\left( x\right) \big |x\in {\mathscr {X}}\right\} \) is to partition (branch) the set of feasible solutions \({\mathscr {X}}=\bigcup _{i=1}^{k}X_{i}\) and then solve the corresponding subproblems \(\min \left\{ v\left( x\right) \big |x\in X_{i}\right\} \) recursively. In order to avoid a complete enumeration, an easy to obtain dual bound \({\underline{v}}\left( X\right) \le \min \left\{ v\left( x\right) \big |x\in X\right\} \) is computed for every considered \(X\subseteq {\mathscr {X}}\) and compared with a primal bound, which is the value of the so far best known solution. In our case, we partition the set of solutions \({\mathscr {X}}={\mathscr {P}}^{\text {ROB}}\cap \left( {\mathbb {Z}}^{n}\times {\mathbb {R}}^{n}\times {\mathscr {Z}}\right) \), where \({\mathscr {Z}}\) contains an optimal choice for z, into subsets \({\mathscr {P}}^{\text {ROB}}\cap \left( {\mathbb {Z}}^{n}\times {\mathbb {R}}^{n}\times Z\right) \) with \(Z\subseteq {\mathscr {Z}}\). For the corresponding robust subproblems \(\text {ROB}\left( Z\right) \), we introduce improved formulations \({\mathscr {P}}\left( Z\right) \) and prove structural properties, from which we derive strong dual bounds on the optimal objective value \(v\left( \text {ROB}\left( Z\right) \right) \). This enables us to prune subsets \(Z\subseteq {\mathscr {Z}}\) containing non-optimal values for z. Furthermore, once the not yet pruned sets Z are sufficiently small, our findings enable us to solve \(\text {ROB}\left( Z\right) \) efficiently as an MILP, sparing us from considering many nominal subproblems \(\text {NOS}\left( z\right) \) separately.
The fourfold contribution of this paper is summarized in the following.
-
We propose a branch and bound algorithm to solve \(\text {ROB}\) and show in an extensive computational study that it outperforms all existing approaches from the literature by far. The code of all tested algorithms is available online [23].
-
For developing the branch and bound algorithm, we first introduce different strong formulations and prove several structural properties for \(\text {ROB}\).
-
We show that these structural properties can as well be used to improve existing approaches from the literature substantially, highlighting the relevance of our findings also for future research.
-
To conduct the computational study, we carefully construct a set of hard robust instances on the basis of real-world nominal problems from MIPLIB 2017 [25]. We make these instances freely available online for future benchmarking in the field of robust optimization [24].
Outline Before we introduce the basic framework of our branch and bound algorithm, we provide the theoretical foundations in Sects. 2 and 3. In Sect. 2, we discuss the weakness of \({\mathscr {P}}^{\text {ROB}}\) and propose a bilinear formulation \({\mathscr {P}}^{\text {BIL}}\) for \(\text {ROB}\), which is as strong as theoretically possible. Although the bilinearity limits the practical use of this formulation, \({\mathscr {P}}^{\text {BIL}}\) will play a critical role in the design of our branch and bound algorithm. Based on the bilinear formulation, we introduce the strong linear formulations \({\mathscr {P}}\left( Z\right) \) for restricted \(z\in Z\) in Sect. 3. Using formulation \({\mathscr {P}}\left( Z\right) \), we present a basic framework of our branch and bound algorithm in Sect. 4, which will then be improved in the subsequent sections by gaining more insight in the structure of \(\text {ROB}\). In Sect. 5, we show how to improve the formulations by using cliques in the so-called conflict graph of the nominal problem. In Sect. 6, we characterize optimal choices of p and z, establishing the theoretical background for many components of the branch and bound algorithm, which we describe in detail in Sect. 7. Finally, in Sect. 8 we conduct our computational study.
2 A strong bilinear formulation
To better understand why formulation \({\mathscr {P}}^{\text {ROB}}\) is problematic, we start by considering an example showing that the integrality gap of \(\text {ROB}\) can be arbitrarily large, even if the integrality gap of the corresponding nominal problem is zero.
Example 1
Consider the trivial task of choosing the smallest out of n elements
whose integrality gap is zero for all \(c\in {\mathbb {R}}^{n}\). Now, consider an instance of the uncertain counterpart \(\text {ROB}\) with \(c=0\), \({\hat{c}}=1\), and \(\varGamma =1\)
Let \(v\left( \text {ROB}\right) \) be the optimal objective value of \(\text {ROB}\) and \(v^{\text {R}}\left( \text {ROB}\right) \) be the optimal value of the linear relaxation. For the above problem, we have \(v\left( \text {ROB}\right) =1\). However, \(\left( x,p,z\right) =\left( \frac{1}{n},\ldots ,\frac{1}{n},0,\ldots ,0,\frac{1}{n}\right) \) is an optimal fractional solution with \(v^{\text {R}}\left( \text {ROB}\right) =\frac{1}{n}\). Thus, the integrality gap is \(\frac{v\left( \text {ROB}\right) -v^{\text {R}}\left( \text {ROB}\right) }{\left| v^{\text {R}}\left( \text {ROB}\right) \right| }=n-1\).
The example shows that choosing fractional values of x in the linear relaxation enables us to meet the constraints \(p_{i}+z\ge {\hat{c}}_{i}x_{i}\) with a relatively low value of z, which marginalizes the influence of the deviations on the objective value. To overcome these problems, we will discuss alternative formulations for modeling \(\text {ROB}\).
Formally, we call \({\mathscr {P}}\subseteq {\mathbb {R}}^{n_{1}+n_{2}}\) a formulation for the problem \(\min \left\{ c^{T}x\big |x\in {\mathscr {X}}\right\} \) with a set of solutions \({\mathscr {X}}\subseteq {\mathbb {Z}}^{n_{1}}\times {\mathbb {R}}^{n_{2}}\) if \({\mathscr {P}}\cap \left( {\mathbb {Z}}^{n_{1}}\times {\mathbb {R}}^{n_{2}}\right) ={\mathscr {X}}\) holds [42]. Using a formulation, we can solve the original problem by solving \(\min \left\{ c^{T}x\big |x\in {\mathscr {P}}\right\} \) and branching on the integer variables. Additionally, \({\mathscr {P}}'\subseteq {\mathbb {R}}^{n+n'}\) is called an extended formulation for a problem if its projection \({\text {proj}}\left( {\mathscr {P}}'\right) \subseteq {\mathbb {R}}^{n}\) into the original solution space is a formulation for that problem. For two formulations \({\mathscr {P}}_{1}\) and \({\mathscr {P}}_{2}\) with \({\mathscr {P}}_{1}\subseteq {\mathscr {P}}_{2}\), we say that \({\mathscr {P}}_{1}\) is at least as strong as \({\mathscr {P}}_{2}\). When considering extended formulations, we compare their projections instead.
To the best of our knowledge, the only results directly targeting the weakness of \({\mathscr {P}}^{\text {ROB}}\) are presented by Atamtürk [5], who proposes four problems \(\text {RP1}\) - \(\text {RP4}\) that are equivalent to \(\text {ROB}\), using different (extended) formulations \({\mathscr {P}}^{\text {RP1}},\ldots ,{\mathscr {P}}^{\text {RP4}}\). The theoretical strength of the four formulations exceeds the one of \({\mathscr {P}}^{\text {ROB}}\) by far. More precisely, we have \({\text {proj}}\left( {\mathscr {P}}^{\text {RP4}}\right) \subsetneq {\text {proj}}\left( {\mathscr {P}}^{\text {RP1}}\right) ={\mathscr {P}}^{\text {RP2}}={\text {proj}}\left( {\mathscr {P}}^{\text {RP3}}\right) \subsetneq {\mathscr {P}}^{\text {ROB}}\) for non-trivial cases. The problem
over the strongest formulation
with \(\left[ n\right] _{0}:=\left\{ 0,\ldots ,n\right\} \), is especially interesting. For every vertex \(\left( x,p,z,\omega ,\lambda \right) \) of the polyhedron \({\mathscr {P}}^{\text {RP4}}\), it holds \(\lambda _{k^{*}}=1\) for a \(k^{*}\in \left[ n\right] _{0}\) and \(\lambda _{k}=0\) for \(k\ne k^{*}\). Choosing \(\lambda \) in such a way reduces \(\text {RP4}\) to solving the nominal subproblem \(\text {NOS}\left( {\hat{c}}_{k^{*}}\right) \). Thus, \(\text {RP4}\) essentially combines the nominal subproblems \(\text {NOS}\left( z\right) \) that are solved in the Bertsimas and Sim approach for all possible values \(z\in \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \) into one problem.
Formulation \({\mathscr {P}}^{\text {RP4}}\) is not only the strongest proposed by Atamtürk, but can be seen as the strongest possible polyhedral formulation overall. This is because it preserves the integrality gap of the nominal problem [5]. However, the disadvantage of all formulations \({\mathscr {P}}^{\text {RP1}},\ldots ,{\mathscr {P}}^{\text {RP4}}\) is that they may become too large for practical purposes, as we will see in the computational study in Sect. 8.
To deal with this issue, we introduce a smaller, although bilinear, formulation for \(\text {ROB}\). For this, we multiply z in the constraints \(p_{i}+z\ge {\hat{c}}_{i}x_{i}\) of the original formulation \({\mathscr {P}}^{\text {ROB}}\) with \(x_{i}\) for all \(i\in \left[ n\right] \). The resulting constraint \(p_{i}+zx_{i}\ge {\hat{c}}_{i}x_{i}\) is valid for all solutions of \(\text {ROB}\), since the inequality becomes \(p_{i}\ge 0\) for \(x_{i}=0\) and is equivalent to the original inequality for \(x_{i}=1\). The new bilinear formulation
is at least as strong as \({\mathscr {P}}^{\text {RP4}}\), as stated in the following theorem.
Theorem 1
It holds \({\mathscr {P}}^{\text {BIL}}\subseteq {\text {proj}}\left( {\mathscr {P}}^{\text {RP4}}\right) \).
Proof
Let \(\left( x,p,z\right) \in {\mathscr {P}}^{\text {BIL}}\) and assume that \(0={\hat{c}}_{0}\le {\hat{c}}_{1}\le \cdots \le {\hat{c}}_{n}\) holds. First, consider the case in which we have \(z\le {\hat{c}}_{n}\). Then there exists an index \(j\in \left[ n-1\right] _{0}\) and a value \(\varepsilon \in \left[ 0,1\right] \) with \(z=\varepsilon {\hat{c}}_{j}+\left( 1-\varepsilon \right) {\hat{c}}_{j+1}\). We define \(\lambda _{k}=0\) for \(k\notin \left\{ j,j+1\right\} \) and \(\lambda _{j}=\varepsilon \) as well as \(\lambda _{j+1}=1-\varepsilon \). Furthermore, we set \(\omega _{i}^{k}=\lambda ^{k}x_{i}\) for all \(i\in \left[ n\right] ,k\in \left[ n\right] _{0}\) and show that \(\left( x,p,z,\omega ,\lambda \right) \in {\mathscr {P}}_{\text {RP4}}\). The first five constraints of formulation \({\mathscr {P}}_{\text {RP4}}\) are trivially satisfied by the definition of \(\varepsilon ,\ \lambda \) and \(\omega \). For the last constraint, we have
for all \(i\in \left[ n\right] \), where equality \(\left( *\right) \) holds since \(\left( {\hat{c}}_{i}-{\hat{c}}_{j}\right) \) and \(\left( {\hat{c}}_{i}-{\hat{c}}_{j+1}\right) \) are either both non-positive if we have \(i\le j\) or both non-negative if we have \(i\ge j+1\).
For the case \(z>{\hat{c}}_{n}\), we define \(\lambda _{k}=0\) for \(k\in \left[ n-1\right] _{0}\) and \(\lambda _{n}=1\). Furthermore, let \(\omega _{i}^{k}=\lambda ^{k}x_{i}\) for all \(i\in \left[ n\right] \) and \(k\in \left[ n\right] _{0}\). Again, \(\left( x,p,z,\omega ,\lambda \right) \) satisfies the first five constraints trivially. Moreover, we have
and thus \(\left( x,p,z,\omega ,\lambda \right) \in {\mathscr {P}}_{\text {RP4}}\), which completes the proof.\(\square \)
Although formulation \({\mathscr {P}}^{\text {BIL}}\) is strong and compact, its bilinearity is rather hindering when solving instances in practice. To understand how we can still make practical use of it, we first consider \({\mathscr {P}}^{\text {BIL}}\) with z restricted to a fixed value. The formulation becomes not only linear, but it also holds \(p_{i}=\left( {\hat{c}}_{i}-z\right) ^{+}x_{i}\) for all \(i\in \left[ n\right] \) in an optimal (fractional) solution \(\left( x,p,z\right) \). Hence, the problem of optimizing over the set \({\mathscr {P}}^{\text {BIL}}\cap \left( {\mathbb {R}}^{2n}\times \left\{ z\right\} \right) \) is equivalent to
which is the linear relaxation of the nominal subproblem \(\text {NOS}\left( z\right) \). This is noteworthy, since this equivalence does not hold for \({\mathscr {P}}^{\text {ROB}}\cap \left( {\mathbb {R}}^{2n}\times \left\{ z\right\} \right) \). The strength of the linearization for fixed z suggests that we may also derive strong linearizations of \({\mathscr {P}}^{\text {BIL}}\) for general restrictions on z, that is \(z\in Z\subseteq \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \). In the next section, we introduce such a linearization, which will be a key component of our branch and bound algorithm.
3 Strong linear formulations for bounded z
Consider a subset \(Z\subseteq \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \) and let \({\underline{z}}=\min \left( Z\right) \) and \({\overline{z}}=\max \left( Z\right) \) for the remainder of this paper. Assuming that there exists an optimal solution \(\left( x,p,z\right) \) to \(\text {ROB}\) with \(z\in Z,\) we can restrict ourselves to the domain \({\mathbb {R}}^{2n}\times \left[ {\underline{z}},{\overline{z}}\right] \). We use this to obtain a linear relaxation of the restricted bilinear formulation \({\mathscr {P}}^{\text {BIL}}\cap \left( {\mathbb {R}}^{2n}\times \left[ {\underline{z}},{\overline{z}}\right] \right) \).
Lemma 1
The linear constraints
and
are valid for all \(\left( x,p,z\right) \in {\mathscr {P}}^{\text {BIL}}\cap \left( {\mathbb {R}}^{2n}\times \left[ {\underline{z}},{\overline{z}}\right] \right) \).
Proof
Since \(p_{i}+zx_{i}\ge {\hat{c}}_{i}x_{i}\) and \(p_{i}\ge 0\) hold for all \(\left( x,p,z\right) \in {\mathscr {P}}^{\text {BIL}}\), the restriction \({\underline{z}}\le z\) implies
Furthermore, due to \(z\le {\overline{z}}\), we obtain
\(\square \)
Note that the Constraints (1) and (2) strictly dominate the inequalities \(p_{i}+z\ge {\hat{c}}_{i}x_{i}\) and \(p_{i}\ge 0\) of \({\mathscr {P}}^{\text {ROB}}\) in the case of \({\underline{z}}>0\) and \({\hat{c}}_{i}>{\overline{z}}\) respectively. Both constraints address the problem of the original formulation, which is that one can decrease \(x_{i}\) in a fractional solution down to \(x_{i}\le \frac{z}{{\hat{c}}_{i}}\) in order to choose \(p_{i}=0\), even if we have \({\hat{c}}_{i}>z\). Given a lower bound \(z\ge {\underline{z}}\), Constraint (1) reduces the benefit of decreasing \(x_{i}\), as the right-hand side only decreases with the factor \(\left( {\hat{c}}_{i}-{\underline{z}}\right) ^{+}\) instead of \({\hat{c}}_{i}\). For an upper bound \(z\le {\overline{z}}\), Constraint (2) guarantees that \(p_{i}\) is not zero for \({\hat{c}}_{i}>{\overline{z}}\) and \(x_{i}>0\) by using the fact that the value of \(p_{i}\) is at least \({\hat{c}}_{i}-{\overline{z}}\) if we have \({\hat{c}}_{i}>{\overline{z}}\) and \(x_{i}=1\).
Using these strengthened constraints, we obtain the robust subproblem
over the linear formulation
As shown in Lemma 1, \({\mathscr {P}}\left( Z\right) \) is a relaxation of the restricted bilinear formulation \({\mathscr {P}}^{\text {BIL}}\cap \left( {\mathbb {R}}^{2n}\times \left[ {\underline{z}},{\overline{z}}\right] \right) \). Note that \({\mathscr {P}}\left( Z\right) \) becomes stronger, the narrower the bounds of Z are, i.e., for \(Z,Z'\) with \(\left[ {\underline{z}},{\overline{z}}\right] \subsetneq \left[ {\underline{z}}',{\overline{z}}'\right] \) it holds \({\mathscr {P}}\left( Z\right) \subsetneq {\mathscr {P}}\left( Z'\right) \cap \left( {\mathbb {R}}^{2n}\times \left[ {\underline{z}},{\overline{z}}\right] \right) \) for non-trivial cases. The following statement shows that \({\mathscr {P}}\left( Z\right) \) is even as strong as \({\mathscr {P}}^{\text {BIL}}\) in the case where z equals one of the bounds \({\underline{z}},{\overline{z}}\).
Proposition 1
It holds \({\mathscr {P}}\left( Z\right) \cap \left( {\mathbb {R}}^{2n}\times \left\{ {\underline{z}},{\overline{z}}\right\} \right) ={\mathscr {P}}^{\text {BIL}}\cap \left( {\mathbb {R}}^{2n}\times \left\{ {\underline{z}},{\overline{z}}\right\} \right) \).
Proof
Consider a solution \(\left( x,p,z\right) \in {\mathscr {P}}\left( Z\right) \cap \left( {\mathbb {R}}^{2n}\times \left\{ {\underline{z}},{\overline{z}}\right\} \right) \). For \(z={\underline{z}}\), it holds
and for \(z={\overline{z}}\), we have
Hence, \(\left( x,p,z\right) \in {\mathscr {P}}^{\text {BIL}}\) and thus \({\mathscr {P}}\left( Z\right) \cap \left( {\mathbb {R}}^{2n}\times \left\{ {\underline{z}},{\overline{z}}\right\} \right) \subseteq {\mathscr {P}}^{\text {BIL}}\cap \left( {\mathbb {R}}^{2n}\times \left\{ {\underline{z}},{\overline{z}}\right\} \right) \). The statement follows together with Lemma 1.\(\square \)
Note that the improved formulation \({\mathscr {P}}\left( Z\right) \) comes with the cost of a larger constraint matrix compared to \({\mathscr {P}}^{\text {ROB}}\), as we have \(p_{i}\ge \left( {\hat{c}}_{i}-{\overline{z}}\right) ^{+}x_{i}\) instead of \(p_{i}\ge 0\). This can be hindering in practice, as smaller constraint matrices tend to be computationally beneficial. We overcome this issue by substituting \(p_{i}=p_{i}'+\left( {\hat{c}}_{i}-{\overline{z}}\right) ^{+}x_{i}\) and \(z=z'+{\underline{z}}\). We then obtain the equivalent substituted problem
over the substituted formulation
The substituted problem \(\text {ROB}^{\text {S}}\left( Z\right) \) is also interesting from a theoretical point of view. Since \(z'\le {\overline{z}}-{\underline{z}}\) holds for all optimal solutions, \(\text {ROB}^{\text {S}}\left( Z\right) \) is equivalent to \(\text {ROB}\) for an instance with objective coefficients \(c_{i}+\left( {\hat{c}}_{i}-{\overline{z}}\right) ^{+}\), deviations \({\hat{c}}'_{i}=\left( \min \left\{ {\hat{c}}_{i},{\overline{z}}\right\} -{\underline{z}}\right) ^{+}\), and an added constant \(\varGamma {\underline{z}}\). This will be useful in subsequent sections, since properties that we prove for \(\text {ROB}\) carry over directly to \(\text {ROB}^{\text {S}}\left( Z\right) \) and \(\text {ROB}\left( Z\right) \).
In the next section, we show how to use formulation \({\mathscr {P}}\left( Z\right) \) in a branch and bound algorithm for solving \(\text {ROB}\).
4 The basic branch and bound framework
The general idea of our branch and bound framework, which is sketched in Algorithm 1, is to solve \(\text {ROB}\) by branching the set \(\left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \) of possible values for z into subsets \(Z\subseteq \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \), for which we then consider the robust subproblem \(\text {ROB}\left( Z\right) \). For each considered subset Z, we store a dual bound \({\underline{v}}\left( Z\right) \) based on the linear relaxation value \(v^{\text {R}}\left( \text {ROB}^{\text {S}}\left( Z'\right) \right) \) for a superset \(Z'\supseteq Z\) using the strong formulation from the previous section. If the dual bound \({\underline{v}}\left( Z\right) \) is greater than or equal to the current primal bound \({\overline{v}}\) then we can prune Z. If Z cannot be pruned, we first asses the strength of formulation \({\mathscr {P}}^{\text {S}}\left( Z\right) \), which converges towards the strength of \({\mathscr {P}}^{\text {BIL}}\cap \left( {\mathbb {R}}^{2n}\times \left\{ {\underline{z}},{\overline{z}}\right\} \right) \) and achieves equality at latest for \(\left| Z\right| =1\) according to Proposition 1. If \({\mathscr {P}}^{\text {S}}\left( Z\right) \) is almost as strong as \({\mathscr {P}}^{\text {BIL}}\cap \left( {\mathbb {R}}^{2n}\times \left\{ {\underline{z}},{\overline{z}}\right\} \right) \) then we may directly solve the substituted robust subproblem \(\text {ROB}^{\text {S}}\left( Z\right) \), sparing us from considering further subsets of Z. Otherwise, if \({\mathscr {P}}^{\text {S}}\left( Z\right) \) is too weak, we continue solving the linear relaxation and branching into subsets \(Z=Z_{1}\cup Z_{2}\).

Note that the framework given in Algorithm 1 only serves for getting a basic intuition, as many components are described vaguely. For example, we leave open for now how to evaluate whether we can stop branching Z due to \({\mathscr {P}}^{\text {S}}\left( Z\right) \) being “strong enough”. We will describe all components of our algorithm in detail in Sect. 7. There, we will not only discuss whether and how we should branch Z (Sect. 7.5) and how to choose the next \(Z\in {\mathscr {N}}\) (Sect. 7.4), but also improve on the computation of dual bounds (Sect. 7.1) and primal bounds (Sect. 7.2) and discuss an efficient pruning strategy (Sect. 7.3).
Before doing so, we first establish some theoretical background in the following two sections that will be crucial for the design of our algorithm.
5 A reformulation using cliques in conflict graphs
In this section, we propose a stronger formulation for \(\text {ROB}\) that depends on so-called conflicts between variables and can also be used to solve the robust subproblems \(\text {ROB}\left( Z\right) \). We already considered the concept of extended formulations in Sect. 2. We now propose a reformulation that is also not in the original variable space, but not an extended formulation. To generalize the concept, we call a problem \(v'=\min \left\{ c'^{T}x'\big |x'\in {\mathscr {X}}'\right\} \) over a polyhedron \({\mathscr {P}}'\subseteq {\mathbb {R}}^{n_{1}'+n{}_{2}'}\) with \({\mathscr {P}}'\cap \left( {\mathbb {Z}}^{n_{1}'}\times {\mathbb {R}}^{n_{2}'}\right) ={\mathscr {X}}'\) a reformulation in a different variable space of \(v=\min \left\{ c^{T}x\big |x\in {\mathscr {X}}\right\} \), if both have the same optimum objective value, i.e., \(v=v'\), and there exists a polynomially time computable, cost preserving mapping \(\phi :{\mathscr {P}}'\rightarrow {\mathbb {R}}^{n_{1}+n{}_{2}}\) with \(\phi \left( {\mathscr {X}}'\right) \subseteq {\mathscr {X}}\). Then, instead of solving the original problem, we can solve the problem over \({\mathscr {X}}'\) and map an optimal solution \(x'\in {\mathscr {X}}'\) to an optimal solution \(\phi \left( x'\right) \in {\mathscr {X}}\). To generalize the concept of strong formulations, we say that \({\mathscr {P}}'_{1}\) is at least as strong as \({\mathscr {P}}'_{2}\) if \(\phi _{1}\left( {\mathscr {P}}'_{1}\right) \subseteq \phi '\left( {\mathscr {P}}'_{2}\right) \) holds.
Here, we reformulate \(\text {ROB}\) in a different variable space by aggregating variables p in a tailored preprocessing step. Preprocessing routines, which aim to reduce the size and improve the strength of a given problem formulation, are key components of modern MILP solvers and critical to their performance [1, 3, 17]. One of these preprocessing routines involves the search for logical implications between binary variables, e.g., \(x_{i}\!=\!1 \!\!\Rightarrow x_{j}\!=\! 0\) for every solution x. These implications can be modeled within a so-called conflict graph, consisting of a node for every binary variable \(x_{i}\) and its complement \({\overline{x}}_{i}=\left( 1-x_{i}\right) \) [6]. There exists an edge between two nodes in the conflict graph if there exists no solution where the corresponding literals are both equal to one. Since every solution to the original problem corresponds to an independent set within the conflict graph, all valid inequalities for the independent set problem on the conflict graph are also valid for the original problem. An interesting type of valid inequalities are set-packing constraints, which are defined by cliques in the conflict graph, i.e., subsets of nodes forming a complete subgraph. For a clique \(\left\{ x_{i_{1}},\ldots ,x_{i_{q}}\right\} \cup \left\{ {\overline{x}}_{j_{1}},\ldots ,{\overline{x}}_{j_{{\overline{q}}}}\right\} \), at most one of the literals can be equal to one, which yields the corresponding set-packing constraint \(\sum _{k=1}^{q}x_{i_{k}}+\sum _{k=1}^{{\overline{q}}}\left( 1-x_{j_{k}}\right) \le 1\).
Here, we are less interested in adding set-packing constraints to our formulations, as they are already used in modern MILP solvers. Instead, we focus on the structural implications of set-packing constraints consisting of positive literals \(x_{i}\) on the variables p and robustness constraints \(p_{i}+z\ge x_{i}\). To ease notation, we call a subset \(Q\subseteq \left[ n\right] \) a clique if the variables \(\left\{ x_{i}\big |i\in Q\right\} \) form a clique in the conflict graph. The following proposition shows that we can use a partitioning \({\mathscr {Q}}\) of \(\left[ n\right] \) into cliques to obtain a stronger reformulation of \(\text {ROB}\) in a smaller variable space.
Proposition 2
Let \({\mathscr {Q}}\) be a partitioning of \(\left[ n\right] \) into cliques. Then the problem
over the formulation
is a reformulation in a different variable space of \(\text {ROB}\) that is at least as strong as \({\mathscr {P}}^{\text {ROB}}\).
Proof
First, note that if \(p'_{Q}=\sum _{i\in Q}p_{i}\) for all \(Q\in {\mathscr {Q}}\) holds then \(\left( x,p,z\right) \) and \(\left( x,p',z\right) \) have the same objective value for their respective problems. Hence, in order to show \(v\left( \text {ROB}\right) =v\left( \text {ROB}\left( {\mathscr {Q}}\right) \right) \), we construct corresponding solutions fulfilling this property.
Let \(\left( x,p,z\right) \) be a solution to \(\text {ROB}\) and consider \(\left( x,p',z\right) \) with \(p'\in {\mathbb {R}}_{\ge 0}^{{\mathscr {Q}}}\) such that \(p'_{Q}=\sum _{i\in Q}p_{i}\). For all cliques \(Q\in {\mathscr {Q}}\), we have \(\sum _{i\in Q}x_{i}\le 1\) and thus there exists an index \(j\in Q\) such that \(x_{i}=0\) for all \(i\in Q\backslash \left\{ j\right\} \). It follows
for all \(Q\in {\mathscr {Q}}\), proving \(\left( x,p',z\right) \in {\mathscr {P}}^{\text {ROB}}\left( {\mathscr {Q}}\right) \), and thus \(v\left( \text {ROB}\left( {\mathscr {Q}}\right) \right) \le v\left( \text {ROB}\right) \).
It remains to show that every \(\left( x,p',z\right) \in {\mathscr {P}}^{\text {ROB}}\left( {\mathscr {Q}}\right) \cap \left( {\mathbb {Z}}^{n}\times {\mathbb {R}}^{\left| {\mathscr {Q}}\right| +1}\right) \) has a corresponding solution \(\phi \left( x,p',z\right) \in {\mathscr {P}}^{\text {ROB}}\cap \left( {\mathbb {Z}}^{n}\times {\mathbb {R}}^{n+1}\right) \) of the same cost. Note that such a mapping \(\phi :{\mathscr {P}}^{\text {ROB}}\left( {\mathscr {Q}}\right) \rightarrow {\mathbb {R}}^{2n+1}\) already implies \(v\left( \text {ROB}\left( {\mathscr {Q}}\right) \right) \ge v\left( \text {ROB}\right) \), and thus \(v\left( \text {ROB}\right) =v\left( \text {ROB}\left( {\mathscr {Q}}\right) \right) \). We define the image of \(\left( x,p',z\right) \in {\mathscr {P}}^{\text {ROB}}\left( {\mathscr {Q}}\right) \) as \(\phi \left( x,p',z\right) =\left( x,p,z\right) \) and consider two different cases for the definition of \(p\in {\mathbb {R}}^{n}\). For cliques \(Q\in {\mathscr {Q}}\) with \(\sum _{j\in Q}{\hat{c}}_{j}x_{j}>0\), we define \(p_{i}=\frac{{\hat{c}}_{i}x_{i}p'_{Q}}{\sum _{j\in Q}{\hat{c}}_{j}x_{j}}\) for all \(i\in Q\). Then \(p_{i}+z\ge {\hat{c}}_{i}x_{i}\) holds, since we have
For cliques \(Q\in {\mathscr {Q}}\) with \(\sum _{j\in Q}{\hat{c}}_{j}x_{j}=0\), we can choose \(p_{i}\) arbitrarily as long as \(p'_{Q}=\sum _{j\in Q}p_{j}\), since \(p_{i}+z\ge 0={\hat{c}}_{i}x_{i}\) holds for any \(p_{i}\ge 0\). This shows not only that \(\phi \left( {\mathscr {P}}^{\text {ROB}}\left( {\mathscr {Q}}\right) \cap \left( {\mathbb {Z}}^{n}\times {\mathbb {R}}^{\left| {\mathscr {Q}}\right| +1}\right) \right) \subseteq {\mathscr {P}}^{\text {ROB}}\cap \left( {\mathbb {Z}}^{n}\times {\mathbb {R}}^{n+1}\right) \) holds, but also proves the strength of \(\text {ROB}\left( {\mathscr {Q}}\right) \), because we did not use the integrality of x and thus have \(\phi \left( {\mathscr {P}}^{\text {ROB}}\left( {\mathscr {Q}}\right) \right) \subseteq {\mathscr {P}}^{\text {ROB}}\).\(\square \)
Reconsider Example 1 from Sect. 2 to see that reformulation \(\text {ROB}\left( {\mathscr {Q}}\right) \) is not only equal, but actually stronger. In the example, \(\left[ n\right] \) is a clique and we thus have
compared to \(v^{\text {R}}\left( \text {ROB}\right) =\frac{1}{n}\).
As mentioned in Sect. 3, the improvement of \(\text {ROB}\) can also be applied to \(\text {ROB}^{\text {S}}\left( Z\right) \). Given a clique partitioning \({\mathscr {Q}}\) of \(\left[ n\right] \) we obtain the stronger reformulation
over
Obviously, in order to obtain these strong reformulations, we first have to compute a conflict graph and a clique partitioning \({\mathscr {Q}}\) of \(\left[ n\right] \). Ideally, this partitioning contains few cliques that are as large as possible. However, finding a partitioning of minimum cardinality is equivalent to computing a minimum clique cover, which was shown to be \({{\mathscr {N}}}{{\mathscr {P}}}\)–hard by Karp [28]. Moreover, building the whole conflict graph itself is also \({{\mathscr {N}}}{{\mathscr {P}}}\)–hard [18]. Consequently, we have to restrict ourselves to a subgraph of the whole conflict graph. If our algorithm was natively implemented in a MILP solver, we could use the conflict graph that is computed during the solver’s preprocessing without spending additional time searching for conflicts. Unfortunately, we cannot access the conflict graph in Gurobi [26], the solver we use for our implementation. Thus, we implement our own heuristics in which we check for each constraint of the nominal problem whether it implies conflicts between variables. Afterwards, we use these conflicts to partition \(\left[ n\right] \) greedily into cliques. As the construction of conflict graphs and clique partitionings are not the focus of this paper, we refer to Appendix A for a detailed description of our implementation. For related work on the construction and handling of conflict graphs, we refer to Achterberg et al. [1], Atamtürk et al. [6], as well as Brito and Santos [18].
Note that our approach of aggregating constraints and variables depends on the variable z being shared by all constraints \(p_{i}+z\ge x_{i}\). Atamtürk et al. [7] propose for the mixed vertex packing problem a similar approach for aggregating constraints containing conflicting binary variables and a common continuous variable. Their mixed clique inequalities are analogous to our clique inequalities and their strengthened star inequalities can be adapted for generalizing these. For now, we leave the adaptation for future research and stick to using clique inequalities depending on clique partitionings, as we otherwise cannot benefit from the reduced number of variables. We will see in our computational study in Sect. 8 that using clique partitionings already yields a substantially stronger reformulation for many instances and improves the performance of our branch and bound algorithm. Before describing the branch and bound algorithm in detail in Sect. 7, we further establish some theoretical background in the next section by characterizing optimal solutions of \(\text {ROB}\). Note that although we solve \(\text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}}\right) \) in practice, for the sake of simplicity, we mostly refer to the equivalent problem \(\text {ROB}\left( Z\right) \) in the remainder of this paper and only refer to \(\text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}}\right) \) when necessary, e.g., when considering its linear relaxation or the strength of the formulation \({\mathscr {P}}^{\text {S}}\left( Z,{\mathscr {Q}}\right) \).
6 Characterization of optimal values for p and z
The central idea of our branch and bound algorithm for solving \(\text {ROB}\) is to restrict the value of z and trying to find an optimal corresponding nominal solution \(x\in {\mathscr {P}}^{\text {NOM}}\). In this section, however, we want to consider the opposite direction. Given a nominal solution \(x\in {\mathscr {P}}^{\text {NOM}}\), what are the optimal values for p and z? The answer to this question will deepen our understanding of the structural properties of \(\text {ROB}\) and is of practical use in many ways. First, we will generalize the result of Lee and Kwon [33], who showed for \(\varGamma \in {\mathbb {Z}}\) that there exists a subset \({\mathscr {Z}}\subseteq \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \), with \(\left| {\mathscr {Z}}\right| \le \left\lceil \frac{n-\varGamma }{2}\right\rceil +1\), containing an optimal choice for z. This reduction is relevant for our branch and bound algorithm, as we only have to consider subsets \(Z\subseteq {\mathscr {Z}}\). Second, given a choice of z, we will be able to restrict our search for a corresponding nominal solution \(x\in {\mathscr {P}}^{\text {NOM}}\) to those for which the chosen z is optimal. We will extensively use this idea within our branch and bound algorithm, especially in Sect. 7.1 where we describe further dual bounding strategies. Third, as we prove the characterization for (potentially fractional) solutions within \({\mathscr {P}}^{\text {BIL}}\), we can compute for any \(x\in {\mathscr {P}}^{\text {NOM}}\) the corresponding objective value for the optimization problem over \({\mathscr {P}}^{\text {BIL}}\). This provides an upper bound on the optimal objective value over \({\mathscr {P}}^{\text {BIL}}\), which we compare to \(v^{\text {R}}\left( \text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}}\right) \right) \) in order to obtain an indicator of the strength of \({\mathscr {P}}^{\text {S}}\left( Z,{\mathscr {Q}}\right) \). We use this indicator in our branch and bound algorithm to decide whether \(\text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}}\right) \) should be solved directly as an MILP or whether Z needs to be shrunk further, as explained in Sect. 7.5. The following theorem states the characterization of optimal values for p and z.
Theorem 2
Let \(x\in {\mathscr {P}}^{\text {NOM}}\) be a (fractional) solution to \(\text {NOM}\). We define
and
The values \(z\in \left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \) are together with \(p_{i}=\left( {\hat{c}}_{i}-z\right) ^{+}x_{i}\) for \(i\in \left[ n\right] \) exactly the optimal values satisfying \(\left( x,p,z\right) \in {\mathscr {P}}^{\text {BIL}}\) and minimizing \(\varGamma z+\sum _{i=1}^{n}p_{i}\).
For integer solutions \(x\in {\mathscr {P}}^{\text {NOM}}\), the theorem states that z should be large enough such that there are at most \(\varGamma \) indices \(i\in \left[ n\right] \) with \(x_{i}=1\) and \({\hat{c}}_{i}>z\). Otherwise, we could increase z while simultaneously decreasing \(p_{i}\) for more than \(\varGamma \) indices, leading to an improvement of the objective value. Conversely, z should be small enough such that there exist at least \(\varGamma \) indices \(i\in \left[ n\right] \) with \(x_{i}=1\) and \({\hat{c}}_{i}\ge z\). Otherwise, we could decrease z and would have to increase \(p_{i}\) for less than \(\varGamma \) indices, also yielding an improvement of the objective value. Obviously, if \(\varGamma \) is so large that \(\sum _{i\in \left[ n\right] }x_{i}<\varGamma \) holds then we need to choose z as small as possible, i.e., \(z=0\).
Before proving Theorem 2, we characterize the bounds \({\underline{z}}\left( x\right) \) and \({\overline{z}}\left( x\right) \) in an additional way. The proof of the following lemma can be found in Appendix B.
Lemma 2
For \(x\in {\mathbb {R}}^{n}\), we have
and
Using the above lemma, we are able to prove Theorem 2.
Proof of Theorem 2
First, note that the interval \(\left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \) is well-defined, since \(\sum _{i\in \left[ n\right] :{\hat{c}}_{i}>z}x_{i}\le \varGamma \) is a weaker requirement than \(\sum _{i\in \left[ n\right] :{\hat{c}}_{i}>z}x_{i}<\varGamma \) and we thus have \({\underline{z}}\left( x\right) \le {\overline{z}}\left( x\right) \) by definition of \({\underline{z}}\left( x\right) \) and Eq. (4). Furthermore, \(p_{i}=\left( {\hat{c}}_{i}-z\right) ^{+}x_{i}\) is optimal for a given x and z, as we minimize and have \(p_{i}\ge \left( {\hat{c}}_{i}-z\right) x_{i}\) and \(p_{i}\ge 0\) for all \(\left( x,p,z\right) \in {\mathscr {P}}^{\text {BIL}}\).
Now, let \(z\ge {\underline{z}}\left( x\right) \) and consider another value \(z'>z\) together with an appropriate \(p'\) such that \(\left( x,p',z'\right) \in {\mathscr {P}}^{\text {BIL}}\). By definition of \({\underline{z}}\left( x\right) \), it holds
and thus
Hence, the objective value is non-decreasing for \(z\ge {\underline{z}}\left( x\right) \). Moreover, for \({\overline{z}}\left( x\right) <\infty \), we even have \(\sum _{i\in \left[ n\right] :{\hat{c}}_{i}>z}x_{i}<\varGamma \) in the case of \(z={\overline{z}}\left( x\right) \) by Eq. (4). Then \((*)\) is a proper inequality and it follows that all choices \(z'>{\overline{z}}\left( x\right) \) are non-optimal.
Now, let \(z\le {\overline{z}}\left( x\right) \) and consider \(z'<z\). This implies \({\overline{z}}\left( x\right) >0\) and together with the definition of \({\overline{z}}\left( x\right) \), we obtain
It follows
Therefore, the objective value is non-increasing for \(z\le {\overline{z}}\left( x\right) \), which shows that all \(z\in \left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \) are optimal. Furthermore, if it holds \(z'<{\underline{z}}\left( x\right) \) then we have \(0<{\underline{z}}\left( x\right) \) and thus \(\sum _{i\in \left[ n\right] :{\hat{c}}_{i}\ge {\underline{z}}\left( x\right) }x_{i}>\varGamma \) by Eq. (3). Then, for \(z={\underline{z}}\left( x\right) \) it follows that \((**)\) is again a proper inequality and all choices \(z'<{\underline{z}}\left( x\right) \) are non-optimal.\(\square \)
As already mentioned, Lee and Kwon [33] showed for \(\varGamma \in {\mathbb {Z}}\) that the number of different values for z to be considered can be reduced from \(n+1\) to \(\left\lceil \frac{n-\varGamma }{2}\right\rceil +1\). To see this, it is helpful to sort the deviations \({\hat{c}}_{i}\). Therefore, for the remainder of this paper, we assume without loss of generality that \({\hat{c}}_{0}\le \cdots \le {\hat{c}}_{n}\) holds. The first observation leading to the reduction of Lee and Kwon is that the values \(z\in \left\{ {\hat{c}}_{n+1-\varGamma },\ldots ,{\hat{c}}_{n}\right\} \) are no better than the value \(z={\hat{c}}_{n-\varGamma }\), i.e., \({\hat{c}}_{n-\varGamma }\ge {\underline{z}}\left( x\right) \) for all solutions \(x\in {\mathscr {P}}^{\text {NOM}}\). The second observation is that if the value \(z={\hat{c}}_{i}\) is optimal then \(z\in \left\{ {\hat{c}}_{i-1},{\hat{c}}_{i+1}\right\} \) also contains an optimal choice. To put it in terms of Theorem 2: if \({\hat{c}}_{i}\in \left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \) holds then we also have \(\left\{ {\hat{c}}_{i-1},{\hat{c}}_{i+1}\right\} \cap \left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \ne \emptyset \). Hence, \({\mathscr {Z}}=\left\{ {\hat{c}}_{0},{\hat{c}}_{2},{\hat{c}}_{4},\ldots ,{\hat{c}}_{n-\varGamma }\right\} \) contains an optimal choice for z. The following statement generalizes the first observation to \(\varGamma \in {\mathbb {R}}_{\ge 0}\). Furthermore, both observations are strengthened by using conflicts and a clique partitioning, which we already compute to obtain the strengthened formulations from Sect. 5, to reduce the set \({\mathscr {Z}}\).
Proposition 3
Let \({\mathscr {Q}}\) be a partitioning of \(\left[ n\right] \) into cliques and \(q:\left[ n\right] \rightarrow {\mathscr {Q}}\) be the mapping that assigns an index \(j\in \left[ n\right] \) its corresponding clique \(Q\in {\mathscr {Q}}\) with \(j\in Q\). For
it holds \({\hat{c}}_{i^{\max }}\ge {\underline{z}}\left( x\right) \) for all solutions \(x\in {\mathscr {P}}^{\text {NOM}}\cap \left\{ 0,1\right\} ^{n}\) and there exists an optimal solution \(\left( x,p,z\right) \) to \(\text {ROB}\) with \(z\in \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{i^{\max }}\right\} \).
Now, let \(G=\left( \left[ n\right] ,E\right) \) be a conflict graph for \(\text {ROB}\) and \(\varGamma \in {\mathbb {Z}}\). Furthermore, let \({\mathscr {Z}}\subseteq \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{i^{\max }}\right\} \) such that \({\hat{c}}_{i^{\max }}\in {\mathscr {Z}}\) and for every \(i\in \left[ i^{\max }-1\right] _{0}\) it holds
-
\({\hat{c}}_{i}\in {\mathscr {Z}}\) or
-
there exists an index \(k<i\) with \({\hat{c}}_{k}\in {\mathscr {Z}}\) and for all \(j\in \left\{ k+1,\ldots ,i-1\right\} \) there exists an edge \(\left\{ j,i\right\} \in E\) in the conflict graph G.
Then there exists an optimal solution \(\left( x,p,z\right) \) to \(\text {ROB}\) with \(z\in {\mathscr {Z}}\).
A proof of the above proposition and an algorithm for computing a set \({\mathscr {Z}}\) meeting the required criteria can be found in Appendix C. Note that the second part of the proposition only holds for \(\varGamma \in {\mathbb {Z}}\). This is because the statement relies on the fact that for \({\hat{c}}_{i}\in \left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \) and \(\varGamma \in {\mathbb {Z}}\), it also holds \({\hat{c}}_{k}\in \left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \). However, for \(\varGamma \notin {\mathbb {Z}}\), we always have \({\underline{z}}\left( x\right) ={\overline{z}}\left( x\right) \), which implies that \({\hat{c}}_{i}\) always needs to be contained in \({\mathscr {Z}}\).
After paving the way with the theoretical results of the previous sections, we now describe the components of our branch and bound algorithm in detail in the next section.
7 The branch and bound algorithm
In the following sections, we will describe our approach for computing dual and primal bounds, our pruning rules as well as our node selection and branching strategies. A summary of the components, merged into one algorithm, is given in Sect. 7.6. An overview on different strategies regarding the components of branch and bound algorithms is provided by Morrison et al. [37].
For the remainder of this paper, \({\mathscr {Z}}\subseteq \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \) will be a set of possible values for z, as constructed by Algorithm 6 from Appendix C. To ease notation, we will refer to the considered subsets \(Z\subseteq {\mathscr {Z}}\) as nodes in a rooted branching tree, where \({\mathscr {Z}}\) is the root node and \(Z'\) is a child node of Z if it emerges directly via branching. Furthermore, we denote with \({\mathscr {N}}\subseteq 2^{{\mathscr {Z}}}\) the set of active nodes, that are the not yet pruned leaves of our branching tree, which are still to be considered.
7.1 Dual bounding
The focus of this paper is primarily on the computation of strong dual bounds \({\underline{v}}\left( Z\right) \). We already paved the way for these in the previous sections by introducing the strong reformulation \(\text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}}\right) ,\) yielding dual bounds \({\underline{v}}\left( Z\right) =v^{\text {R}}\left( \text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}}\right) \right) \). In the following, we show that we can obtain even better bounds by restricting ourselves to solutions fulfilling the optimality criterion in Theorem 2.
7.1.1 Deriving dual bounds from \(\text {ROB}\left( Z\right) \)
Imagine that we just solved a robust subproblem \(\text {ROB}\left( Z\right) \), using the equivalent problem \(\text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}}\right) \), and observed that the optimal objective value \(v\left( \text {ROB}\left( Z\right) \right) \) is significantly higher than the current primal bound \({\overline{v}}\). Furthermore, imagine that there exists a yet to be considered value \(z'\) in an active node \(Z'\in {\mathscr {N}}\) that is very close to one of the just considered values \(z\in Z\). Note that the objective function of the nominal subproblem \(\text {NOS}\left( z\right) \), arising from fixing z, differs only slightly in its objective function \(\varGamma z+\sum _{i=1}^{n}\left( c_{i}+\left( {\hat{c}}_{i}-z\right) ^{+}\right) x_{i}\) from the nominal subproblem \(\text {NOS}\left( z'\right) \). This suggests that the objective value \(v\left( \text {NOS}\left( z'\right) \right) \) is probably not too far from \(v\left( \text {NOS}\left( z\right) \right) \). Since \(v\left( \text {ROB}\left( Z\right) \right) \) is higher than \({\overline{v}}\) and also a dual bound on \(v\left( \text {NOS}\left( z\right) \right) \), we might be able to prune \(z'\) without considering \(\text {ROB}\left( Z'\right) \) if we are able to carry over some information from \(\text {NOS}\left( z\right) \) to \(\text {NOS}\left( z'\right) \). In fact, Hansknecht et al. [27] showed that there exists a relation between the optimal solution values \(v\left( \text {NOS}\left( z\right) \right) \) for different values z.
Lemma 3
[27] For \(z'\le z\), it holds \(v\left( \text {NOS}\left( z'\right) \right) \ge v\left( \text {NOS}\left( z\right) \right) -\varGamma \left( z-z'\right) \).
Proof
The objective function \(\varGamma z+\sum _{i=1}^{n}\left( c_{i}+\left( {\hat{c}}_{i}-z\right) ^{+}\right) x_{i}\) of \(\text {NOS}\left( z\right) \) is non-increasing in z when omitting the constant term \(\varGamma z\). This implies \(v\left( \text {NOS}\left( z'\right) \right) -\varGamma z'\ge v\left( \text {NOS}\left( z\right) \right) -\varGamma z\), which proves the statement.\(\square \)
Accordingly, in addition to the dual bound \({\underline{v}}\left( Z'\right) \) for a node \(Z'\in {\mathscr {N}}\), we can also maintain individual dual bounds \({\underline{v}}\left( z'\right) \) on the optimal objective value \(v\left( \text {NOS}\left( z'\right) \right) \) with \({\underline{v}}\left( z'\right) =v\left( \text {ROB}\left( Z\right) \right) -\varGamma \left( {\underline{z}}-z'\right) \) for \(z'<{\underline{z}}\) after solving \(\text {ROB}\left( Z\right) \). The dual bound for a node \(Z'\) is then the combination of the linear relaxation value \(v^{\text {R}}\left( \text {ROB}^{\text {S}}\left( Z',{\mathscr {Q}}\right) \right) \) and the minimum of all individual bounds \(\min \left\{ {\underline{v}}\left( z'\right) \big |z'\in Z'\right\} \), i.e., we have
While this already strengthens the dual bounds in our branch and bound algorithm, we can improve the results of Hansknecht et al. even more by using the optimality criterion from Theorem 2 and the clique partitioning \({\mathscr {Q}}\) from Sect. 5. Since we are solely interested in optimal solutions to \(\text {ROB}\), it is sufficient to only consider solutions to \(\text {NOS}\left( z'\right) \) that fulfill the optimality criterion, i.e., solutions \(x'\) with \(z'\in \left[ {\underline{z}}\left( x'\right) ,{\overline{z}}\left( x'\right) \right] \). If an optimal solution to \(\text {NOS}\left( z'\right) \) does not fulfill this property then \(z'\) is no optimal choice in the first place and can therefore be pruned. Accordingly, we establish an improved bound that is not a dual bound on \(v\left( \text {NOS}\left( z'\right) \right) \), but a dual bound on the objective value of all solutions to \(\text {NOS}\left( z'\right) \) fulfilling the optimality criterion.
Let \(x'\) be such a solution to \(\text {NOS}\left( z'\right) \) with objective value \(v'\). Note that \(x'\) is also a feasible solution to \(\text {NOS}\left( z\right) \) and let \(v\ge v\left( \text {NOS}\left( z\right) \right) \) be the corresponding objective value. For \(z'<z\), the value \(v'\) is decreased by \(\delta ^{\text {dec}}=\varGamma \left( z-z'\right) \) compared to \(v\), but increased by \(\delta ^{\text {inc}}=\sum _{i=1}^{n}\left( \left( {\hat{c}}_{i}-z'\right) ^{+}-\left( {\hat{c}}_{i}-z\right) ^{+}\right) x_{i}'\). This yields the estimation
on the objective value \(v'\). Note that the decrease by \(\delta ^{\text {dec}}\) is taken into account in the estimation of Lemma 3, but the increase \(\delta ^{\text {inc}}\) is not. Obviously, \(\delta ^{\text {inc}}\) can be zero if we have \(x_{i}'=0\) for all \(i\in \left[ n\right] \) with \({\hat{c}}_{i}>z'\). However, if \(x'\) fulfills the optimality criterion then we know from Theorem 2 that there exist at least \(\varGamma \) indices with \({\hat{c}}_{i}\ge z'\) and \(x_{i}'=1\). Assuming that there do not exist \(\varGamma \) indices with \({\hat{c}}_{i}=z'\), there must exist at least one \(i\in \left[ n\right] \) with \({\hat{c}}_{i}>z'\) and \(x_{i}'=1\), yielding a positive lower bound on \(\delta ^{\text {inc}}\). Taking conflicts between variables \(x_{i}\) into account, we might even deduce that there must exist some indices with \(x_{i}'=1\) and very high \({\hat{c}}_{i}\), which improves the bound on \(\delta ^{\text {inc}}\).
Note that for \(z'>z\), Lemma 3 provides no bound on \(\text {NOS}\left( z'\right) \), although we can apply similar arguments to this case. Observe that Inequality (5) still holds, with \(\delta ^{\text {inc}}\le 0\) and \(\delta ^{\text {dec}}<0\). Unfortunately, if we have \(x_{i}'=1\) for all \(i\in \left[ n\right] \) with \({\hat{c}}_{i}>z\) then \(\delta ^{\text {inc}}<0\) might have a large absolute value, leading to a weak estimation. However, if \(x'\) fulfills the optimality criterion then we know from Theorem 2 that there exist at most \(\varGamma \) indices with \({\hat{c}}_{i}>z\) and \(x_{i}'=1\). From this, we can again deduce a lower bound on \(\delta ^{\text {inc}}\), which can also be improved by taking conflicts between variables \(x_{i}\) into account.
Theorem 3
Let \({\mathscr {Q}}\) be a partitioning of \(\left[ n\right] \) into cliques, \(z,z'\in {\mathbb {R}}_{\ge 0}\), and \(x'\) be an arbitrary solution to \(\text {NOS}\left( z'\right) \) of value \(v'\) that satisfies \(z'\in \left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \). Then we have \(v'\ge v\left( \text {NOS}\left( z\right) \right) -\delta _{z}\left( z'\right) \), where the estimator \(\delta _{z}\left( z'\right) \) is defined as
Proof
For \(z'=0\), the statement follows from Lemma 3. Otherwise, we obtain an estimation
as in Inequality (5), by considering the difference in the objectives of \(\text {NOS}\left( z'\right) \) and \(\text {NOS}\left( z\right) \). Consider the case \(z'>z\). Since it holds \(z'\ge {\underline{z}}\left( x'\right) \), it follows from the definition of \({\underline{z}}\left( x'\right) \) in Theorem 2 that we have
We obtain
where the last equality holds since \({\mathscr {Q}}\) is a partitioning of \(\left[ n\right] \).
Now, let \(0<z'<z\). Since \(z'\le {\overline{z}}\left( x'\right) \) holds, Theorem 2 implies
We obtain
which concludes the proof.\(\square \)
The above statement now enables us not only to compute bounds for \(z'>z\), but also stronger bounds for \(0<z'<z\). Note that for \(z'=0\), we have to use the dual bound from Lemma 3, since Theorem 2 provides no statement on the required structure of \(x'\) in this case.
In our branch and bound algorithm, we use the estimators \(\delta _{{\underline{z}}}\left( z'\right) \) for all \(z'<{\underline{z}}\) and \(\delta _{{\overline{z}}}\left( z'\right) \) for \(z'>{\overline{z}}\) after solving \(\text {ROB}\left( Z\right) \). Accordingly, we define for \(Z\subseteq {\mathscr {Z}}\) the estimators
The improved bounds \(v\left( \text {ROB}\left( Z\right) \right) -\delta _{Z}\left( z'\right) \) come with the cost of a higher computational effort compared to the bounds from Lemma 3. However, the additional overhead is marginal, as we can solve the involved maximization problems in linear time and compute all estimators \(\delta _{{\underline{z}}}\left( z'\right) \), or \(\delta _{{\overline{z}}}\left( z'\right) \) respectively, simultaneously. Algorithm 2 describes our approach for computing the estimators for a set \({\mathscr {Z}}'\subseteq {\mathscr {Z}}\) of remaining values \(z'\).

We first compute \(\delta _{{\overline{z}}}\left( z'\right) \) for \(z'\in \left\{ z'\in {\mathscr {Z}}'\big |z'>{\overline{z}}\right\} \) (lines 1 to 9). For computing \(\delta _{{\overline{z}}}\left( z'_{j}\right) \), we consider all deviations \({\hat{c}}_{k}\) with \({\overline{z}}<{\hat{c}}_{k}\le z'_{j}\) (line 4) and add the corresponding value \({\hat{c}}_{k}-{\overline{z}}\) (line 8). Furthermore, we mark the clique \(q\left( k\right) \) containing k as considered by adding it to the set \({\mathscr {Q}}'\) and we associate the clique \(q\left( k\right) \) with the index k by maintaining a mapping \(q^{-1}:{\mathscr {Q}}'\rightarrow \left[ n\right] \) (line 7). However, if \(q\left( k\right) \) is already contained within \({\mathscr {Q}}'\) then we considered an index \(k'=q^{-1}\left( q\left( k\right) \right) \) with \(q\left( k\right) =q\left( k'\right) \) before k and counted the value \({\hat{c}}_{k'}-{\overline{z}}\) towards \(\delta _{{\overline{z}}}\left( z'\right) \). Hence, either \({\hat{c}}_{k}-{\overline{z}}\) or \({\hat{c}}_{k'}-{\overline{z}}\) has to be subtracted, as we only count the highest value per clique. Since we iterate over the deviations in a non-decreasing order, it holds \({\hat{c}}_{k}-{\overline{z}}\ge {\hat{c}}_{k'}-{\overline{z}}\), which is why we subtract \({\hat{c}}_{k'}-{\overline{z}}\) (line 6). Note that we do not have to consider all values \(\left\{ {\hat{c}}_{k}\big |{\overline{z}}<{\hat{c}}_{k}\le z'_{j}\right\} \) for computing \(\delta _{{\overline{z}}}\left( z'_{j}\right) \) if we already considered the values \(\left\{ {\hat{c}}_{k}\big |{\overline{z}}<{\hat{c}}_{k}\le z'_{j-1}\right\} \) for \(\delta _{{\overline{z}}}\left( z'_{j-1}\right) \). Instead, we construct \(\delta _{{\overline{z}}}\left( z'_{j}\right) \) on the basis of \(\delta _{{\overline{z}}}\left( z'_{j-1}\right) \) and only iterate over \(\left\{ {\hat{c}}_{k}\big |z'_{j-1}<{\hat{c}}_{k}\le z'_{j}\right\} \).
The computation of \(\delta _{{\underline{z}}}\left( z'\right) \) for \(z'\in \left\{ z'\in {\mathscr {Z}}'\big |z'<{\underline{z}}\right\} \) is almost analogous (lines 10 to 24). The difference here is that we only consider up to \(\varGamma \) values \({\underline{z}}-{\hat{c}}_{k}\). Hence, we not only maintain the set \({\mathscr {Q}}'\) and the mapping \(q^{-1}\), but also a list containing the indices of currently added values \({\underline{z}}-{\hat{c}}_{k}\). The list is updated every time we subtract (line 18) or add (line 20) a value \({\underline{z}}-{\hat{c}}_{k}\). Furthermore, since we iterate reversely over \(\left\{ {\hat{c}}_{k}\big |z'_{j}\le {\hat{c}}_{k}<{\underline{z}}\right\} \), the list is ordered non-decreasing with respect to \({\underline{z}}-{\hat{c}}_{k}\). Hence, before assigning \(\delta _{{\underline{z}}}\left( {\hat{c}}_{i_{j}}\right) \), we check whether L contains more than \(\varGamma \) elements and, if necessary, remove the first \(\varGamma -\left| L\right| \) indices together with their value \(z-{\hat{c}}_{k}\) and their clique \(q\left( k\right) \) (lines 21 to 23).
7.1.2 Optimality-cuts
Consider a node \(Z\subseteq {\mathscr {Z}}\) of our branching tree and assume that \(\left( x,p,z\right) \) is a solution to \(\text {ROB}\left( Z\right) \) with \(\left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \cap Z=\emptyset \). We know from Theorem 2 that it is needless to consider x for the subset Z, as there is a different set \(Z'\subseteq {\mathscr {Z}}\) with \(\left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \cap Z'\ne \emptyset \) if x is part of a globally optimal solution. Nevertheless, it is possible that \(\left( x,p,z\right) \) is an optimal solution to \(\text {ROB}\left( Z\right) \), resulting in an unnecessarily weak dual bound \({\underline{v}}\left( Z\right) \). Using the following theorem, we are able to strengthen our formulations such that we only consider solutions \(\left( x,p,z\right) \) with \(\left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \cap Z\ne \emptyset \) and thus raise the dual bound \({\underline{v}}\left( Z\right) \).
Theorem 4
Let \(x\in {\mathscr {P}}^{\text {NOM}}\cap \left\{ 0,1\right\} ^{n}\) be a solution to \(\text {NOM}\) and \(\underline{\text {c}}\le \overline{\text {c}}\) bounds on z. Then \(\left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \cap \left[ \underline{\text {c}},\overline{\text {c}}\right] \) \(\ne \emptyset \) holds if and only if x satisfies
and in the case of \(\underline{\text {c}}>0\) also
Proof
We have \(\left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \cap \left[ \underline{\text {c}},\overline{\text {c}}\right] \) \(\ne \emptyset \) if and only if \({\underline{z}}\left( x\right) \le \overline{\text {c}}\) and \(\underline{\text {c}}\le {\overline{z}}\left( x\right) \) holds. We first show that \({\underline{z}}\left( x\right) \le \overline{\text {c}}\) holds if and only if x fulfills Inequality (6). We know from Theorem 2 that \(\sum _{i\in \left[ n\right] :{\hat{c}}_{i}>{\underline{z}}\left( x\right) }x_{i}\le \varGamma \). Then \({\underline{z}}\left( x\right) \le \overline{\text {c}}\) implies
and thus Inequality (6) due to x being binary. Additionally, x cannot fulfill Inequality (6) if we have \(\overline{\text {c}}<{\underline{z}}\left( x\right) \), as this contradicts the minimality in the definition of \({\underline{z}}\left( x\right) \).
It is clear to see that \(\underline{\text {c}}\le {\overline{z}}\left( x\right) \) applies if we have \(\underline{\text {c}}=0\). Hence, it remains to show that for \(0<\underline{\text {c}}\), it holds \(\underline{\text {c}}\le {\overline{z}}\left( x\right) \) if and only if x fulfills Inequality (7). We know from Theorem 2 that \(\sum _{i\in \left[ n\right] :{\hat{c}}_{i}\ge {\overline{z}}\left( x\right) }x_{i}\ge \varGamma \) holds. Then \(\underline{\text {c}}\le {\overline{z}}\left( x\right) \) implies
and thus Inequality (6). Additionally, x cannot fulfill Inequality (7) if \({\overline{z}}\left( x\right) <\underline{\text {c}}\) holds, as this contradicts the maximality in the definition of \({\overline{z}}\left( x\right) \).\(\square \)
In our branch and bound algorithm, we add the above Inequalities (6) and (7), with \(\underline{\text {c}}={\underline{z}}\) and \(\overline{\text {c}}={\overline{z}}\), as optimality-cuts to the formulation \({\mathscr {P}}^{\text {S}}\left( Z,{\mathscr {Q}}\right) \) when solving the corresponding linear problem. However, the optimality-cuts can cause several problems when added to a robust subproblem \(\text {ROB}\left( Z\right) \), especially with respect to the dual bounds of the last section. Let \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \) be the corresponding problem with added optimality-cuts for bounds \(\underline{\text {c}}\le {\underline{z}}\) and \({\overline{z}}\le \overline{\text {c}}\). Note that in the proof of Theorem 3, we require \(x'\), the solution to \(\text {NOS}\left( z'\right) \), to be feasible for \(\text {NOS}\left( z\right) \) in order to show that \(v\left( \text {NOS}\left( z\right) \right) -\delta _{z}\left( z'\right) \) is a dual bound. Analogously, we require \(x'\) to be a feasible solution to \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \) in order to derive a dual bound from \(v\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) \). That is, if \(x'\) does not meet the optimality-cuts then we can not derive any dual bounds from \(v\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) \). However, if \(\left[ {\underline{z}}\left( x'\right) ,{\overline{z}}\left( x'\right) \right] \cap \left[ \underline{\text {c}},\overline{\text {c}}\right] \ne \emptyset \) holds then \(x'\) is according to Theorem 4 a feasible solution to \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \), leading to the following generalization of Theorem 3.
Corollary 1
Let \(Z\subseteq {\mathbb {R}}_{\ge 0}\) and \(\underline{\text {c}}\le \overline{\text {c}}\) with \(Z\subseteq \left[ \underline{\text {c}},\overline{\text {c}}\right] \). Furthermore, let \(z'\in \left[ \underline{\text {c}},\overline{\text {c}}\right] \) and \(x'\) be an arbitrary solution to \(\text {NOS}\left( z'\right) \) of value \(v'\) satisfying \(z'\in \left[ {\underline{z}}\left( x'\right) ,{\overline{z}}\left( x'\right) \right] \). Then \(v'\ge v\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) -\delta _{Z}\left( z'\right) \) holds.
Accordingly, there is a trade-off in the choice of \(\underline{\text {c}},\overline{\text {c}}\). On the one hand, the optimal objective value \(v\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) \), and thus the derived dual bounds for other \(z'\in \left[ \underline{\text {c}},\overline{\text {c}}\right] \), increases if the bounds \(\underline{\text {c}},\overline{\text {c}}\) are close together. On the other hand, we want to derive dual bounds for as many \(z'\) as possible. Furthermore, the optimality-cuts can be hindering for finding good primal bounds. We resolve this trade-off by adding loose optimality-cuts, corresponding to wide bounds \(\underline{\text {c}},\overline{\text {c}}\), in the beginning and gradually strengthening them as we consider more robust subproblems.
Let \({\mathscr {Z}}^{*}\subseteq {\mathscr {Z}}\) be the union of all nodes \(Z^{*}\subseteq {\mathscr {Z}}\) for which we already solved a robust subproblem \(\text {ROB}\left( Z^{*},\underline{\text {c}}^{*},\overline{\text {c}}^{*}\right) \) and let \({\mathscr {Z}}'=\bigcup _{Z\in {\mathscr {N}}}Z\) be the union of all active nodes. In our branch and bound algorithm, for a node \(Z\in {\mathscr {N}}\), we choose \(\underline{\text {c}},\overline{\text {c}}\in {\mathscr {Z}}'\) as wide as possible around Z such that there exists no \(z^{*}\in {\mathscr {Z}}^{*}\) in between, i.e.,
and
In order to see that it is not reasonable to expand the interval \(\left[ \underline{\text {c}},\overline{\text {c}}\right] \), consider a value \(z'\in {\mathscr {Z}}'\backslash \left[ \underline{\text {c}},\overline{\text {c}}\right] \). By definition, we already considered a subproblem \(\text {ROB}\left( Z^{*},\underline{\text {c}}^{*},\overline{\text {c}}^{*}\right) \) with \(z'\in \left[ \underline{\text {c}}^{*},\overline{\text {c}}^{*}\right] \) for a node \(Z^{*}\) containing a value \(z^{*}\) with \(z'<z^{*}<{\underline{z}}\) or \({\overline{z}}<z^{*}<z'\). Since \(\delta _{Z^{*}}\left( z'\right) \le \delta _{z^{*}}\left( z'\right) <\delta _{Z}\left( z'\right) \) holds, we have already computed a dual bound \({\underline{v}}\left( z'\right) =v\left( \text {ROB}\left( Z^{*},\underline{\text {c}}^{*},\overline{\text {c}}^{*}\right) \right) -\delta _{Z^{*}}\left( z'\right) \) that is probably better than a potential dual bound derived from \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \). Thus, expanding \(\left[ \underline{\text {c}},\overline{\text {c}}\right] \) tends to be useless for obtaining new dual bounds. Now, assume that there exists a nominal solution x with \(\left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \cap \left[ \underline{\text {c}},\overline{\text {c}}\right] =\emptyset \) such that \(\left( x,p,z\right) \) is feasible for \(\text {ROB}\left( Z\right) \) and also defines an improving primal bound \({\overline{v}}\). In this case, it would be beneficial to expand \(\left[ \underline{\text {c}},\overline{\text {c}}\right] \) such that x fulfills the optimality-cuts and we obtain a new incumbent. However, we have seen in the proof of Theorem 2 that the objective value of \(\left( x,p,z\right) \) is non-increasing for \(z\le {\overline{z}}\left( x\right) \) and non-decreasing for \(z\ge {\underline{z}}\left( x\right) \) with the appropriate \(p=\left( {\hat{c}}_{i}-z\right) ^{+}x_{i}\). Using the arguments from above, we should have already found a solution \(\left( x,p^{*},z^{*}\right) \) that is at least as good as \(\left( x,p,z\right) \) for a previous subproblem \(\text {ROB}\left( Z^{*},\underline{\text {c}}^{*},\overline{\text {c}}^{*}\right) \). Accordingly, expanding \(\left[ \underline{\text {c}},\overline{\text {c}}\right] \) is also uninteresting for obtaining new primal bounds.
In the next section, we show what else we can do except for choosing appropriate bounds \(\underline{\text {c}},\overline{\text {c}}\) in order to guide the branch and bound algorithm in the search for primal bounds.
7.2 Primal bounding
We already stated in the introduction that the potentially large optimality gap of \(\text {ROB}\) can cause problems for MILP solvers when trying to compute feasible solutions. Hence, we have to provide guidance for the solver in order to consistently obtain strong primal bounds. As the focus of this paper is on the robustness structures of \(\text {ROB}\), and not the corresponding nominal problem \(\text {NOM},\) we implement no heuristics that explicitly compute feasible solutions x to \(\text {NOM}\). Nevertheless, our branch and bound algorithm naturally aids in the search for optimal solutions by quickly identifying non-promising values of z. This allows us early on to focus on nodes \(Z\subseteq {\mathscr {Z}}\) containing (nearly) optimal choices for z, for which solving \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \) is much easier, using the equivalent problem \(\text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}},\underline{\text {c}},\overline{\text {c}}\right) \), and yields (nearly) optimal solutions to \(\text {ROB}\).
Furthermore, even when considering \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \) for a node \(Z\subseteq {\mathscr {Z}}\) that contains no optimal choice for z, we can potentially derive good primal bounds or even optimal solutions to \(\text {ROB}\). In many cases, an optimal solution \(\left( x,p,z\right) \) to \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \) does not meet the optimality criterion \(z\in \left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \), which leaves potential for improving the primal bound provided by \(v\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) \). Since \({\overline{z}}\left( x\right) \) is easily computable, we can obtain a better primal bound \({\overline{v}}\left( x\right) \) provided by the solution value of \(\left( x,p',{\overline{z}}\left( x\right) \right) \), with \(p_{i}'=\left( {\hat{c}}_{i}-{\overline{z}}\left( x\right) \right) ^{+}x_{i}\). Moreover, we can not only compute \({\overline{v}}\left( x\right) \) for an optimal solution x to \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \), but any feasible solution the solver reports while solving \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \). This increases the chance of finding good primal bounds, as an improved sub-optimal solution may provide an even better bound than an optimal solution to \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \). We will see in our computational study that our branch and bound algorithm quickly finds optimal solutions to \(\text {ROB}\), often while considering the very first robust subproblem. Additionally, the possibility to derive strong primal bounds from sub-optimal solutions, which may be found early on while solving \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \), will be relevant for our pruning strategy in the next section.
7.3 Pruning
In theory, a problem is solved to optimality if the primal bound \({\overline{v}}\) is equal to a proven dual bound \({\underline{v}}\). In practice, however, it is neither always necessary to prove \({\overline{v}}={\underline{v}}\), nor is it always possible due to numerical issues. Instead, one considers a problem to be solved if \({\overline{v}}\) is sufficiently close to \({\underline{v}}\), that is, it either holds \({\overline{v}}-{\underline{v}}\le t^{\text {abs}}\) or \(\frac{{\overline{v}}-{\underline{v}}}{\left| {\overline{v}}\right| }\le t^{\text {rel}}\), where \(t^{\text {abs}}>0\) is the absolute tolerance and \(t^{\text {rel}}>0\) is the relative tolerance. The concept of “sufficiently solved” problems is also applied to the pruning of nodes \(Z\subseteq {\mathscr {Z}}\) within our branching tree. More specifically, we prune Z not only if \({\underline{v}}\left( Z\right) \ge {\overline{v}}\) holds, but as soon as we have \({\overline{v}}-{\underline{v}}\left( Z\right) \le t^{\text {abs}}\) or \(\frac{{\overline{v}}-{\underline{v}}\left( Z\right) }{\left| {\overline{v}}\right| }\le t^{\text {rel}}\). In our computational study, we choose \(t^{\text {abs}}=10^{-10}\) and \(t^{\text {rel}}=10^{-4}\), which are the default tolerances used by Gurobi [26]. Note that for \({\overline{v}}=0\) and \({\overline{v}}>{\underline{v}}\), the relative gap \(\frac{{\overline{v}}-{\underline{v}}}{\left| {\overline{v}}\right| }\) is defined to be \(\infty \). If \({\underline{v}}\ge {\overline{v}}=0\) holds then the relative gap does not matter, since we have \({\overline{v}}-{\underline{v}}\le t^{\text {abs}}\). To simplify notation, we define \({\text {prn}}\left( {\underline{v}},{\overline{v}}\right) =1\) if the dual and primal bounds \({\underline{v}},{\overline{v}}\) are strong enough for pruning and \({\text {prn}}\left( {\underline{v}},{\overline{v}}\right) =0\) otherwise.
Recall that the dual bound \({\underline{v}}\left( Z\right) \) for \(Z\subseteq {\mathscr {Z}}\) is the maximum of the linear relaxation value \(v^{\text {R}}\left( \text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}},{\underline{z}},{\overline{z}}\right) \right) \) and the worst individual bound \(\min \left\{ {\underline{v}}\left( z\right) \big |z\in Z\right\} \) from Sect. 7.1.1. Even if \({\underline{v}}\left( Z\right) \) is too weak for pruning, i.e., \({\text {prn}}\left( {\underline{v}}\left( Z\right) ,{\overline{v}}\right) =0\), it may hold \({\text {prn}}\left( {\underline{v}}\left( z\right) ,{\overline{v}}\right) =1\) for a value \(z\in Z\). Therefore, we apply a further pruning step in addition to the pruning of the whole node Z. Every time we consider a node Z, we check for all \(z\in Z\) whether z can be pruned according to its individual dual bound \({\underline{v}}\left( z\right) \). This is beneficial, as we obtain a stronger formulation for the resulting subset of Z. Furthermore, before solving a robust subproblem \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \), we check for all remaining \(z'\in \bigcup _{Z\in {\mathscr {N}}}Z\) whether \({\text {prn}}\left( {\underline{v}}\left( z'\right) ,{\overline{v}}\right) =1\) holds, so that the bounds \(\underline{\text {c}},\overline{\text {c}}\), as chosen in Sect. 7.1.2, are as narrow as possible.
Once we consider a robust subproblem \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \), we let the MILP solver manage the pruning itself, as the otherwise necessary interference into its solving process would lead to a performance degradation. However, we can monitor the best known dual bound \({\underline{v}}\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) \) and terminate the subproblem as soon as we have \({\text {prn}}\left( {\underline{v}}\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) ,{\overline{v}}\right) =1\). This is especially important for robust subproblems \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \) corresponding to nodes Z containing values that are far from being optimal. In this case, we are usually aware of a primal bound \({\overline{v}}\) that is substantially smaller than the optimal solution value \(v\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) \), allowing for a fast termination. Such a primal bound can either come from a previously considered robust subproblem or from a solution to \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \) that we improved as described in the previous section.
Unfortunately, terminating \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \) prematurely is problematic regarding the dual bounds \(v\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) -\delta _{Z}\left( z'\right) \) computed in Sect. 7.1.1. Note that in practice, we do not necessarily know the optimal solution value \(v\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) \) and thus use the best known dual bound \({\underline{v}}\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) \) instead. Hence, there is a trade-off in saving time by terminating \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \) early and generating strong dual bounds \({\underline{v}}\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) -\delta _{Z}\left( z'\right) \). We resolve this trade-off by computing the estimators \(\delta _{Z}\left( z'\right) \) before solving \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \) and constantly evaluating whether improving \({\underline{v}}\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) \) can potentially lead to the pruning of additional values \(z'\). Let \({\mathscr {Z}}'\cap \left[ \underline{\text {c}},\overline{\text {c}}\right] \) be the remaining values of z for which we computed the estimators \(\delta _{Z}\left( z'\right) \). Furthermore, let \({\overline{v}}\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) \) be the currently best known primal bound for \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \). For evaluating whether \(z'\in {\mathscr {Z}}'\cap \left[ \underline{\text {c}},\overline{\text {c}}\right] \) can potentially be pruned, we consider three different cases.
-
Case 1.
If \({\text {prn}}\left( \max \left\{ {\underline{v}}\left( z\right) ,{\underline{v}}\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) -\delta _{Z}\left( z'\right) \right\} ,{\overline{v}}\right) =1\) holds then \(z'\) can already be pruned.
-
Case 2.
Otherwise, if \({\text {prn}}\left( {\overline{v}}\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) -\delta _{z}\left( z'\right) ,{\overline{v}}\right) =1\) holds then \(z'\) can be pruned if we manage to increase \({\underline{v}}\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) \) up to \({\overline{v}}\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) \).
-
Case 3.
Otherwise, \(z'\) can only be pruned if we find a better global primal bound \({\overline{v}}\).
If Case 1 applies then \(z'\) is irrelevant to the question whether we should terminate \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \) early, as it will be pruned anyway. In contrast, it is unlikely that \(z'\) will be pruned if Case 3 applies. We have already stated in the previous section that our branch and bound algorithm usually finds (nearly) optimal solutions to \(\text {ROB}\) while solving the first robust subproblem. Hence, most of the time, the primal bound \({\overline{v}}\) will not be improved, leaving little chance for \(z'\) to be pruned. Accordingly, in our implementation, we continue solving \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \) as long as there exists a value \(z'\in {\mathscr {Z}}'\cap \left[ \underline{\text {c}},\overline{\text {c}}\right] \) for which Case 2 applies. However, since closing the gap between \({\underline{v}}\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) \) and \({\overline{v}}\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) \) can potentially waste much time, we use an additional termination criterion. In our implementation, we also terminate \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \) if no \(z'\in {\mathscr {Z}}'\cap \left[ \underline{\text {c}},\overline{\text {c}}\right] \) switched to Case 1 within the last 10 s. That is, raising the dual bound did not lead to a pruning of an additional \(z'\) within this time. Of course, this criterion is highly arbitrary, but it leads to an improvement of our algorithm’s performance in our computational study. As heavy engineering is beyond the scope of this paper, we leave a detailed analysis of this component and its potential for future research.
7.4 Node selection
The node selection strategy determines the order in which we explore nodes within our branching tree, and thus directly impacts the number of nodes we consider before finding an optimal solution. Hence, a good node selection strategy is critical to the performance of any branch and bound algorithm, as finding an optimal (or at least good) solution quickly enables us to prune more efficiently. A review of different strategies in the context of mixed integer programming is given by Linderoth and Savelsbergh [34]. A survey on machine learning for node selection is given by Lodi and Zarpellon [35].
Two basic strategies, from which many other strategies emerge as a combination, are depth-first and best-first search. Depth-first search is based on the last-in-first-out principle and thus follows a path down the branching tree until a prunable node is reached. In contrast, best-first search ranks the nodes of the branching tree by assigning a value to each node and always picking a node with the best value. Here, we consider the case where the ranking value is equal to the node’s dual bound. In this case, best-first search is also called best-bound search. Naturally, both strategies, depth-first and best-bound search, have advantages and disadvantages, as discussed by Linderoth and Savelsbergh [34]. An advantage of depth-first search is that it requires less memory, as the number of active nodes \(\left| {\mathscr {N}}\right| \) in the branching tree is relatively small. It also allows for a fast reoptimization after branching, since the optimal dual solution to the parent node’s subproblem is readily available to warm start the, typically similar, subproblem of the child node. Furthermore, depth-first search usually finds feasible solutions quickly, as integer feasible solutions tend to be located deep in the branching tree, where many variables are fixed due to branching. An obvious drawback, however, is that depth-first search may explore many unnecessary nodes and can get stuck in unpromising subtrees if the current primal bound is far from the optimal solution value. In contrast, best-bound search tends to minimize the number of nodes in the branching tree. This is because best-bound search will never select a node whose dual bound is worse than the optimal solution value. However, the drawback of best-bound search is that it may require more memory, as the number of active nodes in the branching tree grows large if there exist many nodes with similar bounds. This can also prevent the algorithm from finding feasible solutions early, since deeper levels of the branching tree are explored late. Furthermore, the reoptimization is hindered, as sequentially considered subproblems are less related compared to the depth-first search.
The strategy for our branch and bound algorithm can be seen as a hybrid of depth-first and best-bound search. Note that our algorithm switches back and forth between two phases. In phase one, we branch the set \({\mathscr {Z}}\) into subsets Z and obtain dual bounds \(v^{\text {R}}\left( \text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}},{\underline{z}},{\overline{z}}\right) \right) \) from solving linear subproblems. In phase two, we stick to a node \(Z\subseteq {\mathscr {Z}}\) and solve the robust subproblem \(\text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}},\underline{\text {c}},\overline{\text {c}}\right) \). Phase two can be seen as a leaning towards depth-first search, since we focus on the chosen values in Z until the problem \(\text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}},\underline{\text {c}},\overline{\text {c}}\right) \) is either solved to optimality or terminated as described in the previous section. Since \(\text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}},\underline{\text {c}},\overline{\text {c}}\right) \) is potentially a hard problem, it would be beneficial to only solve it for promising nodes Z, presumably leading to good solutions. We use the dual bound \({\underline{v}}\left( Z\right) \) of a node \(Z\subseteq {\mathscr {Z}}\) as an indicator for the node’s potential to contain good solutions \(\left( x,p,z\right) \) with \(z\in Z\), and thus perform a best-bound search in phase one. In detail, for the set of active tree nodes \({\mathscr {N}}\), we always process a node \(Z\in {\mathscr {N}}\) for which the current dual bound \({\underline{v}}\left( Z\right) \) is minimum among all nodes, i.e., \(Z\in \text {argmin}\left\{ {\underline{v}}\left( Z\right) \big |Z\in {\mathscr {N}}\right\} \).
Fortunately, the drawbacks of best-bound search described above are not critical in our case. The number of active nodes is at most \(\left| {\mathscr {N}}\right| \le \left| {\mathscr {Z}}\right| \le \left\lceil \frac{n-\varGamma }{2}\right\rceil +1\). Hence, memory consumption should be no limiting factor in phase one. This also allows us to store a solution basis for each node to warm start the simplex algorithm after branching. However, while warm starting usually accelerates the solving process, we observed that it leads to less consistent results in our computational study, as it disables Gurobi’s LP presolve [26]. Therefore, we do not consider warm starts for the evaluation of our branch and bound approach in Sect. 8.
7.5 Branching
Much research has been devoted to the question of how to branch efficiently in integer linear programming, see, e.g., Achterberg et al. [2] or Linderoth and Savelsbergh [34]. However, the main question that is addressed there is on which integer infeasible variable to branch. Obviously, this question is uninteresting in our case, since we solely branch on the variable z and hand the robust subproblems to the chosen MILP solver, which manages the branching on its own. Instead, we have to address the question how to divide a node \(Z\subseteq {\mathscr {Z}}\) so that the branching is efficient. Furthermore, we want to discuss how to decide whether a node Z should be branched at all or whether we solve \(\text {ROB}^{\text {S}}\left( Z,Q,\underline{\text {c}},\overline{\text {c}}\right) \) directly as an MILP.
To answer the latter, let \(\left( x,p,z\right) \in {\mathscr {P}}\left( Z,{\mathscr {Q}},{\underline{z}},{\overline{z}}\right) \) be an optimal solution to the linear relaxation of \(\text {ROB}\left( Z,{\mathscr {Q}},{\underline{z}},{\overline{z}}\right) \). Here, we consider \(\text {ROB}\left( Z,{\mathscr {Q}},{\underline{z}},{\overline{z}}\right) \) instead of the equivalent \(\text {ROB}^{\text {S}}\left( Z,Q,{\underline{z}},{\overline{z}}\right) \) for simplicity. Since x meets the optimality-cuts, there exists a value \(z'\in \left[ {\underline{z}},{\overline{z}}\right] \cap \left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \). The bilinear solution \(\left( x,p',z'\right) \in {\mathscr {P}}^{\text {BIL}}\), with \(p_{i}'=\left( {\hat{c}}_{i}-z'\right) ^{+}x_{i}\), provides an upper bound on the optimal objective value over all solutions in \({\mathscr {P}}^{\text {BIL}}\) fulfilling the optimality-cuts for \(\underline{\text {c}}={\underline{z}}\) and \(\overline{\text {c}}={\overline{z}}\). This upper bound is easily computable, as we have \(v\left( \left( x,p',z'\right) \right) =v\left( \left( x,p'',{\overline{z}}\left( x\right) \right) \right) \), with \(p_{i}''=\left( {\hat{c}}_{i}-{\overline{z}}\left( x\right) \right) ^{+}x_{i}\), and \({\overline{z}}\left( x\right) \) can be determined in linear time. Now, imagine that the objective values \(v\left( \left( x,p,z\right) \right) \) and \(v\left( \left( x,p',z'\right) \right) \) are nearly identical. Since \({\mathscr {P}}^{\text {BIL}}\) is the strongest possible formulation for \(\text {ROB}\), there is not much potential for improving the integrality gap of \(\text {ROB}\left( Z,{\mathscr {Q}},{\underline{z}},{\overline{z}}\right) \) via branching. While this does not necessarily imply for \(\left[ \underline{\text {c}},\overline{\text {c}}\right] \supsetneq \left[ {\underline{z}},{\overline{z}}\right] \) that the integrality gap of \(\text {ROB}\left( Z,{\mathscr {Q}},\underline{\text {c}},\overline{\text {c}}\right) \) is also small enough, we use the relation between the objective values \(v\left( \left( x,p,z\right) \right) \) and \(v\left( \left( x,p',z'\right) \right) \) as an indicator and stop branching Z once they are sufficiently close to each other. In our implementation, we consider the two values to be sufficiently close, if their gap is in the relative tolerance or absolute tolerance, that is \({\text {prn}}\left( v\left( \left( x,p,z\right) \right) ,v\left( \left( x,p',z'\right) \right) \right) =1\), as defined in Sect. 7.3. However, we do not solve \(\text {ROB}^{\text {S}}\left( Z,Q,\underline{\text {c}},\overline{\text {c}}\right) \) right away, but first reinsert the node Z into the set of active nodes \({\mathscr {N}}\) and mark Z to be considered for a robust subproblem by storing a value \(\text {sol}\left( Z\right) =1\). This is because Z was not selected with respect to the just computed dual bound \(v^{\text {R}}\left( \text {ROB}^{\text {S}}\left( Z,Q,{\underline{z}},{\overline{z}}\right) \right) \), but a dual bound based on the linear relaxation value of a parent node. Once Z is chosen again with respect to its new (potentially significantly improved) dual bound, we solve the robust subproblem \(\text {ROB}^{\text {S}}\left( Z,Q,\underline{\text {c}},\overline{\text {c}}\right) \) directly as an MILP.
Now, assume that we have decided otherwise and want to branch the node \(Z\subseteq {\mathscr {Z}}\) further into subnodes \(Z_{1},Z_{2}\). Obviously, \(Z_{1},Z_{2}\) should form “intervals”, that is \(\left[ {\underline{z}}_{1},{\overline{z}}_{1}\right] \cap \left[ {\underline{z}}_{2},{\overline{z}}_{2}\right] =\emptyset \), as otherwise, the bounds on z would be unnecessarily wide, leading to weaker formulations. Hence, we search for a branching-point \(\theta \in \left[ {\underline{z}},{\overline{z}}\right) \) defining \(Z_{1}=\left\{ z'\in Z\big |z'\le \theta \right\} \) and \(Z_{2}=\left\{ z'\in Z\big |z'>\theta \right\} \). Another desirable property of \(Z_{1},Z_{2}\) would be that the computed optimal solution \(\left( x,p,z\right) \in {\mathscr {P}}\left( Z,{\mathscr {Q}},{\underline{z}},{\overline{z}}\right) \) is neither contained in \({\mathscr {P}}\left( Z_{1},{\mathscr {Q}},{\underline{z}}_{1},{\overline{z}}_{1}\right) \), nor in \({\mathscr {P}}\left( Z_{2},{\mathscr {Q}},{\underline{z}}_{2},{\overline{z}}_{2}\right) \). We can achieve this by choosing \(\theta =z\). First, note that \(\theta <\max \left( Z\right) \) holds, since we did not stop branching and thus have \(\left( x,p,z\right) \notin {\mathscr {P}}^{\text {BIL}}\), which implies \(z<\max \left( Z\right) \) due to Proposition 1. Furthermore, if \(z\notin Z\) holds then it is trivial that \(\left( x,p,z\right) \) is not feasible for any child node. In the case of \(z\in Z\), we have \(z={\overline{z}}_{1}\), and thus \(\left( x,p,z\right) \in {\mathscr {P}}\left( Z_{1},{\mathscr {Q}},{\underline{z}}_{1},{\overline{z}}_{1}\right) \) would again imply \(\left( x,p,z\right) \in {\mathscr {P}}^{\text {BIL}}\) due to Proposition 1.
Unfortunately, the computed value z is in practice often near to one of the bounds \({\underline{z}},{\overline{z}}\), leading to an unbalanced branching, where the optimal linear relaxation value \(v^{\text {R}}\left( \text {ROB}\left( Z_{i},{\mathscr {Q}},{\underline{z}}_{i},{\overline{z}}_{i}\right) \right) \) for one child node rises significantly, while the other remains nearly unchanged. This problem is also observed in the context of spatial branch and bound, which is a common approach for solving non-linear optimization problems. In spatial branch and bound, a convex relaxation of the non-linear formulation is considered to obtain lower bounds on the optimal objective value. This relaxation is then strengthened via branching on (continuous) variables occurring in non-linear terms, similar to the branching we perform on z to obtain stronger relaxations \({\mathscr {P}}\left( Z\right) \) of the bilinear formulation \({\mathscr {P}}^{\text {BIL}}\). A common choice for the branching-point in spatial branch and bound is a convex combination of the variable’s value in the current solution and the middle point of the variable’s domain [41]. In our case, this translates to choosing \(\alpha z+\left( 1-\alpha \right) \left( {\overline{z}}+{\underline{z}}\right) /2\) with \(\alpha \in \left[ 0,1\right] \). This value is then often projected into a subinterval to ensure that \(\theta \) is not at the boundaries of its domain, i.e., \(\theta \in \left[ {\underline{z}}+\beta \left( {\overline{z}}-{\underline{z}}\right) ,{\overline{z}}-\beta \left( {\overline{z}}-{\underline{z}}\right) \right] \) with \(\beta \in \left[ 0,0.5\right] \). In summary, the branching point is chosen as
Obviously, the parameters \(\alpha \) and \(\beta \) leave room for engineering and differ between solvers. For example, the solvers SCIP [22] and COUENNE [8] choose \(\theta \) with default values \(\alpha =0.25\) and \(\beta =0.2\), while ANTIGONE (\(\alpha =0.75,\ \beta =0.1\)) and BARON (\(\alpha =0.7,\ \beta =0.01\)) choose a significantly higher value for \(\alpha \), according to [41]. Note that \(\beta \) has actually no effect on \(\theta \) for any of these choices. Again, we don’t dive too deep into the engineering of our branch and bound algorithm in this paper and simply take a middle course by choosing \(\alpha =0.5\) and \(\beta =0\). However, in some cases, this leads to a branching where \(\left( x,p,z\right) \) is still feasible for one of the child nodes. Hence, we check if the branching is effective, by evaluating for both child nodes \(Z_{1},Z_{2}\) if \(\left( x,p,z\right) \notin {\mathscr {P}}\left( Z_{i},{\mathscr {Q}},{\underline{z}}_{i},{\overline{z}}_{i}\right) \) holds. If not, we update \(\theta \) by choosing the middle value between z and \(\theta \). We do this until \(\left( x,p,z\right) \) is infeasible for both nodes, which is guaranteed to happen, as our branching point converges to z.
7.6 Summary and implementation
In this section, we summarize the components of our branch and bound approach and merge them into one algorithm, as described in Algorithm 3. We also discuss some details regarding the implementation of the algorithm, which is written in Java and uses Gurobi [26] as an MILP and LP solver.

Algorithm 3 starts with the preparation for the branch and bound by computing the conflict graph and clique partitioning (line 1), which are then used to compute \({\mathscr {Z}}\) (line 2). Afterwards, the set of active nodes \({\mathscr {N}}\) is initialized with the root node \({\mathscr {Z}}\), which is marked with \(\text {sol}\left( {\mathscr {Z}}\right) =0\), since we don’t know whether \(\text {ROB}^{\text {S}}\left( {\mathscr {Z}},{\mathscr {Q}},\underline{\text {c}},\overline{\text {c}}\right) \) should be solved directly as an MILP (line 3). Afterwards, we initialize the primal and dual bounds (line 4), as well as the set of already considered values \(z\in {\mathscr {Z}}\) for subproblems \(\text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}},\underline{\text {c}},\overline{\text {c}}\right) \) with \(z\in Z\) (line 5). Note that we manage the whole branching tree outside of Gurobi, as it does not provide all callbacks to perform the necessary branching and node-selection [26].
After the initialization, our algorithm starts processing the nodes Z within the set of active nodes \({\mathscr {N}}\) until no node remains, and thus the problem is solved to optimality (line 6). In accordance with Sect. 7.4, we choose a node among those having the lowest dual bound \({\underline{v}}\left( Z\right) \) (line 7). Afterwards, we check whether \(\text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}},\underline{\text {c}},\overline{\text {c}}\right) \) is marked to be solved as an MILP (line 8). If so, we try to prune all remaining values \(z'\) in active nodes (lines 9 and 10) in order to reduce Z as much as possible and allow for a choice of tighter bounds \(\underline{\text {c}},\overline{\text {c}}\) for the optimality-cuts, as described in Sect. 7.1.2 (line 11). We then compute the estimators \(\delta _{Z}\left( z'\right) \) for the remaining values in \(\left[ \underline{\text {c}},\overline{\text {c}}\right] \) (line 12), which we need for our termination strategy of \(\text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}},\underline{\text {c}},\overline{\text {c}}\right) \) and also for updating the dual bounds \({\underline{v}}\left( z'\right) \). We then construct the problem \(\text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}},\underline{\text {c}},\overline{\text {c}}\right) \) and pass it to the solver (line 13). While constructing the robust subproblem in practice, we have to avoid some pitfalls regarding numerical issues. Since the deviations \({\hat{c}}_{i}\), and thus the values \(z\in {\mathscr {Z}}\), can be arbitrarily close to each other, it is possible that our subproblem contains constraints \(p'_{Q}+z'\ge \sum _{i\in Q}\left( \min \left\{ {\hat{c}}_{i},{\overline{z}}\right\} -{\underline{z}}\right) ^{+}x_{i}\) for which the coefficients on the right-hand side are very small. Such constraints may not only be troublesome for the solver’s performance, but also irrelevant in practice, since Gurobi considers per default all constraints that are violated by less than the feasibility tolerance \(10^{-6}\) as satisfied [26]. Hence, we only add the constraint \(p'_{Q}+z'\ge \sum _{i\in Q}\left( \min \left\{ {\hat{c}}_{i},{\overline{z}}\right\} -{\underline{z}}\right) ^{+}x_{i}\) if \(\min \left\{ {\hat{c}}_{i},{\overline{z}}\right\} -{\underline{z}}>10^{-6}\) holds for at least one \(i\in Q\). Once the subproblem is passed to the solver, we monitor the solution process via callbacks. Using these, the solver allows us to access the current best solution of the subproblem, and improve it as in Sect. 7.2, every time a new incumbent is found (line 14). Furthermore, we can query the current primal and dual bounds of the subproblem at every node of its branching tree in order to decide whether the subproblem can be terminated, as in Sect. 7.3 (line 15). After the subproblem is solved or terminated, we remove Z from the set of active nodes, add the values in Z to the set of already considered values \({\mathscr {Z}}^{*}\) (line 16), and update dual bounds using the estimators \(\delta _{Z}\left( z'\right) \) (lines 17 and 18).
If we don’t solve \(\text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}},\underline{\text {c}},\overline{\text {c}}\right) \) directly as an MILP, we remove Z from the set of active nodes, as it will either be pruned or branched (line 20). In order to obtain a formulation that is as strong as possible, we try to prune all values \(z\in Z\), using their individual dual bound \({\underline{v}}\left( z\right) \) (line 21). Afterwards, we let the solver solve the linear relaxation over \({\mathscr {P}}^{\text {S}}\left( Z,{\mathscr {Q}},{\underline{z}},{\overline{z}}\right) \), also avoiding numerical issues as above. If there exists no solution to the linear relaxation then Z can be pruned and there is nothing left to do (line 22). Otherwise, we check whether the optimal solution \(\left( x,p',z'\right) \) is integer feasible and potentially update the best known solution \(\left( x^{*},p^{*},z^{*}\right) \) (lines 23 to 25). If the solution is not integer feasible, we check whether Z can be pruned using the new dual bound \(v\left( \left( x,p',z'\right) \right) \) (line 26). If this is not the case, then we decide whether Z should be branched further, as in Sect. 7.5 (line 27). If we decide to solve \(\text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}},\underline{\text {c}},\overline{\text {c}}\right) \) directly, we reinsert Z into \({\mathscr {N}}\) and mark \(\text {sol}\left( Z\right) =1\) (line 28). Otherwise, we branch Z into subsets \(Z_{1},Z_{2}\), as described in Sect. 7.5 (line 30), compute dual bounds for both child nodes (line 31), and insert them into the set of active nodes (line 32).
After Z is processed, either by solving the robust subproblem or its linear relaxation, we check whether the potentially obtained new primal and dual bounds allow for a pruning of some active nodes (line 33). If any active nodes remain, we continue with choosing the next node, otherwise we report the optimal solution \(\left( x^{*},p^{*},z^{*}\right) \).
Obviously, it will not always be possible to solve \(\text {ROB}\) to optimality within a given time limit. Hence, in practice, we also keep track of a dual bound \({\underline{v}}\left( \text {ROB}\right) \) in order to evaluate the quality of the best solution found. We do this by initializing \({\underline{v}}\left( \text {ROB}\right) =\infty \) and updating it every time a node Z is pruned, using the corresponding dual bound, i.e., \({\underline{v}}\left( \text {ROB}\right) \leftarrow \min \left\{ {\underline{v}}\left( \text {ROB}\right) ,{\underline{v}}\left( Z\right) \right\} \). After the algorithm is terminated, we update \({\underline{v}}\left( \text {ROB}\right) \leftarrow \min \left\{ {\underline{v}}\left( \text {ROB}\right) ,{\underline{v}}\left( Z\right) \right\} \) for all remaining active nodes \(Z\in {\mathscr {N}}\). Doing so, we make sure that the dual bound \({\underline{v}}\left( \text {ROB}\right) \) is equal to the minimum dual bound \({\underline{v}}\left( Z\right) \) of all leaves Z of our branching tree.
The above summary of our branch and bound algorithm closes the theoretical part of this paper. In the next section, we perform an extensive computational study to evaluate the performance of our approach.
8 Computational study
In this section, we first carefully construct a set of hard robust problems, which we then use to experimentally compare our branch and bound algorithm with other approaches from the literature. Afterwards, we perform several tests on the robust knapsack problem to further demonstrate different trends and effects of our branch and bound algorithm. All experiments have been implemented in Java 11 and are performed on a single core of a Linux machine with an Intel® CoreTM i7-5930K CPU @ 3.50GHz, with 4 GB RAM reserved for each calculation. All LPs and MILPs are solved using Gurobi version 9.1.0 [26] in single thread mode and all other settings at default.
All implemented algorithms [23] and benchmark instances [24] are freely available online for further use.
8.1 Instance generation
In order to avoid a bias towards certain combinatorial problems, we generate robust instances on the basis of the diverse MIPLIB 2017 [25]. To transform a given nominal problem from the MIPLIB 2017 into a robust problem, we have to decide which objective coefficients \(c_{i}\) are uncertain, that is \({\hat{c}}_{i}>0\), how large the corresponding deviations \({\hat{c}}_{i}\) are, and what our robustness budget \(\varGamma \) is. In real-world applications, a coefficient is uncertain if, for example, it is the result of a forecast or a measurement. In [12, 14, 16], a coefficient is expected to be a result of such procedures, and thus uncertain, if it is an “ugly” number. In particular, integer values are considered “non-ugly” and are assumed to be certain. However, since many MIPLIB instances only contain integer values, treating all integer objective coefficients as certain would leave us with few instances for our study. Therefore, we take a middle course by considering \(c_{i}\) to be certain only if we have \(c_{i}\in \left\{ -1,0,1\right\} \) in the nominal instance, since it is unlikely that \(c_{i}\) is the result of a forecast or measurement in this case. Coefficients \(c_{i}\in \left\{ -1,1\right\} \) usually do not represent a numerical objective value for \(x_{i}\), but are for counting the number of chosen variables. Moreover, \(c_{i}=0\) suggests that the choice of \(x_{i}\) has no direct effect on the objective at all. Regarding the choice of the deviations, in [12, 14, 16, 20] a fixed percentage of the absolute nominal coefficient is considered, i.e., \({\hat{c}}_{i}=\xi \left| c_{i}\right| \) for uncertain objective coefficients, where \(\xi \) ranges from from \(0.01\%\) to \(2\%\) across the different studies. Furthermore, the robustness budget \(\varGamma \) is chosen from a predefined set of arbitrarily fixed values [14, 16, 20].
Note that the aforementioned studies not only consider uncertain objective coefficients, but also uncertainties in the constraints. Bearing this in mind, the above choices may be appropriate in the respective settings for illustrating the effect of uncertainty [12, 16] and the creation of sufficiently hard instances [14, 20]. Nevertheless, we advocate for a different choice of \({\hat{c}}_{i}\) and \(\varGamma \) in order to construct instances with which we can test our algorithms to their limits. In the following, we study the impact of \({\hat{c}}_{i}\) and \(\varGamma \) on the integrality gap of \(\text {ROB}\) to evaluate how they should be chosen to obtain hard instances.
Just like in the literature, we define our deviations \({\hat{c}}_{i}=\xi _{i}\left| c_{i}\right| \) with respect to the nominal coefficients. However, the factor \(\xi _{i}\) is chosen independently for each uncertain coefficient from an interval \(\left[ {\underline{\xi }},{\overline{\xi }}\right] \). In order to see whether a strong correlation between \({\hat{c}}_{i}\) and \(c_{i}\) raises the integrality gap, we test different ranges \(\left[ {\underline{\xi }},{\overline{\xi }}\right] \) with a fixed middle value \(\left( {\underline{\xi }}+{\overline{\xi }}\right) /2\). We also test much higher values \(\xi _{i}\), compared to the values chosen in [12, 14, 16, 20], since large deviations result in more difficult problems and deviations of even more than \(100\%\) are relevant in practice, as observed in [29].
The choice of \(\varGamma \) must be made especially carefully. For a problem \(\text {ROB}\), let \(n^{\text {ROB}}\) be the number of uncertain variables contributing to an arbitrary optimal solution. If \(\varGamma =0\) or \(\varGamma \ge n^{\text {ROB}}\) holds then either none or all coefficients of the chosen uncertain variables deviate to their maximum. This not only leads the idea of budgeted robust optimization to absurdity, but also results in a relatively small integrality gap. Hence, \(\varGamma \) should be somewhere between 0 and \(n^{\text {ROB}}\) to obtain a difficult instance. Accordingly, choosing \(\varGamma \) from a fixed set of values for all instances is not appropriate for our purpose, as, e.g., \(\varGamma =100\) may be suitable for large instances, while it is way too high for the smaller ones. Obviously, we cannot choose \(\varGamma \) with respect to \(n^{\text {ROB}}\), as we do not know the exact value in advance. Furthermore, in contrast to a practitioner solving a real problem, we have no insight into the structure of the diverse problems from the MIPLIB 2017. Hence, our best bet is to solve the nominal problem first, count the number \(n^{\text {NOM}}\) of uncertain variables appearing in the obtained optimal solution, and choose \(\varGamma \) relative to \(n^{\text {NOM}}\). We will see in the following that for the choice \(\varGamma =\gamma n^{\text {NOM}}\), there is a correlation between \(\gamma \) and the integrality gap of \(\text {ROB}\).
Before determining the integrality gap of \(\text {ROB}\) for different choices of \({\hat{c}}_{i}\) and \(\varGamma \), we have to select the nominal instances to be transformed into robust problems. Naturally, not all instances from the MIPLIB 2017 are suitable for this transformation. Of the available 1065 instances, we consider the ones that are labeled to be feasible, have an objective function, and consist only of binary variables. Furthermore, we only consider instances that have the “easy” label, as we cannot expect to solve the robust counterpart of hard instances. After this first selection, we try to solve the remaining 123 nominal instances within one hour using Gurobi. Of the instances that could be solved, we select those whose computed optimal solution contains at least ten uncertain variables, i.e., \(n^{\text {NOM}}\ge 10\). This ensures that variables with uncertain coefficients have an impact on the optimal solution. From the remaining instances, we also had to exclude pb-fit2d and supportcase11 due to numerical issues. After this final selection, we are left with 67 nominal instances for our computational study.
For these 67 instances, we construct robust problems by choosing \(\varGamma =\left\lceil \gamma n^{\text {NOM}}\right\rceil \), with \(\gamma \in \left\{ 0\%,10\%,20\%,\ldots ,200\%\right\} ,\) as well as \({\hat{c}}_{i}=\xi _{i}\left| c_{i}\right| \), where \(\xi _{i}\) is an independent and uniformly distributed random integer percentage within an interval \(\left[ {\underline{\xi }},{\overline{\xi }}\right] \). Here, we choose \(\left[ {\underline{\xi }},{\overline{\xi }}\right] \in \left\{ \left[ 10\%,90\%\right] ,\left[ 30\%,70\%\right] ,\left[ 45\%,55\%\right] ,\left\{ 50\%\right\} \right\} \). For each resulting robust problem, we solve the linear relaxation, try to compute an optimal integer solution using our branch and bound algorithm, and determine the integrality gap. For a fair comparison of the integrality gap with respect to different choices of \(\gamma \) and \(\left[ {\underline{\xi }},{\overline{\xi }}\right] \), we only consider the 44 underlying nominal instances for which we were able to compute an optimal solution for all combinations of \(\gamma \) and \(\left[ {\underline{\xi }},{\overline{\xi }}\right] \). As we are interested in the impact of \(\gamma \) and \(\left[ {\underline{\xi }},{\overline{\xi }}\right] \), and not of the nominal instance, we normalize the integrality gaps by dividing each gap by the maximum gap over all combinations of \(\gamma \) and \(\left[ {\underline{\xi }},{\overline{\xi }}\right] \) for the respective instance. Figure 1 shows for all combinations of \(\gamma \) and \(\left[ {\underline{\xi }},{\overline{\xi }}\right] \) the mean of the normalized integrality gaps over all considered instances. For all choices of \(\left[ {\underline{\xi }},{\overline{\xi }}\right] \), the mean integrality gap first increases monotonically in \(\gamma \), peaks at latest at \(\gamma =100\%\) and decreases afterwards. This suggests that, at least for most problems, the maximum integrality gap is achieved for a value \(\varGamma \) somewhere in \(\left[ 0,n^{\text {NOM}}\right] \). We take this into account by choosing \(\gamma \in \left\{ 10\%,40\%,70\%,100\%\right\} \) in our computational study. Note that \(\gamma =100\%\) is most likely way too conservative for a practical problem. However, we are not interested in constructing meaningful practical instances, but instances where uncertainty contributes to the difficulty of the problem.
Regarding the deviations, the integrality gap is higher for narrow intervals \(\left[ {\underline{\xi }},{\overline{\xi }}\right] \), suggesting that a strong correlation between \({\hat{c}}_{i}\) and \(c_{i}\) results in hard robust instances. Although choosing \({\underline{\xi }}={\overline{\xi }}\) seems to be beneficial in this regard, we chose \({\underline{\xi }}\ne {\overline{\xi }}\) for our computational study, since fixing \(\xi _{i}\) may result in structural properties that lead to a biased performance of the tested algorithms. For example, Monaci and Pferschy [36] showed that an adaptation of the classical greedy heuristic for the binary knapsack problem has a better worst-case performance for the robust knapsack if \(\max \left\{ \xi _{i}/\xi _{j}\big |i,j\in \left[ n\right] \right\} \) is small. Moreover, our branch and bound algorithm would particularly benefit from choosing \({\underline{\xi }}={\overline{\xi }}\), as this usually provides a smaller set \({\mathscr {Z}}\) of possible values for z. Therefore, we choose \(\left[ {\underline{\xi }},{\overline{\xi }}\right] =\left[ 45\%,55\%\right] \) in our computational study and additionally take smaller and larger deviations into account by also considering \(\left[ {\underline{\xi }},{\overline{\xi }}\right] \in \left\{ \left[ 5\%,15\%\right] \left[ 95\%,105\%\right] \right\} \).
8.2 Impact of components of the branch and bound algorithm
Before comparing the branch and bound algorithm with approaches from literature, we first evaluate the different components described in the previous sections. More precisely, we disable components to test their impact on the performance, leading to the following variants of our branch and bound algorithm.
- BnB:
-
is our branch and bound algorithm as in Algorithm 3.
- BnB-Clique:
-
does not compute the conflict graph and cliques from Sect. 5.
- BnB-Filter:
-
does not filter \({\mathscr {Z}}\) as in Sect. 6, i.e., \({\mathscr {Z}}=\left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \).
- BnB-Estimators:
-
does not derive estimators from one \(\text {ROB}\left( Z\right) \) to another as in Sect. 7.1.1.
- BnB-CutLP:
-
does not use optimality-cuts for solving linear relaxations as in Sect. 7.1.2.
- BnB-CutMILP:
-
does not use optimality-cuts for robust subproblems as in Sect. 7.1.2.
- BnB-Cut:
-
does not use optimality-cuts at all.
- BnB-Primal:
-
does not improve primal bounds as in Sect. 7.2.
- BnB-Terminate:
-
does not terminate robust subproblems as in Sect. 7.3, but solves them to optimality.
- BnB-Branching:
-
does not choose the branching point \(\theta \) as in Sect. 7.3, but chooses \(\theta =z\).
Note that disabling some components can also have an effect on other components. The computation of cliques not only prevents us from using reformulation \(\text {ROB}\left( {\mathscr {Q}}\right) \), but also worsens the filtering of \({\mathscr {Z}}\) and the estimators \(\delta _{z}\left( z'\right) \). Disabling estimators allows us to terminate robust subproblems \(\text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \) more aggressively, as raising the dual bound \({\underline{v}}\left( \text {ROB}\left( Z,\underline{\text {c}},\overline{\text {c}}\right) \right) \) past the current primal bound \({\overline{v}}\) is no longer beneficial. Furthermore, disabling optimality-cuts for robust subproblems allows us to use estimators \(\delta _{z}\left( z'\right) \) for \(z'\notin \left[ \underline{\text {c}},\overline{\text {c}}\right] \).
We use the ten variants above to solve the \(67\cdot 3\cdot 4=804\) robust instances (67 nominal instances, 3 different \(\left[ {\underline{\xi }},{\overline{\xi }}\right] \), 4 different \(\gamma \)) constructed in the previous section within a time limit of 3600 s, including preprocessing, construction of subproblems, etc. Detailed results per instance and algorithm are provided in a supplementary electronic file.
The plots in Fig. 2 give an indicator of the performances on an aggregate level by showing for all variants the proportion of instances that could be solved within a specific number of seconds. Figure 2a suggests that disabling the filtering of the set \({\mathscr {Z}}\) of possible values for z barely makes a difference for our branch and bound algorithm. In contrast, disabling cliques or estimators heavily affects the algorithm’s performance. After 3600 s, the default algorithm solves around 5% instances more than these two variants.
Surprisingly, Fig. 2b shows that disabling optimality-cuts (especially for linear programs) slightly improves the performance for the tested instances. A detailed look at the computational results shows that the impact of optimality-cuts can differ highly between instances. This is partially because the different variants solve different robust subproblems, whose complexity can vary significantly. However, there is also a synergy between our branching strategy, described in Sect. 7.5, and the disabling of optimality-cuts for linear relaxations. Although it seems unintuitive, the addition of optimality-cuts for linear relaxations often results in an increase in the number of nodes in our branching tree, which is partially due to the following reason. Consider a node \(Z\subseteq {\mathscr {Z}}\) such that all solutions x obeying the optimality-cuts for \({\underline{z}},{\overline{z}}\) are far off from being optimal. Furthermore, let \(\left( x,p,z\right) \in {\mathscr {P}}\left( Z,{\mathscr {Q}}\right) \) be an optimal solution for the linear relaxation without optimality-cuts. We observed for many instances that in this case \(z\in \left\{ {\underline{z}},{\overline{z}}\right\} \) holds and thus the linear formulation is as strong as the bilinear formulation according to Proposition 1. Hence, we stop branching the node due to our branching strategy, and directly solve \(\text {ROB}^{\text {S}}\left( Z,{\mathscr {Q}}\right) \) as an MILP, which usually leads to a quick pruning of Z. In contrast, when adding optimality cuts, z usually lies in the inner of the interval \(\left[ {\underline{z}},{\overline{z}}\right] \) which often results in further unnecessary branching. This observation suggests that the current branching strategy has potential for further improvement in future research. In the current state of the algorithm, it is reasonable to test whether using optimality-cuts is useful when solving a practical problem.
Figure 2c shows that terminating robust subproblems prematurely improves the algorithm’s performance and results in solving around \(2\%\) instances more. Choosing the branching point \(\theta \) as a convex combination of the solution value z and the middle of the interval \(\left( {\underline{z}}+{\overline{z}}\right) /2\) seems to have a marginal positive effect. The same holds for the improvement of the primal bound via computing optimal z for incumbent solutions, which suggests that our approach for selecting nodes \(Z\subseteq {\mathscr {Z}}\) containing promising z is very effective. We already stated in Sect. 7.2 that most of the time, we already have a (nearly) optimal solution after solving the very first robust subproblem. For our test instances, the relative gap between the best known solution value after the first robust subproblem and the primal bound after 3600 s is below \(10^{-2}\) for \(99\%\) of all instances and even below \(10^{-4}\) for \(87.8\%\) of all instances. When disabling the improvement of incumbent solutions, this still holds for more than \(94.5\%\) (below \(10^{-2}\)) and \(69\%\) (below \(10^{-4}\)) of all instances respectively.
Another noteworthy setting is the one in which estimators and improvement of primal bounds are disabled together. This version of BnB still solves \(76.7\%\) of all instances, and thus outperforms all approaches from literature, as we will see in the next section. The setting is of particular interest, since it only relies on results that are also generalizable to uncertain constraints with budget uncertainty. Here, the j-th constraint \(\sum _{i\in \left[ n\right] }a_{ji}\ge b_{j}\) of the constraint matrix \(Ax\ge b\) would become \(\sum _{i\in \left[ n\right] }\left( a_{ji}-p_{ji}\right) -\varGamma _{j}z_{j}\ge b\) with additional constraints \(z_{j}+p_{ji}\ge {\hat{a}}_{ji}x_{i}\) for deviations \({\hat{a}}_{ji}\) and a constraint specific budget \(\varGamma _{j}\). Since the additional constraints have the same structure as for the uncertain objective function, we can branch on the variables \(z_{j}\), use clique reformulations, filter possible values for \(z_{j}\), and add optimality cuts. Estimators and the improvement of primal bounds cannot be generalized, since these rely on the fact that a feasible solution for a fixed z has a corresponding feasible solution for a different \(z'\), which does not apply when fixing \(z_{j}\) to different values. The observation that the generalizable results yield a well-performing branch and bound algorithm for uncertain objective functions suggests that our approach and the theoretical results in this paper might also be relevant for robust optimization with uncertain constraints.
8.3 Comparing algorithms from the literature
We now evaluate our branch and bound approach by comparing BnB-CutLP with the following eight algorithms.
- ROB:
-
is the MILP over the standard formulation \({\mathscr {P}}_{\text {ROB}}\).
- SEP:
-
is the cutting-plane approach separating scenarios from the uncertainty set, as described in [14].
- BS:
-
is the approach of Bertsimas and Sim [15] solving nominal subproblems \(\text {NOS}\left( z\right) \) for all \(z\in \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \).
- DnC:
-
is the divide and conquer algorithm of Hansknecht et al. [27] making use of Lemma 3.
- RP1,...,RP4:
-
are the corresponding reformulations of Atamtürk [5].
The approaches ROB, SEP, and BS are widely known and studied, and can thus be considered as the current state-of-the-art approaches. In contrast, DnC has so far only been considered for robust shortest path problems and was not evaluated for general robust optimization problems [27]. To the best of our knowledge, we also present the first study that evaluates the reformulations RP1,...,RP4 on a set of instances based on real-world problems.
In our implementation, we slightly adapt RP2 and RP3 compared to [5]. Reformulation RP2 consists of an exponential number of valid inequalities that are separated in \({\mathscr {O}}\left( n^{2}\right) \) by searching for negative weighted paths in an acyclic directed graph. Atamtürk shows that a subset of these inequalities is sufficient to define the convex hull of
It is easy to see that the graph constructed in [5] can be modified by deleting some arcs, such that there exists a one-to-one correspondence between paths in the graph and inequalities defining the convex hull. We use this reduced graph for our implementation. Reformulation RP3 incorporates the valid inequalities of RP2 by adding \(n+2\) additional variables and \({\mathscr {O}}\left( n^{2}\right) \) constraints. Similar to the graph for the separation problem some of these constraints can be omitted, resulting in a smaller formulation.
Just like in the previous section, we use the different algorithms to solve our 804 robust instances within a time limit of 3600 s. Again, detailed results per instance and algorithm are provided in a supplementary electronic file. Figure 3 shows for all algorithms the proportion of instances that were solved in a specific number of seconds. It is evident that our branch and bound algorithm outperforms all existing approaches from the literature by far, solving \(83.8\%\) of all instances in 3600 s. Among all other algorithms, DnC solves the most instances, ending at \(55.3\%\) after 3600 s. In comparison, BnB-CutLP only needs 220 s to solve \(55.3\%\) of all instances. ROB solves less problems (\(53.1\%\)) than DnC but is faster in the beginning, solving more problems in shorter time. SEP solves only \(31.6\%\) of all instances and thus performs significantly worse than ROB. Interestingly, this is in contrast to the findings of Bertsimas et al. [14], who observed no clear winner between these two approaches for robust problems with uncertain constraints. BS solves more instances (\(45.9\%\)) than SEP but is still clearly worse than ROB and DnC, supporting our claim from the introduction that BS is not practical if the number of different deviations \(\left| \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \right| \) is large. Of the four reformulations of Atamtürk, RP2 is the only practicable one, solving \(49.1\%\) of all instances. This is because RP1, RP3, and RP4 are simply too large for most practical problems. RP1 exceeds the memory limit of 4 GB for \(29.9\%\) of all instances, RP3 for \(20.9\%\) and RP4 even for \(36.1\%\). Even if the models can be build obeying the memory limit, they are most of the time still too large for Gurobi to solve them. RP1 was not even able to solve the linear relaxation of the root node for \(5.8\%\) of all instances. For RP3 and RP4, this was the case for \(44.8\%\) and \(12.1\%\) of all instances respectively.
Obviously, many of the robust instances are very difficult to solve. Thus, in practice, one might also be satisfied obtaining a nearly optimal solution. Figure 4 shows the proportion of instances that are solved up to a specified relative optimality gap within the time limit of 3600 s. Our branch and bound algorithm also clearly outperforms the other algorithms in this regard. BnB-CutLP solves \(94\%\) of all instances to the optimality gap of \(1\%\) and \(98.8\%\) to the gap of \(10\%\). In contrast, ROB, which is the second best performing algorithm, only solves \(78.9\%\) of all instances to the optimality gap of \(10\%\). Note that the line corresponding to BS is nearly horizontal, as the dual bound computed by BS equals the minimum dual bound over all nominal subproblems, and is thus negative infinity before all \(z\in \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \) have been considered. Therefore, we usually either solve an instance to the optimality gap of \(10^{-4}\) or report an infinite gap. The small increase in instances solved before \(1\%\) is due to an error of Gurobi occurring for robust instances emerging from the nominal instance neos-1516309. For these problems, Gurobi solves all nominal subproblems within the time limit, but reports for some a dual bound that is too low. For a fair comparison, we still consider these instances to be solved to optimality.
In order to evaluate the impact of the deviations \({\hat{c}}_{i}\) and the robustness budget \(\varGamma \) on the algorithms’ performances, we report in Table 1 the proportion of instances solved for every combination of \(\left[ {\underline{\xi }},{\overline{\xi }}\right] \) and \(\gamma \). Our branch and bound approach solves consistently for every setting more instances than any other algorithm and has a relatively stable performance for the different choices of \(\left[ {\underline{\xi }},{\overline{\xi }}\right] \). This is in contrast to ROB, which performs significantly worse for higher deviations, as these weaken the formulation. ROB also performs worse for \(\gamma \) around \(40\%\) and \(70\%\), which supports our claim from Sect. 8.1 that choosing \(\varGamma \) somewhere within \(\left[ 0,n^{\text {NOM}}\right] \) results in hard problems. For BnB-CutLP, the performance increases for higher \(\gamma \), as the set of possibly optimal values \({\mathscr {Z}}\) for z decreases. Higher \(\gamma \) are also beneficial for BS, as for these, the optimal choice for z is smaller and thus found faster when iterating over \(\left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \). Hence, we find a good primal bound early on, which can be used to terminate the remaining nominal subproblems once their respective dual bounds are high enough.
8.4 Improving algorithms from literature
We close our computational study on the MILIB instances by showing that the theoretical results from this paper can also be used to significantly improve most of the algorithms considered in the previous section. An obviously improvement for ROB is to compute a partitioning into cliques, determine \({\hat{c}}_{i^{\max }}\), the highest possible optimal value for z as in Sect. 6, and solve the reformulation \(\text {ROB}^{\text {S}}\left( \left[ 0,{\hat{c}}_{i^{\max }}\right] ,{\mathscr {Q}}\right) \) instead of the original one. In the following, we call this approach ROB+. For improving RP4, recall that the reformulation combines the nominal subproblems \(\text {NOS}\left( z\right) \) for all \(z\in \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \) into one problem. However, it is sufficient to define \(\text {RP4}\) for the filtered set \({\mathscr {Z}}\) of possible optimal values for z, instead of the set of all deviations \(\left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \). An analogous reduction can be applied for the reformulation \(\text {RP1}\), which is quite similar to \(\text {RP4}\). In the following, we call the approaches using these reduced reformulations RP1+ and RP4+.
The algorithm that can be improved the most is the DnC of Hansknecht et al. [27]. DnC chooses specific values \(z\in \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \), solves the corresponding nominal subproblems \(\text {NOS}\left( z\right) \), and computes dual bounds for other \(z'\in \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{n}\right\} \) on the basis of Lemma 3 until all z are either pruned or considered for a nominal subproblem. To improve DnC, we only consider values for z within the filtered set \({\mathscr {Z}}\) and use the estimators from Theorem 3 instead of the ones from Lemma 3. Furthermore, we apply optimality-cuts for the nominal subproblems, with \(\underline{\text {c}},\overline{\text {c}}\) chosen analogously as in Sect. 7.1.2. We also improve incumbent solutions by computing the corresponding optimal z and terminate nominal subproblems prematurely, analogously to Sects. 7.2 and 7.3. The improved DnC is called DnC+ in the following.
While the approaches SEP, RP2, and RP3 cannot be improved using our theoretical results, BS could be enhanced similarly to DnC. However, we do not consider an improved version of BS, since it is essentially a strictly weaker algorithm compared to DnC.
We again report results per instance and algorithm in a supplementary electronic file and show aggregate results in Fig. 5. We see that computing a partitioning into cliques and \({\hat{c}}_{i^{\max }}\) pays off, as the improved formulation used for ROB+ enables us to solve \(57.2\%\) instances, compared to \(53.1\%\) for ROB. The filtering of \({\mathscr {Z}}\) is also effective for reducing the size of the reformulations \(\text {RP1}\) and \(\text {RP4}\). RP1+ exceeds the memory limit for \(19.4\%\) of all instances, instead of \(29.9\%\). For RP4+, this reduction is from \(36.1\%\) to \(29.4\%\). Both approaches also solve more instances within the time limit. RP1+ solves \(19.7\%\) instead of \(17.9\%,\) while RP4+ even solves \(20.5\%\) instead of \(11.9\%\). Nevertheless, both reformulations are still way too large for most problems and cannot compete with the other approaches. This is especially true in comparison with DnC+, which performs significantly better than DnC, solving \(83\%\) of all instances instead of \(55.3\%\). In fact, DnC+ performs similar to our branch and bound approach. While DnC+ solves more instances early on, BnB-CutLP solves slightly more instances within 3600s (\(83.8\%\)). A glance at the proportion of instances solved within a specific relative optimality gap, shown in Fig. 6, indicates that our branch and bound is indeed slightly better than DnC+ in solving very hard instances, as BnB-CutLP still solves clearly more instances (\(94\%\)) to the optimality gap of 1% than DnC+ (\(89.4\%\)).
We close this section with an evaluation of the improvements applied to DnC+. We do so by disabling the components individually, analogously to Sect. 8.2. Figure 7a shows that disabling the filtering of \({\mathscr {Z}}\) and the computation of clique partitionings lead to a slight degradation in performance. Both variants solve \(82.5\%\) of all instances instead of \(83\%\). While the effect of disabling the filtering is similar for BnB and DnC+, the partitioning into cliques is much more important for BnB than it is for DnC+. This is because DnC+ only uses the cliques for improving the filtering and the estimators of Theorem 3, but BnB also relies on the strengthened clique reformulation. Using the estimators from Lemma 3 instead of Theorem 3 significantly worsens the algorithm, solving only \(78.9\%\) of all instances. Figure 7b reveals that disabling the improvement of primal bounds, the termination of robust subproblems or optimality-cuts is also hindering. In contrast to BnB, which chooses nodes based on the linear relaxation, DnC+ selects many values for z that are not promising. Accordingly, improving the incumbent solutions for the corresponding subproblems and terminating them early is much more important to DnC+ compared to BnB. Disabling the improvement of primal bounds results in solving 81.5% of all instances. Disabling the termination of robust subproblems even leads to solving only \(77.6\%\) of the instances. Surprisingly, the addition of optimality-cuts has the largest impact on DnC+, although we observed that they slightly worsen BnB in the current implementation. With optimality-cuts disabled, we only solve \(75.6\%\) of all instances. This shows the potential of the optimality-cuts and raises hope that they can also be a helpful addition to our branch and bound approach with further engineering.
8.5 When to use branch and bound or divide and conquer
We have seen that both our branch and bound algorithm and our improved version of the divide and conquer perform exceptionally well compared to the other approaches from literature, with BnB-CutLP solving slightly more instances and DnC+ being faster on the easier ones. We close our computational study with a more detailed comparison of these algorithms, providing some guidance on which algorithm to use in different practical settings.
A major strength of our branch and bound is that we only need to solve very few robust subproblems \(\text {ROB}\left( Z\right) \). Considering only the instances that were solved by both BnB-CutLP and DnC+, BnB-CutLP solves on average 7.9 subproblems, while DnC+solves 13.9 subproblems \(\text {NOS}\left( z\right) \). Furthermore, as already stated in Sect. 8.2, our branch and bound finds (nearly) optimal solutions within the very first subproblem, resulting in a fast termination of the following ones. Despite this advantage, DnC+ solves many instances faster than BnB-CutLP. The reason for this is that solving the linear relaxations over \({\mathscr {P}}^{\text {S}}\left( Z,{\mathscr {Q}}\right) \) can require surprisingly much time. In fact, considering only the solved instances, BnB-CutLP spends on average \(33.1\%\) of its time solving LPs, although we only consider 45.9 of these on average. To further demonstrate the relevance of the LPs for the computation time and better understand the underlying effects, we provide an additional computational study on the robust knapsack problem.
In order to construct hard instances of the robust knapsack problem
for a number of items \(n\in {\mathbb {N}}\), we first select independent and uniformly distributed weights \(a_{i}\in \left[ 10{,}000\right] \) for all \(i\in \left[ n\right] \). Afterwards, we choose profits \(c_{i}=\left\lceil \zeta _{i}a_{i}\right\rceil \), where \(\zeta _{i}\in \left[ 0.95,1.05\right] \) is an independent and uniformly distributed random variable. This choice is based on the observation that the profits and weights should be correlated, as otherwise many items can be excluded easily due to domination [39]. Similar to Sect. 8.1, we choose deviations \({\hat{c}}_{i}=\left\lceil \xi _{i}c_{i}\right\rceil \), where the random variable \(\xi _{i}\in \left[ 0.45,0.55\right] \) is again independent and uniformly distributed. The capacity b and robustness budget \(\varGamma \) depend on the number of items n. We choose \(b=\min \left\{ \frac{n}{2},1000\right\} \cdot 5000\), i.e., we can store \(\min \left\{ \frac{n}{2},1000\right\} \) items of average weight into the knapsack. Note that we choose the minimum of \(\frac{n}{2}\) and 1000 such that the capacity doesn’t become too large for the sake of numerical stability. Finally, we choose \(\varGamma =\frac{\min \left\{ \frac{n}{2},1000\right\} }{2}\), i.e., approximately half of the included items will deviate from their nominal weight, which results in hard instances according to our observations regarding Table 1.
In Table 2, we show computational results for different numbers of items ranging from \(n=50\) to \(n=1{,}000,000\). For every n, we generate 10 different instances to test the algorithms ROB, ROB+, DnC, DnC+, and BnB-CutLP. As before, all algorithms are given a time limit of 3600 s. For ROB and ROB+, Table 2 shows the number of instances that could not be solved to optimality within the time limit and the mean time in seconds used for the instances that could be solved to optimality. The generated instances are apparently quite hard, as ROB and ROB+ already fail to solve nine out of ten instances with \(n=100\) items. Note that ROB+ has a noticeable advantage over ROB although there exist no conflicts between items which ROB+ could make use of. The advantage depends solely on filtering the possible values \({\mathscr {Z}}\) and solving the problem \(\text {ROB}\left( {\mathscr {Z}}\right) \).
Still, the performance of ROB+ is not even close to the performance of the other three algorithms. As DnC, DnC+, and BnB-CutLP are able to solve all instances, we omit the timeout column for these algorithms in Table 2. The mean computation time in seconds reveals that DnC+ performs especially well. This is partially due to the nominal knapsack subproblems \(\text {NOS}\left( z\right) \) being quite easy to solve. Furthermore, DnC+ considers on average only 25.3 subproblems for \(n=1{,}000{,}000\) items, compared to an average of 165.6 subproblems that are solved by DnC.
BnB-CutLP even solves only one robust subproblem \(\text {ROB}\left( Z\right) \) for each knapsack instance and on average 24.2 linear relaxations over \({\mathscr {P}}^{\text {S}}\left( Z\right) \) for \(n=1{,}000{,}000\) items. Nevertheless, its performance degrades for higher n as solving the LPs becomes more and more challenging. For \(n=1{,}000{,}000\), BnB-CutLP spends on average \(93.17\%\) of its time solving linear relaxations. This is due to the up to \(n+1\) additional variables \(p',z'\) and n additional constraints \(p_{i}'+z'\ge \left( \min \left\{ {\hat{c}}_{i},{\overline{z}}\right\} -{\underline{z}}\right) ^{+}x_{i}\) contained in formulation \({\mathscr {P}}^{\text {S}}\left( Z\right) \). Interestingly, the very first LP corresponding to the root node \(Z={\mathscr {Z}}\) is by far the hardest one and requires on average 1062 s for \(n=1,000,000\) items. After branching on z, the LPs become easier, since the tighter bounds \({\underline{z}},{\overline{z}}\) lead to many constraints \(p_{i}'+z'\ge \left( \min \left\{ {\hat{c}}_{i},{\overline{z}}\right\} -{\underline{z}}\right) ^{+}x_{i}\) becoming redundant for \({\underline{z}}\ge {\hat{c}}_{i}\) or at least less impactful for small \({\overline{z}}-{\underline{z}}\). In fact, the single robust subproblem \(\text {ROB}\left( Z\right) \) that we solve for each knapsack instance only requires 74.8 s on average for \(n=1{,}000{,}000\), and is thus significantly easier than the LP of the root node.
These observations suggest that our branch and bound could benefit drastically from further research on how to solve the linear relaxation of the robust problem. As of now, the branch and bound seems to have an advantage for problems where the MILP subproblems \(\text {ROB}\left( Z\right) \) and \(\text {NOS}\left( z\right) \) dominate the problem’s complexity, while our version of the divide and conquer should be used if the linear relaxations over \({\mathscr {P}}^{\text {S}}\left( Z,{\mathscr {Q}}\right) \) are hard to solve.
9 Conclusion
In this paper, we considered robust binary optimization problems with budget uncertainty in the objective, which are tractable in theory, but often hard to solve in practice. We identified that the standard formulation for solving these problems is weak and that the variable z is critical in this regard. To address this issue, we proposed a compact bilinear formulation that is as strong as theoretically possible. To benefit from the formulation’s strength in practice, we derived a strong linear formulation for the case where z is bounded. Building upon this linear formulation and many structural properties of the robust problem, we proposed a branch and bound algorithm in which we obtain bounds on z via branching.
To test the algorithms strength, we compared it to other sophisticated algorithms from the literature within a comprehensive computational study. For this, we carefully generated a set of hard robust instances based on real-world problems from the MIPLIB 2017, which we made available online [24] together with the implemented algorithms [23]. The computational results show that our algorithm outperforms all existing approaches by far. Furthermore, we showed that the structural properties shown in this paper can be used to substantially improve the divide and conquer approach by Hansknecht et al. [27], providing us with two potent algorithms for robust optimization.
For future research, the different components of our approach leave much room for engineering to further enhance the branch and bound algorithm. Additionally, it would be interesting to test our approach for robust optimization with uncertain constraints. We already mentioned that most theoretical results can be generalized to this case and showed that our algorithm performs well relying only on these general results.
Data Availability Statement
All test instances used in our computational study are published and available for download, sharing, and reuse, see [24].
Code availibility
The branch and bound algorithm and all other tested approaches have been implemented in Java and are available on GitHub, see [23].
References
Achterberg, T., Bixby, R.E., Gu, Z., Rothberg, E., Weninger, D.: Presolve reductions in mixed integer programming. INFORMS J. Comput. 32(2), 473–506 (2020)
Achterberg, T., Koch, T., Martin, A.: Branching rules revisited. Oper. Res. Lett. 33(1), 42–54 (2005)
Achterberg, T., Wunderling, R.: Mixed integer programming: analyzing 12 years of progress. In: Facets of Combinatorial Optimization, pp. 449–481. Springer (2013)
Álvarez-Miranda, E., Ljubić, I., Toth, P.: A note on the Bertsimas & Sim algorithm for robust combinatorial optimization problems. 4OR 11(4), 349–360 (2013)
Atamtürk, A.: Strong formulations of robust mixed 0–1 programming. Math. Program. 108(2–3), 235–250 (2006)
Atamtürk, A., Nemhauser, G.L., Savelsbergh, M.W.: Conflict graphs in solving integer programming problems. Eur. J. Oper. Res. 121(1), 40–55 (2000)
Atamtürk, A., Nemhauser, G.L., Savelsbergh, M.W.: The mixed vertex packing problem. Math. Program. 89(1), 35–53 (2000)
Belotti, P., Lee, J., Liberti, L., Margot, F., Wächter, A.: Branching and bounds tightening techniques for non-convex minlp. Optim. Methods Softw. 24(4–5), 597–634 (2009)
Ben-Tal, A., El Ghaoui, L., Nemirovski, A.: Robust Optimization. Princeton university press, Princeton (2009)
Ben-Tal, A., Nemirovski, A.: Robust convex optimization. Math. Oper. Res. 23(4), 769–805 (1998)
Ben-Tal, A., Nemirovski, A.: Robust solutions of uncertain linear programs. Oper. Res. Lett. 25(1), 1–13 (1999)
Ben-Tal, A., Nemirovski, A.: Robust solutions of linear programming problems contaminated with uncertain data. Math. Program. 88(3), 411–424 (2000)
Bertsimas, D., Brown, D.B., Caramanis, C.: Theory and applications of robust optimization. SIAM Rev. 53(3), 464–501 (2011)
Bertsimas, D., Dunning, I., Lubin, M.: Reformulation versus cutting-planes for robust optimization. CMS 13(2), 195–217 (2016)
Bertsimas, D., Sim, M.: Robust discrete optimization and network flows. Math. Program. 98(1–3), 49–71 (2003)
Bertsimas, D., Sim, M.: The price of robustness. Oper. Res. 52(1), 35–53 (2004)
Bixby, R., Rothberg, E.: Progress in computational mixed integer programming: a look back from the other side of the tipping point. Ann. Oper. Res. 149(1), 37–41 (2007)
Brito, S.S., Santos, H.G.: Preprocessing and cutting planes with conflict graphs. Comput. Oper. Res. 128, 105176 (2021)
Fischetti, M., Glover, F., Lodi, A.: The feasibility pump. Math. Program. 104(1), 91–104 (2005)
Fischetti, M., Monaci, M.: Cutting plane versus compact formulations for uncertain (integer) linear programs. Math. Program. Comput. 4(3), 239–273 (2012)
Gabrel, V., Murat, C., Thiele, A.: Recent advances in robust optimization: an overview. Eur. J. Oper. Res. 235(3), 471–483 (2014)
Gamrath, G., Anderson, D., Bestuzheva, K., Chen, W.K., Eifler, L., Gasse, M., Gemander, P., Gleixner, A., Gottwald, L., Halbig, K., et al.: The scip optimization suite 7.0 (2020)
Gersing, T.: Algorithms for robust binary optimization (2022). https://doi.org/10.5281/zenodo.7463371
Gersing, T., Büsing, C., Koster, A.: Benchmark Instances for Robust Combinatorial Optimization with Budgeted Uncertainty (2022). https://doi.org/10.5281/zenodo.7419028
Gleixner, A., Hendel, G., Gamrath, G., Achterberg, T., Bastubbe, M., Berthold, T., Christophel, P.M., Jarck, K., Koch, T., Linderoth, J., Lübbecke, M., Mittelmann, H.D., Ozyurt, D., Ralphs, T.K., Salvagnin, D., Shinano, Y.: MIPLIB 2017: data-driven compilation of the 6th mixed-integer programming library. Math. Program. Comput. (2021). https://doi.org/10.1007/s12532-020-00194-3
Gurobi Optimization, LLC: Gurobi optimizer reference manual, version 9.1 (2021). http://www.gurobi.com
Hansknecht, C., Richter, A., Stiller, S.: Fast robust shortest path computations. In: 18th Workshop on Algorithmic Approaches for Transportation Modelling, Optimization, and Systems (ATMOS 2018). Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik (2018)
Karp, R.M.: Reducibility among combinatorial problems. In: Complexity of Computer Computations, pp. 85–103. Springer (1972)
Koster, A.M., Kutschka, M.: Network design under demand uncertainties: a case study on the abilene and geant network data. In: Photonic Networks, 12. ITG Symposium, pp. 1–8. VDE (2011)
Kouvelis, P., Yu, G.: Robust Discrete Optimization and Its Applications. Kluwer Academic Publishers, Boston (1997)
Kuhnke, S., Richter, P., Kepp, F., Cumpston, J., Koster, A.M., Büsing, C.: Robust optimal aiming strategies in central receiver systems. Renew. Energy 152, 198–207 (2020)
Land, A., Doig, A.: An automatic method of solving discrete programming problems. Econom.: J. Econom. Soc. pp. 497–520 (1960)
Lee, T., Kwon, C.: A short note on the robust combinatorial optimization problems with cardinality constrained uncertainty. 4OR 12(4), 373–378 (2014)
Linderoth, J.T., Savelsbergh, M.W.: A computational study of search strategies for mixed integer programming. INFORMS J. Comput. 11(2), 173–187 (1999)
Lodi, A., Zarpellon, G.: On learning and branching: a survey. TOP 25(2), 207–236 (2017)
Monaci, M., Pferschy, U.: On the robust knapsack problem. SIAM J. Optim. 23(4), 1956–1982 (2013)
Morrison, D.R., Jacobson, S.H., Sauppe, J.J., Sewell, E.C.: Branch-and-bound algorithms: a survey of recent advances in searching, branching, and pruning. Discrete Optim. 19, 79–102 (2016)
Park, K., Lee, K.: A note on robust combinatorial optimization problem. Manag. Sci. Financ. Eng. 13(1), 115–119 (2007)
Pisinger, D.: Where are the hard knapsack problems? Comput. Oper. Res. 32(9), 2271–2284 (2005)
Soyster, A.L.: Convex programming with set-inclusive constraints and applications to inexact linear programming. Oper. Res. 21(5), 1154–1157 (1973)
Speakman, E., Lee, J.: On branching-point selection for trilinear monomials in spatial branch-and-bound: the hull relaxation. J. Global Optim. 72(2), 129–153 (2018)
Wolsey, L.A.: Integer Programming. Wiley, London (2020)
Acknowledgements
We want to thank the anonymous referees for their kind, constructive, and thoughtful feedback which helped in improving the paper.
Funding
Open Access funding enabled and organized by Projekt DEAL. This work was partially supported by the German Federal Ministry of Education and Research (Grants no. 05M16PAA) within the project “HealthFaCT - Health: Facility Location, Covering and Transport”, the Freigeist-Fellowship of the Volkswagen Stiftung, and the German research council (DFG) Research Training Group 2236 UnRAVeL.
Author information
Authors and Affiliations
Contributions
Christina Büsing: Conceptualization, Writing—Review and Editing, Supervision, Project administration, Funding acquisition. Timo Gersing: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Data Curation, Writing—Original Draft, Writing—Review and Editing, Visualization. Arie Koster: Conceptualization, Writing—Review and Editing, Supervision, Project administration, Funding acquisition.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Implementation of conflict graph and clique partitioning
We restrict ourselves here to detecting conflicts between positive literals \(x_{i}\) of uncertain variables, as these are the only ones we need for our clique reformulation. In order to determine if there exists a conflict between two uncertain variables \(x_{i_{1}}\) and \(x_{i_{2}}\), we have to evaluate whether \(\left\{ x\in {\mathscr {X}}\big |x_{i_{1}}=x_{i_{2}}=1\right\} \) is empty. Since this is in general \({{\mathscr {N}}}{{\mathscr {P}}}\)-hard, we resort to a simpler problem. Let \(\sum _{i=1}^{n}a_{ji}x_{i}\le b_{j}\) be a row of the constraint matrix \(Ax\le b\) and let \(l_{i}\le x_{i}\le u_{i}\) be bounds on variable \(x_{i}\) for all \(i\in \left[ n\right] \). If
holds then \(x_{i_{1}}\) and \(x_{i_{2}}\) cannot both be equal to one and we can add an edge \(\left\{ x_{i_{1}},x_{i_{2}}\right\} \) to the conflict graph. In order to evaluate Inequality (8) efficiently for all pairs \(i_{1},i_{2}\), we first compute
by setting \(x_{i}=l_{i}\) for \(a_{ji}>0\) and \(x_{i}=u_{i}\) if \(a_{ji}<0\). Since the uncertain variables \(x_{i_{1}},x_{i_{2}}\) are binary, we have
and thus it is sufficient to evaluate whether
holds. In order to find conflicting variables \(x_{i_{1}},x_{i_{2}}\) having this property, we use Algorithm 4, which is similar to the one presented by Brito and Santos [18]. Instead of performing a pairwise evaluation, Algorithm 4 directly searches for subsets \(h\subseteq \left\{ x_{1},\ldots ,x_{n}\right\} \) forming a clique in the conflict graph. This is not only faster than a pairwise evaluation, but also beneficial for storing the conflict graph. Assume that a row of the constraint matrix implies conflicts of a large clique in the conflict graph. Atamtürk et al. [6] already mentioned that storing these conflicts as a set of edges or using adjacency lists consumes too much memory. Instead, one should use a separate structure to store these conflicts. Here, we store conflicts implied by cliques h with \(\left| h\right| =2\) in adjacency lists, while cliques with \(\left| h\right| >2\) are stored directly as a list of variables. To guarantee fast access to the cliques, we maintain for each variable a list of references to cliques in which it is contained. Thus, the memory requirement of adding a clique h is only \({\mathscr {O}}\left( \left| h\right| \right) \) instead of \({\mathscr {O}}\left( \left| h\right| ^{2}\right) \). In the following, we think of the conflict graph as a hyper graph \(G=\left( V,H\right) \), with \(V=\left\{ x_{1},\ldots ,x_{n}\right\} \) being the variables and \(H\subseteq 2^{V}\) being a set of hyper edges representing cliques in the conflict graph.

Algorithm 4 constructs this hyper graph by iterating over all constraints \(\sum _{i=1}^{n}a_{ji}x_{i} \le b_{j}\). For each constraint, we first compute \(b_{j}'\) (line 3) and the highest coefficient \(a^{*}\) occurring in the constraint (line 4). If we have \(2\max \left\{ a^{*},0\right\} \le b_{j}'\) then the constraint will imply no conflicts, which allows for a fast skipping of uninteresting constraints (line 5). Otherwise, we construct a list of candidates for which we have \(\max \left\{ a^{*},0\right\} +\max \left\{ a_{ji_{l}},0\right\} >b_{j}'\), that is the variable \(x_{i_{l}}\) either defines \(a^{*}\) or has a conflict with the variable defining \(a^{*}\) (line 6). If the list consists of more than one variable, i.e., the variable defining \(a^{*}\), then we have found a conflict (line 7). We sort the list of candidates (line 8) and find the lowest index \(l^{*}\) such that \(x_{i_{l^{*}}}\) and \(x_{i_{l^{*}+1}}\) are in conflict (line 9). Due to the ordering of the list, all variables \(\left\{ x_{i_{l^{*}}},\ldots ,x_{i_{k}}\right\} \) are in conflict with each other and can thus be added as a hyper edge to the conflict graph (line 10). For all variables \(x_{i_{p}}\) that do not belong to the hyper edge, we search for the lowest index \(l'\) such that \(x_{i_{p}}\) and \(x_{i_{l'}}\) are in conflict (line 12). Such an index exists, since \(x_{i_{p}}\) is in conflict with \(x_{i_{k}}\). Again, due to the ordering of the list, the variables \(\left\{ x_{i_{p}},x_{i_{l'}},\ldots ,x_{i_{k}}\right\} \) are in conflict and can be added to our graph (line 13).
Note that the hyper edge added in line 13 consists of a subset of the first hyper edge added to the constraint, starting at an index \(l'\), and an additional variable \(x_{i_{p}}\). Brito and Santos [18] pointed out that this can be used to store the graph more efficiently. Instead of storing the whole hyper edge \(\left\{ x_{i_{p}},x_{i_{l'}},\ldots ,x_{i_{k}}\right\} \), we only store the variable \(x_{i_{p}}\), a reference to the hyper edge \(\left\{ x_{i_{l^{*}}},\ldots ,x_{i_{k}}\right\} \) and the starting index \(l'\), from which we can reconstruct the hyper edge \(\left\{ x_{i_{p}},x_{i_{l'}},\ldots ,x_{i_{k}}\right\} \).

After constructing the conflict graph, we use Algorithm 5 to compute a partitioning of V into cliques. Algorithm 5 is a greedy heuristic that builds on the idea that a minimum clique cover consists without loss of generality only of cliques that are maximal with respect to inclusion. We first initialize a set of cliques \({\mathscr {Q}}=\emptyset \) and remaining nodes \(V'=V\) (line 1). Until there are nodes left for partitioning (line 2), we iteratively select an arbitrary remaining node \(v'\in V'\) (line 3) and construct a maximal clique \(Q\subseteq V'\) containing \(v'\). We initialize \(Q\) as the largest hyper edge on the remaining nodes \(h\cap V'\) containing \(v'\) (line 4 and 5). This speeds up the construction of \(Q\), since we do not have to check whether the variables in h are in conflict. We then expand \(Q\) by iteratively adding remaining nodes that are contained in the neighborhood of all current clique members (lines 6 to 10). Afterwards, we add this clique to our partitioning (line 11), remove the contained nodes from the remaining nodes (line 12), and proceed until no nodes are left.
Proof of Lemma 2
Lemma 2
For \(x\in {\mathbb {R}}^{n}\), we have
and
Proof
Recall that \({\underline{z}}\left( x\right) \) and \({\overline{z}}\left( x\right) \) are initially defined as
and
We first prove Equality (3). If we have \({\underline{z}}\left( x\right) =0\) then for all \(z>0\), it holds
and thus we have
For \({\underline{z}}\left( x\right) >0\), there exists an index \(j\in \left[ n\right] \) with \({\hat{c}}_{j}={\underline{z}}\left( x\right) \) and \({\hat{c}}_{j-1}<{\underline{z}}\left( x\right) \). It holds \(\sum _{i\in \left[ n\right] :{\hat{c}}_{i}\ge {\underline{z}}\left( x\right) }x_{i}>\varGamma \), as otherwise we would have
which contradicts the minimality of \({\underline{z}}\left( x\right) \). Assume that there exists a value \(z>{\underline{z}}\left( x\right) \) with \(\sum _{i\in \left[ n\right] :{\hat{c}}_{i}\ge z}x_{i}>\varGamma \). Then we would have
contradicting the definition of \({\underline{z}}\left( x\right) \).
We now prove Equality (4). If we have \({\overline{z}}\left( x\right) =\infty \) then it holds
and thus
For simplicity, we denote \({\hat{c}}_{n+1}=\infty \). Then in the case of \({\overline{z}}\left( x\right) <\infty \), there exists an index \(j\in \left[ n\right] _{0}\) with \({\hat{c}}_{j}={\overline{z}}\left( x\right) \) and \({\hat{c}}_{j+1}>{\overline{z}}\left( x\right) \). It holds \(\sum _{i\in \left[ n\right] :{\hat{c}}_{i}>{\overline{z}}\left( x\right) }x_{i}<\varGamma \), as otherwise we would have
which contradicts the maximality of \({\overline{z}}\left( x\right) \). Assume that there exists a value \(z<{\overline{z}}\left( x\right) \) with \(\sum _{i\in \left[ n\right] :{\hat{c}}_{i}>z}x_{i}<\varGamma \). Then we would have
contradicting the definition of \({\overline{z}}\left( x\right) \).\(\square \)
Filtering possible values for z
We start with proving the proposition.
Proposition 3
Let \({\mathscr {Q}}\) be a partitioning of \(\left[ n\right] \) into cliques and \(q:\left[ n\right] \rightarrow {\mathscr {Q}}\) be the mapping that assigns an index \(j\in \left[ n\right] \) its corresponding clique \(Q\in {\mathscr {Q}}\) with \(j\in Q\). For
it holds \({\hat{c}}_{i^{\max }}\ge {\underline{z}}\left( x\right) \) for all solutions \(x\in {\mathscr {P}}^{\text {NOM}}\cap \left\{ 0,1\right\} ^{n}\) and there exists an optimal solution \(\left( x,p,z\right) \) to \(\text {ROB}\) with \(z\in \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{i^{\max }}\right\} \).
Now, let \(G=\left( \left[ n\right] ,E\right) \) be a conflict graph for \(\text {ROB}\) and \(\varGamma \in {\mathbb {Z}}\). Furthermore, let \({\mathscr {Z}}\subseteq \left\{ {\hat{c}}_{0},\ldots ,{\hat{c}}_{i^{\max }}\right\} \) such that \({\hat{c}}_{i^{\max }}\in {\mathscr {Z}}\) and for every \(i\in \left[ i^{\max }-1\right] _{0}\) it holds
-
\({\hat{c}}_{i}\in {\mathscr {Z}}\) or
-
there exists an index \(k<i\) with \({\hat{c}}_{k}\in {\mathscr {Z}}\) and for all \(j\in \left\{ k+1,\ldots ,i-1\right\} \) there exists an edge \(\left\{ j,i\right\} \in E\) in the conflict graph G.
Then there exists an optimal solution \(\left( x,p,z\right) \) to \(\text {ROB}\) with \(z\in {\mathscr {Z}}\).
Proof
The first part of the statement is easy to see with Theorem 2, as for all \(x\in {\mathscr {P}}^{\text {NOM}}\cap \left\{ 0,1\right\} ^{n}\), we have
and thus \({\hat{c}}_{i^{\max }}\ge {\underline{z}}\left( x\right) \). Since the objective value is non-decreasing for \(z\ge {\underline{z}}\left( x\right) \), we do not have to consider \(z\in \left\{ {\hat{c}}_{i^{\max }+1},\ldots ,{\hat{c}}_{n}\right\} \).
For the second part, let \(x\in {\mathscr {P}}^{\text {NOM}}\cap \left\{ 0,1\right\} ^{n}\) be an arbitrary solution to \(\text {NOM}\) and \({\mathscr {Z}}\) be a set fulfilling the above properties. It suffices to show \({\mathscr {Z}}\cap \left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \ne \emptyset \). Note that \(0={\hat{c}}_{0}\in {\mathscr {Z}}\) holds, as there exists no index \(k<0\). Hence, we can assume that \({\overline{z}}\left( x\right) >0\) holds, as otherwise there is nothing left to show.
Now, assume that \({\overline{z}}\left( x\right) \ge {\hat{c}}_{i^{\max }}\) holds. Since we have \({\hat{c}}_{i^{\max }}\ge {\underline{z}}\left( x\right) \), it holds \({\hat{c}}_{i^{\max }}\in \left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \) and thus \({\mathscr {Z}}\cap \left[ {\underline{z}}\left( x\right) ,{\overline{z}}\left( x\right) \right] \ne \emptyset \).
We are left with \(0<{\overline{z}}\left( x\right) <{\hat{c}}_{i^{\max }}\). Since
is well-defined, there exists an index \(i^{*}\in \left[ n\right] \) with \(\sum _{i=i^{*}}^{n}x_{i}=\varGamma \) and \(\sum _{i=i^{*}+1}^{n}x_{i}=\varGamma -1\). It holds \({\hat{c}}_{i^{*}}={\overline{z}}\left( x\right) \), as we have
which implies \({\hat{c}}_{i^{*}}\ge {\overline{z}}\left( x\right) \), and
implying \({\hat{c}}_{i^{*}}\le {\overline{z}}\left( x\right) \). If we have \({\hat{c}}_{i^{*}}\in {\mathscr {Z}}\) then there is nothing left to show. Otherwise, there exists an index \(k<i^{*}\) with \({\hat{c}}_{k}\in {\mathscr {Z}}\) and an edge \(\left\{ j,i^{*}\right\} \in E\) in the conflict graph for all \(j\in \left\{ k+1,\ldots ,i^{*}-1\right\} \). Since \(x_{i^{*}}=1\) holds, we have \(\sum _{i=k+1}^{i^{*}-1}x_{i}=0\) and thus
which implies \({\hat{c}}_{k}\ge {\underline{z}}\left( x\right) \). \(\square \)
The above statement already determines the structure of Algorithm 6, which we use to compute a minimal set \({\mathscr {Z}}\) satisfying the requested properties. We start by computing the index \(i^{\max }\) (lines 1 to 5). Afterwards, we add the mandatory deviation \({\hat{c}}_{0}\) (line 6) and check whether \(\varGamma \in {\mathbb {Z}}\) holds (line 7). If so, we evaluate for all \(i\in \left\{ 1,\ldots ,i^{\max }-1\right\} \) if deviation \({\hat{c}}_{i}\) has to be added according to Proposition 3 (lines 8 to 13). Lastly, we add deviation \({\hat{c}}_{i^{\max }}\), which always needs to be considered (line 14). Note that the second part of Proposition 3 only holds for \(\varGamma \in {\mathbb {Z}}\), as otherwise we have \({\underline{z}}\left( x\right) ={\overline{z}}\left( x\right) \), which makes it impossible to skip deviations. Hence, in the case of \(\varGamma \notin {\mathbb {Z}}\), we only use the first part (line 16).

Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Büsing, C., Gersing, T. & Koster, A.M.C.A. A branch and bound algorithm for robust binary optimization with budget uncertainty. Math. Prog. Comp. 15, 269–326 (2023). https://doi.org/10.1007/s12532-022-00232-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12532-022-00232-2