Introduction

Egypt is located in an arid dry climate zone according to Köppen’s climate classification (Köppen 1936). Ninety-four percent of its total area is desert, and the annual rainfall is low (Allam and Allam 2007). Due to arid environmental conditions, water scarcity is considered a critical issue in Egypt, especially in the desert regions. In addition, the population rate has increased in the last decade and the per capita share is dropped below 600 m3/year posting more challenges to Egypt’s water system. Thus, the Egyptian government attaches great importance to purposing future water resources management plans for ensuring sustainable development in the desert communities. One of the desert communities is El-Qaa Plain.

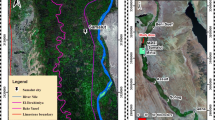
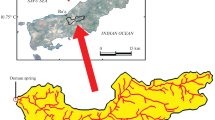
El-Qaa Plain is located in the southwestern portion of Sinai occupying an area of approximately 1930 km2 (Bakr and El-Behiry 2004). The plain is bounded from the east by South Sinai Mountains and from the west by the Gulf of Suez (Abuzied and Alrefaee 2017). A town is located in the study area named El-Tor. El-Tor is the capital of the South Sinai governorate, where the governmental authorities are situated. The town is located along the Gulf of Suez Coastline and is surrounded by reclaimed agricultural farms. The town has a harbor, an airport, and a touristic landmark (Musa wells). Figure 1 shows the location of El-Qaa Plain depicting the location of the nearby towns.

Fig. 1
figure 1

Location map of the study area

Full size image

Groundwater is the main water source in El-Qaa Plain. To ensure future sustainable development, the Egyptian government is currently seeking to plan a future groundwater management strategy in the Plain. To manage groundwater, modeling the future groundwater potential is necessary. As groundwater flow model is a necessary tool that could aid the decision-makers to decide the best future groundwater management plans, thus groundwater flow models should be well-calibrated and validated in order to predict future results accurately and precisely. However, calibrating the groundwater models is complex under limited observed measurements as in the case study. In addition, groundwater models are highly subject to uncertainty (Hendricks Franssen et al. 2009).

The sources of uncertainty in the groundwater flow models are mentioned by Hendricks Franssen et al. (2009) as follows: (i) conceptual model uncertainty, (ii) observation data measurements uncertainty, (iii) parameter uncertainty. The uncertainty related to the aquifer parameters depends significantly on the spatial heterogeneity of the aquifer hydraulic properties including the hydraulic conductivity, the transmissivity, and the mean annual recharge rate.

Some researchers have estimated and measured the hydraulic conductivity and transmissivity based on geophysical methods, pumping tests, and groundwater numerical modeling. Table 1 shows the hydraulic conductivity and transmissivity values assigned for the study area. The table shows that the hydraulic conductivity ranges from around 0.28 to 71 m/day, whereas the transmissivity ranges from around 9 to 2639 m2/day.

Table 1 List of the hydraulic conductivity values measured and estimated by the previous researchers
Full size table

Regarding the mean annual recharge rate, some studies have estimated the mean annual recharge rate using different methods such as hydrological modeling and tracer techniques. The results show that the mean annual recharge rate ranges from around 6.5 mm/year to around 12.5 mm/year. Table 2 shows a list of the mean annual recharge rate assigned by the different researchers.

Table 2 List of the estimated mean annual recharge rate by the previous researchers
Full size table

Although the previous studies have estimated and measured the hydraulic conductivity and the annual mean recharge rate, these parameters are highly variable and uncertain. In addition, they did not take into consideration the spatial heterogeneity of the hydraulic conductivity. In addition, the parameter values are highly uncertain and their values spread in a wide range. To determine the unknown aquifer parameters taking into account the spatial heterogeneity, different methods have been adopted. These methods are categorized as geostatistical methods, stochastic methods.

Geostatistical methods depend mainly on variogram function. Although geostatistics can represent the spatial heterogeneity of the aquifer parameters, the variogram models do not allow the characterizing of the geological settings such as the braided channels and riverbeds. In addition, the variogram models cannot accurately represent complex geological structures. Thus, geostatistical methods cannot predict accurately the spatial heterogeneity of the aquifer parameters.

According to Hendricks Franssen et al. (2009), stochastic methods can represent the aquifer geometrical complexity due to the limitations related to the geostatistical methods. Different stochastic methods (discontinuous facies models) can be adopted as reviewed by De Marsily et al. (1999): Boolean (Haldorsen and Lake 1984), indicator (Gomez-Hernandez and Srivastave 1990), Gaussian threshold (Le Loc’h and Galli 1997), method of transition probabilities (Carrere and Neuman 1986), probability perturbation method (Guardiano and Srivastave 1993; Hu and Chugunova 2008; Strebelle 2002). Stochastic methods could be applied via inverse modeling technique.

Inverse modeling technique could be applied via three steps: (1) setting-up a conceptual model, (2) specifying the model parameters (parameterization), (3) determining the objective function (optimization, parameter calibration). In addition, the choice of the inverse model plays a major role in acquiring accurate results. The choice of the selected models depends on the case study and the data availability.

Hendricks Franssen et al. (2009) has presented a comparison of seven inverse models for representing the aquifer heterogeneity: sequential self-calibration method (SSC), the regularized pilot points method in its Monte Carlo version (RPPM-CS), the Monte Carlo variant of the representer method (RM), the moment equations method (MEM), a linearized semi-analytical method (SAM), the regularised pilot points in its estimation variant (RPPM-CE), and the zonation method (ZM).

They evaluated the performance of these methods to predict the hydraulic conductivity using groundwater level measurements. They found that RPPM-CS, SSC, RM, MEM, and RPPM-CE predict the hydraulic conductivity at the same results. However, these methods utilize different objective functions and different parameterization schemes. On the other hand, ZM and SAM show high errors because these methods do not take into consideration the spatial heterogeneity of the hydraulic conductivity.

Most of researchers have utilized RPPM because it is a flexible and widely-spread technique (Yeh et al. 1996; Lavenue et al. 1995; Ramarao et al. 1992; Vesselinov et al. 2001). The pilot point is based on assigning the aquifer parameters via a group of points distributed along with the model domain instead of assigning the parameters for each grid or mesh (Doherty 2003). The points are interpolated using the geostatistical method (kriging). The objective function is formulated such that the difference is minimized between the groundwater model output and observation measurements.

The main aim of this paper is to specify the range of the main hydrogeological parameters: hydraulic conductivity and transmissivity using the inverse groundwater modeling approach. In addition, a relationship between the mean annual recharge rate and hydrogeological parameters has been developed. To achieve the research objectives, the following steps have been adopted. Firstly, the geological and hydrogeological data were acquired including maps and cross-sections. Secondly, the groundwater abstraction rate and quality were collected. Afterward, a conceptual model has been set up including assigning the boundary conditions and the aquifer thickness. Moreover, the hydrogeological system has been simulated using MODFLOW 2005 code in the groundwater modeling system (GMS) software. The model has been calibrated in the quasi-state conditions using RPPM in the GMS at different mean annual recharge rate values. The model has been validated through a transient run. Finally, the spatial heterogeneity of the model parameter has been represented via mapping and graphical relationships.

Materials and methods

Study area description

Location

El-Qaa Plain is located in the southwestern part of Sinai. It is situated between the latitude of 27°44′ to 28°54′ North and longitude of 33°12′ to 34°15′ East. The area is a portion of the Suez rift margin and it is elongated along the coastline of the Gulf of Suez (around 150 km long, 20–30 km wide) (Said 1962). It is bounded from the northern west by the Gebel Qabeliat Area, and from the East by South Sinai Mountains. A major town is located in El-Qaa Plain area (El-Tor), and some Bedouin communities and agricultural settlements are situated in the study area. The total area of El-Qaa Plain is approximately 1930 km2 (Said 1962).

Geology

Figure 2 depicts the geological map of El-Qaa Plain. The geological age of El-Qaa plains starts from Precambrian basement rocks to Quaternary deposits (Selim et al. 2016). According to Sultan et al. (2013), the geology could be classified into eight units: middle Miocene deposits (boulder, conglromerates, sandstone, shales, sandy shales); middle and lower Eocene deposits (light brown limestone alternating with dolomites, marls, and calcareous shales); Pliocene deposits (greenish gray, shale fractions, gypsum); the Cretaceous deposits, Jurassic deposits (marl limestone); Carbonferious deposits (Abo-Tora formation consisting of sandstone wit clayey beds); Cambrian deposits (sandstone and sandy claystone of Arabah formation); Precambrian basement rocks.

Fig. 2
figure 2

Geological map of El-Qaa Plain (source: Ahmed et al. (2014))

Full size image

The first unit consists of highly fossiliferous reefal limestone from the Pliocene age (Ras Muhammed formation). The middle Miocene age is represented by interbedded anhydrite and limestone (Kareem formation). The middle Eocene comprises a yellowish chalky limestone (Mokhtar formation). The lower Eocene is represented by the Thebes formation. The Cretaceous formation consists of five formations: Sudr (white to gray chalk), Mutullah (limestone and marl with shale), Wata (limestone with sandstone and shale), Galala (marl and claystone), Malaha (sandstone intercalated with mudstone) (Sultan et al. 2013).

Regarding the geological structure characteristics, El-Qaa Plain is located in the Gulf of Suez rift. The Gulf of Suez rift is located in the northwest extension of the Red Sea rift (Said 1962). The rift is situated between the Sinai microplate and the African plate (Landon 1994; Moustafa 2002). The rift is formed due to an uplift, where the rift was elevated by as much as 4 km. The rifting was accommodated by extensional normal faults that strike north and northwest. The uplift eroded the thick sedimentary successions, whereas the extensional faults preserved the successions as subsided blocks (half-grabens) under the Gulf of Suez and the marginal coastal plains.

El-Qaa Plain consists of four aquifer and three aquitards (Ahmed et al. 2014). The four aquifers are as follows from the top to the bottom: Quaternary alluvium, lower Miocene clastics, Nubian sandstone, Precambrian fractured basement. The three aquitards include a massive basement, middle calcareous division, and upper Miocene evaporates (Sultan et al. 2013). The modern precipitation and Nubian sandstone aquifer are replenishing the upper-most aquifers (quaternary alluvium, lower Miocene). However, the lower aquifers (Nubian sandstone and Precambrian fractures are considered as fossil (recharged during the paleo-climatic periods). In this study, we focus on the quaternary alluvium aquifer.

Aquifer hydrogeology

Most geophysical studies have been conducted to understand the potential of groundwater the alluvial quaternary aquifer of El-Qaa Plain (Webster et al. 1982). They have concluded that the aquifer is consisting of gravel, sand, silt, and clay (Selim et al. 2016). The aquifer is bounded from the east by Precambrian rock, and from the west by carbonates and evaporates from the pre-Quaternary era (Darwish and El Azaby 1993; Khalil 2001).

The alluvial quaternary aquifer consists of 2 layers: upper layer and lower layer. The 2 layers are partially separated by a discontinuous clay layer. The upper layer comprises gravel and sand, whereas the lower layer consists of gravel and sand with clay intercalation (El-Fakhrany et al. 2003; Sultan et al. 2013). The thickness of the upper layer ranges from nearly 10 to 140 m, whereas the thickness of the bottom layer varies from proximity 2 to 152 m (Selim et al. 2016). Figure 3 shows the hydrogeological cross-section in the study area, whereas Fig. 4 shows the aquifer geometry including the top and bottom elevation.

Fig. 3
figure 3

Hydrogeological cross-section of the study area (Modified after Gorski and Ghodeif (2001))

Full size image
Fig. 4
figure 4

Aquifer geometry. a Aquifer top elevation (modified after downloading 30 m resolution DEM from USGS website). b Aquifer bottom elevation (modified after Selim et al. (2016))

Full size image

Regarding aquifer properties, the hydraulic conductivity and transmissivity have been measured and estimated by JICA (1999), El-Fakhrany et al. (2003), Bakr and El-Behiry (2004), and Sultan et al. (2009). The hydraulic conductivity ranges from nearly 0.28 to 71 m/day, whereas the transmissivity ranges from around 9 to 2639 m2/day. The effective porosity has been assumed by Bakr and Beheiry (2004) and Sultan et al. (2009), and it varies from around 0.25 to 0.43.

Regarding the groundwater characteristics, groundwater observation head has been acquired from WRRI (2012) from the year 2000 to the year 2011. Additionally, groundwater level and quality have been collected for the year 1999, which is created by JICA (1999) (Fig. 5). The map indicates that groundwater observation head ranges from around 0 to 30 m above MSL, whereas the groundwater salinity ranges from below than 500 to around 2000 mg/L.

Fig. 5
figure 5

Groundwater characteristics. a Groundwater level (year 1999) (modified after JICA (1999)). b Groundwater salinity (year 1999) (modified after JICA (1999))

Full size image

The groundwater recharge has been estimated by USAID (1986), EEC (1993), Abdelrahman (1996), JICA (1999), Elewa & Qaddah (2011), WRRI (2012), Tamaam (2012), and El-sayed et al. (2019). According to the previous studies, the mean annual groundwater recharge ranges from around 5 to 24 Mm3. The groundwater abstraction data has been collected from WRRI (2012). The groundwater exploitation has been started in 1971 with annual abstraction rate of around 0.5 Mm3/year. The groundwater exploitation has been increased from 1971 to 2011 reaching a rate of approximately 11.5 Mm3/year.

Conceptual model

The groundwater model has been set up using GMS. GMS is a graphical user interface for post-processing groundwater softwares such as ModFLOW, MT3DMS, and SeaWAT, ModFLOW is a 3D finite-difference numerical model developed by MacDonald and Harbaugh (1988) and is embedded in GMS. The model simulates the groundwater flow in the quasi-steady and transient state in the porous media. The model is based on a governing equation as described by Hamraz et al. (2015). The equation is based on 2 laws: Darcy’s law and the law of mass conservation.

$$\frac{\partial }{\partial x}\left({K}_{\mathrm{xx}}\frac{\partial h}{\partial x}\right)+\frac{\partial }{\partial y}\left({K}_{\mathrm{yy}}\frac{\partial h}{\partial y}\right)+\frac{\partial }{\partial z}\left({K}_{\mathrm{zz}}\frac{\partial h}{\partial z}\right)={S}_{s}\frac{\partial h}{\partial t}+R$$
(1)

where \({K}_{\mathrm{xx}}\), \({K}_{\mathrm{yy}}\), and \({K}_{\mathrm{zz}}\) are hydraulic conductivity in the directions of x, y, z coordinate orthogonal axes respectively (parallel to the major axes of hydraulic conductivity (L/T)), \(h\) is the potentiometric head (L), \(R\) is the volumetric flux per unit volume including source and sink (1/T), \({S}_{s}\) is the specific storage (1/L), and \(t\) is the time (T).

To build the conceptual model, the Quaternary aquifer has been assigned for the conceptual model. The Quaternary aquifer comprises 3 layer, since the upper-most and lower-most layers consist of sand and gravel with clay intercalation and are connected hydraulically. However, the middle layers comprise discontinuous clay. Therefore, the conceptual model could be represented as a 2D finite-difference model. The model domain is discretized into a grid size of 250 m as modeled by Bakr and Beheiry (2004).

To assign the boundary conditions, the aquifer is bounded by Gulf of Suez from the West (Fig. 6). Thus, constant head boundary has been assigned to represent Gulf of Suez as 0 m above MSL. The aquifer is surrounded by Precambrian mountains from the East (South Sinai mountains) and from the northern west (Gabl El-Qabilliat mountains). Thus, the mountains could be assigned in the model as a no-flow boundary. The model layer thickness has been determined according to the aquifer thickness mapped by Selim et al. (2016).

Fig. 6
figure 6

Conceptual model. a Assigned boundary conditions. b Assigned aquifer thickness (modified after: Selim et al.(2016))

Full size image

Regarding the groundwater recharge and discharge, the model has been run at different mean annual recharge rate values, which were mentioned in Table 2. The groundwater abstraction data has been imported to the model from the year 2000 to 2011. The groundwater level map for the year 1999 has been utilized to calibrate the model. Since the aquifer type is unconfined and porous media is considered as sandy gravel, the specific yield has been assumed by Zaghlool and Eissa (2018) (0.25). Also, groundwater observation data has been imported to the model.

Model calibration and validation

The model is calibrated in a quasi-steady state using the groundwater level map for the year 1999. Then, the model is validated by running the model in a transient state from the year 2000 to the year 2011. To reduce the difference between the observed head and the calculated head, inverse modeling has been performed using the RPPM method. The RPPM method is based on choosing the location of the points with respect to the location of the observation wells. The criteria of selecting the location depend on adjusting the points in the mid-point between the observation wells (Fig. 7). The governing equation for this model is mentioned below as described by Doherty (2003).

$$\phi_m={(d-M(P))}^tQ_1(d-M(P))$$
(2)

where d is a vector of the field measurements (in our case groundwater head measurements), p is a vector of the required estimated parameters (in our case hydraulic conductivity), M describes the model response to generate results, \({Q}_{1}\) incorporated the weights assigned to the various observation, \(\phi_m\) is the objective function which is required to be minimized. In our case, the objective function is the error difference between the observed head and the predicted head.

Fig. 7
figure 7

Model calibration

Full size image

Kriging method is utilized to convert the spatial distribution of the pilot points to the model grid. Kriging requires a variogram function. A variogram is an expression to correlate a relationship between 2 variables. In our case, the first variable is the distance between the grid and the pilot point, whereas the latter is the hydraulic conductivity. The variogram is calculated via Eq. 3 as expressed by Doherty (2003).

$$2\upgamma \left(h\right)={E(\left[Z\left(x+h\right)-Z\left(x\right)\right]}^{2}$$
(3)

where E is the “expected value” operator, Z is some property that varies throughout a study area, and x is the location of a point in space. Where the mean value of Z is uniform over a study area (and hence the mean value of the property differences is zero), it follows from basic manipulation.

Spatial heterogeneity representation

It should be mentioned that the head distribution within the model is function of the ratio of the recharge to the mean value of the hydraulic conductivity rather than the values of each different parameters. To find the optimum value of this ratio, the calibration and validation process are repeated 6 times. In each time, a single value of the mean annual recharge rate presented in Table 2 is used as an input to the model. The corresponding distribution of the hydraulic conductivity is then obtained from the calibration process. Each run has been validated, and it has been found that RMSE is almost the same as the calibrated model. The map has been generated for different mean annual recharge, and the geometric mean of hydraulic conductivity and transmissivity is calculated using ArcGIS. Finally, a relationship has been obtained between the mean annual recharge and the geometric mean of the hydraulic conductivity and transmissivity.

Results and discussions

Figure 8 represents the spatial heterogeneity of the hydraulic at different mean annual recharge rates. The results show that the geometric mean of the hydraulic conductivity ranges from around 1.08 to 2.03 m/day. These values are corresponded to the medium sand porous media. This result strongly agrees with the geophysical studies conducted by El-Fakhrany et al. (2003), Sultan et al. (2009), Ahmed et al. (2014), and Selim et al. (2016), which is related to the porous media. In general, the hydraulic conductivity ranges from around 0.01 to 47 m/day. This agrees with the presence of the clastic sediments (sand and gravel).

Fig. 8
figure 8

Spatial heterogeneity of the hydraulic conductivity

Full size image

Regarding the spatial heterogeneity, the results show that the spatial heterogeneity of the hydraulic conductivity is almost similar at different mean annual recharge rate. The reason is because the spatial variability of mean annual recharge rate has not been taken into account in the model. In other words, the mean annual recharge rate has been assigned for all the model grids.

The maps demonstrate that the high hydraulic conductivity values are situated at the north western portion of the study area. Some sink holes are located in the northeastern portion and in the middle portion of the study area. The middle values are situated in the northeastern region and in the middle of the study area.

A relationship is developed between the geometric mean of hydraulic conductivity and transmissivity from one side and the mean annual recharge rate from the other side (Fig. 8). This relationship agrees significantly with the groundwater flow equation (Eq. 1), as a linear relationship was obtained by fitting the points and it reflects the groundwater flow equation, which states that the slope between the hydraulic conductivity and recharge is constant. The relationship is easily obtained because the porous media of the hydrogeological system does not exhibit high variability and might be accurately presented as a homogenous aquifer with the presence of a discontinuous aquitard layer (clay).

Most groundwater flow models are usually calibrated based on one mean annual recharge rate in most studies. However, in this study, the groundwater flow model is calibrated using 6 different mean annual recharge rates. Thus, a linear relationship is obtained. Therefore, the linear relationship proves that the model calibration has been performed successfully.

The precise value of the hydraulic conductivity could be obtained via this relationship depending on determining the mean annual recharge. Even though the mean annual recharge is estimated by the previous researchers, estimating the recharge precisely could reduce the uncertainty of the hydraulic conductivity and transmissivity. In other words, the mean annual recharge rate could be estimated precisely using different methods such as tracer techniques and numerical hydrological modeling.

To ensure the groundwater sustainable development of the study area, it is necessary to check the mean annual exploitation rate and the mean annual recharge rate values. Based on the literature, it has been perceived that the mean annual recharge rate ranges from around 5 to 24 Mm3. On the other hand, the annual exploitation rate is proximity 11.5 Mm3. This means the hydrogeological system is in a balanced condition and no presence of intensive pumping for agricultural purposes. However, excessive pumping might take place in the future. Therefore, the annual exploitation rate should not exceed the perennial yield.

Conclusion

This paper aims to specify a range of the main hydrogeological parameters for a groundwater flow model: hydraulic conductivity and transmissivity using the inverse groundwater modeling approach. This is accomplished taking into account the spatial heterogeneity of the aquifer parameter. The pilot points method has been selected to predict the aquifer parameters.

The results show that the geometric mean of the hydraulic conductivity ranges from nearly 1 to 2 m/day, whereas the mean annual recharge rate ranges from around 6.5 to 12.5 mm/day. The geometric mean of transmissivity ranges from proximity 200 to 500 m2/day. A relationship has been developed between the geometric mean of the hydraulic conductivity and transmissivity from one side and mean annual recharge rate from the other side. The equation which describes the aforementioned relationship: µ(R) = 6.1 µgeo(K), µ(R) = 0.027 µgeo(T), where µ(R), µgeo(K), and µgeo(T) are respectively the mean annual recharge rate, the hydraulic conductivity, and transmissivity.

Some limitations are present in this study. The first limitation is related to the limited data availability especially the groundwater head observation wells, as the wells do not cover the whole study area. Additionally, the time series of the observation wells starts from the year 2000 to the year 2011. In other words, the longer the observed groundwater head time series is, the more accurate the results are. The latter is the wide variety of the mean annual recharge rate. As reducing uncertainty of the hydraulic conductivity relies on the precise estimation of the mean annual recharge rate.

Some studies could be further conducted including estimating the recharge precisely in order to estimate a precise hydraulic conductivity value. The recharge variable could be calculated using the following methods: numerical modeling, tracer techniques. Additionally, it is recommended to purpose groundwater management plan to mitigate the excessive exploitation in the future using the groundwater flow models and pollution with the aid of the results in this study.

The spatial heterogeneity of the hydraulic conductivity and transmissivity has been represented using maps. These maps could be further utilized by groundwater flow modelers to predict the potential of the groundwater flow and pollution in the future which could aid in purposing a water resources sustainable development plan.