1 Introduction

In the sport of alpine skiing, just a few hundredths of a second can make a significant difference in the results. As an example, in the ladies super-G competition at the 2018 Winter Olympics in Pyeongchang, the difference between the gold medal and fifth place was only 0.16s and just 0.01s separated the gold and silver medalist [1]. The aerodynamic drag is one of the most important factors determining performance in the high-speed disciplines Downhill and Super-G [2, 3], and is also a performance factor in Giant Slalom [4, 5].

Aerodynamic investigation, mostly through wind tunnel measurements, of an alpine skier’s posture has been performed to understand its relationship with the drag force [2, 4, 6,7,8,9]. In general, one can separate the movements of an alpine skier into three main components; I: Extension/flexion of hip, II: Extension/flexion of knees, and III: Arm movements. The movements of the hip and knees are strongly coupled in terms of maintaining balance, turning and have also been the main focus in aerodynamic research in terms of postural changes linked to drag reduction [2, 4, 5, 7, 9]. A straightforward way to reduce the drag in sports aerodynamics is by reducing frontal area, which is effectively achieved by hip flexion, i.e., reduce the frontal area of the torso [10]. Elfmark et al. [2] also revealed that a decrease in torso angle through hip flexion had an additional benefit from a decrease in drag coefficient by less flow separation from the back of the torso. Hence, the main focus when it comes to aerodynamic research on alpine skiing postures has been on legs and torso through hip and knee flexion.

The general knowledge of how postural changes in alpine skiing affect performance in terms of drag reduction have increased through the years [10]. Nevertheless, the movement of the arms and their relationship with aerodynamic drag is still not well understood. Barelle et al. [9] stated that the arms’ influence must be accounted for in alpine skiing and Elfmark et al. [6] revealed that the total drag of an alpine skier changed by \(\sim \)15% by arm abduction and twice that size by placing the arms in front of the torso (outside of the flow). Hence, arm configuration in alpine skiing is highly important for the overall performance as it is a large influence of the total drag. The arms in alpine skiing are also primarily used for stability, and hence arguably offer significant opportunities when it comes to positioning.

Studies on aerodynamic influence of arms configuration in sports are in general scarce. Giljarhus et al. [11] studied the influence of arm configuration in time trial cycling using computational fluid dynamics (CFD) simulations. The optimal configuration was found to be holding underarms close together and keeping the hands slightly higher than the elbows. Another study of arm configuration in cycling was done by Crouch et al. [12], where the influence of arm configuration on flow structures over the torso and hip was measured experimentally. It was found that the transient behavior of the pedaling stroke had an important impact on the flow behavior. Mannion et al. [13] investigated hand configuration in Paralympic hand-cycling. The results showed subtle changes in flow separation patterns leading to a counter-intuitive configuration yielding the lowest drag.

Some insight into arm configuration can also be gained by studying cylinder aerodynamics, as the over- and underarms (and legs) can be thought of as two connected, finite-length cylinders. Flow around a single cylinder is a classical case in fluid mechanics and is treated in several textbooks, e.g., [14]. Although the difference in drag coefficient is not large between a cylinder oriented perpendicular or parallel to the flow, there is a significant difference in frontal area, such that the drag area is increasing as the cylinder angle increases from parallel to vertical. The flow behaviors of two cylinders in various arrangements have been thoroughly studied in the literature, with reviews provided in [15,16,17]. There is a rich variety of flow phenomena, but for high-Reynolds number flow, broadly speaking the drag increases with decreasing distance for two cylinders placed side-by-side, and for a tandem configuration, there is a shielding effect, such that the total drag decreases with decreasing distance.

Given the limited research on how the arms influence the overall aerodynamic drag in alpine skiing, the aim of the present study was to provide insight into the influence of arm configuration in alpine skiing in various leg and torso scenarios, i.e., low-tucked, high- tucked, and flight postures. The work built upon previous work by the authors, where the methodology was first used to study the influence of hip and torso angle [2]. The methodology was based on a combination of experiments on real athletes in a wind tunnel and CFD simulations performed on 3D scanned models of the athletes. This methodology is common in sports aerodynamic research, where the experiments ensure that the considered postures or scenarios are realistic and provide validation for the simulation setup [18,19,20,21,22]. The simulations yield greater details and insight into the flow phenomena causing the change in overall drag.

2 Methods

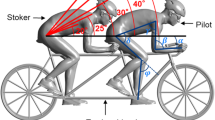
To understand the total impact during a race, three different scenarios, illustrated in Fig. 1, were considered:

  1. 1.

    Low tuck

  2. 2.

    High tuck

  3. 3.

    Flight.

Fig. 1
figure 1

Sample side-view images of the athletes in the wind tunnel (top) and the 3D model used in the simulations (bottom), showing low-tuck posture (left), high-tuck posture (middle), and flight posture with arms along torso (right)

Full size image

The first is the low-tuck scenario, where the alpine skier is able to maintain a steady low-tuck posture, which is considered as an optimal posture athletes will try to attain when possible. In this posture, the alpine skier keeps the arms in front of the body and the angle of the underarms is varied.

Second, the high-tuck scenario, where the alpine skier is forced into a more dynamic high-tuck posture, typically used for sharper turns or in parts of the slope with an uneven surface. Although having the arms tucked together in front of the body is desirable, the athlete often needs to have the arms out to the sides for balancing.

Finally, the flight scenario, where the alpine skier undergoes a flight phase due to a jump. Although a jump only constitutes a few seconds of a full race, it can lead to significant loss of time as a lowering of speed during the jump is propagated further downhill. Since there is no friction force from the skis, all the resistance is due to aerodynamic drag in these situations.

The next sections give a brief overview of the wind tunnel setup and the computational setup. The reader is referred to Elfmark et al. [2] for a more detailed description of the methodology.

2.1 Participants

One female (participant A, height 1.67 m, weight 67 kg) and one male (participant B, height 1.81 m, weight 97 kg) alpine skier from the Norwegian national team participated in the study. The study was conducted in accordance with the ethical guidelines at the University of Stavanger and the Declaration of Helsinki [23]. Prior to formally giving their written consent, both participants were informed of the study’s purpose, benefits, and potential risks, as well as their right to withdraw from the study at any time.

2.2 Experimental setup

The wind tunnel experiment was performed in the Politecnico di Milano high-speed wind tunnel in Milano, Italy. The wind tunnel has a cross-section area of 15.4 m\(^2\) (4 m wide and 3.84 m high), and a low turbulence intensity of less than 0.1%. The drag force is measured using an RUAG Aerospace six-component force balance, where alpine bindings were mounted on the force balance. Ski poles were not used, as they could be a safety hazard and were considered to have negligible influence on the drag.

The wind speed used was 30 ms\(^{-1}\) for participant A and 35 ms\(^{-1}\) for participant B. The slightly different wind speed used was due to safety concerns as the forces are very high, and to match typical differences in male and female speeds. Previous wind tunnel experiments have found the drag area to be independent of wind speed for these high speeds [24]. No blockage correction was applied as the frontal areas of the test participants at all time were below 5% of the cross-section area of the wind tunnel [25, 26].

A live video feed of the side-view of the participant with postural guidelines was displayed on the floor of the wind tunnel, to help the participant find and maintain the intended posture. Three measurements were made for each tested posture with a 20 s sampling time. Unless otherwise noted, the reported drag values are an average of the three samples. Images from the side-view camera taken at the start and finish of each trial were used to both verify that the intended posture was maintained throughout the sampling period, to measure angles and to verify the postures in the digital models.

2.3 Computational setup

Fig. 2
figure 2

Overall mesh structure (left) and close-up of layers near the athlete body (right)

Full size image

Geometry models for both athletes were obtained using an Artec Eva scanner and post-processed with the Artec Studio 14 software. Since the scan could not be performed during testing, the model was adjusted digitally based on pictures from the wind tunnel to ensure that the posture corresponded to the wind tunnel posture. This also allowed isolating changes in arm angles for parameter studies without altering the rest of the athlete body. Figure 1 shows a comparison of pictures from the wind tunnel to the geometry models used in the simulations. Participant B was used for the low-tuck and high-tuck simulations, while participant A was used for the flight posture simulations.

The simulations were performed in the open-source CFD simulation software OpenFOAM, version 7 [27, 28]. The turbulence model used was the k-\(\omega \) SST turbulence model [29]. The SIMPLE algorithm was used for pressure–velocity coupling, with second-order discretization schemes applied for spatial discretization.

The computational mesh is shown in Fig. 2, and the construction was based on the mesh sensitivity study performed in Elfmark et al. [2]. The mesh consisted of approximately 20 million cells, with refinements close to the athlete. The overall cell size near the athlete body was approximately 2 mm, and prism layers were used close to the body giving a distance from the surface to the first cell of approximately 20 \(\upmu \)m.

The total drag area, \(C_\text {D}A\), was calculated with the following formula:

$$\begin{aligned} C_\text {D}A = \frac{2}{\rho V^2_\text {rel}} \left( \underbrace{\iint _S p\cdot n_x \mathrm {d}S}_\text {pressure drag} + \underbrace{\iint _S \tau _{w,x} \mathrm {d}S }_\text {viscous drag} \right) , \end{aligned}$$
(1)

where S denotes the athlete surface, p the pressure, \(n_x\) denotes the component of the surface normal vector in the flow direction, and \(\tau _{w,x}\) denotes the component of the shear stress in the flow direction. Pressure drag is caused by a pressure difference between the front and back of the body, while viscous drag is due to friction. By visualizing the output from Eq. 1 for each individual cell on the surface of the geometry model, local contributions to the total \(C_\text {D}A\) can be identified. Additionally, the cumulative drag along the athlete’s body is calculated by slicing the geometry model into 150 sections perpendicular to the flow direction and integrating the contributions across each individual section.

3 Results

3.1 Low-tuck scenario

Fig. 3
figure 3

Simulation results of cumulative drag along athlete body (Participant B) for different lower arm angles in low-tuck posture

Full size image
Fig. 4
figure 4

Relative drag area as a function of lower arm angle in low-tuck posture. Simulations are based on participant B

Full size image

The impact of arm configuration in a low-tuck posture was studied by changing the angle of the underarms, as illustrated in Fig. 3. The resulting drag areas as a function of lower arm angle are shown in Fig. 4. Overall, the relative change in drag area as a function of the arm angle is appreciable, with a 2.8% change between the lowest and highest values. For the experiment, the athletes were asked to hold a low-, middle-, and high-arm angle with three experimental trials for each defined angle. It was challenging for the athletes to maintain a fixed angle for each of the trials, and hence, the plot shows all of the trials instead of an average. The baseline drag area is taken as the average of the three trials for the middle arm angle.

There is a clear trend in the results, with a minimum in the drag area for an arm angle of approximately 25\(^\circ \) to 30\(^\circ \). This trend is also supported by the simulation results. The higher drag area for higher angles can be explained by the fact that with increasing angle, more of the underarm is exposed to the incoming flow, thereby increasing the drag. Although this will put the overarms in the wake behind the underarms and give some shielding effect, this effect is lower than the additional drag caused by the underarms themselves. This can be seen in Fig. 3, which shows the cumulative drag along the athlete body, extracted from the simulation results.

The development of the cumulative drag can be divided into four sections. In Sect. 1, the drag increases initially as the flow impacts the hands and head. The drag then remains relatively constant as there is a combination of flow acceleration around the head reducing the drag and flow impacting on and separating from the underarms. In this region, the drag is highest for the highest arm angle, as a larger part of the underarms is exposed to the incoming flow. Section 2 starts with an abrupt increase in drag as flow separates from the head creating a recirculation zone in the neck region. This is followed by a second increase as flow impacts the upper arms. The increase is slightly lower for the highest arm angle due to the shielding effect from the underarms, but the total drag remains higher. Next, there is another temporary drop as flow accelerates around the arms before the drag increases again as the flow separates in the elbow region. Section 3 is dominated by a large increase in drag due to flow separating from the lower legs. There is some convergence of the curves towards the end of this section, indicating a complex flow interaction between the arms and the lower leg region. In Sect. 4, there is another increase as flow separates from the trailing end of the body, with similar behavior for all arm angles.

Fig. 5
figure 5

Streamlines showing flow pattern over underarm and lower leg for arm angle of 0\(^\circ \) (top) and 23\(^\circ \) (bottom)

Full size image

The interaction between arms and legs also appears to be the cause of higher drag for the lower arm angles. A low arm angle, with arms parallel to the flow, should intuitively give the lowest drag as the projected frontal area of the arms is lower. This is also the case for Sections I and II as seen in Fig. 3, as an arm angle of 0\(^\circ \) has the lowest drag after Sect. 2. In Sect. 3, however, the drag for this arm angle increases more than the other angles, indicating that the arm angle influences the flow separation behind the lower legs. This is further illustrated in Fig. 5, which shows streamlines of the flow passing over the underarms for arm angle 0\(^\circ \) and 23\(^\circ \), respectively. For the lower arm angle, the flow curves over the elbow before being significantly accelerated around the lower leg. This acceleration gives a lower pressure and hence higher drag. For the higher arm angle, the flow is curved after passing over the underarm and passes directly over the elbow region and lower leg without the sudden acceleration. For angles higher than approximately 30\(^\circ \), the drag increases again, due to the higher frontal area and correspondingly larger wake behind the arms.

3.2 High-tuck scenario

Fig. 6
figure 6

Comparison of drag area relative to the high-tuck baseline posture for different high-tuck postures. Simulations are based on participant B

Full size image
Fig. 7
figure 7

Contour plot comparing the local contribution to drag area, Eq. 1, for the high-tuck postures. Top: front view. Bottom: Close-up of groin area for arms together and arms apart, viewed from below

Full size image

Figure 6 shows the drag area for the three different postures for both experiments and simulations. The baseline is chosen as the posture with arms together in front of the body. The middle posture has the arms slightly apart, while the final posture has the arms out and along the side of the body. The trend is consistent across both participants and the simulations. Having the arms apart increases the drag by 5% to 8%, while having the arms even wider gives a more significant increase of 17% to 21%.

Figure 7 displays the local contribution to drag area for the three simulated arm configurations. By moving the arms slightly apart (middle posture), the frontal area of the alpine skier increase and the groin area gets exposed by the incoming flow, both contributing to an increase in drag area. By moving the arms even wider, so that the elbows are clear of the body gives a stronger wake behind the arms increasing the drag. An even larger area of the groin and thigh areas will also be exposed to the incoming flow, hence the large increase in drag area.

3.3 Flight scenario

Fig. 8
figure 8

Comparison of drag area for four different flight postures, relative to the baseline low-tuck posture. Simulations are based on participant A

Full size image

The four different flight postures considered here are illustrated in Fig. 8, together with their drag area relative to the baseline low-tuck posture. The first flight posture (Arms down) is a neutral posture, and is commonly used by athletes. The second posture (Arms out) represents a posture where the athlete is out of balance and needs to use the arms to counteract rotation in the flight. The third posture (Along torso) is an attempt at an aerodynamically optimal posture, as this would minimize the projected frontal area of the athlete. The final posture (Behind legs) is a modification of the first posture, where the hands are tucked behind the lower legs, again in an attempt to reduce the projected frontal area.

Although there are some differences, the relative drag areas for both participants and the simulated results show the same trends. The arms down configuration gives the highest drag, with a drag even higher than the arms out configuration. An improvement of the arms down configuration is seen in the behind legs, where the hands are tucked behind the legs. A further improvement can be found in the along torso configuration. This posture has the lowest exposure of arm area to the flow as the arms are aligned with the flow along the torso of the athlete.

Figure 9 shows the pressure coefficient around the lower arm and lower leg for the arms out, arms down, and behind legs configurations. When the arm and leg are side-by-side (slice 3), the interaction leads to a higher buildup of pressure in front of the body, and lower pressure behind the body. This results in higher drag compared to the arms out configuration (slice 1 and 2). With the arm behind the leg (slice 4), the leg provides a shielding effect reducing the drag.

Fig. 9
figure 9

Contour plots of pressure coefficient for flight postures for arms out, arms down, and arms behind ankles. The top figure shows the location of the slices, and flow is from left to right

Full size image

4 Discussion

The purpose of this investigation was to examine how the arms of an alpine skier influence the overall drag, hence also performance, in various leg and torso scenarios, i.e., low-tucked, high-tucked, and flight postures. Of the three scenarios considered, the flight posture has the largest variation in the results. Hence, potentially also the largest room for improvement for alpine skiers. This is due to the larger difference in arm configuration for this posture compared to the low- and high-tucked postures. The relative difference between having arms down and the arms along torso is as high as 64%. This is an interesting result as the configuration with arms down is a commonly seen posture in downhill racing. However, having the arms along the torso requires a larger movement from the athlete, as the arms are typically kept either in front of the body or along the sides going into the jump. Moving the arms to the back could be challenging from a balance perspective. Holding the arms down but tucking the hands behind the legs gives an improvement in drag area of approximately 50%. This is a pragmatic improvement to the arms down configuration, as it requires little change for the athlete.

For the low-tuck posture, the angle of the underarms may seem to be of limited influence on the drag, with a maximum difference of 2.8% for the angles considered. The lowest drag area is found with a medium angle of 20\(^\circ \) to 25\(^\circ \). However, this is not an insignificant finding, as the low-tuck position already is assumed to be an aerodynamic optimal posture used through a large proportion of the overall race time. Hence, a 2% to 3% potential improvement of something already assumed to be optimal, used for a large proportion of a competition, has to be considered to be important. The results for the arm angle show some scatter in the results, especially for lower arm angles. This could most likely be contributed to small changes in other parts of the athlete’s posture between each experimental run, which could have an impact on the drag area. Although the CFD simulations allow a more consistent variation in the parameters, it could also be valuable to perform a more detailed experimental study with a physical model instead of a real athlete. This could also allow further insight into the flow interactions between the arms and the legs, which were proposed as the explanation for the optimal arm angle. Since these are complex flow patterns, minor changes in the geometry could change the flow pattern. The simulation results are also expected to be less accurate in these situations with subsequent flow separation and reattachment of the flow, due to the turbulence modelling being less validated for these cases. Nevertheless, the same trends are seen in the experimental results and the simulations offer one viable explanation of the phenomenon.

For the high-tuck posture, separating the arms lead to an increase in the drag area of 5% to 8%, and further opening the posture gives an increase of 17% to 21%. For this scenario, it is more challenging to consistently vary the arm movement, as there are multiple angles involved. The tested arm configurations represent what would be realistic according to the athletes, and should therefore be considered as an approximation of the increase in drag when opening the posture. Nevertheless, the increase is substantial, and there is clear evidence that athletes should strive to maintain a closed posture. This test serves as an example to athletes that even small changes in arm movements could induce large drag differences which could prove to be highly influential of the overall performance.

During a race, the dynamic nature of the slope could make it challenging to apply the findings in this work, especially for the postural changes yielding smaller differences. However, it is also of value to document these smaller differences to let the athletes know where to focus their efforts. The results are also relevant in other applications, such as for developing simpler kinematic models.

The work demonstrated the value of the combined approach with wind tunnel experiments on real athletes and simulations on 3D-scanned models. The simulation method could reproduce trends found in the experiments, and could be further used for systematic parameter studies in future work. Only two athletes were considered in this work, and although the trends were consistent for these two, future studies could investigate individual differences across a larger number of athletes. Future work in this area could also consider further investigating the complex interactions between the arms and legs. More detailed experimental visualization would help in this regard, and also provide further validation data for the computational method.

5 Conclusion

This investigation has given insight into the impact of arm configuration in various scenarios commonly encountered in alpine skiing. Similar trends were observed in the experiments for both athletes and in the simulations. The arms are highly influential of the overall drag, and hence also performance in alpine skiing. For the low-tuck posture, the alpine skiers should try to maintain an angle of the underarm of 20\(^\circ \) to 25\(^\circ \) to improve an already aerodynamic posture. When a higher tuck posture is needed, the athlete should strive to keep the arms tucked in front of the body. Special attention should be paid to the arms in the flight, where the arm configuration could significantly impact the end result.