1 Introduction

The subject of hydrodynamics is one with immense application. The famous Navier–Stokes equations to describe flow of a linearly viscous, incompressible fluid are employed in many branches of applied mathematics and engineering. However, the instantaneous response of the stress to changes in the velocity gradient is not experienced by all types of fluid. There are many fluids which do not react instantaneously and instead remember their history. Such materials are usually put into the category of viscoelastic fluids which incorporate fading memory or other classes of complex fluid. However, the field of complex fluids is intensely studied, as is witnessed by the work of Amendola and Fabrizio [1], Amendola et al. [2], Anand et al. [3], Anand and Christov [4], Christov and Christov [5], Fabrizio et al. [6], Franchi et al. [7], Franchi et al. [8], Franchi et al. [9], Gatti et al. [10], Jordan et al. [11], Jordan and Puri [12], Joseph et al. [13], Payne and Straughan [14], Preziosi and Rionero [15], Yang et al. [16]. By a complex fluid we include not only those displaying viscoelastic behaviour but also such as nanofluid suspensions, cf. Haavisto et al. [17], where the stress may need to incorporate dependence on second gradients of the velocity field to describe such physical effects as the flattening of the parabolic profile in Poiseuille flow, cf. Straughan [18]. We stress that this does not preclude complex solution behaviour in a Newtonian fluid where extremely complicated solutions are known for the Navier–Stokes equations and approximations arising therefrom such as the primitive equations, see e.g. Gargano et al. [19], Kukavica et al. [20].

A very interesting class of complex (viscoelastic) materials are those associated with the names of Kelvin and of Voigt, cf. Chirita and Zampoli [21], Layton and Rebholz [22], and interesting models for Kelvin–Voigt fluids have been presented by Oskolkov [23], Oskolkov [24]. The equations of motion for viscoelastic fluids of Maxwell type, of Oldroyd type, and of Kelvin–Voigt type are succinctly summarized in the article of Oskolkov and Shadiev [25]. Generalizations of the Kelvin–Voigt models to incorporate thermal effects are given by Sukacheva and Matveeva [26], Matveeva [27], Sukacheva and Kondyukov [28]. The latter pieces of work mainly concentrate on solvability issues and on establishing properties of solutions such as existence of a suitable solution and uniqueness questions.

In this work we present analysis of thermal convection of a layer of Kelvin–Voigt fluid heated from below employing the models of Sukacheva and Matveeva [26], Sukacheva and Kondyukov [28]. This is the first analysis of these problems we have seen. We present a computational procedure for calculating the neutral curves for instability associated with thermal convection. This is a non-trivial process for Kelvin–Voigt fluids of variable order since it transpires that to calculate the critical Rayleigh number thresholds of instability one has to first calculate the eigenvalues of the variable order theory and then employ these in the minimization process over all wave numbers. It transpires that for the models of orders 1 and 2 both stationary and oscillatory convection may occur depending on what range of parameters one employs. In practical situations this is of paramount importance, since for example in growing crystals for the semi-conductor industry, oscillatory convection may lead to the formation of striations in the crystal which in turn lead to impurities in the final crystal, cf. Jakeman and Hurle [29].

In the following we firstly describe the equations for thermal convection in a Kelvin–Voigt fluid of order \(0,1,2,\ldots ,L,\) and we then outline the computational procedure in the general case. Following this, the cases of order 0, 1 and 2 are addressed in detail. Practical applications of Kelvin–Voigt fluids are mentioned at the end of Sect. 2.

2 The Kelvin–Voigt equations for thermal convection

Let \(v(\mathbf{x},t),\) \(T(\mathbf{x},t),\) \(p(\mathbf{x},t)\) be the velocity, temperature and pressure at position \(\mathbf{x}\) and time t of a body of fluid. The Kelvin–Voigt equations of non-isothermal fluid flow of variable order may be written, see Sukacheva and Matveeva [26],

$$\begin{aligned} \begin{aligned}&(1-{\hat{\lambda }}\varDelta )v_{i,t}+v_jv_{i,j}=-\frac{1}{\rho _0}p_{,i}+\nu \varDelta v_i+\alpha Tgk_i+\sum ^L_{\alpha =1}\beta _{\alpha }\varDelta W_i^{\alpha },\\&v_{i,i}=0,\\&T_{,t}+v_iT_{,i}=k\varDelta T ,\\&W^{\alpha }_{i,t}+{\hat{\gamma }}^{\alpha }W^{\alpha }_i=v_i,\quad \alpha =1,2,\ldots ,L. \end{aligned} \end{aligned}$$
(1)

Here \({\hat{\lambda }},\nu ,\rho _0,\alpha ,g\) and k are the Kelvin–Voigt coefficient, the kinematic viscosity, a reference density, the coefficient of thermal expansion of the fluid, gravity, and thermal diffusivity. The symbol \(\varDelta \) denotes the Laplacian, \(k_i\equiv \mathbf{k}=(0,0,1)\), (observe that \(k_i\) and k are different), and standard indicial notation together with the Einstein summation convention is employed throughout. For example,

$$\begin{aligned} v_{i,i}\equiv \sum _{i=1}^3v_{i,i}&= \frac{\partial v_1}{\partial x_1}+\frac{\partial v_2}{\partial x_2}+\frac{\partial v_3}{\partial x_3}\\&=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z} \end{aligned}$$

where \(\mathbf{v}=(v_1,v_2,v_3)\equiv (u,v,w)\) and \(\mathbf{x}=(x_1,x_2,x_3)\equiv (x,y,z).\) An example of a nonlinear term is

$$\begin{aligned} v_iT_{,i}\equiv \sum ^3_{i=1}v_iT_{,i}= u\frac{\partial T}{\partial x} +v\frac{\partial T}{\partial y} +w\frac{\partial T}{\partial z}. \end{aligned}$$

The terms \(W_i^{\alpha }\) represent the viscoelastic fading memory effect, and \({\hat{\gamma }}^{\alpha }>0\), are constants, \(\alpha =1,\ldots ,L\). In deriving equations (1) a Boussinesq approximation has been employed whereby the density in the buoyancy force is written as \(\rho =\rho _0[1-\alpha (T-T_0)]\) for a reference temperature \(T_0\) and this gives rise to the \(\alpha gTk_i\) term with the constants appearing as a hydrostatic pressure, cf. Straughan [30], pp. 47–49, Straughan [31], pp. 16–21.

As Oskolkov [23], Oskolkov [24] points out, the \(W^{\alpha }_i\) terms are equivalent to a stress relation of form

$$\begin{aligned} \sigma _{ij}=\kappa _3\frac{\partial d_{ij}}{\partial t}+\nu d_{ij} +\sum _{\beta =1}^L\xi _{\beta }\int _{-\infty }^t\exp \{-{\hat{\gamma }}_{\beta }(t-s)\}\,d_{ij}\,ds, \end{aligned}$$

where \(\kappa _3>0\) and \(\xi _{\beta }>0\) are constants, \(d_{ij}\) is the symmetric part of the velocity gradient, and \(\sigma _{ij}\) is the Cauchy stress tensor. This representation, Oskolkov [23], Oskolkov [24], also arises from a stress representation of form

$$\begin{aligned} \sum _{\alpha =0}^L\lambda _{\alpha }\frac{\partial ^{\alpha }}{\partial t^{\alpha }}\sigma _{ij} =\sum _{\beta =0}^{L+1}\kappa _{\beta } \frac{\partial ^{\beta }}{\partial t^{\beta }}d_{ij} , \end{aligned}$$

for suitable coefficients \(\lambda _{\alpha }\) and \(\kappa _{\beta }\).

If \(L=0\) then equations (1) are sometimes called the Navier–Stokes–Voigt equations, cf. Layton and Rebholz [22], or sometimes the Kelvin–Voigt equations of order zero, or the Oskolkov equations, see Oskolkov [24]. For \(L=1,2,\ldots \) they are known as the Kelvin–Voigt equations of order L.

It is important to note that the Kelvin–Voigt theory is being used in various industrial applications to analyse real materials. For example, Gidde and Pawar [32] use this theory to describe polydimethylsiloxane in a micropump, Jayabal et al. [33] employ the theory in connection with modelling skin in the cosmetics industry, while Jozwiak et al. [34] describe the dynamic behaviour of biopolymer materials. A very important use of Kelvin–Voigt fluids is in viscous fluid dampers which are employed to reduce the effects of vibrations in civil engineering structures, as analysed by Greco and Marano [35] and Xu et al. [36]. Particular cases of this pertain to very high structures such as the tower Taipei 101 in the city Taipei. This is a 1667 ft high structure which is very close to a fault line and has been constructed to withstand typhoons and earthquakes. In order to achieve this Taipei 101 has a 730 ton mass damper fitted and this is connected to 8 viscous fluid dampers which act like shock absorbers when the mass damper moves.

The Kelvin–Voigt theory of order 1 has constitutive equation

$$\begin{aligned} \sigma _{ij}=\kappa _3\frac{\partial d_{ij}}{\partial t}+\nu d_{ij} +\xi _1\int _{-\infty }^t\exp \{-{\hat{\gamma }}_1(t-s)\}\,d_{ij}\,ds, \end{aligned}$$

and this contains 2 extra parameters \(\xi _1\) and \({\hat{\gamma }}_1\) which are not present in the order 0 theory. Kelvin–Voigt theory of order 2 has constitutive equation

$$\begin{aligned} \sigma _{ij}=\kappa _3\frac{\partial d_{ij}}{\partial t}+\nu d_{ij} +\xi _1\int _{-\infty }^t\exp \{-{\hat{\gamma }}_1(t-s)\}\,d_{ij}\,ds +\xi _2\int _{-\infty }^t\exp \{-{\hat{\gamma }}_2(t-s)\}\,d_{ij}\,ds, \end{aligned}$$

and this contains a further two parameters \(\xi _2\) and \({\hat{\gamma }}_2\) and is thus capable of yielding a more accurate fit to experiments than the order 1 or 0 theory, in addition to providing a more refined fit of the fading memory behaviour, which may be required, see e.g. Greco and Marano [35].

3 Thermal convection in a fluid of variable order

We suppose the fluid occupies the horizontal layer \(0<z<d\) with gravity acting downward. Then equations (1) are defined on the spatial region \(\mathbb {R}^2\times \{z\in (0,d)\}\).

The boundary conditions on the planes \(z=0\) and \(z=d\) are given by

$$\begin{aligned} \begin{aligned}&v_i=0,\quad z=0,d;\quad T=T_L,\quad z=0,\quad T=T_U,\quad z=d;\\&W^{\alpha }_i=0,\quad z=0,d,\quad \alpha =1,\ldots ,L, \end{aligned} \end{aligned}$$
(2)

with constant values \(T_L\,^{\circ }\)K, \(T_U\,^{\circ }\)K, where \(^{\circ }\)K denotes degrees Kelvin, and \(T_L>T_U>0\).

The steady solution in whose stability we are interested is given by

$$\begin{aligned} {\bar{v}}_i\equiv 0,\quad {\bar{W}}^{\alpha }_i\equiv 0,\quad {\bar{T}}=-\beta z+T_L , \end{aligned}$$
(3)

where the temperature gradient, \(\beta \), is given by

$$\begin{aligned} \beta =\frac{T_L-T_U}{d} , \end{aligned}$$

and the steady pressure \(\bar{p}\) is a quadratic in z which follows from equation (1)\(_1\).

To investigate stability of the solution (3) we introduce perturbations \((u_i,\theta ,\pi ,q^{\alpha }_i)\) by

$$\begin{aligned} v_i={\bar{v}}_i+u_i,\quad T={\bar{T}}+\theta ,\quad p={\bar{p}}+\pi ,\quad W^{\alpha }_i={\bar{W}}^{\alpha }_i+q^{\alpha }_i . \end{aligned}$$

The equations for the perturbations are then derived and non-dimensionalized with the scalings

$$\begin{aligned}&x_i=x_i^*d,\quad t=t^*{\mathcal T},\quad U=\frac{\nu }{d},\quad {\mathcal T}=\frac{d^2}{\nu }\,,\\&P=\frac{\rho _0\nu U}{d}\,,\quad W=\frac{\nu {\mathcal T}}{d},\quad T^{\sharp }=U\sqrt{\frac{\beta \nu }{kg\alpha }}, \end{aligned}$$

where \({\mathcal T},U,W\) and \(T^{\sharp }\) are the scales for time, velocity, the vectors \(W^{\alpha }_i\), and temperature, respectively. Define the Rayleigh number, \(Ra=R^2\), and the Prandtl number Pr, by

$$\begin{aligned} Ra=\frac{\alpha g\beta d^4}{\nu k} ,\quad Pr=\frac{\nu }{k} , \end{aligned}$$

and rescale the coefficients \({\hat{\gamma }}_{\alpha }\), \({\hat{\lambda }}\), \(\beta _{\alpha }\) by the non-dimensional ones

$$\begin{aligned} \gamma ^{\alpha }={\hat{\gamma }^{\alpha }}{{\mathcal T}} ,\quad \lambda =\frac{\hat{\lambda }}{{\mathcal T}\nu } , \quad \epsilon _{\alpha }=\frac{\beta _{\alpha }d}{\nu U} . \end{aligned}$$

If we drop the *s and now treat \(x_i\) and t as the non-dimensional variables, the non-dimensional form of the perturbation equations to (1) is

$$\begin{aligned} \begin{aligned}&u_{i,t}-\lambda \varDelta u_{i,t}+u_ju_{i,j}=-\pi _{,i}+\varDelta u_i+Rk_i\theta +\sum ^L_{\alpha =1}\epsilon _{\alpha }\varDelta q_i^{\alpha },\\&u_{i,i}=0,\\&Pr(\theta _{,t}+u_i\theta _{,i})=Rw+\varDelta \theta ,\\&q^{\alpha }_{i,t}+\gamma ^{\alpha }q^{\alpha }_i=u_i,\quad \alpha =1,2,\ldots ,L, \end{aligned} \end{aligned}$$
(4)

where \(w=u_3\).

Equations (4) are defined on the domain \(\mathbb {R}^2\times \{z\in (0,1)\}\times \{t>0\}\) and the boundary conditions are

$$\begin{aligned} u_i=0,\quad q^{\alpha }_i=0,\quad \theta =0,\quad z=0,1, \end{aligned}$$
(5)

together with the fact that \(u_i,q^{\alpha }_i,\theta \) and \(\pi \) satisfy a plane tiling periodicity in the x, y plane.

To analyse linear instability we linearize (4) and seek solutions of the form \(u_i=u_i(\mathbf{x})e^{\sigma t},\) \(q^{\alpha }_i=q^{\alpha }_i(\mathbf{x})e^{\sigma t},\) \(\theta =\theta (\mathbf{x})e^{\sigma t},\) \(\pi =\pi (\mathbf{x})e^{\sigma t}.\) This yields from (4)\(_4\)

$$\begin{aligned} (\sigma +\gamma ^{\alpha })q_i^{\alpha }=u_i ,\quad \alpha =1\ldots ,L. \end{aligned}$$
(6)

Then we utilize this in (4) to derive

$$\begin{aligned} \begin{aligned}&\sigma (1-\lambda \varDelta )u_i=-\pi _{,i}+\varDelta u_i+Rk_i\theta +\sum ^L_{\alpha =1}\frac{\epsilon _{\alpha }\varDelta u_i}{(\sigma +\gamma ^{\alpha })} ,\\&u_{i,i}=0,\\&Pr\sigma \theta =Rw+\varDelta \theta . \end{aligned} \end{aligned}$$
(7)

We operate on (7)\(_1\) with \(curl\,curl\) and retain the third component of the resulting equation to find

$$\begin{aligned} \begin{aligned}&\sigma (1-\lambda \varDelta )\varDelta w=\varDelta ^2w+R\varDelta ^*\theta +\sum _{\alpha =1}^L\frac{\epsilon _{\alpha }}{(\sigma +\gamma ^{\alpha })}\varDelta ^2w ,\\&Pr\sigma \theta =Rw+\varDelta \theta , \end{aligned} \end{aligned}$$
(8)

where \(\varDelta ^*= \partial ^2/\partial x^2 +\partial ^2/\partial y^2\) is the horizontal Laplacian. Introduce now the forms \(w=w(z)h(x,y),\) \(\theta =\theta (z)h(x,y)\), where h(x, y) is a planform which reflects the shape of the instability cell, cf. Chandrasekhar [37], pp. 43–52, and \(\varDelta ^*h=-a^2h\), for a wavenumber a. Then (8) may be rearranged as

$$\begin{aligned} \begin{aligned} \sigma (D^2-a^2)w-\sigma \lambda (D^2-a^2)^2w&=(D^2-a^2)^2w\\&\quad -Ra^2\theta +\sum _{\alpha =1}^L\frac{\epsilon _{\alpha }}{(\sigma +\gamma ^{\alpha })}(D^2-a^2)^2w ,\\ Pr\sigma \theta&=Rw+(D^2-a^2)\theta , \end{aligned} \end{aligned}$$
(9)

where \(D=d/dz\) and Eq. (9) hold on \(z\in (0,1)\).

To progress from this point we must specify further information on boundary conditions. The standard boundary conditions for (9) are

$$\begin{aligned} w=0,\quad \theta =0,\quad z=0,1. \end{aligned}$$
(10)

If the surfaces are fixed then we additionally require that

$$\begin{aligned} Dw=0,\quad z=0,1. \end{aligned}$$
(11)

In this case we must employ a numerical technique like the Chebyshev - tau method, see Dongarra et al. [38], together with the QZ-algorithm of Moler and Stewart [39]. This then requires resolution of an \(L+2\) order eigenvalue problem for the \(L+2\) eigenvalues \(\sigma \) before one seeks the particular eigenvalue leading to a minimum problem for the Rayleigh number. Since we believe this is the first analysis to address the thermal convection problem for a Kelvin–Voigt fluid we restrict attention to two stress free surfaces whence (11) is replaced by

$$\begin{aligned} D^2w=0,\quad z=0,1. \end{aligned}$$
(12)

In this case we write w and \(\theta \) as a \(\sin \) series in z of form \(\sin (n\pi z)\), \(n=1,2,\ldots \), cf. Chandrasekhar [37]. Our computations in the cases of Kelvin–Voigt fluids of orders 0, 1 and 2, have always yielded the lowest Rayleigh number instability curves when \(n=1\), and so in our computations reported later we employ this value.

For the case of stationary convection where the growth rate \(\sigma \) is real the instability boundary \(\sigma =0\) yields from (9) the critical Rayleigh number

$$\begin{aligned} Ra_{stat}=\frac{27\pi ^4}{4}\Bigl (1+\sum _{\alpha =1}^L\frac{\epsilon _{\alpha }}{\gamma _{\alpha }}\Bigr ) . \end{aligned}$$
(13)

However, we cannot neglect oscillatory convection and then for the instability boundary \(Re(\sigma )=0\) we may take \(\sigma =i\omega \) in (9). Converting the terms \(1/(\sigma +\gamma ^{\alpha })\) by multiplying top and bottom by the conjugate we find Eq. (9) reduce to in the complex case

$$\begin{aligned} \begin{aligned}&-i\omega (D^2-a^2)w+i\omega \lambda (D^2-a^2)^2w+(D^2-a^2)^2w\\&\quad -Ra^2\theta +\sum _{\alpha =1}^L\frac{\epsilon _{\alpha }}{(\omega ^2+\gamma _{\alpha }^2)}(\gamma ^{\alpha }-i\omega )(D^2-a^2)^2w=0 ,\\&\quad Pr i\omega \theta -(D^2-a^2)\theta -Rw=0 . \end{aligned} \end{aligned}$$
(14)

Insertion of the form \(\sin n\pi z\) with \(n=1\) then yields a determinant equation from (14) of form

$$\begin{aligned} R^2a^2=(\varLambda ^2+Pr\, i\omega )\Bigl (i\omega \varLambda +i\omega \lambda \varLambda ^2+\varLambda ^2 +\sum _{\alpha =1}^L\frac{\epsilon _{\alpha }}{(\omega ^2+\gamma _{\alpha }^2)}\,(\gamma ^{\alpha }-i\omega )\varLambda ^2\Bigr ) . \end{aligned}$$
(15)

Equation (15) must now be resolved into its real and imaginary parts. Recognise the fact that \(R^2\) is real and then the imaginary part yields a polynomial equation of order \(L+2\) in \(\omega ^2\). This must be solved numerically for each \(\omega ^2\) and then be adaptively employed to calculate the minimum of \(Ra=R^2\) in \(a^2\) from the real part of the equation. In this way a network of eigenvalue problems is solved which lead to the solution of the minimum critical Rayleigh number which yields the instability threshold.

The procedure is described in detail in Sects. 5 and 6 where we find the instability thresholds for the order 1 and order 2 problems.

4 Stability for thermal convection in a Navier–Stokes–Voigt fluid

When \(L=0\) and the \(\epsilon _{\alpha }\) terms are not present then (4) reduce to those of Navier–Stokes–Voigt theory incorporating thermal effects, cf. Layton and Rebholz [22], Sukacheva and Kondyukov [28]. The nonlinear perturbation equations in this case become

$$\begin{aligned} \begin{aligned}&u_{i,t}-\lambda \varDelta u_{i,t}+u_ju_{i,j}=\varDelta u_i-\pi _{,i}+Rk_i\theta ,\\&u_{i,i}=0,\\&Pr(\theta _{,t}+u_i\theta _{,i})=Rw+\varDelta \theta , \end{aligned} \end{aligned}$$
(16)

on \(\mathbb {R}^2\times \{z\in (0,1)\}\times \{t>0\}\), together with the boundary conditions

$$\begin{aligned} u_i=0,\quad \theta =0,\quad \mathrm{on}\,\,z=0,1 \end{aligned}$$

and periodicity in the x, y directions.

Let \((\cdot ,\cdot )\) and \(\Vert \cdot \Vert \) denote the inner product and norm on the Hilbert space \(L^2(V)\), where V is a period cell for the solution.

Equation (16) may be written in the abstract form

$$\begin{aligned} Au_t=Lu+N(u), \end{aligned}$$
(17)

cf. Straughan [30], pp. 77–87, where the linear operator L is here symmetric. Then, see general details in Straughan [30], pp. 77–87, one may show that for system (16) the linear instability boundary is equivalent to the nonlinear instability threshold. Thus, we establish the optimum result guaranteeing no subcritical instabilities. One may also show that the instability threshold is the same as that of classical Bénard convection, cf. Chandrasekhar [37], pp. 34–43, Straughan [30], pp. 59–63, where specific details may be found for the classical case.

For the present problem one finds the decay rate of a solution is different from that observed in classical Bénard convection due to the presence of the Kelvin–Voigt term \(\lambda \varDelta u_{i,t}\) and decay is found in the “energy” measure

$$\begin{aligned} E(t)=\frac{1}{2}\Vert \mathbf{u}\Vert ^2+\frac{\lambda }{2}\Vert \nabla \mathbf{u}\Vert ^2+\frac{Pr}{2}\Vert \theta \Vert ^2. \end{aligned}$$

This faster decay rate is also observed by Layton and Rebholz [22], in their Kelvin vortex solutions, see also numerical computations of Matveeva [27].

Remark

We may add a Rayleigh friction term to the right hand side of Eq. (16)\(_1\) as in Di Plinio et al. [40]. In this case the perturbation equations (16) are replaced by

$$\begin{aligned} \begin{aligned}&u_{i,t}-\lambda \varDelta u_{i,t}+u_ju_{i,j}=\varDelta u_i-\xi u_i-\pi _{,i}+Rk_i\theta ,\\&u_{i,i}=0,\\&Pr(\theta _{,t}+u_i\theta _{,i})=Rw+\varDelta \theta , \end{aligned} \end{aligned}$$
(18)

for a constant \(\xi >0\). Again, if one writes (18) in the operator form (17) then the linear operator L is symmetric and one may derive the optimal result that the linear instability and global nonlinear stability boundaries coincide. One may further demonstrate that the Rayleigh number instability threshold is found by minimizing in \(a^2\) the expression

$$\begin{aligned} Ra=\frac{\varLambda ^3}{a^2}+\xi \frac{\varLambda ^2}{a^2} \end{aligned}$$

where \(\varLambda =\pi ^2+a^2\), a being the wavenumber. This threshold is mathematically identical to the one found for thermal convection in a Brinkman porous material. The threshold in the Brinkman case is analysed in depth in Rees [41].

5 Instability for a Kelvin–Voigt fluid of order one

The Kelvin–Voigt perturbation equations of order 1 are given by (4) with \(L=1\). Thus, we must analyse a solution to the system of equations

$$\begin{aligned} \begin{aligned}&u_{i,t}-\lambda \varDelta u_{i,t}+u_ju_{i,j}=-\pi _{,i}+\varDelta u_i+R\theta k_i+\beta \varDelta q_i ,\\&u_{i,i}=0,\\&Pr(\theta _{,t}+u_i\theta _{,i})=Rw+\varDelta \theta ,\\&q_{i,t}+\gamma q_i=u_i, \end{aligned} \end{aligned}$$
(19)

where we have made the identification \(q_i^1\equiv q_i\), \(\epsilon _1\equiv \beta \), \(\gamma _1\equiv \gamma \). The boundary conditions are

$$\begin{aligned} u_i=0,\quad q_i=0,\quad \theta =0,\quad \mathrm{on}\,\,z=0,1, \end{aligned}$$

together with periodicity in x and y.

If we write system (19) in the abstract form (17) then one observes that the solution behaves very differently to that of the Navier–Stokes–Voigt theory in Sect. 4. The linear operator L is now no longer symmetric. The presence of the \(q_i\) term yields a skew–symmetric contribution to L. The classical nonlinear theory of energy stability no longer yields an optimal result regarding the linear instability and nonlinear stability thresholds and there is a possible region of sub-critical instabilities. In this sense the Kelvin–Voigt order 1 problem behaves like thermal convection with rotation, cf. Mulone and Rionero [42], Straughan [43], chapter 8, Straughan [30], chapter 6; or like magnetohydrodynamic thermal convection, Mulone and Rionero [44]; or like double diffusive convection, Mulone [45], Straughan [30], chapter 14, Straughan [46]; or like parallel shear flow, Falsaperla et al. [47], Rionero and Mulone [48], Xiong and Chen [49], Straughan [43], chapter 8; or when Cattaneo–Christov heat flux effects are present in thermal convection, Straughan [50], chapter 8, Straughan [51], Straughan [52], Straughan [53].

To develop an energy stability analysis from (19) we multiply (19)\(_1\) by \(u_i\), (19)\(_2\) by \(\theta \), (19)\(_4\) by \(-\varDelta q_i\), integrate each over V and use the boundary conditions to obtain the equations

$$\begin{aligned} \frac{d}{dt}\Bigl (\frac{1}{2}\Vert \mathbf{u}\Vert ^2+\frac{\lambda }{2}\Vert \nabla \mathbf{u}\Vert ^2\Bigr )= -\Vert \nabla \mathbf{u}\Vert ^2+R(\theta ,w)-\beta (q_{i,j},u_{i,j}), \end{aligned}$$
(20)

and

$$\begin{aligned} \frac{d}{dt}\frac{Pr}{2}\Vert {\theta }\Vert ^2= -\Vert \nabla {\theta }\Vert ^2+R(\theta ,w), \end{aligned}$$
(21)

together with

$$\begin{aligned} \frac{d}{dt}\frac{1}{2}\Vert \nabla \mathbf{q}\Vert ^2= -\gamma \Vert \nabla \mathbf{q}\Vert ^2+(q_{i,j},u_{i,j}). \end{aligned}$$
(22)

Form the combination (20) + (21) + \(\beta \)(22) to arrive at

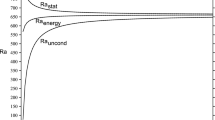
$$\begin{aligned} \frac{d}{dt}&\Bigl (\frac{1}{2}\Vert \mathbf{u}\Vert ^2+\frac{\lambda }{2}\Vert \nabla \mathbf{u}\Vert ^2 +\frac{Pr}{2}\Vert \theta \Vert ^2+\frac{\beta }{2}\Vert \nabla \mathbf{q}\Vert ^2\Bigr )\\&=2R(\theta ,w)-\Vert \nabla \mathbf{u}\Vert ^2-\Vert \nabla \theta \Vert ^2-\gamma \beta \Vert \nabla \mathbf{q}\Vert ^2. \end{aligned}$$

From this equation we may apply the method of energy stability theory, cf. Straughan [30], chapter 4, to find global nonlinear stability provided R does not exceed the classical Bénard threshold. For example, provided \(Ra<27\pi ^4/4\) for two free surfaces, cf. Fig. 1, the region below the line OC. However, as we see from Fig. 1, the linear instability curve increases with \(\beta \) beyond \(27\pi ^4/4\), the lines OA and AB, and there is a region of possible sub-critical instability, in the area OABC. In this respect, the Kelvin–Voigt problem of order 1 behaves very similarly to the thermosolutal convection problem; Fig. 1 is mathematically similar to figure 1, Straughan [46], p. 620.

Fig. 1
figure 1

Graph of \(Ra,\beta \) with \(\gamma =0.2\), \(Pr=25\), \(\lambda =10^{-3}\). The line OA represents the stationery convection curve, whereas the curve AB is the oscillatory convection threshold. The horizontal line OC is the global nonlinear stability boundary. We cannot rule out possible sub-critical instability in the region OABC. Kelvin–Voigt fluid of order one

Full size image

To determine the instability curves in Fig. 1 we return to Eq. (9) and take \(L=1\). For two free surfaces we find that these equations yield the Rayleigh number relation

$$\begin{aligned} R^2a^2=(\varLambda +Pr\sigma )\Bigl [\sigma (\varLambda +\lambda \varLambda ^2)+\varLambda ^2 +\Bigl (\frac{\beta }{\gamma +\sigma }\Bigr )\varLambda ^2\Bigr ] , \end{aligned}$$
(23)

where \(\varLambda =\pi ^2+a^2\). For stationary convection \(\sigma =0\) and then one obtains

$$\begin{aligned} Ra_{stat}=\frac{\varLambda ^3}{a^2}\Bigl (1+\frac{\beta }{\gamma }\Bigr ) \end{aligned}$$

and minimizing over \(a^2\) yields \(a^2=\pi ^2/2\), whence

$$\begin{aligned} Ra_{stat}=\frac{27\pi ^4}{4}\Bigl (1+\frac{\beta }{\gamma }\Bigr ) . \end{aligned}$$
(24)

We might expect oscillatory instability for \(\gamma \) relatively small compared to \(\beta \) since in the formal limit \(\gamma \rightarrow 0\), \(u_i=q_{i,t}\) and then equation (19)\(_1\) essentially becomes hyperbolic, and such instabilities have been seen in other viscoelastic fluids in similar circumstances, see e.g. Joseph et al. [13].

To determine the oscillatory boundary threshold we follow the method in Chandrasekhar [37], section 29. Since we require the boundary where \(Re\,\sigma =0\) we put \(\sigma =i\omega \), \(\omega \in \mathbb {R}\), and then from (23) one finds

$$\begin{aligned} \begin{aligned} R^2a^2=&\varLambda ^3-\omega ^2Pr(\varLambda +\lambda \varLambda ^2)+\frac{\beta \varLambda ^2}{(\gamma ^2+\omega ^2)}\,(\varLambda \gamma +Pr\,\omega ^2)\\&+i\omega \Bigl [\varLambda ^2+\lambda \varLambda ^3+Pr\varLambda ^2+\frac{\beta \varLambda ^2}{(\gamma ^2+\omega ^2)}\,(Pr\gamma -\varLambda )\Bigr ] . \end{aligned} \end{aligned}$$
(25)

Since \(R^2\) and \(a^2\) are real, (25) yields two equations after separating into real and imaginary parts.

We require \(\omega \ne 0\) and then the imaginary part yields

$$\begin{aligned} \omega ^2=-\gamma ^2+\beta \Bigl [\frac{\varLambda ^3-\gamma Pr\varLambda ^2}{\lambda \varLambda ^3+(1+Pr)\varLambda ^2}\Bigr ]>0. \end{aligned}$$
(26)

From this relation one obtains necessary conditions for instability of form

$$\begin{aligned} \beta>\gamma ^2\lambda \quad \mathrm{and}\quad (\beta -\gamma ^2\lambda )\varLambda >\beta \gamma Pr+\gamma ^2(1+Pr). \end{aligned}$$

The real part of (25) yields

$$\begin{aligned} R^2=\frac{1}{a^2}\Bigl [\varLambda ^3+\frac{\beta \gamma \varLambda ^3}{\gamma ^2+\omega ^2}+\beta Pr\varLambda ^2\Bigl (\frac{\omega ^2}{\omega ^2+\gamma ^2}\Bigr ) -Pr \omega ^2(\varLambda +\lambda \varLambda ^2)\Bigr ] . \end{aligned}$$
(27)

One now employs \(\omega ^2\) from (26) in (27) and minimizes the resulting expression numerically in \(a^2\) for fixed \(\beta ,\gamma \) and Pr. Whether stationary or oscillatory convection occurs depends on the relative sizes of \(R^2\) given by (24) or the minimum of (27).

We now present numerical results for the minimization of (27). To present graphical output we fix \(\gamma \) and allow \(\beta \) to vary so that the stationmary convection curve is a straight line as shown as line OA in Fig. 1. For oils the value of the Prandtl number lies typically in the range \(25\le Pr\le 400\), see Rodenbush et al. [54].

Table 1 Transition from stationary to oscillatory convection values. \(\gamma =0.2\), \(Pr=25\). Kelvin–Voigt fluid of order one
Full size table

The stationary convection curve and oscillatory convection curves are given for \(\gamma =0.2,Pr=25\) with \(\lambda \) taking values \(\lambda =1,10^{-3}\), in Fig. 2, and the transition values as the instability switches from stationary to oscillatory convection are given in Table 1 for \(\lambda =10^{-3},10^{-2},0.1\) and 1. The equivalent critical \(a^2\) values are shown in Fig. 3. We see that as the instability switches from stationary to oscillatory convection the \(a^2\) values increase discontinuously and since \(a\propto 1/\)aspect ratio, (aspect ratio = width/depth of a convection cell), this means that the cells switch from a wider to a relatively narrower cell once the convection is oscillatory.

Fig. 2
figure 2

Graph of \(Ra,\beta \) with \(\gamma =0.2\), \(Pr=25\). The transition to oscillatory convection is given for \(\lambda =1\) and \(\lambda =10^{-3}\). The steady solution is unstable above the appropriate stationary–oscillatory curve. The transition values are approximately \(Ra=990.6,\beta =0.1013\) when \(\lambda =10^{-3}\), and \(Ra=1184,\beta =0.160\) when \(\lambda =1\). Kelvin–Voigt fluid of order one

Full size image
Fig. 3
figure 3

Graph of \(a^2,\beta \) with \(\gamma =0.2\), \(Pr=25\). The transition to oscillatory convection is given for \(\lambda =1\) and \(\lambda =10^{-3}\). The stationary convection value of \(a^2=\pi ^2/2\) for all values of \(\beta \). The transition to oscillatory convection occurs at AB when \(\lambda =10^{-3}\) and \(\beta =0.1013\), and occurs at CD when \(\lambda =1\) and \(\beta =0.16\). Kelvin–Voigt fluid of order one

Full size image
Table 2 Transition from stationary to oscillatory convection values. \(\gamma =0.5\), \(Pr=25\). Kelvin–Voigt fluid of order one
Full size table

Figures 4 and 5 give the Ra against \(\beta \) values and the \(a^2\) against \(\beta \) values for \(\gamma =0.5\), \(Pr=25\) and the transition values are given in Table 2. It is noticeable that when \(\gamma =0.5\) the \(a^2\) values at \(\lambda =1\) are considerably smaller for oscillatory convection than the \(\lambda =10^{-3}\) ones. The opposite is true when \(\gamma =0.2\).

Fig. 4
figure 4

Graph of \(Ra,\beta \) with \(\gamma =0.5\), \(Pr=25\). The transition to oscillatory convection is given for \(\lambda =1\) and \(\lambda =10^{-3}\). The steady solution is unstable above the appropriate stationary–oscillatory curve. The transition values are approximately \(Ra=3011,\beta =1.79\) when \(\lambda =10^{-3}\), and \(Ra=4078,\beta =2.60\) when \(\lambda =1\). Kelvin–Voigt fluid of order one

Full size image
Fig. 5
figure 5

Graph of \(a^2,\beta \) with \(\gamma =0.5\), \(Pr=25\). The transition to oscillatory convection is given for \(\lambda =1\) and \(\lambda =10^{-3}\). The stationary convection value of \(a^2=\pi ^2/2\) for all values of \(\beta \). The transition to oscillatory convection occurs at AB when \(\lambda =10^{-3}\) and \(\beta =1.79\), and occurs at CD when \(\lambda =1\) and \(\beta =2.6\). Kelvin–Voigt fluid of order one

Full size image

We computed instability thresholds also for \(Pr=100\). For the parameter ranges we considered only stationary convection was discovered when \(Pr=100\). It would appear that the occurrence of oscillatory convection depends strongly on the Prandtl number not being to high.

6 Instability for a Kelvin–Voigt fluid of order two

We now consider the instability of the conduction solution to the thermal convection problem for a Kelvin–Voigt fluid of order 2. From Eq. (4) the governing system of perturbation equations may be written

$$\begin{aligned} \begin{aligned}&u_{i,t}-\lambda \varDelta u_{i,t}+u_ju_{i,j}=-\pi _{,i}+\varDelta u_i+R\theta k_i+\beta \varDelta W_i+\epsilon \varDelta V_i ,\\&u_{i,i}=0,\\&Pr(\theta _{,t}+u_i\theta _{,i})=Rw+\varDelta \theta ,\\&W_{i,t}+\gamma W_i=u_i,\\&V_{i,t}+\delta V_i=u_i, \end{aligned} \end{aligned}$$
(28)

where \(V_i\) avd \(W_i\) correspond to \(W_i^1\) and \(W_i^2\). The boundary conditions are

$$\begin{aligned} u_i=0,\quad V_i=0,\quad W_i=0,\quad \theta =0,\quad \mathrm{on}\,\,z=0,1, \end{aligned}$$
(29)

together with periodicity in the x, y plane.

These equations are linearized and representations like \(u_i=e^{\sigma t}u_i(\mathbf{x})\) are taken in (28). After removing the pressure the relevant equations may be reduced to

$$\begin{aligned} \begin{aligned}&\sigma (1-\lambda \varDelta )\varDelta w-\varDelta ^2w-\frac{\beta }{(\sigma +\gamma )}\varDelta ^2w-\frac{\epsilon }{(\sigma +\delta )}\varDelta ^2w-R\varDelta ^*\theta =0,\\&\sigma Pr\theta =\varDelta \theta +Rw. \end{aligned} \end{aligned}$$
(30)

The forms \(w=W(z)h(x,y)\), \(\theta =\varTheta (z)h(x,y)\) for a plane tiling planform h are employed and then with \(W(z)={\hat{W}}\sin n\pi z\), and a similar form form \(\theta \), Eq. (30) reduce to a determinant equation. The requirement that \({\hat{W}},{\hat{\varTheta }}\) be non-zero leads to the following equation for \(R^2\),

$$\begin{aligned} R^2a^2=(\varLambda +\sigma Pr)\Bigl [\varLambda ^2\Bigl (\lambda \sigma +1+\frac{\beta }{\sigma +\gamma }+\frac{\epsilon }{\sigma +\delta }\Bigr ) +\sigma \varLambda \Bigr ] , \end{aligned}$$
(31)

where a is the wavenumber and \(\varLambda =\pi ^2+a^2\).

From (31) we find the stationary convection boundary, \(\sigma =0\), as

$$\begin{aligned} R^2_{stat}=\frac{27\pi ^4}{4}\Bigl (1+\frac{\beta }{\gamma }+\frac{\epsilon }{\delta }\Bigr ) . \end{aligned}$$
(32)

To investigate oscillatory convection take \(\sigma =i\omega \), \(\omega \in \mathbb {R}\), and then (31) is written as the real part and the imaginary part. For \(\omega \ne 0\) the imaginary part yields the quadratic equation for \(\omega ^2\),

$$\begin{aligned} X_1\omega ^4+X_2\omega ^2+X_3=0, \end{aligned}$$
(33)

where

$$\begin{aligned} X_1&=\lambda \varLambda ^3+(1+Pr)\varLambda ^2,\\ X_2&=[(\lambda \delta ^2+\lambda \gamma ^2)\varLambda ^3-(\beta +\epsilon )\varLambda ^3]\\&\quad +(1+Pr)\varLambda ^2(\delta ^2+\gamma ^2)+Pr\varLambda ^2(\beta \gamma +\epsilon \delta ),\\ X_3&=\varLambda ^3(\lambda \gamma ^2\delta ^2-\beta \delta ^2-\epsilon \gamma ^2)+(1+Pr)\varLambda ^2\gamma ^2\delta ^2\\&\quad +Pr\varLambda ^2(\beta \gamma \delta ^2+\epsilon \delta \gamma ^2). \end{aligned}$$

Equation (33) is solved numerically for the two solutions \(\omega _+^2\) and \(\omega _-^2\), corresponding to the + and - sign in

$$\begin{aligned} \omega ^2=\frac{-X_2\pm \sqrt{X_2^2-4X_1X_3}}{2X_1} . \end{aligned}$$

Then, both solutions \(\omega _+^2\) and \(\omega _-^2\) are employed in the equation for \(R^2\) which arises from the real part of equation (31). This equation has form

$$\begin{aligned} \begin{aligned} R^2&=\frac{\varLambda ^3}{a^2}\Bigl (1+\frac{\beta \gamma }{\gamma ^2+\omega ^2}+\frac{\epsilon \delta }{\delta ^2+\omega ^2}\Bigr )\\&\quad -\frac{Pr\omega ^2}{a^2}\Bigl [\varLambda ^2\Bigl (\lambda -\frac{\beta }{\gamma ^2+\omega ^2}-\frac{\epsilon }{\delta ^2+\omega ^2}\Bigr )+\varLambda \Bigr ] . \end{aligned} \end{aligned}$$
(34)

Expression (34) is minimized in \(a^2\) for each of \(\omega _+^2\) and \(\omega _-^2\) and the correct minimum is chosen provided the appropriate \(\omega ^2\) is positive. In this manner we find the oscillatory convection instability threshold which is compared to the stationary convection one (32) to assess which type of convection actually occurs.

Table 3 Critical Rayleigh and wave numbers when \(Pr=25\), \(\lambda =0.01\), \(\beta =1.2,\epsilon =1\). The subscripts stat and osc refer to stationary convection or oscillatory convection, respectively. Whether stationary or oscillatory convection occurs is indicated. The symbols *** indicate only stationary convection was found. The stationary convection value of \(a^2\) is always \(\pi ^2/2\approx \,4.9348\). The words approx trans mean that this is close to the transition value from stationary to oscillatory convection. Kelvin–Voigt fluid of order two
Full size table

We present two tables of numerical results taking \(Pr=25\) in both. Table 3 selects \(\beta =1.2,\epsilon =1\), \(\lambda =10^{-2}\), whereas Table 4 employs \(\beta =1,\epsilon =0.9,\lambda =0.1\). For the results presented in both tables we found \(\omega _+^2>0\) and \(\omega _-^2<0\), although if \(\delta \) and \(\gamma \) are relatively large then only stationary convection is found.

Table 4 Critical Rayleigh and wave numbers when \(Pr=25\), \(\lambda =0.1\), \(\beta =1,\epsilon =0.9\). The subscripts stat and osc refer to stationary convection or oscillatory convection, respectively. Whether stationary or oscillatory convection occurs is indicated. The symbols *** indicate only stationary convection was found. The stationary convection value of \(a^2\) is always \(\pi ^2/2\approx \,4.9348\). The words approx trans mean that this is close to the transition value from stationary to oscillatory convection. Kelvin–Voigt fluid of order two
Full size table

In Table 3 we see that relatively small values of \(\delta \) and \(\gamma \) compared to \(\beta \) and \(\epsilon \) result in oscillatory convection, a fact in keeping with the study in a Kelvin–Voigt fluid of order 1 as seen in Sect. 5. When \(\delta \) is kept at fixed value 0.6 stationary convection is witnessed when \(\gamma =0.5\) but once \(\gamma \) is lowered there is a transition point and thereafter lower values of \(\gamma \) yield oscillatory convection. For \(\delta =0.6\) we find an approximate transition value at \(\gamma =0.474\). However, when we keep \(\gamma \) fixed at value 0.4 and increase \(\delta \) we were unable to find stationary convection, even when \(\delta =2\).

In Table 4 the value of \(\lambda \) is larger, but \(\beta \) and \(\epsilon \) are smaller. Here we again witness a transition from stationary to oscillatory convection as the pair \((\delta ,\gamma )\) moves from (0.4,0.3) to (0.35,0.25). The critical Rayleigh number values are much higher in Table 4 than those on Table 3. This shows the layer is more stable for the parameters of Table 4.

In Table 3, oscillatory convection is associated to smaller wave numbers and, therefore, to wider convection cells. This trend is also witnessed in Table 4.

In general, we believe there is a three-dimensional picture where if we fix \(\delta \) and \(\gamma \) and plot Ra against \(\beta \) and \(\epsilon \) we shall find a transition from stationary to oscillatory convection surface analogous to the Ra against \(\beta \) curves in Sect. 5. It is interesting to note that in the order 2 case the oscillatory convection threshold Rayleigh numbers can fall below the transition between the stationary and oscillatory value. Thus, a complete picture in the order 2 case will require substantial computation to create the two dimensional surface as \(\delta ,\gamma ,\epsilon \) and \(\beta \) are varied, once real fluid parameter values are identified.

7 Conclusions

We have analysed the models for viscoelastic flow incorporating thermal effects suggested by Sukacheva and Matveeva [26], Sukacheva and Kondyukov [28], these following from the isothermal models of Oskolkov [23, 24]. A procedure for computing the growth rates and then the stability threshold curves is presented for thermal convection in a layer. In general, the computational procedure needs to be adaptive and will benefit by coding over a network.

We have analysed in detail thermal convection in Kelvin–Voigt fluids of order 0, 1 and 2. The order 0 case is special in that we showed the linear instability curve coincides with the global nonlinear stability one. For Kelvin–Voigt fluids of order 1 and 2 this is not the case and there we witness oscillatory convection and more complex neutral curve behaviour. The order 1 case appears to have a transition value and then the oscillatory curve increases with increasing \(\beta \) values (for fixed \(\gamma \)), as is shown in Figs. 1, 2 and 4. The order 2 case is more complex and yields a two dimensional surface in the Ra, \(\epsilon \), \(\beta \) three dimensional space for fixed \(\gamma ,\delta \). We stress that the computation of oscillatory curves or surfaces is very important in real life fluid mechanics, since as pointed out in the introduction there are situations such as semi-conductor crystal growth where such instabilities are best avoided.

For higher order Kelvin–Voigt fluids the growth rate \(\omega \) will satisfy a polynomial equation of increasing order. The neutral curves must be based on each value of \(\omega ^2\) which is found, and the critical Rayleigh number determined taking all \(\omega ^2\) into account. There may, therefore, be the opportunity for even greater complex behaviour.