Effect of Temperature Upon Double Diffusive Instability in Navier–Stokes–Voigt Models with Kazhikhov–Smagulov and Korteweg Terms

Abstract

We present models for convection in a mixture of viscous fluids when the layer is heated from below and simultaneously the pointwise volume concentration of one of the fluids is heavier below. This configuration produces a problem of competitive double diffusion since heating from below promotes instability, but the greater density of fluid below is stabilizing. The fluids are of linear viscous type which may contain Kelvin–Voigt terms, but density gradients due to the mixture appear strongly in the governing equations. The density gradients give rise to Korteweg stresses, but may also be described by theory due to Kazhikhov and Smagulov. The systems of equations which appear are thus highly nonlinear. The instability surface threshold is calculated and this is found to have a complex nonlinear shape, very different from the linear ones found in classical thermohaline convection in a Navier–Stokes fluid. It is shown that the Kazhikhov–Smagulov terms, Korteweg terms and Kelvin–Voigt term play a key role in acting as stabilizing agents but the associated effect is very nonlinear. Quantitative values of the instability surface are displayed showing the effect Korteweg terms, Kazhikhov–Smagulov terms, and the Kelvin Voigt term have. The nonlinear stability problem is addressed by means of a generalized energy theory deriving different results depending on which underlying theory is employed.

1 Introduction

Recent research is demonstrating that the classes of fluids or fluid mixtures being employed in industrial engineering applications and in particular in renewable energy studies is increasingly diverse. Mixtures of fluids are highly complex and while they may be described by a stess tensor which depends linearly on the velocity gradient it is known that there has to be additionally a dependence on density gradients due to the different constituents. Such complex fluids define a class which is often referred to as generalized Navier–Stokes fluids, and these generalized fluids also encompass those which include viscoelastic effects where the stress tensor depends on the history of the velocity gradient, and this area is vast, as is witnessed by the work of [1,2,3, 16, 17, 23, 33, 34, 75]

In this article we study a mixture of miscible vicous fluids but we also allow the mixture to be comprised of a particular class of viscoelastic fluids associated with the names of Kelvin and of Voigt, cf. [3, 5, 57]. Analysis studies of Kelvin–Voigt fluids (which encompass Navier–Stokes–Voigt) have been presented in much detail by [49, 50], and generalizations of these to incorporate temperature effects are given by [42, 48, 68] and [67], see also [40, 47, 53, 69]. Kelvin–Voigt fluids of order zero are also known as Navier–Stokes–Voigt fluids and the equations for these have been analysed in great detail with respect to questions of existence, behaviour of attractors by e.g. [10, 20, 36, 37]. In connection with classes of viscoelastic fluids we point out that a very useful account of Maxwell, Oldroyd and Kelvin–Voigt fluids of various orders is given by [51] who discuss the solution existence question at length.

Double diffusion is caused by two effects such as a temperature gradient and a concentration gradient and these may often be in opposition. For example if a layer of water (or other solvent) has sodium chloride dissolved in it then instability may be caused by the salt concentration being heavier at the top or by heating the base of the layer and the resulting convective motion is witnessed in the fluid (Newtonian or viscoelastic). This phenomenon is widely studied in the literature, see e.g. [7, 13, 14, 31, 52, 62,63,64,65,66, 73][pp. 238–268]. However, double or multi diffusive instability may also be witnessed in a mixture of miscible liquids subject to a temperature gradient, but where the density gradient due to the different fluids is also an ingredient for instability. Indeed, double or multi diffusive instability for a mixture of miscible fluids is an area which is increasingly occupying application areas. For example, diffusion in glycerol–water mixtures has many applications, see e.g. [12, 21, 74]. Double or multi diffusion convective instability is particularly important in the area of renewable energy. A solar pond is a device which employs the Sun’s rays to produce electricity and recent research in this area is concentrating on using different solvents and dissolved salts, being a precise application of multi fluid mixture convection, see e.g. [4, 59].

In a mixture of viscous fluids one has the usual dependence of the stress tensor upon the symmetric part of the velocity gradient, but there will in general also be a dependence upon gradients of density. The idea of incorporating density gradients into the stress is attributed to Korteweg, see e.g. [70, p. 514]. Further information on Korteweg stress formulations be may found in [41, 46], and these writers analyse in detail thermodynamic aspects and different flow regimes.

Apart from the applications mentioned above, Korteweg stresses are important in real life and have application in vulcanology, see [71], and in other areas of geophysics, see [45]. Beginning with equations of [26, 35] developed a model for a layer of fluid mixture where the stress incorporated Korteweg terms, and they particularly studied the stability of an isothermal liquid layer where convective motion may be driven by gravity if the upper part of the layer is denser than that below. [26] derived a set of Korteweg–Boussinesq equations which are highly useful in this process. The question of uniqueness of a solution to the isothermal Korteweg–Boussinesq equations is addressed by [27]. Temperature effects were incorporated to stability problems involving incompressible viscous fluids with Korteweg stresses by [54]. These writers investigate instability arising due to density gradients via Korteweg stresses, but they do not incorporate buoyancy effects as in [26, 27]. The Korteweg effect will dominate in a zero gravity atmosphere, but even in low gravity conditions the joint effect of buoyancy and density gradients should be important. One of the aims of this work is to include the effect of gravity on instability in addition to the density gradient contribution.

The effect of Korteweg terms upon fluid mechanics is increasingly becoming popular from a continuum mechanics point of view, see e.g. [18, 19, 28], but particularly from a perspective of analysis in partial differential equations, see e.g. [11, 15, 32, 58, 60, 72].

A separate development to deriving a theory for a mixture of isothermal fluids which incorporates density gradient terms is due to [38, 39], and this theory was employed to analyse gravitational instability when the fluid layer is heavier at the top by [24]. The [38, 39], theory has been investigated in some depth from an anlysis viewpoint of existence and solution behaviour by [55, 56], and also by [8, 9]. More recent papers on analysis of the Kazhikhov–Smagulov models is due to [29, 30].

In this work we firstly extend the Korteweg–Boussinesq model of [26] to include temperature effects and thus be applicable to the double diffusive convection scenario. We are particularly interested in the competitive case where temperature is destabilizing whereas the concentration is stabilizing. However, we also develop the [38, 39] model to include temperature effects. To do this we employ a suitable Boussinesq approximation, see [6], and derive the model from the completely nonlinear set of equations analysed in the isothermal case by [8]. This development is very interesting because we show that in addition to the Navier–Stokes terms present in standard double diffusion theory there arise two new sets of terms in the momentum equation. One set of terms we attribute to the Kazhikhov–Smagulov development. The second set of terms has the same form as those which arise from Korteweg theory. Hence, the Kazhikhov–Smagulov full theory analysed by [8] contains the Korteweg terms naturally. Thus, we effectively show that there are three models which arise. One corresponds to the Korteweg theory, the second corresponds to Kazhikhov–Smagulov theory, and the third is a combination of both.

We perform a linear instability analysis and a complementary nonlinear stability analysis for all three models for a mixture of fluids in the competitive double diffusion situation. For the Korteweg model the nonlinear stability obtained is global, in the sense that the stability is for all initial data. For the model derived by [8] from the full set of Kazhikhov– Smagulov equations the nonlinear stability analysis obtained is conditional upon the size of the initial data.

2 Equations

Let $\mathbf{x}$ denote a spatial point in a three-dimensional body and let t denote time. If $\rho (\mathbf{x},t)$ denotes the density of a mixture of two miscible fluids then the Cauchy stress tensor, $t_{ij}$, for a linearly viscous fluid with Korteweg stress terms may be written as

$$\begin{aligned} t_{ij}=(-P+\beta _1\rho _{,k}\rho _{,k}+\beta _2\rho _{,kk})\delta _{ij}+H_1\rho _{,i}\rho _{,j}+H_2\rho _{,ij} +\gamma d_{kk} \delta _{ij} +2\mu d_{ij}\,, \end{aligned}$$

(1)

see [41, 70, p. 514]. Here $d_{ij}$ is the symmetric part of the velocity gradient, i.e.

$$\begin{aligned} d_{ij}=\frac{1}{2}(v_{i,j}+v_{j,i}), \end{aligned}$$

where $v_i$ is the velocity field. We employ standard indicial notation throughout together with the Einstein summation convention. For example, the divergence of the velocity field is

$$\begin{aligned} v_{i,i}\equiv \sum _{i=1}^3v_{i,i}=&\frac{\partial v_1}{\partial x_1}+\frac{\partial v_2}{\partial x_2}+\frac{\partial v_3}{\partial x_3}\\ =&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z} \end{aligned}$$

where $\mathbf{v}=(v_1,v_2,v_3)\equiv (u,v,w)$ and $\mathbf{x}=(x_1,x_2,x_3)\equiv (x,y,z)$. A further example is

$$\begin{aligned} v_iC_{,i}\equiv \sum ^3_{i=1}v_iC_{,i}= u\frac{\partial C}{\partial x} +v\frac{\partial C}{\partial y} +w\frac{\partial C}{\partial z}, \end{aligned}$$

for a function C depending upon $\mathbf{x}$, t. In (1) P is the pressure in the fluid and we here treat the coefficients, $\beta _1,\beta _2,\gamma ,H_1,H_2$ as constants. For an incompressible fluid the $\gamma$ term is omitted from (1) and since the stress tensor appears in the momentum equation as $t_{ij,j}$ the term in $H_2$ can also be incorporated into a modified pressure of form

$$\begin{aligned} p=-P+\beta _1\rho _{,k}\rho _{,k}+(\beta _2+H_2)\Delta \rho . \end{aligned}$$

The momentum equation for a fluid in the Korteweg–Boussinesq equations as derived by [26], employs a Boussinesq approximation, see [6]. The momentum equation of [26] in our notation may be written

$$\begin{aligned} v_{i,t}+v_jv_{i,j}=-\frac{p_{,i}}{\rho _0}+(\nu d_{ij})_{,j}-\frac{g\rho }{\rho _0}\,k_i-K_1C_{,i}\Delta C, \end{aligned}$$

(2)

where $\nu (C)=\mu (C)/\rho _0$ is the kinematic viscosity of the fluid, $\rho _0$ is a constant reference value of density, g is gravity, $\mathbf{k}=(0,0,1)$, and we have written $K_1=-H_1$. [26] mainly discuss the case $H_1<0$ but they leave the possibility that it could be positive. We choose to retain $H_1$ negative since experimental values, cf. [54], suggest this, and also this sign of coefficient arises naturally in the development from the full set of Kazhikhov–Smagulov equations. The function C is the concentration of one of the fluids (the volume fraction) and we observe that [35] defines this quantity for a mixture of water and glycerin to be $C=V_W/V_T$, where $V_W$ is the volume of water and $V_T$ is the total volume. (This must be interpreted in the continuum mixture sense where both constituents exist at each point and one considers a representative elementary volume around a point $\mathbf{x}$ containing both water and glycerin and $V_W$ is the limit as the volume tends to zero. Of course, $V_W$ in this way changes with time, in general.) In [26] the density is written as

$$\begin{aligned} \rho =\rho _0(1+\alpha _c[C-C_0])\,, \end{aligned}$$

(3)

where $C_0$ is a constant reference value, and $\alpha _c$ is the expansion coefficient associated with the concentration variation. Upon employing the density equation (3) in (2) we arrive at the complete momentum equation in the Korteweg–Boussinesq approximation of [26], namely

$$\begin{aligned} v_{i,t}+v_jv_{i,j}=-\frac{p_{,i}}{\rho _0}+(\nu d_{ij})_{,j}-g\alpha _c\,C\,k_i-K_1C_{,i}\Delta C, \end{aligned}$$

(4)

where the constant term in the density, (3), has also been absorbed into the pressure. The fluid is (in a sense) incompressible, see [26], and then the continuity equation is

$$\begin{aligned} v_{i,i}=0. \end{aligned}$$

(5)

The evolution equation for the concentration is

$$\begin{aligned} \frac{\partial C}{\partial t}+v_i\frac{\partial C}{\partial x_i}=\kappa _c\Delta C. \end{aligned}$$

(6)

The Korteweg–Boussinesq system of equations of [26], Eqs. (4.11)–(4.13), is comprised of (4), (5), (6), and for clarity we rewrite them together here,

$$\begin{aligned} \begin{aligned}&\frac{\partial v_i}{\partial t}+v_j\frac{\partial v_i}{\partial x_j}= -\frac{p_{,i}}{\rho _0} +\frac{\partial }{\partial x_j}\bigl (\nu d_{ij}\bigr ) -g\alpha _c\,C\,k_i -K_1\frac{\partial C}{\partial x_i}\Delta C,\\&v_{i,i}=0,\\&\frac{\partial C}{\partial t}+v_i\frac{\partial C}{\partial x_i}=\kappa _c\Delta C\,. \end{aligned} \end{aligned}$$

(7)

To extend the model of [26] to incorporate temperature we need to modify the density in (3) to allow for variable temperature and thus the density is now written as

$$\begin{aligned} \rho =\rho _0(1-\alpha [T-T_0]+\alpha _c[C-C_0])\,, \end{aligned}$$

(8)

where $\rho _0,T_0,C_0$ are constant reference values, $T(\mathbf{x},t)$ is the temperature and $\alpha$ is the expansion coefficient of the fluid.

The evolution equation for the temperature field may now be written as

$$\begin{aligned} \frac{\partial T}{\partial t}+v_i\frac{\partial T}{\partial x_i}=\kappa \Delta T\,, \end{aligned}$$

(9)

cf. [54], where $\kappa$ is the thermal diffusivity which is assumed constant.

There is a case for the viscosity to depend on both temperature and concentration, but as this is the first time we have seen work on the double diffusive convection problem we choose to keep the kinematic viscosity constant and so proceeding in this manner we may arrive at the full system of Korteweg–Boussinesq equations for double diffusive convection in the form

$$\begin{aligned} \begin{aligned}&\frac{\partial v_i}{\partial t}+v_j\frac{\partial v_i}{\partial x_j}= -\frac{p_{,i}}{\rho _0}+\nu \Delta v_i+g\alpha Tk_i-g\alpha _c\,C\,k_i-K_1\frac{\partial C}{\partial x_i}\Delta C,\\&v_{i,i}=0,\\&\frac{\partial T}{\partial t}+v_i\frac{\partial T}{\partial x_i}=\kappa \Delta T,\\&\frac{\partial C}{\partial t}+v_i\frac{\partial C}{\partial x_i}=\kappa _c\Delta C. \end{aligned} \end{aligned}$$

(10)

The momentum equation of the [38, 39] equations is given by [8] as

$$\begin{aligned} \begin{aligned}&\rho (v_{i,t}+v_jv_{i,j})-\mu \Delta v_i-\lambda (v_j\rho _{,ij}+\rho _{,j}v_{i,j})\\&\quad +\frac{\lambda ^2}{\rho }(\rho _{,j}\rho _{,ij}-\frac{1}{\rho }\rho _{,j}\rho _{,j}\rho _{,i}+\rho _{,i}\Delta \rho ) =-P_{,i}+\rho f_i \end{aligned} \end{aligned}$$

(11)

where $\lambda >0$ is a constant we call the Kazhikhov–Smagulov parameter. In Eq. (11), $f_i$ is the body force and P is a modified pressure given by

$$\begin{aligned} P=-\lambda \rho _{,t}+{\hat{p}}+\lambda [({\tilde{\lambda }}+2\mu )\Delta (\log \rho )] \end{aligned}$$

where ${\hat{p}}$ is the actual fluid pressure and $\tilde{\lambda }$ is another constant, cf. [24], Eqs. (2.5), (2.6).

[8] writes that Kazhikhov and Smagulov consider the simplified equation which follows from (11) by omitting the term involving $\lambda ^2$. This simplified system leads to what [24] call the Kazhikhov–Smagulov equations. [8] also notes that Kazhikhov and Smagulov require the condition

$$\begin{aligned} \lambda \ge \frac{2\mu }{M-m}, \end{aligned}$$

(12)

where M and m are the supremum and infimum of the initial density of the mixture. [8] removes the condition (12) and establishes existence of a solution in a precise sense working with the full equation (11).

We divide equation (11) by $\rho >0$ and we observe that the resulting $\lambda ^2$ terms may be rewritten as

$$\begin{aligned} -\frac{1}{2}\bigl (\lambda ^2\vert \nabla (\log \rho )\vert ^2\bigr )_{,i}-\frac{\lambda ^2}{\rho ^2}\,\rho _{,i}\Delta \rho . \end{aligned}$$

Now defined a modified pressure p by

$$\begin{aligned} p=P-\frac{1}{2}\lambda ^2\vert \nabla (\log \rho )\vert ^2 \end{aligned}$$

and then we may write equation (11) as

$$\begin{aligned} \begin{aligned} v_{i,t}+v_jv_{i,j}&=-\frac{1}{\rho }\,p_{,i}+\frac{\lambda }{\rho }(\rho _{,j}v_{i,j}+v_j\rho _{,ij})\\&\quad +\nu \Delta v_i+f_i-\frac{\lambda ^2}{\rho ^2}\,\rho _{,i}\Delta \rho . \end{aligned} \end{aligned}$$

(13)

We next employ a Boussinesq approximation on (13) and in a sense we follow the development of [26] where they proceed from their Eqs. (4.3)–(4.7) to arrive at their Korteweg–Boussinesq Eqs. (4.11)–(4.13). We assume that $\rho$ is a constant, $\rho _0$, when it appears undifferentiated in that equation but we retain the spatial derivative terms. The density in the body force component is assumed given by

$$\begin{aligned} \rho =\rho _0(1-\alpha [T-T_0]+\alpha _c[C-C_0]) \end{aligned}$$

and then we replace the derivatives of $\rho$ in terms of C (the volume concentration) and appending equations (9), (6) for T and C we arrive at a Boussinesq—approximation set of equations arising from the full set of nonlinear equations addressed by [8].

The full system of equations we derive has form

$$\begin{aligned} \begin{aligned} v_{i,t}+v_jv_{i,j}-{\hat{\delta }}\Delta v_{i,t}&=-\frac{1}{\rho _0}\,p_{,i}+\frac{\lambda }{\rho _0}(C_{,j}v_{i,j}+v_jC_{,ij})+\nu \Delta v_i\\&\quad +\alpha gTk_i-\alpha _cgCk_i-\frac{\lambda ^2}{\rho _0^2}\,C_{,i}\Delta C,\\ v_{i,i}&=0,\\ T_{,t}+v_iT_{,i}&=\kappa \Delta T,\\ C_{,t}+v_iC_{,i}&=\kappa _c\Delta C. \end{aligned} \end{aligned}$$

(14)

It should be observed that we have added a Kelvin–Voigt regularizing term, the term involving ${\hat{\delta }}$, to the left hand side, [20]. When ${\hat{\delta }}=0$ we obtain a Navier–Stokes type theory whereas when ${\hat{\delta }}>0$ there results a Navier–Stokes–Voigt type theory. We also note that if we omit the $\lambda /\rho _0$ term then this becomes analogous to the Korteweg theory discussed earlier whereas when we omit the $\lambda ^2/\rho _0^2$ term we have what might be termed a Kazhikhov– Smagulov type theory.

3 Double Diffusive Convection

Suppose Eq. (14) hold in the horizontal layer $\mathbb {R}^2\times \{z\in (0,d)\}$ with the velocity, temperature and concentration prescibed on the boundaries $z=0$ and $z=d$, as

$$\begin{aligned} \begin{aligned}&v_i=0,\quad z=0,d;\\&T=T_L,\quad z=0,\quad T=T_U,\quad z=d;\\&C=C_L,\quad z=0,\quad C=C_U,\quad z=d; \end{aligned} \end{aligned}$$

(15)

for prescribed constant values $T_L,T_U,C_L,C_U$, with $T_L>T_U>0$ and $C_L>C_U$ where $T_L,T_U$ are in $^{\circ }$K. Thus temperature has a tendency to destabilize whereas concentration stabilizes.

The steady solution to (14) and (15) in whose stability we are interested is

$$\begin{aligned} {\bar{v}}_i\equiv 0,\quad {\bar{T}}=-\beta z+T_L\,,\quad {\bar{C}}=-\beta _c z+C_L, \end{aligned}$$

(16)

where the temperature and concentration gradients, $\beta ,\beta _c$, are given by

$$\begin{aligned} \beta =\frac{T_L-T_U}{d}\,, \qquad \beta _c=\frac{C_L-C_U}{d}\,. \end{aligned}$$

The steady pressure $\bar{p}$ may then be derived up to a constant at ones disposal from (14)$_1$.

To investigate stability of the steady solution (16) we introduce perturbations $(u_i,\theta ,\phi ,\pi )$ by

$$\begin{aligned} v_i={\bar{v}}_i+u_i,\quad T={\bar{T}}+\theta ,\quad C={\bar{C}}+\phi ,\quad p={\bar{p}}+\pi \, \end{aligned}$$

where $\bar{p}$ is the steady state pressure arising from (14)$_1$.

The equations for the perturbations are then derived from (14) and these equations are non-dimensionalized with the scalings,

$$\begin{aligned}&u_i=u_i^*U,\quad x_i=x_i^*d,\quad t=t^*{\mathcal T},&\theta =\theta ^*T^{\sharp },\quad \phi =\phi ^*C^{\sharp },\quad \pi =\pi ^*{\tilde{P}}, \end{aligned}$$

where

$$\begin{aligned} U=\frac{\kappa _c}{d}\,,\quad {\mathcal T}=\frac{d^2}{\kappa _c}\,,\quad T^{\sharp }=\frac{\beta d\kappa _c}{\kappa }\,,\quad C^{\sharp }=\beta _c d,\quad {\tilde{P}}=\frac{\rho _0\nu U}{d} \end{aligned}$$

and we define

$$\begin{aligned} \delta =\frac{{\hat{\delta }}}{d^2}\,,\quad Le=\frac{\kappa }{\kappa _c}=\frac{Sc}{Pr}\,,\quad Pr=\frac{\nu }{\kappa }\,,\quad Sc=\frac{\nu }{\kappa _c}\,, \end{aligned}$$

where Le, Sc and Pr are the Lewis, Schmidt and Prandtl numbers. The Rayleigh number, R, and concentration Rayleigh number, S, are introduced as

$$\begin{aligned} R=\frac{\alpha g\beta d^4}{\nu \kappa }\,,\quad S=\frac{\alpha _c\beta _c g d^4}{\kappa _c\nu }\,, \end{aligned}$$

(17)

and we introduce two further non-dimensional parameters, namely the Kazhikhov–Samgulov parameter, $\alpha _2$, and the Korteweg parameter, $\alpha _1$, by

$$\begin{aligned} \alpha _1=\frac{\lambda ^2\nu \kappa _c}{\rho _0^2\alpha _c^2g^2d^6}\,,\qquad \alpha _2=\frac{\lambda \kappa _c}{\rho _0\alpha _cgd^3}\,. \end{aligned}$$

(18)

The fully nonlinear non-dimensional equations for $(u_i,\theta ,\phi ,\pi )$ then become (omitting the *s)

$$\begin{aligned} \begin{aligned}&\frac{1}{Sc}\bigl (u_{i,t}+u_ju_{i,j}\bigr )-\frac{\delta }{Sc}\Delta u_{i,t}=-\pi _{,i}+\Delta u_i+Rk_i\theta -S\phi k_i\\&\quad -\alpha _2Su_{i,3}+\alpha _2S\phi _{,j}u_{i,j}+\alpha _2Su_j\phi _{,ij} +\alpha _1S^2\Delta \phi k_i-\alpha _1S^2\phi _{,i}\Delta \phi \,,\\&u_{i,i}=0,\\&\frac{1}{Le}\bigl (\theta _{,t}+u_i\theta _{,i}\bigr )=w+\Delta \theta \,,\\&\phi _{,t}+u_i\phi _{,i}=w+\Delta \phi \,, \end{aligned} \end{aligned}$$

(19)

where $w=u_3$, and these equations hold on the domain $\mathbb {R}^2\times \{z\in (0,1)\}\times \{t>0\}$.

The boundary conditions to be satisfied are

$$\begin{aligned} u_i=0, \quad \phi =0,\quad \theta =0,\quad z=0,1, \end{aligned}$$

(20)

together with the fact that $u_i,\phi ,\theta$ and $\pi$ satisfy a plane tiling periodicity in the x, y plane.

We believe this is the first analysis of this model and so while $\alpha _1$ and $\alpha _2$ are connected we here treat them as independent constants in order to highlight the Kazhikhov–Smagulov and Korteweg effects on stability and instability. Let us observe that if $\alpha _2=0,\alpha _1\ne 0$, then (19) represents a direct extension of the Korteweg–Boussinesq model of [26], to the double diffusive convection problem. If $\alpha _1=0,\alpha _2\ne 0$, then (19) may be thought of as a Kazhikhov–Smagulov equation model for double diffusive convection. When $\alpha _1\ne 0,\alpha _2\ne 0$, equations (19) are a double diffusive convection model arising from the full set of Kazhikhov–Smagulov equations analysed by [8]. We point out that if we take $\delta =0$ then (19) is representative of Navier–Stokes theory whereas when the Kelvin–Voigt parameter $\delta >0$, (19) is representative of Navier–Stokes–Voigt theory.

4 Linear Instability Analysis

To establish a linear instability analysis of (19), (20), we discard the nonlinear terms and seek a solution representation like $u_i=u_i(\mathbf{x})e^{\sigma t},$ $\phi =\phi (\mathbf{x})e^{\sigma t},$ $\theta =\theta (\mathbf{x})e^{\sigma t},$ $\pi =\pi (\mathbf{x})e^{\sigma t}.$ We then remove the pressure term from equation (19)$_1$ by taking $curl\,curl$ of the linearized version and retaining the third component. In this way one may show that the equations governing linear instability are

$$\begin{aligned} \begin{aligned}&-\frac{\sigma }{Sc}\,\Delta w+\frac{\delta \sigma }{Sc}\,\Delta ^2w=-\Delta ^2w+Ra^2\theta -Sa^2\phi \\&+\alpha _2S\Delta w_{,z}-\alpha _1S^2\Delta ^*\Delta \phi ,\\&\frac{\sigma }{Le}\,\theta =w+\Delta \theta ,\\&\sigma \phi =w+\Delta \phi , \end{aligned} \end{aligned}$$

(21)

where $w=u_3$ and $\Delta ^*=\partial ^2/\partial x^2+\partial /\partial y^2$.

We seek now solutions like $w=W(z)h(x,y)$, $\theta =\Theta (z)h(x,y)$, $\phi =\Phi (z)h(x,y)$, where h is a function compatible with tiling the plane, and h satisfies $\Delta ^*h=-a^2h$, a being a wavenumber. To illustrate the novel effects of the Korteweg and the Kazhikhov–Smagulov terms, in Sect. 6 we concentrate on two stress free surfaces, cf. [22, 31], and then the boundary conditions required are

$$\begin{aligned} W=D^2W=\Theta =\Phi =0,\quad z=0,1, \end{aligned}$$

where $D=d/dz$. Care has to be taken with deriving the boundary conditions. When one solves for two fixed surfaces the condition $D^2W=0$ on $z=0,1$, is replaced by $DW=0$ on $z=0,1$. In deriving the appropriate condition for two stress free surfaces we recall that the Cauchy stress tensor has the form

$$\begin{aligned} t_{ij}=-p\delta _{ij}-K_1C_{,i}C_{,j}+2\mu d_{ij}\,, \end{aligned}$$

and this yields the following conditions on the stress tensor on the planes $z=0,1$,

$$\begin{aligned} t_{\alpha }=t_{\alpha j}n_j=-K_1({\bar{C}}+\phi )_{,\alpha }({\bar{C}}+\phi )_{,z}+\mu (u_{\alpha ,z}+w_{,\alpha })\,, \end{aligned}$$

where $\alpha =1,2$. For the linearized case the $K_1$ term contribution leads to

$$\begin{aligned} -K_1\phi _{,\alpha }{\bar{C}}_{,z}-K_1{\bar{C}}_{,\alpha }\phi _{,z}\,, \end{aligned}$$

on $z=0,1$, and since $\phi =0$ on $z=0,1$, and ${\bar{C}}={\bar{C}}(z)$, these terms vanish, which leads to the condition on $D^2W$.

We firstly study the problem with only Korteweg terms and no Kazhikhov–Smagulov contributions, so that $\alpha _2=0,\alpha _1\ne 0$. In this case the eigenvalue problem for instability reduces to solving the determinant equation

$$\begin{aligned} \begin{vmatrix} \Lambda ^2+\sigma \displaystyle {\Bigl (\frac{\Lambda }{Sc}+\frac{\delta \Lambda ^2}{Sc}\Bigr )}&\quad -Ra^2&\quad Sa^2+\alpha _1S^2a^2\Lambda \\ -1&\quad \displaystyle {\frac{\sigma }{Le}}+\Lambda&\quad 0\\ -1&\quad 0&\quad \Lambda +\sigma \end{vmatrix} =0 \end{aligned}$$

(22)

where $\Lambda =\pi ^2+a^2$.

One sees that the stationary convection boundary, $\sigma =0$, is given by

$$\begin{aligned} R_{stat}=S(1+\alpha _1S\Lambda )+\frac{\Lambda ^3}{a^2}\,, \end{aligned}$$

(23)

and the critical value for instability is obtained by minimizing $R_{stat}$ in $a^2$.

To determine the oscillatory convection critical Rayleigh number one solves (22). This yields a cubic in $\sigma$ which is then resolved into real and imaginary parts. After some calculation one may then show that the oscillatory Rayleigh number is given by

$$\begin{aligned} \begin{aligned} R_{osc}&=\frac{\Lambda ^3}{a^2}\biggl [1+\frac{1}{Le}+\frac{1}{Sc}\Bigl (1+\frac{1}{Le}\Bigr )(1+\delta \Lambda )\biggr ]\\&\quad +S(1+\alpha _1 S\Lambda ) \biggl \{1- \displaystyle {\frac{(1+\delta \Lambda )}{[Sc+Le(1+\delta \Lambda )]}}\, \Bigl (1-\frac{1}{Le}\Bigr ) \biggr \}\,. \end{aligned} \end{aligned}$$

(24)

The critical value for oscillatory convection is found by minimizing $R_{osc}$ in $a^2$.

Numerical results for stationary and oscillatory convection are displayed in Sect. 6.

To determine the critical Rayleigh numbers in general (including for the cases $\alpha _1=0,\alpha _2\ne 0$ or $\alpha _1\ne 0,\alpha _2\ne 0$), requires numerical solution of (21). This we do by employing a Chebyshev-tau method coupled with the QZ algorithm. In this case (21) are written in the form

$$\begin{aligned} \begin{aligned}&(D^2-a^2)W=\chi ,\\&-\frac{\sigma }{Sc}\,\chi +\frac{\delta \sigma }{Sc}\,(D^2-a^2)\chi =-(D^2-a^2)\chi +Ra^2\Theta -Sa^2\Phi \\&+\alpha _2SD\chi +\alpha _1a^2S^2(D^2-a^2)\Phi ,\\&(D^2-a^2)\Theta +W=\frac{\sigma }{Le}\,\Theta ,\\&(D^2-a^2)\Phi +W=\sigma \Phi . \end{aligned} \end{aligned}$$

(25)

For fixed $R,S,Sc,Le,\delta ,\alpha _1,\alpha _2$, the eigenvalues $\sigma$ are computed and the secant method is employed to locate where $\sigma _r=0$ ($\sigma =\sigma _r+i\sigma _1$), and then this value of R is minimized in a to yield the critical values of R.

5 Nonlinear Stability

We now analyse nonlinear stability of the solution (16) for the fully nonlinear equations (19), (20). To facilitate the nonlinear analysis we introduce the variable $\psi$ by the transformation $\psi =\mathfrak {R}\theta ,$ where ${\mathfrak {R}}^2=R$. This changes the $R\theta k_i$ term in (19)$_1$ to $\mathfrak {R}\psi k_i$ and it changes the w term in (19)$_3$ to $\mathfrak {R}w$.

Let V denote the period cell for the perturbation solution and denote by $\Vert \cdot \Vert$ and $(\cdot ,\cdot )$ denote the norm and inner product on $L^2(V)$. We have observed there are effectively three systems of equations of partial differential equations in (19), (20). The Korteweg system with $\alpha _2=0,\alpha _1\ne 0$ is referred to as type I; the second system when $\alpha _1=0,\alpha _2\ne 0$ is type II; and the third system when $\alpha _1\ne 0,\alpha _2\ne 0$ is type III. Suppose H is the space of solutions for equations (19), (20), i.e.

$$\begin{aligned} H=\bigl \{u_i\in H^1_0(V),\theta \in H^1_0(V),\phi \in H^2_0(V)\big \vert u_{i,i}=0,\mathrm{periodic\,\,conditions\,\,in}\,\,x,y\bigr \}. \end{aligned}$$

Define $R_{EFI}$ to be the solution to the maximization problem for the standard Bénard problem

$$\begin{aligned} \frac{1}{R_{EFI}}=\max _{H}\,\frac{I_B}{D_B}\,, \end{aligned}$$

(26)

where

$$\begin{aligned} I_B=2(\theta ,w),\qquad D_B=\Vert \nabla \mathbf{u}\Vert ^2+\Vert \nabla \theta \Vert ^2, \end{aligned}$$

and H in (26) is understood to refer only to $u_i$ and $\theta$. It may be shown that $R_{EFI}=1707.76$ for two fixed surfaces and $R_{EFI}=27\pi ^4/4$ for two stress free surfaces, cf. [62] pp. 68, 69 and p. 97.

We state the following theorem.

Theorem. A. The steady solution (16) to system I is globally nonlinearly stable (i.e. for all initial data) if $R<R_{EFI}$.

B. The steady solution (16) for system III is nonlinearly stable if $R<R_{EFI}$ and the initial data satisfies $E(0)<c$, where E(0) is the measure

$$\begin{aligned} E(0)=\frac{1}{2Sc}\Vert \mathbf{u}(0)\Vert ^2+\frac{\delta }{2}\Vert \nabla \mathbf{u}(0)\Vert ^2 +\frac{R}{2Le}\Vert \theta (0)\Vert ^2+\frac{S}{2}\Vert \phi (0)\Vert ^2+\frac{\alpha _1S^2}{2}\Vert \nabla \phi (0)\Vert ^2, \end{aligned}$$

and

$$\begin{aligned} c=\frac{\sqrt{2}\,c_1^2S\sqrt{\alpha _1\delta }\,(R_{EFI}-R)}{R_{EFI}(1+2c_1^2c_3)}, \end{aligned}$$

with the constants in c being defined in the proof.

Proof.

Multiply (19)$_1$ by $u_i$ (with $R\theta \equiv \mathfrak {R}\psi$) and integrate over V. After some integration by parts and use of the boundary conditions one finds

$$\begin{aligned} \begin{aligned} \frac{d}{dt}\Bigl (\frac{1}{2Sc}\Vert \mathbf{u}\Vert ^2&+\frac{\delta }{2Sc}\Vert \nabla \mathbf{u}\Vert ^2\Bigr )= -\Vert \nabla \mathbf{u}\Vert ^2+\mathfrak {R}(\psi ,w)-S(\phi ,w)+\alpha _2S(\phi _{,j}u_{i,j},u_i)\\&+\alpha _2S(u_j\phi _{,ij},u_i)+\alpha _1S^2(\Delta \phi ,w)-\alpha _1S^2(u_i,\phi _{,i}\Delta \phi ). \end{aligned} \end{aligned}$$

(27)

Next multiply equations (19)$_3$ and (19)$_4$ by $\psi$ and $\phi$, respectively, recalling $\mathfrak {R}\theta =\psi$, and integrate each over V to obtain

$$\begin{aligned} \frac{d}{dt}\frac{1}{2Le}\Vert \psi \Vert ^2=\mathfrak {R}(w,\psi )-\Vert \nabla \psi \Vert ^2\,, \end{aligned}$$

(28)

and

$$\begin{aligned} \frac{d}{dt}\frac{1}{2}\Vert \phi \Vert ^2=(w,\phi )-\Vert \nabla \phi \Vert ^2\,. \end{aligned}$$

(29)

We require a further identity and so we follow an idea in [26, 27]. Hence, multiply (19)$_4$ by $-\Delta \phi$ and integrate over V to find

$$\begin{aligned} \frac{d}{dt}\frac{1}{2}\Vert \nabla \phi \Vert ^2=-(w,\Delta \phi )-\Vert \Delta \phi \Vert ^2+(u_i,\phi _{,i}\Delta \phi )\,. \end{aligned}$$

(30)

From (27)–(30) we may now arrive at a generalized energy equation of form

$$\begin{aligned} \frac{dE}{dt}=\mathfrak {R}I-D+N, \end{aligned}$$

(31)

where

$$\begin{aligned} E=\frac{1}{2Sc}\Vert \mathbf{u}\Vert ^2+\frac{\delta }{2Sc}\Vert \nabla \mathbf{u}\Vert ^2+\frac{1}{2Le}\Vert \psi \Vert ^2+\frac{S}{2}\Vert \phi \Vert ^2 +\frac{\alpha _1S^2}{2}\Vert \nabla \phi \Vert ^2, \end{aligned}$$

and

$$\begin{aligned} I=2\mathfrak {R}(\psi ,w), \end{aligned}$$

and

$$\begin{aligned} D=\Vert \nabla \mathbf{u}\Vert ^2+\Vert \nabla \psi \Vert ^2+S\Vert \nabla \phi \Vert ^2+\alpha _1S^2\Vert \Delta \phi \Vert ^2, \end{aligned}$$

and

$$\begin{aligned} N=\alpha _2S(u_i,\phi _{,j}u_{i,j})+\alpha _2S(u_j\phi _{,ij},u_i). \end{aligned}$$

For part A of the theorem, $\alpha _2=0$, and then $N=0$, and we set

$$\begin{aligned} \frac{1}{R_E}=\max _H\frac{I}{D}\,. \end{aligned}$$

From (31) we find

$$\begin{aligned} \frac{dE}{dt}\le -D\Bigl (1-\frac{R}{R_E}\Bigr )\,. \end{aligned}$$

(32)

Since I only involves w and $\theta$, $R_E$ may be replaced by $R_{EFI}$ and using Poincaré’s inequality

$$\begin{aligned} D\ge c_2E, \end{aligned}$$

(33)

where

$$\begin{aligned} c_2=\min \,\Bigl \{Sc\,\pi ^2,\frac{1}{\delta },2Le\,\pi ^2,2\pi ^2\Bigr \}\,. \end{aligned}$$

For $R<R_{EFI}(\equiv R_E)$ then put $k=1-R/R_{EFI}>0$, and using (32) and (33) we may arrive at

$$\begin{aligned} \frac{dE}{dt}\le -kc_2E, \end{aligned}$$

and so

$$\begin{aligned} E(t)\le E(0)\exp (-kc_2t). \end{aligned}$$

Thus we have global nonlinear stability in the measure E(t), and part A is proved.

To prove part B we note that using integration by parts

$$\begin{aligned} (u_i,\phi _{,j}u_{i,j})=&-\frac{1}{2}(u_iu_i,\Delta \phi )\,,\nonumber \\ \le&\frac{1}{2}\Vert \mathbf{u}\Vert ^2_4\,\Vert \Delta \phi \Vert \,,\nonumber \\ \le&\frac{1}{2c_1^2}\Vert \nabla \mathbf{u}\Vert ^2\,\Vert \Delta \phi \Vert \,, \end{aligned}$$

(34)

where $\Vert \cdot \Vert _4$ denotes the norm on $L^4(V)$ and $c_1$ is the constant in the Sobolev embedding of $H^1_0(V)\subset L^4(V)$. Furthermore,

$$\begin{aligned} (u_i,\phi _{,ij}u_j)=&-(u_{i,j}\phi _{,j},u_i)\,,\nonumber \\ =&(u_{j,i}u_{i,j},\phi )\,,\nonumber \\ \le&\sup _V\,\vert \phi \vert \,\Vert \nabla \mathbf{u}\Vert ^2\,,\nonumber \\ \le&c_3\Vert \Delta \phi \Vert \,\Vert \nabla \mathbf{u}\Vert ^2\,, \end{aligned}$$

(35)

where the constant $c_3$ may be found in [25, pp. 280–283]. From the forms for E(t) and D(t) one may show

$$\begin{aligned} \Vert \Delta \phi \Vert \,\Vert \nabla \mathbf{u}\Vert ^2\le \frac{\sqrt{2}}{S\sqrt{\alpha _1\delta }}\,DE^{1/2}\,, \end{aligned}$$

and so employ this inequality together with the bounds (34) and (35) to obtain

$$\begin{aligned} N\le c_4DE^{1/2}, \end{aligned}$$

(36)

where

$$\begin{aligned} c_4=\frac{\sqrt{2}}{S\sqrt{\alpha _1\delta }}\Bigl (\frac{1}{2c_1^2}+c_3\Bigr )\,. \end{aligned}$$

Next, employ (36) in (31) together with the procedure leading to (32), (33) to find

$$\begin{aligned} \frac{dE}{dt}\le -D(k-c_4E^{1/2}). \end{aligned}$$

(37)

If now $E^{1/2}(0)<k/c_4$ then one may use a continuity argument to show $E(t)\rightarrow 0$, exponentially, see e.g. [62, pp. 14–16], and part B follows.

Remark.

When $\alpha _2\ne 0,\alpha _1=0$ the above proof does not work. [24] also found difficulty numerically to proceed with the reduced equations of Kazhikhov–Smagulov in their analysis of convective overturning in the isothermal problem.

6 Numerical Results

To understand the novel effects of this work we firstly discuss the instability diagram for classical thermohaline convection in a linearly viscous fluid, see Fig. 1. This is when $\alpha _1=0,\alpha _2=0,\delta =0$. Note that for S less than the threshold value $S=51.9$ the instability curve is a straight line of slope one which is intersected by another straight line which is the oscillatory convection threshold. Once S is larger than the transition value oscillatory convection is the mechanism leading to instability.

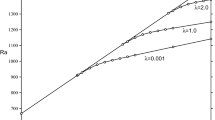
In Fig. 2 we show a typical analogous picture when Korteweg terms are present, i.e. $\alpha _2=0,\delta =0$, but $\alpha _1\ne 0$. Observe that the Korteweg terms have a very strong effect on the instability curves. The curve for stationary convection is very nonlinear as S increases. Once again there is a transition to oscillatory convection but at a much smaller value of $S=5.6$, indicating the strong stabilizing effect of the Korteweg terms. The oscillatory convection curve is actually also very nonlinear. For example, using the parameter values in Fig. 2, R increases from 709.424 at $S=0$ to 713.043 when $S=10$. However, when $S=100$, R has value 1193.81. Figure 3 shows the stationary and oscillatory curves for the same parameter values as Fig. 2, but now the effect of the Kelvin–Voigt parameter, $\delta$, is seen. This parameter only affects oscillatory convection, but it is seen that $\delta$ has a stabilizing effect. We have only presented details for $Le=20$ and $Sc=40$, but similar behaviour is observed for all the other values of Le and Sc we have employed. A referee has pointed out that oscillatory convection only occurs when $Le>1$. This is true, although for most fluids encountered in real life this condition holds.

The effect of the Kazhikhov–Smagulov parameter, $\alpha _2$, upon the stationary convection threshold is observed in Tables 1 and 2. The parameter $\alpha _2$, like $\alpha _1$, has a strong stabilizing effect. For the scaling chosen here the effect of $\alpha _1$ is greater than that of $\alpha _2$, as seen in Table 1, but both parameters have a pronounced effect on the threshold of convective motion. We also observe that as $\alpha _1$ increases $a^2$ displays a strong decrease whereas when $\alpha _2$ increases, $a^2$ increases. This means that as $\alpha _1$ increases the aspect ratio of the convection cells at the onset of convection is increasing and so the cells become wider with increasing $\alpha _1$. Thus increasing internal stresses due to density gradients are leading to wider cells. The Kazhikhov–Smagulov parameter has the opposite effect. As $\alpha _2$ increases the cells become narrower. Hence, while both effects stabilize the onset of stationary convection, each term has a very different effect on the behaviour of the cell shape. We should point out that the eigenvalue problem to calculate $\sigma$ is a difficult one numerically, and spurious eigenvalues are definitely witnessed.

7 Conclusions

We have produced a model to describe the behaviour of a mixture of two miscible fluids where differences in concentration by volume of a given fluid lead to density gradients in addition to the expansion by heating. The double diffusive convection problem is analysed in detail by a linear instability technique, but also by a fully nonlinear energy argument. There are two sources of terms which are not present in classical thermosolutal convection, these being associated with Korteweg effects and also with effects due to work of Kazhikhov and Smagulov. Both effects are shown to have a strong influence on the convection threshold and also upon the size of the resulting convection cells.

Froma mathematical viewpoint the novelty of the Korteweg and of the Kazhikhov–Smagulov terms may be seen by examining the linearized theory. Omitting the nonlinear terms in (19) the equations governing linearized instability theory are

$$\begin{aligned} \begin{aligned}&\frac{1}{Sc}u_{i,t}-\frac{\delta }{Sc}\Delta u_{i,t}= -\pi _{,i}+\Delta u_i+\mathfrak {R}k_i\psi -S\phi k_i-\alpha _2Su_{i,3}+\alpha _1S^2\Delta \phi k_i\,,\\&u_{i,i}=0,\\&\frac{1}{Le}\psi _{,t}=\mathfrak {R}w+\Delta \psi \,,\\&\phi _{,t}=w+\Delta \phi \,. \end{aligned} \end{aligned}$$

(38)

It is convenient to cast equations (38) together with the boundary conditions (20) in the setting of an abstract system, defined in a Hilbert space,

$$\begin{aligned} Au_t+Lu+N(u)+\epsilon Mu=0, \end{aligned}$$

(39)

cf. [61, p. 156]. For our purpose A and L are symmetric, unbounded linear operators, M is a skew-symmetric linear operator, and N(u) is a nonlinear operator.

We operate on (38)$_4$ by $S-\alpha _1S^2\Delta$, and derive the following equation

$$\begin{aligned} (S-\alpha _1S^2\Delta )\phi _{,t}= (S-\alpha _1S^2\Delta )w +(S-\alpha _1S^2\Delta )\Delta \phi \,. \end{aligned}$$

(40)

Then (38) and (40) may be written in the form (39) where $u=(u,v,w,\psi ,\phi )^T$ and essentially L and $\epsilon M$ have the forms

$$\begin{aligned} -L= \begin{pmatrix} \Delta &{}\quad 0\quad &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \Delta &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \Delta &{}\quad \mathfrak {R} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \mathfrak {R} &{}\quad \Delta &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad S\Delta - \alpha _1S^2\Delta ^2 \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} -\epsilon M= \begin{pmatrix} -\alpha _2S\,\frac{\partial }{\partial z} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -\alpha _2S\,\frac{\partial }{\partial z} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -\alpha _2S\,\frac{\partial }{\partial z} &{}\quad 0 &{}\quad -S+\alpha _1S^2\Delta \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad S-\alpha _1S^2\Delta &{}\quad 0 &{}\quad 0 \end{pmatrix} \end{aligned}$$

[61, p. 156] points out that when $\epsilon =0$ (i.e. $\alpha _1=\alpha _2=0$, or $S=0$) then, under suitable conditions on N, the linear and nonlinear stability boundaries coincide. If M is bounded then $\sigma$ will be real and the instability and nonlinear stability boundaries remain within $O(\epsilon )$ of each other if $\epsilon$ is small enough. However, he also notes that there are many problems in applied mathematics in which $\epsilon$ is not small, citing the rotating Bénard problem and the magnetohydrodynamic Bénard problem as examples. The current work is also a novel example of this. It is typical that non-zero skew symmetric terms in (39) lead to stabilizing effects and the $\alpha _1$ and $\alpha _2$ terms are each involved with skew symmetric operators.

We also draw attention to the fact that [43, 44] have identified interesting attractors and behaviour for ordinary differential equation systems derived from double diffusive convection theory. We believe the new effects identified here could reveal yet further interesting attractor behaviour.

It is worth stressing the application area of solar ponds for the type of work investigated here. Use of sodium chloride in a solar pond can have an adverse effect on agriculture fields, and salts such as muriate of potash and urea are being investigated as alternatives. Other phase change materials and nanofluids may lead to better thermal efficiency and storage, cf. [59], and a solvent of Navier–Stokes–Voigt type may be preferable.

Table 1 Critical Rayleigh and wave numbers for stationary convection versus S

Table 2 Critical Rayleigh and wave numbers for stationary convection versus $\alpha _1$ or $\alpha _2$

Fig. 1

Graph of R versus S for standard thermohaline convection, $\alpha _1=0$, $\alpha _2=0$, $Le=20$, $Sc=40$, $\delta =0$. The transition value to oscillatory convection is approximately $R=709.4$, $S=51.9$

Fig. 2

Graph of R versus S for double diffusive convection with Korteweg stress, $\alpha _1=0.1$, $\alpha _2=0$, $Le=20$, $Sc=40$, $\delta =0$. The transition value to oscillatory convection is approximately $R=709.42$, $S=5.6$

Fig. 3

Graph of R versus S for double diffusive convection with Korteweg stress, effect of Kelvin–Voigt term, $\alpha _1=0.1$, $\alpha _2=0$, $Le=20$, $Sc=40$, $\delta =0$, $\delta =0.1$. The transition values to oscillatory convection are approximately $R=709.42$, $S=5.6$ and $R=734.62$, $S=6.9$