Complex dynamics of a fractional-order SIR system in the context of COVID-19

Abstract

This paper proposes and analyses a new fractional-order SIR type epidemic model with a saturated treatment function. The detailed dynamics of the corresponding system, including the equilibrium points and their existence and uniqueness, uniform-boundedness, and stability of the solutions are studied. The threshold parameter, basic reproduction number of the system which determines the disease dynamics is derived, and the condition of occurrence of backward bifurcation is also determined. Some numerical works are conducted to validate our analytical results for the commensurate fractional-order system. Hopf bifurcations for the fractional-order system are studied by taking the order of the fractional differential as a bifurcation parameter.

1 Introduction

Disease is an integral part of modern civilization. As long as human lives, illnesses will last in our society. But, the extent of these diseases can be reduced, and even we can eradicate the disease from the population. Among various types of diseases, infectious diseases are the most vulnerable diseases. Any contagious disease, caused by the pathogen of bacteria, viruses, fungi, or some parasites can transmit from an infected human to a susceptible human either through direct contact (viz. influenza, tuberculosis, rubella, measles, HIV-AIDS, etc.) or via some medium (viz. malaria, dengue, chikungunya, etc.). Among all infectious diseases, the recent pandemic COVID-19 caused by the virus SARS-CoV-2 (severe acute respiratory syndrome coronavirus 2), the first pandemic of the twenty-first century has affected the lifestyle of human population of every country throughout the globe. The disease COVID-19 was first noticed in the Wuhan city of the Republic of China in December of last year [38]. Till today except for very few countries, COVID-19 pandemic has worsened the situation all over the globe [37]). It should be noted that till May 2020, more than six million world populations have been affected by the disease COVID-19, where almost 50% closed cases, including 12% death (see [37]).

The rate of progression of infectious diseases including COVID-19 depends on the amount of pathogen living within a host, its rate of growth, and the interaction with the host’s immunity. A mathematical model can perfectly capture these relations. Mathematical models help to represent all the scenarios in a compact form. It also captures how disease propagates, its long-term behavior, and ultimately helps to determine possible interventions to restrain the infectious disease. The mathematical model of an infectious disease was first introduced by Kermack and McKendrick [19]. They have used a simple SIR model to formulate the mathematical model. After this theoretical epidemiology has come a long way. Several works on control strategies like vaccination, treatment, isolation were taken into consideration by many researchers [17, 20, 24]. But, in all the works done so far, researchers have considered the integer order system while constructing the mathematical model. Recently some researchers have also developed some model-based works to examine the detailed dynamical behavior of the COVID-19. The researchers including Ahmed et al. [3], Kucharski et al. [21], Prem et al. [32], etc. have also developed some mathematical models and presented rigorous analysis. In an article, Ribeiro et al. [33] have used some stochastic-based regression models to forecast the phenomena in ten most affected states of Brazil. Noting that isolation is a good measure to control the disease, Hellewell et al. [14] have used the operative techniques of COVID-19 diseases using separation. In the recent works, Mandal et al. [25, 27] have constructed and analyzed a mathematical model on the COVID-19 in the pandemic scenario of three states of India. In other recent work, a balance between lockdown and compliance to investigate the COVID-19 scenes has been proposed by Zegarra et al. [2]. Some more theoretical works on COVID-19 can be found in [25, 27, 34].

The shortcoming of the integer order system is that it does not rely on the previous history of the system. But, when a disease transmits, the susceptible population uses their memory to prevent infection. A dynamical system involving fractional-order derivatives bears the information regarding its present and also its past states [12]. Hence, fractional-order systems give more in-depth knowledge about the system than integer order systems. Also, as there are many developments in fractional calculus (See the articles [1, 4, 28, 29]), so, it is logical to apply a fractional-order differential equation to represent a biological phenomenon through mathematical modeling. According to Du et al. [10], if the parameter $\alpha (\in (0,1])$, the order of the fractional-order system tends to 0, the model has full memory, and when $\alpha =1$, the model system is known as memoryless. Hartley et al. [13] used fractional differentiation for the first time for a physical system in demonstrating the behavior of the semi-infinite lossy (RC) line. Torvik et al. [35] have studied that fractional derivatives appear naturally to describe some properties of motions of a Newtonian fluid. At present, there are several works involving the application of fractional-order systems in various fields including epidemic models [15, 26].

In human society, any epidemic can not be thought without the effect of memory. Whenever an infectious disease propagates in human society, the knowledge or experience of each people about that particular disease should affect their response [36]. People apply several precautions (e.g. vaccination, if it is available) for a disease if they have a past experience of the disease. In this regard, some important control measures can suppress the spreading of the disease. But, mere knowledge about a disease may not protect all the time. That is why people are willing to adopt some new paths to control these diseases. The memory of an infectious disease from the previous situation has more contribution on the recent situation as compared to no memory. It is anticipated that the long-time impact of memory decreases in future time more tardily than exponential decay, but generally, its behavior is a similar way of power-law damping function.

In this work, we have formulated a new SIR type epidemic model with the help of fractional differential equations. Although there are many ways to define a fractional-order differential equation in the sense of Riemann-Liouville, Gr$\ddot{u}$nwald-Letnikov, and the Caputo. In this work, we use the Caputo definition due to its similarity in using the initial conditions with the integer-order differential equation. From this perspective, we develop a mathematical model considering a system of fractional-order differential equations and analyze the thorough dynamics of the proposed model. Moreover, we apply this model to predict the COVID-19 situation of India after the second wave.

The whole manuscript is structured in the following way: An SIR type model with the fractional differential equation is formulated in Sect. 2. The equilibrium points, existence and uniqueness of solution, their dynamical behavior, stability of the system, and the occurrence of Hopf bifurcation are discussed in Sect. 3. Several numerical simulations are performed in Sect. 4, and the application of the model on some real-world data is discussed in Sect. 5, and lastly, in Sect. 6, we present a concise discussion and conclusion.

2 Model formulation

In this section, a new SIR type model is considered. We divide the whole population into susceptible S(t), infected I(t), and recovered R(t), the three mutually exclusive time-dependent classes. First, we consider that at any time t,  A be the newly recruitment rate, $\beta$ be the disease transmission rate, d be the natural death rate, $\delta$ be the rate of death due to the disease, $\epsilon$ be the natural recovery rate. We assume that some infected person will be recovered due to available treatment control. Let v denote the treatment control parameter for the infected population. The rate of recovery is considered as $\frac{\gamma v}{1+vI}$ with $\gamma$ representing the effectiveness of the treatment due to saturated type treatment control (see Jana et al. [16]). Every country, including the most developed countries in the world, has limitations in providing medical resources like proper medicines, availability of beds in hospitals, etc. Particularly, the contagious disease like COVID-19, which has appeared all of a sudden, it is not possible to provide treatment to every patient when the number of patients becomes very large. From this point of view, we have used the saturated type recovered rate due to treatment. A schematic diagram of the above assumptions is described in Fig. 1. Based on these assumptions, we define our model in the following manner:

Fig. 1

Flow chart of the disease transmission

$$\begin{aligned} \begin{aligned} \frac{dS}{dt}=&A - \beta SI-dS, \\ \frac{dI}{dt}=&\beta SI - \left( \epsilon +\frac{\gamma v}{1+vI}\right) I-(d+\delta )I,\\ \frac{dR}{dt}=&\left( \epsilon +\frac{\gamma v}{1+vI}\right) I-dR, \end{aligned} \end{aligned}$$

(2.1)

with initial conditions

$$\begin{aligned} S(t_0)=S_0\ge 0, I(t_0)=I_0\ge 0, R(t_0)=R_0\ge 0. \end{aligned}$$

According to Du et al. [10] a memory process usually consists of two stages: the fresh stage and the working stage. The fresh memory is used to just remember things while the working memory helps to do cognitive works. In the fractional model, we capture the working memory. The critical point between the fresh stage and the working stage is usually not the origin. This observation is quite different from the traditional fractional models of one stage. For example, the fractional Maxwell’s model is a one-stage model. As the combination of two simple models, it has a more complicated expression than Eq. (2.1). We also find that the order of fractional. Also, in reality, no individual has the same memories, it changes from person to person. Once infected an individual gains knowledge about the disease which helps to obstruct the transmission of infectious disease. We consider this fact into the fractional form of the system (2.1). Here we assume that $\alpha _1$, $\alpha _2$ and $\alpha _3$ are such properties corresponding to the susceptible, infected and recovered population respectively, where $\alpha _i \in (0,1],~ i=1,2,3$. Whereas, the recovered will have better working memory than infected one but less working memory than susceptible. So, the fractional order form of the system (2.1) takes the form

$$\begin{aligned}&{}_{t_0}D_t^{\alpha _1}S(t)= A^{'} - \beta ^{'} SI-d^{'}S, S(t_0)\ge 0\nonumber \\&{}_{t_0}D_t^{\alpha _2}I(t)= \beta ^{'} SI - \big (\epsilon ^{'}+\frac{\gamma ^{'} v^{'}}{1+v^{'}I}\big )I-(d^{'}+\delta ^{'})I, I(t_0)\ge 0 \nonumber \\&{}_{t_0}D_t^{\alpha _3}R(t)= \big (\epsilon ^{'} +\frac{\gamma ^{'} v^{'}}{1+v^{'}I}\big )I-d^{'}R, R(t_0)\ge 0. \end{aligned}$$

(2.2)

Here $D_t^{\alpha _i}$ is the fractional-order derivative in Caputo sense [30, 31] for $i= 1, 2, 3$. In the system (2.2) we replace the parameters of the system (2.1) in such a way that the problem of dimension mismatch is solved.

For simplicity, we set $A{'}=A,~\beta {'}=\beta ,~d{'}=d,~\epsilon {'}=\epsilon ,~\gamma {'}=\gamma ,~v{'}=v,~\delta {'}=\delta$.

Using these transformations into the system (2.2), we have

$$\begin{aligned} \begin{aligned} {}_{t_0}D_t^{\alpha _1}S(t)=&A - \beta SI-dS, \\ {}_{t_0}D_t^{\alpha _2}I(t)=&\beta SI - \big (\epsilon +\frac{\gamma v}{1+vI}\big )I-(d+\delta )I,\\ {}_{t_0}D_t^{\alpha _3}R(t)=&\left( \epsilon +\frac{\gamma v}{1+vI}\right) I-dR \end{aligned} \end{aligned}$$

(2.3)

with initial conditions $S(t_0)=S_0\ge 0,~I(t_0)=I_0\ge 0,~R(t_0)=R_0\ge 0$. Here $D_t^{\alpha _i}$ is the fractional-order derivative in Caputo sense [30, 31] for $i= 1, 2, 3$. The system (2.3) is called to be an incommensurate fractional-order system. If $\alpha _1=\alpha _2=\alpha _3=\alpha \in (0,1]$, then the system is said to be a commensurate fractional-order system which is given by

$$\begin{aligned} \begin{aligned} {}_{t_0}D_t^{\alpha }S(t)=&A - \beta SI-dS, \\ {}_{t_0}D_t^{\alpha }I(t)=&\beta SI - \big (\epsilon +\frac{\gamma v}{1+vI}\big )I-(d+\delta )I, \\ {}_{t_0}D_t^{\alpha }R(t)=&\left( \epsilon +\frac{\gamma v}{1+vI}\right) I-dR \end{aligned} \end{aligned}$$

(2.4)

with initial conditions $S(t_0)=S_0\ge 0,~I(t_0)=I_0\ge 0,~R(t_0)=R_0\ge 0$. Here $D_t^{\alpha }$ is the fractional-order derivative in Caputo sense [30, 31].

3 The analysis of fractional-order system

At this stage, we analyze the dynamical behavior of the fractional-order system (2.4).

3.1 Equilibrium points

Now we discuss the existence of nonnegative equilibrium points of the system (2.4). We observe that the system (2.4) has three equilibrium points. One is disease free equilibrium (DFE) $E_0=\big (\frac{A}{d},0,0 \big )$ and the other two equilibrium points are endemic equilibrium (EE) if they exist $E_1(S^{*},I^{*}, R^{*})$ and $E_2(S^{**},I^{**}, R^{**})$ where $I^{*}$ and $I^{**}$ are the roots of the following quadratic equation

$$\begin{aligned} a_0I^2+a_1I+a_2=0 \end{aligned}$$

(3.1)

where $a_0= \beta v(\epsilon +d+\delta ),$ $a_1= [(\epsilon +d+\delta )(\beta +dv)-(A-\gamma )\beta v],$ $a_2= d(\epsilon +d+\delta +\gamma v)(1-R_0),$ and $R_0=\frac{\beta A}{d(\epsilon +d+\delta +\gamma v)}.$

Here the parameter $R_0$ is recognized as the basic reproduction number. Hence we can derive $S^{*}=\frac{1}{\beta }[\epsilon + d + \delta + \frac{\gamma v}{1+vI^{*}}],$ $R^{*}=\frac{1}{d}(\epsilon +\frac{\gamma v}{1+vI^{*}})I^{*}$ and $S^{**}=\frac{1}{\beta }[\epsilon + d + \delta + \frac{\gamma v}{1+vI^{**}}],$ $R^{**}=\frac{1}{d}(\epsilon +\frac{\gamma v}{1+vI^{**}})I^{**}$.

Let $D= a_1^{2}-4a_0a_2$ be the discriminant of the Eq. (3.1).

If $R_0>1$, (i.e. if $a_2<0$) then (3.1) has a unique positive root, $I^{*}=\frac{-a_1+\sqrt{D}}{2a_0}$. Thus we can say that the system (2.1) has a positive unique EE $(S^{*},I^{*},R^{*})$ if $R_0>1$.

If $R_0=1$, then $a_2=0$ which implies $(a_0I+a_1)I=0$. From this we can get a positive EE of the system (2.4) as $-\frac{a_1}{a_0}$ if and only if $a_1<0$. Now, $a_1<0$ gives the treatment control parameter to be $v>\frac{\beta (\epsilon +d+\delta )}{(A-\gamma )\beta -d(\epsilon +d+\delta )}$.

If $R_0<1$, (i.e. if $a_2>0$) and $D<0$, then the system (2.1) possesses no EE. Also if $R_0<1$ and $a_1\ge 0$ i.e. $0<v\le \frac{\beta (\epsilon +d+\delta )}{(A-\gamma )\beta -d(\epsilon +d+\delta )}$ then there is no endemic equilibrium points.

We formulate the next theorem which is grounded on the above discussions.

Theorem 3.1

(i) The system (2.4) possesses two EE points if $R_0<1$, $D>0$, $a_1<0$ and no EE point if $R_0<1$, $D>0$, $a_1 \ge 0$.

• (ii) The system (2.4) possesses two equal EE points if $R_0<1$, $D=0$, $a_1<0$ and no EE points if $R_0<1$ and $D<0$.

• (iii) If the basic reproduction number, $R_0=1$, then the system (2.4) possesses a unique EE point if $a_1<0$ i.e. $v>\frac{\beta (\epsilon +d+\delta )}{(A-\gamma )\beta -d(\epsilon +d+\delta )}$, where v is the control parameter and no EE points if $a_1 \ge 0$.

• (iv) The system (2.4) possesses a unique EE point if $R_0>1$.

From the above theorems we experience that the system (2.4) has two different equilibrium points even when $R_0<1$. Hence we can conclude that the proposed model experiences a backward bifurcation at $R_0 < 1$ which shown in Fig. 2. Thus the condition $R_0 < 1$ is not sufficient to eradicate the disease from the population.

Fig. 2

Backward bifurcation of the system (2.4) with the parameter values $A=0.85$ , $\beta =0.1$, $d=0.01$, $\delta =0.5$, $\epsilon =0.001$, $\gamma =0.01$, and $v=1$

Theorem 3.2

[5] The system (2.4) passes through a backward bifurcation at $R_0=1$ if and only if $R_0{'}<R_0,$ where $R_0{'}$ is determined in subsequent steps.

Here the treatment control parameter v is selected as the backward bifurcation parameter. Observe that if the case (iii) of theorem (3.1) is true then the system (2.4) undergoes a backward bifurcation at $R_0=1$. Hence it can be explained that the system possesses two EE point in some interval $[R_0{'},R_0]$, where $R_0=1$ and $R_0{'}=R_0{'}(v^{*})$. $v^{*}$ can be derived from $D=0$ i.e. $a_1^{2}=4a_0a_2$. Now, $a_1^{2}=4a_0a_2$ gives $B{v^{*}}^{2}-2Cv^{*}+\beta ^{2}(\epsilon +d+\delta )^{2}=0$ where $B={[\beta (A-\gamma )-(\epsilon +d+\delta )d]}^{2},$ and $C=\beta (d+\epsilon +\delta )[d(d+\epsilon +\delta )-\beta (\gamma +A)].$ Solving we have $v=\frac{C \pm \sqrt{C^{2}-B\beta ^{2}(\epsilon +d+\delta )^{2}}}{B}.$ Now, this case occurs only when $a_1<0$ and $R_0<1$. Thus we get,

$$\begin{aligned} v>max\left\{ \frac{\beta (\epsilon + d+ \delta )}{\beta (A-\gamma )-d(d+\epsilon +\delta )}, \frac{\beta A-d(\epsilon + d +\delta )}{\gamma d}\right\} \end{aligned}$$

From the above conditions we have derived at the critical value of v as $v^{*}=\frac{C + \sqrt{C^{2}-B\beta ^{2}(\epsilon +d+\delta )^{2}}}{B}.$ Thus the new threshold value at which the diseases eradicates from the population $R_0{'}$ (say) is $R_0{'}=\frac{\beta A}{d(\epsilon +d+\delta +\gamma v^{*})}.$ Therefore, depending on the above discussion we can state the next theorem.

Theorem 3.3

The system (2.4) holds

• (i) a unique EE point if $R_0>1$ and the disease will remain in the population.

• (ii) two EE points if $R_0{'}< R_0<1$ which implies that the system passes through a backward bifurcation.

• (iii) a unique DFE point if $R_0<R_0{'}<1$ which implies that the disease will die out.

3.2 Existence and uniqueness of the solutions

We now state and prove the following lemma which helps us to conclude that our constructed model has a unique solution.

Lemma 3.4

[22] Consider the fractional-order system

$$\begin{aligned} {}_{t_0}D_t^{\alpha }x(t)=f(t,x), t_0>0,~ \text {and}~ x(t_0)=x_0 \end{aligned}$$

(3.2)

where $\alpha \in (0,1],~ f:[t_0,\infty )\times {\mathcal {R}}\rightarrow {\mathbb {R}}^{n},~{\mathcal {R}} \subset \mathbb R^{n}.$ If the Lipschitz condition with respect to x is satisfied by the function f(t, x), then the system (3.2) has a unique solution on the interval $[t_0,\infty )\times {\mathcal {R}}$.

Theorem 3.5

The system (2.4) has a unique solution in the region $[t_0,P]\times {\mathcal {R}}$ where, ${\mathcal {R}}=\{(x,y,z)\in {\mathbb {R}}^{3}: \max \{|S|,|I|,|R|\}\le Q\}$, and $P,Q\in {\mathbb {R}}^{+}$.

Proof

We prove the existence and uniqueness criterion for the fractional-order system (2.4). For that purpose we consider the region $[t_0,P]\times {\mathcal {R}}$ where ${\mathcal {R}}=\{(x,y,z)\in {\mathbb {R}}^{3}: max \{|S|,|I|,|R|\}\le Q\}$. Let $X=(S, I, R)$ and $Y=(S_1, Y_1, R_1)$ be arbitrary two points in the region ${\mathcal {R}}$ and define the mapping $H:{\mathcal {R}}\rightarrow {\mathbb {R}}^{3}$ by $H(X)=(H_1(X),H_2(X),H_3(X))$, where

$$\begin{aligned}&H_1(X)=A-\beta SI-dS,~ H_2(X)=\beta SI-\left( \epsilon +\frac{\gamma v}{1+vI}\right) I-(d+\delta )I, ~\text {and}\\&H_3(X)=\left( \epsilon +\frac{\gamma v}{1+vI}\right) I-dR. \end{aligned}$$

For any $X, Y \in {\mathcal {R}}$, we have

$$\begin{aligned} \begin{aligned}&||H(X)-H(Y)||\\&\quad =\sum _{i=1}^{3}|H_i(X)-H_i(Y)|\\&\quad =|A-\beta S I-dS-A+\beta S_1 I_1+dS_1| + |\beta SI-(\epsilon +\frac{\gamma v}{1+vI})I\\&\qquad -(d+\delta )I-\beta S_1I_1\\&\qquad +\, (\epsilon -\frac{\gamma v}{1+vI_1})I+(d+\delta )I_1|+|(\epsilon +\frac{\gamma v}{1+vI})I-dR\\&\qquad -(\epsilon +\frac{\gamma v}{1+vI_1})I_1+dR_1|\\&\quad \le 2\beta |SI-S_1I_1|+ d|S-S_1|+2\epsilon |I-I_1|+2\gamma v|\frac{I}{1+vI}\\&\qquad -\frac{I_1}{1+vI_1}|+(d+\beta )|I-I_1|\\ {}&\qquad +\, d|R-R_1|\\&\quad \le (2\beta Q+d)|S-S_1|+(2d+2\epsilon +2\gamma v+\delta )|I-I_1|+d|R-R_1|\\&\quad \le K||X-Y||, \text {where}~ K=max\{2\beta Q+d,~2(d+\epsilon +\gamma v)+\delta ,~d\} \end{aligned} \end{aligned}$$

Therefore, the function H(X) fulfills the criteria of the Lipschitz’s condition with respect to $X=(S, I, R)\in {\mathcal {R}}$. Then by using the Lemma 3.4, we can conclude that our system (2.4) has a unique solution $X\in {\mathcal {R}}$ with initial conditions $X_{t_0}=(S_{t_0}, I_{t_0}, R_{t_0})\in {\mathcal {R}}$. $\square$

3.3 Nonnegativity and boundedness of solutions

In mathematical biology, our main concern is on the nonnegative and bounded solutions. Hence, we try to find the solutions that possess the (i) non-negativity and (ii) bounded properties. For this purpose, we consider the following region ${\mathcal {R}}^{+}=\{(S,I,R)\in {\mathcal {R}}: S, I, R \in \mathbb {R^{+}}\}$.

Theorem 3.6

Every solutions of the fractional system (2.4) whose initial values start in $\mathbb {R^{+}}^{3}$ i.e. $S_{t_0}\ge 0, I_{t_0}\ge 0, R_{t_0}\ge 0$ are all nonnegative and bounded.

Proof

To prove the nonnegativity of the solution, we use Lemma 3.2 [15]. We have discussed the existence of solution of the system (2.1) in Theorem 3.1. As (2.4) is a homogeneous system of equations with initial conditions $S(t)\ge 0,~I(t)\ge 0,~R(t)\ge 0$ we can conclude that the solutions of (2.4) is non-negative. Furthermore, the solutions are nondecreasing in t. Now to prove the uniform boundedness of the solutions, we consider a mapping $F(t)=S(t)+I(t)+R(t)$. Then we have,

$$\begin{aligned} \begin{aligned}&{}_{t_0}D_t^{\alpha }F(t)+dF(t)\\&\quad ={}_{t_0}D_t^{\alpha }S(t)+{}_{t_0}D_t^{\alpha }I(t)+{}_{t_0}D_t^{\alpha }R(t)+dS(t)+dI(t)+dR(t)\\&\quad = A-\beta SI-dS+\beta SI-\left( \epsilon +\frac{\gamma v}{1+vI}\right) I\\&\qquad -\, (d+\delta )I+\left( \epsilon +\frac{\gamma v}{1+vI}\right) I-dR+dS(t)+dI(t)+dR(t)\\&\quad = A-\delta I \le A ~\text {as}~ I(t)\ge 0. \end{aligned} \end{aligned}$$

Using the Lemma 3.2 [15], we have $F(t)\le (F(t_0)-\frac{A}{d})E_{\alpha }[-d(t-t_0)^{\alpha }]+\frac{A}{d}\rightarrow \frac{A}{d}~ as ~ t\rightarrow \infty$. Therefore, all the solution of the fractional system (2.4) whose initial conditions start in the region ${\mathcal {R}}^{+}$ is bounded and it lies in the region $\{(S+I+R)\in {\mathcal {R}}^{+}: S+I+R \le \frac{A}{d}\}$. $\square$

3.4 Dynamical behavior

In this portion of the research article, we study the stability conditions of each equilibrium point. Here, we assume that the fractional system (2.4) possesses unique EE point. The local stability investigation of the system (2.4) is done with the help of making linearization around each equilibrium point. The Jacobian matrix of the fractional system (2.4) at the DFE point $(\frac{A}{d},0,0)$ is

$$\begin{aligned} J\left( \frac{A}{d},0,0\right) =\begin{pmatrix} -d &{} 0 &{} 0\\ 0 &{} \frac{\beta A}{d}-(d+\epsilon + \delta )-\gamma v &{} 0\\ 0 &{}\epsilon +\gamma v &{} -d\\ \end{pmatrix} \end{aligned}$$

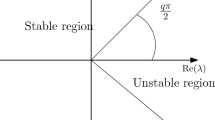
The eigenvalues of the above Jacobian matrix are $\lambda _1=-d, \lambda _2=-d, \lambda _3=\frac{\beta A}{d}-(\epsilon +d+\delta +\gamma v)$. Therefore, $|arg(\lambda _1)|=|arg(\lambda _2)|=\pi >\frac{\alpha \pi }{2}$, where $\alpha \in (0,1]$ and $|arg(\lambda _3)|=\pi >\frac{\alpha \pi }{2}$ if $\frac{\beta A}{d}-(d+\epsilon + \delta )-\gamma v<0$ i.e. if $R_0<1$. Again we have established that the system undergoes backward bifurcation iff $R_0{'}<R_0.$ Hence, by the Lemma 3.3 [15], we can conclude that the system is asymptotically stable around the DFE if $R_0< min\{1,R_0{'}\}$. Thus, we can state the next theorem.

Theorem 3.7

The DFE $\left( \frac{A}{d},0,0\right)$ of the fractional system (2.4) is locally asymptotically stable iff

$$\begin{aligned} R_0<min\{1,R_0{'}\}. \end{aligned}$$

Next, we discuss the local stability criteria of EE point $(S^{*},I^{*},R^{*})$. J, the Jacobian matrix at $(S^{*},I^{*},R^{*})$ of the system (2.4) is given by

$$\begin{aligned} J(S^{*},I^{*},R^{*})=\begin{pmatrix} -d-\beta I^{*} &{} -\beta S^{*} &{} 0\\ \beta I^{*} &{} \beta S^{*}-( d+ \epsilon +\delta )-\frac{\gamma v}{(1+vI^{*})^{2}} &{} 0\\ 0 &{} \epsilon +\frac{\gamma v}{(1+v I^{*})^{2}} &{} -d\\ \end{pmatrix} \end{aligned}$$

One eigenvalue of the matrix is $\lambda _1=-d$ and the other two eigenvalues are obtained from the matrix

$$\begin{aligned} J^*=\begin{pmatrix} -d-\beta I^{*} &{} -\beta S^{*}\\ \beta I^{*} &{} \beta S^{*}-(d+\epsilon + \delta )-\frac{\gamma v}{(1+vI^{*})^{2}}\\ \end{pmatrix} \end{aligned}$$

The characteristic equation of the Jacobian matrix at the EE, $(S^{*},I^{*},R^{*})$ is given by

$$\begin{aligned} \lambda ^{2}-2 a_1(\gamma )\lambda +a_2(\gamma )=0 \end{aligned}$$

(3.3)

where $a_1(\gamma )=\frac{1}{2}[\frac{\gamma v^{2}I^{*}}{(1+vI^{*})^{2}}-(\beta I^{*}+d)]$, and $a_2(\gamma )= \beta I^{*}(\epsilon +d+\delta +\frac{\gamma v}{1+vI^{*}})-(\beta I^*+d)\frac{\gamma v^{2}I^{*}}{(1+v I^{*})^{2}}.$

Let $\lambda _2 ~\text {and}~ \lambda _3$ be the eigenvalues of the matrix $J^*$. Now, $a_1$ will be negative if

$$\begin{aligned} 0<\gamma < \frac{(\beta I^{*}+d)(1+v I^{*})^2}{v^{2} I^{*}} =\gamma _{0},~\text {say} \end{aligned}$$

(3.4)

Then the eigenvalues are

$$\begin{aligned} \lambda _{2,3}=a_1 \pm \sqrt{a_1^{2}-a_2} \end{aligned}$$

(3.5)

Previously, we have determined one eigenvalue $\lambda _1=-d$ whose argument i.e. $|arg(-d)|=\pi >\frac{\alpha \pi }{2}$, for $\alpha \in (0,1)$. Now, we consider different cases considering different values of $b_{1} ~\text {and}~ a_2$.

• (i) If $a_1^{2}\ge a_2$ and $a_1< 0$, then both the eigenvalues are negative. So, $|arg(\lambda _{2,3})|=\pi >\frac{\alpha \pi }{2}, \alpha \in (0,1)$. Hence from Lemma 3.3 and Lemma 3.4 of the article by Jana et al. [15], the EE is asymptotically stable.

• (ii) If $a_1^{2}\ge a_2$ and $a_1\ge 0$, then one of the eigenvalues will be non negative. Then, $|arg(\lambda _i)|=0<\frac{\alpha \pi }{2}$ for i=2 or, 3, and $\alpha \in (0,1)$. Hence, by Lemma 3.3 and 3.4 [15], the EE is unstable.

• (iii) If the conditions $a_1^{2}< a_2$ and $a_1>0$ hold, then both the eigenvalues will be complex conjugates. $\lambda _{2,3}= a_1\pm i\sqrt{a_2-a_1^{2}}$, where $i=\sqrt{-1}$. Therefore, the EE point will be asymptotically stable if $|arg(\lambda _{2,3})|=tan^{-1}|\frac{\sqrt{a_2-a_1^{2}}}{a_1}|>\frac{\alpha \pi }{2}$. Hence, for the order of differentiation $\alpha \in \left( 0,\frac{2}{\pi }tan^{-1}|\frac{\sqrt{a_2-a_1^{2}}}{a_1}|\right)$ the EE is locally asymptotically stable.

• (iv) If $a_1^{2}< a_2$ and $a_1^{2}<0$, then $|arg(\lambda _{2,3})|=\pi -tan^{-1}|\frac{\sqrt{a_2-a_1^{2}}}{a_1}|$. Therefore, EE will be asymptotically stable if $\pi -tan^{-1}|\frac{\sqrt{a_2-a_1^{2}}}{a_1}|>\frac{\alpha \pi }{2}$. Hence, for the order of differentiation $\alpha \in \left( 0,2-\frac{2}{\pi }tan^{-1}|\frac{\sqrt{a_2-a_1^{2}}}{a_1}|\right)$

• (v) If $a_1^{2}< a_2$ and $a_1<0$, then $|arg(\lambda _{2,3})|=\frac{\pi }{2}> \frac{\alpha \pi }{2}$. Then EE is locally asymptotically stable.

From the above discussions we may state the next theorem about the stability of the EE point.

Theorem 3.8

The conditions for the local stability of EE of the system (2.4) are followed by:

• (i) The EE is locally asymptotically stable if $a_1^{2}\ge a_2$ and $a_1<0$.

• (ii) The EE is locally unstable if $a_1^{2}\ge a_2$ and $a_1\ge 0$.

• (iii) The EE is locally asymptotically stable if $a_1^{2}< a_2$ and $a_1>0$.

• (iv) The EE is locally asymptotically stable if $a_1^{2}< a_2$ and $a_1<0$.

• (v) The EE is locally asymptotically stable if $a_1^{2}< a_2$ and $a_1=0$.

3.5 Global stability of DFE

We now demonstrate the asymptotic global stability of the DFE point.

Theorem 3.9

The DFE point $E_0\left( \frac{A}{d}, 0, 0\right)$ of the fractional system (2.4) is globally asymptotically stable if $R_0<min\{1,R_0{'}\}.$

Proof

We prove the theorem using the Lemma 4.3 of the article [15]. Consider a function in the following way:   $V=I$.

Then the solution of the fractional system (2.4) and the constructed function V together imply that

$$\begin{aligned} \begin{aligned} {}_{t_{0}}D_{t}^{\alpha }V={}_{t_{0}}D_{t}^{\alpha }I(t)&=\beta SI-\left( \epsilon +\frac{\gamma v}{1+vI}\right) I-(\delta +d)I\\&\le \left[ \frac{\beta A}{d}-\gamma v-\epsilon -(\delta +d)\right] I\\&=(d+\epsilon +\delta +\gamma v)[R_0-1]I\le 0~\text {if}~R_0<1.\\ \end{aligned} \end{aligned}$$

The Lemma 4.3 [15] suggests that any solution of (2.1) starting in the region ${\mathcal {R}}$ tends to largest invariant set $S=\{(S, I, R) \in {\mathcal {R}}:{}_{t_{0}}D_{t}^{\alpha }V=0\}$. Hence, $\displaystyle {\lim _{t \rightarrow \infty }}I(t)=0$, the fractional system (2.4) changes to the equations

$$\begin{aligned} {}_{t_{0}}D_{t}^{\alpha }S(t)=A-dS,~ {}_{t_{0}}D_{t}^{\alpha }R(t)=-dR \end{aligned}$$

(3.6)

The solution of (3.6) is $S(t)=\left( -\frac{A}{d}+S(0)\right) E_{\alpha }[-dt^{\alpha }]+\frac{A}{d}~\text {and}~R(t)=R(0)E_{\alpha }[-dt^{\alpha }]$

Then we have $S(t)=\frac{A}{d}~\text {and}~R(t)=0$ as $t \rightarrow \infty$. Further, we have already established that the DFE is locally asymptotic stable if $R_0<min\{1,R_0{'}\}.$ Combining both results, we may conclude that the DFE point of the limit set (3.6) is globally stable asymptotically for $R_0<min\{1,R_0{'}\}$. Hence the proof. $\square$

3.6 Analysis of Hopf bifurcation

The existence and analysis of Hopf bifurcation for a system is modeled by ordinary differential equations is studied by many researchers [17, 18]. In this portion, we analyze Hopf bifurcation of the fractional-order system (2.4) for different values of $\alpha \in (0,1)$. Here we assume the effectiveness of the saturated treatment control parameter $\gamma$ and the fractional-order $\alpha$ as bifurcation parameters.

It is known that Hopf bifurcation may take place in spite of stability of a system at the critical value of bifurcation parameter for an integer order system. Therefore, all the roots of the Eq. (3.3) are all real. Hence, $a_1(\gamma )=0$ delivers us the necessary critical value $\gamma _{0}$ of the bifurcation parameter

$$\begin{aligned} \gamma _{0}=\frac{(\beta I^{*}+d)(1+v I^{*})^2}{v^{2} I^{*}}. \end{aligned}$$

In this case, the Hopf bifurcation occurs at $\gamma _{0}$ if the succeeding conditions are fitted i.e.

$$\begin{aligned} \frac{d}{d\gamma }Re[\lambda (\gamma _{0})]\ne 0,~Im[\lambda (\gamma _{0})]\ne 0. \end{aligned}$$

Now we state some necessary conditions for the existence of Hopf bifurcation in our fractional system.

Here we take $\alpha$ as the bifurcation parameter. Using the Lemma 3.4 [15], we can say that stability of the fractional system (2.4) depends on sign of $(\frac{\alpha \pi }{2}-|arg(\lambda _{i})|)~~i=1,~2,~3$. Based on this observation, we define the function $F(\alpha )$ by

$$\begin{aligned} f_2(\alpha )=\frac{\alpha \pi }{2}-|arg(\lambda _{i})|,~~i=1,~2,~3. \end{aligned}$$

The Lemma 3.4 [15] implies that the EE point will be stable asymptotically if $f_2(\alpha )<0$ and it will be unstable if $f_2(\alpha )>0$.

Theorem 3.10

[23] If the bifurcation parameter $\alpha$ crosses the critical value $\alpha =\alpha ^{*}\in (0,1)$, then the fractional system (2.4) passes through a Hopf bifurcation at EE point $(S^{*}, I^{*}, R^{*})$, if the given singularity conditions [(i), (ii)] and also the transversality condition [(iii)] are satisfied.

• (i) the Jacobian J at the EE point of the system (2.4) induces complex conjugate eigenvalues $\lambda _{2,3}=a(\alpha ) \pm ib(\alpha )$ with $a(\alpha )>0$.

• (ii) $f_2(\alpha ^{*})=0$ and

• (iii) $\frac{d}{d\alpha }f_2(\alpha )\ne 0~ \text {at}~ \alpha =\alpha ^{*}$.

3.7 Incommensurate fractional-order model

Let us assume the incommensurate fractional system (2.4), $\alpha _i\in (0,1],~i=1, 2, 3$ and $\zeta =\frac{1}{L}$ where $L= lcm(q_1,q_2, q_3)$ and $\alpha _i=\frac{p_i}{q_i}$, and $p_i$, $q_i$ are relatively prime for $i=1, 2, 3$. Then by Lemma 3.5 [15], an equilibrium point E(S, I, R) is locally stable asymptotically iff $|arg(\lambda )|>\frac{\zeta \pi }{2}$ for all the roots $\lambda$’s of the characteristic equation

$$\begin{aligned} det(M-J)=0 \end{aligned}$$

(3.7)

where $M=diag(\lambda ^{L\alpha _1}, \lambda ^{L\alpha _2}, \lambda ^{L\alpha _3})$ and J, Jacobian matrix evaluated at the same equilibrium point E(S, I, R).

4 Numerical experiments

In the numerical experiments, we apply predictor-corrector P(EC)$^m$E (Predict, multi-term(Evaluate, Correct), Evaluate) method which is the modified method of PECE (Predict, Evaluate, Correct, Evaluate) and Adams-Moulton algorithm [8, 9, 11] in the environment of MATLAB-16 software. For this purpose, we use the solver function as implicit fractional linear multi-step methods (FLMMs) for fractional-order systems. To perform numerical works, we choose the set of parameters as

$$\begin{aligned} A=0.85,~\beta =0.1,~d=0.01,~v=1,~\epsilon =0.01,~\delta =0.5. \end{aligned}$$

These parameters yield the EE $E^{*}$ of the fractional system (2.4) as $E^{*}=(5.2+ \frac{10\gamma }{1+I^{*}},I^{*},(1+\frac{5}{1+I^{*}})I^{*})$ where $I^{*}=0.1(3-10\gamma +\sqrt{169-80\gamma +100 {\gamma }^2})$. $E^{*}$ exists if $I^{*}>0$ which implies that the feasible region of $\gamma$ is $0<\gamma <8$. The EE $E^{*}$ of the ordinary system will be stable if $a_{1}(\gamma )=0$ and $a_{1}(\gamma )=0$ gives $\gamma =0.47~(\text {say}, ~\gamma _{0})$. For $\gamma <\gamma _{0}$, the eigenvalues contain negative real parts and hence $|arg(\lambda _{2,3})|>\frac{\alpha \pi }{2}$. Therefore the EE point is asymptotically stable and converges to $E^{*}=(7.343, 1.056, 22.79)$ for all $\alpha \in (0,1)$. If $\gamma >\gamma _{0}$, for $\alpha =1$, the EE is unstable as the eigenvalues contain positive real parts. Now, we depict some figures for the solutions of the fractional system (2.4) in the presence of the initial conditions $S(0)=0.045,~I(0)=0.04,~R(0)=0.037$. If $\gamma >\gamma _{0}$ and $\alpha \in (0,1]$, then it can be said that the EE point is stable by Theorem 3.8. If we choose $\gamma = 0.49$ then the eigenvalues are $\lambda _{2,3}=0.004\pm 0.257i$. When $\alpha <\frac{2}{\pi }|arg(\lambda _{2,3})|=0.987$, EE point will be asymptotically stable and it will be unstable whenever $\alpha >0.987$. These behaviors are shown in Fig. 3 for $\gamma =0.44$, Fig. 4 for $\gamma =0.47$, and Fig. 5 for $\gamma =0.49$.

Fig. 3

Time series plot of S(t), I(t) and R(t) for $\gamma =0.44$ of system (2.4) corresponding to the orders $\alpha =0.9, 0.95, 1$

Fig. 4

Time series plot of S(t), I(t) and R(t) for $\gamma =0.47$ of system (2.4) corresponding to the orders $\alpha =0.9, 0.95, 1$

Fig. 5

Time series plot of S(t), I(t) and R(t) for $\gamma = 0.49$ of system (2.4) corresponding to the orders $\alpha =0.9,~0.95,~1$

Next we assume $\gamma =0.9$, the eigenvalues are $0.068 \pm 0.216i$. When the value of $\alpha <\frac{2}{\pi }|arg(\lambda _{2,3})|=0.803$, EE point will be asymptotically stable and for $\alpha >0.803$ the EE point will be unstable. Figure 6 depicts the behavior.

Fig. 6

Time series plot for $\gamma = 0.9$ of system (2.4) corresponding to the order $\alpha = 0.8,~0.95$ respectively

Fig. 7

Stability region of the commensurate system (2.4)

Fig. 8

Limit cycles for $\gamma =0.97$ at $\alpha =0.802,~0.89,~0.98$

From the above discussion it can be said that with changing values of $\gamma$, we can get different region of $\alpha$ for which the EE points remain asymptotically stable. The fractional order system will be asymptotically stable if $\gamma <f_1(\alpha )=\frac{\alpha }{2}-|arg(\lambda )|$. Here, $f_1(0)=1.90,~f_1(1)=0.45$. So, $f_1(\alpha )$ is a decreasing function. The stability region in terms of $\alpha ~\text {and}~\gamma$ are shown in Fig. 7.

Now we demonstrate Hopf bifurcation for the fractional system (2.4). To satisfy the singularity condition (i) of Theorem 3.10, we must have $a_{1}(\gamma )>0$ and $\sqrt{{a_1(\gamma )}^{2}-a_{2}(\gamma )}<0$ of the equation (3.5). We see that Hopf bifurcation of the system (2.4) occurs for $\alpha \in (0,1)$ if the parameter $\gamma$ representing the effectiveness of treatment control lies in the interval (0, 1.5). We choose $\gamma = 0.97$ then the critical value of $\alpha$ as $\alpha *$ is determined from condition (ii) of Theorem 3.10 and we get the critical value $\alpha * = 0.802$. The third condition holds good since, $\frac{d}{d\alpha }f_2(\alpha )=\frac{\pi }{2}$ at $\alpha =\alpha ^{*}$. Hence, we see that Hopf bifurcation undergoes at $\alpha ^{*}=0.802$ and with increasing value of $\alpha$ from $\alpha ^{*}$ the orbits of the limit cycles also increase. Figure 8. depicts such behavior. The eigenvalues at EE of the incommensurate fractional system (2.3) can be determined by the help of the equation (3.7) which is, in general, a higher-order polynomial based on the values of $\alpha _1,~\alpha _2,~\alpha _3$. Now we choose $\gamma =0.95$. Then we obtain the EE point (10.89, 0.703, 2.769). We set the fractional orders as $\alpha _1=0.9,~\alpha _2=0.7,~\alpha _3=0.8$ and obtain the eigenvalues from equation (3.7). We see that the absolute value of the minimum of arguments of the eigenvalues is $0.133 <\frac{\pi \zeta }{2}=0.157$. Hence, in this case, the eigenvalues are unstable. Again we choose $\alpha _1=0.7,~\alpha _2=0.5,~\alpha _3=0.6$ and find the absolute value of the minimum of argument of the eigenvalues of the equation (3.7) as $0.180>\frac{\pi \zeta }{2}=0.157$. Hence, in this case, the EE point is asymptotically stable. These behavior are presented in Fig. 9.

Fig. 9

Time series plot for $\gamma = 0.95$ of system (2.3) corresponding to the order $\alpha _1=0.9,~\alpha _2=0.7,~\alpha _3=0.8$ and $\alpha _1= 0.7,~\alpha _2=0.5,~\alpha _3=0.6$

Now we state the theorem for existence criteria of Hopf Bifurcation due to the parameter $\gamma$.

Here we define a function $f_3(\gamma )$ by

$$\begin{aligned} f_3(\gamma )=\frac{\alpha \pi }{2}-|arg(\lambda _{i}(\gamma ))|,~i=1,~2,~3. \end{aligned}$$

From Theorem 2 in [7], we can say that the EE point will be stable asymptotically if $f_3(\gamma )<0$ and it will be unstable if $f_3(\gamma )>0$. Now we state the theorem for existence criterion of Hopf bifurcation about the parameter $\gamma$.

Theorem 4.1

[23] If the bifurcation parameter $\gamma$ crosses its critical value $\gamma ^{*}$ (say), then the system (2.4) passes through a Hopf bifurcation at the EE point $(S^{*}, I^{*}, R^{*})$, if the following singularity conditions (i) and (ii) and the transversality condition (iii) are satisfied.

• (i) the Jacobian J computed at the EE point of the system (2.4) determines a pair of complex conjugate eigenvalues $\lambda _{2,3}=c(\gamma ) \pm i d(\gamma )$ with $c(\gamma )>0$.

• (ii) $f_3(\gamma ^{*})=0$ and

• (iii) $\frac{d}{d\gamma }f_3(\gamma )\ne 0~ \text {at}~ \gamma =\gamma ^{*}$.

4.1 Numerical simulation of Hopf bifurcation

Fig. 10

Limit cycles for $\alpha =0.98$ at $\gamma =0.587,~0.727,~0.969$

We now choose $\gamma$ as a bifurcation parameter. Here also we obtain the eigenvalues from the equation (3.5). The first condition of Theorem 4.1 implies that the eigenvalues obtained from equation (3.5) must contain positive real parts. Then we must have $a_1>0$ and $a_2^{2}-a_1<0$. Hence, a Hopf bifurcation of the system (2.4) occurs if $\gamma \in (0,1.5).$

The critical value $\gamma ^{*}$ of $\gamma$ is obtained from $f_3(\gamma )=0$ and which implies

$$\begin{aligned} \frac{\alpha \pi }{2}=tan^{-1}\left( \frac{\sqrt{a_2^2-a_1}}{a_1}\right) \end{aligned}$$

Let us choose the order of fractional derivative $\alpha =0.98$ then the equation $f_3(\gamma )=0$ yields the critical value of the bifurcation parameter as $\gamma ^{*}=0.587$ and at this point $\frac{d}{d\gamma }h(\gamma ) =0.00919 \ne 0$. Therefore, the transversality criteria [(iii)] is also satisfied. Thus, the existence of Hopf bifurcation confirms at $\gamma ^{*}=0.587$ and with increasing value of $\gamma$ from $\gamma ^{*}$ the orbits of the limit cycles also increase. Figure 10. depicts such behavior.

4.2 Hopf bifurcation of the incommensurate system

Here we consider the incommensurate system (2.3) where the fractional orders $\alpha _1,~\alpha _2,~\alpha _3 ~\in (0,1)$ are taken as bifurcation parameter. We study the stability criteria of the fractional system (2.3) by using Theorem 2 in [7]. It shows that the stability depends on the sign of $(\frac{\alpha \zeta }{2}-|arg(\lambda _{i})|)$. Here we see that the number of eigenvalues, i depends on the term $\zeta =\frac{1}{L}$ which depends on the different fractional orders (generally, i is greater than the number of equations of the given system). Here we consider the orders of fractional derivative $\alpha _1,~\alpha _2,~\alpha _3$ as the bifurcation parameters.

Now we define a function

$$\begin{aligned} w(\zeta (\alpha _1,~\alpha _2,~\alpha _3))=\frac{\zeta \pi }{2}-\min _{i}|arg(\lambda _{i})| \end{aligned}$$

From Theorem 2 in [7], we can see that EE point will be stable asymptotically if $w(\zeta )<0$ and it will be unstable if $w(\zeta )>0$.

To examine the existence of the Hopf bifurcation for incommensurate fractional system, we state the pursuing theorem.

Theorem 4.2

[7] If the bifurcation parameters $(\alpha _{1},~\alpha _{2},~\alpha _{3})$ meets its critical value $(\alpha _{1}^{*},~\alpha _{2}^{*},~\alpha _{3}^{*})\in (0,1)$, then the system (2.3) passes through Hopf bifurcation at the EE point $E^{*}=(S^{*},I^{*},R^{*})$, if the given singularity criteria [(i)] and also the transversality criteria [(ii)] are satisfied.

• (i) $w((\alpha _{1}^{*},~\alpha _{2}^{*},~\alpha _{3}^{*}))=0$

• (ii) $\Delta w((\alpha _{1}^{*},~\alpha _{2}^{*},~\alpha _{3}^{*})).\mathbf {\rho } \ne 0$, where $\mathbf {\rho }$ is the directional derivative of the vector curve $w(\zeta (\alpha _{1},~\alpha _{2},~\alpha _{3}))=0$ at the critical value of bifurcation parameter $(\alpha _{1}^{*},~\alpha _{2}^{*},~\alpha _{3}^{*})$.

Fig. 11

Limit cycles for $\gamma =0.97$ at $\alpha _1=0.692,~0.88,~0.98$ and $\alpha _2=0.94$ $\alpha _3=0.96$

We calculate $(\alpha _1^*,\alpha _2^*,\alpha _3^*)$, the critical value of the parameter for fixed $\gamma =0.97$. Let us choose fixed $\alpha _2^*=0.94$ and $\alpha _3^*=0.96$. Then the equation $w(\zeta (\alpha _1^*,\alpha _2^*,\alpha _3^*)=0$ determine $(\alpha _1^*,\alpha _2^*,\alpha _3^*)$ as (0.692, 0.94, 0.96). At the critical value $\alpha _1^*$, Fig. 11 establishes that the Hopf bifurcation occurs. Also if $\alpha _1$ increases beyond the critical value $\alpha _1^*$, the limit cycles will be an attractor with larger radius.

5 Numerical application for some real world data

In this section, we apply the above system (2.1) to predict the COVID-19 situation of India after the second wave. For this, we collect the data of daily (cumulative) active infected of India from 1st March 2021 to 15th August 2021 from the official websites of the Government of India [6] and taking the parameter set as $A=85620,~\beta =0.084,~d=0.001,~\epsilon =0.00125,~\gamma =0.0825,~v=0.1,~\delta =0.00157$ and $\alpha =0.90.$ At this environment, to fit the above data with the above model, we use the MATLAB-16 software to drow the prediction graph up to February 2022 which is shown in Fig. 12 and we see that the number of daily active infected will be decreased and at 28th February 2022, the number of active infected will be approximately 19100. From this graph, we can predict the daily active infected of any day between this period of time.

Fig. 12

Future prediction of daily active infected of COVID-19 cases in India

6 Conclusions

In this research work, we have constructed and studied a new SIR epidemic model with the help of fractional differential equations where the disease transmission and disease treatment control get saturated after a certain time. Both commensurate and incommensurate fractional differential equations are used to investigate the complete nature and dynamics of infectious diseases. The uniqueness, positiveness, and uniform boundedness of the solutions of the system (2.4) have been established. The threshold parameter to discuss the infectious disease dynamics is commonly known as basic reproduction number $(R_0)$ is derived, and it has also been confirmed that the DFE is locally and also globally stable when the threshold condition $R_0<\min \{1,R_0{'}\}$ holds. On the other hand, the system also passes through a backward bifurcation at the EE point for the threshold range $R_0{'}<R_0 \le 1.$ Moreover, several computer simulations works enrich our theoretical results. A stability region for the corresponding fractional system is identified. Along with the Hopf bifurcation phenomenon considering the fractional derivative i.e., $\alpha$ as bifurcation parameter is visualized graphically. We have further observed that with the increasing value of $\alpha ,$ the length of the cycle increases, and this phenomenon established that by increasing the importance of $\alpha$, the system repels away from the equilibrium point. Moreover, the Hopf bifurcation scenario for the incommensurate fractional system is also derived with bifurcation parameters $\alpha _{1}$, $\alpha _{2}$, and $\alpha _{3}$. We also experienced the significance of $\alpha$ with the help of the model fitting.

Also, we have drow a prediction curve of daily active infected of India from 1st March 2021 to 28 February 2022, i.e., of one year with help of the existing data from 1st March 2021 to 15th August 2021. From this prediction curve, we can conclude that if the present situation (i.e., the value of the parameter that we have assumed here) does not change, there will be no chance of a third wave before February 2022.