The three-dimensional Fueter equation and divergence-free frames

Abstract

This paper extends hyperkähler Floer theory with flat target manifolds from the case where the source is a 3-sphere or 3-torus, equipped with a standard frame, to the case where the source is a general closed orientable 3-manifold, equipped with a regular divergence-free frame. Regular divergence-free frames are characterized by the nonexistence of nonconstant solutions to the unperturbed linear Fueter equation. They form a dense open subset of the space of all divergence-free frames. A gauged version of the Fueter equation is introduced, which unifies various geometric equations in gauge theory.

Appendices

Appendix A: Divergence-free frames

Let M be a closed connected oriented 3-manifold and $\operatorname {dvol}_{M}\in {\varOmega}^{3}(M)$ be a positive volume form. Denote the set of positive frames by

and the set of divergence-free positive frames by

Given three deRham cohomology classes a ₁,a ₂,a ₃∈H ²(M;ℝ), denote the set of divergence-free positive frames that represent the classes a _i by

The following theorem is an application of Gromov’s h-principle and is proved in [21, page 182] and [10, Corollary 20.4.3]. Although the result is stated in these references in the weaker form that every frame can be deformed in to a divergence-free frame, the proofs give the stronger result stated below (as explained to the author by Yasha Eliashberg).

Theorem A.1

(Gromov)

The inclusion is a homotopy equivalence for all a ₁,a ₂,a ₃∈H ²(M;ℝ), and so is the inclusion .

Lemma A.2

(Gromov)

Let V be a 3-dimensional real vector space and S:V×V→V be a skew-symmetric bilinear map. Let $\mathcal{R}\subset\operatorname{Hom}(V,\operatorname{End}(V))$ be the set of all linear maps $L:V\to\operatorname{End}(V)$ such that the map

$$\varLambda^2V\to V:u\wedge v\mapsto S(u,v)+L(u)v-L(v)u $$

is a vector space isomorphism. Fix a 2-dimensional linear subspace E⊂V and a linear map $\lambda:E\to\operatorname{End}(V)$. Define

$$\mathcal{L}:= \bigl\{L\in\operatorname{Hom}\bigl(V,\operatorname {End}(V)\bigr) \,|\,L|_E=\lambda \bigr\}. $$

If $\mathcal{L}\cap\mathcal{R}$ is nonempty, then it has two connected components and the convex hull of each connected component of $\mathcal{L}\cap\mathcal{R}$ is equal to $\mathcal{L}$.

Proof

The proof is a special case of the argument given by Eliashberg–Mishachev in [10, pages 183/184]. Assume without loss of generality that

$$V={\mathbb{R}}^3,\quad E= \bigl\{x\in{\mathbb{R}}^3\,| \,x_1=0 \bigr\}. $$

Write S in the form

$$S(u,v) =: \sum_{i<j}u_iv_jS_{ij}, \quad S_{ij}=-S_{ji}\in{\mathbb{R}}^3, $$

and write a linear map $L:{\mathbb{R}}^{3}\to\operatorname {End}({\mathbb{R}}^{3})$ in the form

$$L(u)v = \sum_{i,j=1}^3u_iv_jL_{ij}, \quad L_{ij}\in{\mathbb{R}}^3. $$

Then $L\in\mathcal{R}$ if and only if

$$ \det (S_{23}+L_{23}-L_{32},S_{31}+L_{31}-L_{13},S_{12}+L_{12}-L_{21}) \ne0. $$

(52)

Denote by $\mathcal{R}^{+}$, respectively $\mathcal{R}^{-}$, the set of all $L\in\mathcal{R}$ for which the sign of the determinant in (52) is positive, respectively negative.

Fix a linear map $\lambda:E\to\operatorname{End}({\mathbb{R}}^{3})$. This map is determined by the coefficients L _ij with i=2,3. Thus an element $L\in\mathcal{L}\cap\mathcal{R}$ is determined by the choice of L ₁₁, L ₁₂, L ₁₃. If S ₂₃+L ₂₃−L ₃₂=0 then the determinant in (52) vanishes for every $L\in\mathcal{L}$ and so $\mathcal{L}\cap\mathcal{R}=\emptyset$. Hence assume S ₂₃+L ₂₃−L ₃₂≠0. Then $\mathcal{L}\cap\mathcal{R}^{+}$ and $\mathcal{L}\cap\mathcal {R}^{-}$ are nonempty connected submanifolds of ℝ³×ℝ³×ℝ³. (Namely, L ₁₁ is any vector in ℝ³, L ₁₂ is required to be in the complement of an affine line, and then L ₁₃ is required to be in the complement of an affine plane depending smoothly on L ₁₂.)

Choose x,y∈ℝ³ such that

$$\det(S_{23}+L_{23}-L_{32},x,y) > 0. $$

Then, for t>0 sufficiently large,

Given $L\in\mathcal{L}$ choose $L',L''\in\mathcal{L}$ such that

Then $L',L''\in\mathcal{L}\cap\mathcal{R}^{+}$ and $L=\frac{1}{2}(L'+L'')$. Hence the convex hull of $\mathcal{L}\cap\mathcal{R}^{+}$ is equal to $\mathcal{L}$. A similar argument shows that the convex hull of $\mathcal{L}\cap \mathcal{R}^{-}$ is also equal to $\mathcal{L}$. This proves Lemma A.2. □

Proof of Theorem A.1

Fix a Riemannian metric on M, let a∈H ²(M;ℝ)³, and let σ _i ∈Ω ²(M) be the harmonic representative of a _i , i=1,2,3. Define

Let

be the projection defined by π _a (β)=v for , where $\iota(v_{i})\operatorname{dvol}_{M}:=\sigma_{i}+d\beta_{i}$. This is a homotopy equivalence. A homotopy inverse assigns to the unique co-exact triple of 1-forms $\beta\in\pi_{a}^{-1}(v)$.

Consider the vector bundle

$$X:=T^*M\oplus T^*M\oplus T^*M $$

over M and denote by X ⁽¹⁾ the 1-jet bundle. Use the Riemannian metric on M to identify X ⁽¹⁾ with the set of tuples (y,β ₁,β ₁,β ₃,L ₁,L ₂,L ₃) with y∈M, $\beta_{i}\in T_{y}^{*}M$, and $L_{i}\in\operatorname {Hom}(T_{y}M,T_{y}^{*}M)$. Denote by

the open subset of all (y,β,L)∈X ⁽¹⁾ such that the 2-forms $\tau_{i}\in\varLambda^{2}T_{y}^{*}M$, defined by

$$ \tau_i(u,v):=\sigma_i(u,v)+ \bigl \langle L_i(u), v \bigr\rangle - \bigl\langle L_i(v), u \bigr\rangle,\quad i=1,2,3, $$

(53)

are linearly independent. Denote by the space of sections of . Thus an element of is a tuple (β,L)=(β ₁,β ₂,β ₃,L ₁,L ₂,L ₃) with β _i ∈Ω ¹(M) and L _i ∈Ω ¹(M,T ^∗ M) such that the 2-forms τ _i ∈Ω ²(M), defined by (53) are everywhere linearly independent. Then is a bundle over . The projection is given by π _a (β,L)=v, where $\iota(v_{i})\operatorname{dvol}_{M}:=\tau_{i}$ and τ _i is as in (53). This map is a homotopy equivalence. A homotopy inverse of π _a is the inclusion given by ι _a (v):=(0,L), where $L_{i}(u):=\frac{1}{2} (\operatorname{dvol}_{M}(v_{i},u,\cdot )-\sigma_{i}(u,\cdot ) )$. Namely, , both maps are linear between open subsets of topological vector spaces, and the kernel of π _a is the space of tuples (β,L) such that each L _i is symmetric.

The previous discussion shows that there is a commutative diagram

where the vertical maps are homotopy equivalences and the differential operator is given by . Thus is the space of all sections β of X such that satisfies the differential relation . By Lemma A.2, is ample in the sense of [10, page 167]. Hence satisfies the h-principle (see [10, Theorem 18.4.1]). In particular, every section of is homotopic, through sections of , to a section of the form (β,∇β). Equivalently, every frame can be deformed within to a divergence-free frame in . In fact, by the parametric h-principle, the inclusion induces isomorphisms on all homotopy groups, and is therefore a homotopy equivalence (see [10, 6.2.A]). Hence the inclusion is a homotopy equivalence.

To explain the extension of this result to the inclusion of into , it is convenient to spell out the details of the parametric h-principle in the present setting. Choose a smooth manifold Λ and a smooth map a:Λ→H ²(M;ℝ)³. Consider the vector bundle

$${\widetilde{X}}:=\varLambda\times T^*M\oplus T^*M\oplus T^*M \to{ \widetilde{M}}:=\varLambda\times M. $$

Define as the set of tuples $(\lambda,y,\beta_{1},\beta_{2},\beta_{3},{\widetilde{L}}_{1},{\widetilde {L}}_{2},{\widetilde{L}}_{3})$, with λ∈Λ, y∈M, $\beta_{i}\in T^{*}_{y}M$, and ${\widetilde{L}}_{i}\in\operatorname{Hom}(T_{\lambda}\varLambda\times T_{y}M,T_{y}^{*}M)$, such that the 2-forms $\tau_{i}=\tau_{\lambda,i}\in\varLambda^{2}T_{y}^{*}M$ in (53) are linearly independent. Here σ _i =σ _λ,i is the harmonic representative of the class a _i (λ) and $L_{i}\in\operatorname{Hom}(T_{y}M,T_{y}^{*}M)$ is the restriction of ${\widetilde{L}}_{i}$ to 0×T _y M. Define the operator from sections of ${\widetilde{X}}$ to sections of ${\widetilde{X}}^{(1)}$ as the covariant derivative

Let be the space of sections of and denote by its preimage under . Thus an element of is a map Λ→Ω ¹(M)³:λ↦β _λ such that the 2-forms

$$ \tau_{\lambda,i}:=\sigma_{\lambda,i}+d \beta_{\lambda,i},\quad i=1,2,3, $$

(54)

are everywhere linearly independent for every λ. An element of is a smooth section that assigns to λ∈Λ a tuple

$$ (\beta_{\lambda,1},\beta_{\lambda,2},\beta_{\lambda,3}, {\widetilde{L}}_{\lambda,1},{\widetilde{L}}_{\lambda,2},{\widetilde {L}}_{\lambda,3}) \in{\varOmega}^1(M)^3\times \operatorname{Hom}\bigl(T_\lambda\varLambda ,{\varOmega}^1 \bigl(M,T^*M\bigr)\bigr)^3 $$

(55)

such that the 2-forms τ _λ,i ∈Ω ²(M), defined by (53), are everywhere linearly independent for every λ∈Λ. As before there is a commutative diagram

Here is the space of maps such that and is the space of all smooth maps from Λ to . The projection , respectively , assigns to the section λ↦β _λ , respectively (55), the section λ↦v _λ with $\iota(v_{\lambda,i})\operatorname {dvol}_{M}=\tau _{\lambda,i}$, where τ _λ,i is given by (54), respectively (53). Both projections are homotopy equivalences.

By Lemma A.2, the open differential relation is ample. Hence it follows from the h-principle in [10, Theorem 18.4.1] that every smooth map from Λ to can be deformed within to a smooth map that satisfies . With Λ=S ^k this implies that the homomorphism is surjective for all a ₁,a ₂,a ₃∈H ²(M;ℝ).

The relation also satisfies the relative h-principle in [10, 6.2.C]. For the (k+1)-ball Λ=B ^k+1 with boundary ∂B ^k+1=S ^k this means that, if a map extends over B ^k+1 in , and one chooses any smooth extension of the projection over B ^k+1, then this extension lifts to a smooth map , equal to the given map over the boundary (and homotopic to the given map in ). Hence the homomorphism is injective. This proves Theorem A.1. □

Appendix B: Self-adjoint Fredholm operators

This appendix is included for the benefit of the reader. It discusses two well known results about self-adjoint Fredholm operators, that are used in Sect. 2. Lemma B.1 characterizes unbounded self-adjoint Fredholm operators and Lemma B.2 shows that regular crossings are isolated. While Lemma B.2 follows from the Kato selection theorem (see [34, Lemma 4.7]), the proof given below is simpler and more direct.

Let H be a Hilbert space and V⊂H be a dense linear subspace that is a Hilbert space in its own right. Suppose that the inclusion V↪H is a compact operator. Denote the inner product on H by 〈⋅,⋅〉, the norm on H by $\Vert x\Vert _{H}:=\sqrt{\langle x,x\rangle}$ for x∈H, and the norm on V by ∥x∥ _V for x∈V. Let be the space of symmetric bounded linear operators A:V→H and be the subset of self-adjoint operators. Thus a bounded linear operator D:V→H is an element of if and only if 〈Dx,ξ〉=〈x,Dξ〉 for all x,ξ∈V and, for every x∈H, the following holds

$$ \sup_{0\ne\xi\in V}\frac{\vert \langle x, D\xi \rangle \vert }{\Vert \xi \Vert _H}<\infty \quad\iff\quad x\in V. $$

(56)

Every is a Fredholm operator of index zero and regular crossings of differentiable paths are isolated. Proofs of these well known observations are included here for completeness of the exposition.

Lemma B.1

Let . Then the following are equivalent.

• (i) .

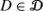• (ii) $(\operatorname{im}\,D)^{\perp}\subset V$ and there is a constant c>0 such that, for all x∈V,

  $$ \Vert x\Vert _V\le c \bigl(\Vert Dx\Vert _H+\Vert x\Vert _H \bigr). $$

  (57)

• (iii) D is a Fredholm operator of index zero.

In particular, is an open subset of in the norm topology.

Proof

We prove that (i) implies (ii). Assume . By (56) $(\operatorname{im}\,D)^{\perp}\subset V$. We show that the graph of D is a closed subspace of H×H. Let x _n ∈V and x,y∈H be such that lim _n→∞∥x−x _n ∥ _H =0 and lim _n→∞∥y−Dx _n ∥ _H =0. Then 〈x,Dξ〉=lim _n→∞〈x _n ,Dξ〉=lim _n→∞〈Dx _n ,ξ〉=〈y,ξ〉 for ξ∈V. Hence x∈V by (56) and, since D is symmetric, it follows that Dx=y. Thus D has a closed graph. Now V→graph(D):x↦(x,Ax) is a bijective bounded linear operator and so has a bounded inverse. This proves (57).

We prove that (ii) implies (iii). Since V↪H is a compact operator, it follows from (57) that D has a finite-dimensional kernel and a closed image (see [27, Lemma A.1.1]). Since $(\operatorname{im}\,D)^{\perp}\subset V$ and D is symmetric, it follows that $(\operatorname{im}\,D)^{\perp}=\ker\,D$. Hence $\dim\,\operatorname{coker}\,D=\dim\,\ker\,D$.

We prove that (iii) implies (i). Let be a Fredholm operator of index zero. Then D has a finite-dimensional kernel and a closed image. Since D is symmetric, $\ker\,D\subset(\operatorname{im}\,D)^{\perp}$. Since D has Fredholm index zero, $\ker\,D = (\operatorname{im}\, D)^{\perp}$ and hence $\operatorname{im}\,D=(\ker\,D)^{\perp}$. Now let x∈H and suppose that there is a constant c such that |〈x,Dξ〉|≤c∥ξ∥ _H for every ξ∈V. By the Riesz representation theorem, there exists an element y∈H such that 〈x,Dξ〉=〈y,ξ〉 for ξ∈V. Choose y ₀∈ker D such that y−y ₀⊥ker D. Then $y-y_{0}\in\operatorname{im}\,D$. Choose x ₁∈V such that Dx ₁=y−y ₀. Then 〈x−x ₁,Dξ〉=〈y,ξ〉−〈Dx ₁,ξ〉=〈y ₀,ξ〉 for every ξ∈V. Given ξ∈V choose ξ ₀∈ker D such that ξ−ξ ₀⊥ kerD. Then

$$\langle x-x_1, D\xi \rangle = \bigl\langle x-x_1, D(\xi- \xi_0) \bigr\rangle = \langle y_0, \xi-\xi_0 \rangle=0. $$

Hence $x-x_{1}\in(\operatorname{im}\,D)^{\perp}=\ker\,D\subset V$ and hence x∈V.

Since (i) and (iii) are equivalent it follows from the perturbation theory for Fredholm operators (see [27, Theorem A.1.5]) that  is an open subset of with respect to the norm topology. This proves Lemma B.1. □

Let I⊂ℝ be an open interval and be a continuous path with respect to the norm topology on . The path is called weakly differentiable if the map I→ℝ:s↦〈x,D(s)ξ〉 is differentiable for every x∈H and every ξ∈V. A crossing is an element s∈I such that D(s) has a nontrivial kernel. A crossing s∈I is called regular if the quadratic form

$$\varGamma_s:\ker\,D(s)\to{\mathbb{R}},\qquad \varGamma_s( \xi):= \bigl\langle\xi, \dot{D}(s)\xi \bigr\rangle, $$

is nondegenerate.

Lemma B.2

Let be a weakly differentiable path of self-adjoint operators and let s ₀∈I be a regular crossing. Then there is a δ>0 such that D(s):V→H is bijective for every s∈I with 0<|s−s ₀|<δ.

Proof

Assume without loss of generality that s ₀=0. By Lemma B.1 there is a constant c>0 such that

$$ \Vert x\Vert _V\le c \bigl(\bigl \Vert D(s)x\bigr \Vert _H+\Vert x\Vert _H \bigr) $$

(58)

for every x∈V and every s in some neighborhood of zero. Shrinking I, if necessary, we may assume that (58) holds for every s∈I.

Assume, by contradiction, that there is a sequence s _n ∈I such that s _n →0 and D(s _n ) is not injective for every n. Then there is a sequence x _n ∈V such that D(s _n )x _n =0 and ∥x _n ∥ _H =1. Thus ∥x _n ∥ _V ≤c by (58). Passing to a subsequence we may assume that x _n converges in H to x ₀. Then ∥x ₀∥ _H =1 and 〈x ₀,D(0)ξ〉=lim _n→∞〈x _n ,D(s _n )ξ〉=0 for ξ∈V. Hence x ₀∈ker D(0). Moreover, for every ξ∈ker D(0), the sequence D(s _n )ξ/s _n converges weakly to $\dot{D}(0)\xi$ and is therefore bounded, so

$$\bigl\langle\dot{D}(0)\xi, x_0 \bigr\rangle = \lim _{n\to\infty} \biggl\langle\frac{D(s_n)\xi}{s_n}, x_0 \biggr \rangle = \lim_{n\to\infty} \biggl\langle\frac{D(s_n)\xi}{s_n}, x_n \biggr\rangle = 0. $$

This contradicts the nondegeneracy of Γ ₀ and proves Lemma B.2. □

Let I be a compact interval and be a weakly differentiable path with only regular crossings such that D(s) is bijective at the endpoints of I. The spectral flow is the sum of the signatures of the crossing forms Γ _s over all crossings. It is invariant under homotopy with fixed endpoints and is additive under catenation. (See [34] for an exposition.)