1 Introduction

High energy gas fracturing (HEGF) is a technique to stimulate wellbores by producing several radial cracks around the holes. The cracks are generated by high pressure gas produced from burning a propellant. This approach creates multiple fractures and avoids the inherent limitations of other common well stimulating techniques such as hydraulic fracturing (HF) and explosive fracturing (EF). Hydraulic fractures are generated using a fluid which needs pumping equipment on the top of the well, and the result is usually in the form of two fractures perpendicular to the minimum principle stress orientation. Explosive fracturing can also generate several fractures, but releasing a very high amount of energy in a few milliseconds may cause considerable crushing of rock and leaving a residual compressive stress zone around the wellbore. HEGF produces a higher pressure in a shorter time than HF but a significantly lower pressure in a longer time than EF, so multiple cracks can be generated without causing substantial damage to the rock structure.

Since a higher recovery is obtained by HF due to the possibility of having very long fractures, HEGF has not been accepted as the first choice for increasing the recovery. Despite the disadvantageous of short crack lengths, HEGF has its own applications and advantages: no need for special pumping equipment, low overall costs, simple and fast procedure, and the possibility of having multiple fractures without causing an extensive damage. Krilove et al. (2008) investigated the capability of this technique by applying it on petrophysical laboratory samples and inside production wells. They concluded that HEGF is an effective and efficient method which can increase the oil production rate by a factor of 2 to 3. It has also been experimentally observed that HEGF is rather suitable for exploratory wells or wells with natural fissures around them (Yang et al. 1992; Wu et al. 2012). In addition, this method has been successfully implemented in other applications such as enhancing the injectivity of gas injection wells (Salazar et al. 2002), prefracturing before hydraulic fracturing to reduce the friction pressure losses near the wellbore (Jaimes et al. 2012), stimulating geothermal wells (Chu et al. 1987), extracting gas from coal seams (Chao et al. 2013), etc.

The procedure of crack initiation and propagation has been comprehensively studied for blasting applications, and the role of different effects has been determined through numerous experimental and numerical investigations which will be briefly discussed in this section. According to these studies, one can conclude that a conventional blasting process has two major stages which contribute to crack propagation and rock fragmentation: (a) stress wave and (b) gas pressure. The role of the stress wave is to create initial cracks, while the gas pressure leads to crack propagation. In fact, the stress wave can only initiate limited cracking and crushing of the rock near the borehole which would not exceed more than several hole diameters (Kutter and Fairhurst 1971). Based on some field and laboratory experiments, McHugh (1983) concluded that the effect of gas pressure could be more noticeable than the effect of stress wave. The same result was confirmed by Daehnke et al. (1997). The peak pressure of propellant in HEGF is not as high as an explosive charge and this pressure is released over a longer period of time, as a result, the HEGF procedure can be assumed to be very similar to the second stage of blasting (Nilson et al. 1985).

Possibility of unexpected results during such complicated and fast engineering actions, which may cause major safety and economic problems, motivates implementation of numerical and analytical simulations to predict a wide range of problems. Several attempts have been devoted to simulating the complex process of blasting, but only those related to this research are briefly reviewed. Nilson et al. (1985) developed equations of conservation of mass and momentum for penetration of a gas through a crack. These equations were solved numerically, while analytical solutions were implemented for analyzing the solid media. Munjiza et al. (2000) suggested a simple model for evaluation of gas pressure through cracks. Gas pressure was only considered in a specific area around the source, and the combined finite-discrete element method was used for the analysis of the cracked solid. The Nilson equations were implemented by Cho et al. (2004b) to investigate the dynamic fracture process of rock. A dynamic FEM code equipped with a re-meshing algorithm was used to consider crack growth, and the gas pressure was estimated as a one-dimensional flow through cracks. In a different approach, Mohammadi and Bebamzadeh (2005) developed an approach to model gas–solid interaction. This model used two separate but coupled meshes for the computation of solid and gas phases based on the mechanics of porous media. Then Mohammadi and Pooladi (2007) improved the method proposed by Munjiza et al. (2000) to non-uniform gas flow through fractures to account for the effects of cracking and deformation induced by blasting on the pressure and density of the gas. The same idea was used and further developed by Mohammadi and Pooladi (2012) to efficiently simulate the process of gas flow through a complex system of fractures. Different benchmark examples were simulated to assess the performance of their proposed approach. Other numerical techniques such as discrete element method (DEM) for particulate media have also been implemented to simulate rock fragmentation by high energy gas (Ruest et al. 2006). This method can handle highly complex fracture networks but the computational cost is extremely high.

Similar to blasting, the gas fracturing procedure can be classified into two stages; rapid rising of gas pressure which causes some cracking around the hole and the gas penetration which leads to crack extension. The crack initiation step can be simulated using sophisticated rate-dependent constitutive models. Several models have been proposed for random generation of cracks in rocks under dynamic loading, including Cho et al. (2004a, 2008), Cho and Kaneko (2004), Zhu et al. (2004, 2007), and Ma and An (2008). The second stage of gas fracturing, gas penetration into existing cracks, is of great importance because it predominantly determines the final crack extension. It has been considered as a quasi-static phenomenon due to a lower rate of loading (Paine and Please 1995; Nilson et al. 1985).

HEGF can be regarded as an engineering problem in highly complicated conditions with several uncertainties. The final results depend on many factors such as rock strength (tensile strength, toughness), in situ stresses, type of propellant and quality of sealing. The first stage of HEGF procedure is not in the scope of this study and the main focus is to simulate the process of gas penetration and crack extension to obtain quantitatively acceptable results. For simulating the solid medium, the powerful extended finite element method (XFEM) is implemented. This method simulates the existing and propagating cracks independent of the generated mesh, so avoiding the difficult re-meshing and stress transfer algorithms. This method has been used to study hydraulic fractures in concrete dams by (Ren et al. 2009), in which the fluid pressure was applied as a uniform constant pressure through the entire crack surfaces. Different coupled hydro-mechanical formulations of XFEM were also proposed in several studies to simulate hydraulic fracturing in porous media, while the injected fluid can permeate into the surrounding rocks (Mohammadnejad and Khoei 2013; Gordeliy and Peirce 2013; Gholami et al. 2013). Here, to consider the gas flow through the fractures, a one-dimensional transient flow model governed by conservation of mass and momentum (Nilson and Griffiths 1983; Nilson et al. 1985) is adopted. These equations are solved using an explicit finite difference method (FDM). In each time step, the geometrical parameters of fractures are given to the FDM code, and the resultant solution for the gas pressure along the crack is applied as the boundary conditions on the solid medium. These equations were previously used by Cho et al. (2004b) and Goodarzi et al. (2011, 2013) to simulate a laboratory scale experiment conducted by Cho et al. (2002) to study the gas flow inside a crack. Applicability of these equations was confirmed by the good agreement obtained between numerical and experimental values of the average gas velocity inside the crack.

In this paper, after introducing the gas flow and XFEM equations, the provided XFEM code is validated against an analytical solution, and the effects of different numerical parameters are assessed in order to achieve a reasonable accuracy for the numerical results. The proposed algorithm is then evaluated by simulating two field experiments of gas fracturing, with comprehensive sensitivity analyses to investigate the effect of each parameter.

2 Numerical modeling of gas flow

After a blast, a small zone with many cracks would appear around the blast-hole, and just a few of them can surpass the others and extend. Experimental investigations have also shown that the number of major cracks around a blast-hole is between 3 and 8 (Garnsworthy 1990). Accordingly, in this research, the gas flow is only considered in those surpassing fractures. The gas penetration through the cracks is assumed to be a one-dimensional transient flow. Moreover, because of the insignificant loss of mass and heat into the surrounding rock, it is reasonable to presume that the gas expansion is an adiabatic process, and the rock is impermeable (Nilson et al. 1985).

The one-dimensional equations of gas flow, governed by the laws of conservation of mass and momentum, can be written as follows:

$$\frac{\partial (\rho h)}{\partial t} + \frac{\partial (\rho vh)}{\partial x} = 0,$$
(1)
$$\rho h\left( {\frac{1}{\rho }\frac{\partial P}{\partial x} + \psi } \right) = 0,$$
(2)

where ρ is the density; v is the velocity; P is the gas pressure; and Ψ is the viscous shear stress, which can be approximated by Eq. (3a) and (3b) for laminar and turbulent flow, respectively (Paine and Please 1995),

$$\psi = \frac{12\mu v}{{\rho h^{2} }},$$
(3a)
$$\psi = a\left( {\frac{\varepsilon }{h}} \right)^{b} \frac{{v^{2} }}{h},$$
(3b)

where μ is the viscosity of fluid; h is the fracture opening; ε is the fracture roughness; and a and b are experimental constants: a = 0.1 and b = 0.5 (Nilson et al. 1985). Cho et al. (2004b) showed that the turbulent model for gas flow through the fracture is much more reasonable, so Eq. (3b) is chosen for the rest of this study.

Replacing the viscous shear stress in Eq. (2) by Eq. (3b) and after simple manipulations, the velocity can be determined from

$$v = \sqrt {\frac{h}{{f_{t} \rho }}\left( { - \frac{\partial P}{\partial x}} \right)} ;\quad f_{t} = a(\varepsilon /h)^{b} .$$
(4)

Substituting Eq. (4) into Eq. (1), the discretized form of Eq. (1) on the mesh shown in Fig. 1, can be written as follows:

Fig. 1
figure 1

The finite difference mesh for one-dimensional gas flow, w and x are in the middle of the elements

Full size image
$$\rho_{N}^{t + \Delta t} - \rho_{N}^{t} = - \frac{4\Delta t}{{(\Delta x_{R} + \Delta x_{L} )(h_{w} + h_{x} )}} \times \left( {h_{x} \sqrt { - \rho^{t}_{x} \frac{{h_{x} }}{f}\frac{{(P^{t}_{L} - P^{t}_{N} )}}{{\Delta x_{L} }}} - h_{w} \sqrt { - \rho^{t}_{w} \frac{{h_{w} }}{f}\frac{{(P^{t}_{N} - P^{t}_{M} )}}{{\Delta x_{R} }}} } \right),$$
(5)

where h is a constant input associated with an element, and the density of elements is calculated as the average of the densities of their nodes. Despite the fact that an advanced equation of state such as JWL can better predict the explosive pressure, the JWL parameters for the propellant used in our verification examples are not available in the literature. As a result, to estimate the detonation gas pressure along the fractures, an ideal gas equation of state is implemented (Paine and Please 1995; Mortazavi and Katsabanis 2001).

$$P = P_{0} \left( {\frac{\rho }{{\rho_{0} }}} \right)^{\gamma } ,$$
(6)

where P 0 and ρ 0 are the initial pressure and density of the gas; P and ρ are the current values and γ is the coefficient of the ideal gas.

3 Extended finite element method

3.1 Formulation

The finite element method (FEM) is one of the most powerful methods in engineering analyses, frequently used to model various problems in solid media. One of the main approaches of FEM in modeling crack propagation problems is to use the technically difficult and time-consuming adaptive re-meshing approach. The extended finite element method, on the other hand, simulates the cracks by enriching the shape functions of the elements which are involved with cracks. In this way, after each step of crack propagation, there is absolutely no need to change the initial mesh and only the new involved elements should be detected for proper enrichments.

When an element takes part in a crack simulation, its XFEM displacement approximation can be defined as follows (Mohammadi 2008):

$${\mathbf{u}}({\mathbf{x}}) = \sum\limits_{j = 1}^{n} {N_{j} ({\mathbf{x}}){\mathbf{u}}_{j} } + \sum\limits_{h = 1}^{m} {N_{h} ({\mathbf{x}})H(\xi ({\mathbf{x}})){\mathbf{a}}_{h} } + \sum\limits_{k = 1}^{mt} {N_{k} ({\mathbf{x}})\left( {\sum\limits_{l = 1}^{mf} {F_{l} ({\mathbf{x}}){\mathbf{b}}_{k}^{l} } } \right)}.$$
(7)

Here u is the conventional FEM nodal displacements; n is the number of nodes of the element; m is the number of nodes which are involved with the crack length; mt is the number of nodes being related to the crack tip; mf is the number of functions that are used for enriching the crack tip element; and a h and b l k are the additional degrees of freedom associated with crack discontinuity and crack tip singularity enrichments, respectively; N is the conventional shape functions of FEM; and H is the Heaviside function for simulation of displacement discontinuity across a crack,

$$H(\xi (x)) = \left\{ {\begin{array}{*{20}c} 1, & {\xi (x) \ge 0} \\ 0, & {\xi (x) < 0} \\ \end{array} } \right..$$
(8)

In Eq. (7), F is a set of functions which are obtained from analytical solution of displacement around a crack tip. The crack tip enrichment function F for an isotropic elastic material can be defined as follows:

$$F_{\alpha } (r,\theta ) = \left\{ {\sqrt r \sin \frac{\theta }{2},\sqrt r \cos \frac{\theta }{2},\sqrt r \sin \theta \sin \frac{\theta }{2},\sqrt r \sin \theta \cos \frac{\theta }{2}} \right\}.$$
(9)

Selection of the enriched nodes is performed according to the crack position, as shown in Fig. 2.

Fig. 2
figure 2

Selection of the nodes for enrichments, squares show the crack tip enrichment, and circles are related to the Heaviside enrichment

Full size image

The conventional FEM formulation should be updated to account for the additional degrees of freedom. If a cracked body subjected to body force b and internal pressure p on the crack surfaces is assumed, as depicted in Fig. 3, the global governing equation for determining the unknown vectors u can be defined as follows:

Fig. 3
figure 3

A cracked solid domain subjected to an internal pressure on crack surfaces

Full size image
$${\mathbf{Ku = f}},$$
(10)

where the unknowns vector u, the stiffness matrix K, and the external force vector f, for each element, can be determined from the equations as follows:

$${\mathbf{u}}^{e} = \left\{ {{\mathbf{u}}_{j} ,{\mathbf{a}}_{h} ,{\mathbf{b}}_{k}^{l} } \right\}^{T} ,$$
(11)
$${\mathbf{k}}_{ij}^{e} = \left[ {\begin{array}{*{20}c} {k_{ij}^{uu} } & {k_{ij}^{ua} } & {k_{ij}^{ub} } \\ {k_{ij}^{au} } & {k_{ij}^{aa} } & {k_{ij}^{ab} } \\ {k_{ij}^{bu} } & {k_{ij}^{ba} } & {k_{ij}^{bb} } \\ \end{array} } \right],\quad (r,s = u,a,b),$$
(12)
$${\mathbf{f}}_{i}^{e} = \left\{ {{\mathbf{f}}_{i}^{u} ,{\mathbf{f}}_{i}^{a} ,{\mathbf{f}}_{i}^{bl} } \right\}.$$
(13)

Considering B and D as the matrix of the shape function derivatives and the constitutive matrix, respectively, different terms in Eq. (12) and (13) can be determined as following:

$$k_{ij}^{rs} = \int\limits_{{\varOmega^{e} }} {\left( {{\mathbf{B}}_{i}^{r} } \right)}^{T} {\mathbf{DB}}_{j}^{s} \text{d} \varOmega ,$$
(14)
$${\mathbf{f}}_{i}^{u} = \int\limits_{\varOmega } {N_{i} {\mathbf{b}}\text{d} } \varOmega + \int\limits_{{L_{f} }} {N_{i} {\mathbf{t}}\text{d} } \varGamma ,$$
(15)
$${\mathbf{f}}_{i}^{a} = \int\limits_{\varOmega } {N_{i} H{\mathbf{b}}\text{d} } \varOmega + \int\limits_{{L_{f} }} {N_{i} H{\mathbf{t}}\text{d} } \varGamma + 2\int\limits_{{L_{c} }} {n.N_{i} {\mathbf{p}}\text{d} } \varGamma ,$$
(16)
$${\mathbf{f}}_{i}^{bl} = \int\limits_{\varOmega } {N_{i} F_{l} {\mathbf{b}}\text{d} } \varOmega + \int\limits_{{L_{f} }} {N_{i} F_{l} {\mathbf{t}}\text{d} } \varGamma + 2\int\limits_{{L_{c} }} {n\sqrt r .N_{i} {\mathbf{p}}\text{d} } \varGamma ,\quad (l = 1 - 4).$$
(17)

3.2 Numerical integration

Despite the simple idea of XFEM, specific details are required for its implementation. One of them, which is critical to achieve proper accuracy, is the integration on the elements that are involved with a crack. The Gauss quadrature method is usually adopted for this purpose in conventional FEM simulation. However, it may not be accurate enough for singular or discontinuous functions usually encountered in XFEM simulations. One way to improve the results is to subdivide the both sides of the enriched element into subtriangles in such a way that their edges conform to the geometry of the crack and the element (Mohammadi 2008). Figure 4 shows a simple typical procedure for subdividing a crack element and a crack tip element; a larger number of triangles may be required to achieve sufficient accuracy. It should be noted that integration in each triangle is performed by a standard Gauss quadrature rule.

Fig. 4
figure 4

Subtriangles for integration on a crack tip element (left) and a cracked element (right)

Full size image

More details about the formulation, implementation, and applications of XFEM can be found in Mohammadi (2008, 2012).

4 Coupling process and crack propagation

The two numerical approaches for solving the gas flow and the cracked solid medium have to be coupled. At first, initial lengths of cracks are assumed as a result of the first phase of blasting (the shock wave propagation), which is not directly simulated in this paper. The initial FDM mesh is generated on the existing cracks and the gas flow algorithm is performed for a small time span (time step). Then the calculated gas pressure is applied as the boundary conditions into the XFEM code for simulating the cracked domain. The new crack lengths and the crack opening displacements (COD) are computed and exported to the gas flow algorithm for the next step of calculation.

A criterion is also required for crack propagation. The stress intensity factor (SIF) is calculated and compared with the critical value in each step. There are several methods for numerical evaluation of SIF, but due to the assumption of linear elasticity in this study, the computationally inexpensive displacement extrapolation method is adopted. As the problem is solved in a quasi-static condition, cracks propagate and extend to a specific value when the criterion is satisfied. In other word, a pseudo-velocity is assumed for crack propagation, and the specific value of propagation extent for each step is obtained from this velocity multiplied by the time step. The proposed algorithm is described in Fig. 5.

Fig. 5
figure 5

The flowchart for the proposed algorithm

Full size image

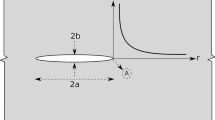
Assuming a linear elastic analysis, the SIF can be calculated using the analytical solution of displacements around the crack tip (Eq. 18). Rewriting these expressions in terms of SIF and substituting the numerically obtained displacements for several points on a radial line emanating from the crack tip, a set of data for SIF in mode I (K I) or mode II (K II) with respect to the distance r from the crack tip is generated. The SIF at the crack tip is the extrapolated value for r = 0. Figure 6 shows the procedure of this approach,

Fig. 6
figure 6

Displacement extrapolation method; the SIF at the crack tip is estimated from the best fitted line on the sampling points

Full size image
$$\begin{aligned} 4G\sqrt {\frac{2\pi }{r}} \left\{ \begin{aligned} u \hfill \\ v \hfill \\ \end{aligned} \right\} = & \;K_{\text{I}} \left\{ \begin{aligned} (2k - 1)\cos \frac{\theta }{2} - \cos \frac{3\theta }{2} \hfill \\ (2k + 1)\sin \frac{\theta }{2} + \sin \frac{3\theta }{2} \hfill \\ \end{aligned} \right\}, \\ 4G\sqrt {\frac{2\pi }{r}} \left\{ \begin{aligned} u \hfill \\ v \hfill \\ \end{aligned} \right\} = & \;K_{\text{II}} \left\{ \begin{aligned} - (2k + 3)\sin \frac{\theta }{2} - \sin \frac{3\theta }{2} \hfill \\ (2k - 3)\cos \frac{\theta }{2} + \cos \frac{3\theta }{2} \hfill \\ \end{aligned} \right\}. \\ \end{aligned}.$$
(18)

5 Numerical results

5.1 Validation of XFEM code

To verify the accuracy of the presented XFEM code, a classic problem with available analytical solution is simulated. A pressurized hole with two radiating cracks in an infinite plate (Fig. 7) has the following closed-form solution for the stress intensity factor,

Fig. 7
figure 7

Geometry of the hole with two radiating cracks

Full size image
$$K = \beta P\sqrt {\pi a},$$
(19)

where β is a coefficient related to the ratio of crack tip distance from the center of the hole to the hole radius. A hole with 5 cm radius and two 15 cm radiating cracks is assumed and a uniform internal pressure of 1 MPa is applied inside the hole and the cracks. β for this problem is 0.9976 (Saouma 2000), so the analytical stress intensity factor (Eq. 19) is computed, 7.91 MPa m0.5.

Due to the axial symmetry of the problem, one half of the geometry is simulated with the developed XFEM code. Figure 8 shows the generated mesh of 2200 nodes, the enriched nodes and the distribution of Gauss points around the cracks. It is noted that only 54 extra degrees of freedom are required to simulate the crack. Increasing the number of Gauss points around the crack tip can reduce the error but increases the computational time, so an optimum distribution should be obtained for each type of problem. The numerically predicted stress intensity factor for this model is 7.7 MPa m0.5 with an acceptable error of about 2.7 %.

Fig. 8
figure 8

Generated mesh and extra degrees of freedom for enrichments (left) and the distribution of Gauss points (right)

Full size image

5.2 Gas fracturing simulation

In order to investigate the capability of the proposed approach to simulate gas fracturing problems, the experimental studies conducted by the Sandia National laboratory (Nilson et al. 1985) in deep tunnels excavated in a homogenous Tuff with 10 MPa hydrostatic stress are modeled. Two of these examples are chosen for this study. One of them is a low-power fracturing, which produced only two fractures and the other one is a high energy fracturing with 6 major radiating cracks. The details of the experiments and the rock properties are presented in Tables 1 and 2.

Table 1 The details and results of the experiments (after Nilson et al. 1985)
Full size table
Table 2 Properties of the host rock (Nilson et al. 1985)
Full size table

The gas produced from the propellant burning is considered as an ideal gas, while its expansion is assumed as an adiabatic expansion. These are reasonable assumptions for high temperature gases produced by blasting (Mortazavi and Katsabanis 2001). Initial tiny cracks around the borehole are assumed to initiate the crack propagation. In addition, the rapid phase of pressure rise is ignored. In fact, the simulation starts immediately after the peak pressure is reached. The fluid pressure acts normal to the crack surface and in these particular examples, the stress state is hydrostatic; therefore, the crack propagation occurs in pure Mode I which means no change in the direction of the crack during its propagation. It should be noted that it will not be the case when the in situ stress state becomes anisotropic. In addition, there are two unknown parameters in this simulation which are determined based on calibration of the experiments: the constant of equation of state (γ) and the crack propagation velocity.

Figure 9 shows the generated model for the first experiment (D1) which contains 3000 nodes. The initial crack length is 2 cm, the time step for analyzing the solid medium is 100 μs, and the crack velocity is assumed to be 100 m/s. According to the observed cracking pattern for this experiment, the average final crack length is equal to 0.7 m, so the constant of equation of state can be calibrated. Performing a back analysis on the results, the value of 1.29 is obtained which is in the expected range of 1.2–3 for blast-induced high temperature and high density gases, as proposed by Mortazavi and Katsabanis (2001) (Fig. 10). The calibrated value for the constant of equation of state might not be exactly equal to the real value, due to so many unavoidable uncertainties in these complex problems and the simplifications and assumptions that are essential to make the simulation possible. The obtained value may cover some of them but it can generate the same overall result.

Fig. 9
figure 9

Generated mesh (left) and enriched nodes (right) for the D1 experiment

Full size image
Fig. 10
figure 10

Calibration of the constant of equation of state

Full size image

To better investigate the effects of other parameters, a sensitivity analysis is carried out on the crack propagation velocity, the initial crack length and the time step. Values for these parameters are changed in reasonable ranges and their effects on the final crack length are studied. Figure 11 clearly shows that the results for the final crack length remain practically insensitive to these numerical assumptions.

Fig. 11
figure 11

Sensitivity of the final crack length with respect to the initial crack length, crack propagation velocity, and the time step

Full size image

Despite the fact that the final solution is not sensitive to the assumption of the crack propagation velocity, its value should be set in a logical range. Nilson et al. (1985) argued that in a dynamic state, the maximum velocity for crack propagation mostly depends on the mechanical properties of the solid medium and it can be roughly estimated around 50 % of the Rayleigh wave speed in the medium. In contrast, in hydraulic or gas fracturing, the fluid-dynamic considerations control the crack propagation velocity and it depends on how fast the driving pressure can push fluid into the fracture, so the crack speed becomes slower than the dynamic mode. As the Rayleigh wave speed is slightly less than the shear wave speed which is 100 m/s (Table 2) for this rock. The assumed pseudo-crack propagation velocity should be less than 600 m/s. Figure 12 shows the effect of crack velocity and the constant of equation of state on the borehole pressure decay of the D1 experiment. It can be concluded that it is the crack propagation velocity that mainly determines the rate of pressure drop in the borehole. The crack extension velocity of 50 m/s can well be matched with the field data, which is also in agreement with the description provided by Nilson et al. (1985) that fluid-driven fracturing is slower than dynamic fracturing.

Fig. 12
figure 12

The effect of crack propagation velocity and the constant of EOS (γ) on the decay of borehole pressure

Full size image

Another important issue that should be clarified is the effect of in situ stress, as HEGF might be applied in different depths. The final results of this test with different in situ stresses (Fig. 13) reveal that this parameter has a significant non-linear effect on the final results and it should be considered in the design procedure of a successful HEGF operation.

Fig. 13
figure 13

The effect of in situ stress on the final crack length

Full size image

Additionally, to investigate the effect of mesh size on the results, the same problem is simulated by different number of nodes. The results are summarized in Table 3 which indicates that for around 3000 nodes or more, for this particular simulation, the final result will converge and become mesh insensitive. It should be noted that the mesh size can also slightly change the loading evaluated inside the crack and consequently affects to some extent the accuracy of the predicted stress intensity factor.

Table 3 Sensitivity analysis of the final crack length with respect to the mesh size
Full size table

The calibrated parameters obtained from the first experiment (D1) are now used to simulate the second experiment (GF2) because the host rock and the propellant are the same for both tests. Figure 14 shows the adopted mesh for the GF2 experiment which has 2750 nodes. The crack propagation velocity and the initial crack length are assumed to be 200 m/s and 5 cm, respectively, which may not be the real values, but the results are expected to be insensitive to them, as it was investigated in the previous simulation.

Fig. 14
figure 14

Generated mesh for the GF2 experiment (left), crack positions, and the enriched nodes (right)

Full size image

After 16 ms, the final crack length becomes 2.3 m. According to the reference description and the borehole pressure sensor results, after this time, the test sealing had broken, and the gas pressure was lost so, this time is considered as the end of the simulation. The stress states at this time are shown in Fig. 15.

Fig. 15
figure 15

Radial and tangential stresses at GF2 model after 16 ms (stress dimension is Pa)

Full size image

The observed difference between the average of final crack lengths in the numerical model (2.3 m) and the experimental test (1.7 m) can be discussed on the basis of some unavoidable sources of error. Firstly, the evaluated material properties, especially the toughness, involve some level of uncertainties. Secondly, due to the short rise time (0.5 ms), small cracks are generated around the hole which absorb a portion of the gas energy through its penetration into these small spaces. As a result, the final crack length is shortened. Generally, because of high level of uncertainties, some authors believe that a precise quantitatively prediction of such a complex problem with a conventional computational model seems very difficult and unlikely, and they may even accept a model that can predict with twofold difference for practical purposes (Nilson et al. 1985).

6 Conclusions

In this paper, a simple model was proposed and evaluated to predict the final length of gas fractures. The available equations of gas flow through a crack were implemented and solved on a 1D finite difference mesh. The novel and computationally efficient XFEM approach was used for simulation of the cracked solid. A simple fracture mechanics problem with an analytical solution was also utilized for validation of the XFEM code. Moreover, the details of XFEM integration and evaluation of the stress intensity factor were determined in such a way that with a reasonable computational effort, a sufficient accuracy could be obtained. Two experimental studies were chosen to calibrate and evaluate the model. Although the predicted results of numerical simulation could not be perfectly matched with the experimental study, the error remained in an acceptable level for practical purposes. In addition, comprehensive sensitivity analyses were performed and the influential parameters were clarified. The in situ stress was found to be a very critical factor on the final result which should be considered for HEGF designs. The final lengths of the cracks were found to be independent of the initial crack lengths. As a result, in a blasting process, the role of gas pressure on the extension of cracks remained more important than the role of the stress wave. This model can be easily improved for complicated geometries, stress states, and material properties as a general computational tool for checking the initial or finalized designs of HEGF operations. Moreover, similar engineering problems such as control blasting in mining industry can be simulated with this algorithm.