Introduction

Many organisms exhibit plastic phenotypic responses to environmental cues. Higher plants adjust stem length in response to different light regimes (Smith 1982; Dudley and Schmitt 1995, 1996; Schmitt et al. 1995) and root morphology and physiology in response to soil nutrient concentrations (Hodge 2004). Phytoplankton adjust uptake of different nutrients in response to surrounding nutrient concentrations (Klausmeier et al. 2007). Heterotrophic bacteria adjust metabolism in response to changing substrate availability (Stevenson and Cole 1999; Dekel and Alon 2005; Kalisky et al. 2007). Yeasts adjust growth form and reproductive cycles in response to differential nutrient limitation (Granek and Magwene 2010). The underlying genetic regulation of phenotypic plasticity is increasingly well-known (Scheiner 1993; Alon 2006). In this paper, we focus on the plasticity of autotrophic traits with direct biogeochemical implications, but there exists a vast literature on phenotypic plasticity in many types of organisms (see van Kleunen and Fischer 2005; Pigliucci 2005; Auld et al. 2010, for recent reviews).

Although plasticity is widespread in autotrophs, it is not ubiquitous across traits. In addition to the hare-like strategy of plastic change, some autotrophs seem to employ a tortoise-like fixed strategy of little or no change for certain traits. Some fixed (which we treat as synonymous with “canalized” or “obligate”) traits such as the development of basic organs are clearly essential for organism function, so the existence of obligate traits per se does not pose a paradox. At first glance, however, many fixed traits seem like they could lower fitness and therefore require explanation. Classic ecophysiology theory suggests that autotrophs should plastically adjust their resource allocation such that growth is co-limited by multiple essential resources (Bloom et al. 1985; Chapin et al. 1987; Field et al. 1992), but fixed traits involved with resource acquisition would prevent co-limitation in all but the most stable equilibrium environments. For example, the rate of N fixation appears to be plastic in some plant–microbe symbioses (Pearson and Vitousek 2001; Barron et al. 2010) and fixed in others (Binkley et al. 1992; Menge and Hedin 2009). In this case, fixing more N than is necessary to meet demand seems maladaptive since it is known that N fixation is expensive (Gutschick 1981; Hedin et al. 2003, 2009). The over-consumption of non-limiting nutrients observed in phytoplankton chemostats (Rhee 1978; Ahlgren 1985) is similarly perplexing, given that phytoplankton in many natural environments maintain constant N/P ratios across environmental conditions (Hall et al. 2005). Such luxury uptake may incur a cost in natural environments not realized in the laboratory, but the mechanism responsible for triggering a plastic response is unknown. Why might tortoise strategies win in some cases and hare strategies in others?

One explanation for the existence of fixed resource acquisition strategies could be called the sluggish hare: The rate of plastic change is constrained such that organisms cannot keep up with changing environments. Theoretical support for this explanation comes from modeling studies for a variety or organisms. In a model of phytoplankton with flexible stoichiometry competing for two essential resources, hare-like phytoplankton always invaded and outcompeted fixed types if plasticity could be fast enough, but if the rate of plasticity was forced below a certain threshold, a tortoise strategy outcompeted the sluggish hare (Klausmeier et al. 2007). In a model of plastic and fixed (called “facultative” and “obligate” in the paper) N fixers competing for two resources, sufficiently large time lags in plastic N fixation engendered cycles and allowed the fixed type to dominate (Menge et al. 2009a). Time lags have also been shown to limit plasticity in a more general model with environmental stochasticity (Padilla and Adolph 1996).

Another explanation for the existence of fixed types is that plasticity might carry costs apart from being mismatched to the environment. Although this mismatch is a cost that plastic types can experience—due to inaccuracy in plasticity (Moran 1992; Sultan and Spencer 2002; Wolf et al. 2005) as well as time lags—fixed types can also be mismatched to the environment, so this is not a cost of plasticity per se (Auld et al. 2010). DeWitt et al. (1998) defined true costs of plasticity as when “in a focal environment a plastic organism exhibits lower fitness while producing the same mean trait value as a fixed organism.” A recent review (Auld et al. 2010) categorized various costs proposed by others (DeWitt et al. 1998; van Kleunen and Fischer 2005) into those that are environment independent, such as the building and maintenance of infrastructure to detect and respond to the environment, and those that are environment dependent, such as the energetic costs of building new physiological structures or new proteins to change a trait. In this paper, we adopt this useful distinction, which helps extend our analogy. Compared with the tortoise, the hare has a higher basal metabolic rate to maintain the ability to move quickly (environment-independent cost) and burns more energy by accelerating faster (environment-dependent cost). A number of theoretical models have examined how plasticity costs affect fitness (Moran 1992; Padilla and Adolph 1996; Sultan and Spencer 2002; Ernande and Dieckmann 2004; Menge et al. 2009a), generally finding that plasticity costs constrain the success of plastic types in some environments. In addition to theoretical arguments, there is some empirical evidence that plasticity costs exist, although the type of cost (environment-dependent versus independent) is rarely measured. van Kleunen and Fischer (2005) found that 27 of 207 (13%) published analyses on plants revealed plasticity costs and suggested that the role of costs may be higher than indicated by the 13% due to inadequacies in many studies.

A key element missing from the above discussion is the dynamic nature of plastic responses. Rather than a discrete difference between plastic and fixed, one can envision a continuous range of plasticity in which a fixed strategy is merely one end of the continuum. Two important components of plasticity are the maximum rate of change for the plastic trait and the response function to environmental conditions. The response functions—called reaction norms in the quantitative genetics literature (Gavrilets and Scheiner 1993)—describe the sensitivity of plastic change to the environment: always changing at maximal rates unless at the optimum strategy, only at maximal rates when far away from the optimum, or something in between? Different response functions are depicted on Fig. 1, which shows the rate of change of a generic strategy, s, as a function of its distance from the optimum, s *, where s * is determined by environmental conditions. The maximum rate is controlled by the scale of the vertical axis (i.e., the parameter c), and the sensitivity is controlled by the shape of the curve. Importantly, plasticity costs likely depend on these plasticity dynamics. Environment-dependent costs should depend on the rate of change of the plastic trait (the y value in Fig. 1), which corresponds to the building of new physiological structures or proteins. Environment-independent costs, i.e., the costs of infrastructure necessary to be plastic, likely depend on the maximum rate of trait change. Organisms that can respond rapidly must have sensitive detection systems and detailed response networks, which must cost more than the rudimentary infrastructure that would be sufficient for less dynamic plasticity.

Fig. 1
figure 1

Rate of change of the strategy s in response to distance from co-limitation (s * − s), as defined in Eq. 2. The strategy s is defined as the proportion of effort devoted to acquiring nutrient 1, so it varies from 0 to 1. The value s * is the co-limitation point, which is a function of the nutrient concentrations (see Eq. 7) so it changes through time. In this figure, s * is 0.5. The parameter c is the maximum absolute rate of change, realized for s = 0, s * = 1 or vice versa for each p. The curves are Eq. 2 with different values of p: p < 1 is concave downward to the left of s *, p = 1 is linear, and p > 1 is concave upward to the left of s *

Full size image

Different plasticity response functions have been investigated in a number of theoretical contexts. For example, Gavrilets and Scheiner (1993) showed that a linear response (straight, negative-sloped line in Fig. 1) was selected for in their general quantitative genetics model, whereas a sigmoidal response to lactose concentration seems to be the most fit for Escherichia coli (Dekel and Alon 2005; Kalisky et al. 2007). However, to our knowledge, different plasticity response functions have not been investigated in biogeochemical models with essential nutrients.

In this paper, we use a mathematical model of essential nutrients cycling through autotrophs and the environment to investigate how different plasticity dynamics affect fitness in different environmental conditions. Our basic question is: Under what conditions are different plasticity dynamics—tortoise versus hare—adaptive? We study the maximum rate as well as the sensitivity of plastic change, and our model includes all the costs described above. Inherent to the population growth function (i.e., the fitness function) is the effect of each trait on fitness in a given environment, so the trait value and environmental state at a given time determine how well the organism is matched to the environment. Environment-independent costs of being plastic are included as a fitness decrease for plastic types, which is proportional to their maximum rate of plastic change (corresponding to the extent of their environmental detection infrastructure). Environment-dependent costs of being plastic are expressed as a decrease in fitness that depends on the rate of change of the trait itself.

We offer a number of conjectures based on our intuition and previous studies of plasticity. First, optimal fixed strategies will outcompete plastic strategies in environments that tend toward equilibrium because the environment-independent costs of plasticity outweigh the negligible benefits of plasticity in a stable environment. A corollary of this conjecture is that less dynamic plastic strategies outcompete faster plastic strategies in equilibrium environments. Second, as environmental fluctuations increase, there will be a threshold beyond which sufficiently rapid plastic strategies will outcompete slower plastic or fixed strategies. Third, when plastic strategies are adaptive, the most adaptive plastic strategy will depend on the benefit of approaching co-limited growth relative to the cost of rapidly changing strategy. That is, there will be no simple “faster is better” or “slower is better” rule. After describing the model, we utilize a combination of analytic and simulation methods to evaluate these conjectures.

Methods

Model description

Our model includes two essential nutrients (“1” and “2”) that cycle through autotrophs (synonymous here with “plants”) and the surrounding environment (“soil”). Autotrophs of type j (B j ) take available nutrients (A i , i = 1,2) from the soil and return unavailable nutrients (D i ) to the soil when they die or when tissues turn over. The basic structure of our model builds on previous models of two nutrients cycling through autotrophs and the environment (Tilman 1982; Legovic and Cruzado 1997; Daufresne and Hedin 2005; Klausmeier et al. 2007; Ballantyne et al. 2008; Menge et al. 2009a; Menge and Weitz 2009; Ballantyne et al. 2010). One major difference from most of these models is the inclusion of a differential equation for the proportion of uptake effort devoted to nutrient 1, although Klausmeier et al. (2007) also included such an equation. We call this proportion s j for type j, so 1 − s j is the proportion that type j allocates to taking up nutrient 2. Another major difference is the inclusion of costs associated with plasticity, which are commonly included in evolutionary models of plasticity (DeWitt et al. 1998; Auld et al. 2010) but only in one of the autotroph-nutrient models (Menge et al. 2009a). Together, the explicit consideration of dynamic nutrient uptake and costs of plasticity set this study apart from others and allow us to address our main questions. Some additional differences between these approaches are fixed autotroph stoichiometry (this model; Tilman 1982; Daufresne and Hedin 2005; Menge et al. 2009a; Menge and Weitz 2009) versus flexible autotroph stoichiometry (Legovic and Cruzado 1997; Klausmeier et al. 2007; Ballantyne et al. 2008, 2010) and the inclusion of nutrient recycling (this model; Daufresne and Hedin 2005; Ballantyne et al. 2008; Menge et al. 2009a; Menge and Weitz 2009) versus no recycling (Tilman 1982; Legovic and Cruzado 1997; Klausmeier et al. 2007).

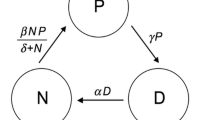
A cartoon of our model is shown in Fig. 2, and the basic equations for our model are

  • Autotroph biomass:

    $$\dot{B_j}=B_j\left( g_j\left( A_1,A_2,s_j\right) - \mu_j\left( \dot{s_j}\right)\right) $$
    (1)

  • Nutrient uptake strategy:

    $$ \dot{s_j}= \begin{cases} c_j\left| s_j^* - s_j\right|^{p_j} &s_j \le s_j^* \\ -c_j\left| s_j^*-s_j\right|^{p_j} &s_j>s_j^* \end{cases} $$
    (2)

  • Unavailable nutrients:

    $$ \dot{D}_i = \sum\limits_j\frac{B_j\mu_j\left( \dot{s_j}\right)}{\omega_{ij}} - m_iD_i - \phi_iD_i $$
    (3)

  • Available nutrients:

    $$ \dot{A}_i = I_i - k_iA_i - \sum\limits_j\frac{B_jg_j\left( A_1,A_2,s_j\right)}{\omega_{ij}} + m_iD_i $$
    (4)
    $$ \begin{array}{rll} &&{\kern-6pt}g_j\left( A_1,A_2,s_j\right) \\ &&{\kern6pt} = \text{MIN}\left( s_j\omega_{1j}\nu_{1j}A_1,(1-s_j)\omega_{2j}\nu_{2j}A_2\right) \end{array} $$
    (5)
    $$ \mu_j\left(\dot{s_j}\right) = \mu_{0j} + \psi_j c_j + \gamma_j\left|\dot{s_j}\right| $$
    (6)
    $$ s_j^* = \frac{\omega_{2j}\nu_{2j}A_2}{\omega_{1j}\nu_{1j}A_1+\omega_{2j}\nu_{2j}A_2} = \frac{1}{1+\frac{\omega_{1j}\nu_{1j}A_1}{\omega_{2j}\nu_{2j}A_2}} $$
    (7)

Plant growth (Eq. 5) follows Liebig’s law of the minimum, a standard function (Tilman 1982; Legovic and Cruzado 1997) which specifies that relative growth is limited by one nutrient except at the perfectly balanced ratio that yields co-limitation. The components of plant growth for each nutrient are the proportion of effort allocated to acquiring that nutrient (s j or 1 − s j for plant type j), the nutrient use efficiency (ω ij for nutrient i and plant type j), the nutrient uptake rate (ν ij for nutrient i and plant type j), and the concentration of the nutrient itself (A i ). Turnover/mortality (Eq. 6) includes a plasticity-independent term (μ 0j ), an environment-independent cost of plasticity proportional to the maximum rate of plastic change (ψ j c j ), and an environment-dependent cost proportional to the absolute rate of plastic change (\(\gamma_j\left|\dot{s_j}\right|\)). These distinct costs of plasticity have not yet been examined in a biogeochemical model with dynamic uptake strategies.

Fig. 2
figure 2

Cartoon diagram of the model. a The strategy (Fig. 1) is defined by the proportion of effort allocated to acquiring nutrient 1. The circles depict autotroph uptake areas, such as root surface area for higher plants or cell surface area for unicellular phytoplankton. b, c The model ecosystem consists of two nutrients cycling through autotroph biomass and the environment. Nutrients in the environment exist in forms that are unavailable and available to the autotroph. Autotroph growth and nutrient uptake depend on whichever nutrient is more limiting, which itself is affected by the strategy. Because of plasticity costs, the nutrient uptake strategy also affects autotroph turnover/mortality, which returns nutrients to the environment. Unavailable nutrients are broken down into available nutrients and can also be lost from the system. Available nutrients can be taken up or lost from the system and come from an external source as well as the decomposition of unavailable nutrients. Multiple autotroph types interact with each other solely through their effects on nutrients in the environment

Full size image

Nutrient dynamics are similar to many other models that include recycling and fixed stoichiometry. Plant turnover/mortality (\(B_j\mu_j(\dot{s_j})\)) goes into the plant-unavailable nutrient pools based on plant stoichiometry (ω ij for nutrient i and plant type j). Plant-unavailable nutrients become available at the rates m i and are lost at the rates ϕ i . There are inputs (I i ) and losses (k i A i ) from the plant-available nutrient pool. All parameters are positive.

The strategy itself for each type changes as in Fig. 1. The value \(s_j^*\) (Eq. 7) is defined as the strategy that yields co-limitation between the two resources (from setting the two parts of Eq. 5 equal and solving for s j ), and as such is a function of the current values of the resources. The parameter c j controls the maximum rate of change of the strategy. Because we are examining plastic rather than evolutionary change, c j is faster than generation times. The parameter p j controls the shape of the curve: p j  = 1 gives a linear decrease as a function of s j , 0 < p j  < 1 gives a highly sensitive function that is concave-downward when positive and concave-upward when negative, and 1 < p j  < ∞ gives a less sensitive function with the opposite concavity. In other words, decreasing p increases the sensitivity of plastic responses.

Because we are interested in comparing different nutrient strategies that vary in plasticity, we let the plasticity parameters (c j and p j ) vary but assume hereafter that the other plant parameters are the same for each plant type (ω i1 = ω i2 = ω i and similarly for ν i , μ 0, ψ, and γ). Importantly, because ω i and ν i do not vary between plant types and all competitors have equal access to the available resources, the co-limitation point s * is the same for each plant type.

Model analysis

Some of our questions pertain to environments at or near equilibrium. In these cases, we examine the invasion dynamics of different types with different maximum rates of plastic change, c, and different response functions controlled by p, by examining the sign of \(\frac{\dot{B}_{\rm inv}}{B_{\rm inv}}|_{\rm res}\), i.e., the relative growth rate (RGR; which in such models is akin to fitness) of the invading type in the equilibrium environment of the resident. This technique from adaptive dynamics (Geritz et al. 1998) assumes that the invader is at a sufficiently low density that it does not affect the environment, that the strategy of interest is constant on the timescale of the model, and that successful invaders displace resident types and come to equilibrium before new invaders appear.

Equilibrium dynamics tell only part of the story, however, given that biogeochemical systems are slow to equilibrate (Walker and Syers 1976; Vitousek 2004; Menge et al. 2009b) and the benefits of plasticity are only expected to appear in non-equilibrium environments. Therefore, we use analytical and numerical techniques to examine non-equilibrium dynamics in addition to our equilibrium analyses. First, we attempt to gain analytical insight into the dynamics of the benefits and costs of plasticity following a perturbation. Nutrient pulses and periodic forcing from seasonal or diurnal cycles are sources of environmental fluctuations in biogeochemical systems, so examining the benefits and costs of plasticity following such perturbations or during such cycles is a useful way to begin to understand plasticity dynamics in different fluctuation regimes. We initially look at the effect of plasticity on the autotroph’s RGR following a perturbation. For example, the effect of c on the integrated benefits and costs of plasticity following a perturbation is given by

$$ \frac{\partial{}}{\partial{c}}\int_0^T g(s,A_1,A_2) - \mu(\dot{s}) {\rm d}t $$
(8)

If Eq. 8 is positive, types with higher c—more hare-like strategies—would have higher net benefits and vice versa. The time period of integration T is the relevant period over which benefits and costs are calculated. We interpret this as a crude approximation of the average perturbation interval of the environment, since the next perturbation would begin the integration with a new set of starting conditions.

Fully analyzing Eq. 8 is likely impossible due to the multidimensionality and nonlinearity of the system, but taking advantage of the natural timescale separation inherent in biogeochemical systems (Vitousek 2004; Menge et al. 2009b) allows some progress to be made. For example, in terrestrial ecosystems, the timescale over which plant-available nutrients equilibrate (hours to days, controlled primarily by plant uptake) is typically much faster than the timescale of plants themselves (years to centuries, controlled by mortality), which in turn is faster than plant-unavailable nutrients (centuries to millennia, controlled by the plant-unavailable nutrient loss rate; Menge et al. 2009b). Because we are examining plastic change, i.e., change within the lifespan of a single organism, the dynamics of s are also faster than plants and plant-unavailable nutrients except in cases tending toward fixed strategies. If we confine our analysis to the case where the rate of plastic change is substantially faster than plant-available nutrients (minutes to hours), some progress is possible.

The above analysis does not yield tractable results in many cases and makes assumptions that might not hold in other cases. Moreover, scaling up the short-term analysis to long-term perturbation or fluctuation dynamics is tenuous. Therefore, we also simulate the system numerically with periodic forcing using Matlab’s ode45 function. This allows us to compare different strategies that exist at any starting populations in the same ecosystem and to relax all assumptions about timescales, but the results are only valid for the particular parameter ranges we use. In previous work, we have parameterized models for aquatic (Ballantyne et al. 2008; Menge and Weitz 2009; Ballantyne et al. 2010) or terrestrial (Ballantyne et al. 2008; Menge et al. 2009a, b) ecosystems, but here we use a generalized set of parameters (Table 1) for heuristic purposes. To force fluctuations in the simulations, we allow nutrient inputs to vary periodically (as sines and cosines) through time, with the two nutrients fluctuating out of phase. Because nutrient inputs come from different sources, particularly in terrestrial ecosystems (N primarily from biological N fixation and atmospheric deposition, P from rock weathering), such out-of-phase inputs are not unreasonable and have been used elsewhere (Klausmeier et al. 2007). We use different fluctuation periods for our different simulations. The particulars of each simulation are given on the figures or in figure captions. Specific questions we address via simulation are: (1) What are the competitive dynamics of different plasticity strategies under different fluctuation regimes? (2) For a given fluctuation regime, what are the evolutionarily and convergence stable plasticity strategies?

Table 1 Parameter definitions, units, and values for model simulations
Full size table

Results

Equilibrium dynamics

Equilibrium solutions are in the Electronic Supplementary Materials. Here we draw attention to some notable features of the equilibrium. As can be seen from Eq. 2, the equilibrium value of s is \(\bar{s}^*\), meaning that the plant is always co-limited at equilibrium unless it has a fixed strategy (s f—where the subscript f indicates “fixed”—corresponding to c = 0). Co-limitation of the plastic strategy at equilibrium was built into the model rather than a result from it, but we felt that this was warranted given the plethora of studies showing that co-limitation at equilibrium is optimal or evolutionary and convergence stable in multiple-nutrient models (Tilman 1982; van den Berg et al. 2002; Klausmeier et al. 2007; Menge and Weitz 2009). Another feature of the equilibrium is that the parameters associated with the environment-dependent plasticity cost (γ and p) have no effect. This happens because this cost depends on the rate of change of the strategy, but by definition the strategy is not changing at equilibrium. Although we have not conducted a full stability analysis, simulations suggest that the system with a single plant type is stable when a positive internal equilibrium exists.

Optimal fixed types outcompete plastic types in equilibrium environments

Types with different values of c invade residents with different c at equilibrium when the RGR of the invader,

$$ \frac{\dot{B}_{\rm inv}}{B_{\rm inv}}|_{\rm res} = \psi\left( c_{\rm res}-c_{\rm inv}\right), $$
(9)

is positive, i.e., when the invader has a lower c. This means that fixed but co-limited types (c = 0, constant \(s_{\rm f} = \bar{s}^*\)) can invade any resident and cannot be invaded. Because both types are co-limited at equilibrium, the environment-dependent cost (the \(\gamma |\dot{s}|\) term) is null and there is no differential benefit due to better matching the environment for different c types. Hence, the environment-independent costs of plasticity (ψc) dominate in equilibrium environments, selecting for co-limited fixed types over any other type.

Suboptimal fixed types can outcompete plastic types or vice versa in equilibrium environments

The case of fixed types that are not co-limited deserves special attention. Because the plastic type is co-limited and resources 1 and 2 are arbitrarily defined, examining limitation by resource 1 suffices. A fixed strategy can invade a co-limited plastic resident when

$$ \frac{\dot{B}_{\rm f,inv}}{B_{\rm f,inv}}|_{\rm p,res} = \mu_0\left(\frac{s_{\rm f,inv}}{\bar{s}_{\rm p,res}} - 1\right) + \frac{s_{\rm f,inv}}{\bar{s}_{\rm p,res}}\psi c_{\rm p,res} > 0 $$
(10)
$$ \frac{\psi c_{\rm p,res}}{\mu_0} > \frac{\bar{s}_{\rm p,res}}{s_{\rm f,inv}} - 1 $$
(11)

Because the fixed type is limited by resource 1 and the plastic type is co-limited, \(s_{\rm f,inv} < \bar{s}_{\rm p,res}\). Therefore, if the environment-independent cost of plasticity (ψc) is small relative to the base mortality cost (μ 0), single-limited fixed types never invade co-limited plastic types.

Assuming that the plastic invader comes to co-limitation fairly rapidly in its new environment, a plastic strategy can invade a fixed resident when

$$ \frac{\psi c_{\rm p,inv}}{\mu_0} < \frac{\bar{s}_{\rm p,inv}}{s_{\rm f,res}} - 1 $$
(12)

Again, the right-hand term is always positive, but the cost of being plastic can prevent the invasion of the plastic type if it is sufficiently large relative to the distance of the fixed type from co-limitation.

Evaluating the reciprocal invasion conditions 11 and 12 together for a single fixed type (s f,inv = s f,res = s f) and a single plastic type (c p,inv = c p,res = c p) yields coexistence conditions. Algebraically,

$$\text{Coexistence: } \bar{s}_{\rm p,inv} > s_{\rm f}\left( 1 + \frac{\psi c}{\mu_0}\right) > \bar{s}_{\rm p,res} $$
(13)
$$ \text{Fixed strategy wins: } \bar{s}_{\rm p,inv}, \bar{s}_{\rm p,res} < s_{\rm f}\left( 1 + \frac{\psi c}{\mu_0}\right) $$
(14)
$$ \text{Plastic strategy wins: } \bar{s}_{\rm p,inv}, \bar{s}_{\rm p,res} > s_{\rm f}\left( 1 + \frac{\psi c}{\mu_0}\right) $$
(15)
$$ \text{Founder control: } \bar{s}_{\rm p,inv} < s_{\rm f}\left( 1 + \frac{\psi c}{\mu_0}\right) < \bar{s}_{\rm p,res} $$
(16)

Note that the \(\bar{s}_{\rm p}\) terms in conditions 11 and 12 are not the same even for a single plastic type because they are the strategies that yield co-limitation in different environments: the environment set by a co-limited type in condition 11 and the environment set by a single-limited type in condition 12. Exploration of parameter space indicates that one type always wins, but we have not proven that coexistence or founder control cannot occur.

Different response functions have no effect on competitive success in equilibrium environments

Because p has no effect on the equilibrium values, the RGR of invaders with different p types is always 0. This neutral invasion stems from the continued co-limitation of both types and the lack of an effect of p on the environment-independent costs of plasticity.

Non-equilibrium dynamics

Lower plasticity is adaptive in rapidly or slowly fluctuating environments but intermediate plasticity is adaptive in intermediately fluctuating environments

Here we examine how the benefits and costs of plasticity vary with the maximum rate of plastic change, c, assuming a linear response (p = 1). To integrate the expressions for the benefits (g(s, A 1)) and costs (\(\mu(\dot{s})\)), we first need the expression for s(t). To make the analysis tractable, we assume that the strategy changes faster than plant-available nutrients, so s * is constant. Little is known about the timescale of changing strategy, and in some situations, available nutrients might change as fast as or faster than plant strategies. However, our simulation results are similar to this analytical simplification despite nutrients changing faster than the strategy, so the insights from this simplification might be useful beyond the strict assumption of timescale separation. Assuming s * is constant, the solution of Eq. 2 is

$$ s(t) = s^* + (s(0) - s^*)e^{-ct} $$
(17)

which begins at s(0) and approaches the co-limitation value for the given {A 1, A 2}, s *, in a saturating manner. This means that limitation does not switch from one type to another, which simplifies our analysis.

Substituting Eq. 17 in Eqs. 5–6 and differentiating reveals the effects of c on the instantaneous benefits (Eq. 18) and costs (Eq. 19) of plasticity. For the case of limitation by nutrient 1, these are

$$ \frac{\partial{}}{\partial{c}}\left( g(A_1,s(t)\right) = \omega_1\nu_1A_1\left( s^*-s(0)\right) te^{-ct} $$
(18)
$$ \frac{\partial{}}{\partial{c}}\left( \mu\left(\dot{s}\right)\right) = \psi + \gamma\left( s^*-s(0)\right)\left( 1-ct\right) e^{-ct} $$
(19)

Because we have assumed limitation by nutrient 1, s * > s(0), so the instantaneous benefits (Eq. 18) and environment-independent costs (first term in Eq. 19) always increase with higher plasticity. However, although the environment-dependent costs (second term in Eq. 19) are initially higher for higher plasticity because of more rapid change, at \(t=\frac{1}{c}\) after the perturbation this flips because the more plastic type is nearer co-limitation so it changes more slowly. Instantaneous benefits and costs of plasticity are plotted as functions of the time since perturbation (t) for low ψ (Fig. 3a) and high ψ (Fig. 3b).

Fig. 3
figure 3

Benefits and costs of plasticity. Top panels show instantaneous benefits (due to being nearer co-limitation), environment-independent (E-I) costs (due to increased detection infrastructure), and environment-dependent (E-D) costs (due to more rapid changing of the strategy) of increasing plasticity as a function of time since a perturbation. Bottom panels show the integrated benefits and costs of increasing plasticity as a function of time between perturbations, i.e., integrated to a particular point on the horizontal axis in the top panel. Panels show effects of increasing c for low (a, d) and high (b, e) E-I costs and decreasing p (c, f). For the maximum rate of change, increasing plasticity is maladaptive (integrated costs exceed benefits, (d, e)) at high and low perturbation frequency but can be adaptive at intermediate perturbation frequency if E-I costs are sufficiently low (d). For the sensitivity of change, increasing plasticity is maladaptive at high perturbation frequency but adaptive at low perturbation frequency (f). These figures correspond to Eqs. 18–21, which assume that the strategy changes faster than other variables

Full size image

These results show that for small t, instantaneous costs always exceed instantaneous benefits, regardless of the parameter values. Therefore, for very short perturbation intervals, the integrated costs of increased plasticity exceed the integrated benefits, suggesting that sufficiently rapid perturbation frequencies always select for decreased plasticity. At the other end of the time gradient, because the environment-independent costs continue as the plant approaches co-limitation while the benefits and environment-dependent costs vanish, sufficiently slow perturbation frequencies also select for decreased plasticity. Can there be an intermediate perturbation frequency that yields net benefits of increasing plasticity? The integrated benefits and costs over a particular perturbation time interval T are given by

$$ \begin{array}{rll} &&{\kern-6pt} \frac{\partial{}}{\partial{c}}\left( \int_0^T s(t)\omega_1\nu_1A_1 {\rm d}t\right) \\ &&{\kern1pc} = \frac{1}{c^2}(s^*-s(0))\omega_1\nu_1A_1\left( 1-e^{-cT}\left( 1+cT\right)\right) \end{array} $$
(20)
$$ \begin{array}{rll} &&{\kern-6pt} \frac{\partial{}}{\partial{c}}\left( \int_0^T \left(\mu_0 + \psi c + \gamma c\left( s^* - s(t)\right)\right) {\rm d}t\right) \\ &&{\kern1pc} = \psi T + \gamma T( s^* - s(0))e^{-cT} \end{array} $$
(21)

Equations 20 and 21 are always positive, meaning that unlike the instantaneous case, integrated plasticity benefits and costs increase as the maximum rate of plastic change increases. The increased benefits of a faster c derive from the growth increase of a more rapid approach to co-limitation, whereas the higher costs stem from physiologically adjusting more machinery (e.g., converting N uptake receptors to P uptake receptors) and the need for greater plasticity infrastructure. As the perturbation frequency decreases (i.e., as T increases), three things happen. First, integrated benefits of higher c saturate at a positive value because all types approach co-limitation but faster types had longer periods of time nearer co-limitation. Second, integrated environment-independent costs grow linearly over time because higher infrastructure costs are ever-present. Third, integrated environment-dependent costs vanish because all types have changed the same number of receptors by the time they reach co-limitation.

The integrated benefits (Eq. 20) and costs (Eq. 21) are plotted as functions of the perturbation interval (T) for low ψ (Fig. 3d) and high ψ (Fig. 3e). From the instantaneous analysis, we determined that costs always exceeded benefits for low T and high T. The integrated results support this and also show that there can be an intermediate perturbation interval where integrated benefits of higher c exceed costs. Therefore, there can be a progression of perturbation regimes such that very rapid perturbation frequency favors lower c, intermediate perturbation frequency favors higher c, and low perturbation frequency favors lower c again. Equating Eqs. 20 and 21 and solving for T would reveal these threshold periods, but we cannot derive a closed form solution of this transcendental equation. This progression of perturbation frequency regimes does not always exist, however, because integrated costs can always exceed benefits if plasticity costs are sufficiently high (Fig. 3e).

These results rely on many simplifying assumptions such as the timescale of adjusting the strategy being faster than the timescales of available nutrients and the other variables. Simulations of the full system (Eqs. 1–7) with periodically varying input ratios of the two nutrients show that these results are robust to these assumptions and lend additional insight into the mechanisms behind the competitive hierarchy. Figure 4 shows the time course of competition between types with high c (plastic) and low c (fixed) in environments ranging from highly fluctuating (Fig. 4a, b) to stable (Fig. 4e, f). In relatively stable, equilibrium-type environments, fixed types (low c) outcompete plastic types (higher c; Fig. 4e, f) because of the environment-independent costs of being plastic. For an intermediate fluctuation period, the plastic type can win (Fig. 4c, d) because it keeps pace with the environment and the benefits of co-limitation exceed the costs of changing strategy. For a rapid fluctuation period, however, the obligate type wins again (Fig. 4a, b) because the cost of the rapid plastic change needed to keep pace with the environment is prohibitive.

Fig. 4
figure 4

Competition between different plasticity c strategies. Biomass (a, c, e) and strategy (b, d, f) of the fixed (green, s = 0.75) and plastic (blue, variable s) types are shown for a, b a highly fluctuating environment, c, d an environment with intermediate fluctuations in the nutrient input ratio, and e, f an equilibrium environment. In the rapidly fluctuating environment (a, b), the fixed type wins because the plastic type pays a cost to change rapidly. In the intermediately fluctuating environment (c, d), the plastic type wins because its ability to match the environment outweighs the plasticity costs. In the equilibrium environment (e, f), the fixed type invades and displaces the plastic type even though it is not co-limited because of the environment-independent costs of plasticity

Full size image

We also studied competition between the winning type (fixed or plastic) from Fig. 4 and a range of the opposite type (Fig. 5) by determining whether the winning type could be invaded. In highly fluctuating environments (Fig. 5a), the fixed type we chose outcompeted all plastic types we examined, whereas in the intermediately fluctuating environment (Fig. 5b), the plastic type we chose outcompeted all fixed types. In some cases, exclusion was slow (insets in Fig. 5). Similar exclusion dynamics occurred in simulations starting with equal biomasses of each type, as observed in Fig. 4. All of our simulations employ periodic forcing rather than the intermittent perturbations assumed in the analytical section, yet they both yield the same changing competitive hierarchy from low to intermediate to high fluctuations.

Fig. 5
figure 5

Competition between a range of plastic and fixed strategies. Average biomass (a) of a range of plastic types competing against the fixed type s f = 0.56 in a highly fluctuating environment and (b) of a range of fixed types competing against the plastic type c = 3, p = 1 in an intermediately fluctuating environment. Each simulation began with the resident near its stable attractor and the invader at small biomass and ran for 12,000 time steps. Biomass averages are over the last 4,000 time steps of each simulation. Insets in each panel show the temporal dynamics of the type that is excluded most slowly

Full size image

When plasticity is favored, an intermediate level of plasticity appears to be most adaptive. We examined reciprocal invasion conditions for a wide range of c types at an intermediate level of environmental fluctuation by examining how invader biomass changed over multiple fluctuation periods. Figure 6 is a pairwise invasion plot showing the success of different c types for the intermediate fluctuation period from Fig. 4. Types with an intermediate c (near 0.5 with these parameters) can invade any type (a horizontal line through c inv = 0.5 is always in the “+” region) and cannot be invaded by any type (a vertical line through c res = 0.5 is always in the “−” region), so the intermediate c is globally stable. In the parlance of adaptive dynamics, it is convergence stable (will be approached from nearby types) and evolutionarily stable (cannot be invaded by nearby types), and thus, a continuously stable strategy (CSS; Levin and Muller-Landau 2000). In addition to this globally stable intermediate c, there is an evolutionary repellor at about c = 0.07. This type cannot invade any other types and can be invaded by all other types. Low c (near zero) is also a CSS, but because low c can be invaded by the globally stable intermediate c, it is only locally stable.

Fig. 6
figure 6

Pairwise invasibility plot. The axes are the c value for the resident (horizontal) and the invader (vertical), and the regions are indicated by whether the invader invades (white region with plus sign) or not (black region with minus sign). We followed the outline of the technique in Klausmeier et al. (2007) for invasion in a model with forced fluctuations. Beginning near the stable limit cycle of the resident, we introduced invaders at small biomass with the same s. Invasion success was calculated by comparing maximum invader biomass from the first half of the simulation time to the second half. Simulation time after introducing the invader varied from four to 500 fluctuation periods. Longer periods were necessary near the transitions because some invading types initially decreased in biomass (see Electronic Supplementary Materials). Input fluctuations occurred over a period 32π. Other parameters are as in Table 1 except for μ 0 (0.03), ψ (0.006), and γ (0.02). Types with c > 1.738 for these parameters go extinct. The figure shows two locally stable points—c → 0 and intermediate c—separated by an evolutionary repellor. The intermediate c is also globally stable: It invades any type and cannot be invaded by any type

Full size image

More sensitive response functions are adaptive in slowly fluctuating environments but less sensitive response functions are adaptive in rapidly fluctuating environments

Here we examine how the benefits and costs of plasticity vary with p. The shape of the response function has no impact on the environment-independent costs, so the net benefit of changing p depends on the balance of nearing co-limitation and the environment-dependent costs of change itself. As for the c analysis, we need the dynamics of a rapid s when \(p \ne 1\), which are given by

$$ s(t) = s^* - \left(\left( s^* - s(0)\right)^{1-p} - \left( 1-p\right) ct\right)^{\frac{1}{1-p}} $$
(22)

For p > 1, the strategy monotonically approaches the asymptote s *, but slower than when p = 1. For p < 1, the strategy monotonically approaches s *, reaching s * at

$$ t_{s\rightarrow s^*} = \frac{\left(s^*-s(0)\right)^{1-p}}{c\left( 1-p\right)} $$
(23)

at which point s(t) remains at s *. Higher c, lower p, and a smaller initial distance from co-limitation decrease the time it takes to reach co-limitation. Using Eq. 22, the effects of changing p on instantaneous and integrated benefits and costs of plasticity can be calculated. The expressions are cumbersome, but graphing them reveals that instantaneous benefits increase with plasticity (decreasing p; solid line in Fig. 3c is positive). Also, instantaneous costs increase with plasticity for a period but decrease after a threshold time (when the dashed line in Fig. 3c switches sign) because more plastic types approach co-limitation faster. As with increasing c, decreasing p yields net integrated costs for sufficiently high perturbation frequencies (when the dashed line is greater than the solid line in Fig. 3f). However, unlike increasing c, decreasing p is always adaptive for sufficiently slow perturbation frequencies because there are no environment-independent costs associated with p.

Discussion

Our results reveal three distinct regions of environmental heterogeneity that select for distinct types of plasticity. For sufficiently stable environments, the most adaptive strategy is a tortoise—very low or no plasticity (low c in our model)—because the costs of being able to respond to environmental change (environment-independent costs in the parlance of Auld et al. (2010)) remain significant but plasticity benefits are negligible when the environment does not change. However, if any plasticity remains in stable environments, it should be highly sensitive (low p) over the limited range of plastic change. Such sensitivity carries no environment-independent cost, and although the benefits of such sensitivity are small, the environment-dependent cost over long time periods is zero.

For rapidly fluctuating environments, the most adaptive strategy is again a tortoise because the costs of changing strategy to keep pace with environmental change (environment-dependent costs, which derive, for example, from building new structures or synthesizing new proteins) outweigh the benefits of remaining near co-limitation. Environment-independent costs can also play a role in rapidly fluctuating environments, but the environment-dependent costs alone exceed benefits. Unlike the stable environment, rapidly fluctuating environments select for low sensitivity (high p) as well as low maximum plastic change (low c).

Klausmeier et al. (2007) found a somewhat similar result that sufficiently rapid fluctuations selected for low c, but our result differs in an important way. An inability to keep pace with the environment was the reason that plastic types were maladaptive in the Klausmeier et al. (2007)’s model as well as other models looking at time lags in plasticity (Padilla and Adolph 1996; Menge et al. 2009a). Our model reveals another mechanism that is related to the cost of changing strategy. Because of this cost, even if the plastic type is sufficiently nimble to keep pace perfectly with environmental change, the costs of doing so become prohibitive, so plastic types cannot win even if there is no limit on their maximum rate of change. The ecosystem-level effects of these two selection mechanisms—an inability to keep pace with environmental variability versus suffering reduced fitness due to the costs of rapid change—are similar in the end because they both select for low or no plasticity. However, before the selective endpoints are reached, the ecosystem-level effects vary. Types that keep pace with the environment maintain co-limitation, minimizing nutrient accumulation and loss, whereas types that cannot keep pace might yield nutrient pulses (Hedin et al. 2009; Menge et al. 2009a).

Another difference between the current model and Klausmeier et al. (2007) is the nature of autotroph stoichiometry. Flexible stoichiometry, as in Klausmeier et al. (2007), could buffer variation in nutrient supply, whereas the fixed stoichiometry of the current paper does not permit such a buffer. Explicitly incorporating the costs of luxury consumption into flexible quota models would be an interesting comparison of fixed versus flexible stoichiometry strategies.

The third region of environmental heterogeneity, an intermediate level of fluctuation, selects for a more hare-like strategy. This region does not exist if the environment-independent costs of plasticity are sufficiently high, but given the existence of many plastic types, it seems reasonable to assume that these costs are not always prohibitive. Even when plasticity is favored, however, the fastest hare does not necessarily win. The most adaptive strategy keeps pace with the environment but is not faster because an increased ability to change rapidly would carry higher environment-independent costs. In other words, within the sweet spot of environmental fluctuations where plasticity is beneficial, there is a sweet spot of plasticity that is neither too fast nor too slow.

This dominance of intermediate rates of change has been seen in other contexts such as bet-hedging, also known as stochastic phenotype switching (Cohen 1966; Slatkin 1974). In a model of clonal bacterial populations in fluctuating environments, optimal switching rates mirrored the rates of environmental fluctuations (Kussell and Leibler 2005). There are well-documented empirical examples of such strategies, such as the appearance of bet-hedging mutations in bacteria subjected to randomly fluctuating experimental conditions (Beaumont et al. 2009). In our model, the success of intermediate plasticity stems from costs of changing, whereas in the model of Kussell and Leibler (2005), the success of intermediate plasticity stems from better matching for the random switching.

Other recent results from models examining bacterial bet hedging in fluctuating environments offer interesting comparisons to the work presented here. In a model including both periodic and stochastic environmental fluctuations, Thattai and van Oudenaarden (2004) found that bacteria that cannot keep pace with environmental change have the highest net growth rates when they employ stochastic switching. Kussell and Leibler (2005) found that random switching outperformed sensory switching when the sensory cost was sufficiently high relative to environmental unpredictability. Wolf et al. (2005) examined the impact of imperfect environmental detection, finding that stochastic switching is evolutionarily stable when sensory information is unreliable. These results showing that stochastic switching can outperform slow, costly, or unreliable environmental sensing are intriguing, and examining stochastic switching would be an interesting extension to our model, which currently employs only sensory responses.

Our model focuses on autotrophic nutrient uptake and thus has direct biogeochemical and community implications. When hare strategies are favored—in intermediately fluctuating environments—co-limitation is the norm, whereas when tortoise strategies are favored—in rapidly or slowly fluctuating environments—single limitation is more likely, although tortoise strategies in perfectly stable equilibrium environments tend toward co-limitation as well (Reynolds and Pacala 1993; van den Berg et al. 2002; Klausmeier et al. 2007; Menge and Weitz 2009). Co-limitation tends to produce lower nutrient losses from ecosystems because plants are acquiring nutrients in a perfectly balanced ratio, whereas single nutrient limitation produces large nutrient losses of the non-limiting nutrient (Hedin et al. 2003, 2009) unless luxury consumption is indefinite. Although luxury consumption undoubtedly occurs, field studies (Tripler et al. 2002; Hall et al. 2005) and theoretical examination of large datasets (Ballantyne et al. 2010) suggest that it has distinct limits. The extent of nutrient losses has a number of implications for human well-being. Hydrologic nutrient losses from terrestrial ecosystems control downstream eutrophication and thus the dead zones that ravage fisheries (Rabalais et al. 2002). Gaseous nutrient losses of N in particular occur when N is not limiting (Hall and Matson 1999, 2003), and some chemical forms of these losses are strong greenhouse gasses (N2O) or play a role in ozone formation (NO x ). In addition to these biogeochemical implications, the dominance of co-limited types makes it harder to explain species coexistence (Klausmeier et al. 2007). Therefore, the environmental fluctuation regime could have large implications for basic and applied ecological issues as it does in evolutionary contexts.

The relevance of our results to real ecosystems depends in large part on parameters for which there are currently few data. In particular, the plasticity cost parameters ψ and γ and the plasticity dynamics (controlled by c and p) are little known yet play huge roles in determining whether plasticity is favored or not. We suggest that increased empirical attention to plasticity costs and benefits is necessary to better understand ecosystem functioning in noisy environments. Many extensions or further analyses of our model are also possible. The periodic fluctuations in our model make it a candidate for analysis with Floquet theory (Jordan and Smith 1999; Klausmeier 2008), which could add analytical rigor to our results. Including random fluctuations would make the model more realistic and lend credence to the need of organisms to detect the environment (rather than predicting, as could happen with purely periodic fluctuations (Kussell and Leibler 2005)). The contrasting effects of stochastic switching versus sensory switching are likely to be interesting. Predation and parasitism are known to be important in many systems and may have interesting effects on uptake plasticity and therefore ecosystem function. Analogous processes have been observed in predator–prey dynamics within grassland communities (Schmitz 2008). With the exception of our descriptions of changing strategy, the mathematical functions for most of our nutrient fluxes are basic, and more realistic functions could add subtleties to our results.