Threshold dynamics of a non-autonomous SEIRS model with quarantine and isolation

Abstract

A model for assessing the effect of periodic fluctuations on the transmission dynamics of a communicable disease, subject to quarantine (of asymptomatic cases) and isolation (of individuals with clinical symptoms of the disease), is considered. The model, which is of a form of a non-autonomous system of non-linear differential equations, is analysed qualitatively and numerically. It is shown that the disease-free solution is globally-asymptotically stable whenever the associated basic reproduction ratio of the model is less than unity, and the disease persists in the population when the reproduction ratio exceeds unity. This study shows that adding periodicity to the autonomous quarantine/isolation model developed in Safi and Gumel (Discret Contin Dyn Syst Ser B 14:209–231, 2010) does not alter the threshold dynamics of the autonomous system with respect to the elimination or persistence of the disease in the population.

Introduction

It is well known that some infectious diseases, such as measles, mumps and chickenpox, exhibit periodic fluctuations in their transmission dynamics. For instance, the city of New York recorded yearly outbreaks of chickenpox and mumps, and a biennial pattern of measles outbreaks, between 1929 and 1970 (Cooke and Kaplan 1976; London and Yorke 1973). Furthermore, contact rates may vary during a time period due to a number of factors such as environmental (weather changes; emergence of insects caused by seasonal variation) and the fact that children are in school during certain months etc. (Diekmann and Heesterbeek 2000). London and Yorke (1973) showed such variations in contact rates by studying data for mumps, chickenpox and measles. Other diseases show seasonal behavior as well (see, for instance, Bacaër (2009), Bacaër and Guernaoui (2006), Cornelius (1971), Dowell (2001), Earn et al. (2002), Hethcote and Levin (1989), London and Yorke (1973)). As noted by Cooke and Kaplan (1976), since periodic fluctuation in contact rate is crucial to a number of diseases, it is instructive and theoretically evaluate the effect of such fluctuations on the transmission dynamics of the relevant diseases in a population.

During outbreaks of a communicable disease in human populations, basic public health control measures, notably quarantine (of individuals suspected of being exposed to the disease) and isolation (of individuals with clinical symptoms of the disease) are generally implemented aimed at controlling or mitigating the disease burden (measured in terms of number of new cases, hospitalization, morbidity, mortality). Over the decades, such control measures have been successfully applied to effectively combat the spread of some emerging and re-emerging diseases such as leprosy, plague, cholera, typhus, yellow fever, smallpox, diphtheria, tuberculosis, measles, ebola, pandemic influenza and, more recently, severe acute respiratory syndrome (SARS) (Chowell et al. 2004a, b; Donnelly et al. 2003; Gumel et al. 2004; Hethcote et al. 2002; Lipsitch et al. 2003; Lloyd-Smith et al. 2003; McLeod et al. 2006; Riley et al. 2003; Wang and Ruan 2004; Webb et al. 2004). However, as noted by McLeod et al. (2006), such basic control measures are gradually refined during the course of a disease outbreak (as more data and knowledge about the epidemiology and biology of the disease become available). Thus, it is reasonable to include periodicity in disease transmission models that involve the use quarantine and isolation.

The purpose of the current study is to qualitatively assess the impact of periodicity on the transmission dynamics of communicable disease in the presence of quarantine and isolation. In particular, to determine whether or not adding periodicity to the autonomous quarantine/isolation model considered in Safi and Gumel (2010) affects the dynamics of the quarantine/isolation model with respect to the elimination and persistence of the disease. To achieve this objective, a deterministic non-autonomous system of non-linear differential equations, which takes into account the aforementioned periodicity, will be designed and analyzed.

Model formulation

The model to be considered is that for the transmission dynamics of an infectious disease, in the presence of quarantine of exposed individuals and isolation of infected individuals with clinical symptoms of the diseases (infectious and symptomatically-infected individuals are used interchangeably in this study). It is based on splitting the total population at time t, denoted by N(t), into the sub-populations of susceptible (S), exposed (infected, but not yet show clinical symptoms of the disease; E), infected with symptoms (I), quarantined (Q), hospitalized (H) and recovered (R) individuals (it is assumed that individuals in the Q class are infected but do not display clinical symptoms of the disease).

It is worth mentioning that, although (in general) the process of quarantine also involves the isolation of susceptible individuals who are suspected of being exposed to the disease (see, for instance, Feng et al. (2007), Lipsitch (2003)), the quarantine class (Q) involves only newly-infected (asymptomatic) individuals (detected either via contact tracing of symptomatic cases or random testing). That is, in this study quarantine refers to the removal of newly-infected individuals from having contact with the general population (i.e. individuals who remain susceptible at the end of the quarantine period are not counted in the Q class). The justification for this is based on the fact that, for large total population sizes (N), the quarantine of susceptible individuals is unlikely to have a significant impact on the disease dynamics (Feng et al. 2007). It is known, for instance, that the mass quarantine implemented during the SARS outbreaks in the Greater Toronto Area of Canada only resulted in the detection of very few confirmed SARS cases (Day et al. 2006).

The model is given by the following non-autonomous system of non-linear differential equations:

$$ \begin{aligned} \frac{{\hbox{d}}S}{{\hbox{d}}t}&=\Uppi+\psi R(t)-\lambda_a(t) S(t) -\mu S(t),\\ \frac{{\hbox{d}}E}{{\hbox{d}}t}&= \lambda_a(t)S(t)-[\kappa(t)+\sigma(t)+\mu]E(t),\\ \frac{{\hbox{d}}I}{{\hbox{d}}t}&=\kappa(t)E(t)-[\gamma_{1}(t)+\phi(t)+\mu+\delta_1]I(t),\\ \frac{{\hbox{d}}Q}{{\hbox{d}}t}&=\sigma(t)E(t)-[\alpha(t)+\gamma_2(t)+\mu]Q(t),\\ \frac{{\hbox{d}}H}{{\hbox{d}}t}&=\alpha(t)Q(t)+\phi(t)I(t)-[\gamma_3(t)+\mu+\delta_2]H(t),\\ \frac{{\hbox{d}}R}{{\hbox{d}}t}&=\gamma_1(t) I(t) +\gamma_2(t)Q(t)+\gamma_3(t)H(t)-(\psi+\mu )R(t), \end{aligned} $$

(1)

where λ _a (t) is the time-dependent infection rate, given by

$$ \lambda_a(t)=\beta(t)\frac{I(t)+\eta_E(t)E(t)+\eta(t)[\epsilon_1Q(t)+\epsilon_2H(t)]}{N_a(t)}, $$

(2)

and N _a (t) is the total actively-mixing population, given by

$$ N_a(t)= S(t)+E(t)+I(t)+\epsilon_1Q(t)+\epsilon_2H(t)+R(t). $$

(3)

In (2), β(t) is the effective time-dependent contact rate, the modification parameter 0 ≤ η(t) < 1 accounts for the assumed reduction of infectiousness of quarantined and hospitalized individuals in relation to the symptomatically-infected (infectious) individuals in the I class. This study assumes that exposed individuals can transmit infection (at a assumed reduced rate β(t)η _E (t), where 0 ≤ η _E (t) < 1 accounts for the reduction of transmission rate of exposed individuals in relation to individuals in the I class). It should be mentioned that many disease modeling studies that include quarantine tend to assume that quarantined individuals do not transmit infection (because individuals in quarantine are typically asymptomatic; and, for some diseases such as HIV, there is positive correlation between infectiousness and viral load). This assumption is relaxed in this study by allowing for the possibility of disease transmission by individuals in quarantine. Transmission by asymptomatically-infected individuals (such as those in the E and Q classes) occurs in the context of some diseases, such as influenza.

In (3), $\epsilon_1$ and $\epsilon_2$ (with $0\leq \epsilon_1,\epsilon_2\leq 1$) are modification parameters used to measure the efficacy of quarantine and isolation in preventing quarantined and isolated individuals from having contact with the general public (thereby not partaking in the disease transmission process). If $\epsilon_1=\epsilon_2=0,$ then quarantine and isolation are perfectly implemented (so that individuals in the quarantine and isolation classes are not part of the actively-mixing population, and do not transmit infection). This is in line with one of the six incidence function formulations (quarantine-adjusted) in Hethcote et al. (2002). Leaky quarantine and isolation is represented by the case with $0<\epsilon_1,\epsilon_2<1.$ The case $\epsilon_1=\epsilon_2=1$ represents the scenario when individuals in quarantine and isolation are equally likely to have contact with the general public than anyone else in the population. The vast majority of quarantine and isolation models published in the literature, such as those in Chowell et al. (2004), Feng (2007a, b, Gumel et al. (2004), Hethcote et al. (2002), McLeod et al. (2006), Mubayi et al. (2010), Safi and Gumel (2010), Webb et al. (2004), adopt the case with $\epsilon_1=\epsilon_2=1.$ It is worth stating that quarantine is not always administered via the healthcare system. That is, it may be administered at home, and there is no guarantee that individuals in quarantine strictly adhere to the stipulated guidelines (this may be the reason for the choice of the scenario with $\epsilon_1=\epsilon_2=1).$

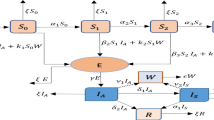
Susceptible individuals acquire infection, following effective contacts with infected individuals (in the E, Q, I and H classes), at the time-dependent rate λ _a (t). It should be mentioned that, in (2), the transmission rate for individuals in the quarantine and hospitalized classes (β(t)η(t)) is further reduced by their respective contact efficacy ($\epsilon_1$ and $\epsilon_2$). The parameter $\Uppi$ in (1) represents recruitment rate into the population and ψ is the rate of loss of infection-acquired immunity. Exposed individuals are quarantined at a rate σ(t). These individuals develop symptoms at a rate κ(t). Quarantined and symptomatically-infected (infectious) individuals are hospitalized at the rates α(t) and ϕ(t), respectively. The parameters γ₁(t), γ₂(t) and γ₃(t) represent the recovery rates for symptomatic, quarantined and hospitalized individuals, respectively, while μ is the natural death rate (so that 1/μ is the average lifespan). Finally, δ₁ and δ₂ are disease-induced death rates for infectious and hospitalized individuals, respectively. It is worth emphasizing that the model (1) monitors humans populations. Hence, all its state variables and parameters are assumed to be non-negative (and bounded) for all time t ≥ 0. A flow diagram of the model is given in Fig. 1, and the associated variables and parameters are described and estimated in Tables 1 and 2.

Fig. 1

Flow diagram of the model (1)

Table 1 Description of the variables and parameters of the model (4)

Table 2 Estimated values of the parameters of the model

The non-autonomous model (1) is an extension of the autonomous quarantine/isolation model studied in Safi and Gumel (2010), by considering some of the parameters (namely, $\beta,\eta,\kappa,\sigma,\phi,\gamma_1,\gamma_2, \gamma_3\;\hbox {and}\;\alpha$) to be periodic positive continuous functions in t with period ω > 0 (unlike in the autonomous model (Safi and Gumel 2010), where all the model parameters are assumed to be constant; it is worth stating that the model in Safi and Gumel (2010) does not account for the recovery of quarantined individuals). The non-autonomous system reduces to the autonomous system in Safi and Gumel (2010) by setting $\beta(t)=\beta,\;\eta(t)=\eta,\;\kappa(t)=\kappa,\;\phi(t)=\phi,\;\alpha(t)=\alpha,\;\gamma_1(t)=\gamma_1,\; \gamma_2(t)=0,\; \gamma_3(t)=\gamma_3$ and σ(t) = σ.

Using the definition N = S + E + I + Q + H + R, the non-autonomous system (1) can be re-written as:

$$ \begin{aligned} \frac{{\hbox{d}}S}{{\hbox{d}}t}&=\Uppi+\psi [N(t)-S(t)-E(t)-I(t)-Q(t)-H(t)]\ \\ &-\beta(t)\frac{I(t)+\eta_E(t)E(t)+\eta(t)[\epsilon_1Q(t)+\epsilon_2H(t)]}{N(t)-(1-\epsilon_1)Q(t)-(1-\epsilon_2)H(t)}S(t) -\mu S(t),\\ \frac{{\hbox{d}}E}{{\hbox{d}}t}&=\beta(t)\frac{I(t)+\eta_E(t)E(t)+\eta(t)[\epsilon_1Q(t)+\epsilon_2H(t)]}{N(t)+(\epsilon_1-1)Q(t)+(\epsilon_2-1)H(t)}S(t)-[\kappa(t)+\sigma(t)+\mu]E(t),\\ \frac{{\hbox{d}}I}{{\hbox{d}}t}&= \kappa(t) E(t)-[\gamma_{1}(t)+\phi(t)+\mu+\delta_1]I(t),\\ \frac{{\hbox{d}}Q}{{\hbox{d}}t}&=\sigma(t)E(t)-[\alpha(t)+\gamma_2(t)+\mu]Q(t),\\ \frac{{\hbox{d}}H}{{\hbox{d}}t}&=\alpha(t)Q(t)+\phi(t)I(t)-[\gamma_3(t)+\mu+\delta_2]H(t),\\ \frac{{\hbox{d}}N}{{\hbox{d}}t}&=\Uppi-\delta_1 I(t)-\delta_2 H(t)-\mu N(t). \end{aligned} $$

(4)

Following Liu et al. (2009), the parameter β(t) is defined as $\beta(t)=\beta_0\left\{ 1.1+\sin\left[\frac{\pi (t+1)}{6}\right]\right\},$ where β₀ > 0. Although seasonality (or periodicity) has not played any role in the transmission dynamics of SARS, the parameter values in Table 2, used to simulate the model (4), are consistent with those associated with the spread of SARS in a population (since the autonomous version of the model was used to study SARS dynamics) (Chowell et al. 2004a, b; Donnelly et al. 2003; Gumel et al. 2004; Lipsitch et al. 2003; Lloyd-Smith et al. 2003; McLeod et al. 2006; Riley et al. 2003; Wang and Ruan 2004; Webb et al. 2004).

Basic properties

The basic properties of the non-autonomous model (4) (which is equivalent to system (1)) will now be studied.

Lemma 1

System (4) has a unique and bounded solution with the initial value ${(S^0,E^0,I^0,Q^0,H^0,N^0)\in X=\{(S,E,I,Q,H,N)\in \mathbb{R}^{6}_{+}: N\ge S+E+I+Q+H\}.}$ Further, the compact set

$$ {{\cal {D}}}=\{(S,E,I,Q,H,N){\in X}: N\le \Uppi /\mu\} $$

is positively-invariant and attracts all positive orbits in X.

Proof Following Liu et al. (2009), let ${g\in(\mathbb{R}^{6}_{+},\mathbb{R})}$ be defined by

$$ g(S,E,I,Q,H,N)=\left\{\begin{array}{lll} 0,{(S,E,I,Q,H,N)=(0,0,0,0,0,0);} \\ \frac{S[I(t)+\eta_E(t)E(t)+\eta(t)[\epsilon_1Q(t)+\epsilon_2H(t)]}{N-(1-\epsilon)Q-(1-\epsilon_2)H}, & {\rm otherwise.} \end{array}\right. $$

Using the definition of the function g, the system (4) can also be re-written as:

$$ \begin{aligned} \frac{{\hbox{d}}S}{{\hbox{d}}t}&=\Uppi+\psi[N(t)-S(t)-E(t)-I(t)-Q(t)-H(t)]-\beta(t) g(S,E,I,Q,H,N)\\&-\mu S(t),\\ \frac{{\hbox{d}}E}{{\hbox{d}}t}&=\beta(t)g(S,E,I,Q,H,N)-[\kappa(t)+\sigma(t)+\mu]E(t),\\\frac{{\hbox{d}}I}{{\hbox{d}}t}&= \kappa(t)E(t)-[\gamma_{1}(t)+\phi(t)+\mu+\delta_1]I(t),\\\frac{{\hbox{d}}Q}{{\hbox{d}}t}&=\sigma(t)E(t)-[\alpha(t)+\mu]Q(t),\\\frac{{\hbox{d}}H}{{\hbox{d}}t}&=\alpha(t)Q(t)+\phi(t)I(t)-[\gamma_2(t)+\mu+\delta_2]H(t),\\\frac{{\hbox{d}}N}{{\hbox{d}}t}&=\Uppi-\delta_1 I(t)-\delta_2H(t)-\mu N(t). \\ \end{aligned} $$

(5)

Thus, the function g(S, E, I, Q, H, N) is continuous on ${\mathbb{R}^{6}_{+}. }$ Furthermore, it can be shown that g(S, E, I, Q, H, N) is globally-Lipschitz on ${\mathbb{R}^{6}_{+}}$ (with Lipschitz constant L = 6). Theorem 5.2.1 of Smith (1995) can then be applied to show that, for any ${(S^0,E^0,I^0,Q^0,H^0,N^0)\in\mathbb{R}^{6}_{+},}$ the system (4) has a unique local non-negative solution (S, E, I, Q, H, N), with

$$ [S(0),E(0),I(0),Q(0),H(0),N(0)]=(S^0,E^0,I^0,Q^0,H^0,N^0). $$

It follows from the last equation of the system (4) that

$$ \frac{{\hbox{d}}N}{{\hbox{d}}t}=\Uppi-\delta_1 I-\delta_2 H-\mu N\le\Uppi-\mu N, $$

from which it is clear that the associated linear differential equation,

$$ \frac{{\hbox{d}}N}{{\hbox{d}}t}=\Uppi-\mu N, $$

has a unique equilibrium $N^{*}=\Uppi/\mu,$ which is globally-asymptotically stable (GAS). Finally, it can be shown, using comparison theorem (Smith and Waltman 1995), that N(t) is bounded. Thus, the solution of the system (4) exists globally on the interval $[0,\infty).$ $\square$

Stability of disease-free equilibrium (DFE)

Local stability of DFE

Although the concept of basic reproduction number has been extensively addressed (over the decades) for autonomous models for disease transmission, such a concept has not been extended to disease transmission models with periodic coefficients until very recently (see, for instance, the notable contributions of Bacaër (2007, 2009), Bacaër and Guernaoui (2006), Bacaër and Ouifki (2007), Bacaër and Abdurahman (2008), Bacaër and Ait Dads (2011) and Zhao and co-workers (2009, 2010a, b, 2008)). This article uses the methodology in Wang and Zhao (2008) to compute the reproduction number (or ratio) associated with the non-autonomous SEIRS model with quarantine and isolation, given by (4).

The DFE of the system is given by

$$ {\mathcal{E}}_0=(S_0,{E}_0,I_0,Q_0,H_0,N_0)=\left(\frac{\Uppi}{\mu},0,0,0,0,\frac{\Uppi}{\mu}\right). $$

(6)

The equations for the rates of change of the infected components (E, I, Q, H) of the linearized version of the system (4) at the DFE $(\mathcal{E}_0)$ are given by

$$ \begin{aligned} \frac{{\hbox{d}}E}{{\hbox{d}}t}&= \beta(t)\{[I(t)+\eta_E(t)E(t)+\eta(t)[\epsilon_1Q(t)+\epsilon_2H(t)]\}-[\kappa(t)+\sigma(t)+\mu]E(t),\\ \frac{{\hbox{d}}I}{{\hbox{d}}t}&= \kappa(t) E(t)-[\gamma_1(t)+\phi(t)+\mu+\delta_1]I(t),\\ \frac{{\hbox{d}}Q}{{\hbox{d}}t}&=\sigma(t)E(t)-[\alpha(t)+\gamma_2(t)+\mu]Q(t),\\ \frac{{\hbox{d}}H}{{\hbox{d}}t}&=\alpha(t)Q(t)+\phi(t)I(t)-[\gamma_3(t)+\mu+\delta_2]H(t).\\ \end{aligned} $$

Using the notation in Wang and Zhao (2008), the next generation matrix F(t) (of the new infection terms) and the M-matrix V(t) (of the remaining transfer terms) associated with the model (4) are given, respectively, by

$$ F(t)=\left(\begin{array}{llll} \eta_E(t)\beta(t)&\beta(t) & \epsilon_1\eta(t)\beta(t) & \epsilon_2\eta(t) \beta(t) \\ 0 & 0 &0&0\\ 0 & 0 &0&0\\ 0 & 0 &0&0\\ \end{array}\right), $$

and,

$$ V(t)=\left(\begin{array}{llll} \kappa(t)+\sigma(t)+\mu & 0 &0&0\\ -\kappa(t) & \gamma_1(t)+\phi(t)+\mu+\delta_1&0&0\\ -\sigma(t)&0&\alpha(t)+\gamma_2(t)+\mu&0\\ 0&-\phi(t)&-\alpha(t)&\gamma_3(t)+\mu+\delta_2 \end{array}\right). $$

Following Wang and Zhao (2008), let $\Upphi_M$ be the monodromy matrix of the linear ω-periodic system

$$ \frac{{\hbox{d}}Z}{{\hbox{d}}t}=M(t)Z, $$

and $\rho(\Upphi_M(\omega))$ be the spectral radius of $\Upphi_M(\omega).$ Further, let

$$ Y(t,s),\;\;t\ge s, $$

be the evolution operator of the linear ω-periodic system

$$ \frac{{\hbox{d}}y}{{\hbox{d}}t}=-V(t)y. $$

In other words, for each ${s\in\mathbb{R},}$ the associated 4 × 4 matrix Y(t, s) satisfies

$$ \frac{{\hbox{d}}Y(t,s)}{{\hbox{d}}t}=-V(t)Y(t,s)\;\;\forall t\ge s,\;\;\;Y(s,s)=I. $$

It is further assumed that ϕ(s) (ω-periodic in s) is the initial distribution of infectious individuals. That is, F(s)ϕ(s) is the rate at which new infections are produced by infected individuals who were introduced into the population at time s (Wang and Zhao 2008). Since t ≥ s, it follows then that Y(t, s)F(s)ϕ(s) represents the distribution of those infected individuals who were newly-infected at time s, and remain infected at time t.

Hence, the cumulative distribution of new infections at time t, produced by all infected individuals (ϕ(s)) introduced at a prior time s = t, is given by

$$ \Uppsi(t)=\int\limits_{-\infty}^{t}{Y(t,s)F(s)\phi(s){\hbox{d}}s}=\int\limits_{0}^{\infty}{Y(t,t-a)F(t-a)\phi(t-a)da}. $$

Let ${\mathbb{C}_{\omega}}$ be the ordered Banach space of all ω-periodic functions from ${\mathbb{R}}$ to ${\mathbb{R}^{4},}$ which is equipped with maximum norm $\|.\|$ and positive cone

$$ {\mathbb{C}}_{\omega}^{+}=\{ \phi\in{\mathbb{C}}_{\omega}:\phi(t)\ge0,\;\;\forall t\in {\mathbb{R}} \}. $$

Define a linear operator ${L:\mathbb{C}_{\omega}\rightarrow\mathbb{C}_{\omega}}$ (Wang and Zhao 2008)

$$ (L\phi)(t)=\int\limits_{0}^{\infty}{Y(t,t-a)F(t-a)\phi(t-a)da}\;\;\;\forall t\in{\mathbb{R}},\phi\in{\mathbb{C}}_{\omega}. $$

The reproduction ratio $(\mathcal{R}_0)$ is then given by the spectral radius of L, denoted by ρ(L). That is, $\mathcal{R}_0=\rho(L)$ (Wang and Zhao 2008). It can be verified that system (4) satisfy the Assumptions A1–A7 in Wang and Zhao (2008) (see Appendix). Thus, using Theorem 2.2 in Wang and Zhao (2008), the following result is established.

Lemma 2

The DFE of the model (4), given by (6), is locally-asymptotically stable if $\mathcal{R}_0<1,$ and unstable if $\mathcal{R}_0>1.$

To compute the reproduction ratio $\mathcal{R}_{0},$ associated with the model (4), the following result will be used.

Theorem 1

(Wang and Zhao (2008)). Let W(t, λ) t ≥ 0 be the standard fundamental matrix of

$$ \frac{{\hbox{d}}w}{{\hbox{d}}t}=\left( -V(t)+\frac{1}{\lambda}F(t)\right)w,\;\;\; w\in {\mathbb{R}}^n, \lambda\in(0,\infty), $$

with W(0,λ) = I. The following statements are valid:

• (i) If ρ(W(ω, λ)) = 1 has a positive solution λ₀, then λ₀ is an eigenvalue of L, and hence $\mathcal{R}_0>0;$

• (ii) If $\mathcal{R}_0>0,$ then $\lambda=\mathcal{R}_0$ is the unique solution of ρ(W(ω, λ)) = 1;

• (iii) $\mathcal{R}_0=0,$ if and only if ρ(W(ω, λ)) < 1 for all $\lambda>0.$

The computation for $\mathcal{R}_0$ is then carried out via the following steps (Wang and Zhao 2008) (see also Bacaër (2007) for other particular examples based on using Floquet theory):

• (a) First of all, for a given value of λ, the matrix W(ω, λ) is numerically computed using a standard numerical integrator (such as the forward-Euler or Runge-Kutta finite-difference method (Kincaid and Cheney 1991));

• (b) Then, the spectral radius ρ(W(λ)) is calculated;

• (c) Let f(λ) = ρ(W(λ)) − 1. Then, a root finding method (such as the bisection method (Kincaid and Cheney 1991)) is used to find the zero of f.

The epidemiological implication of the result in Lemma 2 is that the disease can be eliminated from the community (when $\mathcal{R}_0<1$) if the initial sizes of the sub-populations of the model are in the basin of attraction of the DFE ($\mathcal{E}_0$). To ensure that disease elimination is independent of the initial sizes of the sub-populations of the model, it is necessary to show that the DFE is GAS if $\mathcal{R}_0<1.$ This is explored below.

Global stability of DFE

Theorem 2

The DFE of the model (4), given by (6), is GAS in $\mathcal{D}$ whenever $\mathcal{R}_0<1.$

Proof. First of all, using the fact that $S(t)\le N(t)-[(1-\epsilon_1)Q(t)+(1-\epsilon_2)H(t)]$ for all t ≥ 0 in $\mathcal{D},$ the system (4) can be re-written as

$$ \begin{aligned} \frac{{\hbox{d}}E}{{\hbox{d}}t}&\le \beta(t) [\eta_E(t)E(t)+I(t)+\eta(t) (\epsilon_1Q(t)+\epsilon_2H(t)) ]-[\kappa(t)+\mu]E(t),\\ \frac{{\hbox{d}}I}{{\hbox{d}}t}&= \kappa(t) E(t)-[\gamma_1(t)+\phi(t)+\mu+\delta_1]I(t),\\ \frac{{\hbox{d}}Q}{{\hbox{d}}t}&=\sigma(t)E(t)-[\alpha(t)+\gamma_2(t)+\mu]Q(t),\\ \frac{{\hbox{d}}H}{{\hbox{d}}t}&=\alpha(t)Q(t)+\phi(t)I(t)-[\gamma_3(t)+\mu+\delta_2]H(t). \end{aligned} $$

(7)

The equations in (7), with equality used in place of the inequality, can be re-written in terms of the matrices F(t) and V(t), as follows:

$$ \frac{{\hbox{d}}W}{{\hbox{d}}t}=[F(t)-V(t)]W(t). $$

(8)

It follows from Lemma 2.1 in Zhang and Zhao (2007) that there exists a positive ω-periodic function, $w(t)=(\underline {E}(t),\underline {I}(t),\underline {Q}(t),\underline {H}(t)),$ such that

$$ W(t)=e^{\theta t}w(t),\;\; \rm{with} \;\;\theta=\frac{1}{\omega}ln\rho[\phi_{F-V}(\omega)], $$

is a solution of the equation given by (8). However, $\mathcal{R}_0<1$ implies that ρ(ϕ _F-V (ω)) < 1 (by Theorem 2.2 in Wang and Zhao (2008)). Hence, θ is a negative constant. Thus, $W(t)\rightarrow 0$ as $t\rightarrow \infty.$ This implies that the trivial solution of system (8), given by W(t) = 0, is GAS.

For any non-negative initial solution (E(0), I(0), Q(0), H(0))^T of the system (8), there exists a sufficiently large M ^* > 0 such that

$$ (E(0),I(0),Q(0),H(0))^T\le M^*(\underline {E}(0),\underline {I}(0),\underline {Q}(0),\underline {H}(0))^T. $$

Thus, by comparison theorem (Smith and Waltman 1995), it follows that

$$ (E,I,Q,H)\le M^* W(t) \;\;\hbox {for all} \;\;t>0, $$

where, M ^* W(t) is also a solution of (8). Hence, $(E(t),I(t),Q(t),H(t))\rightarrow(0,0,0,0)$ as $t\rightarrow\infty.$ Finally, by Theorem 1.2 in Thiem (1992), it follows that $N(t)\rightarrow \Uppi/\mu$ and $S(t)\rightarrow\Uppi/\mu$ as $t\rightarrow \infty.$ In summary,

$$ \lim_{t\rightarrow\infty}{[S(t),E(t),I(t),Q(t),H(t),N(t)]}\rightarrow {\mathcal{E}}_0, \;\;\rm{whenever}\;\; {\mathcal{R}}_0<1. $$

Hence, noting that $\mathcal{E}_0$ is asymptotically-stable when $\mathcal{R}_0<1$ (Lemma 2), it follows that $\mathcal{E}_0$ is globally-attractive if $\mathcal{R}_0<1.$ $\square$

The epidemiological implication of Theorem 2 is that the use of quarantine and isolation can lead to disease elimination in the community if it brings (and keeps) the threshold quantity, $\mathcal{R}_0,$ to a value less than unity. That is, the threshold condition $\mathcal{R}_0 < 1$ is necessary and sufficient for disease elimination from the community. Figure 2 depicts the numerical results obtained by simulating the model (4) using various initial conditions for the case $\mathcal{R}_0 <1.$ It is evident from this figure that all solutions converged to the DFE, $\mathcal{E}_0$ (in line with Theorem 2). It is worth mentioning that the DFE of the corresponding autonomous model was also shown to be globally-asymptotically stable when the associated reproduction number is less than unity (see Safi and Gumel (2010)). Thus, this study shows that adding periodicity to the corresponding autonomous quarantine/isolation model given in Safi and Gumel (2010) does not alter the stability properties of the associated DFE of the autonomous model.

Fig. 2

Simulation of the model (4) showing the total number of infected individuals as a function of time for $\mathcal{R}_0<1.$ Parameter values used are as given in Table 2, with β₀ = 0.08 (so that, $\mathcal{R}_0= 0.75833351.$)

The following result can be proved for the system (4) using persistence theory (see, for instance, Liu et al. (2009), Zhang and Zhao 2007, Zhao 2003)):

Theorem 3

If the reproduction ratio $\mathcal{R}_0>1,$ then there exists τ > 0 such that any solution (S(t), E(t), Q(t), H(t), N(t)) of the system (4) with initial value $(S^0,E^0,I^0,Q^0,H^0,N^0)\in \{(S,E,I,Q,H,N)\in X : E>0,I>0,Q>0,H>0\}$ satisfies

$$ \liminf_{t\rightarrow \infty}I\ge\tau,\;\; \liminf_{t\rightarrow \infty}E\ge\tau,\;\; \displaystyle{\liminf_{t\rightarrow \infty}Q\ge\tau},\;\;\hbox {and}\;\;\liminf_{t\rightarrow \infty}H\ge\tau. $$

The epidemiological implication of Theorem 3 is that the disease will persist in the population if $\mathcal{R}_0 > 1.$ Figure 3 shows a time series plot of the total number of infected individuals for two sets of initial conditions. It should be mentioned that the solutions did not converge to zero as they appear to in Fig. 3 (see Fig. 4 for a depiction of the zoomed version of the tail end of Fig. 3). Figures 3 and 4 clearly show convergence of the solutions to the non-trivial periodic solution for the case $\mathcal{R}_0>1$ (in line with Theorem 3). Phase portraits of the solutions are also provided (Fig. 5).

Fig. 3

Simulations of the model (4) showing the total number of infected individuals as a function of time. Parameter values used are given as in Table 2, with β₀ = 1 (so that, $\mathcal{R}_0>1$)

Fig. 4

Blow up of the tail end of Fig. 3

Fig. 5

Phase portraits of the model (4). Parameter values used are as given in Table 2, with β₀ = 1.6 (so that, $\mathcal{R}_0>1$)

Figure 6 shows the fixed-points of the Poincar$\acute{\hbox {e}}$ map associated with the system (4). The fixed-points are calculated as follows:

• (i) For each value of β₀, the model is run 5000 times, and the transient solutions are removed by discarding the first 4900 iterates;

• (ii) An arbitrary point (typically the first local maximum) is picked out of the remaining 100 iterates;

• (iii) A time period of 12 days is arbitrarily selected;

• (iv) The fixed-points of the Poincar$\acute{\hbox {e}}$ map are then plotted, starting from the first local maximum.

For all the iterations carried out, the local maxima (corresponding to each period) are the same (as plotted in Fig. 6). It follows from Fig. 6 that for β₀ < β_0c (i.e. $\mathcal{R}_0<1$), the map has a unique trivial fixed-point (corresponding to the DFE, $\mathcal{E}_0$). Furthermore, for β₀ > β_0c (i.e. $\mathcal{R}_0>1$), the map has a unique non-trivial fixed-point (corresponding to non-trivial periodic solution). Hence, the system (4) undergoes a forward (transcritical) bifurcation at β₀ = β_0c (for the parameter values used in the simulations, this bifurcation occurs at the point $\beta_0=\beta_{0c}\,\backsimeq\,0.10497$). It should be recalled that for $\beta_0=\beta_{0c}=0.10497,\mathcal{R}_0\,\backsimeq\,1$ (which is in line with the result depicted in Fig. 6). A detailed bifurcation diagram of the periodic solution is given in Fig. 7 (this figure is plotted using the same approach as that for plotting Fig. 6, except that, here, the absolute minimum and maximum of the number of infectious individuals in class I, denoted by I _min and I _max, are depicted). Clearly, Fig. 7 shows that β₀ must exceed a certain critical value (β₀ > β_0c  = 0.10497) for the disease to persist in the population. In summary, Figs. 3, 4, 5, 6,7 show disease persistence (via the existence of a periodic solution) when ${{\mathcal{R}}_{0}>1.}$ It should be recalled that the corresponding autonomous model given in Safi and Gumel (2010) was shown to have a stable unique endemic equilibrium whenever its associated reproduction number is less than unity (so that the disease persists). Thus, the analyses in this article show that adding periodicity to the autonomous model in Safi and Gumel (2010) does not alter its qualitative dynamics with respect to the elimination and persistence of the disease in the population.

Fig. 6

Simulations of the model (4) showing the fixed-points of the Poincar$\acute{\hbox {e}}$ map as β₀ varies from 0 to 0.5. Parameter values used are as given in Table 2

Fig. 7

Bifurcation diagram of the non-trivial periodic solution; showing the number of infectious individuals in class I as a function of $\beta_0\in[0,0.5].$ Parameter values used are as given in Table 2

Conclusions

A deterministic non-autonomous model for assessing the impact of quarantine (of asymptomatic cases) and isolation (of symptomatic cases) on curtailing the spread of a communicable disease is presented. The model is simulated using a reasonable set of parameter values (consistent with the 2002/2003 SARS outbreaks). The study shows that the associated disease-free solution is globally-asymptotically stable whenever the reproduction threshold is less than unity. The disease persists in the population if the threshold exceeds unity. The study shows that adding periodicity to the corresponding autonomous model in Safi and Gumel (2010) does not alter its qualitative dynamics with respect to the elimination and persistence of the disease.

Appendix

Verification of Assumptions A1–A7 in Wang and Zhao (2008). The purpose here is to check whether the system (4) (or, equivalently, (1)) satisfies Conditions A1–A7 in Wang and Zhao (2008). Since the system (1) is equivalent to (4), the former system will be used in this analysis (for mathematical convenience). Using the notation in Wang and Zhao (2008), system (1) can be re-written as:

$$ \frac{{\hbox{d}}}{{\hbox{d}}t}x(t)={\mathcal{F}}(t,x(t))-{\mathcal{V}}(t,x(t))=f(t,x(t)), $$

(9)

where,

$$ x=\left(\begin{array}{l} S(t) \\ E(t) \\ I(t) \\ Q(t) \\ H(t)\\ R(t) \end{array}\right), \;\;{\mathcal{F}}=\left(\begin{array}{l} 0 \\ \frac{\beta(t)S(t)\left\{\eta_E(t)E(t)+I(t)+\eta(t) [\epsilon_1Q(t)+\epsilon_2H(t)]\right\}}{S(t)+E(t)+I(t)+\epsilon_1Q(t)+\epsilon_2H(t)+R(t) }\\ \kappa(t) E(t) \\ \sigma(t) E(t)\\ \alpha(t) Q(t)\\ 0\end{array}\right),\;\;\; $$

and,

$$ {\mathcal{V}}=\left(\begin{array}{l} -\Uppi-\psi R(t)+\frac{\beta(t)S(t)\left\{\eta_E(t)E(t)+I(t)+\eta(t) [\epsilon_1Q(t)+\epsilon_2H(t)]\right\}} {S(t)+E(t)+I(t)+\epsilon_1Q(t)+\epsilon_2H(t)+R(t)} +\mu S(t) \\ (\kappa(t)+\sigma(t)+\mu)E(t) \\ (\gamma_1+\phi+\mu+\delta_1)I(t)\\ (\alpha(t)+\gamma_2+\mu)Q(t)\\ (\gamma_3+\mu+\delta_2)H(t)\\ -\gamma_1 I(t)-\gamma_2Q(t)-\gamma_3H(t)+(\psi+\mu)R(t) \end{array}\right). $$

Furthermore, let,

$$ {\mathcal{V}}^+=\left(\begin{array}{l} \Uppi+\psi R(t)\\ 0\\ 0\\ 0\\ 0\\ \gamma_1 I(t)+\gamma_2Q(t)+\gamma_3H(t) \end{array}\right), {\mathcal{V}}^-=\left(\begin{array}{l} \frac{\beta(t)S(t)\left\{\eta_E(t)E(t)+I(t)+\eta(t) [\epsilon_1Q(t)+\epsilon_2H(t)]\right\}} {S(t)+E(t)+I(t)+\epsilon_1Q(t)+\epsilon_2H(t)+R(t)}+\mu S(t)\\ (\kappa(t)+\sigma(t)+\mu)E(t) \\ (\gamma_1+\phi+\mu+\delta_1)I(t)\\ (\alpha(t)+\gamma_2(t)+\mu)Q(t)\\ (\gamma_2+\mu+\delta_2)H(t)\\ (\psi+\mu)R(t) \end{array}\right). $$

It is easy to see that $\mathcal{V}=\mathcal{V}^--\mathcal{V}^+.$ The functions $\mathcal{F},\mathcal{V}^+$ and $\mathcal{V}^-$ satisfy the following:

• (A1) For each 1 ≤ i ≤ 6, $\mathcal{F}_i(t,x),\;\;\mathcal{V}^+_{i}(t,x)\;\;\hbox{and}\;\;\mathcal{V}^-_{i}(t,x)$ are non-negative, continuous on ${\mathbb{R}\times \mathbb{R}^6_{+}}$ and continuously differential with respect to x (since each function denotes a direct non-negative transfer of individuals).

• (A2) By assumption (it should be noted that it is assumed that some of the model parameters are ω-periodic functions), there exists a real number ω > 0, such that $\mathcal{F}_i(t,x),\;\;\mathcal{V}^+_{i}(t,x)$ $\hbox{and}\;\;\mathcal{V}^-_{i}(t,x)$ are ω-periodic in t.

• (A3) If x _i  = 0, then $\mathcal{V}^-_{i}=0$ for i = 2, 3, 4, 5.

• (A4) $\mathcal{F}_{i}=0$ for i = 1, 6.

• (A5) Define $X_s=\{ x\ge0:\; x_i=0\; \hbox {for} \;i=2,3,4,5\}.$ It is clear that if x ∈ X _s , then $\mathcal{F}_{i}=\mathcal{V}_i^{+}=0$ for i = 2, 3, 4, 5. System (1) has a disease-free solution, given by x ^* = (${\Uppi}/{\mu}$, 0, 0, 0, 0, 0). Define a 2 × 2 matrix

  $$ M(t)=\left(\frac{\partial f_i(t,x^*)}{\partial x_j}\right)_{i,j=1,6}. $$

  It follows from (9), and the definitions of the matrices ${\mathcal{F}}$ and ${\mathcal{V}},$ that

  $$ M(t)=\left[\begin{array}{ll} -\mu & \psi \\ 0 & -(\mu+\psi)\\ \end{array}\right]. $$

• (A6) Since M(t) is a diagonalizable matrix with negative eigenvalues, then

  $$ \rho(\Upphi_M(\omega))<1. $$

• (A7) Similarly,−${\mathcal{V}}$(t) is a diagonalizable matrix with negative eigenvalues. Hence,

  $$ \rho(\Upphi_{-V}(\omega))<1.$$

  Thus, the system (1) , or (equivalently) (4), satisfies Conditions A1–A7 in Wang and Zhao (2008).