Skip to main content
SpringerLink
Log in

Nonlinear stability analysis of coupled azimuthal interfaces between three rotating magnetic fluids

  • Published:
Pramana Aims and scope Submit manuscript

Abstract

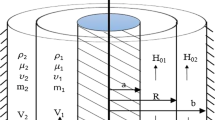
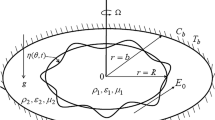
The current work deals with the nonlinear azimuthal stability analysis of coupled interfaces between three magnetic fluids. The considered system consists of three incompressible rotating magnetic fluids throughout the porous media. Additionally, the system is pervaded by a uniform azimuthal magnetic field. Therefore, for simplicity, the problem is considered in a planar configuration. The adopted nonlinear approach depends mainly on solving the linear governing equations of motion with the implication of the corresponding convenient nonlinear boundary conditions. The linear stability analysis resulted in a quadratic algebraic equation in the frequency of the surface waves. Consequently, the stability criteria are theoretically analysed. A set of diagrams is plotted to discuss the implication of various physical parameters on the stability profile. On the other hand, the nonlinear stability approach revealed two nonlinear partial differential equations of the Schrödinger type. With the aid of these equations, the stability of the interface deflections is achieved. Subsequently, the stability criteria are theoretically accomplished and numerically confirmed. Regions of stability/instability are addressed to illustrate the implication of various parameters on the stability profile.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. J M D Coey, Magnetism and magnetic material (Camdridge University Press, New York, 2009)

    Google Scholar 

  2. R E Rosensweig, Adv. Electron. Electron. Phys. 48, 103 (1979)

    Article  Google Scholar 

  3. R E Zelazo and J R Melcher, J. Fluid Mech. 39, 1 (1969)

    Article  ADS  Google Scholar 

  4. S K Malik and M Singh, Quart. Appl. Math. 47, 59 (1989)

    Article  MathSciNet  Google Scholar 

  5. A R F Elhefnawy, M A A Mahmoud and G M Khedr, Can. Appl. Math. Q 12, 323 (2004)

    MathSciNet  Google Scholar 

  6. Y O El-Dib, G M Moatimid and A A Mady, Pramana – J. Phys. 93: 82 (2019)

    Google Scholar 

  7. H H Bau, Phys. Fluids 25, 1719 (1982)

    Article  ADS  Google Scholar 

  8. K Zakaria, M A Sirwah and S A Alkharashi, Phys. Scr. 77, 025401 (2008)

    Article  ADS  Google Scholar 

  9. S A Al-Karashi and Y Gamiel, Theor. Math. Phys. 191, 580 (2017)

    Article  Google Scholar 

  10. G M Moatimid, Y O El-Dib and M H Zekry, Chin. J. Phys. 56, 2507 (2018)

    Article  Google Scholar 

  11. G M Moatimid, Y O El-Dib and M H Zekry, Pramana – J. Phys. 92: 22 (2019)

    Google Scholar 

  12. G M Moatimid, N T Eldabe and A Sayed, Heat Transfer - Asian Res. 48, 4074 (2019)

    Article  Google Scholar 

  13. N E Kochin, I A Kibel and N V Roze, Theoretical hydromechanics (Interscience, New York, 1965)

    MATH  Google Scholar 

  14. G I Taylor, Phil. Trans. R. Soc. A 223, 289 (1923)

    ADS  Google Scholar 

  15. J L Synge, Proc. R. Soc. A 167, 250 (1938)

    ADS  Google Scholar 

  16. M V Abakumov, Comput. Math. Math. Phys. 59, 584 (2019)

  17. V Ya Rudyak and E G Bord, Fluid Dyn. 53, 729 (2018)

  18. Y O El-Dib and A A Mady, J. Comput. Appl. Mech. 49, 261 (2018)

    Google Scholar 

  19. D Lu, A R Seadawy, J Wang, M Arshad and U Farooq, Pramana – J. Phys. 93: 44 (2019)

    Google Scholar 

  20. W Liu and Y Zhang, Opt. Quant. Electron. 51, 65 (2019)

  21. M Asadzadeh and C Standard, J. Math. Sci. 239, 233 (2019)

  22. A H Nayfeh, J. Appl. Mech. 43, 584 (1976)

    Article  ADS  Google Scholar 

  23. A R F Elhefnawy, ZAMM 77, 19 (1997)

    Article  ADS  MathSciNet  Google Scholar 

  24. D S Lee, Eur. Phy. J. B 28, 495 (2002)

    Article  ADS  Google Scholar 

  25. K Zakaria, Physica A 327, 221 (2003)

    Article  ADS  MathSciNet  Google Scholar 

  26. Y O El-Dib, Nonlinear Dyn. 24, 399 (2001)

    Article  MathSciNet  Google Scholar 

  27. G M Moatimid, J. Phys. A 36, 11343 (2003)

    Article  ADS  MathSciNet  Google Scholar 

  28. A RF Elhefnawy, G M Moatimid and A K Elcoot, ZAMP 55, 63 (2004)

  29. M Eghbali and B Farokhi, Pramana – J. Phys. 84, 637 (2015)

    Google Scholar 

  30. A R Seadawy and K El-Rashidy, Pramana – J. Phys. 87: 20 (2016)

    Google Scholar 

  31. J Zhang, W Hu and Y Ma, Pramana – J. Phys. 87: 93 (2016)

    Google Scholar 

  32. G M Moatimid, Y O El-Dib and M H Zekry, Arabian J. Sci. Eng. 45, 391 (2020)

    Article  Google Scholar 

  33. Y O El-Dib, G M Moatimid and A A Mady, Chin. J. Phys. 66, 285 (2020)

    Google Scholar 

  34. S Chandrasekhar, Hydrodynamic and hydromagnetic stability (Clarendon Press, Oxford, 1961)

    MATH  Google Scholar 

  35. J R Melcher, Field coupled surface waves (MIT Press, Cambridge, 1963)

    Google Scholar 

  36. Y O El-Dib and G M Moatimid, Z. Naturforsch. A 57a, 159 (2002)

  37. Y O El-Dib, J. Phys. A 30, 3585 (1997)

    Article  ADS  MathSciNet  Google Scholar 

  38. G Rüdiger, M Geller, R Hollerbach, M Schultz and F Stefani, Phys. Rep. 741, 1 (2018)

    Article  ADS  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Education, Ain Shams University, Roxy, Cairo, Egypt

    Galal M Moatimid

  2. Department of Mathematics and Computer Science, Faculty of Science, Beni-Suef University, Beni-Suef, Egypt

    Marwa H Zekry

Authors
  1. Galal M Moatimid
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Marwa H Zekry
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Marwa H Zekry.

Appendix

Appendix

The coefficients appearing in eqs (27) and (28) may be listed as follows:

$$\begin{aligned} L_{1}\equiv & {} a_{1}\frac{\partial ^{2}}{\partial t^{2}}+b_{1}\frac{\partial ^{2}}{\partial \theta ^{2}}+c_{1}\frac{\partial ^{2}}{\partial \theta \partial t}\\&+(h_{1}+ik_{1})\frac{\partial }{\partial t}+(g_{1}+if_{1})\frac{\partial }{\partial \theta }\\ a_{1}= & {} 2m^{2}R_{1}^{13}R_{2}^{4}\left( (\mu _{1}-\mu _{2})^{2}(\mu _{2}-\mu _{3})^{2}R_{1}^{4m}\right. \\&\left. +2(\mu _{1}^{2}-\mu _{2}^{2})(\mu _{2}^{2}-\mu _{3}^{2})R_{1}^{2m}R_{2}^{2m}\right. \\&\left. +(\mu _{1}+\mu _{2})^{2}(\mu _{2}+\mu _{3})^{2}R_{2}^{4m} \right) \\&\times \left( (\rho _{1}-\rho _{2})R_{1}^{4m}\right. \\&\left. -2\rho _{1}R_{1}^{2m}R_{2}^{2m}+(\rho _{1}+\rho _{2})R_{2}^{4m} \right) ,\\ b_{1}= & {} -2T_{1} m^{2}R_{1}^{10} R_{2}^{4} (R_{1}^{2m} -R_{2}^{2m} )\left( (\mu _{1} -\mu _{2} )^{2}(\mu _{2}\right. \\&\left. -\mu _{3} )^{2}R_{1}^{4m} +2(\mu _{1}^{2} -\mu _{2}^{2} )(\mu _{2}^{2} -\mu _{3}^{2} )R_{1}^{2m} R_{2}^{2m}\right. \\&\left. +(\mu _{1} +\mu _{2} )^{2}(\mu _{2} +\mu _{3} )^{2}R_{2}^{4m} \right) ,\\ c_{1}&{=}&2m^{2}R_{1}^{13}R_{2}^{4}\left( (\mu _{1}{-}\mu _{2})^{2}(\mu _{2}{-}\mu _{3})^{2}R_{1}^{4m}\right. \\&\left. {+}2(\mu _{1}^{2}{-}\mu _{2}^{2})(\mu _{2}^{2}{-}\mu _{3}^{2})R_{1}^{2m}R_{2}^{2m}\right. \\&\left. +(\mu _{1}{+}\mu _{2})^{2}(\mu _{2}{+}\mu _{3})^{2}R_{2}^{4m} \right) \\&\times \left( (\rho _{1}{\Omega }_{1}-\rho _{2}{\Omega }_{2})R_{1}^{4m}-2\rho _{1}{\Omega }_{\mathrm {1}}R_{1}^{2m}R_{2}^{2m}\right. \\&\left. +(\rho _{1}{\Omega }_{\mathrm {1}}+\rho _{2}{\Omega }_{\mathrm {2}})R_{2}^{4m} \right) {,}\\ h_{1}&{=}&2m^{2}R_{1}^{13} R_{2}^{4} (R_{1}^{2m} -R_{2}^{2m} )\\&\times \left( (\mu _{1} -\mu _{2} )(\mu _{2} -\mu _{3} )R_{1}^{2m}\right. \\&\left. +(\mu _{1} +\mu _{2} )(\mu _{2} +\mu _{3} )R_{2}^{2m} \right) ^{2}\\&\times \left( {(\rho _{1} \nu _{1} -\rho _{2} \nu _{2} )R_{1}^{2m} -(\rho _{1} \nu _{1}} \right) \\&+\rho _{2} \nu _{2} )R_{2}^{2m} \\ k_{1}= & {} 2m^{2}R_{1}^{13}R_{2}^{4}(R_{1}^{2m}-R_{2}^{2m})\left( (\mu _{1}-\mu _{2})\right. \\&\left. \times (\mu _{2}-\mu _{3})R_{1}^{2m}+(\mu _{1}+\mu _{2})(\mu _{2}+\mu _{3})R_{2}^{2m} \right) ^{2}\\&\mathbf {\times } \left( (m-2)(\rho _{1}{\Omega }_{\mathrm {1}}-\rho _{2}{\Omega }_{\mathrm {2}})R_{1}^{2m}\right. \\&\left. -((m-2)\rho _{1}{\Omega }_{\mathrm {1}}{+}(m{+}2)\rho _{2}{\Omega }_{\mathrm {2}})R_{2}^{2m} \right) ,\\ g_{1}= & {} 2m^{2}R_{1}^{13}R_{2}^{4}(R_{1}^{2m}-R_{2}^{2m})\left( (\mu _{1}-\mu _{2})\right. \\&\left. \times (\mu _{2}-\mu _{3})R_{1}^{2m}+(\mu _{1}+\mu _{2})(\mu _{2}+\mu _{3})R_{2}^{2m} \right) ^{2}\\&\times \left( (\rho _{1}\nu _{1}{\Omega }_{1}-\rho _{2}\nu _{2}{\Omega }_{2})R_{1}^{2m}\right. \\&\left. -(\rho _{1}\nu _{1}{\Omega }_{1}+\rho _{2}\nu _{2}{\Omega }_{\mathrm {2}})R_{2}^{2m} \right) \\ f_{1}&{=}&-2m^{2}R_{1}^{11} R_{2}^{4} (R_{1}^{2m} {-}R_{2}^{2m} )\left( (\mu _{1} -\mu _{2} )\right. \\&\left. \times (\mu _{2}-\mu _{3} )R_{1}^{2m}+(\mu _{1} +\mu _{2} )(\mu _{2} +\mu _{3} )R_{2}^{2m} \right) \\&\,\times \left( {mH_{0}^{2} } (R_{1}^{2m} -R_{2}^{2m} )(\mu _{1}-\mu _{2} )^{2}\right. \\&\left. \times \left( (\mu _{2} -\mu _{3} )R_{1}^{2m} +(\mu _{2} +\mu _{3} )R_{2}^{2m} \right) \right. \\&\left. -R_{1}^{2} \left( (\mu _{1} -\mu _{2} )(\mu _{2} -\mu _{3} )R_{1}^{2m}\right. \right. \\&\left. \left. +(\mu _{1} +\mu _{2} )(\mu _{2} +\mu _{3} )R_{2}^{2m} \right) \,\left( (m-2)(\rho _{1} \Omega _{1}^{2}\right. \right. \\&\left. \left. -\rho _{2} \Omega _{2}^{2} )R_{1}^{2m} -((m-2)\rho _{1} \Omega _{1}^{2}\right. \right. \\&\left. \left. +(m+2)\rho _{2} \Omega _{2}^{2} )R_{2}^{2m} \right) \right) , \end{aligned}$$
$$\begin{aligned} L_{2}\equiv & {} a_{2}\frac{\partial ^{2}}{\partial t^{2}}+b_{2}\frac{\partial ^{2}}{\partial \theta ^{2}}\\&+c_{2}\frac{\partial ^{2}}{\partial \theta \partial t}+(h_{2}+ik_{2})\frac{\partial }{\partial t}+(g_{2}+if_{2})\frac{\partial }{\partial \theta }\\&a_{2} =2m^{2}R_{1}^{12+m} R_{2}^{5+m} \left( (\mu _{1} -\mu _{2} )^{2}(\mu _{2} -\mu _{3} )^{2}R_{1}^{4m}\right. \\&\left. +2(\mu _{1}^{2} -\mu _{2}^{2} )(\mu _{2}^{2} -\mu _{3}^{2} )R_{1}^{2m} R_{2}^{2m}\right. \\&\left. +(\mu _{1} +\mu _{2} )^{2}(\mu _{2} +\mu _{3} )^{2}R_{2}^{4m} \right) \rho _{2} ,\\ b_{2}= & {} 0,\\&c_{2} =4m^{2}R_{1}^{12+m} R_{2}^{5+m} (R_{1}^{2m} -R_{2}^{2m} )\left( (\mu _{1} -\mu _{2} )^{2}(\mu _{2}\right. \\&\left. -\mu _{3} )^{2}R_{1}^{4m} +2(\mu _{1}^{2} -\mu _{2}^{2} )(\mu _{2}^{2} -\mu _{3}^{2} )R_{1}^{2m} R_{2}^{2m}\right. \\&\left. +(\mu _{1} +\mu _{2} )^{2}(\mu _{2} +\mu _{3} )^{2}R_{2}^{4m} \right) \rho _{2} \Omega _{2},\\&h_{2}=\nu _{2}c_{2}/{\Omega }_{\mathrm {2}}\\&k_{2}=mc_{2}\\&g_{2} =4m^{2}R_{1}^{12+m} R_{2}^{5+m} (R_{1}^{2m} -R_{2}^{2m} )\\&\times \left( (\mu _{1} -\mu _{2} )(\mu _{2} -\mu _{3} )R_{1}^{2m}\right. \\&\left. +(\mu _{1} +\mu _{2} )(\mu _{2} +\mu _{3} )R_{2}^{2m} \right) ^{2}\rho _{2} \nu _{2} \Omega _{2} ,\\&f_{2}=-4m^{3}R_{1}^{11+m}R_{2}^{4+m}(R_{1}^{2m}-R_{2}^{2m})\\&\times \left( (\mu _{1}-\mu _{2})(\mu _{2}-\mu _{3})R_{1}^{2m}\right. \\&\left. +(\mu _{1}+\mu _{2})(\mu _{2}+\mu _{3})R_{2}^{2m} \right) \\&\times \left( H_{0}^{2} (R_{1}^{2m}-R_{2}^{2m})(\mu _{1}-\mu _{2})(\mu _{2}-\mu _{3})\right. \\&\left. - R_{1}R_{2}\left( (\mu _{1}-\mu _{2})(\mu _{2}-\mu _{3})R_{1}^{2m}\right. \right. \\&\left. \left. +(\mu _{1}+\mu _{2})(\mu _{2}+\mu _{3})R_{2}^{2m} \right) \rho _{2}\Omega _{2}^{2} \right) , \\ L_{3}\equiv & {} a_{3}\frac{\partial ^{2}}{\partial t^{2}}+b_{3}\frac{\partial ^{2}}{\partial \theta ^{2}}\\&+c_{3}\frac{\partial ^{2}}{\partial \theta \partial t}+(h_{3}+ik_{3})\frac{\partial }{\partial t}+(g_{3}+if_{3})\frac{\partial }{\partial \theta }\\ a_{3}= & {} 4m^{2}R_{1}^{5+m} R_{2}^{12+m} (R_{1}^{2m} -R_{2}^{2m} )\left( (\mu _{1} -\mu _{2} )^{2}(\mu _{2}\right. \\&\left. -\mu _{3} )^{2}R_{1}^{4m} +2(\mu _{1}^{2} -\mu _{2}^{2} )(\mu _{2}^{2} -\mu _{3}^{2} )R_{1}^{2m} R_{2}^{2m}\right. \\&\left. +(\mu _{1} +\mu _{2} )^{2}(\mu _{2} +\mu _{3} )^{2}R_{2}^{4m} \right) \rho _{2} ,\\ b_{3}= & {} 0,\\ c_{3}= & {} 4m^{2}R_{1}^{5+m} R_{2}^{12+m} (R_{1}^{2m} -R_{2}^{2m} )\left( (\mu _{1} -\mu _{2} )^{2}(\mu _{2}\right. \\&\left. -\mu _{3} )^{2}R_{1}^{4m} +2(\mu _{1}^{2} -\mu _{2}^{2} )(\mu _{2}^{2} -\mu _{3}^{2} )R_{1}^{2m} R_{2}^{2m}\right. \\&\left. +(\mu _{1} +\mu _{2} )^{2}(\mu _{2} +\mu _{3} )^{2}R_{2}^{4m} \right) \rho _{2} \Omega _{2},\\ h_{3}= & {} 4m^{2}R_{1}^{5+m}R_{2}^{12+m}(R_{1}^{2m}-R_{2}^{2m})\\&\times \left( (\mu _{1}-\mu _{2})(\mu _{2}-\mu _{3})R_{1}^{2m}\right. \\&\left. +(\mu _{1}+\mu _{2})(\mu _{2}+\mu _{3})R_{2}^{2m} \right) ^{2}\rho _{2}\nu _{2},\\ k_{3}= & {} m{\Omega }_{2}h_{3}/\nu _{2},\\ g_{3}= & {} h_{3}\Omega _{2},\\ f_{3}= & {} -4m^{3}R_{1}^{4+m}R_{2}^{11+m}(R_{1}^{2m}-R_{2}^{2m})\left( (\mu _{1}-\mu _{2})(\mu _{2}\right. \\&\left. -\mu _{3})R_{1}^{2m}+(\mu _{1}+\mu _{2})(\mu _{2}+\mu _{3})R_{2}^{2m} \right) \left( H_{0}^{2} (R_{1}^{2m}\right. \\&\left. -R_{2}^{2m})\mu _{2}(\mu _{1}-\mu _{2})(\mu _{2}-\mu _{3})\right. \\&\left. - R_{1}R_{2}\left( (\mu _{1}-\mu _{2})(\mu _{2}-\mu _{3})R_{1}^{2m}\right. \right. \\&\left. \left. +(\mu _{1}+\mu _{2})(\mu _{2}+\mu _{3})R_{2}^{2m} \right) \rho _{2}{\Omega }_{2}^{2} \right) , \end{aligned}$$
$$\begin{aligned} L_{4} \,\equiv & {} a_{4} \frac{\partial ^{2}}{\partial t^{2}}+b_{4} \frac{\partial ^{2}}{\partial \theta ^{2}}+c_{4} \frac{\partial ^{2}}{\partial \theta \,\partial t}\\&+(h_{4} +ik_{4} )\frac{\partial }{\partial t}+(g_{4} +if_{4}) \frac{\partial }{\partial \theta } \\ a_{4}= & {} 2m^{2}R_{1}^{4}R_{2}^{13}\left( (\mu _{1}-\mu _{2})^{2}(\mu _{2}-\mu _{3})^{2}R_{1}^{4m}\right. \\&\left. +2(\mu _{1}^{2}-\mu _{2}^{2})(\mu _{2}^{2}-\mu _{3}^{2})R_{1}^{2m}R_{2}^{2m}\right. \\&\left. +(\mu _{1}+\mu _{2})^{2}(\mu _{2}+\mu _{3})^{2}R_{2}^{4m} \right) \\&\times \left( (\rho _{3}-\rho _{2})R_{1}^{4m}-2\rho _{3}R_{1}^{2m}R_{2}^{2m}\right. \\&\left. +(\rho _{1}+\rho _{3})R_{2}^{4m} \right) , \\ b_{4}= & {} -2T_{2} m^{2}R_{1}^{4} R_{2}^{10} (R_{1}^{2m} -R_{2}^{2m} )\left( (\mu _{1} -\mu _{2} )^{2}(\mu _{2}\right. \\&\left. -\mu _{3} )^{2}R_{1}^{4m} +2(\mu _{1}^{2} -\mu _{2}^{2} )(\mu _{2}^{2} -\mu _{3}^{2} )R_{1}^{2m} R_{2}^{2m}\right. \\&\left. +(\mu _{1} +\mu _{2} )^{2}(\mu _{2} +\mu _{3} )^{2}R_{2}^{4m} \right) ,\\ c_{4}= & {} 2m^{2}R_{1}^{4}R_{2}^{13}\left( (\mu _{1}-\mu _{2})^{2}(\mu _{2}-\mu _{3})^{2}R_{1}^{4m}\right. \\&\left. +2(\mu _{1}^{2}-\mu _{2}^{2})(\mu _{2}^{2}-\mu _{3}^{2})R_{1}^{2m}R_{2}^{2m}\right. \\&\left. +(\mu _{1}+\mu _{2})^{2}(\mu _{2}+\mu _{3})^{2}R_{2}^{4m} \right) \\&\times \left( (\rho _{3}{\Omega }_{3}-\rho _{2}{\Omega }_{2})R_{1}^{4m}-2\rho _{3}{\Omega }_{\mathrm {3}}R_{1}^{2m}R_{2}^{2m}\right. \\&\left. +(\rho _{3}{\Omega }_{3}+\rho _{2}{\Omega }_{2})R_{2}^{4m} \right) , \end{aligned}$$
$$\begin{aligned} h_{4}= & {} 2m^{2}R_{1}^{4} R_{2}^{13} (R_{1}^{2m} -R_{2}^{2m} )\\&\times \left( (\mu _{1} -\mu _{2} )(\mu _{2} -\mu _{3} )R_{1}^{2m} +(\mu _{1}\right. \\&\left. +\mu _{2} )(\mu _{2}+\mu _{3} )R_{2}^{2m} \right) ^{2}\left( (\rho _{2} \nu _{2}\right. \\&\left. -\rho _{3}\nu _{3} )R_{1}^{2m} +(\rho _{2} \nu _{2}+\rho _{3} \nu _{3} )R_{2}^{2m}\right) ,\\ k_{4}= & {} 2m^{2}R_{1}^{4}R_{2}^{13}(R_{1}^{2m}-R_{2}^{2m})\left( (\mu _{1}-\mu _{2})(\mu _{2}\right. \\&\left. -\mu _{3})R_{1}^{2m}+(\mu _{1}+\mu _{2})(\mu _{2}+\mu _{3})R_{2}^{2m} \right) ^{2}\\&\times \left( (m+2)(\rho _{2}{\Omega }_{2}-\rho _{3}{\Omega }_{3})R_{1}^{2m}\right. \\&\left. +((m-2)\rho _{2}{\Omega }_{\mathrm {2}}+(m+2)\rho _{3}{\Omega }_{\mathrm {3}})R_{2}^{2m} \right) ,\\ g_{4}= & {} -2m^{2}R_{1}^{4}R_{2}^{11}(R_{1}^{2m}-R_{2}^{2m})\\&\times \left( (\mu _{1}-\mu _{2})(\mu _{2}-\mu _{3})R_{1}^{2m}\right. \\&\left. +(\mu _{1}+\mu _{2})(\mu _{2}+\mu _{3})R_{2}^{2m} \right) ^{2}\\&\times \left( (\rho _{2}\nu _{2}{\Omega }_{2}-\rho _{3}\nu _{3}{\Omega }_{3})R_{1}^{2m}\right. \\&\left. +(\rho _{2}\nu _{2}{\Omega }_{2}+\rho _{3}\nu _{3}{\Omega }_{3})R_{2}^{2m} \right) , \end{aligned}$$

and

$$\begin{aligned} f_{4}= & {} -2m^{2}R_{1}^{4}R_{2}^{11}(R_{1}^{2m}-R_{2}^{2m})\\&\times \left( (\mu _{1}-\mu _{2})(\mu _{2}-\mu _{3})R_{1}^{2m}\right. \\&\left. +(\mu _{1}+\mu _{2})(\mu _{2}+\mu _{3})R_{2}^{2m} \right) \\&\times \left( mH_{0}^{2} (R_{1}^{2m}-R_{2}^{2m})(\mu _{2}\right. \\&\left. -\mu _{3})^{2}\left( (\mu _{1}-\mu _{2})R_{1}^{2m}(\mu _{1}+\mu _{2})R_{2}^{2m} \right) \right. \\&\left. -R_{2}^{2}\left( (\mu _{1}-\mu _{2})(\mu _{2}-\mu _{3})R_{1}^{2m}\right. \right. \\&\left. \left. +(\mu _{1}+\mu _{2})(\mu _{2}+\mu _{3})R_{2}^{2m} \right) \right. \\&\left. \times \left( (m+2)(\rho _{2}{\Omega }_{2}^{2}-\rho _{3}{\Omega }_{\mathrm {3}}^{\mathrm {2}})R_{1}^{2m}\right. \right. \\&\left. \left. +((m-2)\rho _{2}{\Omega }_{\mathrm {2}}^{\mathrm {2}}+(m+2)\rho _{3}{\Omega }_{3}^{2})R_{2}^{2m} \right) \right) . \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Moatimid, G.M., Zekry, M.H. Nonlinear stability analysis of coupled azimuthal interfaces between three rotating magnetic fluids. Pramana - J Phys 94, 115 (2020). https://doi.org/10.1007/s12043-020-01962-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12043-020-01962-5

Keywords

PACS Nos

Search

Navigation