Skip to main content
SpringerLink
Log in

EHD azimuthal instability of two rigid-rotating columns with Marangoni effect in porous media

  • Original Paper
  • Published:
Indian Journal of Physics Aims and scope Submit manuscript

Abstract

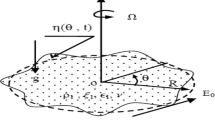
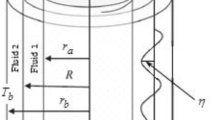
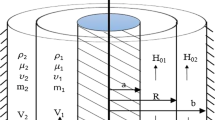
This current work is concerned with the analysis of the azimuthal instability of a circular interface between two rotating cylindrical nano-fluids under the influence of a uniform azimuthal electric field. The fluids are considered as dielectric, viscous, homogeneous, incompressible, and saturated in porous media. To simplify the mathematical manipulation, the viscous potential theory along with the normal modes analysis is employed. Motivated by the potential implication of mass and heat transfer in physics, engineering and biology, the existing configuration is intended to be a miscible one. Additionally, apart from Hsieh’s simplified formulation (J Basic Eng 94:156, 1972, Phys Fluids 21:745, 1978), the governing equations of motion include energy as well as volumetric nanoparticles fraction equations. The surface tension depends on temperature and concentration distributions. Consequently, the influence of Marangoni convection takes place. The linear stability results in an exceedingly complicated transcendental dispersion relation. Typically, this equation has no exact (closed) solution. Subsequently, numerical calculations are performed to validate the theoretical outcomes and describe the relationship between the real part of the growth rate and the radius of the cylindrical interface. The analysis reveals a set of non-dimensional numbers, all of which are restricted by the stability criteria.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. J R Melcher and G I Taylor Ann. Rev. Fluid Mech. 1 111 (1969)

    Article  ADS  Google Scholar 

  2. J R Melcher Field Coupled Surface Waves. (Cambridge: MIT Press) (1963)

    Google Scholar 

  3. J M Reynolds Phys. Fluids 8 161 (1965)

    Article  ADS  MathSciNet  Google Scholar 

  4. X Chen Sci. Bull. 48 1055 (2003)

    Article  Google Scholar 

  5. Z Ding, T N Li and H Wong Phys. Fluids 25 124103 (2013)

    Article  ADS  Google Scholar 

  6. G I Taylor and A D McEwan J. Fluid Mech. 22 1 (1965)

    Article  ADS  Google Scholar 

  7. J F Hoburg and J R Melcher J. Fluid Mech. 73 333 (1976)

    Article  ADS  Google Scholar 

  8. M F El-Sayed, G M Moatimid and N M Hafez Prog. Appl. Math. 2 35 (2011)

    Google Scholar 

  9. G M Moatimid and M H Zekry Microsyst. Technol. 26 2013 (2020)

    Article  Google Scholar 

  10. G M Moatimid and M H Zekry Pramana-J. Phys. 94 115 (2020)

    Article  ADS  Google Scholar 

  11. Y O El-Dib J. Phys. 66 285 (2020)

    MathSciNet  Google Scholar 

  12. S Chandrasekhar Proc. R. Soc. A 217 306 (1953)

    ADS  Google Scholar 

  13. J Ahmed J. Phys. 60 22 (2019)

    Google Scholar 

  14. B Rao and T J Simons Tellus 22 493 (1970)

    Article  ADS  Google Scholar 

  15. J Pedlosky Geophysical Fluid Dynamics (Springer) (1979)

  16. A V Coward and P Hall Theor. Comput. Fluid Dyn. 5 269 (1993)

    Article  Google Scholar 

  17. Y O El-Dib Fluid Dyn. Res. 18 17 (1996)

    Article  ADS  Google Scholar 

  18. G M Moatimid and Y O El-Dib Int. J. Eng. Sci. 32 1183 (1994)

    Article  Google Scholar 

  19. Y O El-Dib and G M Moatimid Physica A 205 511 (1994)

    Article  ADS  Google Scholar 

  20. Y O El-Dib and A A Mady J. Comput. Appl. Mech. 49 261 (2018)

    Google Scholar 

  21. Y O El-Dib Phys. 93 82 (2019)

    Google Scholar 

  22. I A Badruddin and A A A Al-Rashed J. Heat Mass Transf. 55 2184 (2012)

    Article  Google Scholar 

  23. V Prasad and F Kulacki Int. J. Heat Mass Transf. 27 207 (1984)

    Article  Google Scholar 

  24. N S Ahmed, I A Badruddin and J Kanesan J. Heat Mass Transf. 54 3822 (2011)

    Article  Google Scholar 

  25. A D Obembe J. Sci. Eng. 41 4719 (2016)

    Google Scholar 

  26. L Rayleigh Edinburgh J. Sci. 32 529 (1916)

    Google Scholar 

  27. S Chandrasekhar Hydrodynamic and Hydromagnetic Stability (Clarendon Press:Oxford University Press) (1961)

  28. S B N Kumar Technol. 32 629 (2020)

    Google Scholar 

  29. Q F Fu Sprays. 24 555 (2014)

    Google Scholar 

  30. Q F Fu J. Heat Mass Transfer 104 644 (2017)

    Article  Google Scholar 

  31. Q F Fu, X D Deng, B Q Jia and L J Yang AIAA J. 56 1 (2018)

    Article  Google Scholar 

  32. D Y Hsieh J. Basic. Eng. 94 156 (1972)

    Article  Google Scholar 

  33. D Y Hsieh Phys. Fluids 21 745 (1978)

    Article  ADS  Google Scholar 

  34. G M Moatimid Technol. 26 2123 (2020)

    Google Scholar 

  35. J Buongiorno J. Heat Transfer 128 240 (2006)

    Article  Google Scholar 

  36. M Sheikholeslami and A J Chamkha J. Mol. Liq. 225 750 (2017)

    Article  Google Scholar 

  37. G M Moatimid and M A Hassan J. Comput. Theor. Nanosci. 15 1495 (2018)

    Article  Google Scholar 

  38. M A Hassan J. Egyptian Math. Soc. (JOEMS) 26 58 (2018)

    Article  Google Scholar 

  39. M Madhu Power Res. 6 31 (2017)

    Google Scholar 

  40. K Bhattacharyya and G C Layek Phys. Res. Int. 2014 1 (2014)

    Article  Google Scholar 

  41. M R Krishnamurthy Sci. Technol. Int. J. 19 53 (2016)

    Google Scholar 

  42. M Sheikholeslami and A J Chamkha J. Mol. Liq. 225 750 (2016)

    Article  Google Scholar 

  43. T Funada and D D Joseph J. Fluid Mech. 445 263 (2001)

    Article  ADS  MathSciNet  Google Scholar 

  44. T Funada and D D Joseph Int. J. Multiphase Flow 28 1459 (2002)

    Article  Google Scholar 

  45. T Funada and D D Joseph J. Non- Newtonian Fluid Mech. 111 87 (2003)

    Article  Google Scholar 

  46. J P Kubitschek and P D Weidman J. Fluid Mech. 572 261 (2007)

    Article  ADS  MathSciNet  Google Scholar 

  47. S C Hirata Porous Med. 78 525 (2009)

    Article  Google Scholar 

  48. C Bringedal M. Sc. Thesis (University of Bergen) (2011)

  49. G M Moatimid and M A Hassan Int. J. Eng. Sci. 54 15 (2012)

    Article  Google Scholar 

  50. M F El-Sayed and G M Moatimid Sprays. 26 349 (2016)

    Google Scholar 

  51. M F El-Sayed and G M Moatimid J. Fluid Mech. Res. 44 93 (2017)

    Article  Google Scholar 

  52. M F E Amer and G M Moatimid At. Sprays. 29 1087 (2019)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Education, Ain Shams University, Roxy, Cairo, Egypt

    Galal M. Moatimid, Mohamed F. E. Amer & Mona A. A. Mohamed

Authors
  1. Galal M. Moatimid
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mohamed F. E. Amer
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mona A. A. Mohamed
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mona A. A. Mohamed.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

It should be noted that all the constants that obtained here are calculated in the non-dimensional form after dropping the star mark.

  • The constants that appear in Eqs. (23)–(25) are defined as:

    $$\begin{aligned} & a_{11} = i\left( {\frac{\mu }{{R^{m - 1} }}\frac{{\Delta_{1} }}{\Delta }\left( {(\omega + im\Omega_{1} ) - \rho_{0} (\omega + im\Omega_{2} )} \right) + \frac{{\rho_{0} \sigma_{0} }}{{2\mu_{1} R^{m - 1} \delta }}\frac{{\Delta_{2} }}{\Delta }} \right)\,\delta \,, \\ & a_{21} = \frac{{iR^{m + 1} }}{{\Delta \delta^{2m} }}\left( {(1 - m)\left( {(\omega + im\Omega_{1} ) - \rho_{0} (\omega + im\Omega_{2} )} \right) - \frac{{m\sigma_{0} }}{{2\mu_{1} \delta }}\left( {H(R) + \frac{{\delta E_{0}^{2} (\varepsilon_{1} - \varepsilon_{2} )}}{{\sigma_{0} }}} \right)} \right)\delta \,\,, \\ & a_{22} = - b^{2m} a_{21} , \\ \end{aligned}$$

    where \(\Delta = - m\mu \left( {(1 - m)R^{2m} + (1 + m)b^{2m} } \right) + m(1 - m)\rho_{0} \left( {R^{2m} - b^{2m} } \right)\),

    $$\Delta_{1} = (1 - m)R^{2m} + (1 + m)b^{2m} \,\,,$$

    and \(\Delta_{2} = m\left( {b^{2m} - R^{2m} } \right)\left( {H(R) + \frac{{\delta \varepsilon_{1} E_{0}^{2} (1 - \varepsilon )}}{{\sigma_{0} }}} \right)\,.\)

  • The constants that appear in Eq. (27) are defined as:

    $$b_{11} = \frac{{\Delta_{{T_{1} }} }}{{\Delta_{T} }}T_{b} \,\,,\,\,b_{21} = \frac{{\Delta_{{T_{2} }} }}{{\Delta_{T} }}T_{b} \,\,\,,\,\,{\text{and}}\,\,\,b_{22} = \frac{{\Delta_{{T_{3} }} }}{{\Delta_{T} }}T_{b} \,\,,$$

    where

    $$\begin{aligned} \Delta_{T} & = n_{1} I_{m}^{^{\prime}} (n_{1} R)\left[ {I_{m} (n_{2} R)K_{m} (n_{2} b) - I_{m} (n_{2} b)K_{m} (n_{2} R)} \right] \\ & \quad + n_{2} k_{f} I_{m} (n_{1} R)\left[ {I_{m} (n_{2} b)K_{m}^{^{\prime}} (n_{2} R) - I_{m}^{^{\prime}} (n_{2} R)K_{m} (n_{2} b)} \right]\,\,, \\ \end{aligned}$$
    $$\Delta_{{T_{1} }} = n_{2} k_{f} \left[ {I_{m} (n_{2} R)K_{m}^{^{\prime}} (n_{2} R) - I_{m}^{^{\prime}} (n_{2} R)K_{m} (n_{2} R)} \right]\,\,,$$
    $$\Delta_{{T_{2} }} = n_{2} k_{f} I_{m} (n_{1} R)K_{m}^{^{\prime}} (n_{2} R) - n_{1} I_{m}^{^{\prime}} (n_{1} R)K_{m} (n_{2} R)\,\,\,,$$
    $$\Delta_{{T_{3} }} = n_{1} I_{m}^{^{\prime}} (n_{1} R)I_{m} (n_{2} R) - n_{2} k_{f} I_{m} (n_{1} R)I_{m}^{^{\prime}} (n_{2} R)\,\,.$$

  • The constants that appear in Eq. (28) are defined as:

    $$c_{11} = \frac{{\Delta_{{C_{1} }} }}{{\Delta_{C} }}\,\,,\quad c_{21} = \frac{{\Delta_{{C_{2} }} }}{{\Delta_{C} }}\,\,,\quad {\text{and}}\quad c_{22} = \frac{{\Delta_{{C_{3} }} }}{{\Delta_{C} }}\,,$$

where

$$\begin{aligned} \Delta_{C} & = s_{1} I_{m}^{^{\prime}} (s_{1} R)\left( {I_{m} (s_{2} R)K_{m} (s_{2} b) - I_{m} (s_{2} b)K_{m} (s_{2} R)} \right) \\ & \quad + s_{2} D_{B} I_{m} (s_{1} R)\left( {I_{m} (s_{2} b)K_{m}^{^{\prime}} (s_{2} R) - I_{m}^{^{\prime}} (s_{2} R)K_{m} (s_{2} b)} \right), \\ \end{aligned}$$
$$\begin{aligned} \Delta_{{C_{1} }} & = s_{2} D_{B} \left( {I_{m} (s_{2} b)K_{m}^{^{\prime}} (s_{2} R) - I_{m}^{^{\prime}} (s_{2} R)K_{m} (s_{2} b)} \right)\lambda_{1} + \,\left( {I_{m} (s_{2} R)K_{m} (s_{2} b) - I_{m} (s_{2} b)K_{m} (s_{2} R)} \right)\lambda_{2} \\ & \quad + s_{2} D_{B} \left( {I_{m} (s_{2} R)K_{m}^{^{\prime}} (s_{2} R) - I_{m}^{^{\prime}} (s_{2} R)K_{m} (s_{2} R)} \right)\lambda_{3} , \\ \end{aligned}$$
$$\begin{aligned} \Delta_{{C_{2} }} & = - s_{1} \left( {I_{m}^{^{\prime}} (s_{1} R)K_{m} (s_{2} b)} \right)\lambda_{1} + \,\left( {I_{m} (s_{1} R)K_{m} (s_{2} b)} \right)\lambda_{2} \\ & \quad + \left( {s_{2} D_{B} I_{m} (s_{1} R)K_{m}^{^{\prime}} (s_{2} R) - s_{1} I_{m}^{^{\prime}} (s_{1} R)K_{m} (s_{2} R)} \right)\lambda_{3} , \\ \end{aligned}$$
$$\begin{aligned} \Delta_{{C_{3} }} & = s_{1} \left( {I_{m}^{^{\prime}} (s_{1} R)I_{m} (s_{2} b)} \right)\lambda_{1} - \,\left( {I_{m} (s_{1} R)I_{m} (s_{2} b)} \right)\lambda_{2} \\ & \quad + \left( {s_{1} I_{m} (s_{2} R)I_{m}^{^{\prime}} (s_{1} R) - s_{2} I_{m}^{^{\prime}} (s_{2} R)I_{m} (s_{1} R)} \right)\lambda_{3} , \\ \end{aligned}$$

where

$$\lambda_{1} = \frac{{D_{{T_{1} }} }}{{D_{{B_{1} }} }}\left( {\frac{{n_{1}^{2} }}{{n_{1}^{2} - s_{1}^{2} }}T_{1} (R) - \frac{{D_{T} }}{{D_{B} }}\frac{{n_{2}^{2} }}{{n_{2}^{2} - s_{2}^{2} }}T_{2} (R)} \right),$$
$$\lambda_{2} = \frac{{D_{{T_{1} }} }}{{D_{{B_{1} }} \delta }}\left( {\frac{{n_{1}^{2} }}{{n_{1}^{2} - s_{1}^{2} }}T_{1}^{^{\prime}} (R) - D_{T} \frac{{n_{2}^{2} }}{{n_{2}^{2} - s_{2}^{2} }}T_{2}^{^{\prime}} (R)} \right),$$

and \(\lambda_{3} = \frac{{D_{{T_{1} }} }}{{D_{{B_{1} }} }}\left( {\frac{{D_{T} }}{{D_{B} }}\frac{{n_{2}^{2} }}{{n_{2}^{2} - s_{2}^{2} }}T_{2} (b) + \frac{{C_{b} }}{{{\text{Na}}}}} \right)\,\,.\)

  • The constants that appear in Eqs. (37) and (38) are defined as follows:

    $$d_{11} = \frac{{ - iE_{0} \delta (\varepsilon_{1} - \varepsilon_{2} )(R^{2m} + b^{2m} )}}{{R^{m} \left( {R^{2m} (\varepsilon_{1} - \varepsilon_{2} ) + b^{2m} (\varepsilon_{1} + \varepsilon_{2} )} \right)}},$$
    $$d_{21} = \frac{{ - iE_{0} \delta (\varepsilon_{1} - \varepsilon_{2} )R^{m} }}{{\left( {R^{2m} (\varepsilon_{1} + \varepsilon_{2} ) + b^{2m} (\varepsilon_{1} + \varepsilon_{2} )} \right)}},$$

and

$$d_{22} = \frac{{ - iE_{0} \delta (\varepsilon_{1} - \varepsilon_{2} )R^{m} b^{2m} }}{{R^{2m} (\varepsilon_{1} - \varepsilon_{2} ) + b^{2m} (\varepsilon_{1} + \varepsilon_{2} )}}.$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Moatimid, G.M., Amer, M.F.E. & Mohamed, M.A.A. EHD azimuthal instability of two rigid-rotating columns with Marangoni effect in porous media. Indian J Phys 96, 2855–2871 (2022). https://doi.org/10.1007/s12648-021-02199-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12648-021-02199-7

Keywords

Search

Navigation