Assessment in the service of learning: challenges and opportunities or Plus ça Change, Plus c’est la même Chose

Abstract

This paper begins with a brief overview of literature indicating that, although there have been significant advances in the field’s capacity to conduct both formative and summative assessments over the past decades, those advances have not been matched by comparable impact. The bulk of the paper is devoted to a series of examples from the Mathematics Assessment Project that illustrate issues of methods, and the unrealized potential for advances.

1 Introduction and overview

The main focus of this paper concerns the distance between the current state of assessment as practised and what the field actually knows about formative and summative assessment. In Sect. 2 we offer a brief reprise of the state of the art, including some significant changes in the research landscape over the past half-century or so. The discussion indicates that, for the most part, these advances have not made their way into practice. Our claim is that practical solutions to the “implementation problem” do exist, at scale (see, e.g., Swan & Burkhardt 2014). Section 3 documents how large numbers of teachers can learn to implement formative assessment, with significant changes in their practice and significant improvements in their students’ mathematical performance. Section 4 provides examples of assessment items that address mathematical practices and processes as well as concepts and procedures—items that are parts of cost-effective, viable and robust assessments.¹ Section 5 discusses reasons that such advances have not become more prevalent. Our examples are taken from experience in US and UK but we believe the lessons learned, and not learned, are of wider international relevance.

2 Changes over the past half century

2.1 On understanding mathematical thinking, and goals for students

We begin with a description of trends in the US, then abstract to trends world-wide. Mathematics instruction in the US through the middle of the twentieth century was largely focused on computational proficiency, as indicated by this overview quotation from the 1951 Yearbook of the National Society for the Study of Education:

Criticisms of the high school program usually center around the lack of computational facility of the graduate. However, there is a more fundamental criticism…. The failure to get the right sum for a column of numbers or the failure to get the proper result in a percentage situation is merely a symptom of the real difficulty…. arithmetic is still taught as a series of rules that produce the right answer to isolated number situations (provided the student remembers the rules). (Van Engen, 1951, p. 103).

The situation changed radically after the launch of Sputnik in 1955. Nearly 20 years after the volume quoted above, Edward Begle, a major architect of the “New Math,” introduced the 1970 NSSE Yearbook, also devoted to mathematics education, with the following description of the “revolution” in school mathematics that had taken place: “No longer is computational skill the be-all and end-all of mathematics. Now there is an equal emphasis on understanding the basic concepts of mathematics and of their interrelationships, i.e., the structure of mathematics.” (Begle, 1970, p. 1).

As is well known, developments like the “New Math” in the US, “Modern Mathematics” in the UK, and associated changes in other nations were short-lived; in the US in particular the 1970s were the decade of “back to basics.” In reaction, in its Agenda for Action the US National Council of Teachers of Mathematics (1980) declared the 1980s to be the “decade of problem solving.” With underpinnings grounded in research conducted over the 1970s and 1980s (e.g., Hatfield, 1978; Schoenfeld, 1985), NCTM issued in 1989 the Curriculum and evaluation standards for school mathematics. The Standards, as they are known, declared process goals to be as important as content goals: the first four standards were “mathematics as problem solving,” “mathematics as communication,” “mathematics as reasoning,” and “mathematical connections.” Problem solving became a main theme, with subsequent volumes in the US (NCTM, 2000; Common Core State Standards Initiative, 2010) elaborating on mathematical processes and practices students should learn. There were similar development in the UK, notably the 1989 introduction of a National Curriculum that, while setting out broad aims, unfortunately specified assessment standards only in terms of detailed content criteria. The recent Proceedings of the 13th International Congress on Mathematical Education (Kaiser, 2017) shows the acceptance of these broader goals around the world—and the challenges in making them a reality in practice. Simply put, no research-based description of mathematical proficiency today would be complete without significant attention to mathematical processes and practices. Research continues to identify attributes of classrooms from which students emerge as knowledgeable, flexible and resourceful thinkers and problem solvers; see, e.g., Schoenfeld (2013, 2015).

Every nation has its own traditions and cultural context, of course; the “math wars” in the US over the 1990s (see, e.g., Schoenfeld, 2004) were clearly the product of national politics. At the same time, general trends in research regarding “what counts” were consistent internationally (see, e.g., English, 2008). More importantly, to various degrees, nations around the world were grappling with issues of problem solving. As seen in Törner, Schoenfeld, & Reiss, (2008), nations around the world were making attempts to infuse problem solving processes into their own curricula. Policy documents and the degree of national homogeneity differed widely, of course, but it is safe to say that by the first decade of the twenty-first century, mathematical practices and processes were recognized as important. The question, then, is how they were and are represented in assessment, curricula, and professional development (the latter two being related to formative assessment).

2.2 On assessment technologies

On the one hand, there is little question that over that past decades there have been significant advances in the field’s capacity to assess aspects of student understanding in summative terms—consider, for example, item response theory (Baker, 2001; deBoeck & Wilson, 2004; Lord, 1980) and increasing use of the Rasch model (Bond & Fox, 2015; Fischer & Molenaar, 1995; Rasch, 1960), or the widespread adoption of computer-adaptive testing, or CAT (see, e.g., Van der Linden & Glas, 2000; Wainer & Mislevy, 2000).

On the other hand, there are strong arguments that these advances have not served the purposes of learning well (Baird, Andrich, Hopfenbeck & Stobart, 2017; Briggs, 2017; Hopfenbeck, 2017; Kane, 2017; Schoenfeld, 2007). For one thing, almost all of the advances made concern the ability to assess students’ detailed conceptual and procedural understanding to a high level of psychometric precision; by and large, the measurement community has not devoted significant attention to assessing student’s mathematical practices or processes (problem solving, substantial reasoning, communicating, and making connections, as discussed above.) In fact, technologies such as CAT have, thus far, made it increasingly difficult to focus on such practices. In the American and British contexts, at least, the goal of efficient scoring has reified the standard content-oriented testing model, which focuses on short items that are expected to be answered in short order. For example, the UK General Certificate of Secondary Education (GCSE) in Mathematics has consisted entirely of short items that occupy the successful student for around 90 seconds.² At a more advanced level, the US Graduate Record Exam (GRE) Advanced Mathematics Test “consists of approximately 66 multiple-choice questions drawn from courses commonly offered at the undergraduate level. Testing time is 2 h and 50 min.” (Educational Testing Service, 2018). Some years ago the second author of this paper was a member of the ETS advisory committee that oversaw the construction of the exam. The committee recommended constructing a new exam, with open-ended (“essay”) questions that would be hand graded—the idea being to provide opportunities for problem solving, extended chains of reasoning, etc. Preliminary testing indicated that such an exam would be viable. At that time, however, ETS as a whole decided to move from its then-current format (“bubble-in” answers to multiple-choice problems) to computer-adapted tests. Given that hand-grading was not an option for CAT, ETS terminated the committee’s explorations of alternative testing modes employing problems that demanded the use of the practices discussed above. Examples from socially significant “high-stakes” examinations from other countries³ suggest a similar fragmentation of performance in mathematics.

As will be seen in Sect. 4, which goes into much greater detail, there are viable and robust methods for evaluating processes, that satisfy psychometricians’ concerns regarding reliability and validity. The challenge is one of political will. The challenges with regard to formative assessment differ.

2.3 On formative assessment

Before proceeding, it should be noted that the concept of formative assessment, like the concept of “pedagogical content knowledge” (Shulman, 1986, 1987) to give another example, existed long before it was named: for centuries teachers have attended to evidence of their students’ thinking and adjusted their instruction accordingly. What has changed over the past few decades are the goals of instruction, as described in Sect. 2.1. As classroom goals have become more ambitious (and less well defined!), the major challenge has been in providing a meaningful form of professional development (whether through curriculum materials, coaching, teacher learning communities, or combinations thereof) that would enable teachers to craft richer learning environments.

The naming process began with Scriven (1967) and Bloom (1969), although there was some confusion about the relationship between formative evaluation (using tests as measures of performance) and formative assessment (in which a wide range of indicators could be used). In the US, a focus on formative assessment was catalyzed by the issuance by the US National Council of Teachers of Mathematics (1989)  of the 1989 NCTM Standards. In 1991 NCTM produced the Professional Standards for Teaching Mathematics, and in 1995  (National Council of Teachers of Mathematics 1991, 1995) it followed up with Assessment Standards for School Mathematics—this latter volume having sections explicitly devoted to monitoring students’ progress and making instructional decisions. The National Science Foundation supported conferences related to what was still called “classroom assessment” (see, e.g., Bright & Joyner, 1998). Most importantly in 1998, two fundamental and catalytic papers by Paul Black and Dylan Wiliam, “Assessment and Classroom learning” (Black & Wiliam, 1998a) and “Inside the Black Box: Raising Standards Through Classroom Assessment” (Black & Wiliam, 1998b) documented the importance of the phenomenon and its potential, when well done, for enhancing student learning. This focused attention on formative assessment, which continues.

Fast-forward twenty years to 2018, and what is the state of the art? It is, shall we say, contested. A balanced and extensive overview can be found in Wiliam (2016), in particular in Chapter 4, “Formative Assessment.” There is, in the literature, general agreement that formative Assessment is not clearly defined. (This is, of course, an endemic problem: decades after Ausubel (1968) introduced the term “advanced organizers” the literature on them was inconclusive because they had been implemented in a wide variety of ways.) Dunn and Mulvenon (2009) make this argument, saying that as a result, the impact of formative assessment is challenging to evaluate. Bennett (2011) concludes likewise, saying that “the term, ‘formative assessment’, does not yet represent a well-defined set of artefacts or practices. Although research suggests that the general practices associated with formative assessment can facilitate learning, existing definitions admit such a wide variety of implementations that effects should be expected to vary widely from one implementation and student population to the next” (p. 5). Similar claims are found in Kingston & Nash (2011). But definition is only half of the challenge. The second half has to do with implementation. Teaching with an eye toward process and practices is hard—it demands knowledge and skills that extend far beyond what many teachers know. Together these two sources of “noise”, in definition and implementation, explain the wide variation in effect sizes, over a third of them negative, reported by Black and Wiliam (1998a), see also Kluger & Denisi (1996).

Using feedback in the service of such student learning is a form of the “adaptive expertise” described by Hatano & Inagaki (1986, see also Swan 2006). The question, if one cares about impact, is how to help teachers develop such adaptive expertise, at scale (see, e.g., Wiliam, 2017).

In Sects. 3, and 4 we focus on specifics, using examples from the Mathematics Assessment Project and its antecedents, drawing attention to general principles embodied in this exemplification. Our intention is to show that practical solutions to many of the challenges identified in Sect. 2 do exist.

3 Implementing formative assessment

We shall use the following characterization (Wiliam and Thompson 2007, p. 67):⁴

As noted in Sect. 2.2, a major challenge is to help large numbers of teachers develop the kind of adaptive expertise required to use formative assessment successfully. What is involved and how teachers may be enabled to acquire these skills is the theme of this section.

To use formative assessment successfully, one must be sensitive to the phenomenon of student misconceptions, and on the lookout for signs of them. A mistake ‘in the moment’ may simply go corrected, without the teacher having the time or inclination to look for the root cause of the error. Many of the issues are subtle: there is a large misconceptions literature, but few teachers are likely to have dipped into its complexities. And, of course, there are the everyday pressures of ‘covering’ content, which seem to work against time spent delving into student thinking and responding to it. As a result, though some degree of this adaptive expertise does exist au naturel, there is wide variation. A key goal is to scaffold it, so that, ultimately, this kind of adaptive expertise becomes part of the teacher’s pedagogical tool kit.

The standard approach to extending teachers’ expertise is through professional development. Following their review, Black and Wiliam with the team at Kings College (Black et al., 2003), and others launched programs of work that aimed to turn the insights into impact on practice, mainly focusing on the professional development of teachers. They found, however, that regular meetings over a period of years were needed to enable a substantial proportion of the teachers to acquire and deploy the adaptive expertise needed for self-directed formative assessment. This is clearly an approach that is difficult to implement on a large scale—live professional development is costly and the number of potential leaders with the necessary expertise is limited. This approach was brought together in a practical guide by Wiliam and Thompson (2007), while Black and Wiliam (2009, 2014) have developed further the theoretical aspects.

The other standard form of support for teachers is teaching materials; in contrast to live professional development these are readily reproducible. The question then arises as to how far well-engineered (Burkhardt, 2006) teaching materials can enable teachers to acquire the new pedagogical and mathematical skills needed to make high-quality formative assessment an integral part of the implemented curriculum in their classrooms, even where linked professional development support is limited or non-existent. This design challenge is recognized as formidable, since formative assessment involves a much wider range of teaching strategies and skills than traditional mathematics curricula demand. The Mathematics Assessment Project was set up, with support from the Bill & Melinda Gates Foundation, to explore this issue. It led over 5 years to the design of teaching materials for 100 Formative Assessment Lessons (FALs)—20 for each year across the age range 11 to 16 or 17. The research-based design of these lessons, called Classroom Challenges, is described in detail by Swan and Burkhardt (2014). He we summarize the key elements.

The goal of the project was to conduct relevant research and to produce 100 FALs—most concept focused, others problem solving focused—that would have the following properties:

• The lessons would focus on key mathematical concepts and practices.

• Each lesson could be “inserted” into the regular grade level curriculum, so that for particular topics they would help teachers discover what their students had learned, what challenges they face and, crucially, provide ways to address those challenges.

• The lesson materials support a pre-assessment followed soon after with about two hours of classroom time, helping teachers to:

  • uncover some misconceptions by using the pre-assessment, with time to think through the ways in which the content of the lesson addresses them;

  • be prepared for the main lesson with a list of “common issues” that the lesson would likely uncover, and ways to respond to those issues without simply re-teaching the content—e.g., by using questions that cause the students to consider a particular example that challenges their statement;

  • launch the main lesson in ways that student ideas (often contradictory!) are made public, so it became apparent to all that there were issues to resolve;

  • lead a number of small group activities in which students build on each other’s ideas in posters for presentation, supported from time to time by the teacher;

  • close the lesson with activities that expand on and solidify student learning.

• Perhaps most ambitious, the project had the goal that the formative assessment lessons would support teachers in changing their pedagogy. The idea was that, having been supported in teaching this new way with very carefully guided lessons, the teachers could begin to generalize from this experience so that their “regular” lessons were taught differently—constructive learning by teachers.

Design principles and objectives are one thing; executing them is another. The lessons profited from a design and development process that reflected standard methods from other research-based fields. It was developed by the Shell Centre team over many years and refined over the first few years of MAP (see Swan & Burkhardt, 2014). It involves two rounds of revision, based on rich structured observational feedback from a small number of classrooms. An independent team, in this case from Inverness Research Associates, provided quality control, documenting processes and products and suggesting ongoing improvements.

This process, although typical for products in research-based fields, is far more extensive, and expensive, than the authoring methods used to generate the vast majority of instructional materials. But the carefully staged iterative design process, with feedback from a sample of classrooms large enough to distinguish the generic from the idiosyncratic, explains why these educationally ambitious materials work well—and why there have been more than 7,000,000 lesson downloads so far from map.mathshell.com.

The evidence that there is significant student and teacher learning came from the trials themselves, and from a variety of independent sources. A team from the National Center for Research on Evaluation, Standards, and Student Testing (CRESST) reported on their study in Kentucky (Herman et al., 2014), where the Challenges were introduced as the “Mathematics Development Collaborative” (MDC). The evaluators created a measure of algebraic growth based on Kentucky’s statewide mathematics assessment. Participating teachers were expected to implement between four and six of the Classroom Challenges, meaning that students were engaged in this work for 8–12 days of the school year. CRESST used recently developed methodology to convert the observed effect size for these classes into a gross indicator of the number of months of learning represented (see Hill et al., 2007). Relative to typical growth in mathematics from ninth to tenth grade, the effect size for the MDC classes represents 4.6 months of schooling.

That is, the average content gains as a result of 8–12 days of instruction using formative assessment lessons were 4.6 months. How could that be? There are various factors. In content terms, the formative assessment lessons are synthetic: they pull together prior learning and enhance it by making these connections, thus having an impact beyond the direct days of instruction.

But the pedagogy of the lessons, and its impact on the teachers is at least as important. We note, first, that the pedagogy in the formative assessment lessons is entirely consistent with the Teaching for Robust Understanding of Mathematics (TRU Math) framework (Schoenfeld 2013, 2014, 2015), which indicates that powerful learning will take place to the degree that a classroom environment provides the following: (1) engagement with rich mathematical content and practices; (2) opportunities for sense making at an appropriate level of cognitive demand, so students can learn via “productive struggle”; (3) equitable access to the content for all students; (4) opportunities to develop a sense of disciplinary agency and identity by contributing to classroom discussion, building on others’ ideas and having one’s own ideas built on; and (5) formative assessment. The formative assessment lessons support teaching in all these five dimensions. But, as noted in the description of goals above, they were designed with the intention that, having been supported in teaching this new way by the formative assessment lessons, the teachers might begin to teach their ‘regular’ lessons in ways more consistent with TRU.

The evidence is that the formative assessment lessons did achieve some of this pedagogical transfer. A study by Research for Action (2015) found that almost all (98%) participating teachers indicated that the role of teacher as instructional ‘facilitator’ or ‘coach’, which is embodied in the Challenges, supports increasing students’ mathematical understanding. Compared to providing direct instruction, coaching enables students to take on a more active learning role.

“I’ve been teaching for 36 years, and teaching the same way. It’s hard to change; to teach an old dog new tricks. But now that I’m doing it, I love it…. At first, I felt like, I’m not teaching! [laughs] But now I realize that they really are learning, and doing more on their own. And I don’t have to stand up there, and teach my heart out, and they [are] just looking at me and still not getting it. Now… they’re probably learning more”. High school math teacher (p. 3)

The vast majority (91%) of the teachers reported that the lessons provided them with effective strategies for teaching math and strengthening mathematical discourse in their classrooms.

“The students actually talk about math and they are actually having debates and they are debating between who is correct. Before, without this type of teaching, they never talked about math. It was always the teacher talking and they never got into good discussions or justify their answers, and they were never responsible for understanding what other people were thinking as well.” High school math teacher (p. 4).

In addition, teachers reported that the practices were affecting their instruction, even when they weren’t using the Challenges. At least three-quarters of the teachers said that the lessons had become important to their instructional practice and that they were infusing strategies from the Classroom Challenges into their ongoing instruction. High school math teachers reported:

This has expanded me to do more work in groups, even more than I have done in the past.

I think it’s helping us grow as teachers in how we question the students.

“It has definitely made me more aware of putting the responsibility on them – for them to be their own learners and I love the questioning technique and being their facilitator to learning. It has definitely changed my way of teaching.” (pp. 4–5)

These findings mesh with a case study (Kim 2017) done in Bay Area classrooms under similar conditions: a teacher who taught five formative assessment lessons wound up doing half as much “telling” at the end of the year as at the beginning, and twice as much asking questions that expect explanations, not just answers. Additional documentation is found in Inverness Research Associates’ (2014) MAP project portfolio.

In sum, these formative assessment lessons produce improved learning and teacher change that is significant. Their development and implementation provide rich sites for research.

4 Summative assessments

4.1 Assessments that support and advance systemic learning goals

Formative assessment is essential to support individual student learning. It is, of necessity, fine-grained. Other purposes, e.g., monitoring the health of the system at various levels (school, district, state) require summative measures—summative in the sense that they integrate information about student performance at a particular time into a more compact form.

When one considers any such measure, it is worth asking (following Burkhardt, 2007)

• 1. Who does this assessment inform? Students? Teachers? Employers? Universities? Governments?

• 2. What is the assessment for? To monitor progress? To guide instruction? To aid or justify selection? To guide policy making?

• 3. What aspects of mathematical proficiency are important and should be assessed? Quick calculation? The ability to construct chains of reasoning? The ability to use knowledge in a new situation? The ability to communicate precisely?

• 4. When should assessment occur in order to achieve these goals? Daily? Monthly? Yearly? Once?

• 5. What will the consequences of assessment be? For students? For teachers? For schools? For parents? For politicians?

• 6. What will it cost, and is the necessary amount a cost-effective use of resources?

Looking at the first two questions, we have seen in Sect. 3 how formative assessment can provide students and teachers with a rich stream of information in a form that, if collected and used intelligently, can be directly and effectively applied to enhance learning at every level—from metacognitive processes, through solving rich problems, down to individual concepts and skills. But the other potential users listed in Question 1, including policy makers and administrators at every level, simply cannot handle the huge quantity of evidence that formative assessment, day by day, involves and requires. They need compact summative data. Their answer has usually been in the form of tests, taking a few hours at most. In this section we look at the many issues that this kind of testing raises, summarized in the other questions above.

We start with Question 5, on consequences, and make an important distinction. For some tests the results of their performance have little direct effect on individual students, teachers or schools. Examples of this kind are surveys like PISA or the National Assessment of Educational Progress (NAEP) in the US. They may guide policy decisions of governments but have no direct consequences in schools and, crucially, no impact on “the zone of instruction”—teachers and students in classrooms. In some countries, national and local testing is of this kind but in others, including both the UK and the US, scores on high stakes tests are used by government to change the budgets of schools and the career prospects of teachers, as well as of students. In these cases, the nature of the test has profound influence on the zone of instruction, with the range of learning activities in most classrooms narrowed to focus on the task types covered in the tests. In these circumstances, this range of different task types is crucial if the test is to support the learning and performance goals of the system, rather than undermining it. In advising a test development agency on this we wrote:

It is now widely recognized that high stakes assessments establish the ceiling with regard to performance expectations in most classrooms. Thus it is essential ... to insist on a meaningful, balanced implementation of ... [performance goals]. The lower the bar, the lower people will aim. This is the nation’s best chance – for the next decade at least – to move the system in the right directions.

This was summarized long ago (Burkhardt et al, 1990) as WYTIWYG: What You Test Is What You Get. Despite oft-expressed discouragement from leadership of all kinds, teachers will teach to the test—their “bottom line” in such a system. It follows that a system that wants to combine high-stakes with high quality educational outcomes must develop and implement tests worth teaching to—the global answer to Question 3 above. Although teachers have long recognized WYTIWYG, the responsibility that it entails has only recently been accepted in principle by test providers and government; it is still rarely achieved in practice.

The balance of this section focuses on addressing Question 3 in more detail, describing the essential elements in the design of mathematics tests that will advance the quality of classroom teaching and thus of student learning. Issues of implementation reflecting Questions 4 and 6 will also be addressed. A more extended discussion can be found in the report on High-stakes Examinations to Support Policy of a working group of the International Society for Design and Development in Education (ISDDE, 2012).

The range of mathematical expertise that adults need in the modern world, and thus the goals of high-quality curricula, has been summarized in various forms. PISA speaks of the components of “mathematical literacy” (OECD, 2016) and the modeling process, while the Danish national curriculum talks of eight “competencies.” The US Common Core State Standards describe eight Mathematical Practices, which expect students to learn to: make sense of problems and persevere in solving them; reason abstractly and quantitatively; construct viable arguments; model with mathematics; use appropriate tools strategically; attend to precision; look for and make use of structure; look for and express regularity in repeated reasoning. Though these principles differ in detail, the overall intentions are similar. One thing is clear: these objectives go far beyond the objectives reflected in traditional tests of skills in the procedures of arithmetic and algebra, and in reproducing proofs of theorems in geometry.

In order to meet these broader and deeper learning and performance goals, assessments need to:

• provide students with the opportunity to demonstrate their understanding of core mathematical content in the context of mathematical practices,

• exemplify and reward the various kinds of performances to which students and teachers should aspire,

• be reliably score-able and have appropriate psychometric properties, including content and construct validity and reliability,

• be doable within a reasonable time period.

Here we outline, and briefly exemplify, a set of specifications for assessments with the characteristics delineated above. First we review some fundamental facts in the light of the mathematical practices above:

• 1. It is impossible to assess these goals using only short “items”⁵—short tasks focused on one fragment of mathematics that take only a minute or two. Making sense of problems and persevering in solving them takes time, as does constructing viable arguments and critiquing the arguments made by others. Modelling with mathematics essentially involves extended chains of reasoning. Assessing students’ capacity to employ these practices demands the use of what have been called “performance tasks”—non-routine tasks involving substantial chains of reasoning.

  Mathematics is not a checklist of fragments to be mastered; doing and using mathematics involves the integrated use of knowledge and practices. It is appropriate that each test sample the various aspects of mathematical proficiency in a balanced way, testing at each grade level mainly for understanding of the big connected ideas of the “content domains,” rather than trying to assess mastery of all the fine-grained skills. This approach sustains the non-routine aspect that is central to the practices—i.e., to doing and using mathematics.

• 2. The difficulty of a task increases with its complexity, unfamiliarity, technical demand, and the level of autonomy expected of the student-solver. For consistent levels of difficulty, if some elements present greater challenge, the others must be less demanding. In the world of short tasks, the technical demand dominates because the others are minimal. For the more complex, non-routine tasks that ask the student to devise a solution path and construct a substantial chain of reasoning, the technical demand must be lower, focused on concepts and skills that students have thoroughly absorbed and connected—which means those first met in earlier grades.

  In consequence, short tasks (focusing largely on freshly learned material) and performance tasks (which ask students to do real problem solving, using tools and techniques over which they have some level of mastery) have complementary roles in well-balanced assessment.

• 3. To be faithful to the goals, some assessment tasks must allow multiple solution paths. The aim is to support classroom practices that engage students in meaningful and powerful mathematical problem solving activities. Complex problems can often be approached in multiple ways—some more elegant than others perhaps, and calling upon different mathematics. This means that one cannot guarantee that a student will use a particular piece of mathematics. (We have been told of a case where an assessment board refused to use a particular task, because they could not tell a priori whether it would be solved using algebraic or geometric methods. That is most unfortunate, given that problems in the real world don’t come packaged with labels that say “use this method.” The highest priority goal is to solve the problem!)

• 4. This is not an issue in terms of assessment coverage: scaffolded tasks or short tasks can sample appropriately from individual content domains. Rather, the issue is that tasks that provide opportunities for mathematical thinking often afford multiple approaches. The following task, Skeleton Tower, is an example.

  

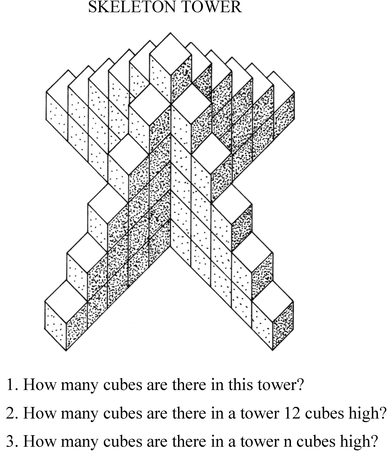
  Most age-16 students begin by tackling Skeleton Tower numerically, first counting and then showing some structured algebraic thinking (e.g., 4(1 + 2 + 3+…5) + 6). Some then sum the series for n algebraically. A few see that breaking off opposite arms and inverting them on the other two arms can produce a rectangle. (This pictorial-symbolic version is prized by many mathematicians, because it helps to explain the algebraic formula.) Multiple and sometimes non-overlapping solution pathways are inherent to rich mathematical thinking; high-quality balanced assessments must include such tasks. (We note in addition that such tasks, once released, become the basis of rich classroom conversations about mathematical content and connections—another primary goal of high-quality assessment.)

• 5. An assessment consistent with the broader goals must be faithful to that description of the mathematics, taken holistically, and not simply to individual items of content. Such assessments can be constructed (Daro and Burkhardt 2012) by:

  • (a) assembling a collection of rich tasks that cover the range of performances that the goals imply;

  • (b) selecting a sample from them that is balanced along the dimensions of content and practice coverage, difficulty, and levels of scaffolding; and then

  • (c) fleshing out content sampling coverage with a set of short tasks.

There is a substantial history internationally (see e.g. Burkhardt 2009) of such assessments being developed and implemented systemically and successfully in a cost-effective form.

In what follows we begin by illustrating the properties of another complex assessment task, showing how the task provides information about multiple aspects of content and practices. We then abstract from this example, showing how a collection of such tasks—buttressed by a collection of short tasks—can meet the criteria discussed above.

What are the essential features of a complex performance task, suitable for a timed written test? It should ask a student to integrate conceptual understanding and technical skills with some of the mathematical practices. Skeleton Tower is an example that focuses on problem solving, with much of the challenge coming in how to tackle the problem. We complement this first with a task that focuses on mathematical concepts and skills - in this case in the interpretation of line graphs of a real world situation.

Hurdles Race (Swan et al. 1985) is a 15-min assessment task, suitable for students age 14–16. It taps into a number of major content understandings and common misunderstandings, such as seeing graphs as pictures. Here is the task.

We will not give a complete solution here. (It would look something like this: “And they’re off. Runner C is off to a quick lead, with A and B trailing. Oh no, runner C trips on a hurdle and he’s down! Runner A is now in the lead, although B is catching up slowly. But wait, A starts to fade…”). We do note, however, that a full solution involves the following mathematical insights:

• (1) A section of runner C’s graph is horizontal. Over that time span (from approximately 15 s), the runner is not getting further from the starting point of the race. That is, the runner must have stopped—“trips on a hurdle” is a natural assumption linking with the context. (It is well known that students have difficulty interpreting horizontal portions of graphs; thus this part of the task examines a common student difficulty, in the context of a meaningful interpretation.)

• (2) In a race, the person who reaches the end in the shortest time is the winner—hence the winner is the one whose graph “ends” furthest to the left. This requires analysis—many students will, without thinking things through, assume that the graph that goes furthest to the right must be that of the winner—who will be to the right when viewed from the stands. The “graph is a picture” confusion.

• (3) A point of intersection indicates that two runners are at the same distance from the start at the same time - i.e., that they are side-by-side, with one having caught up and about to pass the other.

• (4) A graph that curves upward indicates that the person graphed is moving more rapidly as time passes, while a downward curve indicates that the runner is slowing down. Figuring this out is an important interpretive act, indicating a deep understanding of the representation. (This is where, at the end of the race, runner A fades while runner B speeds up and wins.)

All of these points have to do with interpreting a fundamental mathematical representation, a graph. They also call for making fundamental use of the concepts of rate and ratio, with speed being the ratio of the change in distance traveled over a unit of time.

However, as with all good tasks, Hurdles Race is more than those things. It asks students to integrate their interpretation into a coherent story in the form of a commentary—such integration is an essential feature⁶ of mathematical practice.

To summarize the generalizable points from this analysis of Hurdles Race:

• It is essential to understand that the content understandings and practices a student can demonstrate by working the Hurdles Race task can not be examined coherently by a series of multiple choice tasks or some other testing equivalent. Breaking up the task destroys it—the context is essential, as is the capacity to create explanations. It should also be noted that this particular assessment task has been widely used; it is reliable and can be scored with accuracy.

• Empirically, this task is appropriately challenging for high school students in good programs, though they will have learned the basic concepts of line graphs in earlier grades (illustrating the general point about task difficulty in 3 above).

• The expertise that is assessed by tasks presented, like Hurdles Race, in a non-pre-digested natural form is all that will be useful to the student beyond the math classroom. It must be a focus of any valid assessment.

The variety of tasks needs to be broad. We have space for only two more kinds. Even simple tasks on traditional topics can be designed, like 25% Sale below, to require thinking - and to extend mathematical horizons, in this case to geometric/exponential behavior.

Modeling is the competency for being able to use mathematics to understand the world better. It can be, and has been (MARS 2002–2004), assessed in examinations with real-world problem solving tasks like Traffic Jam.

4.2 Designing tests that reward good teaching

It is possible to design tests that pass psychometric muster and are reasonably cost-effective. We will sketch two outstanding examples from the past (see Burkhardt, 2009) before describing in a little more detail a recent example from the US.

In the Testing Strategic Skills project, the Shell Centre team worked with England’s then-largest examination board. The board recognized that the tasks in the tests did not begin to cover the board’s list of “knowledge and abilities to be tested”.⁷ The brief was to improve the alignment by introducing one of the missing task types each year, providing schools with well-engineered teaching materials (Shell Centre, 1984, 1987–1989; Swan et al. 1985) that would enable typical teachers to prepare their students for the new challenge. This gradual approach proved effective from both an assessment and an education perspective, with reliable scoring and substantially improved student performance on these important task types—hardly surprising, since they had not previously been taught! Equally important strategically, the annual 5% changes were popular with both teachers and students.

In Australia in the late 1980s, the State of Victoria introduced a new Certificate of Education (VCE) with a variety of assessment components that covered the broad spectrum of goals we have referred to (Stephens and McCrae, 1995). This highly ambitious program was gradually modified in the light of pushback but remained an outstanding exemplar for at least a decade.⁸ Some educational effects were impressive: Barnes, Clarke, and Stephens (2000) found that, although this was a school leaving examination for age 18, the kinds of problem-solving it introduced became part of the curriculum throughout secondary schools.

These two examples show how high-quality summative assessment on a large scale can forward student learning of high-level skills.

In 2010 the authors were asked by the Smarter Balanced Assessment Consortium (SBAC, one of the two assessment consortia in the US chartered to construct assessments that fully reflect the goals of the Common Core State Standards) to draft the content specifications for their tests in Mathematics (Schoenfeld et al., 2012). The specification was an embodiment of the principles set out above, assessing student performance in mathematics across a wide range of task types, which were exemplified in the appendix that accompanied the specifications. Our design included extended performance tasks such as those given in this paper. The specifications were reviewed by SBAC’s statistical consultants, and were declared to meet the relevant psychometric standards for large scale, high stakes testing. We also described methods of scoring that would be cost-effective, would provide professional development for the teachers who scored the assessments, and would provide reasonable safeguards against cheating.

In some respects, the design was revolutionary. Scores would be reported under four headings: concepts and procedures, problem solving, communicating reasoning, and modeling and data analysis.⁹ Thus, for the first time, students and teachers would receive meaningful feedback regarding key mathematical practices. SBAC’s resident psychometricians were perfectly happy to give such a high-stakes test on a very large scale—at one point, half the US.

Had the tests been implemented as designed, the result would have been a cost-effective assessment that drove instruction in the right directions—if several things are being tested and scored separately, people will pay separate attention to all of them. However, the test was never implemented the way specified - or, indeed, in a way consistent with its declared goals and the Common Core Standards. We explore the reasons in Sect. 5.

5 Why is high-quality assessment still so rare?

We have seen that the design of the various aspects of assessment in ways that will support student learning and the teachers on whom it so largely depends, though challenging, involves nothing that is not well understood within the mathematics education research and development community. Yet, despite the “proof of concept” large-scale working examples of formative assessment (as exemplified in Sect. 3), and of summative assesssment (as in Sect. 4), it is still rare to find large-scale uses of assessments that come close to the kind of description we have given here. In this final section we look at the reasons that seem to underlie this mismatch and what might be done about them.

How reliably to do better at system level is an unsolved problem but we have presented evidence on approaches that have worked ‘at scale’ and hypothesized how they might be extended. Without considering these issues, unusual though it is in research papers on assessment, it seems to us that the exercise is in danger being “academic”, in the pejorative sense. Inadequate attention to the question “Why is high-quality assessment still so rare?” may well be part of the reason that high-quality assessment is still so rare.

In Sect. 3 we recognized that formative assessment for learning requires most teachers of mathematics to move outside their comfort zone of established practice, and discussed at some length how they can be supported in meeting these challenges. There are indications of progress, with formative assessment becoming more widespread. In contrast, despite some effort in various countries including our own, national testing has changed only marginally and superficially. So here we will focus on the reasons for that. In doing this we will discuss Questions 4, 5 and 6 from Sect. 4.1: on timing, consequences and cost for those who commission and provide the tests.

First it is worth noting some common myths:

• Myth 1: Tests are precision instruments. They are not, as test-producers’ fine print usually makes clear. Testing and then retesting the same student on parallel forms, “equated” to the same standard, usually produces significantly different scores. This inherent variation is ignored by most test-buyers who know that measurement uncertainty is not politically palatable, when life-changing decisions are made on the basis of test scores. The drive for precision leads to narrow assessment objectives and simplistic tests.¹⁰

• Myth 2: Each test should cover all the important mathematics in a unit or grade. It does not and cannot, even when the range of mathematics is narrowed to short content-focused items; testing is always a sampling exercise. This does not matter as long as the samples in different tests range across all the goals—but some object: “We taught (or learned) X but it wasn’t tested this time.” This concern is a peculiar to mathematics. Such sampling is accepted as the inevitable norm in other subjects. History examinations, year-by-year, ask for essays on different aspects of the history curriculum; final examinations in literature or poetry courses do not necessarily expect students to write about every book or poem studied. Science subjects also expect to sample from a wide range of topics and problems.

• Myth 3: “We don’t test that but, of course, all good teachers teach it.” If so, then there are few “good teachers”; as we have noted, the rest take very seriously the measures by which society chooses to judge them and, for their own and their students’ futures, concentrate on these.

• Myth 4: Testing takes too much time. This is true if testing is a distraction from the curriculum. It need not be, if the assessment tasks are also good learning (i.e., good curriculum) tasks. Feedback is important in every system; below we look at the cost-effectiveness of assessment time.

• Myth 5: High-validity broad-spectrum tests are expensive. This view arises from a kind of “tunnel vision”—not examining all the costs of different kinds of test, and relating them to the total cost of educating a student in mathematics - around $2,000 a year in the U.S. Informal surveys suggest teachers spend around 20 days of ‘math time’ in ‘test prep’ practice that is otherwise unproductive—short items do not represent mathematics ‘in the round’. That’s around $200 per student to be added to the $2 cost of the test. Test prep for a test based on tasks that involve substantial chains of reasoning is, in contrast, valuable learning time—indeed, students would benefit if teachers did more of it. Thus, a $20 test that focuses on such understandings looks highly cost-effective when all costs are taken into account. One can have different views on what proportion of the $2,000 should be spent on testing, but 1% is surely not excessive!

Beyond the myths, there are some political pressures that discourage policy makers from improving high-stakes tests.

• Changing high-stakes assessment inevitably causes trouble for politicians and policy makers. People have become used to the existing system and are concerned about any change. Teachers, parents and others tend to fear the worst—and a few of them will be outspoken in their opposition.

• This leads to less concern about what is assessed, provided it is socially acceptable. We noted above the difference between the properties of the assessment of English and Mathematics in the US and UK. Equally, though life-changing decisions are made on the basis of test scores, their crudeness and inaccuracy as measures, evidenced by the test–retest variation in scores, is ignored.

Some of these reasons were, we believe, among the reasons that the SBAC specs were not implemented in the ways we had hoped. For one thing, reporting four scores (or even three), no matter how valuable for students and teachers, makes life much more complex for administrators and politicians, who find it much simpler to deal with univariate indicators (“Test scores rose 3% this past year!”). For another, the wish to ultimately have all tests graded solely by computers (read: “cheaply”) mitigated against institutionalizing longer, more complex problems. The costs of wasted classroom time are invisible, as opposed to the costs of paying teachers to grade papers. (We note that groups such as the Silicon Valley Mathematics Initiative have organized grading sessions in which teachers discussed student work, and learned a great deal about student thinking, thus obtaining significant professional development. So the money spent on teacher grading was well spent professional development money. But, it was still real money.) Finally, using computer-based tests also “solved” a security problem—what if teachers colluded, in scoring papers? We note that there are mechanisms to cope with such issues—teachers from District A grade papers from district B, a certain per cent of papers are double-graded by experts, etc. In any case, SBAC’s governing board opted for versions of the tests that fall far short of what could have been done.¹¹

This is not an American issue; in the UK there has been a similar process of degradation in implementation in the recent revision of GCSE Mathematics. There the three broad assessment objectives (concepts and skills, reasoning, problem solving) were divided into 21 sub-objectives by the body (Ofqual) that is responsible for ensuring comparability of standards across the various test providers, with further detailed rules about the distribution of score points. This again fragments performance in a way that effectively excludes rich substantial tasks—in the design of which the providers have no experience!

Policy makers greatly underestimate the design and development challenges in producing good tests. Designing and developing rich tasks that require high-level thinking in a form that enable all students to show what they know and can do is much more like designing learning materials than writing “short items” (Burkhardt, 2006). To assume, despite all the evidence to the contrary, that test providers who have only delivered simple multiple-choice tests of separate skills can deliver whatever kind of test you commission is educationally negligent. How much of this is naiveté and how much corporate power we cannot judge. But the resulting low-quality high-stakes tests are now the single most formidable barrier to improving our students’ mathematical understandings.

When political pressure clashes with educational improvement, it is not surprising if the former wins. The challenge to the educational community is to find ways to mitigate this—policy makers are, after all, part of the education system that we aim to improve. Though this is not the place for a full discussion of these issues, we mention two features that have proven helpful.

• Gradual change—when improvements are made incrementally, the adverse reaction is largely avoided, since the test remains “mostly the same as last year’s”.

• Lowering the stakes—when many measures and circumstantial factors are explicitly included in the policy maker’s decision, it lessens the focus on, and concern about, test scores.

These are, of course, not easy to achieve; but they are not impossible. Burkhardt (2009) discusses these issues, giving examples of successful initiatives. If we as a community are to see the fruits of our academic labors having impact in practice, some portion of our efforts will need to be devoted to finding better ways to influence the system that governs that practice.