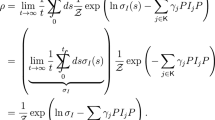Abstract
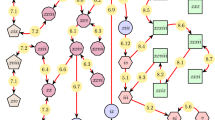
We show here that any two finite state irreducible Markov chains of the same entropy are finitarily Kakutani equivalent. By this we mean they are orbit equivalent by an invertible measure preserving mapping that is almost continuous and monotone in time when restricted to some cylinder set. Smorodinsky and Keane have shown that any two irreducible Markov chains of equal entropy and period are finitarily isomorphic. Hence, all that is necessary to obtain our result is to show that for every entropy h > 0 and period p ∈ ℕ there exists two irreducible Markov chains σ 1, σ 2 both of entropy h, where
(1) σ 1 is mixing
(2) ς 2 has period p and
(3) σ1 and σ 2 are finitarily Kakutani equivalent.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
H. Dye, On groups of measure preserving transformations I, American Journal of Mathematics 81 (1959), 119–159.
T. Hamachi and M. Keane, Finitary orbit equivalence of odometers, Bulletin of London Mathematical Society, to appear.
T. Hamachi, M. S. Keane and M. K. Roychowdhury, Finitary orbit equivalence and measured Bratteli diagrams, Mathematische Zeitschrift, submitted.
T. Hamachi and M. Osikawa, Ergodic groups of automorphisms and Krieger’s theorems, Seminar on Math. Keio Univ., 3 (1981).
M. Keane and M. Smorodinsky, Finitary isomorphism of irreducible Markov shifts, Israel Journal of Mathematics 34 (1979), 281–286.
M. Keane and M. Smorodinsky, A class of finitary codes, Israel Journal of Mathematics 26 (1977), 352–371.
M. Keane and M. Smorodinsky, Bernoulli schemes of the same entropy are finitarily isomorphic, Annals of Mathematics 109 (1979), 397–406.
D. J. Rudolph, A characterization of those processes finitarily isomorphic to a Bernoulli shift, in Ergodic theory and dynamical systems I, (College Park, Md., 1979–80), Birkhäuser Boston, Mass., 1981, pp. 1–64.
D. J. Rudolph, A mixing Markov chain with exponentially decaying return times is finitarily Bernoulli, Ergodic Theory Dynamical Systems 2 (1982), 85–97.
M. K. Roychowdhury, {m n }-odometer and the binary odometer are finitarily orbit equivalent, Contemporary Mathematics, AMS, Edited by I. Assani, UNC Chapel Hill, to appear.
M. K. Roychowdhury, Irrational rotation of the circle and the binary odometer are finitarily orbit equivalent, RIMS of Kyoto, to appear.
M. K. Roychowdhury and D. Rudolph, Any two irreducible Markov chains are finitarily orbit equivalent, preprint.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Roychowdhury, M.K., Rudolph, D.J. Any two irreducible Markov chains of equal entropy are finitarily Kakutani equivalent. Isr. J. Math. 165, 29–41 (2008). https://doi.org/10.1007/s11856-008-1002-5
Received:
Issue Date:
DOI: https://doi.org/10.1007/s11856-008-1002-5