Abstract
The practice of verification of shell finite element formulations is discussed from a variety of viewpoints: The provenance of benchmark target values, the suitability of benchmark problems for different classes of shell models, the importance of reporting limit values, and the completeness of the benchmark sets are critically examined. A set of benchmark problems that are most suitable across common shell finite element models is identified.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Structures that can be modeled as shells have a permanent place in the structural engineering vocabulary. Finite element models of shells tend to be quite complicated, yet the payoff in terms of computational efficiency is significant, and the literature on the development of shell finite elements has been expanding at a great rate. The review of shell finite elements from 1990 listed 288 references [1], and 10 years later the list grew to 368 references [2]. Since not every single publication made it into the list included in a review, and considering also that this piece of information refers to a situation 20 years ago, the number of papers published about shell finite element technology clearly has grown quite rapidly. As a further source of information we may also recommend the chapter [3]. While there does not seem to be a newer review paper on shell technology, an excellent summary of the methodological developments in recent years written by Bischoff is available [4].
It has become a custom to illustrate the performance of new contribution to numerical models of shells using some benchmark problems, with the aim of establishing some reason for being: higher accuracy, more robust or more efficient formulation, etc. The computational mechanics community has endeavoured over the past decades to establish the art and science of verification in research, development and in engineering practice [5]. However, it would appear that in the recent past, even in flagship journals, the verification of shell models has not been up to standard, and that that problem persists even today. Several of the issues are discussed in this paper. Foremost, any publication of a finite element model needs to demonstrate convergence with benchmark tests. Alas, often the results may be published only in graphical form, which makes it hard or impossible to establish convergence. Even if the results are provided in tabular form, it is often left up to the reader to attempt to use the numerical data to draw conclusions as to whether or not the convergence can be (has been) verified. Also, often the benchmark data is not of sufficiently high quality as will be demonstrated here. Further, benchmarks are not of much use if they are not selected properly. Some benchmarks are applicable only to a particular class of shell models [4], for example, in the case of concentrated loads to be discussed here. Another vexing problem is that the convergence reporting may be selective: only those benchmarks that work for the proposed method are included. Evidently, this makes the reader’s task of separating wheat from the chaff so much harder. Finally, we may propose the basic tenet of publishing reproducible results: make it possible for your readers to reproduce your results for themselves. This would usually mean making the software used to compute the results available together with the paper itself. Unfortunately, this approach is a distinct rarity at the moment.
While we focus our attention on linear static benchmarks, many of our conclusions will be applicable to dynamics (steady-state and free vibration, and transient). The complicating factor for these types of problem is how to describe the solutions. This becomes particularly acute in frequency–response computations and transient simulations, where the results are typically presented with charts, and robustly comparing curves is a notoriously difficult problem.
Most computational models for shell structures these days fall into the category of finite element methods. However, alternative models, such as finite difference formulations, mesh-free formulations, or boundary element formulations, are subject to the same general rules of verification. The observations we offer in this paper apply to all of these models.
For simplicity, we will deal in this paper with only first-order models: shear-rigid and shear-flexible. By the shear-rigid designation we mean the Kirchhoff–Love (KL) class of models, and by shear-flexible we mean the Mindlin-Reissner (MR) class of models.
The plan for the present paper is as follows. Section 2 undertakes to illustrate how benchmark values come about. How they develop, how they come to be the authoritative source of information, and how they are (sometimes) corrected. Section 3 discusses the importance of reporting the results as limit values, not as a sequence of raw numbers. The limits of the refinement of the model have the power of providing evidence of convergence. Too many papers have presented non-convergent models over the years, as we demonstrate using a simple metanalysis. Section 4 discusses a pain point that afflicts many papers even today: a benchmark problem is applied where it is not applicable. Concentrated forces lead to infinite displacements for shear flexible shells, yet many shear-flexible models are tested using benchmark problems where such loading is used. In Sect. 5 we address the issue of the completeness of benchmarks. The verification of a particular model may be considered complete only if all known conditions in which the model can fail have been tested. Section 6 presents a selection of suitable benchmarks for both shear-flexible and shear-rigid shell models. Finally, in Sect. 7 we offer some conclusions and recommendations.
2 Reference Values
A necessary precondition for successful benchmarking is a reliable value of the quantity of interest. The benchmark value should be computed repeatedly by independent researchers, each new result confirming or disputing the credibility of the other results. If and when a sufficient number of independent results that are in agreement has accumulated, the benchmark value can be established.
2.1 The Curious Case of the Scordelis–Lo Benchmark
The cylindrical roof supported on diaphragms, subjected to self-weight load, often referred to as the Scordelis–Lo roof, has appeared in almost every paper on computational shell analysis since the 1970s. The deflection of the midpoint of the free edge in the direction of the applied self-weight loading is the quantity of interest in this particular benchmark. How reliable is this number?
The value of the deflection of 0.3024ʹ (3.6288ʺ) is the magnitude often incorrectly attributed to [6] (1964). Upon closer inquiry we find that no value of the target quantity was given in [6], in fact this shell structure was neither defined, nor analyzed, in [6]. Rather, Ref. [6] described a computer program for cylindrical shells based on a shallow-shell theory (Donell-Jenkins) adopted from [7], somewhat inconsistently applied as elucidated in [8], and not taking into account shear deformations.
The computer program described in [6] was used in [9] (1968) to produce the graphs reported there, but no numerical data was given, and the source of the computer program was listed as a personal communication from Scordelis. The “exact” solution to the problem now known as the Scordelis–Lo roof was apparently first computed by Johnson [10] (1968), who in his thesis explicitly acknowledged using the program presented in [6], but only graphs were shown, not numerical data. A numerical value for the mid-edge deflection was first given by Carr, quoted as 3.696ʺ (0.3080ʹ) [11] (1967). Carr cited [6], but might have adopted the “exact” solution from [10]. Clough and Johnson [12] (1968) also showed only graphs and cited [6]. The paper [13] (1970) reported the deflection as 3.7033ʺ (0.3086ʹ): the provenance of this numerical value is uncertain, because [6] was cited as the source.
Where does the deflection of 0.3024ʹ come from then? It makes its first appearance in the well-known benchmark paper [14] (1985). The authors cited [6], rejected the 0.3086ʹ value with the words “… many finite elements converge to a lower value”, and proposed 0.3024ʹ in its stead. Unfortunately, with no indication of how the number was obtained. So this is the origin of the 0.3024ʹ benchmark value, further reinforced in its place by the well-known “obstacle course” paper [15] (1985), which cites [14] as the authority on this benchmark.
The computer program cited in [6] is of limited value these days, unless a shallow-shell result is really desired: a shallow-shell theory was used, not the (more realistic) deep-shell theory. Of course, the deficiency of the approach presented in [6] was noticed quite early on. A deep-shell solution had already been reported by Forsberg [16] (1970) for the finite difference code STAGS, and the deflection of the shell was reported as approximately 0.3ʹ (the limited accuracy of 3.6ʺ is all that could be recovered from a graph presented in [16], as no numbers were provided). The deep-shell solution was subsequently cited in a number of articles: for instance in [8], where the magnitude of the deflection was not provided, and the figure disagreed with the linked table; in [13], where the magnitude of the deep-shell solution was given vaguely in relation to the shallow-shell solution of [6]; and in [17], where the result of [16] was cited (without any justification) as 0.3008ʹ (3.607ʺ) (recall that [16] reported no numbers).
The study of Szabo and Sahrmann of shear-flexible deep shells [18] (1988) also cited [16]: the deflection 3.53ʺ (0.2941ʹ) given for the deep shell did not agree with [16] though. The mid-edge deflection of 3.613ʺ (0.3011ʹ) computed in [18] with a hierarchical shell model is a credible value to be used as a reference for shear-flexible shells, and agrees reasonably well with the solution of approximately 3.6ʺ computed for the Kirchhoff–Love (KL) shell model without transverse shear deformations given in [16] (refer to the caveat concerning absence of quantitative information mentioned above, though).
So, while many papers have found results quite different from the benchmark value, the questionable deflection at the midpoint of the straight edge of 0.3024ʹ persisted in dozens of articles and textbooks. Occasionally the discrepancy may be noted: for instance [19] described convergence of a shear-rigid model to 0.3006ʹ (3.6072ʺ), but 0.3024ʹ (3.6288ʺ) of [6] was still provided as the reference value. In the paper [20], the converged result for a shear-flexible shell was listed as 0.3020ʹ, but again 0.3024ʹ was given as the target value.
We should mention that the convoluted story of this benchmark was noted already by Ashwell [21] (1976): the first citation of the Scordelis–Lo benchmark was attributed to Cantin and Clough [9] (1968). Ashwell mentioned the contradictory values for the deflection of the shallow shell model noted above, and listed deflection for the deep shell “about 3 percent lower”, attributing this result to Forsberg [16]. Three percent lower than 3.70ʺ comes to 3.589ʺ (0.2991ʹ), which incidentally is the value cited in the Abaqus documentation [22], citing Ashwell as the source of this number.
Sobering story indeed. Perhaps the time has come to ascertain this benchmark quantity at its correct value? Computed separately for shear-flexible and shear-rigid shells? Benchmarks based on unreliable numbers may be worse than no benchmarks.
We propose to establish two separate values of the target quantity, one for shear-rigid shells (KL), and one for shear-flexible shells (MR), using evidence available from the existing literature, and carrying out careful analyses with established finite element shell models.
For the shear-flexible (MR) shells we have the following evidence. The hierarchical shell model of Szabo and Sahrmann of [18] resulted in the deflection of 3.613ʺ (0.3011ʹ). Our own results obtained with the commercial software Abaqus, using quadrilateral shear-flexible elements with full integration S4 (modification of the well-known MITC4 element) resulted in the deflection of approximately 0.30204ʹ: refer to Table 1. Table 1 presents mid-edge deflections obtained with progressively finer meshes, which were obtained by doubling the number of element edges in each direction. Since the element size increased in constant proportion, Richardson extrapolation to the limit of infinite refinement [23] could be attempted using the formula
Here \({q}_{1}\) is the result for the coarsest mesh, \({q}_{3}\) is the result for the finest mesh, and \({q}_{2}\) is the result computed for the intermediate mesh. The estimate of the solution in the limit of infinite refinement, \({q}_{t}\), is what we mean by “extrapolated” result.
The result of 0.30204ʹ also agrees quite well with the Abaqus linear and quadratic reduced-integration shell elements S4R (Table 2, deflection of 0.30202ʹ) and S8R (Table 3, deflection of 0.30203ʹ). Next, the converged result for a shear-flexible isogeometric shell in [20] was listed as 0.3020ʹ. The shear-flexible flat-facet shell element model implemented in [24], used with extremely refined meshes, generated the extrapolated value of 0.30148ʹ (refer to Table 4). Finally, the geometry-exact shear-flexible shell formulation based on the reproducing kernel particle method (RKPM) [25] produced the extrapolated deflection of 0.3022ʹ (refer to Table 5). In the light of this evidence, we propose that for shear-flexible shells the value of the mid edge deflection is likely to be in the interval from 0.30200ʹ to 0.30204ʹ.
For the shear-rigid (KL) shells we propose 0. 3006ʹ (3.6072ʺ) for the mid-edge deflection. This is supported by the isogeometric results [19] described above, and our own results obtained with the commercial software Abaqus [22]: The shear-rigid triangular finite element STRI3, based on enforcing a discrete KL condition, hence known as DKT, used with very fine meshes, yields the extrapolated result of 0. 300534ʹ, consistent with [19] (refer to Table 6).
There are three more purportedly shear-rigid shell finite elements in Abaqus: the quadrilaterals S4R5, S8R5, and the quadratic triangle STRI65. Unfortunately, these three types of elements do not appear to converge to the shear-rigid solution. As shown in Tables 7, 8, and 9, these elements converge to values in excess of the results of the shear-flexible models, and hence cannot be trusted, as the deflections computed with shear-flexible model are expected to exceed the deflections computed with shear-rigid models, not the other way around.
2.2 Hemispherical Shell Variants
The cylindrical roof benchmark is not the only one that might benefit from some serious investigative work. The hemisphere with an 18° opening at the top is another of the “obstacle course” benchmarks [15]. The problem was recommended as a benchmark in [14]. An analytical solution of a similar problem involving one half of the entire sphere, i.e. without an opening, was cited as resulting in the deflection under the force of 0.0924 [26]. MacNeal and Harder recommended, without much justification, the deflection of 0.0940 for the open-top hemisphere [14]. Later, Simo et al. [27] cited a private communication, on the strength of which they recommended the deflection of 0.093 for the open-top hemisphere. Our own calculation of the deflection of the closed sphere using Richardson extrapolation with a Kirchhoff–Love curved quadrilateral shell finite element resulted, in the limit of element size approaching zero, in the deflection of 0.092469. Analogous calculation for the open-top hemisphere resulted in 0.093597.
In order to demonstrate convergence, solid numbers are needed, with several digits of accuracy. We don’t know if our calculated answers will withstand the test of time, but it is rather likely that the traditionally cited reference values for the two hemisphere benchmarks are not sufficiently accurate. The literature already provides data in support of this contention: refer to Table 5 in [28].
3 Approach to the Limit
It is currently common practice to demonstrate convergence of shell formulations by solving on 2–4 progressively refined meshes, and then, when the finest-mesh solution can get close to the reference value, the formulation is claimed to be convergent. (There are some exceptions: convergence is taken seriously in [29,30,31,32,33], for instance.)
There are obvious problems with the above approach. Whether or not a formulation produces convergent answers needs to be decided with the approach to the limit: as the model is refined, the solutions produced must approach a limit. It is the limit value that needs to be compared with the benchmark value, not the individual results obtained with finite element sizes.
We shall illustrate some of the problems with examples based on actual published papers, but in order not to single out anyone, we shall leave the sources anonymous. In all examples shown below the element size was halved with each progressive refinement.
Illustration 1: The three results,\({q}_{1}=99.8\%\),\({q}_{2}=99.9\%\), and\({q}_{3}=100.0\%\), which are expressed as percentages of the benchmark value, were obtained. Since the element size increased in constant proportion, Richardson extrapolation may be attempted using the formula (1), which results in \({q}_{t}\) blowing up: no limit exists because\(2{q}_{2}-{q}_{1}-{q}_{3}=0\). So, while the results look impressively close to the benchmark value, the model does not converge. At least, its convergence to any finite value cannot be demonstrated using the computed numbers.
Illustration 2: The three results, \({q}_{1}=65.1\%\), \({q}_{2}=96.8\%\), and \({q}_{3}=99.3\%\), which are expressed as percentages of the benchmark value, were calculated. Again, Richardson extrapolation may be attempted using formula (1), yielding \({q}_{t}=99.51\%\). Hence, the formulation converges to a value different from the benchmark value by approximately 0.5%. This then may serve as a basis for a discussion of whether or not the formulation is actually convergent; the simple fact that the last computed number is within 1% of the benchmark value is not sufficient.
Illustration 3: The three results, \({q}_{1}=63.6\%\), \({q}_{2}=95.1\%\), and \({q}_{3}=101.6\%\), which are expressed as percentages of the benchmark value, were computed. The model was hailed as “quickly converging”. Richardson extrapolation (1) yields the limit value of \({q}_{t}=103.3\%\). Hence, rather than being quickly convergent relative to the benchmark, the model converges to the wrong deflection and is therefore suspect.
3.1 Meta-Analysis of Convergence for the Cylindrical Roof
It may be illustrative to look at a meta-analysis of the results reported for the cylindrical roof benchmark (referred to as to Scordelis–Lo above). We take 68 distinct sets of results used to “demonstrate convergence” from the papers [27, 34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76] and from works cited therein. Our own calculations presented in the tables above are not included among the sets of results studied in the meta-analysis.
There were 11 studies that implemented the shear-rigid shell models and 57 studies that reported shear-flexible shell models. We keep the individual data points presented below anonymous, but the data is obviously available to anyone wishing to reproduce our results from the list of references above.
We intend to measure the degree to which each study managed to demonstrate convergence to the benchmark value. We attempt to use Richardson extrapolation to ascertain the limit of the deflection to which the formulation converges. The typical practice in the past has been to report 3 or 4 digits for the results, which are typically normalized and reported as a fraction of the reference solution, or a percentage thereof. This may to some degree affect the result of the extrapolation. However, given our goal, poor published data still allows us to draw conclusions about the study's ability to show convergence.
Out of the total of 68 studies, 15 were unsuitable for extrapolation (for instance when the magnitude of the difference between successive solutions increased with refinement instead of decreasing). This could be due to the dataset having been obtained in the pre-asymptotic range, or it could be due to the tested formulation being divergent. Put differently, for these fifteen studies, extrapolation from the computed results would not be possible at all.
The remaining 53 sets of data resulted in estimates of the limit value to which the formulations appeared to converge. These extrapolated values would not be rejected by the analyst at first sight, in other words they appear to be reasonable (that does not mean the extrapolation was actually warranted, as will be discussed below). Figure 1 shows the deviation of the limit value from the assumed benchmark quantity of 0.3024ʹ. The deviations were sorted algebraically. However, 11 studies produced extrapolated values that were more than (±)2.0% away from the assumed benchmark value. These studies are not included in the figure. Either the results of such studies do not converge to the correct benchmark value, or the extrapolation did not actually work and the dataset was not suitable for the approach to the limit after all. Figure 1 therefore shows only the results of 42 studies.
We proposed the “corrected” values of the benchmark target for both shear-rigid and shear-flexible shells in Sect. 2. For shear-rigid shells, the deflection should be 0.3006ʹ, i.e. roughly 0.6% below 0.3024ʹ. The bottom gray bar in Fig. 1 represents a (±)0.1% band around the correct deflection for the shear-rigid shells. The results for the studies that implemented the shear-rigid shells are shown with filled dots. Clearly, only two such studies lie within the band, which we could take to mean that the formulations correctly converged. (Admittedly, the width of the band was taken arbitrarily as 0.2%, but a different choice would just change the quantity, not the quality.)
The studies of shear-flexible models are marked in Fig. 1 with a “+” sign. There are a number of these markers within the bottom gray bar for KL models or just above it. These markers represent studies which failed to converge to the correct solution: recall that the proposed value for shear-flexible shells was 0.3020ʹ, or approximately 0.15% below the value of 0.3024ʹ, and well above the range for the KL models. The top gray bar in Fig. 1 represents a (±)0.1% band around the correct deflection for the shear-flexible shells. Six (6) studies that employed shear-flexible models fall within this band, and hence can be considered converged.
Thus, of the 68 studies (formulations) only 8 can be shown to have converged to a plausible result, 2 for the shear-rigid shell model, and 6 for the shear-flexible shell. The other 60 published formulations either converge to an incorrect value, or the data provided does not allow for conclusions to be drawn as to the correctness of the solution.
This seems to us a thoroughly distressing result. We think one would be justified in the hope that the peer-review process would take verification seriously, and not let through formulations that do not actually work, or whose verification could not be completed because the data included in the paper were insufficient for that purpose.
4 Point Loads
In 1992, Babuška and Oden published a brief article on the meaning of benchmarks [77]. One of the illustrative examples was a point load on a shell: Belytschko’s pinched sphere benchmark was criticized because a finite value for the deflection under the load was provided, without the necessary caveats having been mentioned concerning infinite displacement under the point load that ensues in three dimensional analysis and for shear-flexible shells. The target quantity in any benchmark must be finite, and this dictum was violated in this benchmark. Therefore, the pinched sphere benchmarks are inadmissible as tests for shear-flexible shells. Alas, in the intervening decades hundreds of researchers have ignored this observation, having “tested” shear-flexible shells on these benchmarks.
For a shear-flexible shell with a point load no convergence of the deflection is possible [4]. How is it then that researchers conclude from a sequence of finite element simulations with progressively refined meshes that a convergence for the deflection under a point load occurred? The subject of point loads on shells was studied in [78], where it was stipulated that a region of dimension \(\sqrt{Rt}\) existed around the point of application of the force in which the “singular” character of the deflection was manifest. It was referred to as the “hotspot”. The solution could be split into two parts: a smooth part, with a finite deflection under the force, and the singular, infinite, part. Here \(R\) is the radius of curvature of the shell, and \(t\) is the thickness of the shell.
Consider for instance the pinched-cylinder benchmark. Here \(R=300\) and \(t=3\). The hotspot size is then \(\sqrt{Rt}=10\). If the finite element model is constructed for one eighth of the entire structure, the element size is \(h=\pi R/(2n)\), where \(n\) is the number of element edges along each of the four sides of the computational domain (assuming uniform mesh). For instance, for \(n=32\), the element size is \(h=\frac{\pi R}{64}\approx 14.7\). Consequently, the entire hotspot is covered by a single element with room to spare. No wonder that the hotspot isn’t visible in the solution. Note that usually \(n\le 32\) in the literature. And this is then the reason why the progression of the solutions with refinement appears to give the false hope of convergence: the sequence of solutions simply doesn’t go far enough to resolve the hotspot, and therefore the singularity of the deflection is missed.
The point-loaded benchmarks are fine for KL shells, but should be avoided for shear-flexible shells: The ill-defined outcome outlined above, and the false sense of having proved convergence where no convergence is really possible, should give all researchers pause.
5 Completeness of the Benchmarks
The task of proving the robustness of a numerical approach to the solution of the deformation of shells (i. e., verification of the model) may be based on mathematical arguments, provided the formulation is amenable to mathematical analysis [79, 80]. Few are, and then the task may be partially accomplished by testing the formulation on a selection of benchmarks. Provided we can identify all the distinct required modes of deformation that the formulation needs to accommodate in order to be convergent, we can construct a sub-set of tests that exercise the model for the one or more of the required modes of deformation. If the model passes these tests, we may be confident that the formulation is convergent for the class of problems considered. Of course, provided the set of tests is complete.
What do we mean here by modes of deformation? Take for instance papers by Briassoulis [81,82,83] and Bathe et al. [84] and da Veiga [85,86,87]: Asymptotic arguments identify bending-dominated, membrane-dominated, and intermediate modes of deformation. In addition, for individual finite element formulations one can discern subcategories: flat shells versus warped shells, with and without coupling between bending and membrane stretching, with and without membrane rotations, with and without geometrical distortion (irregularity) of the element shapes. Furthermore, behavior at shell junctions and folds needs to be tested.
We are not very likely to know for sure whether the set of tests is complete. Rather, we may find out the set was incomplete when a new test is discovered which some of the formulations passing the other tests fail. This happened for instance in 1997: Failure of the Nastran quadrilateral to converge was reported by Raasch (as cited in Knight [88]). The investigated structure consisted of two strips of circular arcs which were responding to a transverse load by torsion. Consequently, the transfer of twisting moments from element to element was crucial, and shear-flexible shell element formulations were found to diverge from the correct deflection as a result of uncontrolled spurious transverse shear [89].
The articles cited in this work include at least three formulations which pass the tests of the obstacle course, but fail the Raasch test. Evidently, in order to test the reliability of shell finite element formulations, the Raasch benchmark should be added to the standard set of tests: a test which breaks finite element formulations previously considered robust is clearly valuable in calibrating the analyst’s ability to spot failing formulations.
6 Proposed Set of Benchmarks
The two popular sets of benchmarks for shells include the “obstacle course” [90] (closed-top pinched sphere, pinched cylinder, Scordelis–Lo cylindrical roof) and the proposed set of benchmarks [14] (open-top pinched hemisphere, twisted beam, Scordelis–Lo cylindrical roof). Occasionally, these benchmark problems are supplemented with others (such as the Raasch hook). In our opinion, given the current state of understanding, the standard set of benchmarks from the above references needs to be both pruned and expanded. Pruned by removing the benchmarks with point loads, and expanded to include any benchmark which managed to break previously respectable finite element formulations (as explained above, the Raasch hook).
Why do we start from a set of existing benchmarks rather than from scratch? To establish a benchmark takes a collaborative effort. Much effort and know-how went into the current set of benchmarks. They may not be perfect, but they have value that is worth preserving. Each independent solution of the benchmark problem may be able to contribute either by burnishing the credentials of the reference values, or by prompting incremental adjustments of these values where warranted.
For all of the benchmarks proposed here, the reference (target) solutions should be computed both for shear-flexible and shear-rigid shells. At the moment this is not available across the board. Evidently, such lack of discrimination will result in discrepancies. For very thin shells those discrepancies can be expected to be small (negligible?), but for thicker shells we should demand separate numbers for shear-flexible (MR) and shear-rigid (KL) shells.
Computing the deflection at some feature of the geometry (corner or a midpoint) has historically been the target quantity of choice: the targets are easily explained and easily communicated. In addition to pointwise deflection or stress values, it would be extremely valuable to describe full-field target data, i.e. displacements, stress resultants, stresses, defined over the entire surface of the shell. Evidently, this would present formidable challenges, as we may realize just by looking for possible ways in which such data could be communicated for a general shell shape. But, a benchmark described in this way would represent a significant step up in terms of the thoroughness of testing. We hope that such benchmarks will materialize eventually.
Realistically, the place to start formulating a better set of benchmarks today is to consider scalar target quantities. However, we endeavor to select benchmarks that address convergence in more than just the deflection at a single point.
An important pointwise quantity that should be included in any suite of benchmarks is a measure of stress: either an invariant (von Mises, for example), or a stress component. Alternatively, a stress resultant (membrane or shear sectional force, or the section bending or twisting moment) could be the target quantity. Alas, benchmarks with these types of target outputs are decidedly rare: in fact, we were able to locate only a single benchmark, the Z-section cantilever.
An alternative to a pointwise quantity is a globally computed quantity, such as strain energy. The advantage of the strain energy measure is that it is only necessary to communicate a single number as the target quantity. Two of the benchmarks proposed below include strain energy as the target quantity.
The list of proposed benchmarks are as follows.
6.1 Scordelis–Lo Roof
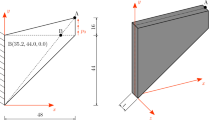
The Scordelis–Lo cylindrical roof is one of the original obstacle course benchmarks, and was discussed at length above. This shell is known to be respond to the applied loading with a mixed membrane-bending stress state [83, 84]. Figure 2 shows one quarter of the barrel vault. The dimensions shown in Fig. 2 are in feet, and the thickness is 0.25ʹ. Consistent values for the material properties are: Young’s modulus \(4.32\times {10}^{8}\text{ lbf/f}{\text{t}}^{2}\), Poisson ratio 0.0. The shell is loaded by self-weight of 90 \(\text{lbf/f}{\text{t}}^{2}\) (as loading per unit area) in the negative Z direction. The target quantity is the displacement of point \(A\) in the direction of the load. We provided evidence above to support the reference values of the target quantity to be likely in the interval from 0.30200ʹ to 0.30204ʹ for shear-flexible shells, and approximately 0.3006ʹ for the shear-rigid shells.
6.2 Twisted Beam
The generating section of the surface is a straight line segment of length 1.1ʹʹ, extruded in the \(x\) direction to a total cantilevered length of 12ʹʹ with a 90° counterclockwise twist about the \(x\) axis (Fig. 3). This benchmark is geared towards quadrilateral finite elements, as it tests the ability of these elements to handle warping of the element surface to accommodate the pre-twist of the structure [91]. The structure is loaded by total shear forces of 1.0 lbf in the \(y\) or the \(z\) direction, uniformly distributed along the edge \(A\). The Young’s modulus is \(29\times {10}^{6} {\text{psi}}\), and the Poisson ratio is 0.22.
The thickness of the shell was taken variously as 0.32ʹʹ in [14], 0.05ʹʹ in [27], and 0.0032ʹʹ in [52]. The test was proposed with the thickness 0.32ʹʹ by MacNeal and Harder [14], who reported the deflections of the midpoint of edge \(A\) as 0.001754ʹʹ (for load \({F}_{y}\)), and 0.005424ʹʹ (for load \({F}_{z}\)) [14]. These numbers were apparently derived from a beam analytical model, but no details concerning the assumptions and limitations were provided. A couple of works introduced thinner variants of this structure. The motivation was to test locking behaviors, in addition to the test of the sensitivity to warping. Simó et al. [27] (thickness 0.05ʹʹ) and Belytschko et al. [52] (thickness 0.0032ʹʹ) provide even fewer details concerning the reference values. Belytschko et al. [52] reported 0.001294 ʹʹ (for load \({F}_{y}\)), and 0.005256ʹʹ (for load \({F}_{z}\)), where the loads were scaled down with a factor of 1.0e6.
In an attempt to address this uncertainty, we computed a set of reference values for the thicknesses 0.32ʹʹ and 0.0032ʹʹ. The commercial finite element software, Abaqus, was employed with linear finite elements, both shear-rigid (S4R5—quadrilateral, and STRI3—triangle), and shear-flexible (S4—quadrilateral, and S3—triangle). The results of extrapolations from datasets obtained with uniform meshes, the coarsest of which had 16 elements across the width, and 192 elements along the length of the shell, and where each successively finer mesh was obtained by bisection, are shown in Table 10. For the thickness 0.0032ʹʹ, the applied forces were scaled down to \(1.0\times {10}^{-6} {\text{lbf}}\). For the thinner variant, the results are in excellent agreement among the four element types: the differences are less than 0.02%. The agreement is not that close for the thicker variant, the maximum difference amounting to approximately 0.5%. The source of the differences could potentially be attributed to shear flexibility. It is also noteworthy that the “exact” solutions of Belytschko et al. [52] both overestimate, for one loading direction, and underestimate, for the other loading direction, the deflections obtained with the finite element models. Again, the source of the discrepancy is not known, given that no details were provided for the “exact” solution.
6.3 Z-Section Cantilever (LE5)
The Z-section cantilever under torsional loading is a test recommended by the National Agency for Finite Element Methods and Standards (U.K.) [92]. This appears to be the only test of a shell structure where the target quantity is stress. Figure 4 illustrates the structure. All dimensions are in meters. The cantilever is 10 m long, the flanges are 1 m wide, and the width of the web is 2 m. The thickness is uniform, \(0.1\, {\text{m}}\). The structure is subject to torsional moment of \(2.0 {\text{MNm}}\), generated by the two forces uniformly distributed across the flanges, \(S=0.6 {\text{MN}}\). The Young’s modulus is taken as \(210 {\text{GPa}}\), and the Poisson ratio is 0.3. The target quantity is the mid-surface axial stress (\({\sigma }_{x}\)) at point \(A\) (at the edge of a flange, 2.5 m from the clamped end) of value \(-108 {\text{MPa}}\) (compressive) [92]. In addition to being the only test in which stress is the target quantity, this is also the only benchmark which features folded shells.
The original target value of the stress really is not very reliable. An investigation using extrapolation from very fine meshes using the robust flat-facet triangular finite element [24] resulted in the limit-value estimate of \(-111.06 {\text{MPa}}\). In addition, we provide supporting evidence obtained with the commercial finite element software, Abaqus, using shear-flexible linear (S4) and quadratic (S8R) quadrilateral finite elements: Refer to Tables 11 and 12. The linear finite element resulted in data that could be extrapolated to support our own prediction, while the data obtained with the quadratic finite element was not suitable for extrapolation, but nevertheless approached our predicted values of stress. Furthermore, Table 13 presents the data for the quadratic shear-rigid element S8R5. The extrapolated value is an excellent agreement with Table 11.
6.4 Partially Clamped Hyperbolic Paraboloid Shell
The partially clamped hyperbolic paraboloid shell has been proposed as a good test of inextensible bending response in thin shells [93]. Figure 5 shows the surface that can be expressed in the global cartesian coordinates with the formula \(z=-{x}^{2}+{y}^{2}\), where \(-1/2\le x\le 1/2\) and \(-1/2\le y\le 1/2\) (dimensions in meters). The material properties are \(E=2\times {10}^{11} \mathrm{Pa}, \nu =0.3\), and the loading is a body load of \(8000 {\text{N/m}}^{3}\).
This is one of the few benchmarks where both local (pointwise deflection) and global (strain energy) target quantities are provided. The solution is proposed in Ref. [31] for the strain energy and the displacement in the load direction at point \(A\). The values of the target quantities are only provided for shear-flexible shells, but as long as the shell ratio of span to thickness is quite large, the difference of results obtained with shear-rigid models relative to the benchmark values will not be excessive.
The target data from Ref. [31] is summarized in Table 14. Importantly, these results were computed for one specific mesh (cubic MITC16 quadrilateral, with 48 elements per side), and therefore should not be used as a benchmark target quantity. Here we compute the solution in the limit of zero element size using Richardson extrapolation. Firstly, we employ a commercial finite element software, Abaqus, using the shear-flexible linear element S4. Table 15 shows the deflection of point \(A\) computed for the three considered thicknesses. The predictions exceed the values in Table 14. For the two moderately thin shell configurations, the difference is slight; for the very thin shell (\(L/t=10000\)) the difference amounts to approximately 1%. The reason for this discrepancy is not obvious. The results for the strain-energy target quantity are shown in Table 16, and they follow a similar trend as the deflection data.
Secondly, we provide evidence by solving the problem with the robust shear-flexible flat-facet triangular finite element of [24]. Tables 17 and 18 show the estimates of the deflection and strain energy targets. These numbers are generally within a fraction of a percent off the results reported in [31]. Therefore, the extrapolation numbers reported in Tables 17 and 18 are the best estimates of the target quantities in this benchmark.
6.5 Hyperboloid of Revolution with \(cos(2\phi )\)—Distributed Pressure
Two benchmarks are represented here: the difference between them is a support condition at one of the edges. These tests have been proposed by Hiller and Bathe [33]. The structure is a single-sheet hyperboloid of revolution. It is loaded with a self-equilibrated normal pressure in the interior, with circumferential variation around the axis of the hyperboloid according to \(cos(2\phi )\). Three planes of symmetry are used to reduce the geometry to one eighth of the full shell. The fourth edge is either free, or clamped. The goal is to study a non-trivial shell, with nonzero Gaussian curvature, either to explore bending-dominated response (when the circular edge is free), or to subject the shell to membrane-dominated response and to produce a boundary layer (when the circular edge is clamped). Figure 6 shows the surface that can be expressed in the global Cartesian coordinates with the formula \(1+{y}^{2}={x}^{2}+{z}^{2}\), where \(-1\le y\le 1\) (dimensions in meters). The material properties are \(E=2\times {10}^{11} \mathrm{Pa}, \; \nu =0.3\), and the magnitude of the applied pressure is \({p}_{0}=1.0 \mathrm{MPa}.\)
The reference solutions in terms of strain energy have been obtained in [33] and are presented for the free hyperboloid in Table 19, and for the clamped hyperboloid in Table 20. In addition, the flat-facet triangular element of [24] (T3FF) was used to verify the solutions of [33]. Both formulations are shear flexible, and both formulations are robust for very small thicknesses (i.e. they avoid thickness locking).
Note the scaling of the strain energy: changing the thickness of the shell with a factor of 10 scales the energy with the factor of \({10}^{3}\) in the bending-dominated case, whereas the scaling is linear in the membrane-dominated case.
The two independent sets of results, from Ref. [33] and from Ref. [24], are in excellent agreement. The maximum difference can be found to be approximately 1% for the third row in the Table 19, and appears to be a bit of an anomaly; the reason for that is at the moment unknown.
6.6 Raasch Hook
The Raasch hook structure consists of two joined strips of circular arcs, which are responding to a transverse load by torsion. Consequently, the transfer of twisting moments from element to element is crucial, and shear-flexible shell element formulations are known to diverge from the correct deflection due to uncontrolled spurious transverse shear [88, 89, 94]. Figure 7 describes the geometry. The strip is of cross section \(2\times 20 {\text{in}}\). Shear load in the Z direction is applied at the free edge, of magnitude \(0.05 \text{lbf/in}\). The elastic properties are \(E=3300 {\text{psi}}\), \(\nu =0.35\). The target quantity is the displacement of point \(A\) in the direction of the applied load (positive Z direction).
The original source listed solution obtained with hybrid solid elements of \(4.9352^{\prime\prime}\) [88]. However, this result was provided for the finest considered mesh only, not as a limit value. Schoop computed an analytical solution using a theory of curved beams as \(4.7561^{\prime\prime}\), [94]. This model incorporated warping of the cross section, but not shear deformation. According to [88], the contribution of transverse shear flexibility can account for around 5% of the tip deflection. The shear-compensated result of Schoop is \(4.7561\times 1.05=4.9939^{\prime\prime}\), which is in reasonable agreement with \(4.9352^{\prime\prime}\) of [88] (i.e. 1.2% higher). A further data point has been provided in Kemp et al. [95] using a solid-shell finite element: \(5.027^{\prime\prime}\). However, it is not clear whether this number represented the solution on a particular mesh or an approach to the limit. Finally, the Abaqus verification manual states the reference solution of \(5.020^{\prime\prime}\) obtained for a 20 × 144 × 2 mesh of C3D20R hexahedral elements. Our own computation with the serendipity 20-node hexahedral elements extrapolated to the limit produced a refined estimate of \(5.022^{\prime\prime}\).
Strictly speaking, the reference values discussed above are only appropriate for shear-flexible shells. This does not mean that the benchmark is useless for shear-rigid formulations, but an appropriate value of the target quantity is at the moment not available. (That deflection magnitude will be lower, probably by a couple of percent.)
6.7 Open-Source Implementation
In order to facilitate correctness checks that anyone wishes to perform on the data from these benchmarks, we provide the Github repository, ShellBenchmarking.jl [96], where we solve all the above benchmark problems using the shear-flexible flat-facet triangular shell element [24].
7 Conclusions
Providing evidence that a finite element formulation is convergent represents a very important constituent of papers on this subject. The present paper strives to point out where many publications fall short of the state-of-the-art verification practices.
Too often the results are provided only in graphical form (charts), which makes it hard or impossible to verify convergence (or the lack thereof). Also, even if the results are provided in tabular form, it is often left up to the reader to attempt to use the numerical data to draw conclusions as to whether or not the formulation can be verified by predicting the limit value obtained by infinite refinement. This practice needs to change, and all developers of finite element formulations must provide evidence that their formulation converges to the correct numbers. Richardson extrapolation is an invaluable tool in this respect.
Benchmarks are not of much use if they are not designed properly. Some benchmarks are applicable only to a particular class of shell models. We considered the case of concentrated loads, which are an “illegal” load case for shear-flexible shells: deflections under the forces are infinite in the limit of infinite refinement, and therefore those deflections must be considered illegitimate target benchmark values. Clearly, the answer is to apply such benchmarks only to the class of shell models that will not result in infinitely large deflections (Kirchhoff–Love).
A crucial component of the verification process is a reliable collection of benchmarks, which is as complete as possible. We discuss a couple of examples of the process through which the benchmark value is determined. At times we may be surprised to find how flimsy the supporting evidence can be. Searching the benchmark value based on the best available evidence is imperative. We provide a list of benchmarks that we deem suitable for both shear-flexible (Mindlin-Reissner) and shear-rigid (Kirchhoff–Love) shells. An important aspect of verification is to include all benchmarks which have failed some formulations in the past. Put another way, if we suspect that our formulation might be susceptible to some failure, we should test it with a benchmark problem capable of detecting that failure. Publishing only benchmarks in which our formulation succeeded is evidently wrong.
Finally, we wish to stress the importance of making it possible for the readers of our papers to reproduce our results for themselves. This would usually mean making the software used to compute the results available together with the paper itself. While this is rare at the moment, we are hopeful that this practice will become established in the future. Reproducible science via published open-source benchmarking is invaluable for the field. In order to lead by example, the benchmark problems presented in this paper are solved in the open-source package indicated in the data availability statement.
Data Availability
The source code and data used to produce our own results in this article are freely available in the repository https://github.com/PetrKryslUCSD/ShellBenchmarking.jl.
References
Yang HTY, Saigal S, Liaw DG (1990) Advances of thin shell finite-elements and some applications. 1. Comput Struct 35(4):481–504
Yang HTY et al (2000) A survey of recent shell finite elements. Int J Numer Methods Eng 47(1–3):101–127
Bischoff M et al (2004) Models and finite elements for thin-walled structures. In: Stein E, de Borst R (eds) Encyclopedia of computational mechanics. Wiley, Chichester
Bischoff M (2018) Finite elements for plates and shells. In: Altenbach H, Öchsner A (eds) Encyclopedia of continuum mechanics. Springer, Berlin, pp 1–23
Babuska I, Oden JT (2004) Verification and validation in computational engineering and science: basic concepts. Comput Methods Appl Mech Eng 193(36–38):4057–4066
Scordelis AC, Lo KS (1964) Computer analysis of cylindrical shells. ACI J Proc. https://doi.org/10.14359/7796
Gibson J (1961) The design of cylindrical shell roofs, 2nd edn. E & F N Spon, New York
Dawe DJ (1975) High-order triangular finite element for shell analysis. Int J Solids Struct 11(10):1097–1110
Cantin G, Clough RW (1968) A curved, cylindrical-shell, finite element. AIAA J 6(6):1057–1062
Johnson CP (1968) The analysis of thin shells by a finite element procedure. In: Civil Engineering. Universe of California, Berkeley, Berkeley
Carr AJ (1967) A refined finite element of thin shells. In: Civil Engineering. University of California, Berkeley, Berkeley, CA
Clough RW, Johnson CP (1968) A finite element approximation for the analysis of thin shells. Int J Solids Struct 4(1):43–60
Cowper GR, Lindberg GM, Olson MD (1970) A shallow shell finite element of triangular shape. Int J Solids Struct 6(8):1133–1156
Macneal RH, Harder RL (1985) A proposed standard set of problems to test finite element accuracy. Finite Elem Anal Des 1(1):3–20
Belytschko T et al (1985) Stress projection for membrane and shear locking in shell finite-elements. Comput Methods Appl Mech Eng 51(1–3):221–258
Forsberg K, Hartung K (1970) An evaluation of finite difference and finite element techniques for analysis of general shells. In: Symposium on High Speed Computing of Elastic Structures. IUTAM, Liege
Argyris J et al (1986) Trunc for shells—an element possibly to the taste of Irons, Bruce. Int J Numer Methods Eng 22(1):93–115
Szabo BA, Sahrmann GJ (1988) Hierarchic plate and shell models based on P-extension. Int J Numer Methods Eng 26(8):1855–1881
Kiendl J et al (2009) Isogeometric shell analysis with Kirchhoff-Love elements. Comput Methods Appl Mech Eng 198(49–52):3902–3914
Kiendl J, Marino E, De Lorenzis L (2017) Isogeometric collocation for the Reissner-Mindlin shell problem. Comput Methods Appl Mech Eng 325:645–665
Ashwell DG (1976) Strain Elements, with application to arches, rings and cylindrical shells. In: Conference on Finite Elements Applied to Thin Shells and Curved Members. Wiley, Cardiff
ABAQUS/Standard User's Manual (2018) Dassault Systemes Simulia Corp
Krysl P (2021) Finite element modeling with Abaqus and Python for thermal and stress analysis, 3rd edn. Pressure Cooker Press, San Diego
Krysl P (2022) Robust flat-facet triangular shell finite element. Int J Numer Methods Eng 123:2399
Chen J-S, Wang D (2006) A constrained reproducing kernel particle formulation for shear deformable shell in Cartesian coordinates. Int J Numer Methods Eng 68(2):151–172
Morley LSD, Morris AJ (1978) “Conflict between finite elements and shell theory”, Technical report, Royal Aicraft Establishment Report, London
Simo JC, Fox DD, Rifai MS (1989) On a stress resultant geometrically exact shell-model. 2. The linear-theory—computational aspects. Comput Methods Appl Mech Eng 73(1):53–92
Winkler R, Plakomytis D (2016) A new shell finite element with drilling degrees of freedom and its relation to existing formulations. In Eccomas Proceedia, MS 908—verification and validation of structural mechanics simulation models
Ko Y, Lee PS, Bathe KJ (2016) The MITC4+shell element and its performance. Comput Struct 169:57–68
Lee PS, Bathe KJ (2004) Development of MITC isotropic triangular shell finite elements. Comput Struct 82(11–12):945–962
Bathe KJ, Iosilevich A, Chapelle D (2000) An evaluation of the MITC shell elements. Comput Struct 75(1):1–30
Bathe KJ, Lee PS (2011) Measuring the convergence behavior of shell analysis schemes. Comput Struct 89(3–4):285–301
Hiller JF, Bathe KJ (2003) Measuring convergence of mixed finite element discretizations: an application to shell structures. Comput Struct 81(8–11):639–654
Ko Y, Lee PS, Bathe KJ (2017) A new 4-node MITC element for analysis of two-dimensional solids and its formulation in a shell element. Comput Struct 192:34–49
Sangtarash H et al (2021) A high-performance four-node flat shell element with drilling degrees of freedom. Eng Comput 37(4):2837–2852
Shin CM, Lee BC (2014) Development of a strain-smoothed three-node triangular flat shell element with drilling degrees of freedom. Finite Elem Anal Des 86:71–80
Allman DJ (1994) A basic flat facet finite-element for the analysis of general shells. Int J Numer Methods Eng 37(1):19–35
Krysl P, Belytschko T (1996) Analysis of thin shells by the element-free Galerkin method. Int J Solids Struct 33(20–22):3057–3078
Ko Y et al (2017) Performance of the MITC3+and MITC4+shell elements in widely-used benchmark problems. Comput Struct 193:187–206
Rezaiee-Pajand M, Yaghoobi M (2018) An efficient flat shell element. Meccanica 53(4–5):1015–1035
de Sousa RJA et al (2005) A new one-point quadrature enhanced assumed strain (EAS) solid-shell element with multiple integration points along thickness: part I—geometrically linear applications. Int J Numer Methods Eng 62(7):952–977
Hu P, Xia Y, Tang LM (2011) A four-node Reissner-Mindlin shell with assumed displacement quasi-conforming method. CMES-Comput Model Eng Sci 73(2):103–135
De Sousa RJA et al (2003) A new volumetric and shear locking-free 3D enhanced strain element. Eng Comput (Swansea, Wales) 20(7–8):896–925
Nguyen-Thanh N et al (2008) A smoothed finite element method for shell analysis. Comput Methods Appl Mech Eng 198(2):165–177
Moreira RAS, Dias Rodrigues J (2011) A non-conforming plate facet-shell finite element with drilling stiffness. Finite Elem Anal Des 47(9):973–981
Abed-Meraim F, Combescure A (2002) SHB8PS—a new adaptative, assumed-strain continuum mechanics shell element for impact analysis. Comput Struct 80(9–10):791–803
Allman DJ (1984) A compatible triangular element including vertex rotations for plane elasticity analysis. Comput Struct 19(1–2):1–8
Andelfinger U, Ramm E (1993) EAS-elements for 2-dimensional, 3-dimensional, plate and shell structures and their equivalence to HR-elements. Int J Numer Methods Eng 36(8):1311–1337
Areias PMA et al (2003) Analysis of 3D problems using a new enhanced strain hexahedral element. Int J Numer Methods Eng 58(11):1637–1682
Areias PMA, Song JH, Belytschko T (2005) Finite-strain quadrilateral shell element based on discrete Kirchhoff-Love constraints. Int J Numer Methods Eng 64(9):1166–1206
Belytschko T, Leviathan I (1994) Physical stabilization of the 4-node shell element with one-point quadrature. Comput Methods Appl Mech Eng 113(3–4):321–350
Belytschko T, Wong BL, Stolarski H (1989) Assumed strain stabilization procedure for the 9-node Lagrange shell element. Int J Numer Methods Eng 28(2):385–414
Choi CK, Lee PS, Park YM (1999) Defect-free 4-node flat shell element: NMS-4F element. Struct Eng Mech 8(2):207–231
Cook RD (1993) further development of a 3-node triangular shell element. Int J Numer Methods Eng 36(8):1413–1425
Cook RD (1994) 4-Node flat shell element—drilling degrees of freedom, membrane bending coupling, warped geometry, and behavior. Comput Struct 50(4):549–555
de Sa J et al (2002) Development of shear locking-free shell elements using an enhanced assumed strain formulation. Int J Numer Methods Eng 53(7):1721–1750
de Sousa RJA et al (2006) A new one-point quadrature enhanced assumed strain (EAS) solid-shell element with multiple integration points along thickness—Part II: nonlinear applications. Int J Numer Methods Eng 67(2):160–188
Groenwold AA, Stander N (1995) An efficient 4-node 24 dof thick shell finite element with 5-point quadrature. Eng Comput 12(8):723–747
Gruttmann F, Wagner W (2005) A linear quadrilateral shell element with fast stiffness computation. Comput Methods Appl Mech Eng 194(39–41):4279–4300
Hauptmann R et al (2001) “Solid-shell” elements with linear and quadratic shape functions at large deformations with nearly incompressible materials. Comput Struct 79(18):1671–1685
Hauptmann R, Schweizerhof K (1998) A systematic development of “solid-shell” element formulations for linear and non-linear analyses employing only displacement degrees of freedom. Int J Numer Methods Eng 42(1):49–69
Hughes TJR, Liu WK (1981) Non-linear finite-element analysis of shells. 2. Two-dimensional shells. Comput Methods Appl Mech Eng 27(2):167–181
Ibrahimbegovic A, Frey F (1994) Stress resultant geometrically nonlinear shell theory with drilling rotations. 3. Linearized kinematics. Int J Numer Methods Eng 37(21):3659–3683
Kim KD, Liu GZ, Han SC (2005) A resultant 8-node solid-shell element for geometrically nonlinear analysis. Comput Mech 35(5):315–331
Kim KD, Lomboy GR, Voyiadjis GZ (2003) A 4-node assumed strain quasi-conforming shell element with 6 degrees of freedom. Int J Numer Methods Eng 58(14):2177–2200
Klinkel S, Gruttmann F, Wagner W (2006) A robust non-linear solid shell element based on a mixed variational formulation. Comput Methods Appl Mech Eng 195(1–3):179–201
Liu J, Riggs HR, Tessler A (2000) A four-node, shear-deformable shell element developed via explicit Kirchhoff constraints. Int J Numer Methods Eng 49(8):1065–1086
Liu ML, To CWS (1998) A further study of hybrid strain-based three-node flat triangular shell elements. Finite Elem Anal Des 31(2):135–152
Liu WK et al (1986) Resultant-stress degenerated-shell element. Comput Methods Appl Mech Eng 55(3):259–300
Mostafa M (2016) An improved solid-shell element based on ANS and EAS concepts. Int J Numer Meth Eng 108(11):1362–1380
Mostafa M, Sivaselvan MV, Felippa CA (2013) A solid-shell corotational element based on ANDES, ANS and EAS for geometrically nonlinear structural analysis. Int J Numer Methods Eng 95(2):145–180
Nguyen-Van H, Mai-Duy N, Tran-Cong T (2009) An improved quadrilateral flat element with drilling degrees of freedom for shell structural analysis. CMES Comput Model Eng Sci 49(2):81–111
Providas E, Kattis MA (2000) An assessment of two fundamental flat triangular shell elements with drilling rotations. Comput Struct 77(2):129–139
Rhiu JJ, Lee SW (1987) A new efficient mixed formulation for thin shell finite-element models. Int J Numer Methods Eng 24(3):581–604
Saleeb AF, Chang TY, Graf W (1987) A quadrilateral shell element using a mixed formulation. Comput Struct 26(5):787–803
Wang CS, Hu P (2012) Quasi-conforming triangular Reissner-Mindlin shell elements by using Timoshenko’s Beam Function. CMES Comput Model Eng Sci 88(5):325–350
Babuska I, Oden JT (1992) Benchmark computation: what is the purpose and meaning? IACM Bull 7(4):83–84
Niemi AH, Hakula H, Pitkäranta J (2008) Point load on a shell. In: Kunisch K, Of G, Steinbach O (eds) Numerical mathematics and advanced applications. Springer, Berlin
Chapelle D, Bathe KJ (2000) The mathematical shell model underlying general shell elements. Int J Numer Methods Eng 48(2):289–313
Chapelle D, Bathe KJ (2001) Optimal consistency errors for general shell elements. C R Acad Sci Ser I-Math 332(8):771–776
Briassoulis D (2002) Testing the asymptotic behaviour of shell elements—Part I: the classical benchmark tests. Int J Numer Methods Eng 54(3):421–452
Briassoulis D (2002) Testing the asymptotic behaviour of shell elements—Part II: new limit tests: analytical solutions and the RFNS element case. Int J Numer Meth Eng 54(5):631–670
Briassoulis D (2005) Asymptotic deformation modes of benchmark problems suitable for evaluating shell elements. Comput Methods Appl Mech Eng 194(21–24):2385–2405
Lee PS, Bathe KJ (2002) On the asymptotic behavior of shell structures and the evaluation in finite element solutions. Comput Struct 80(3–4):235–255
Da Veiga LB (2003) Asymptotic energy behavior of two classical intermediate benchmark shell problems. Math Models Methods Appl Sci 13(9):1279–1302
da Veiga LB, Chinosi C (2004) Numerical evaluation of the asymptotic energy behavior of intermediate shells with application to two classical benchmark tests. Comput Struct 82(6):525–534
Da Veiga LB, Hakula H, Pitkaranta J (2008) Asymptotic and numerical analysis of the eigenvalue problem for a clamped cylindrical shell. Math Models Methods Appl Sci 18(11):1983–2002
Knight NF (1997) Raasch challenge for shell elements. In: AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference (37 ; Salt Lake City, UT 1996-04-15). American Institute of Aeronautics and Astronautics, Reston, VA, pp 375–381
MacNeal RH et al (1998) The treatment of shell normals in finite element analysis. Finite Elem Anal Des 30(3):235–242
Belytschko T et al (1985) Stress projection for membrane and shear locking in shell finite elements. Comput Methods Appl Mech Eng 51(1–3):221–258
Zupan D, Saje M (2004) On “A proposed standard set of problems to test finite element accuracy”: the twisted beam. Finite Elem Anal Des 40(11):1445–1451
NAFEMS (1990) Z-section cantilever—analysis type: linear elastic. In: The standard NAFEMS Benchmarks. National Agency for Finite Element Methods and Standards (U.K.)
Bathe KJ, Chapelle D (2003) The finite element analysis of shells—fundamentals. Springer, Berlin, p 330
Schoop H, Hornig J, Wenzel T (2002) Remarks on Raasch’s Hook. Tech Mech 22(4):259–270
Kemp BL, Cho C, Lee SW (1998) A four-node solid shell element formulation with assumed strain. Int J Numer Methods Eng 43(5):909–924
Krysl P (2022) ShellBenchmarking.jl. https://github.com/PetrKryslUCSD/ShellBenchmarking.jl
Acknowledgements
The reviewers are thanked for insightful and helpful comments. The manuscript benefited tremendously from their input.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Krysl, P., Chen, JS. Benchmarking Computational Shell Models. Arch Computat Methods Eng 30, 301–315 (2023). https://doi.org/10.1007/s11831-022-09798-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11831-022-09798-5