Global Properties of Eigenvalues of Parametric Rank One Perturbations for Unstructured and Structured Matrices

Abstract

General properties of eigenvalues of $A+\tau uv^*$ as functions of $\tau \in {\mathbb {C} }$ or $\tau \in {\mathbb {R} }$ or $\tau ={{\,\mathrm{{e}}\,}}^{{{\,\mathrm{{i}}\,}}\theta }$ on the unit circle are considered. In particular, the problem of existence of global analytic formulas for eigenvalues is addressed. Furthermore, the limits of eigenvalues with $\tau \rightarrow \infty$ are discussed in detail. The following classes of matrices are considered: complex (without additional structure), real (without additional structure), complex H-selfadjoint and real J-Hamiltonian.

1 Introduction

The eigenvalues of matrices of the form $A+\tau uv^*$, viewed as a rank one parametric perturbation of the matrix A, have been discussed in a vast literature. We mention the classical works of Lidskii [23], Vishik and Lyusternik [43], as well as the more general treatment of eigenvalues of perturbations of the matrix in the books by Kato [18] and Baumgärtel [4]. Recently, Moro, Burke and Overton returned to the results of Lidskii in a more detailed analysis [32], while Karow obtained a detailed analysis of the situation for small values of the parameter [17] in terms of structured pseudospectra. Obviously, parametric perturbations appear in many different contexts. The works most closely related to the current one concern rank two perturbations by Kula, Wojtylak and Wysoczański [21], matrix pencils by De Terán, Dopico and Moro [6] and Mehl, Mehrmann and Wojtylak [29, 30] and matrix polynomials by De Terán and Dopico [7].

While the behaviour of eigenvalues for $\tau \rightarrow 0$ (i.e. local behaviour), is fully understood, the behaviour for $\tau$ converging to infinity needs a separate analysis, as we will show in the course of the paper. Furthermore, the problem of global properties of eigenvalues as functions of the parameter (loosely speaking, the behaviour for intermediate values of $\tau$) still has open ends, cf. e.g. the recent paper by C.K. Li and F. Zhang [22]. The main difficulty lies in the fact that the eigenvalues cannot be defined neither analytically nor uniquely, even if we restrict the parameter $\tau$ to real numbers. As is well-known the problem does not occur in the case of Hermitian matrices where an analytic function of $\tau$ with Hermitian values has eigenvalues and eigenvectors which can be arranged such that they are analytic as functions of $\tau$ (Rellich’s theorem) [35]. Other cases where the difficulty is detoured appear, e.g., in a paper by Gingold and Hsieh [12], where it is assumed that all eigenvalues are real, or in the series of papers of de Snoo (with different coauthors) [8, 9, 38, 39] where only one distinguished eigenvalue (the so called eigenvalue of nonpositive type) is studied for all real values of $\tau$.

Let us review now our current contribution. To understand the global properties with respect to the complex parameter $\tau$ we will consider parametric perturbations of two kinds: $A+t uv^*$, where $t\in {\mathbb {R} }$, or $A+{{\,\mathrm{{e}}\,}}^{{{\,\mathrm{{i}}\,}}\theta } uv^*$, where $\theta \in [0,2\pi )$. The former case was investigated already in our earlier paper [34], we review the basic notions in Sect. 2. However, we have not found the latter perturbations in the literature. We study them in Sect. 3, providing elementary results for further analysis.

Joining these two pictures together leads to new results on global behaviour of the eigenvalues in Sect. 4. Our main interest lies in generic behaviour of the eigenvalues, i.e., we address a question what happens when a matrix A (possibly very untypical and strange) is fixed and two vectors u, v are chosen numerically (we intentionally do not use the word ‘randomly’ here). One of our main results (Theorem 11) shows that the eigenvalues of $A+\tau uv^\top$ can be defined globally as analytic functions in this situation for real $\tau$. On the contrary, if one restricts only to real vectors u, v this is no longer possible (Theorem 13).

In Sect. 5 we study the second main problem of the paper: the limits of eigenvalues for large values of the parameter. Although similar results can be found in the literature we have decided to provide a full description, for all possible (not only generic) vectors u, v. This is motivated by our research in the following Sect. 6, where we apply these results to various classes of structured matrices. We also note there the classes for which a global analytic definition of eigenvalues is not possible (see Theorem 24). In Sect. 7 we apply the general results to the class of matrices with nonnegative entries.

Although we focus on parametric rank one perturbations, we mention here that the influence of a possibly non-parametric rank one perturbation on the invariant factors of a matrix has a rich history as well, see, e.g., the papers by Thompson [41] and M. Krupnik [20]. Together with the the works by Hörmander and Melin [16], Dopico and Moro [33], Savchenko [36, 37] and Mehl, Mehrmann, Ran and Rodman [24,25,26] they constitute a linear algebra basis for our research, developed in our previous paper [34]. What we add to these methods is some portion of complex analysis, by using the function $Q(\lambda )=v^\top (\lambda I_n- A)^{-1}u$ and its holomorphic properties. This idea came to us through multiple contacts and collaborations with Henk de Snoo (cf. in particular the line of papers on rank one perturbations [1, 13,14,15, 38, 39]), for which we express our gratitude here.

2 Preliminaries

If X is a complex matrix (in particular, a vector) then by ${\bar{X}}$ we define the entrywise complex conjugate of X, further we set $X^*={\bar{X}}^\top$. We will deal with rank one perturbations

$$\begin{aligned} B(\tau )=A+\tau uv^*, \end{aligned}$$

with $A\in {\mathbb {C} }^{n\times n}$, $u,v\in {\mathbb {C} }^n$. The parameter $\tau$ is a complex variable, we will often write it as $t{{\,\mathrm{{e}}\,}}^{{{\,\mathrm{{i}}\,}}\theta }$ and fix either one of t and $\theta$. We review now some necessary background and fix the notation.

Let a matrix A be given. We say that a property (of a triple A, u, v) holds for generic vectors $u,v\in {\mathbb {C} }^n$ if there exists a finite set of nonzero complex polynomials of 2n variables, which are zero on all u, v not enjoying the property. Note that the polynomials might depend on the matrix A. In some places below a certain property will hold for generic $u,{\bar{v}}$. This happens as in the current paper we consider the perturbations $uv^*$, while in [34] $uv^\top$ was used (even for complex vector u, v) . In any case, i.e., either u, v generic or $u,{\bar{v}}$ generic, the closure of the set of ‘wrong’ vectors has an empty interior.

By $m_A(\lambda )$ we denote the minimal polynomial of A. Define

$$\begin{aligned} p_{uv}(\lambda )= v^* m_A(\lambda )(\lambda I_n -A)^{-1} u \end{aligned}$$

(1)

and observe that it is a polynomial, due to the formula for the inverse of a Jordan block (cf. [34]). Let $\lambda _1 , \ldots , \lambda _r$ be the (mutually different) eigenvalues of A, and corresponding to the eigenvalue $\lambda _j$, let $n_{j,1} \ge n_{j,2} \ge \cdots \ge n_{j,\kappa _j}$ be the sizes of the Jordan blocks of A. We shall denote the degree of the polynomial $m_A(\lambda )$ by l, so

$$\begin{aligned} l=\sum _{j=1}^r n_{j,1}. \end{aligned}$$

Then

$$\begin{aligned} \deg p_{uv}(\lambda )\le l-1 \end{aligned}$$

(2)

and equality holds for generic vectors $u,v\in {\mathbb {C} }^n$, see [34].

It can be also easily checked (see [36] or [34]) that the characteristic polynomial of $B(\tau )$ satisfies

$$\begin{aligned} \det (\lambda I_n-B(\tau ))= & {} \det (\lambda I_n-A)\cdot \left( 1-\tau v^*(\lambda I_n-A)^{-1}u\right) \nonumber \\= & {} \frac{\det (\lambda I_n - A)}{m_A(\lambda )}\left( m_A(\lambda )-\tau p_{uv}(\lambda )\right) . \end{aligned}$$

(3)

Therefore, the eigenvalues of $A+\tau uv^*$ which are not eigenvalues of A, are roots of the polynomial

$$\begin{aligned} p_{B(\tau )}(\lambda ) = m_A(\lambda )- \tau p_{uv}(\lambda ) . \end{aligned}$$

(4)

Note that some eigenvalues of A may be roots of this polynomial as well. Saying this differently, we have the following inclusion of spectra of matrices

$$\begin{aligned} \sigma (B(\tau ))\setminus \sigma (A)\subseteq p_{B(\tau )}^{-1}(0) \subseteq \sigma (B(\tau )),\quad \tau \in {\mathbb {C} }, \end{aligned}$$

(5)

but each of these inclusions may be strict. Further, let us call an eigenvalue of A frozen (by u, v) if it is an eigenvalue of $B(\tau )$ for every complex $\tau$. Directly from (3) we see that each frozen eigenvalue is either a root of $\det (\lambda I_n-A)/m_A(\lambda )$, then we call it structurally frozen, or a root of both $m_A(\lambda )$ and $p_{uv}(\lambda )$, and then we call it accidentally frozen. Note that, due to a rank argument, $\lambda _j$ is structurally frozen if and only if it has more than one Jordan block in the Jordan canonical form. Obviously, both types of freezing can occur simultaneously: a structurally frozen eigenvalue can be, additionally, accidentally frozen by a specific choice of vectors u, v, cf. Example 1 below.

Recall that the Jordan form of $B(\tau )$ at structurally frozen eigenvalues may vary for different u, v, which was a topic of many papers, see, e.g., [16, 34, 36]. Nonetheless, being structurally frozen obviously does not depend on u, v. In contrast, generically $m_A(\lambda )$ and $p_{uv}(\lambda )$ do not have a common zero [34], i.e., a slight change of u, v leads to defrosting of $\lambda _j$ (which explains the name accidentally). In spite of this, we still need to tackle such eigenvalues in the course of the paper. The main technical problem is shown by the following, almost trivial, example.

Example 1

Let $A=0\oplus A_1$, where $A_1\in {\mathbb {C} }^{(n-1)\times (n-1)}$ has a single eigenvalue at $\lambda _1\ne 0$ with a possibly nontrivial Jordan structure and let $u=v=e_1$. The eigenvalues of $B(\tau )$ are clearly $\tau$ and $\lambda _1$ and the eigenvalue $\lambda _1$ is accidentally frozen. (n.b., if the Jordan structure of $A_1$ at $\lambda _1$ consists of at least two blocks, then $\lambda _1$ is also a structurally frozen eigenvalue of A). Observe that if we define $\lambda _0(\tau )=\tau$ then for $\tau =\lambda _1$ there is a sudden change in the Jordan structure of $B(\tau )$ at $\lambda _0(\tau )$.

To handle the evolution of eigenvalues of $B(\tau )$ without getting into the trouble indicated above we introduce the rational function

$$\begin{aligned} Q(\lambda ):=v^* (\lambda I_n-A)^{-1} u= \frac{p_{uv}(\lambda )}{m_A(\lambda )}. \end{aligned}$$

(6)

It will play a central role in the analysis. Note that $Q(\lambda )$ is a rational function with poles in the set of eigenvalues of A, but not each eigenvalue is necessarily a pole of $Q(\lambda )$. More precisely, if $\lambda _j$ ($j\in \{1,\dots r\}$) is an accidentally frozen eigenvalue of A then $Q(\lambda )$ does not have a pole of the same order as the multiplicity of $\lambda _i$ as a root of $m_A(\lambda )$, i.e, in the quotient $Q(\lambda )=\frac{p_{uv}(\lambda )}{m_A(\lambda )}$ there is pole-zero cancellation.

Proposition 2

Let $A\in {\mathbb {C} }^{n\times n}$, let $\tau _0\in {\mathbb {C} }$, let $u,v\in {\mathbb {C} }^n$ and assume that $\lambda _0\in {\mathbb {C} }$ is not an eigenvalue of A. Then $\lambda _0$ is an eigenvalue of $A+\tau _0 uv^*$ of algebraic multiplicity $\kappa \in \{1,2,\dots \}$ if and only if

$$\begin{aligned} Q(\lambda _0)=\frac{1}{\tau _0},\ Q'(\lambda _0)=0,\dots ,Q^{(\kappa -1)}(\lambda _0)=0,\ Q^{(\kappa )}(\lambda _0)\ne 0. \end{aligned}$$

(7)

If this happens, then $\lambda _0$ has geometric multiplicity one, i.e., $A+\tau _0 uv^*$ has a Jordan chain of size $\kappa$ at $\lambda _0$. Finally, $\lambda _0$ is not an eigenvalue of $A+\tau _1 uv^*$ for all $\tau _1\in {\mathbb {C} }{\setminus }\{\tau _0\}$.

Remark 3

If $\kappa =1$ condition (7) should be read as $Q(\lambda _0)=1/\tau _0$, $Q'(\lambda _0)\ne 0$. In this case the implicit function theorem tells us that the eigenvalues can be defined analytically in the neigbourhood of $\tau _0,\lambda _0$. If $\kappa >1$ then the analytic definition is not possible and the eigenvalues expand as Puiseux series, that is, they behave locally as the solutions of $(\lambda -\lambda _0)^\kappa =\tau -\tau _0$, see, e.g., [4, 18, 19].

Remark 4

One may be also tempted to define the eigenvalues via solving the equation $Q(\lambda )=1/\tau$ at $\lambda _0$ being an accidentally frozen eigenvalue of A for which $Q(\lambda )$ does not have a pole at $\lambda _0$. This would be, however, a dangerous procedure, as $\lambda _0$ might get involved in a larger Jordan chain. For example let

$$\begin{aligned} B(\tau )=\begin{bmatrix} 1 &{}\quad 1 \\ 0 &{}\quad \tau \end{bmatrix} \end{aligned}$$

with an accidentally frozen eigenvalue 1 and $Q(\lambda )=1/\lambda$. Here for $\tau =1$ we get a Jordan block of size 2, but clearly the eigenvalues in a neighbourhood of $\lambda _0=1$ and $\tau _0=1$ do not behave as 1 plus the square roots of $\tau - 1$. For this reason we will avoid the accidentally frozen eigenvalues.

Remark 5

Note that in case $m_A$ and $p_{uv}$ have no common zeroes, i.e., there are no accidentally frozen eigenvalues, $Q^\prime (\lambda )$ can be expressed in terms of $m_A$ and $p_{uv}$ as follows

$$\begin{aligned} Q^\prime (\lambda )= \frac{p_{uv}^\prime (\lambda )m_A(\lambda )-p_{uv}(\lambda )m_A^\prime (\lambda )}{m_A(\lambda )^2}, \end{aligned}$$

(8)

where cancellation of roots between numerator and denominator occurs in an eigenvalue of A when corresponding to that eigenvalue there is a Jordan block of size bigger than one.

Proof of Proposition 2

For the proof of the first statement we start from the definition of $Q(\lambda )$. Note that $m_A(\lambda _0)$ is necessarily non zero, and so $p_{uv}(\lambda _0)$ is non-zero as well. If $\lambda _0$ is an eigenvalue of $B(\tau _0)$ which is not an eigenvalue of A, then, since $p_{B(\tau _0)}(\lambda _0)=0$, we have from (6) that $Q(\lambda _0)=\frac{1}{\tau _0}$, which proves the first equation in (7).

Furthermore, from the definition of $Q(\lambda )$ we have $p_{uv}(\lambda )-Q(\lambda )m_A(\lambda )$ is identically zero. So, for any $\nu$ also the $\nu$-th derivative is zero. By the Leibniz rule this gives

$$\begin{aligned} p_{uv}^{(\nu )}(\lambda )- \sum _{j=0}^\nu \begin{pmatrix} \nu \\ j\end{pmatrix} Q^{(j)}(\lambda )m_A^{(\nu -j)}(\lambda ) =0. \end{aligned}$$

We rewrite this slightly as follows:

$$\begin{aligned} p_{uv}^{(\nu )}(\lambda ) -Q(\lambda )m_A^{(\nu )}(\lambda ) =\sum _{j=1}^\nu \begin{pmatrix} \nu \\ j\end{pmatrix} Q^{(j)}(\lambda )m_A^{(\nu -j)}(\lambda ) . \end{aligned}$$

(9)

Now, if $\lambda _0$ is an eigenvalue of algebraic multiplicity $\kappa$ of $B(\tau _0)$ and not an eigenvalue of A, then for $j=0, 1, \ldots , \kappa -1$ we have $m^{(j)}_A(\lambda _0)-\tau _0 p_{uv}^{(j)}(\lambda _0)=0$. Take $\nu =1$ in (9), and set $\lambda =\lambda _0$:

$$\begin{aligned} p_{uv}^\prime (\lambda _0)-\frac{1}{\tau _0}m_A'(\lambda _0)=Q^\prime (\lambda _0)m_A(\lambda _0). \end{aligned}$$

Since $m_A(\lambda _0)\not =0$ it now follows that $Q^\prime (\lambda _0)\not =0$ when $\kappa =1$, while $Q^\prime (\lambda _0)=0$ when $\kappa >1$. Now proceed by induction. Suppose we have already shown that $Q^{(i)}(\lambda _0)=0$ for $i=1, \ldots , k <\kappa -1$. Then set $\nu =k+1$ in (9) to obtain, using the induction hypothesis, that

$$\begin{aligned} 0=p_{uv}^{(k+1)}(\lambda _0) -Q(\lambda _0)m_A^{(k+1)}(\lambda _0) = Q^{(k+1)}(\lambda _0)m_A(\lambda _0). \end{aligned}$$

Once again using the fact that $m_A(\lambda _0)\not =0$, we have that $Q^{(k+1)}(\lambda _0)=0$. Finally, for $\nu =\kappa$ in (9), and using what we have shown so far in this paragraph, we have

$$\begin{aligned} 0\not =p_{uv}^{(\kappa )}(\lambda _0) -Q(\lambda _0)m_A^{(\kappa )}(\lambda _0)=Q^{(\kappa )}(\lambda _0)m_A(\lambda _0), \end{aligned}$$

and so (7) holds.

Conversely, suppose (7) holds. Then by the definition (6) of Q we have $m_A(\lambda _0)-\tau _0p_{uv}(\lambda _0)=0$, so by (4) $\lambda _0$ is an eigenvalue of $B(\tau _0)$. Moreover, by (9) we have $m_A^{(j)} (\lambda _0)-\tau _0 p_{uv}^{(j)}(\lambda _0)=0$ for $j=1, \ldots , \kappa _1$, while $m_A^{(\kappa )} (\lambda _0)-\tau _0 p_{uv}^{(\kappa )}(\lambda _0)=\tau _0Q^{(\kappa )}(\lambda _0)m_a(\lambda _0)\not =0$. Hence, $\lambda _0$ is an eigenvalue of $B(\tau _0)$ of algebraic multiplicity $\kappa$, completing the proof of the first statement.

For the proof of the second statement, note that as $\lambda _0 I_n-A$ is invertible, any rank one perturbation of $\lambda _0 I_n-A$ can have only a one dimensional kernel. Therefore, the Jordan structure of the perturbation at $\lambda _0$ is fixed. The last statement for $\tau _1=0$ follows from the assumption that $\lambda _0\notin \sigma (A)$ and for $\tau _1\notin \{0,\tau _0\}$ directly from (7). $\square$

The statements in Proposition 2 can also be seen by viewing $1-\tau v^*(\lambda I_n-A)^{-1} u$ as a realization of the (scalar) rational function $1-\tau Q(\lambda )$. From that point of view the connection between poles of the function and eigenvalues of A, respectively, zeroes of the function and eigenvalues of $B(\tau )=A+\tau uv^*$ is well-known. For an in-depth analysis of this connection, even for matrix-valued rational matrix functions, see [2], Chapter 8. We provided above an elementary proof of the scalar case for the reader’s convenience.

Note the following example, now more involved than the one in Remark 4.

Example 6

In this example we return to the consideration of accidentally frozen eigenvalues. Let $A=\begin{bmatrix} 1 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 2\end{bmatrix}, u=v=e_1$. Then we have:

$$\begin{aligned} m_A(\lambda )&= (\lambda -1)^2(\lambda -2)=\lambda ^3-4\lambda ^2+5\lambda -2,\\ Q(\lambda )&=\frac{1}{\lambda -1}, \quad Q^\prime (\lambda )=-\frac{1}{(\lambda -1)^2},\\ p_{uv}(\lambda )&=(\lambda -1)(\lambda -2)=\lambda ^2-3\lambda +2. \end{aligned}$$

Also $B(\tau )=A+\tau uv^*=\begin{bmatrix} \tau +1 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 2\end{bmatrix}$, which has eigenvalues 1, 2 and $\tau +1$. Note that both 1 and 2 are, by definition, accidentally frozen eigenvalues, although their character is rather different.

Let us consider Proposition 2 for this example. Note that $Q^\prime (\lambda )$ has no zeroes, which tells us that there are no double eigenvalues of $B(\tau )$ which are not eigenvalues of A. However, note that the zeros of $m_A(\lambda )$ and $p_{uv}(\lambda )$ are not disjoint. In particular,

$$\begin{aligned} p_{uv}^\prime (\lambda )m_A(\lambda )-p_{uv}(\lambda )m_A^\prime (\lambda ) =(\lambda -1)^2(\lambda -2)^2, \end{aligned}$$

which detects the double eigenvalue of B(0) at $\lambda _1=1$ and a double semisimple eigenvalue of B(1) at $\lambda _2=2$, however, as can be seen from (8) the roots of this polynomial are cancelled by the roots of $m_A^2(\lambda )$.

3 Angular Parameter

In this section we will study the perturbations of the form

$$\begin{aligned} A+t {{\,\mathrm{{e}}\,}}^{{{\,\mathrm{{i}}\,}}\theta }uv^*,\quad \theta \in [0,2\pi ), \end{aligned}$$

where $t>0$ is a parameter. More precisely, we will be interested in the evolution of the sets

$$\begin{aligned} \sigma (A,u,v;t)=\bigcup _{0\le \theta <2\pi } \sigma (A+t {{\,\mathrm{{e}}\,}}^{{{\,\mathrm{{i}}\,}}\theta }uv^*){\setminus }\sigma (A), \end{aligned}$$

with the parameter $t>0$.

It should be noted that the sets $\sigma (A,u,v;t)$ are strongly related to the pseudospectral sets as introduced in e.g., [17], Definition 2.1. In fact they can be viewed as the boundaries of pseudospectral sets for the special case of rank one perturbations. The interest in [17], see in particular the beautiful result in Theorem 4.1 there, is in the small t asymptotics of these sets. Our interest below is hence more in the intermediate values of t and in the large t asymptotics of these sets.

By $z_1,\dots , z_{d}$ we denote the (mutually different) zeroes of $Q'(\lambda )$, note that some of them might happen to be accidentally frozen eigenvalues, a slight modification of Example 6 is left to the reader, see also Remark 9 below. We define $t_j$ as

$$\begin{aligned} t_j =\frac{1}{|Q(z_j)|},\ \quad j=1, \ldots ,d. \end{aligned}$$

We group some properties of the sets $\sigma (A,u,v;t)$ in one theorem. Below by a smooth closed curve we mean a ${\mathcal {C}}^\infty$–diffeomorphic image of a circle.

Theorem 7

Let $A\in {\mathbb {C} }^{n\times n}$ and let $u,v\in {\mathbb {C} }^n$ be two nonzero vectors, then the following holds.

• (i) For $t>0$, $t\ne t_j$ $(j=1,\dots , d)$ the set $\sigma (A,u,v;t)$ consists of a union of smooth closed algebraic curves that do not intersect mutually.

• (ii) For $t= t_j$ $(j=1,\dots , d)$ the set $\sigma (A,u,v;t)$ is locally diffeomorphic with the interval, except the intersection points at those $z_i$ for which $t_j=1/|Q(z_i)|$ (possibly there are several such $z_i$’s).

• (iii) For generic $u,v\in {\mathbb {C} }^n$ and for all $j=1,\dots d$ the point $z_j$ is a double eigenvalue of $A+\tau uv^*$, for $\tau =1/Q(z_j)$. Two of the curves $\sigma (A,u,v,t)$ meet for $t=t_j$ at the point $z_j$. These curves are at the point $z_j$ not differentiable, they make a right angle corner, and meet at right angles as well.

• (iv)
  $$\begin{aligned} \sigma (A)\cup \bigcup _{t>0} \sigma (A,u,v;t) \cup Q^{-1}(0)={\mathbb {C} }. \end{aligned}$$

  (10)

• (v) The function $t\rightarrow \sigma (A,u,v;t)$ is continuous in the Hausdorff metric for $t>0$.

• (vi) $\sigma (A,u,v;t)$ converges to $Q^{-1}(0)\cup \{\infty \}$ with $t\rightarrow \infty$.

Proof

First observe that

$$\begin{aligned} \sigma (A,u,v;t)=\left\{ z\in {\mathbb {C} }: \frac{1}{|Q(z)|}=t\right\} ,\quad t>0. \end{aligned}$$

Indeed, the inclusion ‘$\subseteq$’ follows from the definition of $\sigma (A,u,v;t)$ and Proposition 2. To see the converse inclusion let $1/Q(z)=\tau$, with some complex nonzero $\tau$, then again by Proposition 2z is an eigenvalue of $A+\tau uv^*$, i.e. $z\in \sigma (A,u,v;|\tau |)$.

One may rephrase the above by saying that $\sigma (A,u,v;t)$ is a level set of the modulus of a rational function 1/Q(z). Since these level sets can also be written as the set of all points $z\in \mathbb {C}$ for which $|m_A(z)|^2=t^2|p_{uv}(z)|^2$ it is clear that for each t they are algebraic curves. For $t\not = t_j$ ($j=1, \ldots , d$) the curves have no self-intersection and hence are smooth. This shows statements (i) and (ii).

Let us now prove (iii). First note that for generic $u,v\in {\mathbb {C} }^n$ there are no accidentally frozen eigenvalues, as remarked in the end of Sect. 2. Hence, every eigenvalue of $A+\tau uv^*$ of multiplicity $\kappa$, which is not an eigenvalue of A, is necessarily a zero of $Q(\lambda )-1/\tau$ of multiplicity $\kappa$, see Proposition 2. However, by Theorem 5.1 of [34] for generic $u,v\in {\mathbb {C} }^n$ all eigenvalues of $A+\tau uv^*$ which are not eigenvalues of A are of multiplicity at most two, and by Proposition 2 the geometric multiplicity is one. Therefore the meeting points are at $z_j$ with $Q'(z_j)=0$, $Q''(z_j)\ne 0$. The behaviour of the eigenvalue curves concerning right angle corners follows from the local theory on the pertubation of an eigenvalue of geometric and algebraic multiplicity two for small values of $t-t_j$ (see e.g., the results of [23], but in particular, because of the connection with pseudospectra, see [17]).

To see (iv) let $\lambda _0\in {\mathbb {C} }$ be neither an eigenvalue of A nor a zero of $Q(\lambda )$. Then $Q(\lambda _0)=1/\tau _0$ for some $\tau _0\in {\mathbb {C} }$, hence $\lambda _0\in \sigma (A,u,v;|\tau _0|)$. Statement (v) follows from Proposition 2.3 part (c) in [17]. To see (vi) note that $1/|Q(\lambda )|$, as an absolute value of a holomorphic function, does not have any local extreme points on ${\mathbb {C} }{\setminus } p_{uv}^{-1}(0)$ and it converges to infinity with $|\lambda |\rightarrow \infty$. $\square$

In Sect. 5 we will study in detail the rate of convergence in point (v) above.

Example 8

Consider the matrix

$$\begin{aligned} A=\begin{bmatrix} -2 &{} \quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 4 &{}\quad 1\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 4 \end{bmatrix} \end{aligned}$$

and the vectors

$$\begin{aligned} u =\begin{bmatrix} -0.2 + 0.7{{\,\mathrm{{i}}\,}}\\ 1.5 - 1.2{{\,\mathrm{{i}}\,}}\\ 1.5 + 0.5{{\,\mathrm{{i}}\,}}\\ 1.5 + 1.5{{\,\mathrm{{i}}\,}}\end{bmatrix} \quad \text{ and } \quad v =\begin{bmatrix} 0.5 + 0.3{{\,\mathrm{{i}}\,}}\\ 1 - 0.8{{\,\mathrm{{i}}\,}}\\ 0.8 + 0.9{{\,\mathrm{{i}}\,}}\\ -0.3 - 1.2{{\,\mathrm{{i}}\,}}\end{bmatrix}. \end{aligned}$$

In Fig. 1 one may find the graph of the corresponding function $|1/Q(\lambda )|$, and a couple of curves $\sigma (A,u,v,t)$ at values of t where double eigenvalues occur. Observe that these curves are often called level curves or contour plots of the function $|1/Q(\lambda )|$.

Fig. 1

The plot of $|1/Q(\lambda )|$ and the curves $\sigma (A,u,v,t)$ for the values of t for which there is a double eigenvalue

Remark 9

Observe that one may easily construct examples with $z_1,\dots ,z_d$ given. Let

$$\begin{aligned} A=\begin{bmatrix} 0 &{}\quad 1 &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ \vdots &{}\quad &{} \ddots &{}\quad \ddots &{}\quad 0\\ 0 &{}\quad \cdots &{}\quad \cdots &{}\quad 0 &{}\quad 1\\ a_1 &{}\quad a_2 &{}\quad \cdots &{}\quad \cdots &{}\quad a_n \end{bmatrix}, \quad u=\begin{bmatrix} 0 \\ \vdots \\ \vdots \\ 0 \\ 1\end{bmatrix}, \quad v=\begin{bmatrix} {\overline{a}}_1\\ {\overline{a}}_2\\ \vdots \\ \vdots \\ {\overline{a}}_n\end{bmatrix} \end{aligned}$$

with $a_1,\dots a_n\in {\mathbb {C} }{\setminus }\{0\}$. Then for $\tau =1$ the matrix $B(\tau )=A+\tau uv^*$ is equal to the $n\times n$ Jordan block with eigenvalue zero, and hence has an eigenvalue of multiplicity n. By a construction similar to Example 6 we may also make this eigenvalue accidentally frozen.

Example 10

In a concrete example, let

$$\begin{aligned} A=\begin{bmatrix} 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \\ 1 &{}\quad -1 &{}\quad 1\end{bmatrix}, \quad u=\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}, \quad v=\begin{bmatrix} 1 \\ -1 \\ 1\end{bmatrix}. \end{aligned}$$

Then $m_A(\lambda )=(\lambda -1)(\lambda ^2+1)$ so the eigenvalues of A are $1, \pm {{\,\mathrm{{i}}\,}}$. Further $p_{uv}(\lambda )=\lambda ^2-\lambda +1$ with roots at $\frac{1}{2}\pm \frac{\sqrt{3}}{2}{{\,\mathrm{{i}}\,}}$, and the zeroes of $Q^\prime (\lambda )$ are the zeroes of $p_{uv}^\prime (\lambda )m_A(\lambda )-p_{uv}(\lambda )m_A^\prime (\lambda )=-\lambda ^2(\lambda ^2-2\lambda +3)$ which has roots at 0 and at $1\pm \sqrt{2}{{\,\mathrm{{i}}\,}}$. The corresponding values of t are, respectively, $\frac{1}{|Q(0)|}=1$ and $\frac{1}{|Q(1\pm \sqrt{2}{{\,\mathrm{{i}}\,}})|}=\frac{4}{\sqrt{3}}$. The eigenvalues of $A+\tau uv^*$ are plotted for the values $\tau =te^{{{\,\mathrm{{i}}\,}}\theta }$ with $t=1$ and $t=\frac{4}{\sqrt{3}}$ in the graph below (Fig. 2).

Fig. 2

Eigenvalue curves (right) showing a triple eigenvalue at zero for $\tau =1$ and double eigenvalues at $1\pm \sqrt{2}i$ for $\tau =\frac{4}{\sqrt{3}}$. On the left the graph of $1/|Q(\lambda )|$ with the same eigenvalue curves plotted in the ground plane. Green stars indicate the eigenvalues of A, blue stars the roots of $p_{uv}(\lambda )$ and triangles the zeroes of $Q^\prime (\lambda )$

4 Eigenvalues as Global Functions of the Parameter

We return now to the problem of defining the eigenvalues as functions of the parameter. Recall that l stands for the degree of the minimal polynomial of A. We start with the case where we consider the parameter $\tau$ to be real.

Theorem 11

Let $A\in {\mathbb {C} }^{n\times n}$ and $u\in {\mathbb {C} }^n{\setminus }\{0\}$ be fixed. Then for all $v\in {\mathbb {C} }^n$ except some closed set with empty interior the following holds.

• (i) The eigenvalues of

  $$\begin{aligned} B(\tau )=A+\tau uv^*,\quad \tau \in (0,+\infty ), \end{aligned}$$

  which are not eigenvalues of A, can be defined uniquely (up to ordering) as functions $\lambda _1(\tau ),\dots ,\lambda _l(\tau )$ of the parameter $\tau \in (0,+\infty )$.

• (ii) The remaining part of the spectrum of $B(\tau )$ consists of structurally frozen eigenvalues of A, i.e., there are no accidentally frozen eigenvalues (see formula (5) and the paragraphs following it for definitions).

• (iii) For $i,j=1,\dots d$, $i\ne j$ one has $\lambda _i(\tau )\ne \lambda _j({\tilde{\tau }})$ for all $\tau ,{\tilde{\tau }}\in (0,+\infty )$.

• (iv) The functions $\lambda _j(t)$ can be extended to analytic functions in some open complex neighbourhood of $(0,+\infty )$.

Proof

First let us write explicitly for which u, v all the statements will hold. Due to Proposition 2 and Remark 3 the necessary and sufficient condition for this is the following: there are no accidentally frozen eigenvalues and $Q(z_j)\notin {\mathbb {R} }$ for all zeros $z_j$ of $Q'(\lambda )$. We will now show that given arbitrary $u_0,v_0$ which do not satisfy the above condition one may construct u, v, lying arbitrarily close to $u_0,v_0$ such that the condition holds on some open neighbourhood of u, v. We will do this in two steps. First let us choose ${\tilde{u}},{\tilde{v}}$ such that there are no accidentally frozen eigenvalues, i.e., there are no common eigenvalues of $m_A(\lambda )$ and $p_{{\tilde{u}}{\tilde{v}}}(\lambda )$. By [34] one may pick ${\tilde{u}}$ and ${\tilde{v}}$ arbitrarily close to $u_0,v_0$ and the desired property will hold in some small neighbourhood of ${\tilde{u}},{\tilde{v}}$. Furthermore, ${\tilde{u}},{{\,\mathrm{{e}}\,}}^{{{\,\mathrm{{i}}\,}}\theta }{\tilde{v}}$ will also obey this property for all $\theta \in (-\pi ,\pi )$. Note that one may find $\theta \ne 0$ arbitrarily small enough, so that with $v={{\,\mathrm{{e}}\,}}^{{{\,\mathrm{{i}}\,}}{\tilde{\theta }}}v$ ($|\theta -{\tilde{\theta }}|$ small enough) and $u={\tilde{u}}$ one has $Q(z_i)\notin {\mathbb {R} }$ for $i=1,\dots d$. $\square$

Observe that the statement is essentially stronger and the proof is much easier than in Theorem 6.2 of [34].

Proposition 12

The statements of Theorem 11 are also true for the angular parameter, i.e., if one replaces $\tau \in (0,+\infty )$ by $\tau ={{\,\mathrm{{e}}\,}}^{{{\,\mathrm{{i}}\,}}\theta }$, $\theta \in (0,2\pi )$ in all statements.

Proof

The equivalent condition for all the statements is in this case: there are no accidentally frozen eigenvalues and $|Q(z_j)|\ne 1$ for all zeros $z_j$ of $Q'(\lambda )$. Hence, in the last step of the proof we need to replace ${\tilde{v}}$ by $t{\tilde{v}}$ with $t>0$ small enough. $\square$

However, note that if we replace the complex numbers by the real numbers the statement is false, as the following theorem shows.

Theorem 13

Let $A\in {\mathbb {R} }^{n\times n}$ and $u,v\in {\mathbb {R} }^n$ be such that for some $\tau _0>0$ an analytic definition of eigenvalues of $A+\tau uv^\top$ is not possible due to

$$\begin{aligned} Q(x)=1/ \tau _0,\quad Q'(x)=0,\quad Q''(x)\ne 0 \end{aligned}$$

for some $x\in {\mathbb {R} }$ which is not an eigenvalue of A, cf. Remark 3. Then for all ${\tilde{A}}\in {\mathbb {R} }^{n\times n}$, ${\tilde{u}}\in {\mathbb {R} }^n$, ${\tilde{v}} \in {\mathbb {R} }^n$ with $\left\| {\tilde{v}}-v\right\|$, $\left\| {\tilde{u}}-u\right\|$ and $\left\| {\tilde{A}}-A\right\|$ sufficiently small the analytic definition of eigenvalues of ${\tilde{A}}+\tau {\tilde{u}}{\tilde{v}}^*$ is not possible due to existence of ${\tilde{x}}\in {\mathbb {R} }$, ${\tilde{\tau }}_0>0$, depending continuously on ${\tilde{A}},{\tilde{u}},{\tilde{v}}$ with

$$\begin{aligned} {\widetilde{Q}}({\tilde{x}})=1/{{\tilde{\tau }}_0},\quad {\widetilde{Q}}'({\tilde{x}})=0,\quad {\widetilde{Q}}''({\tilde{x}})\ne 0, \end{aligned}$$

where ${\widetilde{Q}}(z)$ corresponds to the perturbation ${\tilde{A}}+\tau {\tilde{u}}{\tilde{v}}^*$ as in (6).

Proof

Recall the formulas (6) and (8) and set

$$\begin{aligned} q_0(\lambda )=p_{uv}^\prime (\lambda )m_A(\lambda )-p_{uv}(\lambda )m_A^\prime (\lambda ) , \end{aligned}$$

(11)

so that

$$\begin{aligned} Q^\prime (\lambda )= \frac{q_0(\lambda )}{m_A(\lambda )^2}. \end{aligned}$$

(12)

By assumption we have that $m_A(x)\ne 0$ and $q_0(x)=0$. We also get that $q_0'(x)\ne 0$, as otherwise $Q''(x)=0$. We define ${\tilde{q}}_0(\lambda )$ analogously as $q_0(\lambda )$, i.e.,

$$\begin{aligned} {\widetilde{Q}}^\prime (\lambda )=\frac{{\tilde{q}}_0(\lambda )}{m_{{\tilde{A}}}(\lambda )}. \end{aligned}$$

Both polynomials ${\tilde{q}}_0(\lambda )$ and $m_{{\tilde{A}}}(\lambda )$ have coefficients depending continuously on the entries of ${\tilde{A}},{\tilde{u}},{\tilde{v}}$. As x is a simple zero of the polynomial $q_0(\lambda )$, which is additionally real on the real line, we have that there is a real ${\tilde{x}}$ near x such that ${\tilde{q}}_0({\tilde{x}})=0$ and $m_{{\tilde{A}}}({\tilde{x}})\ne 0$ for ${\tilde{u}}$, ${\tilde{v}}$, ${\tilde{A}}$, as in the statement. Defining ${\tilde{t}}:=1/{\widetilde{Q}}({\tilde{x}})$ finishes the proof. $\square$

Remark 14

To give a punch line to Theorem 13 we make the obvious remark that A, u, v satisfying the assumptions do exist. For each such A the set of vectors $u,v\in {\mathbb {R} }^n$ for which a double eigenvalue appears has a nonempty interior in ${\mathbb {R} }^n$, contrary to the complex case discussed in Theorem 11.

Note another reason for which the eigenvalues cannot be defined globally analytically for real matrices.

Proposition 15

Assume that the matrix $A\in {\mathbb {R} }^{n\times n}$ has no real eigenvalues and let u, v be two arbitrary nonzero real vectors. Then for some $\tau _0\in {\mathbb {R} }{\setminus }\{ 0\}$ an analytic definition of eigenvalues of $A+\tau uv^\top$ is not possible due to

$$\begin{aligned} Q(x)=1/\tau _0,\quad Q'(x)=0 \end{aligned}$$

for some $x\in {\mathbb {R} }$, cf. Remark 3.

Proof

Note that $Q(\lambda )$ is real and differentiable on the real line, due to the assumptions on A. As $Q(\tau )\rightarrow 0$ with $|\tau |\rightarrow \infty$, one has a local real extreme point of $Q(\lambda )$. $\square$

5 The Eigenvalues of $A+\tau uv^*$ for Large $|\tau |$

We shall also be concerned with the asymptotic shape of the curves $\sigma (A,u,v;t)$. The proof of the following result was given in [42]: let A be an $n\times n$ complex matrix, let u, v be generic complex n-vectors. Asymptotically, as $t\rightarrow \infty$, these curves are circles, one with radius going to infinity centered at the origin, and the others with radius going to zero, and centers at the roots of $p_{uv}(\lambda )$. The result will be restated in a more precise form below, in Theorem 17, part (v). For this we first prove the following lemma.

Lemma 16

Let $m_A(\lambda )=\sum _{k=0}^l m_k\lambda ^k$. Then

$$\begin{aligned} p_{uv}(\lambda )&= {\displaystyle \sum _{i=0}^{l-1} \left( \sum _{\begin{array}{c} k-j=i+1\\ k,j\ge 0 \end{array}} m_kv^*A^{j} u\right) }\lambda ^i . \end{aligned}$$

(13)

Proof

Recall that $p_{uv}(\lambda )=m_A(\lambda )v^*(\lambda I_n-A)^{-1}u$. Expanding $(\lambda I_n-A)^{-1}$ in Laurent series for $|\lambda |\ge \Vert {A}\Vert$ we obtain

$$\begin{aligned} p_{uv}(\lambda )= m_A(\lambda )v^*(\lambda I_n-A)^{-1}u =\sum _{k=0}^l \sum _{j=0}^\infty m_kv^*A^{j} u \lambda ^{k-j-1}. \end{aligned}$$

Put $k-j-1=i$ and interchange the order of summation to see that

$$\begin{aligned} p_{uv}(\lambda )= \sum _{i=-\infty }^{l-1} \left( \sum _{\begin{array}{c} k-j-1=i\\ k,j\ge 0 \end{array}} m_k v^*A^{j}u\right) \lambda ^i . \end{aligned}$$

However, $p_{uv}(\lambda )$ is a polynomial in $\lambda$, hence the sum from $i=-\infty$ to $-1$ vanishes, and we arrive at formula (13). $\square$

Next, we analyze the roots of the polynomial $p_{B(\tau )}= m_A(\lambda )- \tau p_{uv}(\lambda )$ as $\tau \rightarrow \infty$. We have already shown in [34] that if $u^*v\not = 0$, then $l-1$ of these roots will approximate the roots of $p_{uv}(\lambda )$, while one goes to infinity. The condition $u^*v\ne 0$ obviously holds for generic u, v, however the next theorem presents the full picture in view of later applications to structured matrices.

Theorem 17

Let $A\in {\mathbb {C} }^{n\times n}$, $u,v\in {\mathbb {C} }^n$ and let $l\in \mathbb {N}$ denote the degree of the minimal polynomial $m_A(\lambda )$. Assume also that

$$\begin{aligned} v^*u=\cdots =v^*A^{\kappa -1}u=0,\quad v^*A^{\kappa }u\not = 0, \end{aligned}$$

(14)

for some $\kappa \in \{0,\dots ,l-1 \}$ and put

$$\begin{aligned} v^*A^{\kappa }u=r_{\kappa }e^{{{\,\mathrm{{i}}\,}}\theta _{\kappa }}. \end{aligned}$$

Then

• (i) $p_{uv}(\lambda )$ is of degree $l-\kappa -1$;

• (ii) $l-\kappa -1$ eigenvalues of $B(\tau )$ converge to the roots of $p_{uv}(\lambda )$ as $\tau \rightarrow \infty$;

• (iii) there are $\kappa +1$ eigenvalues $\lambda _1(\tau ),\dots ,\lambda _{\kappa +1}(\tau )$ of $A+\tau uv^*$ which go to infinity with $r=|\tau |\rightarrow \infty$ as

  $$\begin{aligned} \lambda _j(re^{{{\,\mathrm{{i}}\,}}\theta }) = \root \kappa +1 \of {rr_{\kappa }} e^{ {{\,\mathrm{{i}}\,}}(\frac{1}{\kappa +1} (\theta +\theta _{\kappa }) +\frac{2j}{\kappa +1}\pi )}+O(1), \qquad j=1, 2, \ldots , \kappa +1, \end{aligned}$$

  where $\theta \in [0,2\pi )$ is fixed, and for all of them we have

  $$\begin{aligned} \frac{d\lambda _j}{d\tau }= \frac{v^*A^\kappa u}{l\lambda _j^{\kappa }} +O\left( \lambda ^{-(\kappa +1)}\right) . \end{aligned}$$

  so these eigenvalues can be parametrized by a curve

  $$\begin{aligned} \Gamma (\theta )= (rr_\kappa )^{\frac{1}{\kappa +1}}\exp ({{\,\mathrm{{i}}\,}}\theta ) + O(1),\quad (r\rightarrow \infty ); \end{aligned}$$

• (iv) as $\theta \rightarrow 2\pi$ one has, after possibly reordering the eigenvalues $\lambda _1(\tau ),\dots ,\lambda _{\kappa +1}(\tau )$, that

  $$\begin{aligned} \lambda _j(re^{{{\,\mathrm{{i}}\,}}\theta })\rightarrow \lambda _{j+1}(r), \quad j=1,\dots , \kappa , \quad \lambda _{\kappa +1} (re^{{{\,\mathrm{{i}}\,}}\theta })\rightarrow \lambda _1(r); \end{aligned}$$

• (v) additionally, let $\zeta _1,\dots , \zeta _\nu$ denote the roots of the polynomial $p_{uv}(\lambda )$ with multiplicities respectively $k_1,\dots k_\nu$. Denote

  $$\begin{aligned} v^*(\zeta _j I_n-A)^{-(k_j+1)}u=\rho _{j}e^{{{\,\mathrm{{i}}\,}}\theta _j}, \qquad j=1, \ldots , \nu . \end{aligned}$$

  Then $\sigma (A,u,v;t)$ for sufficiently large $\tau$ can be parametrized by disjoint curves $\Gamma _1(\theta ),\dots ,\Gamma _{\nu +1}(\theta )$, where the $\kappa +1$ eigenvalues which go to infinity trace out a curve

  $$\begin{aligned} \Gamma _{\nu +1}(\theta )= (rr_\kappa )^{\frac{1}{\kappa +1}}\exp ({{\,\mathrm{{i}}\,}}\theta ) + O(1) \end{aligned}$$

  while the $k_j$ eigenvalues near $\zeta _j$ trace out a curve $\Gamma _j(\theta )$ which is of the form

  $$\begin{aligned} \Gamma _j(\theta )=\zeta _j+|\tau |^{-\frac{1}{k_j}}\rho _j^{-\frac{1}{k_j}}e^{{{\,\mathrm{{i}}\,}}\theta }+O\left( |\tau |^{-\frac{2}{k_j}}\right) ,\qquad 0\le \theta \le 2\pi , \end{aligned}$$

  with $r=|\tau |\rightarrow \infty$.

Proof

Statement (i) results directly from Lemma 16.

Statement (ii) is a consequence of formulas (3) and (4) expressing the characteristic polynomial of $A+\tau uv^*$ in terms of $p_B(\tau )=m_A(\lambda )-\tau p_{uv}(\lambda )$ (formula (4)). Then, by [18, Sect. II.1.7] statement (ii) follows.

For statement (iii) and following, by (13)

$$\begin{aligned} p_{B(\tau )}(\lambda )&= \sum _{i=0}^l m_i\lambda ^1 -\tau \sum _{i=0}^{l-1} \left( \sum _{\begin{array}{c} k-j=i+1\\ k,j\ge 0 \end{array}} m_kv^*A^ju\right) \lambda ^i \\&=\lambda ^l +\sum _{i=0}^{l-1}\left( m_i-\tau \left( \sum _{\begin{array}{c} k-j=i+1\\ k,j\ge 0 \end{array}} m_kv^*A^ju\right) \lambda ^i \right) . \end{aligned}$$

In case $v^*u=0, v^*Au=0, \ldots , v^*A^{\kappa -1 } u=0$ and $v^*A^\kappa u\not =0$, this becomes

$$\begin{aligned} p_{B(\tau )}(\lambda )&= \lambda ^l +\lambda ^{l-1}m_{l-1} + \cdots + \lambda ^{l-\kappa }m_{l-\kappa } \\&\quad +\lambda ^{l-\kappa -1}(m_{l-\kappa -1}-\tau v^*A^\kappa u) + \text{ lower } \text{ order } \text{ terms } . \end{aligned}$$

For large values of $\lambda$ and $\tau$ the dominant terms are $\lambda ^{l-\kappa -1} (\lambda ^{\kappa +1}-\tau v^*A^\kappa u)$, showing that indeed, the largest roots behave asymptotically as the $(\kappa +1)$-th roots of $\tau v^*A^\kappa u$.

Moreover, for the derivative of $\lambda$ with respect to $\tau$ we have by the implicit function theorem

$$\begin{aligned} \frac{d\lambda }{d\tau } = -{\frac{\partial p_{B(\tau )}}{\partial \tau }}/{\frac{\partial p_{B(\tau )}}{\partial \lambda }} = \frac{p_{uv}(\lambda )}{m_A^\prime (\lambda )-\tau p_{uv}^\prime (\lambda )}. \end{aligned}$$

Now $p_{uv}(\lambda )=\lambda ^{l-\kappa -1}v^*A^\kappa u +\text{ lower } \text{ order } \text{ terms }$, and

$$\begin{aligned} m_A^\prime (\lambda )-\tau p_{uv}^\prime (\lambda ) =l\lambda ^{l-1} +\text{ lower } \text{ order } \text{ terms }. \end{aligned}$$

So

$$\begin{aligned} \frac{d\lambda }{d\tau } =\frac{\lambda ^{l-\kappa -1}v^*A^\kappa u +\text{ lower } \text{ order } \text{ terms } }{l\lambda ^{l-1} +\text{ lower } \text{ order } \text{ terms } }. \end{aligned}$$

Dividing by $\lambda ^{l-\kappa -1}$ in numerator and denominator we arrive at

$$\begin{aligned} \frac{d\lambda }{d\tau } =\frac{v^*A^\kappa u}{l} \frac{1}{\lambda ^\kappa } + O\left( \lambda ^{-(k+1)}\right) . \end{aligned}$$

which concludes the proof of part (iii).

Note that also part (iv) follows directly from part (iii) combined with the continuity of the eigenvalues as a function of $\theta$ (even when taking $\theta \in \mathbb {R}$, rather than restricting to $\theta \in [0, 2\pi )$).

For part (v) and the remaining parts of part (iii) in the general case, recall that the eigenvalues of $A+\tau uv^*$ which are not eigenvalues of A are (among the) roots of $m_A(\lambda )-\tau p_{uv}(\lambda )$, which are the same as the roots of the polynomial $\frac{1}{\tau }m_A(\lambda )-p_{uv}(\lambda )$. First we take $\theta =0$, so $\tau =t$.

Put $s=1/t$, and consider the polynomial $sm_A(\lambda )-p_{uv}(\lambda )$ as a small perturbation of the polynomial $-p_{uv}(\lambda )$. By general theory concerning the behavior of the roots of a polynomial under such a perturbation (see, e.g., [4] Appendix, [19] or Puiseux’s original 1850 paper) for small s the roots of $sm_A(\lambda )-p_{uv}(\lambda )$ near the roots of $p_{uv}(\lambda )$ are locally described by a Puiseux series of the form

$$\begin{aligned} \zeta _j+c_{1j}s^{\frac{1}{k_j}}+c_{2j}s^{\frac{2}{k_j}}+\cdots , \qquad j=1, \ldots , \nu \end{aligned}$$

with $c_{1j}\not = 0$. Here $k_j$ is the multiplicity of $\zeta _j$ as a root of $p_{uv}(\lambda )$, and there are $k_j$ roots of $sm_A(\lambda )-p_{uv}(\lambda )$ near $\zeta _j$.

Next we do not consider $t \in \mathbb {R}$ but $\tau =te^{{{\,\mathrm{{i}}\,}}\theta } \in \mathbb {C}$. Replacing u by $e^{{{\,\mathrm{{i}}\,}}\theta }u$ we see that the roots of $m_A(\lambda )-\tau p_{uv}(\lambda )$ for large $\tau$ near $\zeta _j$ behave as $\zeta _j+c_{1j}\tau ^{-1/k_j}$. For fixed $|\tau |=r$ these $k_j$ roots near $\zeta _j$ trace out a curve $\Gamma _j(\theta )=\zeta _j+c_{1,j} r^{-1/k_j}exp({{\,\mathrm{{i}}\,}}\theta )+o(r^{-1/k_j})$ with $r\rightarrow \infty$.

We shall make these arguments much more precise as follows. Remember that an eigenvalue $\lambda _0$ of $A+\tau uv^*$ which is not also an eigenvalue of A is a solution to $Q(\lambda )=1/\tau$. Consider large values of $|\tau |$ and consider also the large eigenvalues of $A+\tau uv^*$, for instance for $\tau$ large enough there is at least one eigenvalue with $|\lambda |>\Vert A\Vert$. Then $\lambda$ satisfies

$$\begin{aligned} 1=\tau v^*\sum _{j=0}^\infty \frac{A^j}{\lambda ^{j+1}}u=\tau \sum _{j=\kappa }^\infty \frac{v^*A^j u}{\lambda ^{j+1}} \end{aligned}$$

by the definition of $\kappa$. Hence

$$\begin{aligned} \lambda ^{\kappa +1}=\tau v^*A^\kappa u+\frac{\tau }{\lambda } v^*A^{\kappa +1}u+ \frac{\tau }{\lambda ^2} v^*A^{\kappa +2}u+\cdots , \end{aligned}$$

(15)

and so

$$\begin{aligned} \left( \frac{\lambda ^{\kappa +1}}{\tau }-v^*A^\kappa u\right) =O\left( \frac{1}{\lambda }\right) \end{aligned}$$

Thus

$$\begin{aligned} \lambda \approx (\tau )^{\frac{1}{\kappa +1}}(v^*A^\kappa u)^{\frac{1}{\kappa +1}}. \end{aligned}$$

Again, we can be much more precise than this: we know that $\lambda$ as a function of $\tau$ has a Puiseux series expansion, and if we set

$$\begin{aligned} \lambda =c_{-1}\tau ^{\frac{1}{\kappa +1}}+ c_0+ c_1\tau ^{-\frac{1}{\kappa +1}}+\cdots \end{aligned}$$

one checks from the equation (15) that the following hold:

$$\begin{aligned} c_{-1}&=(v^*A^ku)^{\frac{1}{\kappa +1}},\\ c_0&=\frac{1}{k+1}\cdot \frac{v^*A^{k+1}u}{v^*A^ku},\\ c_1&=\frac{1}{k+1}\cdot \frac{1}{(v^*A^ku)^{\frac{k+2}{k-1}}}\cdot (v^*A^{k+2}u-(k+2)v^*A^{k+1}u). \end{aligned}$$

Hence

$$\begin{aligned} \lambda = (\tau )^{\frac{1}{\kappa +1}}(v^*A^\kappa u)^{\frac{1}{\kappa +1}} + \frac{1}{k+1}\cdot \frac{v^*A^{k+1}u}{v^*A^ku}+O\left( \tau ^{-\frac{1}{k+1}}\right) \end{aligned}$$

This completes the proof of part (iii), and gives the precise form of $\Gamma _{\nu +1}(\theta )$ for $r=|\tau |$ large enough.

Next we consider the eigenvalues of $A+\tau uv^*$ which are close to $\zeta _j$ for large $\tau$. Recall that $\zeta _j$ is a root of $p_{uv}(\lambda )$, so $m_A(\zeta _j)v^*(\zeta _j I_n-A)^{-1}u=0$. If $\zeta _j$ would be a zero of $m_A(\lambda )$, then $\zeta _j$ is an accidentally frozen eigenvalue for A, u, v and so is an eigenvalue of $B(\tau )$ for all $\tau$. Otherwise, $\zeta _j$ is not an eigenvalue of A, and we have $v^*(\zeta _j I_n-A)^{-1}u=0$. For $\lambda$ near $\zeta _j$ write

$$\begin{aligned} v^*(\lambda I_n-A)^{-1}u&= v^*((\lambda -\zeta _j)+(\zeta _j I_n-A))^{-1}u\\&= v^*((\lambda -\zeta _j)(\zeta _j I_n-A)^{-1}+I)^{-1}(\zeta _j I_n-A)^{-1}u\\&=v^*\sum _{k=0}^\infty (\lambda -\zeta _j)^k(\zeta _j I_n-A)^{-(k+1)}u\\&=v^*(\zeta _j I_n-A)^{-1}u+v^*\sum _{k=1}^\infty (\lambda -\zeta _j)^k(\zeta _j I_n-A)^{-(k+1)}u. \end{aligned}$$

Since the first term is zero, we have

$$\begin{aligned} v^*(\lambda I_n-A)^{-1}u =(\lambda -\zeta _j)v^*(\zeta _j I_n-A)^{-2)}u +(\lambda -\zeta _j)^2v^*(\zeta _j I_n-A)^{-3)}u+\cdots \end{aligned}$$

Again use the fact that any eigenvalue of $A+\tau uv^*$ which is not an eigenvalue of A satisfies

$$\begin{aligned} \frac{1}{\tau }=v^*(\lambda I_n-A)^{-1}u. \end{aligned}$$

So, if the root $\zeta _j$ of $p_{uv}(\lambda )$ has multiplicity $k_j$, then

$$\begin{aligned} \frac{1}{\tau }=(\lambda -\zeta _j)^{k_j}v^*(\zeta _j I_n-A)^{-(k_j+1)}u +(\lambda -\zeta _j)^{k_j+1}v^*(\zeta _j I_n-A)^{-(k_j+2)}u+\cdots . \end{aligned}$$

For the moment, let us denote $v^*(\zeta _j I_n-A)^{-k}u$ by $a_{j,k}$. We know from the considerations in an earlier paragraph of the proof that $\lambda$ can be expressed as a Puiseux series in $\tau ^{-1}$, let us say

$$\begin{aligned} \lambda =\zeta _j+c_{1,j}\tau ^{-\frac{1}{k_j}}+c_{2,j}\tau ^{-\frac{2}{k_j}}+\cdots . \end{aligned}$$

Then $\lambda -\zeta _j=c_{1,j}\tau ^{-\frac{1}{k_j}}+c_{2,j}\tau ^{-\frac{1}{k_j}}+\cdots$, and inserting that in the above equation we obtain

$$\begin{aligned} \frac{1}{\tau }&= \frac{1}{\tau }c_{1,j}^{k_j}a_{j,k_j+1} + k_jc_{1,j}^{k_j-1}\tau ^{-\frac{k_j-1}{k_j}}\cdot c_{2,j}\tau ^{-\frac{2}{k_j}}a_{j,k_j+1} \\ {}&\quad \ + c_{1,j}^{k_j+1}\tau ^{-\frac{k_j+1}{k_j}}a_{j,k_j+2} + \mathrm{smaller\ order\ terms} \\&=\frac{1}{\tau }c_{1,j}^{k_j}a_{j,k_j+1} +\tau ^{-\frac{k_j+1}{k_j}}\left( k_j c_{1,j}^{k_j-1} c_{2,j}a_{j,k_j+1} + c_{1,j}^{k_j+1}a_{j,k_j+2}\right) +\cdots . \end{aligned}$$

Equating terms of equal powers in $\tau$ gives

$$\begin{aligned} c_{1,j}=a_{j,k_j+1}^{-k_j}=\left( \frac{1}{v^*(\zeta _j I_n-A)^{-(k_j+1)}u}\right) ^{\frac{1}{k_j}} \end{aligned}$$

and using this we can derive a formula for $c_{2,j}$, which after some computation becomes

$$\begin{aligned} c_{2,j}=-\frac{1}{k_j}\cdot \frac{v^*(\zeta _j I_n-A)^{-(k_j+2)}u}{v^*(\zeta _j I_n-A)^{-(k_j+1)}u}. \end{aligned}$$

Let us denote

$$\begin{aligned} v^*(\zeta _j I_n-A)^{-(k_j+1)}u=\rho _{j}e^{{{\,\mathrm{{i}}\,}}\theta _j}, \qquad j=1, \ldots , \nu . \end{aligned}$$

Then $c_{1,j}=\rho _j^{-\frac{1}{k_j}} e^{{{\,\mathrm{{i}}\,}}\frac{\theta _j}{k_j}}$ and the $k_j$ eigenvalues near $\zeta _j$ trace out a curve $\Gamma _j(\theta )$ which is of the form

$$\begin{aligned} \Gamma _j(\theta )=\zeta _j+|\tau |^{-\frac{1}{k_j}}\rho _j^{-\frac{1}{k_j}}e^{{{\,\mathrm{{i}}\,}}\theta }+O\left( |\tau |^{-\frac{2}{k_j}}\right) ,\qquad 0\le \theta \le 2\pi . \end{aligned}$$

This completes the proof of part (v). $\square$

Remark 18

As an alternative argument to much of the results of the previous theorem in the generic case, consider $\tilde{B}(s)=uv^*+sA$, where $s=\frac{1}{\tau }=\frac{1}{t}e^{-{{\,\mathrm{{i}}\,}}\theta }$. For $t\rightarrow \pm \infty$ and thus $s\approx 0$ we will denote the eigenvalues of $\tilde{B}(s)$ by $\nu _j(s)$ for $j=1,\ldots ,n$. Note that there is a close relationship between $\nu _j(\tau ^{-1})$ and $\lambda _j(\tau )$, namely, $\lambda _j(\tau )=\tau \nu _j(\tau ^{-1})$.

Consider $\tilde{B}(s)$ as a perturbation of $uv^*$. Note that $uv^*$ has eigenvalues $v^*u$ and 0, the latter with multiplicity $n-1$, and that generically, when $v^*u\not = 0$, $uv^*$ is diagonalizable. In the non-generic case, when $v^*u=0$, $uv^*$ has only eigenvalue 0, with one Jordan block of size two, and $n-2$ Jordan blocks of size one.

In the generic case where $v^*u \ne 0$, according to [18], Sect. II.1.2, in particular formula (1.7) there, also Sect. II.1.7 and Theorem 5.11 in Sect. II.5.6, and Lidskii’s Theorem [23], see also [4], and for a nice exposition [32], we have that B(s) has n separate eigenvalues given by

$$\begin{aligned} \sigma (\tilde{B}(s)) = \{\nu _j(s)\} = \bigg \{ \begin{array}{ll} v^*u + sk_{1,1} + s^2k_{2,1} + \cdots &{} j=1 \\ 0 + sk_{1,j} + s^2k_{2,j} + \cdots &{} j=2,\ldots ,n. \\ \end{array} \end{aligned}$$

First we take $\theta =0$, so $\tau =t$. In that case $s=\frac{1}{\tau }=\frac{1}{t}$. For $j=2,\ldots ,n$ we have $\nu _j(\frac{1}{t}) = \frac{1}{t}k_{1,j} + \frac{1}{t^2}k_{2,j} + \cdots$ and therefore

$$\begin{aligned} \lambda _j(t) = t\nu _j(\frac{1}{t}) = k_{1,j} + \frac{1}{t}k_{2,j} + \cdots . \end{aligned}$$

This works the same for $j=1$, then $\lambda _1(t)=tv^*u+k_{1,1}+\frac{1}{t}k_{2,1}+\cdots$.

Now consider the limit of $\lambda _j(t)$ as $t\rightarrow \pm \infty$ for $j=2, \ldots , n$. By (ii) this is one of the roots of $p_{uv}(\lambda )$ or an eigenvalue of A. Generically, the roots of $p_{uv}(\lambda )$ will be simple. After possibly rearranging the eigenvalues we may assume that for $j=2, \ldots , l$ the eigenvalue $\lambda _j(t)$ converges to one of the roots of $p_{uv}(\lambda )$, while for $j=l+1, \ldots , n$ the eigenvalue $\lambda _j(t)$ is constantly equal to an eigenvalue of A. Then

$$\begin{aligned} \lim _{t\rightarrow \infty } \lambda _j(t) = \lim _{t\rightarrow \infty } t\nu _j(\frac{1}{t}) = k_{1,j} \text{ for } j=2,\ldots , l \end{aligned}$$

where $k_{1,j}$ is either one of the roots of $p_{uv}(\lambda )$ or an eigenvalue of A. Thus $\lambda _j(t) = k_{1,j} + \frac{1}{t}k_{2,j}+O\left( \frac{1}{t^2}\right)$ for $j=2,\ldots , l$.

Next we do not consider $t \in \mathbb {R}$ but $\tau =te^{{{\,\mathrm{{i}}\,}}\theta } \in \mathbb {C}$. Make the following transformation:

$$\begin{aligned} \sigma (A + \tau uv^*) = \sigma (A + te^{{{\,\mathrm{{i}}\,}}\theta }uv^*) = \sigma (A + t\tilde{u}v^*) \end{aligned}$$

where $\tilde{u} = e^{{{\,\mathrm{{i}}\,}}\theta }u$. Note that $p_{uv}(\lambda )$ and $p_{\tilde{u}v}(\lambda )$ only differ by the constant $e^{{{\,\mathrm{{i}}\,}}\theta }$ and so they have the same roots. Applying the arguments from the previous paragraphs we obtain

$$\begin{aligned} \lambda _1(\tau ) = \lambda _1(te^{{{\,\mathrm{{i}}\,}}\theta }) = te^{{{\,\mathrm{{i}}\,}}\theta }v^*u +O(1) \end{aligned}$$

and

$$\begin{aligned} \lambda _j(\tau ) = \lambda _j(te^{{{\,\mathrm{{i}}\,}}\theta }) = k_{1,j} + \frac{1}{t}e^{-{{\,\mathrm{{i}}\,}}\theta }k_{2,j}+O\left( \frac{1}{t^2}\right) , j=2,\ldots , l. \end{aligned}$$

Consider for fixed t the curve

$$\begin{aligned} \zeta _{2,t} = \{ \lambda _j(te^{{{\,\mathrm{{i}}\,}}\theta }) \mid j=2,\ldots ,n, 0 \le \theta < 2\pi \}. \end{aligned}$$

The arguments above show that asymptotically $\zeta _{2,t}$ is a circle with radius $\frac{1}{t}k_{2,j}$ centered at $k_{1,j}$, which is a root of $p_{uv}(\lambda )$.

Remark 19

Note that if (14) holds for $\kappa =l-1$ then $p_{uv}(\lambda )\equiv 0$ and by (4) the characteristic polynomial of the perturbed matrix coincides with the characteristic polynomial of A.

Remark 20

Consider the case $\kappa =2$. Then the eigenvalues that go to infinity will trace out a circle, but each of them only traces out half a circle. In addition the speed with which the eigenvalues go to zero is considerably slower than when $\kappa =1$.

Example 21

As an extreme example, consider $A=J_n(0)$, the $n\times n$ Jordan block with zero eigenvalue, and let $u=e_n$ and $v=e_1$, where $e_j$ is the j’th unit vector. Then $p_{uv}(\lambda )=1$, and the eigenvalues of $A+\tau uv^*$ are the n’th roots of $\tau$, $\lambda _k(\tau )= \root n \of {r}e^{i\frac{2k}{n}\pi }$ for $k=1, \ldots ,n$, and $\frac{d\lambda }{d\tau } = \frac{1}{n}\tau ^{\frac{1}{n}-1}= \frac{e_1^*A^{n-1}e_n}{n}\cdot \frac{1}{\lambda ^{n-1}}$, as predicted by the theorem.

Example 22

Consider $A=I_2$, and the same u and v as in the previous example. In this case $v^*A^ku=0$ for all k. Consequently, as is also immediate by looking at the matrix, none of the eigenvalues moves. More generally, this happens as soon as A is upper triangular and $uv^*$ is strictly upper triangular.

Example 23

As an example consider $A=\begin{bmatrix} 0 &{} 1 \\ -1 &{} -1\end{bmatrix}$, take $u=\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ and $v=\begin{bmatrix} 1 \\ 1\end{bmatrix}$. Then $m_A(\lambda )=\lambda ^2+\lambda +1$, $p_{uv}(\lambda )=\lambda +1$, and one computes $p_{uv}^\prime (\lambda )m_A(\lambda )-p_{uv}(\lambda )m_A^\prime (\lambda ) =-\lambda (\lambda +2)$. So $Q^\prime (0)=0, Q^\prime (-2)=0$, and so $z_1=0,z_2=-2$. Finally the corresponding $t_1=\frac{1}{|Q(0)|}=1$, and $t_2=\frac{1}{|Q(-2)|}=3$. The eigenvalue curves are shown below (Fig. 3). Note the difference in scales between the individual graphs.

Fig. 3

Eigenvalue curves of $A+te^{{{\,\mathrm{{i}}\,}}\theta }uv^*$ as functions of $\theta$ for several values of t. Green stars indicate the eigenvalues of A, the blue star indicates the root of $p_{uv}(\lambda )$ and the triangles the zeroes of $Q^\prime (\lambda )$. The final graph also illustrates the asymptotic circular behaviour for large values of t

6 Structured Matrices

Generic rank one perturbations for several classes of structured matrices were studied intensively over the last decade. We refer the reader to: [24] for complex J-Hamiltonian complex H-symmetric matrices, [25] for complex H-selfadjoint matrices including the effects on the sign characteristic, [27] for complex H-orthogonal and complex J-symplectic as well as complex H-unitary matrices, [28] for the real cases including the effects on the sign characteristic, [11] for the case of H-positive real matrices and [40] for symplectic matrices. In [3] higher rank perturbations of structured matrices were considered. Another type of structure was treated in [5], where nonnegative rank one perturbations of M-matrices are discussed. Finally, the quaternionic case was discussed in [31].

In the present section we will treat the classes of complex H-selfadjoint and real J-Hamiltonian matrices, analysing the global definition of eigenvalues and the convergence for large values of the parameter. First let us recall the definitions.

We say that an $n\times n$ matrix A is

• (H) H-selfadjoint if $A\in {\mathbb {C} }^{n\times n}$, $HA=A^*H$, where $H\in {\mathbb {C} }^{n\times n}$ is some Hermitian nonsingular matrix.

• (J) J-Hamiltonian if $A\in {\mathbb {R} }^{n\times n}$, $JA=-A^\top J$, where $J\in {\mathbb {R} }^{n\times n}$ is a nonsingular real matrix satisfying $J=-J^\top$.

Note that rank one matrices in these classses are, respectively, of the form

• (H) $uu^*H$, for some $u\in {\mathbb {C} }^n{\setminus }\{0\}$,

• (J) $uu^\top J$ for some $u\in {\mathbb {R} }^n{\setminus }\{0\}$.

Consequently, the function $Q(\lambda )$ takes, respectively, the form

• (H) $Q(\lambda )=u^*H(\lambda I_n-A)^{-1}u$,

• (J) $Q(\lambda )=u^\top J(\lambda I_n-A)^{-1}u$.

It appears that in both these classes global analytic definition of eigenvalues is not a generic property, similarly to Theorem 13 in the real unstructured case. By inspection one sees that the proof remains almost the same, the key issue is that all polynomials involved are real on the real line and x is a simple real zero of $q_0(\lambda )$.

Theorem 24

Assume one of the following

• (H) $A\in {\mathbb {C} }^{n\times n}$ is H-selfadjoint with respect to some nonsingular Hermitian H, and $u\in {\mathbb {C} }^n{\setminus }\{0\}$,

• (J) $A\in {\mathbb {R} }^{n\times n}$ is J-Hamiltonian with respect to some nonsingular skew-symmetric J, and $u\in {\mathbb {R} }^n{\setminus }\{0\}$.

If for some $\tau _0>0$ an analytic definition of the eigenvalues of $A+\tau uv^*$ is not possible due to

$$\begin{aligned} Q(x)=1/\tau _0,\quad Q'(x)=0,\quad Q''(x)\ne 0 \end{aligned}$$

for some $x\in {\mathbb {R} }$, cf. Remark 3, then for all

• (H) ${\tilde{A}}\in {\mathbb {C} }^{n\times n}$ being H-selfadjoint, ${\tilde{u}}\in {\mathbb {C} }^n$

• (J) ${\tilde{A}}\in {\mathbb {R} }^{n\times n}$ being J-symmetric, ${\tilde{u}}\in {\mathbb {R} }^n$ (respectively)

with $\left\| {\tilde{u}}-u\right\|$ and $\left\| {\tilde{A}}-A\right\|$ sufficiently small the analytic definition of the eigenvalues is not possible due to existence of ${\tilde{x}}\in {\mathbb {R} }$, ${\tilde{\tau }}_0>0$, depending continuously on ${\tilde{A}},{\tilde{u}},{\tilde{v}}$ with

$$\begin{aligned} {\widetilde{Q}}({\tilde{x}})=1/{{\tilde{\tau }}_0},\quad {\widetilde{Q}}'({\tilde{x}})=0,\quad {\widetilde{Q}}''({\tilde{x}})\ne 0, \end{aligned}$$

where ${\widetilde{Q}}(z)$ corresponds to the perturbation of ${\tilde{A}}$ as described above the theorem.

Remark 25

We remark here, that Proposition 15 holds for J-Hamiltonian matrices as well, and also for complex H-selfadjoint matrices.

We continue the section with corollaries from Theorem 17. While statement (ii) below is not surprising if one takes into account the symmetry of the spectrum of a J-Hamiltonian matrix with respect to both axes, statement (i) cannot be derived using symmetry principles only.

Corollary 26

• (i) Let $A\in {\mathbb {R} }^{n\times n}$, consider the perturbation $A+\tau uu^\top J$, where J is real, nonsingular and skew symmetric, and $u\in {\mathbb {R} }^n{\setminus }\{0\}$ and $\tau \in \mathbb {R}$. Then there are (at least) two eigenvalues of $A+t uu^\top J$ going to infinity as described by part (ii) of Theorem 17.

• (ii) If, additionally to (i), A is also J-Hamiltonian the number of such eigenvalues is even, and

• (iii) In case A is J-Hamiltonian and $u^\top JAu >0$ then there are two real eigenvalues converging to infinity as $\tau$ goes to $+\infty$, and two purely imaginary eigenvalues going to infinity as $\tau$ goes to $-\infty$. In case $u^\top JAu <0$ the situation is reversed.

• (iv) In case A is J-Hamiltonian and $u^\top JAu=0$ there are at least four eigenvalues going to infinity as $\tau$ goes to $+\infty$ and as $\tau$ goes to $-\infty$. More precisely, let $\kappa$ be the first (necessarily odd) integer for which $u^\top JA^\kappa u\not = 0$. If $u^\top JA^\kappa u >0$ then for $\tau \rightarrow + \infty$ there are at least two real eigenvalues going to infinity, and two purely imaginary eigenvalues going to infinity. If $u^\top JA^\kappa u <0$ then for $\tau \rightarrow - \infty$ there are at least two real eigenvalues going to infinity, and two purely imaginary eigenvalues going to infinity.

Proof

Part (i) follows from Theorem 17 and the fact that for any vector u we have $u^\top Ju=0$ by the skew-symmetry of J.

Part (ii) follows from the same reasoning taking into account that for any even k the matrix $JA^k$ is skew-symmetric, from which one has $u^\top JA^ku=0$ for even k.

Parts (iii) and (iv) follow from Theorem 17, part (iii), using the fact that $Q(\lambda )$ is real on both real and imaginary axis. $\square$

Example 27

Consider the following matrices J and A and vector u:

$$\begin{aligned} J=\begin{bmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad -1 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ -1 &{}\quad 0 &{}\quad 0 &{}\quad 0\end{bmatrix}, \quad A=\begin{bmatrix} 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -1 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -1\end{bmatrix}, \quad u=\begin{bmatrix} 0 \\ 1 \\ 1 \\ 1 \end{bmatrix}. \end{aligned}$$

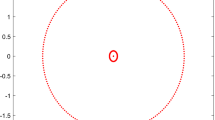
Then, one checks easily that A is J-Hamiltonian, and that $u^\top JAu=0$, while $u^\top JA^3 u=-4\not =0$. The polynomial $p_{uv}(\lambda )$ for $v=-Ju$ is constant, equal to $-4$. Hence all four eigenvalues of $A+t uu^\top J$ are going to infinity, as is shown in Fig. 4. Note also that the rate of convergence to infinity in this example should be as the fourth root of t, which is confirmed by the graph (the fourth root of 125000 is about 19).

Fig. 4

Four eigenvalues going to infinity. The plot shows the eigenvalues of $A+tuu^\top J$ for $0\le t\le 125000$ in red, and the eigenvalues of $A-tuu^\top J$ for the same range of t in cyan, cf. Example 27

7 Nonnegative Matrices

We will apply Theorem 17 to the setting of nonnegative matrices. Recall that a nonnegative matrix A is called irreducible if there is no permutation matrix P such that $P^\top A P$ is of a block form

$$\begin{aligned} P^\top A P = \begin{bmatrix} X &{}\quad Y \\ 0 &{}\quad Z \end{bmatrix} \end{aligned}$$

with X and Z being nontrivial square matrices. By the graph associated with the matrix $A=[a_{ij}]_{ij=1}^n$ we understand the directed graph with vertices $1,\dots ,n$ and with the set of edges consisting of only those pairs (i, j) for which $a_{ij}>0$. By a cycle we understand a directed path from the vertex i to itself.

Theorem 28

Let $A=[a_{ij}]_{ij=1}^n\in {\mathbb {R} }^{n\times n}$ be a nonnegative, irreducible matrix. Let also l denote the length of the shortest cycle in the graph of the matrix $A+e_{i_0}e_{j_0}^\top$ containing the $(i_0,j_0)$ edge. Then the matrix

$$\begin{aligned} A+\tau e_{i_0}e_{j_0}^\top ,\quad \tau >0 \end{aligned}$$

has precisely l eigenvalues converging to infinity with $\tau \rightarrow +\infty$

Proof

Note that

$$\begin{aligned} e_{j_0}^\top A^k e_{i_0} = (A^k)_{j_0i_0}=0 \end{aligned}$$

if and only if $k<l$, as l is the length of the smallest cycle going through the $(i_0,j_0)$ edge. By Theorem 17 the matrix $A+\tau uv^\top$ has precisely l eigenvalues converging to infinity. $\square$

Note that the number l of eigenvalues converging to infinity may be greater than the number of eigenvalues of A on the spectral circle, i.e, the imprimitivity index. However, by the theory of nonnegative matrices l, as the length of the (shortest) cycle, is always a multiple of the imprimitivity index, see, e.g., Theorem 1.6. of [10].

Example 29

Consider the matrix $A=\begin{bmatrix} 1 &{}\quad 1 \\ 1 &{}\quad 1 \end{bmatrix}$ and the vectors $u=\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ and $v= \begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Then $B(\tau ) = \begin{bmatrix} 1 &{}\quad 1+\tau \\ 1 &{}\quad 1 \end{bmatrix}$. Then $v^\top u=0$, while $v^\top Au\not = 0$. So both eigenvalues of $B(\tau )$ will go to infinity. For $\tau \ge 0$ the matrix $B(\tau )$ is an entrywise positive matrix, so one of the eigenvalues will be the spectral radius. By Theorem 17, both eigenvalues go to zero at the same rate, but as the eigenvalues are $\sqrt{1+\tau } \pm 1$ their moduli are not equal.