Abstract
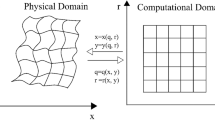
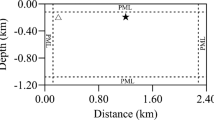
The perfectly matched layer (PML) is a highly efficient absorbing boundary condition used for the numerical modeling of seismic wave equation. The article focuses on the application of this technique to finite-element time-domain numerical modeling of elastic wave equation. However, the finite-element time-domain scheme is based on the second-order wave equation in displacement formulation. Thus, the first-order PML in velocity-stress formulation cannot be directly applied to this scheme. In this article, we derive the finite-element matrix equations of second-order PML in displacement formulation, and accomplish the implementation of PML in finite-element time-domain modeling of elastic wave equation. The PML has an approximate zero reflection coefficients for bulk and surface waves in the finite-element modeling of P-SV and SH wave propagation in the 2D homogeneous elastic media. The numerical experiments using a two-layer model with irregular topography validate the efficiency of PML in the modeling of seismic wave propagation in geological models with complex structures and heterogeneous media.
Similar content being viewed by others
References
Bao, H., Bielak, J., Ghattas, O., Kallivokas, L. F., O’ Hallaron, D. R., Shewchuk, J. R., and Xu, J., 1998, Large-scale simulation of elastic wave propagation in heterogeneous media on parallel computers: Computer Methods in Applied Mechanics and Engineering, 152, 85–102.
Bécache, E., Fauqueux, S., and Joly, P., 2003, Stability of perfectly matched layers, group velocities and anisotropic waves: Journal of Computational Physics, 188(2), 399–433.
Bérenger, J. P., 1994, A perfectly matched layer for the absorption of electromagnetic waves: Journal of Computational Physics, 114(2), 185–200.
Cerjan, C., Kosloff, D., Kosloff, R., and Reshef, M., 1985, A nonreflecting boundary condition for discrete acoustic and elastic wave equation: Geophysics, 50(4), 705–708.
Chew, W. C., and Liu, Q., 1996, Perfectly matched layers for elastodynamics: A new absorbing boundary condition: Journal of Computational Acoustics, 4(4), 341–359.
Chew, W. C., and Weedon, W. H., 1994, A 3-D perfectly matched medium from modified Maxwell’s equations with stretched coordinates: Microwave and Optical Technology Letters, 7(13), 599–604.
Clayton, R., and Engquist, B., 1977, Absorbing boundary conditions for acoustic and elastic wave equations: Bulletin of the Seismological Society of America, 67(6), 1529–1540.
Cohen, G. C., 2002, Higher-order Numerical Methods for Transient Wave Equations: Springer: Berlin.
Collino, F., and Tsogka, C., 2001, Application of the PML absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media: Geophysics, 66(1), 294–307.
Courant, R., Friedrichs, K. O., and Lewy, H., 1928, Über die partiellen Differenzengleichungen der mathematischen Physik: Mathematische Annalen, 100, 32–74.
Drake, L.A. 1972, Rayleigh wave at continental boundary by the finite element method, Bulletin of the Seismological Society of America, 62(5), 1259–1268
Engquist, B., and Majda, A., 1977, Absorbing boundary conditions for the numerical simulation of waves: Proceedings of the National Academy of Science, 74(5), 1765–1766.
Hastings, F. D., Schneider, J. B., and Broschat, S. L., 1996, Application of the perfectly matched layer PML absorbing boundary condition to elastic wave propagation: Journal of the Acoustical Society of America, 100(5), 3061–3069.
Higdon, R. L., 1991, Absorbing boundary conditions for elastic waves: Geophysics, 56(2), 231–241.
Katsibas, T. K., and Antonopoulos, C. S., 2002, An efficient PML absorbing medium in FDTD simulations of acoustic scattering in lossy media: IEEE Proceeding on Ultrasonic Symposium, 1, 551–554.
Komatitsch, D., and Tromp, J., 2003, A perfectly matched layer absorbing boundary condition for the secondorder seismic wave equation: Geophysical Journal International, 154(1), 146–153.
Liu, Q., and Tao, J., 1997, The perfectly matched layer for acoustic waves in absorptive media: Journal of the Acoustical Society of America, 102(4), 2072–2082.
Liu, Q. H., 1999, Perfectly matched layers for elastic waves in cylindrical and spherical coordinates: Journal of the Acoustical Society of America, 105(4), 2075–2084.
Madariaga, R., 2007, Seismic source theory. Treatise on Geophysics, Amsterdam: Elsevier, 59–82.
Marfurt, K. J., 1984, Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equation: Geophysics, 49(5), 533–549.
Meza-Fajardo, K. C., and Papageorgiou, A. S., 2008, A nonconvolutional, split-field, perfectly matched layer for wave propagation in isotropic and anisotropic elastic media: Stability analysis: Bulletin of the Seismological Society of America, 98(4), 1811–1836.
Newmark, N. M., 1959, A method of computation for structural dynamics: ASCE Journal of the Engineering Mechanics Division, 85(3), 67–94.
Quarteroni, A., Tagliani, A., and Zampieri, E., 1998, Generalized Galerkin approximations of elastic waves with absorbing boundary conditions: Computer Methods in Applied Mechanics and Engineering, 163, 323–341.
Shi, R., Wang, S., and Zhao, J., 2012, An unsplit complex-frequency-shifted PML based on matched Z-transform for FDTD modeling of seismic wave equations: Journal of Geophysics and Engineering, 9, 218–229.
Sochacki, J., Kubichek, R., George, J., Fletcher, W. R., and Smithson, S., 1987, Absorbing boundary conditions and surface waves: Geophysics, 52(1), 60–71.
Stacey, R., 1988, Improved transparent boundary formulations for the elastic wave equation: Bulletin of the Seismological Society of America, 78(6), 2089–2097.
Zeng, Y. Q., He, J. Q., and Liu, Q. H., 2001, The application of the perfectly matched layer in numerical modeling of wave propagation in poroelastic media: Geophysics, 66(4), 1258–1266.
Zienkiewicz, O. C., Taylor, R. L., and Zhu, J., 2005, The Finite Element Method: its Basis and Fundamentals (6th edition): Elsevier Butterworth-Heinemann, London.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work is sponsored by the National Natural Science Foundation of China Research (Grant No. 41274138), and the Science Foundation of China University of Petroleum (Beijing) (No. KYJJ2012-05-02).
Zhao Jian-Guo, Associate Professor, obtained his bachelor and PhD degrees in Exploration Geophysics from Changchun College of Geology in 1998 and 2002, respectively, and his PhD degree in Exploration Geophysics from Tohoku University, Japan, in 2006. He joined China University of Petroleum (Beijing) in 2006 after his PhD research. His research interests include seismic full-wave modeling and inversion, seismic data processing, seismic-electromagnetic high-accuracy joint inversion, and rock physics.
Rights and permissions
About this article
Cite this article
Zhao, JG., Shi, RQ. Perfectly matched layer-absorbing boundary condition for finite-element time-domain modeling of elastic wave equations. Appl. Geophys. 10, 323–336 (2013). https://doi.org/10.1007/s11770-013-0388-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11770-013-0388-y