1 Introduction and contribution

In this paper, we deal with a reverse imaging problem introduced recently in [19]. Given an image filter \({\varvec{y}}={\varvec{f}}({\varvec{x}})\) with input \({\varvec{x}}\in \mathbb {R}^d\) and output \({\varvec{y}}\in \mathbb {R}^d\), the problem consists of restoration of \({\varvec{x}}\) from \({\varvec{y}}\) under the condition that we can apply the filter \({\varvec{f}}(\cdot )\) as many times as needed but without any knowledge of its internal structure. In particular, it means that we cannot directly invert the filter. Following [19], we call such a restoration process reverse filtering or defiltering.

The reverse image filtering schemes introduced in [19] and in the subsequent works [4, 12] are aimed at removing slight filtering effects. In contrast, our work is focused on removing, at least partially, severe filtering effects. Three examples are shown in Fig. 1, where reverse filtering of images filtered by a Gaussian, Laplace-of-Gaussian (LoG), and the adaptive manifold filter (AMF) [6] is demonstrated.

Mathematically, the defiltering problem consists of numerically solving the equation

$$\begin{aligned} {\varvec{y}}={\varvec{f}}({\varvec{x}}),\quad {\varvec{x}},{\varvec{y}}\in \mathbb {R}^d, \end{aligned}$$
(1)

for \({\varvec{x}}\), given \({\varvec{y}}\). Here, \({\varvec{x}}\) is an (unknown) input image, \({\varvec{f}}(\cdot )\) is a (black-box) filter, and \({\varvec{y}}\) is the (given) output image.

Numerical methods for solving (1) include the Newton’s method and its relatives, various gradient descent schemes, and fixed-point iterations. Straightforward uses of the Newton’s and gradient descent methods require an estimation of the Jacobian of \({\varvec{f}}(\cdot )\) and are not computationally feasible, as a typical image consists of tens of thousands to millions of pixels.

A simple and efficient fixed-point iteration scheme for image defiltering was recently proposed by Tao et al. [19]. The scheme consists of the following iterations

$$\begin{aligned} {\varvec{x}}_{n+1}\!=\!{\varvec{T}}({\varvec{x}}_n)\equiv {\varvec{x}}_n+{\varvec{h}}_n,\!\quad {\varvec{h}}_n={\varvec{y}}-{\varvec{f}}({\varvec{x}}_n),\!\quad {\varvec{x}}_0={\varvec{y}}\end{aligned}$$
(2)

and can be considered as an iterative unsharp masking with filter \({\varvec{f}}(\cdot )\). Mathematically, (2) corresponds to the Picard’s iterative method \({\varvec{x}}_{n+1}={\varvec{f}}({\varvec{x}}_n)\), a simple and popular method for numerically solving nonlinear equation (1) (see, for example, [1] for a comprehensive study of fixed-point iteration methods). A rigorous convergence analysis of (2) for image filters satisfying certain conditions is given in [19].

Fig. 1
figure 1

Top row: test images we deal with in this paper: Trui, cameraman, and Barbara. Middle row: the images are filtered by a Gaussian imgaussfilt(x,5), Laplace-of-Gaussian imfilter(x,fspecial(’log’,7,0.4)), and the adaptive manifold filter (AMF) adaptive_manifold_filter(x,20,0.4)[6], respectively (Matlab notations are used to specify the parameters of the filters). Bottom row: defiltering results; notice how well the fine image details are restored

Full size image

As shown in [19], (2) demonstrates excellent results for removing light filtering effects but, according to our experiments, often fails when dealing with severe image deformations. So in this paper, we introduce two iterative methods

$$\begin{aligned}&{\varvec{x}}_{n+1}\!=\!{\varvec{P}}({\varvec{x}}_n)\!\equiv {\varvec{x}}_n+\lambda _n\,\frac{{\varvec{f}}({\varvec{x}}_n+{\varvec{h}}_n)-{\varvec{f}}({\varvec{x}}_n-{\varvec{h}}_n)}{2},\nonumber \\&\quad \lambda _n=\frac{4\Vert {\varvec{h}}_n\Vert ^2}{\Vert \,{\varvec{f}}({\varvec{x}}_n+{\varvec{h}}_n)-{\varvec{f}}({\varvec{x}}_n-{\varvec{h}}_n)\Vert ^2},\nonumber \\&\quad {\varvec{h}}_n={\varvec{y}}-{\varvec{f}}({\varvec{x}}_n),\quad {\varvec{x}}_0={\varvec{y}}\end{aligned}$$
(3)

and

$$\begin{aligned} {\varvec{x}}_{n+1}\!=\!{\varvec{S}}({\varvec{x}}_n)\!\equiv \!{\varvec{x}}_n+\frac{{\varvec{h}}_n\Vert {\varvec{h}}_n\Vert }{\Vert {\varvec{f}}({\varvec{x}}_n+{\varvec{h}}_n)-{\varvec{f}}({\varvec{x}}_n)\Vert },\!\quad {\varvec{x}}_0={\varvec{y}}\end{aligned}$$
(4)

which are inspired by a gradient descent scheme studied by Polyak [15] and Steffensen’s method [17], respectively (hence the notations \({\varvec{P}}(\cdot )\) and \({\varvec{S}}(\cdot )\)). We propose a brief analysis of (2), (3) and (4) in the next section.

Given \({\varvec{x}}_n\) the reconstructed image at the n-th step of the iterative process, we consider two error functions in order to measure the reconstruction accuracy

$$\begin{aligned} E_x({\varvec{x}}_n)=\frac{\Vert \,{\varvec{x}}-{\varvec{x}}_n\Vert }{\Vert {\varvec{x}}\Vert } \quad \text{ and }\quad E_y({\varvec{x}}_n)=\frac{\Vert \,{\varvec{y}}-{\varvec{f}}({\varvec{x}}_n)\Vert }{\Vert {\varvec{y}}\Vert }. \end{aligned}$$
(5)

Although we use both error functions to evaluate the T, P, and S-iterative processes, only \(E_y\) can be used in practice, as \({\varvec{x}}\) is not known a priori.

Figure 2 presents the \(E_x\) and \(E_y\) error graphs corresponding to the reverse filtering examples shown in Fig. 1.

Fig. 2
figure 2

The error graphs for \(E_x\) (top row) and \(E_y\) (bottom row) for the reverse filtering examples of Fig. 1. Results for the first 200 iterations are presented (additional iterations are needed for defiltering the Gaussian and LoG filtering effects). For LoG, middle column, log–log plots are used to keep the results of the T and S-iterations visible in the graph

Full size image

2 Analysis of the previous and proposed methods

Numerical methods for solving (1) include Newton’s method and its relatives, as well as various gradient descent schemes, and fixed-point iterations [13]. Unfortunately, the vast majority of these methods require knowledge of the gradient of \({\varvec{f}}(\cdot )\) or impose too many restrictions on the behavior of \({\varvec{f}}(\cdot )\).

Tao et al. [19] use a fixed-point iteration method to analyze convergence properties of their T-iterations (2). Unfortunately, their analysis can be applied only to linear mappings.

A similar scheme

$$\begin{aligned} {\varvec{x}}_{n+1}\!=\!{\varvec{M}}({\varvec{x}}_n)\!\equiv \!(1-\gamma \mu ){\varvec{x}}_n+\gamma \!\left( {\varvec{y}}-{\varvec{f}}({\varvec{x}}_n)\right) ,\quad \!\!\!\!{\varvec{x}}_{0}={\varvec{y}}, \end{aligned}$$
(6)

was proposed by Milanfar [12] who used different considerations. Here, \(\gamma \) and \(\mu \) are positive parameters chosen such that both \(\gamma <1\) and \(\gamma \mu \) is small. Although the iterative scheme (6) is supported by a solid analysis of its convergence properties [12], our experiments have not revealed practical advantages of (6) over (2). In Fig. 3 we present the \(E_x\)-error graphs for defiltering six linear and nonlinear filters using (2) and (6) with \(\gamma \mu =0.001\) and \(\mu =0.5^k\), \(k=0,1,2,3\). One can see that in the majority of cases, (2) slightly outperforms (6).

In [4], an interesting iterative scheme for solving (1) was proposed

$$\begin{aligned} {\varvec{x}}_{n+1}=\mathcal {F}^{-1}\left( \frac{\mathcal {F}({\varvec{y}})\mathcal {F}({\varvec{x}}_n)}{\mathcal {F}({\varvec{f}}({\varvec{x}}_n))}\right) . \end{aligned}$$
(7)

Here, \(\mathcal {F}\) stands for the Fourier transform and element-wise multiplication and division are used. Interestingly, (7) can be considered as a variant of (6) employed in the frequency domain and used with variable parameter \(\gamma _n\) instead of \(\gamma \) and \(\mu =0\). Indeed, the iterative process

$$\begin{aligned}&\mathcal {F}({\varvec{x}}_{n+1})=\mathcal {F}({\varvec{x}}_n)+\gamma _n\left( \mathcal {F}({\varvec{y}})-\mathcal {F}({\varvec{f}}({\varvec{x}}_n))\right) \\&\quad \hbox {with}\quad \gamma _n=\mathcal {F}({\varvec{x}}_n)\big /\mathcal {F}({\varvec{f}}({\varvec{x}}_n)) \end{aligned}$$

yields (7). This iterative scheme shows an excellent performance for linear filters \({\varvec{f}}(\cdot )\), provided that periodic boundary conditions are imposed, as demonstrated by the top-left and top-middle images of Fig. 4. Unfortunately, if other types of boundary conditions are chosen, (7) does not lead to good defiltering results, as shown by the bottom-left and bottom-middle images. In addition, this method does not show a good performance for some nonlinear filters, as seen in the right images of Fig. 4.

Fig. 3
figure 3

\(E_x\)-error graphs for defiltering (2) and (6). Top-left: Gaussian; top-right: AMF [6]; middle-left: bilateral filtering; middle-right: RTV [24]; bottom-left: WMF [26]; bottom-right: RGF [25]. In the majority of these tests (2), corresponding to the curves in black, slightly outperforms (6)

Full size image
Fig. 4
figure 4

Defiltering imgaussfilt(x,5,’Padding’,’circular’)  (top-left) and imgaussfilt(x,5)  (bottom-left) by (7). Similar defiltering results for imfilter(x,fspecial(’log’,7,0.4))  with (top-middle) and without (bottom-middle) periodic boundary conditions by (7). Top-right: defiltering RTV [24]  with default settings by (7). Bottom-right: defiltering AMF [6]  adaptive_manifold_filter(x,20,0.4)  by (7)

Full size image

It is interesting to note that the problem of reverse image filtering is closely related to stochastic approximation [2, 9], an active research area initiated by Robbins and Monro (RM) almost seventy years ago [16]. Remarkably, the RM algorithm looks very similar to (2). Given noisy measurements

$$\begin{aligned} {\varvec{y}}_n={\varvec{f}}({\varvec{x}}_n)+\eta _n, \end{aligned}$$

where \(\{\eta _n\}\) are measurement errors, the algorithm implements a simple iterative procedure for solving the equation \({\varvec{y}}={\varvec{f}}({\varvec{x}})\)

$$\begin{aligned} {\varvec{x}}_{n+1}={\varvec{x}}_n+a_n({\varvec{y}}-{\varvec{y}}_n), \end{aligned}$$

where \(\{a_n\}\) is a sequence of nonnegative real numbers satisfying \(\sum a_n=\infty \) and \(\sum a_n^2<\infty \).

Our P-iterations (3) can be considered as an approximation of the gradient descent with a variable step-size for minimizing least-square energy

$$\begin{aligned} \mathcal {E}({\varvec{x}})=\Vert {\varvec{y}}-{\varvec{f}}({\varvec{x}})\Vert ^2 \end{aligned}$$
(8)

whose anti-gradient is approximated by a symmetric finite difference

$$\begin{aligned} -\nabla \mathcal {E}({\varvec{x}}_n)=2\nabla {\varvec{f}}({\varvec{x}}_n){\varvec{h}}_n\approx {\varvec{f}}({\varvec{x}}_n+{\varvec{h}}_n)-{\varvec{f}}({\varvec{x}}_n-{\varvec{h}}_n), \end{aligned}$$

where, as before, \({\varvec{h}}_n={\varvec{y}}-{\varvec{f}}({\varvec{x}}_n)\) is assumed to be sufficiently small.

Fig. 5
figure 5

Results obtained on several state-of-the-art edge-preserving filters. From top to bottom: first row: filtered images; second row: the images are defiltered by T-iterations (2); third row: the images are defiltered by P-iterations (3); fourth row: the images are defiltered by S-iterations (4); fifth row: the corresponding \(E_x\)-error graphs. For each image, its \(E_x\)-error value is shown. For each filtering method, the image with the minimum \(E_x\)-error value is marked by a thick color line, where black corresponds to the T-iterations (2), red to the P-iterations (3), and blue to the S-iterations (4)

Full size image

It turns out that in the one-dimensional case (single-pixel images), our iterative scheme (3) approximates the standard Newton iterations for numerically solving \(y=f(x)\). Indeed, the Newton iterations for solving \(F(x)\equiv y-f(x)=0\) are given by

$$\begin{aligned} x_{n+1}=x_n-\frac{F(x_n)}{F^\prime (x_n)}=x_n+\frac{h_n}{f^\prime (x_n)},\quad h_n=y-f(x_n). \end{aligned}$$

Now we can observe that in the one-dimensional case (3) is reduced to

$$\begin{aligned} x_{n+1}=x_n+\frac{2h_n^2}{f(x_n+h_n)-f(x_n-h_n)}\approx x_n+\frac{h_n}{f^\prime (x_n)}. \end{aligned}$$
Table 1 For each filter, the best defiltering method is indicated
Full size table

It is also worth mentioning a link between (3) and the Kiefer–Wolfowitz (KW) stochastic approximation method [8]. The KW algorithm for a univariate function \(y=f(x)\) consists of an iterative process

$$\begin{aligned} x_{n+1}=x_n+a_n\frac{f(x_n+c_n)-f(x_n-c_n)}{2c_n}, \end{aligned}$$
(9)

where \(c_n\rightarrow 0\) in addition to some other conditions imposed on the sequences \(\{a_n\}\) and \(\{c_n\}\). A multivariate version of the KW algorithm can be found, for example, in [9] (initially both the RM and KW algorithms were proposed by their authors for univariate functions).

In the one-dimensional case, our S-iterations (4) become Steffensen’s method [17]

$$\begin{aligned} x_{n+1}=x_n+\frac{h_n}{f(x_n+h_n)-f(x_n)}h_n,\quad h_n=y-f(x_n), \end{aligned}$$

which delivers a numerical solution to \(y=f(x)\) and has quadratic convergence like Newton’s method.

3 Numerical experiments and discussion

In this section, we test our methods (3) and (4), and compare them against (2) using a wide selection of edge-preserving image filters, in addition to the two linear filters (Gaussian and LoG) and the adapted manifold filter (AMF) [6] considered in Sect. 1.

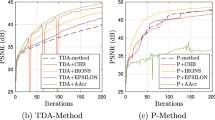
Results obtained are shown in Fig. 5 for the image filters: WMF [26], RTV [24], RGF [25], ILS [11], WLS [5] and L\(_0\) [23], and in Fig. 6 for the bilateral filter (BF), LLF [14] and LE [18]. For each image filter, we show an example of a filtered test image (top row), followed by the results obtained from T-iterations of Tao et al. [19] (2), P-iterations (3) and S-iterations (4) in the second, third and fourth row (from the top). For each method, the minimal \(E_x\)-error is indicated under the image. The bottom row provides error graphs for \(E_x\) (5) for the three methods. The best method is decided based on the error function \(E_x\) (5) and indicated by a thick color line. Table 1 summarizes the best methods for each filter according to the \(E_x\)-error function.

Fig. 6
figure 6

Further experiments with the state-of-the-art edge-preserving image filters. From top to bottom: first row: filtered images; second row: the images are defiltered by T-iterations (2); third row: the images are defiltered by P-iterations (3); fourth row: the images are defiltered by S-iterations (4); fifth row: the corresponding \(E_x\)-error graphs. For each image, its \(E_x\)-error value is presented. For each filtering method, the image with the minimum \(E_x\)-error value is marked by a thick color line, where black corresponds to the T-iterations (2), red to the P-iterations (3), and blue to the S-iterations (4)

Full size image

For the filters used in our experiments and shown in Figs. 5 and 6, we use the Matlab implementations provided by the authors of the corresponding papers with the following settings (we use Matlab notations for the filters and their arguments):

  • WMF [26]: jointWMF(x),

  • RTV [24]: tsmooth(x),

  • RGF [25]: RollingGuidanceFilter(x,3,0.05,4),

  • ILS [11]: ILS_LNorm(x,1,0.8,0.0001,4),

  • WLS [5]: wlsFilter(x),

  • L\(_0\) [23]: L0Smoothing(x,0.01),

  • BF: imbilatfilt(x,0.05,3),

  • LLF [14]: double(locallapfilt(im2uint8(x),0.2,10.0))/255,

  • LE [18]: localExtrema(x,x,7).

Surprisingly, reverse filtering of linear filters (in this paper, we consider Gaussian and LoG filters) turns out to be a difficult task. In the case of periodic boundary conditions, perfect defiltering is delivered by the method of Dong et al. (7) proposed in [4]. However, (7) is very sensitive to small perturbations and fails to recover images resulting from linear filters with non-periodic boundary conditions (see, e.g., Fig. 4).

The method of Tao et al. (2) [19] works well when it is used for defiltering Gaussians with small variances. In our example of Gaussian defiltering (see the left images in Figs. 1 and 2), the variance is \(\sigma ^2=5\) and (2) fails to produce a reasonably good result. Our experiments show that (2) also fails to recover the LoG filtering results (see, for example, Figs. 1 and 2, middle column).

Our P-iteration scheme (3) is capable of defiltering the Gaussian and LoG filters, as demonstrated in Figs. 1 and 2. However, the convergence can be slow. For example, restoring the left and middle images of Fig. 1 requires 100K iterations.

In addition to the Gaussian and LoG filters, we test ten state-of-the-art edge-preserving filters, see Figs. 5 and 6 and the right images of Figs. 1 and 2. For some filters, e.g., AMF, excellent defiltering results are obtained. For some others, e.g., LE, only very modest results are achieved. In general, we see that our P-iteration and S-iteration schemes together outperform the T-iteration method (2) [19]. However, for zero-order reverse filtering, (2) is the fastest method, as it requires only one call of function \({\varvec{f}}(\cdot )\) per iteration and, if it approaches an error minimum value, does it quickly.

We find it surprising that for the majority of the tested filters, small-scale image details can be accurately recovered if a proper defiltering method is applied. This means that typically edge-preserving filters only suppress those small-scale details but do not remove them completely.

In our experiments, we observe only a weak correlation between the two error functions \(E_x\) and \(E_y\) (5) for an iteratively defiltered image \({\varvec{x}}_n\). Namely, if \(E_y\) does not grow, then it is very likely that the defiltered image has its main features preserved, as demonstrated by Fig. 7. In real-life scenarios when only \(E_y\) is available, the number of reverse filtering iterations has to be selected manually. This is the only user-specified parameter in our approach.

Fig. 7
figure 7

Overrestoration examples. Left: WMF defiltering with 100 iterations of (4) amplifies certain middle-range frequencies. Right: BF defiltering with 1K iterations of (4) amplifies some high frequencies. Compare these results with those for WMF and BF from Figures 5 and 6, respectively

Full size image
Fig. 8
figure 8

R-iterations (10) achieve the smallest \(E_x\)-errors for the LE filter [18] (left) and WLS filter [5] (right). Top: images defiltered by (10). Bottom: the corresponding \(E_x\)-error graphs

Full size image
Fig. 9
figure 9

Top row: original images. Middle row: filtered images. Bottom row: the corresponding defiltered images. For each filtered image, for each channel, the number of reverse filtering iterations is determined by (11) with \(t=0.0005\). a Wiener filtering and defilering with (3). b Pillbox filtering and defiltering with (3). c Motion blur filtering and defiltering with (3). d Image-guided filtering and defiltering with (4). e Image-guided filtering using a smoothed guidance and defiltering with (4). See the main text for details. Zoom in the images to see how well small-scale details are restored

Full size image

While, in this paper, we deal with deterministic reverse filtering methods, we feel that randomized algorithms could be very successful at achieving high-quality defiltering results. As an example, let us consider the following simple stochastic iterative process

$$\begin{aligned} {\varvec{x}}_{n+1}\!=\!{\varvec{R}}({\varvec{x}}_n)\!\equiv \!{\varvec{x}}_n\!-\!\frac{\mathcal {E}\left( {\varvec{x}}_n\!+\!{\varvec{r}}\displaystyle {\frac{c_n}{\,2\,}}\right) \!-\!\mathcal {E}\left( {\varvec{x}}_n\!-\!{\varvec{r}}\displaystyle {\frac{c_n}{\,2\,}}\right) }{c_n} \end{aligned}$$
(10)

where quadratic energy \(\mathcal {E}\) is defined by (8), \({\varvec{r}}\) is a random image whose components are random numbers uniformly distributed on the interval [0, 1] and \(c_n=1/\sqrt{n}\). One can see that (10) combines (9) with stochastic gradient descent ideas. While (10) shows a modest performance for the majority of the considered filters, it allows us to achieve some progress with defiltering the LE filter [18] for which (10) shows the lowest \(E_x\) error. In Fig. 8, we show the result obtained by (10) for defiltering the LE and WLS filters. The top row shows the best obtained results, while the bottom row compares the result of the R-iterations (10) against the results of the T, S and P-iterations for the \(E_x\) error function. Visually (10) does a better work for retrieving fine details and high frequency texture in the image.

When dealing with color images, the simplest approach consists of defiltering each RGB channel. Obviously, more sophisticated strategies should lead to better results. Figure 9 shows several examples of color images, defiltered with our approach, from different domains (nature, architecture, humans, animals). In these examples, we test defiltering capabilities of our schemes (3) and (4) using popular image filters which have not yet been considered so far in this paper: (a) Wiener filter, (b) circular averaging filter (pillbox), (c) motion blur, (d) image guided filter [7], and (e) image guided filter, where Gaussian smoothing is applied to the guidance image:

  1. (a)

    wiener2(x,[5,5],0.1)

  2. (b)

    imfilter(x,fspecial(’disk’,3))

  3. (c)

    imfilter(x,fspecial(’motion’,20,45))

  4. (d)

    imguidedfilter(x)

  5. (e)

    imguidedfilter(x,imgaussfilt(x,5))

For the linear filters (first three filters), reverse filtering was done by applying (3). The remaining nonlinear filters were defiltered by (4). In these five examples, for each color channel, we stop iterative processes (3) and (4) immediately after the relative change in successive iterations becomes less than a user-specified threshold \(t>0\)

$$\begin{aligned} \Vert {\varvec{x}}_{n+1}-{\varvec{x}}_n\Vert \big /\Vert {\varvec{x}}_n\Vert < t. \end{aligned}$$
(11)

Better results could be obtained if an optimal number of iterations is chosen for each filter. Achieving reasonably good threshold t in (11) (for all the examples in Fig. 9 defilering is done with \(t=0.0005\)) demonstrates the robustness of our schemes (3) and (4).

One seemingly promising application of defiltering schemes lies in image enhancing. It seems natural to use the proposed reverse image filtering schemes as follows: The image \({\varvec{x}}\) in (1) can be considered as an enhanced version of the input image \({\varvec{y}}\) if \({\varvec{f}}(\cdot )\) is an appropriate filter. In Fig. 10, we combine AMF [6] with P-iterations (3) for image sharpening and with S-iterations (4) for image dehazing.

Fig. 10
figure 10

Original (left) and enhanced (right) images. Top: visually pleasant sharpening results can be achieved by combining AMF [6] and the P-iteration scheme (3) (in this example, ten iterations of (3) are used). Bottom: an image dehazing result is achieved by applying five S-iterations (4) based on the AMF filtering scheme

Full size image

4 Conclusion and directions for future work

In this work, we have considered the problem of reverse filtering, or defiltering, a severely filtered image \({\varvec{y}}={\varvec{f}}({\varvec{x}})\). We assume no knowledge of the internal structure of the filter \({\varvec{f}}(\cdot )\) (and thus cannot compute its inverse). Two proposed methods (3) and (4) are compared against the existing method (2) introduced in [19]. The comparison is done on severely filtered images.

Possible directions of future work on defiltering include the use of stochastic approximation methods for image defiltering and adapting image reverse filtering schemes for geometric modeling applications (see, for example, the recent work [22] devoted to reverse geometry filtering).

Using reverse filtering schemes for image enhancing and sharpening constitutes another direction for future work. See a very recent work [3] where single-step polynomial defiltering is used for fast and natural-looking sharpening large-size images.

Iterative schemes (3) and (4) can be considered as zero-order optimization methods. Problems requiring zero-order optimization appear frequently in signal processing and machine learning [10].

As (3) and (4) can be used to estimate how much of high-frequency image content is partially suppressed but remains preserved by an image filtering method, it would be interesting to establish a link with the ability of the method to protect deep learning schemes against adversarial attacks which often target high-frequency image components invisible to the human eye [20, 21].