Skip to main content
SpringerLink
Log in

A novel finite element formulation for static bending analysis of functionally graded porous sandwich plates

  • Research Article
  • Published:
Frontiers of Structural and Civil Engineering Aims and scope Submit manuscript

Abstract

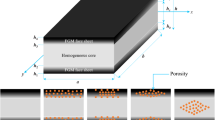
This article aims to propose a finite element formulation based on Quasi-3D theory for the static bending analysis of functionally graded porous (FGP) sandwich plates. The FGP sandwich plates consist of three layers including the bottom skin of homogeneous metal, the top skin of fully ceramic and the FGP core layer with uneven porosity distribution. A quadrilateral (Q4) element with nine degrees of freedom (DOFs) per node is derived and employed in analyzing the static bending response of the plate under uniform and/or sinusoidally distributed loads. The accuracy of the present finite element formulation is verified by comparing the obtained numerical results with the published results in the literature. Then, some numerical examples are performed to examine the effects of the parameters including power-law index k and porosity coefficient ξ on the static bending response of rectangular FGP sandwich plates. In addition, a problem with a complicated L-shape model is conducted to illustrate the superiority of the proposed finite element method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Vo T P, Thai H T, Nguyen T K, Maheri A, Lee J. Finite element model for vibration and buckling of functionally graded sandwich beams based on a refined shear deformation theory. Engineering Structures, 2014, 64: 12–22

    Article  Google Scholar 

  2. Asghari M, Ahmadian M T, Kahrobaiyan M H, Rahaeifard M. On the size-dependent behavior of functionally graded micro-beams. Materials & Design, 2010, 31(5): 2324–2329

    Article  Google Scholar 

  3. Trinh L C, Vo T P, Osofero A I, Lee J. Fundamental frequency analysis of functionally graded sandwich beams based on the state space approach. Composite Structures, 2016, 156: 263–275

    Article  Google Scholar 

  4. Vo T P, Thai H T, Nguyen T K, Inam F. Static and vibration analysis of functionally graded beams using refined shear deformation theory. Meccanica, 2014, 49(1): 155–168

    Article  MathSciNet  MATH  Google Scholar 

  5. Reddy J. Analysis of functionally graded plates. International Journal for Numerical Methods in Engineering, 2000, 47(1–3): 663–684

    Article  MATH  Google Scholar 

  6. Luat D T, Van Thom D, Thanh T T, Van Minh P, Van Ke T, Van Vinh P. Mechanical analysis of bi-functionally graded sandwich nanobeams. Advances in Nano Research, 2021, 11: 55–71

    Google Scholar 

  7. Nguyen V H, Nguyen T K, Thai H T, Vo T P. A new inverse trigonometric shear deformation theory for isotropic and functionally graded sandwich plates. Composites. Part B, Engineering, 2014, 66: 233–246

    Article  Google Scholar 

  8. Zenkour A M. Generalized shear deformation theory for bending analysis of functionally graded plates. Applied Mathematical Modelling, 2006, 30(1): 67–84

    Article  MATH  Google Scholar 

  9. Li S, Zheng S, Chen D. Porosity-dependent isogeometric analysis of bi-directional functionally graded plates. Thin-walled Structures, 2020, 156: 106999

    Article  Google Scholar 

  10. Tran T T, Le P B. Nonlocal dynamic response analysis of functionally graded porous L-shape nanoplates resting on elastic foundation using finite element formulation. Engineering with Computers, 2022, 1–17

  11. Zhao X, Lee Y, Liew K M. Free vibration analysis of functionally graded plates using the element-free kp-Ritz method. Journal of Sound and Vibration, 2009, 319(3–5): 918–939

    Article  Google Scholar 

  12. Nguyen-Xuan H, Tran L V, Nguyen-Thoi T, Vu-Do H. Analysis of functionally graded plates using an edge-based smoothed finite element method. Composite Structures, 2011, 93(11): 3019–3039

    Article  Google Scholar 

  13. Nguyen H N, Canh T N, Thanh T T, Ke T V, Phan V D, Thom D V. Finite element modelling of a composite shell with shear connectors. Symmetry, 2019, 11(4): 527

    Article  MATH  Google Scholar 

  14. Karamanlı A, Vo T P. Size dependent bending analysis of two directional functionally graded microbeams via a quasi-3D theory and finite element method. Composites. Part B, Engineering, 2018, 144: 171–183

    Article  Google Scholar 

  15. Thai C H, Zenkour A M, Abdel Wahab M, Nguyen-Xuan H. A simple four-unknown shear and normal deformations theory for functionally graded isotropic and sandwich plates based on isogeometric analysis. Composite Structures, 2016, 139: 77–95

    Article  Google Scholar 

  16. Tran T T, Pham Q H, Nguyen-Thoi T. Static and free vibration analyses of functionally graded porous variable-thickness plates using an edge-based smoothed finite element method. Defence Technology, 2021, 17(3): 971–986

    Article  Google Scholar 

  17. Tran T T, Nguyen P C, Pham Q H. Vibration analysis of FGM plates in thermal environment resting on elastic foundation using ES-MITC3 element and prediction of ANN. Case Studies in Thermal Engineering, 2021, 24: 100852

    Article  Google Scholar 

  18. Tran T T, Pham Q H, Nguyen-Thoi T. Dynamic analysis of functionally graded porous plates resting on elastic foundation taking into mass subjected to moving loads using an edge-based smoothed finite element method. Shock and Vibration, 2020, 2020: 8853920

    Article  Google Scholar 

  19. Pham Q H, Tran V K, Tran T T, Nguyen-Thoi T, Nguyen P C, Pham V D. A nonlocal quasi-3D theory for thermal free vibration analysis of functionally graded material nanoplates resting on elastic foundation. Case Studies in Thermal Engineering, 2021, 26: 101170

    Article  Google Scholar 

  20. Pham Q H, Thanh Tran T, Ke Tran V, Nguyen P C, Nguyen-Thoi T. Free vibration of functionally graded porous non-uniform thickness annular-nanoplates resting on elastic foundation using ES-MITC3 element. Alexandria Engineering Journal, 2022, 61(3): 1788–1802

    Article  Google Scholar 

  21. Pham Q H, Tran T T, Tran V K, Nguyen P C, Nguyen-Thoi T, Zenkour A M. Bending and hygro-thermo-mechanical vibration analysis of a functionally graded porous sandwich nanoshell resting on elastic foundation. Mechanics of Advanced Materials and Structures, 2021, 1–21

  22. Thanh T T, Van Ke T, Hoa P Q, Trung N T. An edge-based smoothed finite element for buckling analysis of functionally graded material variable-thickness plates. Vietnam Journal of Mechanics, 2021, 43: 221–235

    Google Scholar 

  23. Nguyen P C, Pham Q H, Tran T T, Nguyen-Thoi T. Effects of partially supported elastic foundation on free vibration of FGP plates using ES-MITC3 elements. Ain Shams Engineering Journal, 2022, 13(3): 101615

    Article  Google Scholar 

  24. Tran T T, Pham Q H, Nguyen-Thoi T. An edge-based smoothed finite element for free vibration analysis of functionally graded porous (FGP) plates on elastic foundation taking into mass (EFTIM). Mathematical Problems in Engineering, 2020, 2020: 8278743

    Article  MathSciNet  Google Scholar 

  25. Sobhy M. A comprehensive study on FGM nanoplates embedded in an elastic medium. Composite Structures, 2015, 134: 966–980

    Article  Google Scholar 

  26. Tornabene F. Free vibration analysis of functionally graded conical, cylindrical shell and annular plate structures with a four-parameter power-law distribution. Computer Methods in Applied Mechanics and Engineering, 2009, 198(37–40): 2911–2935

    Article  MATH  Google Scholar 

  27. Mantari J L. Refined and generalized hybrid type quasi-3D shear deformation theory for the bending analysis of functionally graded shells. Composites. Part B, Engineering, 2015, 83: 142–152

    Article  Google Scholar 

  28. Torabi J, Kiani Y, Eslami M R. Linear thermal buckling analysis of truncated hybrid FGM conical shells. Composites. Part B, Engineering, 2013, 50: 265–272

    Article  Google Scholar 

  29. Rezaei A, Saidi A. Application of Carrera Unified Formulation to study the effect of porosity on natural frequencies of thick porous-cellular plates. Composites. Part B, Engineering, 2016, 91: 361–370

    Article  Google Scholar 

  30. Rezaei A, Saidi A. Exact solution for free vibration of thick rectangular plates made of porous materials. Composite Structures, 2015, 134: 1051–1060

    Article  Google Scholar 

  31. Zhao J, Xie F, Wang A, Shuai C, Tang J, Wang Q. A unified solution for the vibration analysis of functionally graded porous (FGP) shallow shells with general boundary conditions. Composites. Part B, Engineering, 2019, 156: 406–424

    Article  Google Scholar 

  32. Zhao J, Xie F, Wang A, Shuai C, Tang J, Wang Q. Vibration behavior of the functionally graded porous (FGP) doubly-curved panels and shells of revolution by using a semi-analytical method. Composites. Part B, Engineering, 2019, 157: 219–238

    Article  Google Scholar 

  33. Li Q, Wu D, Chen X, Liu L, Yu Y, Gao W. Nonlinear vibration and dynamic buckling analyses of sandwich functionally graded porous plate with graphene platelet reinforcement resting on Winkler—Pasternak elastic foundation. International Journal of Mechanical Sciences, 2018, 148: 596–610

    Article  Google Scholar 

  34. Sahmani S, Aghdam M M, Rabczuk T. Nonlocal strain gradient plate model for nonlinear large-amplitude vibrations of functionally graded porous micro/nano-plates reinforced with GPLs. Composite Structures, 2018, 198: 51–62

    Article  Google Scholar 

  35. Guo H, Zhuang X, Chen P, Alajlan N, Rabczuk T. Stochastic deep collocation method based on neural architecture search and transfer learning for heterogeneous porous media. Engineering with Computers, 2022, 1–26

  36. Guo H, Zhuang X, Chen P, Alajlan N, Rabczuk T. Analysis of three-dimensional potential problems in non-homogeneous media with physics-informed deep collocation method using material transfer learning and sensitivity analysis. Engineering with Computers, 2022, 1–22

  37. Zhuang X, Guo H, Alajlan N, Zhu H, Rabczuk T. Deep autoencoder based energy method for the bending, vibration, and buckling analysis of Kirchhoff plates with transfer learning. European Journal of Mechanics. A, Solids, 2021, 87: 104225

    Article  MathSciNet  MATH  Google Scholar 

  38. Guo H, Zheng H, Zhuang X. Numerical manifold method for vibration analysis of Kirchhoff s plates of arbitrary geometry. Applied Mathematical Modelling, 2019, 66: 695–727

    Article  MathSciNet  MATH  Google Scholar 

  39. Guo H, Zheng H. The linear analysis of thin shell problems using the numerical manifold method. Thin-walled Structures, 2018, 124: 366–383

    Article  Google Scholar 

  40. Zenkour A. A comprehensive analysis of functionally graded sandwich plates: Part 1—Deflection and stresses. International Journal of Solids and Structures, 2005, 42(18–19): 5224–5242

    Article  MATH  Google Scholar 

  41. Zenkour A M. The effect of transverse shear and normal deformations on the thermomechanical bending of functionally graded sandwich plates. International Journal of Applied Mechanics, 2009, 1(4): 667–707

    Article  MathSciNet  Google Scholar 

  42. Zenkour A, Alghamdi N. Bending analysis of functionally graded sandwich plates under the effect of mechanical and thermal loads. Mechanics of Advanced Materials and Structures, 2010, 17(6): 419–432

    Article  Google Scholar 

  43. Zenkour A, Sobhy M. Thermal buckling of various types of FGM sandwich plates. Composite Structures, 2010, 93(1): 93–102

    Article  Google Scholar 

  44. Zenkour A, Alghamdi N. Thermomechanical bending response of functionally graded nonsymmetric sandwich plates. Journal of Sandwich Structures & Materials, 2010, 12(1): 7–46

    Article  Google Scholar 

  45. Zenkour A M. Bending analysis of functionally graded sandwich plates using a simple four-unknown shear and normal deformations theory. Journal of Sandwich Structures & Materials, 2013, 15(6): 629–656

    Article  MathSciNet  Google Scholar 

  46. Daikh A A, Zenkour A M. Free vibration and buckling of porous power-law and sigmoid functionally graded sandwich plates using a simple higher-order shear deformation theory. Materials Research Express, 2019, 6(11): 115707

    Article  Google Scholar 

  47. Zenkour A. A comprehensive analysis of functionally graded sandwich plates: Part 2—Buckling and free vibration. International Journal of Solids and Structures, 2005, 42(18–19): 5243–5258

    Article  MATH  Google Scholar 

  48. Daikh A A, Zenkour A M. Effect of porosity on the bending analysis of various functionally graded sandwich plates. Materials Research Express, 2019, 6(6): 065703

    Article  Google Scholar 

  49. Zenkour A M. A quasi-3D refined theory for functionally graded single-layered and sandwich plates with porosities. Composite Structures, 2018, 201: 38–48

    Article  Google Scholar 

  50. Thai H T, Nguyen T K, Vo T P, Lee J. Analysis of functionally graded sandwich plates using a new first-order shear deformation theory. European Journal of Mechanics. A, Solids, 2014, 45: 211–225

    Article  MathSciNet  MATH  Google Scholar 

  51. Sid Ahmed Houari M, Tounsi A, Anwar Bég O. Thermoelastic bending analysis of functionally graded sandwich plates using a new higher order shear and normal deformation theory. International Journal of Mechanical Sciences, 2013, 76: 102–111

    Article  Google Scholar 

  52. Nguyen T K, Nguyen V H, Chau-Dinh T, Vo T P, Nguyen-Xuan H. Static and vibration analysis of isotropic and functionally graded sandwich plates using an edge-based MITC3 finite elements. Composites. Part B, Engineering, 2016, 107: 162–173

    Article  Google Scholar 

  53. Pham Q H, Nguyen P C, Tran T T, Nguyen-Thoi T. Free vibration analysis of nanoplates with auxetic honeycomb core using a new third-order finite element method and nonlocal elasticity theory. Engineering with Computers, 2021, 1–19

  54. Li D, Deng Z, Xiao H, Zhu L. Thermomechanical bending analysis of functionally graded sandwich plates with both functionally graded face sheets and functionally graded cores. Mechanics of Advanced Materials and Structures, 2018, 25(3): 179–191

    Article  Google Scholar 

  55. Li D, Deng Z, Xiao H, Jin P. Bending analysis of sandwich plates with different face sheet materials and functionally graded soft core. Thin-walled Structures, 2018, 122: 8–16

    Article  Google Scholar 

  56. Tounsi A, Houari M S A, Benyoucef S, Adda Bedia E A. A refined trigonometric shear deformation theory for thermoelastic bending of functionally graded sandwich plates. Aerospace Science and Technology, 2013, 24(1): 209–220

    Article  Google Scholar 

  57. Tlidji Y, Daouadji T H, Hadji L, Tounsi A, Bedia E A A. Elasticity solution for bending response of functionally graded sandwich plates under thermomechanical loading. Journal of Thermal Stresses, 2014, 37(7): 852–869

    Article  Google Scholar 

  58. Zaoui F Z, Ouinas D, Tounsi A. New 2D and quasi-3D shear deformation theories for free vibration of functionally graded plates on elastic foundations. Composites. Part B, Engineering, 2019, 159: 231–247

    Article  Google Scholar 

  59. Neves A, Ferreira A, Carrera E, Cinefra M, Roque C, Jorge R, Soares C M. Static, free vibration and buckling analysis of isotropic and sandwich functionally graded plates using a quasi-3D higher-order shear deformation theory and a meshless technique. Composites. Part B, Engineering, 2013, 44(1): 657–674

    Article  Google Scholar 

  60. Farzam-Rad S A, Hassani B, Karamodin A. Isogeometric analysis of functionally graded plates using a new quasi-3D shear deformation theory based on physical neutral surface. Composites. Part B, Engineering, 2017, 108: 174–189

    Article  Google Scholar 

  61. Vafakhah Z, Navayi Neya B. An exact three dimensional solution for bending of thick rectangular FGM plate. Composites. Part B, Engineering, 2019, 156: 72–87

    Article  Google Scholar 

  62. Vo T P, Thai H T, Nguyen T K, Inam F, Lee J. A quasi-3D theory for vibration and buckling of functionally graded sandwich beams. Composite Structures, 2015, 119: 1–12

    Article  Google Scholar 

  63. Reddy J N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis. Boca Raton: CRC press, 2003

    Book  Google Scholar 

  64. Sobhy M. An accurate shear deformation theory for vibration and buckling of FGM sandwich plates in hygrothermal environment. International Journal of Mechanical Sciences, 2016, 110: 62–77

    Article  Google Scholar 

  65. Touratier M. An efficient standard plate theory. International Journal of Engineering Science, 1991, 29(8): 901–916

    Article  MATH  Google Scholar 

  66. Soldatos K P. A transverse shear deformation theory for homogeneous monoclinic plates. Acta Mechanica, 1992, 94(3–4): 195–220

    Article  MathSciNet  MATH  Google Scholar 

  67. Karama M, Afaq K, Mistou S. Mechanical behaviour of laminated composite beam by the new multi-layered laminated composite structures model with transverse shear stress continuity. International Journal of Solids and Structures, 2003, 40(6): 1525–1546

    Article  MATH  Google Scholar 

  68. Mahi A, Adda Bedia E A, Tounsi A. A new hyperbolic shear deformation theory for bending and free vibration analysis of isotropic, functionally graded, sandwich and laminated composite plates. Applied Mathematical Modelling, 2015, 39(9): 2489–2508

    Article  MathSciNet  MATH  Google Scholar 

  69. Pham Q H, Nguyen P C, Thanh Tran T. Dynamic response of porous functionally graded sandwich nanoplates using nonlocal higher-order isogeometric analysis. Composite Structures, 2022, 290: 115565

    Article  Google Scholar 

  70. Vasiraja N, Nagaraj P. The effect of material gradient on the static and dynamic response of layered functionally graded material plate using finite element method. Bulletin of the Polish Academy of Sciences. Technical Sciences, 2019, 67(4): 827–838

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Mechanical Engineering, Le Quy Don Technical University, Hanoi, Vietnam

    Van Chinh Nguyen & Trung Thanh Tran

  2. Laboratory for Applied and Industrial Mathematics, Institute for Computational Science and Artificial Intelligence, Van Lang University, Ho Chi Minh City, Vietnam

    Trung Nguyen-Thoi

  3. Faculty of Mechanical-Electrical and Computer Engineering, Van Lang University, Ho Chi Minh City, Vietnam

    Trung Nguyen-Thoi

  4. Faculty of Engineering and Technology, Nguyen Tat Thanh University, Ho Chi Minh City, Vietnam

    Quoc-Hoa Pham

Authors
  1. Van Chinh Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Trung Thanh Tran
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Trung Nguyen-Thoi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Quoc-Hoa Pham
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Quoc-Hoa Pham.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nguyen, V.C., Tran, T.T., Nguyen-Thoi, T. et al. A novel finite element formulation for static bending analysis of functionally graded porous sandwich plates. Front. Struct. Civ. Eng. 16, 1599–1620 (2022). https://doi.org/10.1007/s11709-022-0891-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11709-022-0891-4

Keywords

Search

Navigation